Computation Offloading Based on a Distributed Overlay Network Cache-Sharing Mechanism in Multi-Access Edge Computing

Abstract

Multi-access edge computing (MEC) enhances service quality for users and reduces computational overhead by migrating workloads and application data to the network edge. However, current solutions for task offloading and cache replacement in edge scenarios are constrained by factors such as communication bandwidth, wireless network coverage, and limited storage capacity of edge devices, making it challenging to achieve high cache reuse and lower system energy consumption. To address these issues, a framework leveraging cooperative edge servers deployed in wireless access networks across different geographical regions is designed. Specifically, we propose the Distributed Edge Service Caching and Offloading (DESCO) network architecture and design a decentralized resource-sharing algorithm based on consistent hashing, named Cache Chord. Subsequently, based on DESCO and aiming to minimize overall user energy consumption while maintaining user latency constraints, we introduce the real-time computation offloading (RCO) problem and transform RCO into a multi-player static game, prove the existence of Nash equilibrium solutions, and solve it using a multi-dimensional particle swarm optimization algorithm. Finally, simulation results demonstrate that the proposed solution reduces the average energy consumption by over 27% in the DESCO network compared to existing algorithms.

1. Introduction

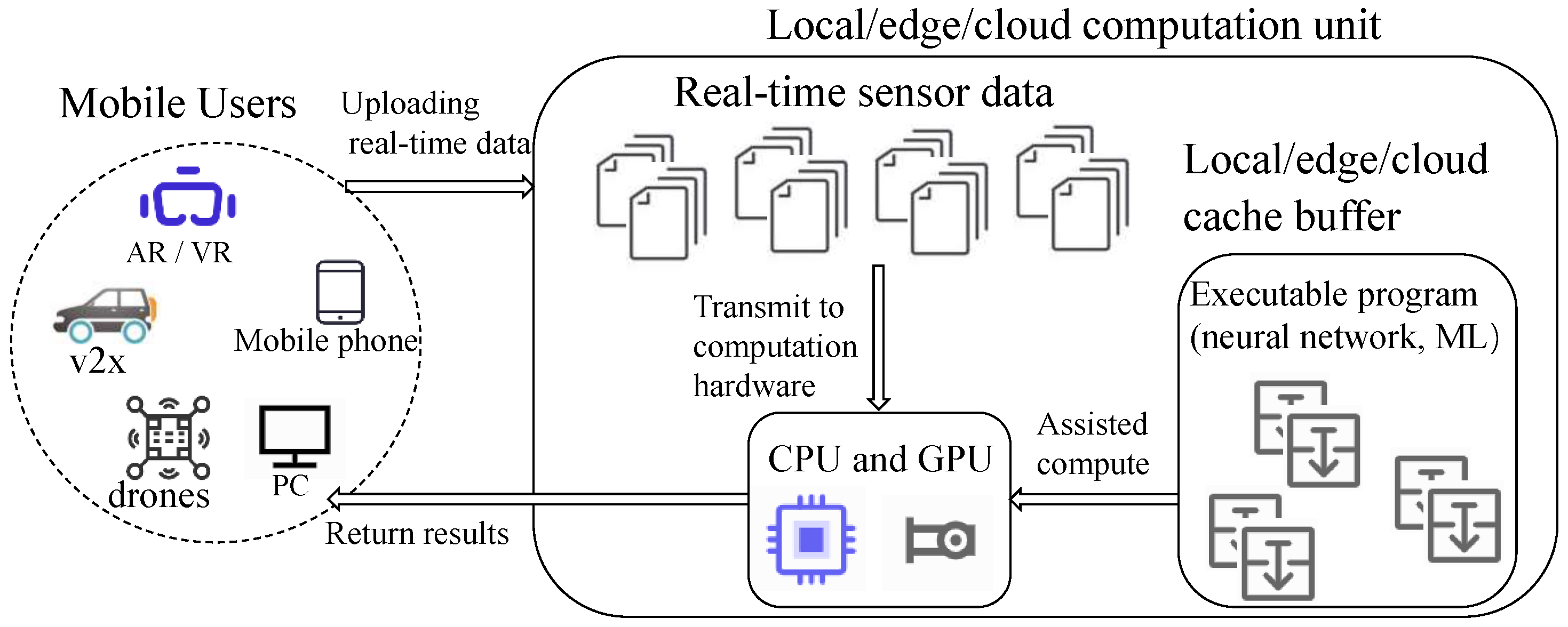
In recent years, with the rapid proliferation of wireless IoT applications such as connected vehicles, VR/AR, smart cities, and personalized streaming videos, there has been a surge in computation-sensitive and real-time services in mobile networks [1]. These services typically require completion within a short time frame (20–125 ms) [2]. Figure 1 illustrates the workflow of real-time services. Generally, three steps are involved: generation, processing, and transmission [3]. Firstly, mobile users (MUs) such as connected vehicles, AR/VR devices, mobile phones, or drones would continuously generate sensor or user data (infrared, radar, video streams, health, and so on) when requesting specific real-time services. Subsequently, MUs can process these tasks locally or transmit them to server units located in the cloud or edge to obtain computing services. The computing operations will be carried out with the assistance of application data (executable programs). The computing results return to the MUs at the end of the time frame. For example, vehicles requiring autonomous driving services would detect environment data from fusion monitoring devices (in-vehicle cameras, millimeter-wave or ultrasonic radar, etc.) while driving. After preprocessing, these raw data are sent to computing units deployed with corresponding target detection algorithms (or processed directly by locally embedded computing units) to perceive road conditions and provide optimal driving decisions.

This necessitates an efficient, cost-effective service model that minimizes user energy consumption while ensuring service quality. Traditional cloud computing architectures, as a centralized solution, encounter challenges such as severe wide-area network latency and fluctuating service quality when handling these new types of services.

Multi-access edge computing (MEC) [4] emerges as a computing paradigm capable of addressing these issues. It leverages the distributed computing power and communication resources at the network edge, particularly at the edge of the mobile wireless access network (RAN), by deploying communication entities such as road side units (RSUs), smart gateways, and small cell base stations to construct a network topology. It deploys corresponding computing and storage units at wireless access points (WAPs) to provide personalized services to MUs. MUs can directly access computing services from edge servers located at WAPs, avoiding traffic bottlenecks in the core and backhaul network during routing, thus partially alleviating the cache and computational burdens on data centers.

Additionally, MEC offers performance-optimizing technologies such as computation offloading (CO) [5] and edge caching (EC) [6]. Computation offloading, as a service optimization paradigm, allows MUs to delegate complex interactive computing tasks to edge nodes and receive computation results via the wireless downlinks between WAPs and MUs, thereby greatly alleviating the problem of high computational energy consumption in terminal devices with limited computational resources during service usage. Edge caching allows users to cache application data at communication nodes, enabling different MUs requesting the same service to directly upload locally generated real-time data for computation, avoiding the redundant transmission of the same application data and thus alleviating high latency and heavy load in the fronthaul network.

As an evolution of traditional mobile base stations, the MEC architecture allows for the scheduling and management of parallel communication resources at the network edge layer. This provides a new solution for designing cache data-sharing strategies among MEC nodes using backhaul networks, further optimizing system performance. It also offers cloud service providers more flexible computation offloading solutions by changing the execution and storage locations of data to optimize system performance.

Although the MEC network paradigm can overcome some of the drawbacks of cloud computing and meet the service constraints of real-time applications, there are still many challenges. Specifically, from the perspective of data sharing, in the current edge computing domain, the most well-known approach is based on blockchain [7] for distributed data storage and synchronized data sharing. However, this approach faces serious performance issues for high-throughput applications due to the low performance of blockchain networks, high costs associated with storing block data, and scalability challenges posed by large-scale data synchronization. These issues present difficulties in scheduling real-time applications.

To address these issues, our work focuses on leveraging performance optimization methods in MEC networks to provide real-time services for MUs. The main contributions of this study can be summarized as follows:

• The thesis proposes a Distributed Edge Service Caching and Offloading (DESCO) architecture based on edge servers’ collaboration to provide real-time services for mobile users. Within DESCO, the optimization problem of minimizing the long-term average energy consumption of users while satisfying latency constraints is established, for which cache sharing, replacement, and computation offloading methods are leveraged to further optimize user costs.
• A decentralized consistent hashing-based cache-sharing mechanism named “Cache Chord” is designed. This mechanism leverages the communication backhaul links at the edge layer and expands the DESCO framework by allowing edge servers to self-organize into a circular logical topology, facilitating application data sharing. Additionally, a cache IP list mechanism is devised to link application resource key-values in the overlay network with actual data in the real network.
• The real-time computation offloading (RCO) problem is transformed into a multi-player static game among MUs within the wireless network coverage of each server in order to reduce the current time slot energy consumption. A multi-dimensional discrete particle swarm optimization algorithm is applied to solve this problem after proving the existence of the Nash equilibrium (NE) solution for the game. Furthermore, the exploration coefficients and iteration rules of the algorithm are designed to meet environment constraints.
• Finally, simulation experiments are conducted to evaluate the performance of the proposed framework and algorithms. Results demonstrate that the proposed offloading method effectively reduces overall energy consumption at the user layer and obtains better converges compared to baseline algorithms.

The remainder of the paper is organized as follows: Section 2 introduces the related work of computation offloading and cache-sharing technology. Section 3 describes the system model of DESCO, and further introduces the cache-sharing mechanism. In Section 4, we transfer the RCO problem into a static game and proof the existence of NE solutions, then design the MDPSO algorithm. Section 5 presents simulation experiments to explore the superiority of the MDPSO algorithm and Cache Chord. Finally, the conclusion is given in Section 6.

2. Related Works

With the development of real-time applications, resource requests generated by terminal devices tend to be independent and the service requests from MUs exhibit more dynamic characteristics. Specifically, as noted in [8,9], within MU groups, the popularity of services follows a Zipf distribution, implying that a single server-based service requires maintaining a large cache database to improve hit rates, leading to significantly increase system redundancy. Simultaneously, computation offloading services impose considerable pressure on the transmission bandwidth of the wireless uplink from end to edge, while the computational capabilities of terminal MU devices are limited and consume a considerable amount of energy [10]. Therefore, coordinating energy consumption and service efficiency to maximize the system’s offloading benefits is a worthy issue to explore. Given the current state of limited infrastructure capacity and the limited computational capabilities of user devices in edge networks, the effective use of network resources to improve resource utilization and system performance has become an urgent challenge for network service providers.

To address this situation, researchers primarily employ two methods: firstly, by designing fine-grained and efficient computation offloading algorithms, and secondly, by considering the heterogeneity of edge devices and their geographical distribution characteristics, leveraging collaborative services between edges to enable on-demand resource mobility and fully utilize existing computing devices to ensure service quality. The following two subsections will provide detailed explanations of these approaches.

2.1. Computation Offloading Strategy

The real-time computation offloading (RCO) can enhance the QoE of interactive gaming [11]. In this scenario, MEC servers would process real-time action data offloaded by players (MUs) and render them into corresponding in-game scenes. The rendered data are then compressed via a video encoder and transmitted back to users through video-streaming. The RCO strategy allows servers to wisely offload service requests from multiple users, maximizing overall user satisfaction. RCO can also be applied in energy-constrained drones [12] and wearable devices [13] to reduce the computational overhead of local devices. Complex neural networks or machine learning computations can drain battery life for these devices. Additionally, requests from similar types of devices often exhibit popularity (e.g., health monitoring, object detection, and path planning algorithms). The RCO algorithm can select a strategy that maximizes offloading benefits based on the application categories stored on the server and the user cluster’s requests, thereby reducing the computational energy consumption of MUs and extending device battery life.

Multiple mobile users can achieve resource-sharing and collaborative computing, while nearby MUs may request similar tasks [14]. Based on this scenario, a fine-grained collaborative computing offloading and caching strategy is proposed to minimize the overall execution latency of MUs within the network [15]. Additionally, the concept of a call graph is utilized to model the offloading and caching relationships among MUs. It is noteworthy that [16] considers software-fetching and multicasting in network modeling, mathematically characterizing the processes of data uploading, task execution, and computation result downloading to minimize cache and weighted deadline as optimization objectives. They employ a joint algorithm combining ADMM and a penalty convex–concave procedure to obtain the optimal offloading strategy.

The ADMM algorithm is also applied in [17] to obtain distributed offloading decisions. In this work, the authors propose a computation offloading scheme where computational tasks generated by ground users can be computed locally, on Low Earth Orbit (LEO) satellites, or on cloud servers. The authors also consider the limited computational capabilities and coverage time of each LEO satellite. They subsequently investigate the optimization problem of minimizing the total energy consumption of ground users, which is discrete and non-convex, and convert it into a linear programming problem.

In Time-Division Multiple Access (TDMA)-based MEC systems, a partial offloading strategy based on an iterative heuristic algorithm is proposed [18] to minimize the total energy consumption of MUs while ensuring the task delay constraints. This strategy jointly optimizes task offloading rates, channel allocation, and MEC computing resource allocation. The authors decompose the problem into a series of offloading subproblems and design a two-stage algorithm to iteratively solve the offloading task set until achieving the minimum energy consumption.

When addressing performance optimization problems with computation offloading algorithms, it is observed that the discussion on the economies of scale brought by multi-server clusters is insufficient. Most articles only conduct research based on single-server scenarios, while in reality, MEC servers are often densely deployed in scenarios such as streets, malls, and schools to provide services to users. This cluster effect can be applied to the design of distributed network models and data-sharing algorithms. Wired backhaul links between edges can transmit large amounts of real-time data, which are also beneficial for the on-demand allocation of cached content related to real-time tasks.

2.2. Data-Sharing Mechanism

The authors of [19,20] focus on algorithm design to explore the cache-sharing strategy in distributed edge environments. To address the problem of MUs’ difficulty in discovering required IoT resources due to device heterogeneity, a Fog Computing-based resource discovery solution named FDS-RD is proposed [19]. FDS-RD employs a Distributed Hash Table (DHT) to map resources to a structured peer-to-peer (P2P) network, facilitating resource discovery in large-scale IoT environments.

VCNS [20] is a content-sharing network, tailored for the vehicular ad hoc network (VANET) scenario. It presents an edge caching scheme based on cross-entropy and dynamically adjusts caching based on content popularity within the request scope. Additionally, it designs a collaborative content delivery mechanism for RSUs to further reduce system latency overhead. Meanwhile, the authors of [21,22] focus on network logical topology design, exploring both structured and unstructured network topologies. The emphasis is on managing resource nodes to organize decentralized sharing networks, providing cached content to users to optimize system overheads.

Considering cooperative caching among edge servers, ref. [21] proposes a distributed edge data indexing system called EDIndex. In this system, any server maintains a hierarchical counting bloom filter (HCBF) tree index structure, which indexes the data stored in nearby edge servers, enabling fast querying at the edge. SA-Chord [22] is a pure edge computing-based adaptive distributed overlay network architecture. Based on the chord protocol, it designs a two-layer circular routing overlay composed of peer nodes and super nodes. Peer nodes only participate in content reception and transmission without routing, while super node clusters are responsible for maintaining routing tables for message-forwarding, achieving decentralized content-sharing based on the dual-layer structure.

From the above works, it can be observed that decentralized application caching and retrieval based on distributed hash can efficiently achieve data sharing, effectively reducing various overheads of the system, considering the limited storage capacity of geographically distributed edge service nodes. Therefore, this paper will explore the optimal task scheduling strategy based on a heuristic algorithm. Additionally, it will leverage the edge backhaul links’ path in existing multi-server–multi-user MEC networks to construct a structured data-sharing mechanism based on DHT.

3. System Descriptions and Assumptions

3.1. DESCO Network Model

We designed an Edge Service Caching and Offloading (DESCO) architecture based on the multi-server–multi-user end–edge two-layer network paradigm [22], as illustrated in Figure 2. In the DESCO network, the end layer consists of MU clusters, distributed across the coverage areas of various wireless networks, organized by different edge servers, and each of them is connected to the nearest server to obtain computing and offloading services. In the edge layer, MEC servers are deployed within wireless access points (WAPs) and equipped with computing and storage units. MEC servers communicate with each other through wired backhaul links and are self-organized at the application layer into a decentralized ring network called Cache Chord. The maintenance of this network structure relies solely on the consistent hashing protocol followed by server nodes, with detailed design discussed in Section 3.3.

Three computing modes exist in the DESCO network: local computing, pure offloading, and cache-based offloading. Local computing means MUs processing real-time tasks by themselves; pure offloading signifies that the MEC server’s local cache pool does not store the application programs required to execute user requests, so MUs need to offload real-time data and application data to the server. Cache-based offloading indicates that the server stores the application data for the task, and all users requesting the service only need to offload real-time data to the server, reducing some of the transmission energy consumption. This will be elaborated further in Section 3.4.

Table 1. Notation summary.

Notation	Definition
$\mathrm{T}$,$\tau$	Set of time sequence; time frame length
${\theta }_k$, ${\omega }_k$, ${\varphi }_k$	Real-time data volume of k; application data size of k; necessary FLOPs of task k
$\Delta$, D	MEC server set; number of MEC server
$\mathrm{N}d$, N	User request under server d; request of user n
$o_{d,n}$	MUs’ local compute power
$\mathrm{K}$, NID, KID	Service feature set; MEC server IP address set; application identifier set
$U_{{\mathrm{N}}_d}^t$, ${\mu }_n^t$	User request under server d; request of user n
b	Wireless subchannel bandwidth of server d
$l_n^{d,t}$	Minimum efficient uplink transmission rate of user k in range d
${\psi }_n$	Transmit power of user n
${\mathrm{V}}^{d,t}$	RCO decision of server d in slot t
${\upsilon }_n^{d,t}$	RCO policy of user n
${\mathrm{P}}^{d,t}$	Application cache replacement operation of d
${\rho }_k^{d,t}$	Operation of task k in server d at time t
${\mathrm{Y}}_{n,d,k,t}$	Energy consumption of user n in range d

summarizes the main parameters included in this study. The total number of MEC servers joining the DESCO network edge layer is denoted by the set $\Delta =\{1,2,3,\dots ,D\}$. Each distributed MEC server node uses its IP address as a unique identifier, represented by the set $\mathrm{NID}=\{ni{p}_1,ni{p}_2,\dots ,ni{p}_D\}$. The set $\mathrm{KID}=\{ki{d}_1,ki{d}_2,\dots ,ki{d}_K\}$ signifies unique resource identifiers for applications, utilized for identifying and indexing services within the Cache Chord network. Here, the subscript K indicates the total number of tasks that any user n at different geographical locations might request at any moment.

In the DESCO system, every entity operates in the time series $\mathrm{T}=\{1,2,\dots ,T\}$. This value serves as the fundamental unit for both the system’s offloading and caching decisions and the variations in user task requests. The duration of any arbitrary time slot $t\in \mathrm{T}$ is set as a constant value, denoted by $\tau$, representing the latency constraint of real-time applications. This means that at time t, when an MU generates a service request and produces corresponding real-time data, the computation result must be returned before the end of time t.

Let $\mathrm{K}=\{\langle {\theta }_1,{\omega }_1,{\varphi }_1\rangle ,\langle {\theta }_2,{\omega }_2,{\varphi }_2\rangle ,\dots ,\langle {\theta }_K,{\omega }_K,{\varphi }_K\rangle \}$ be the set of task features, where a task $k\in \{1,2,\dots ,K\}$ can be represented by a tuple $\langle {\theta }_k,{\omega }_k,{\varphi }_k\rangle$. In this tuple, ${\theta }_k$ represents the real-time data generated by the user request task (such as sensor data generated in real-time by IoT devices, video data, etc.), ${\omega }_k$ represents the size of the application data of the task, and ${\varphi }_k$ represents the necessary floating-point operations (FLOPs) required for task completion [23]. Let $\Delta =\{1,2,\dots ,N\}$ represent the set of users governed by the server. Furthermore, the set $U_{N_d}^t=\{{\mu }_1^t,{\mu }_2^t,...,{\mu }_N^t\}$ denotes the task requests of each user within the server d’s range at time t. At the beginning of each time slot, MUs can either execute a new computation task different from ${\mu }_n^{t-1}$, maintain the request from the previous time slot, or not request any service. Additionally, any user’s request satisfies ${\mu }_n^t\in \{\mathrm{K}\cup \left\{0\right\}\}$.

The set ${\mathrm{P}}^{d,t}=\{p_1^{d,t},p_2^{d,t},...,p_K^{d,t}\}$ is utilized to denote the application data retained in the cache pool of the MEC server node $d\in \Delta$ at time t. The element in the set satisfies $p_k^{d,t}\in \{0,1\}$; 0 and 1, respectively, represent the absence or presence of application data k in the cache pool of server node d. Meanwhile, the set ${\mathrm{P}}_{d,t}=\{{\rho }_1^{d,t},{\rho }_2^{d,t},...,{\rho }_K^{d,t}\}$ represents the cache replacement strategy. Each ${\rho }_k^{d,t}$ can assume one of three values: −1, 0, or 1, corresponding to the deletion, maintenance, or addition operation. Based on this, the cache replacement operation for application k on server d should adhere to

$$p_k^{d,t}=p_k^{d,t-1}+{\rho }_k^{d,t-1},\forall p_k^{d,t}\ge 0.$$

(1)

The inequality $\forall p_k^{d,t}\ge 0$ represents the MEC server unable to delete data that do not exist in their cache pool. Further, considering the cache pool capacity $\mathrm{S}$ of server d, the system’s cache status and replacement decisions at any given moment must subject to

$$\sum _{k=1}^K{\omega }_k(p_k^{d,t}+{\rho }_k^{d,t})\le \mathrm{S},\forall t\in T,\forall d\in \Delta .$$

(2)

This ensures the integrity and efficiency of data management in the DESCO system.

3.2. Communication Model

MEC servers are homogeneous devices with the same computing, communication, and storage capabilities [24,25]. The available bandwidth of server d is bHz, with F orthogonal wireless subchannels. The bandwidth of subchannels $f\in F$ is $b=B/F$, where $\forall f\in \{1,2,\dots ,F\}$. Each user can only occupy one channel to communicate with the server. The set ${\mathrm{V}}^{d,t}=\{{\upsilon }_1^{d,t},{\upsilon }_2^{d,t},...,{\upsilon }_N^{d,t}\}$ represents a server’s wireless channels’ allocation strategy while providing RCO service, and elements subjects to $\forall {\upsilon }_n^{d,t}\in \{0,1,2,...,F\}$, where 0 signifies that the user processes computational data on their local device. However, users will generate transmission energy consumption, which is determined by two variables: the volume of transmitted data and the uplink transmission rate. The uplink transmission rate is influenced by the number of users occupying the channel $Q\in [0,N]$, user’s channel gain ${\zeta }_n$, and the transmission power ${\psi }_n$. According to the Shannon–Hartley theorem, the minimum effective uplink transmission rate for mobile user n managed by server d in time slot t is [26]

$$l_n^{d,t}=b{log}_2(1+\frac{{\zeta }_n{\psi }_n}{{\displaystyle \sum _{m\in \{Q-n\},{\upsilon }_m^{d,t}={\upsilon }_n^{d,t}}}{\zeta }_m{\psi }_m+{\sigma }^2}),$$

(3)

where ${\sigma }^2$ represents the second central moment of Gaussian white noise. It is observed that the effective transmission power of user n decreases as the number of users Q occupying the same channel increases. Too many users occupying the same channel will increase noise interference ${\sum }_{m\in \{Q-n\},{\upsilon }_m^{d,t}={\upsilon }_n^{d,t}}{\zeta }_m{\psi }_m+{\sigma }^2$, resulting in a decrease in energy consumption benefits for task offloading, reducing the energy efficiency of task offloading and increasing task latency. Therefore, the impact of channel allocation must be considered in task offloading strategies to optimize performance.

3.3. Cache Chord Mechanism

In this section, we present a decentralized real-time resource access mechanism by orchestrating the network resources of MEC server clusters in the edge layer, utilizing a DHT-based consistent hashing ring network topology. Our discussion focuses on three key aspects: mapping, indexing, and updating for the Cache Chord.

3.3.1. Identifier Mapping

The initial step involves performing a consistent hashing operation on the $NID$ of server nodes, and $KID$ of application resource identifiers to construct a ring topology. The Hash algorithm maps these identifier data into a space of size $2^m$, creating a unique m-bit string. The data in this space are arranged in ascending order, proceeding clockwise, to form a virtual circular “ring”. This ring is numerically labeled with integers within the range of $[0,2^m-1]$, assigning numbers to both the server and application data, which follows

$$\begin{array}{c}\hfill X=\mathrm{Hash}〈\mathrm{NID}〉modm,\end{array}$$

(4)

$$\begin{array}{c}\hfill Y=\mathrm{Hash}〈\mathrm{KID}〉modm,\end{array}$$

(5)

where $\mathrm{Hash}\langle \rangle$ is the mapping function. Both random variables X and Y are defined as positive integers within interval $[0,2^m-1]$. The position of server node within the ring is denoted by $\mathrm{Nod}X$, while the location of application node is represented by $\mathrm{Key}Y$.

In the ring network, resource $\mathrm{Key}Y$ is updated by the first server node $\mathrm{Nod}X$ encountered in the clockwise direction. $\mathrm{Nod}X$ maintains a cache IP list for resource localization. Specifically, the list comprises a dataset formed by tuple $〈\mathrm{Key}Y,\mathrm{ServerI}{\mathrm{P}}_Y〉$, the first element of this tuple represents the position Y of the application data within the ring, the IP address of each physical device that stores application data Y at time t is reperensted by

$${\mathrm{ServerIP}}_Y^t=\{ni{d}_1,ni{d}_2,...,ni{d}_S\}\cup \left\{0\right\},\forall ni{d}_s\in \mathrm{NID},$$

(6)

where {0} signifies that the application data do not exist in edge layer. Utilizing this table, any user requesting service k for application data ${\omega }_k$ can determine the resource’s position in the ring network by processing its resource identifier $ki{d}_k$ through Formula (5), and index which machine stored the application data through ${\mathrm{ServerIP}}_Y^t$. It should be clarified that the positions and adjacent relationships of nodes within the Cache Chord merely represent a logical topology at the overlay network level, rather than actual storage locations. Additionally, the cache IP list on the server stores only indices of certain application data, not the application data themselves within the cache pool.

3.3.2. IP Indexing

In the ring topology, each server node $\mathrm{Nod}X$ identifies the first server node encountered in the clockwise direction as its successor node, and the first server node encountered in the counterclockwise direction as its predecessor node. $\forall \mathrm{Nod}X$ maintains the IP addresses of its successor and predecessor nodes, facilitating rapid access to the resources and cache IP lists of adjacent nodes.

Based on this structure, any server node d can determine the application’s relative position based on the hash value of the corresponding identifier $ki{d}_k$. By sequentially querying other server nodes in the order of the ring, the corresponding resource can be found in the respective successor node. However, the complexity of this query algorithm is not optimal. Assuming there are D servers in the ring, the query complexity is $O\left(D\right)$, and in the worst case, all nodes need to be traversed to find the target element.

To accelerate search processes, Cache Chord introduces the finger table mechanism [27]. Specifically, each server node $\mathrm{Nod}X$ maintains a table consisting of successor nodes, each with a length of m. This list includes the IP addresses corresponding to these nodes. The sequence of nodes in this table is subject to $\mathrm{Nod}\left\{\right(X+2^{i-1})mod{2}^m\}$, where $i\in \{1,2,...,m\}$. However, if the i-th server node does not exist in the ring, the node closest to the i-th position is saved as the i-th entry in the finger table, denoted as $\mathrm{FingerTable}(i)$. When $\mathrm{Nod}X$ seeks to retrieve a resource node $\mathrm{Key}Y$, it initially searches for the IP address of the resource among its stored successor and predecessor nodes. If the corresponding identifier Y for the task is not found, the server searches the finger table to locate the server node with a hash value greater than Y and that is closest to it. If the node with the highest number in the finger table is still less than Y, the process jumps to $\mathrm{Nod}(X+2^{m-1})$, which is $\mathrm{FingerTabl}{\mathrm{e}}_{max}\left(i\right)$, and repeats the aforementioned steps until Y is found, as detailed in Algorithm 1.

The integration of the finger table and cache IP list mechanisms enables a binary search-like method in Cache Chords, effectively converging the time complexity of resource searches to $O\left(\log D\right)$, where D is the total number of server nodes. Comparing the complexity of the finger table-based Algorithm 1 with the previously mentioned exhaustive search, according to L’Hôpital’s rule, we can obtain $\underset{D\to \infty }{lim}{D}^{-1}logD=0$. This implies that such a nonlinear search method can locate the corresponding resources with fewer execution cycles. Figure 3 shows a simulation of a Cache Chord of size $2^7$, demonstrating the process of server node $ni{d}_d$ mapping to the Cache Chord and searching for application $\mathrm{Key}78$.

Algorithm 1 Application Key Routing

1: Initialize $\mathrm{Nod}X.\mathrm{successor}$, $\mathrm{Nod}X.CacheIPlist$, $\mathrm{Nod}X.FingerTable$, length of finger table m  2: repeat  3:    Search in $\mathrm{Nod}X.CacheIPlist$ and $\mathrm{Nod}X.\mathrm{successor}$  4:    if $\mathrm{Nod}X.FingerTable\left(i\right)>\mathrm{Key}Y$ and maximum i then  5:        ship application search request to $\mathrm{Nod}X.FingerTable\left(i\right)$  6:    else if $\mathrm{Key}Y>\mathrm{Nod}X.FingerTable\left(m\right)$  7:        ship request to $\mathrm{Nod}X.FingerTable\left(m\right)$  8:        let $\mathrm{Nod}X.FingerTable\left(m\right)$ be new $\mathrm{Nod}X$  9:    end if 10: until find $\mathrm{Nod}X$ which stored $\mathrm{Key}Y$ in its finger table 11: return $\mathrm{Key}Y$ IP address to original server node $\mathrm{Nod}X$

3.3.3. Identifier Mapping

At the end of time slot t, each server node in the edge layer executes strategy ${\ae }_{d,t}$ to update the cache IP list. Specifically, if server d stores or deletes an application task in the local cache pool, i.e., ${\rho }_k^{d,t}=-1$ or 1, it requires executing Algorithm 2 to update the cache IP list. This ensures consistency between the data index in the overlay network and the storage status of data in the actual environment.

Algorithm 2 Cache IP List Update

1: Initialize $NID$, $KID$, $\mathrm{Nod}X.CacheIPlist$, $\mathrm{Nod}X.FingerTable$, cache replacement decision ${\ae }_{d,t}$ of $\mathrm{Nod}X$  2: for each server d in cluster $\Delta$ do  3:    for each task k in server d do  4:      if ${\rho }_k^{d,t}\ne 0$ then  5:         search Task k through execute Algorithm 1 and get IP address of target server node $\mathrm{Nod}T$  6:         if ${\rho }_k^{d,t}=1$ then  7:           add $\mathrm{Nod}X$ IP address into corresponding ${\mathrm{ServerIP}}_Y^t$ of $\mathrm{Nod}T.CacheIPlist$  8:         end if  9:      end if 10:   end for 11: end for 12: return $\mathrm{Key}Y$ IP address to original server node $\mathrm{Nod}X$

3.4. DESCO Task Processing Model

Algorithm 3 outlines the workflow of the mechanism. Initially, the server gathers individual user requests and searches its local cache pool $\mathbb{R}$ for corresponding application data ${\omega }_k$. If the data are not already stored, the server then executes Algorithm 1 to locate the server node managing that application within the Cache Chord network by retrieving the cache IP list. If ${\mathrm{ServerIP}}_Y^t\ne 0$, the IP of the node storing the application is returned to server d. Subsequently, the server derives the RCO strategy ${\mathrm{V}}^{d,t}$ based on the local cache status and Cache Chord information. In the final phase, Algorithm 2 updates the resource index within the Cache Chord network. The output is the user layer energy consumption at that moment, which comprises computational and communication energy costs.

Algorithm 3 DESCO Network Overall Mechanism

1: Initialize MEC server cluster $\Delta$, Cache Chord $\mathbb{C}$, MEC server local cache buffer $\mathbb{R}$  2: for each server d in cluster $\Delta$ do  3:    server d gathering user request set $U_{{\mathrm{N}}_d}^t$  4:    for each user request ${\mu }_n^t$ do  5:      search corresponding application data ${\omega }_k$ in cache buffer $\mathbb{R}$  6:      if $p_k^{d,t}=0$ then  7:         play Algorithm 1 in Cache Chord $\mathbb{C}$ to search application data of task k  8:         server d compute offloading strategy ${\mathrm{V}}^{d,t}$ based on application caching state and Cache Chord by playing RCO decision  9:      end if 10:    for each offloading vector ${\upsilon }_n^{d,t}$ do 11:        if ${\upsilon }_n^{d,t}\ne 0$ and $\mathrm{ServerI}{\mathrm{P}}_k\vee p_k^{d,t}=0$ then 12:          user transmit task data ${\omega }_k$ and task data ${\theta }_k$ to server d, execute task on MEC server 13:        else if ${\upsilon }_n^{d,t}\ne 0$ and $\mathrm{ServerI}{\mathrm{P}}_k\vee p_k^{d,t}=0$ 14:          user transmit task data ${\theta }_k$ to server d, execute task on MEC server 15:        else 16:          local compute 17:        end if 18:        user n generated energy consumption ${\mathrm{Y}}_{n,d,k,t}$ 19:     end for 20:   end for 21:   update application state in Cache Chord through Algorithm 2 22: end for 23: return user layer energy consumption ${\displaystyle \sum _{d\in \Delta }}{\displaystyle \sum _{n\in {\mathrm{N}}_d,k\in U_{{\mathrm{N}}_d}^t}}{\mathrm{Y}}_{n,d,k,t}$

3.4.1. Local Computing Mode

We derive the pure computational cost $o_{d,n}^2{\varphi }_k\varsigma$ based on the mobile device computational model [14], where the parameter $o_{d,n}$ represents the performance of the mobile user’s computing unit, measured in floating-point operations per second (FLOPS). This metric can be adjusted through power control technology DVFS [28]. Additionally, the coefficient $\varsigma$ correlates with the power consumption and is inherently linked to the hardware architecture of the mobile device. Considering the time constraint $\tau$ of task ${\mu }_n^t$, we ascertain that when $o_{d,n}={\varphi }_k/\tau$, the MUs can execute services with minimal power consumption without breaching the user’s latency constraints, represented by

$$\varsigma \frac{{{\varphi }_k}^3}{{\tau }^2}.$$

(7)

Meanwhile, we can conclude that the latency of local computation is equal to the maximum value of the time slot, $\tau$.

3.4.2. Pure Offloading Mode

Communication cost is determined by the transmitted data volume, channel coherence parameters, and the user’s transmission power. Notably, when both the local cache pool of server and the Cache Chord lack the application data ${\omega }_k$ for task k, i.e., ${\mathrm{ServerIP}}_k^t\vee p_k^{d,t}=0$, the user should upload both the application data ${\omega }_k$ and the real-time computational data ${\theta }_k$ to the edge. Consequently, it can be inferred that the current energy consumption of the n is

$${\psi }_n\frac{{\omega }_k+{\theta }_k}{l_n^{d,t}},$$

(8)

where ${\psi }_n$ represents the transmission power of a user. Furthermore, we can infer that the latency of pure offloading is

$$T_{n,k,d,t}^P=\frac{{\varphi }_k}{{\eta }_d}+\frac{{\omega }_k+{\theta }_k}{l_n^{d,t}},$$

(9)

where the rightmost term represents the transmission delay for user n when sending data of task k, and the middle term represents the computation delay for server d.

3.4.3. Cache-Based Offloading Mode

When user n requests a service that is stored locally in the cache pool of d, or when the service k is located in another server through executing Algorithm 1 (denoted as ${\mathrm{ServerIP}}_k^t\vee p_k^{d,t}=1$), MUs only need to transmit ${\theta }_k$ to server. The corresponding transmission cost is then quantified as

$${\psi }_n\frac{{\theta }_k}{l_n^{d,t}};$$

(10)

similarly, the latency in cache-based offloading can be expressed as

$$T_{n,k,d,t}^C=\mathrm{sgn}(1-p_k^{d,t})T_{d,k,t}^R+\frac{{\varphi }_k}{{\eta }_d}+\frac{{\theta }_k}{l_n^{d,t}},$$

(11)

where signum function $\mathrm{sgn}\left(x\right)$ be subjected to

$$sgn\left(x\right)=\left\{\begin{array}{c}1,\\ 0,\end{array}\begin{array}{c}x>0\\ x=0.\end{array}\right.$$

(12)

In Equation (12), $\mathrm{sgn}(1-p_k^{d,t})T_{d,k,t}^R$ denotes the latency of executing the routing algorithm to acquire application data ${\omega }_k$ in the Cache Chord. In this state, users do not need to further transmit data ${\omega }_k$ for task k, thereby reducing some of the time overhead. To simplify the model, consistent with other studies [3,29,30], we assume that the computational capacity of MEC servers is much greater than that of MUs, i.e., ${\eta }_d\gg o_{d,n}$. Therefore, the latency caused by MEC servers performing computations can be eliminated.

During the process of MEC servers utilizing the Cache Chord to execute indexing algorithms, the data volume transmitted between MEC nodes is very small, containing only information such as the IP address of the resources and the hash value of the destination server node address. Additionally, as MEC nodes are geographically adjacent and communicate through ideal wired backhaul links, without any transmission bottlenecks, the propagation delay of MEC servers transmitting application data to each other can be neglected. Therefore, in our modeling, we assume that the delay of MEC servers retrieving and transmitting corresponding application data ${\omega }_k$ in the Cache Chord can be ignored. This can be represented by the following inequality:

$$\frac{{\varphi }_k}{{\eta }_d}+T_{d,k,t}^R\ll \frac{{\varphi }_k}{o_{d,n}}\le \tau$$

(13)

3.4.4. User Layer Energy Consumption

Let $\mathbb{E}=\{{\epsilon }_1^t,{\epsilon }_2^t,...,{\epsilon }_K^t\},\forall {\epsilon }_k^t\in \{0,1\}$ represent whether the edge layer holds application data ${\omega }_k$, when the application data exist, the formula ${\mathrm{ServerIP}}_k^t\vee p_k^{d,t}=1,{\epsilon }_k^t=1$ can be derived; otherwise, ${\mathrm{ServerIP}}_k^t\vee p_k^{d,t}=0$, and ${\epsilon }_k^t=0$. Based on these, it can be concluded that at any slot t, the service request ${\mu }_n^t\in \{0,1,2,...,K\}$ of local user n on server d satisfies the following energy consumption formula:

$$\begin{array}{cc}\hfill {\mathrm{Y}}_{n,d,k,t}=& sgn\left({\mu }_n^t\right)\left\{\right(1-sgn({\upsilon }_n^{d,t}\left)\right)\varsigma \frac{{{\varphi }_k}^3}{{\tau }^2}\hfill \\ \hfill +& sgn({\upsilon }_n^{d,t}\left)\right((1-{\epsilon }_k^t{)\psi }_n\frac{{\omega }_k+{\theta }_k}{l_n^{d,t}}+{\epsilon }_k^t{\psi }_n\frac{{\theta }_k}{l_n^{d,t}}\left)\right\},\hfill \end{array}$$

(14)

3.5. Problem Formulation

Based on the above modeling, the optimization objective can be transformed as follows. Under the assistance of the Cache Chord mechanism, take the RCO action ${\mathrm{V}}^{d,t}$ in order to minimize the long-term average energy consumption of the user layer in the DESCO model, which can be formulated as the following problem:

$$\begin{array}{cc}\hfill \mathrm{P}:& \underset{{\mathbb{V}}^t}{min}(\underset{T\to \infty }{lim}\frac{1}{TD}\sum _{t=1}^T\sum _{d=1}^D{\sum }_{n\in {\mathrm{N}}_d,k\in U_{{\mathrm{N}}_d}^t}{\mathrm{Y}}_{n,d,k,t})\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& ni{d}_s\in \mathrm{NID},\forall s\in S,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & p_k^{d,t}=p_k^{d,t-1}+{\rho }_k^{d,t-1},\forall p_k^{d,t}\ge 0,\forall t=T,\forall d\in \Delta ,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & {\sum }_{k\in [1,K]}{\omega }_k(p_k^{d,t}+{\rho }_k^{d,t})\le \mathrm{S},\forall t\in T,\forall d\in \Delta ,\forall k\in \mathrm{K},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & {\rho }_k^{d,t}\in \{1,0,-1\},\forall k\in U_{{\mathrm{N}}_d}^t,\forall t\in T,\forall d\in \Delta ,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & {\upsilon }_n^{d,t}\in \{0,1,2,...,F\},\forall n\in {\mathrm{N}}_d,\forall t\in T,\forall d\in \Delta .\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & \mathrm{sgn}\left({\upsilon }_n^{d,t}\right)\left(\mathrm{sgn}\left({\epsilon }_k^t\right)T_{n,k,d,t}^C+\mathrm{sgn}(1-{\epsilon }_k^t)T_{n,k,d,t}^P\right)\le \tau .\hfill \end{array}$$

(21)

Set ${\mathbb{V}}^t=\{{\mathrm{V}}^{1,t},{\mathrm{V}}^{2,t},\dots ,{\mathrm{V}}^{D,t}\}$ represents the entire server cluster of RCO decisions. (16) mandates that the storage location for any application data must reside within the servers at the edge layer. (17) specifies that the application cache status $p_k^{d,t}$ of MEC server at time t is determined by its cache status at $(t-1)$ and the application replacement decisions ${\rho }_k^{d,t-1}$ based on that status. (18) asserts that for any MEC server d, the current tasks and those newly added at the next moment, based on the application replacement decision, must not exceed the server’s own cache pool capacity S. (19) illustrates the cache replacement policy of pool ${\mathrm{P}}^{d,t}$: addition, deletion, or retention. (20) represents the offloading decision for server d towards user n at time t, where $\{1,2,\dots ,F\}$ denotes data offloading through the server’s subchannel, and 0 indicates local computation of the task. The next section will detail how to decouple the complex problem P and address it through a joint algorithmic approach. (21) represents the latency constraint of real-time computing tasks.

4. Distributed Real-Time Computation Offloading Algorithm Based on MDPSO

4.1. Modeling the RCO Problem Based on Multi-Player Static Game

The coherent noise of a channel increases as the number of users occupying the channel rises. Consequently, users require more energy to transmit real-time sensor data, as indicated by Formula (3). Consequently, the offloading benefits of MUs selecting that channel decrease. Based on the above analysis, it can be observed that there exists an evident competitive relationship among MUs in the process of offloading data (selecting offloading channels). Moreover, user requests in any time slot occur concurrently rather than sequentially, which introduces the RCO problem into the realm of multi-player static game theory. In this chapter, discussions will be conducted on this game problem, and the NE solution will be sought based on the multi-dimensional particle swarm method in heuristic algorithms.

In the computation offloading problem, as the popularity of tasks does not change due to users being in different coverage areas of MEC, the requests ${\mu }_n^t$ of any MUs in the terminal layer follow the same probability distribution. Additionally, the RCO decision of any MEC server only affects the data upload efficiency and latency of local users. Therefore, the scope of the computation offloading problem can be atomized, with each server making decisions assisted by the cache ring. This can be represented by each server minimizing its real-time energy consumption function $q_{d,t}\left(V^{d,t}\right)$. Thus, the optimization problem becomes

$$\begin{array}{cc}\hfill \mathrm{P}1:& \underset{{\mathrm{V}}^{d,t}}{min}{q}_{d,t}\left({\mathrm{V}}^{d,t}\right)={\sum }_{n\in {\mathrm{N}}_d,k\in U_{{\mathrm{N}}_d}^t}{\mathrm{Y}}_{n,d,k,t}\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\left(17\right),\left(20\right),\left(21\right)\hfill \end{array}$$

(22)

where ${\mathrm{V}}^{d,t}$ represents an N-dimensional discrete random variable, and each dimension corresponds to the RCO strategy ${\upsilon }_n^{d,t}$ of user n. The effectiveness of a decision is quantified by the difference between the user’s computational energy consumption and communication energy consumption. The offloading benefit for user $n\in {\mathrm{N}}_d$ is defined as

$${\Gamma }_n\left({\upsilon }_n^{d,t}\right)=sgn\left({\upsilon }_n^{d,t}\right)(\varsigma \frac{{{\varphi }_k}^3}{{\tau }^2}-{\psi }_n\frac{{\theta }_k+(1-{\epsilon }_k^t){\omega }_k}{blog(1+\frac{{\zeta }_n{\psi }_n}{{\displaystyle \sum _{m\in \{Q-n\},{\upsilon }_m^{d,t}={\upsilon }_n^{d,t}}}{\zeta }_m{\psi }_m+{\sigma }^2})}),$$

(23)

where ${\Gamma }_n\left({\upsilon }_n^{d,t}\right)>0$ represents that implementing the offloading strategy ${\upsilon }_n^{d,t}$ can conserve energy for MUs in comparison to local computations. It is evident that the total offloading benefit ${\sum }_{n\in {\mathrm{N}}_d}{\Gamma }_n\left({\upsilon }_n^{d,t}\right)$ for the local user cluster of server d is inversely proportional to the real-time energy consumption function $q_{d,t}\left({\mathrm{V}}^{d,t}\right)$, which implies that

$$q_{d,t}\left({\mathrm{V}}^{d,t}\right)\propto \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\sum }_{n\in {\mathrm{N}}_d}{\Gamma }_n\left({\upsilon }_n^{d,t}\right)$}\right..$$

(24)

In further analysis, we deduce that for user $\forall n\in {\mathrm{N}}_d$, the selection of channel $f\in F$ for transmission introduces coherent noise ${\sum }_{m\in \{Q-n\},{\upsilon }_m^{d,t}={\upsilon }_n^{d,t}}{\zeta }_m{\psi }_m+{\sigma }^2$ impacting both the individual benefit ${\Gamma }_n\left({\upsilon }_n^{d,t}\right)$ and the overall energy consumption $q_{d,t}\left({\mathrm{V}}^{d,t}\right)$.

This suggests that the RCO strategy ${\upsilon }_n^{d,t}$ of user n, in conjunction with other users’ RCO strategies ${\mathrm{V}}_{n-}^{d,t}={\mathrm{V}}^{d,t}-\left\{{\upsilon }_n^{d,t}\right\}$, formed a multi-player static game problem [31]. Consequently, this game can be characterized as

$$\mathcal{G}=〈{\mathrm{N}}_d,\{{\mathrm{P}}_{n,t}\},{\Gamma }_n\left({\upsilon }_n^{d,t}\right)〉,$$

(25)

where ${\mathrm{N}}_d$ represents the set of players, $\left\{{\mathrm{P}}_{n,t}\right\}$ symbolizes the pure strategy set of player n, and ${\Gamma }_n\left({\upsilon }_n^{d,t}\right)$ denotes the offloading payoff compared to local computing. However, it is known that not all finite-strategy static games have pure-strategy Nash equilibrium. Therefore, we will analyze the existence of Nash equilibrium solutions for the given N-player static game problem $\mathcal{G}$.

Firstly, the number of players participating in this finite-strategy static game $\mathcal{G}$ is denoted as N. Let the n-th player’s pure channel strategy available at time t be represented as

$${\mathrm{P}}_{n,t}=\left\{A_1^n,A_2^n,...,A_F^n\right\},n\in {\mathrm{N}}_d.$$

(26)

The strategy space composed of pure strategies for $N_d$ players is

$${\mathrm{P}}_t={\mathrm{P}}_{1,t} \times {\mathrm{P}}_{2,t} \times \dots \times {\mathrm{P}}_{N,t}.$$

(27)

Any strategy combination in strategy space A is

$$p_t=\left({\mathrm{A}}_{j_1,t}^1,{\mathrm{A}}_{j_2,t}^2,...,{\mathrm{A}}_{j_N,t}^N\right),{\mathrm{A}}_{j_n,t}^n\in {\mathrm{P}}_{n,t},n=1,2,\dots ,N.$$

(28)

Denote

$${\tilde{\mathrm{P}}}_t^{n-1}={\mathrm{P}}_{1,t},{\mathrm{P}}_{2,t},\dots ,{\mathrm{P}}_{n-1,t}(1<n\le N),{\tilde{\mathrm{P}}}_t^{n-1}=\Phi \left(n=1\right),$$

(29)

$${\overline{\mathrm{P}}}_t^{n+1}={\mathrm{P}}_{n+1,t},{\mathrm{P}}_{n+2,t},\dots ,{\mathrm{P}}_{N,t}(1\le n<N),{\overline{\mathrm{P}}}_t^{n+1}=\Phi \left(n=N\right).$$

(30)

Apparently

$${\mathrm{P}}_t=\left\{\begin{array}{ll}{\mathrm{P}}_{1,t}\times {\overline{\mathrm{P}}}_t^{n+1},\hfill & n=1\\ {\tilde{\mathrm{P}}}_t^{n-1}\times {\mathrm{P}}_{n,t},\hfill & n=N\\ {\tilde{\mathrm{P}}}_t^{n-1}\times {\mathrm{P}}_{n,t}\times {\overline{\mathrm{P}}}_t^{n+1},\hfill & 1<n<N.\end{array}\right.$$

(31)

Without loss of generality, when $1<n<N$, the following exists:

$$\begin{array}{c}\forall p_t^{n-1}\in {\tilde{\mathrm{P}}}_t^{n-1},p_t^{n-1}=\left({\mathrm{A}}_{j_1,t}^1,{\mathrm{A}}_{j_2,t}^2,...,{\mathrm{A}}_{j_{n-1},t}^{n-1}\right),{\mathrm{A}}_{j_k,t}^k\in {\mathrm{P}}_{k,t},k=1,2,...,n-1,\hfill \\ \forall p_t^{n-1}\in {\overline{\mathrm{P}}}_t^{n+1},p_t^{n+1}=\left({\mathrm{A}}_{j_{n+1},t}^1,{\mathrm{A}}_{j_{n+2},t}^2,...,{\mathrm{A}}_{j_N,t}^N\right),{\mathrm{A}}_{j_k,t}^k\in {\mathrm{P}}_{k,t},k=n+1,n+2,...,N.\hfill \end{array}$$

(32)

According to the utility function ${\Gamma }_n\left({\upsilon }_n^{d,t}\right)$ of the n-th player, if there exists the following:

$$p_t^{*}=\left(p_t^{n-1*},{\mathrm{A}}_{j_n,t}^{n*},p_t^{n+1*}\right),$$

(33)

let

$${\Gamma }_n\left(p_t^{*}\right)={\Gamma }_n\left(p_t^{n-1*},{\mathrm{A}}_{j_n,t}^{n*},p_t^{n+1*}\right)⩾{\Gamma }_n\left(p_t^{n-1*},{\mathrm{A}}_{k,t}^n,p_t^{n+1*}\right),\forall {\mathrm{A}}_{k,t}^n\in {\mathrm{P}}_{n,t}.$$

(34)

Then, $p_t^{*}$ is referred to as a pure-strategy Nash equilibrium of the finite-strategy static game $\mathcal{G}$. Building upon the above, we can continue the derivation; let

$$\begin{array}{c}{T}_{i,t}(p_t^{n-1},p_t^{n+1})=\left\{(p_t^{n-1},A_{j_k,t}^n,p_t^{n+1})|\underset{A_k^n\in {\mathrm{P}}_{n,t}}{\max }{U}_i(p_t^{n-1},A_{k,t}^n,p_t^{n+1})\right\},i=1,2,\cdots ,N\hfill \\ T_{i,t}=\underset{(p_t^{n-1},p_t^{n+1})\in {\tilde{\mathrm{P}}}_t^{n-1}\times {\overline{\mathrm{P}}}_t^{n+1}}{\cup }{T}_i(p_t^{n-1},p_t^{n+1})=\hfill \\ \left\{(p_t^{n-1},A_{j_k,t}^n,p_t^{n+1})|\underset{A_k^n\in {\mathrm{P}}_{n,t}}{\max }{U}_i(p_t^{n-1},A_k^n,p_t^{n+1})\right\},\hfill \\ \forall (p_t^{n-1},p_t^{n+1})\in {\tilde{\mathrm{P}}}_t^{n-1}\times {\overline{\mathrm{P}}}_t^{n+1}|i=1,2,\cdots ,N.\hfill \end{array}$$

(35)

If the game $\mathcal{G}$ has a Nash equilibrium, then

$$p_t=\left(p_t^{n-1},{\mathrm{A}}_{j_n,t}^n,p_t^{n+1}\right)=\left({\mathrm{A}}_{j_1,t}^1,{\mathrm{A}}_{j_2,t}^2,...,{\mathrm{A}}_{j_N,t}^N\right).$$

(36)

According to the definition of pure NE, we have

$${\Gamma }_i(p_t^{n-1},A_{j_n,t}^n,p_t^{n+1})⩾{\Gamma }_i(p_t^{n-1},A_{k,t}^n,p_t^{n+1}),\forall A_{k,t}^n\in {\mathrm{P}}_{n,t}.$$

(37)

Therefore, there exists:

$$(p_t^{n-1},A_{j_n,t}^n,p_t^{n+1})\in T_n\left(p_t^{n-1},p_t^{n+1}\right)\subset T_n,n=1,2,\dots ,N.$$

(38)

Thereby

$$(p_t^{n-1},A_{j_n,t}^n,p_t^{n+1})\in \underset{i=1}{\overset{N}{\cap }}{T}_{i,t}.$$

(39)

So, we have

$$\underset{i=1}{\overset{N}{\cap }}{T}_{i,t}\ne \Phi .$$

(40)

If the above equation holds, then we may assume the following:

$$p_t=\left(p_t^{n-1},{\mathrm{A}}_{j_n,t}^n,p_t^{n+1}\right)=\left({\mathrm{A}}_{j_1,t}^1,{\mathrm{A}}_{j_2,t}^2,...,{\mathrm{A}}_{j_N,t}^N\right)\in T_{i,t},i=1,2,\dots ,N.$$

(41)

From the definition of $T_{i,t}$, we can infer that

$$\begin{array}{c}{\Gamma }_n\left({\mathrm{A}}_{j_1,t}^1,{\mathrm{A}}_{j_2,t}^2,...,{\mathrm{A}}_{j_N,t}^N\right)=\underset{A_k^n\in {\mathrm{P}}_{n,t}}{max}{\Gamma }_n\left(p_t^{n-1},A_{k,t}^n,p_t^{n+1}\right)\\ \ge {\Gamma }_n\left(p_t^{n-1},A_{k,t}^n,p_t^{n+1}\right),\forall A_{k,t}^n\in {\mathrm{P}}_{n,t}.\end{array}$$

(42)

According to the definition of pure-strategy Nash equilibrium, a pure-strategy Nash equilibrium of a finite-strategy static game is $\left({\mathrm{A}}_{j_1,t}^1,{\mathrm{A}}_{j_2,t}^2,...,{\mathrm{A}}_{j_N,t}^N\right)$. Based on the above derivation, it can be concluded that the sufficient and necessary condition for the existence of a pure-strategy Nash equilibrium solution is $\underset{n=1}{\stackrel{N}{\cap }}{T}_{n,t}\ne \Phi$.

Clearly, there exists a set of solution vectors for the game $\mathcal{G}$, such that

$${\Gamma }_n({\mathrm{V}}_{n-}^{d,t},{\upsilon }_n^{d,t\ast })\ge {\Gamma }_n({\mathrm{V}}_{n-}^{d,t},{\upsilon }_n^{d,t}),{\upsilon }_n^{d,t}\in \{0,1,2,...,F\}.$$

(43)

Therefore, the Nash equilibrium solution for the game problem $\mathcal{G}$ exists.

4.2. Solving RCO Using Multi-Dimensional Discrete Particle Swarm Optimization Algorithm

To resolve this game problem, we employed a multi-dimensional discrete particle swarm algorithm [32] to search for NE point ${\tilde{\mathrm{V}}}^{d,t}$. The modeling process begins by initializing a set of multi-dimensional random particles, represented by the set ${\mathcal{J}}_{{\mathrm{N}}_d}^{l,i}=\{J_1^{l,i},J_2^{l,i},...,J_N^{l,i}\},\forall i\in I,\forall l\in L$. Here, i denotes the iteration rounds of the particles, L represents the population size, and the particle dimension corresponds to the total number of users $\mathrm{N}d$ participating in the RCO game.

Each particle symbolizes a feasible solution set for the game, with the solution vector’s domain in any dimension n following $\forall J_n^{l,i}\in \{0,1,2,...,F\}$. It is important to note that for users without service requests at slot t, the corresponding dimensional value remains consistently zero, as indicated by the expression ${\mu }_n^t=0\to J_n^{l,i}\equiv 0$.

These particles are initially distributed randomly within the solution space and are assessed for estimated energy consumption $q_{d,t}\left({\mathcal{J}}_{{\mathrm{N}}_d}^{l,i}\right)$ based on the fitness function $q_{d,t}\left(\right)$, which reflects the quality of the particle’s current position. The solution vector with the best fitness in the global historical iterations for population L is designated as ${\mathcal{J}}_{{\mathrm{N}}_d}^{globe}=\{J_1^{globe},J_2^{globe},...,J_N^{globe}\}$, while the local historical optimal fitness solution vector for particle $\forall l\in L$ is named by ${\mathcal{J}}_{{\mathrm{N}}_d}^{local}=\{J_1^{local},J_2^{local},...,J_N^{local}\}$. In the i-th iteration, particles determine their displacement vector ${\mathcal{Z}}_{{\mathrm{N}}_d}^{l,i}=\{Z_1^{l,i},Z_2^{l,i},...,Z_N^{l,i}\}$ for the subsequent iteration by considering the global optimal solution in the $(i-1)$-th iteration, local optimal solution, and the particle’s current position, where positive integer $\forall Z_n^{l,i}\in [0,F]$. The formula for updating the displacement vector in the n-th dimension for the i-th iteration is as follows:

$$Z_n^{l,i}=Z_n^{l,i-1}+⌊H1\left(x_1\right)\times (J_n^{local}-J_n^{l,i-1})⌋+⌊H2\left(x_2\right)\times (J_n^{globe}-J_n^{l,i-1})⌋$$

(44)

In cases where the user request is null, the particle displacement vector should be zero. To increase the randomness of particle movement, we set two exploration coefficients, $H1\left(x_1\right)$ and $H2\left(x_2\right)$. Both of them follow uniform distribution. The random variables $x_1$ and $x_2$ have value ranges of $[h{1}_{min},h{1}_{max}]$ and $[h{2}_{min},h{2}_{max}]$, respectively, and satisfy the following equation:

$$\begin{array}{c}\hfill H1\left(x_1\right)=\left\{\begin{array}{c}\frac{1}{(h{1}_{max}-h{1}_{min})},\\ 0,\end{array}\begin{array}{c}{x}_1\in [h{1}_{min},h{1}_{max}]\\ \mathrm{elsewhere},\end{array}\right.\\ \hfill H2\left(x_2\right)=\left\{\begin{array}{c}\frac{1}{(h{2}_{max}-h{2}_{min})},\\ 0,\end{array}\begin{array}{c}{x}_2\in [h{2}_{min},h{2}_{max}]\\ \mathrm{elsewhere}.\end{array}\right.\end{array}$$

(45)

Nevertheless, the exploration coefficient results in the weighted displacement vector fail to comply with the domain definition of the action space, specifically concerning decimal values. To mitigate the impact of the decimal component in our calculations, we employed the floor function $⌊\ast ⌋$ to handle the increments. This approach guarantees that the displacement vector adheres to the constraints imposed by the offloading space. The iterative formula to determine the particle’s position is delineated as follows:

$${\mathcal{J}}_{{\mathrm{N}}_d}^{l,i}={\mathcal{J}}_{{\mathrm{N}}_d}^{l,i-1}+{\mathcal{Z}}_{{\mathrm{N}}_d}^{l,i}.$$

(46)

After i iterations, the algorithm arrives at the final global optimal solution vector ${\mathcal{J}}_{{\mathrm{N}}_d}^{final}$, which minimizes the real-time energy consumption function $q_{d,t}^{min}\left({\mathcal{J}}_{{\mathrm{N}}_d}^{final}\right)$. This solution vector also represents the NE point ${\tilde{\mathrm{V}}}^{d,t}$ of the game problem $\mathcal{G}$. The specific process of the RCO decision is detailed in Algorithm 4.

Algorithm 4 Discrete Multi-dimensional PSO-based RCO Algorithm

1: Initialize: MEC server d, Cache Chord $\mathbb{C}$, MEC server local cache buffer $\mathbb{R}$, user request set $U_{{\mathrm{N}}_d}^t$, communication channel F, game $\mathcal{G}$, particle population quantity L, particle iteration i, fitness function $q_{d,t}\left(\right)$, particle displacement vector ${\mathcal{Z}}_{{\mathrm{N}}_d}^{l,i}$, particle ${\mathcal{J}}_{{\mathrm{N}}_d}^{l,i}$  2: for each iteration i do  3:    for each particle ${\mathcal{J}}_{{\mathrm{N}}_d}^{l,i}$ do  4:      for each dimension n do  5:         calculate displacement vector ${\mathcal{Z}}_{{\mathrm{N}}_d}^{l,i}$ through function (44)  6:         update particle position ${\mathcal{J}}_{{\mathrm{N}}_d}^{l,i}$ through function (46)  7:      end for  8:      calculate fitness $q_{d,t}\left({\mathcal{J}}_{{\mathrm{N}}_d}^{l,i}\right)$  9:    end for 10:  if $q_{d,t}\left({\mathcal{J}}_{{\mathrm{N}}_d}^{l,i}\right)>q_{d,t}\left({\mathcal{J}}_{{\mathrm{N}}_d}^{local}\right)$ then 11:      ${\mathcal{J}}_{{\mathrm{N}}_d}^{local}={\mathcal{J}}_{{\mathrm{N}}_d}^{l,i}$ 12:  end if 13:  if $q_{d,t}\left({\mathcal{J}}_{{\mathrm{N}}_d}^{l,i}\right)>q_{d,t}\left({\mathcal{J}}_{{\mathrm{N}}_d}^{local}\right)$ and $\forall q_{d,t}\left({\mathcal{J}}_{{\mathrm{N}}_d}^{\xi ,i}\right)<q_{d,t}\left({\mathcal{J}}_{{\mathrm{N}}_d}^{l,i}\right),\forall \xi \in L$ then 14:      ${\mathcal{J}}_{{\mathrm{N}}_d}^{globe}={\mathcal{J}}_{{\mathrm{N}}_d}^{l,i}$ 15:  end if 16: end for 17: ${\mathcal{J}}_{{\mathrm{N}}_d}^{final}={\mathcal{J}}_{{\mathrm{N}}_d}^{globe}$ 18: return Global Optimal Solution ${\mathcal{J}}_{{\mathrm{N}}_d}^{final}$ to server d

5. Performance Evaluation

Simulation experiments were developed on the Python platform for the DESCO network environment. The MDPSO algorithm was deployed based on this distributed environment. The service coverage area of distributed MEC nodes is a regular hexagonal region with a diagonal length of 200 m. The values of system time slots, system operating cycle, server’s wireless transmission bandwidth, server’s and MUs’ computing power, user’s channel gain ${\zeta }_n$, and the local computing energy consumption coefficient $\varsigma$ are all constants and remain unchanged in the subsequent comparative experiments. The specific values are shown in

Table 2. Simulation setting.

Parameter	Value
Number of MEC servers $\Delta$	3
Subchannel bandwidth b	3
$\varsigma$	$5\times {10}^{-27}$
${\sigma }^2$	$2\times {10}^{-13}$
${\psi }_n$	0.5 W
F	10
D	2000
$o_{d,n}$	1 GHz
${\theta }_{max},{\omega }_{max},{\varphi }_{max}$	5
$[h{1}_{min},h{1}_{max}]$ and $[h{2}_{min},h{2}_{max}]$	$[0,3]$
Particle number L	500
Particle iteration i	100

.

During the initialization phase, DESCO randomly generates the data for all services in the set $\mathrm{K}$. The values are sampled from the intervals ${\theta }_k\in [1,{\theta }_{max}]$, ${\omega }_k\in [1,{\omega }_{max}]$, and ${\varphi }_k\in [1,{\varphi }_{max}]$, where the maximum values ${\varphi }_{max},{\omega }_{max},{\theta }_{max}$ are all set to 5. The service cache capacity S of MEC server d is fixed at 2GB, and the cache replacement policy is set to random caching by default. In the subsequent experiments, we will investigate the average energy consumption of users under different numbers of MEC servers. The environment configuration is the same as [3,31,33]. The state transition probabilities of user requests follow a Zipf distribution parameterized by $〈R,L,\vartheta 〉$, where

$$Pr\{{\mu }_n^{t+1}=b|{\mu }_n^t=a\}=\left\{\begin{array}{c}R,\mathrm{a}\ne 0,b=0\hfill \\ \frac{1-R}{L},a\ne 0,b=(a+l)mod(K+1),l\in [1,K]\hfill \\ \frac{1-R}{b^{\vartheta }{\sum }_{i\in [1,K]}{\left(\frac{1}{i}\right)}^{\vartheta }},a=0,b\ne 0,\hfill \end{array}\right.$$

(47)

whereby $\vartheta$ represents the Zipf distribution parameter. L denotes the number of adjacent services that may be requested in the next stage. R signifies the probability that user n will not request any service in the subsequent phase. We will adjust parameters L and R to evaluate the performance of the algorithm under varying transition probabilities.

(1) The Greedy–Random algorithm: combines Greedy RCO with random cache replacement strategy. In the initialization phase, MEC servers randomly generate the RCO strategies for the user. Then, based on this initial strategy, the algorithm traverses each user’s offloading decision in the set $N_d$. At each step, it searches for the channel occupancy strategy that minimizes the energy consumption for that user. Meanwhile, the MEC server adopts a random cache replacement strategy for local cache space. This strategy randomly replaces the stored application data with the application data offloaded by users in the current time slot after the cache space becomes saturated, satisfying Equation (18) during this process.

(2) Random cache replacement with multi-dimensional discrete particle swarm offloading (MDPSO-Random): The MDPSO strategy is utilized to solve RCO strategy. By assigning initial momentum to random multi-dimensional particles, the RCO strategy explores the optimal strategy in the solution space based on the fitness function. It is worth noting that this algorithm is deployed only in DESCO networks with a single MEC server.

(3) The MDPSO-Random algorithm with Cache Chord (MDPSO-Random with CC) builds upon the MDPSO-Random algorithm: This mechanism allows MUs to access the application cache resources across the entire edge layer.

The effectiveness of the MDPSO algorithm and Cache Chord is verified from three aspects: convergence of the MDPSO algorithm, energy consumption performance, and cache hit rate.

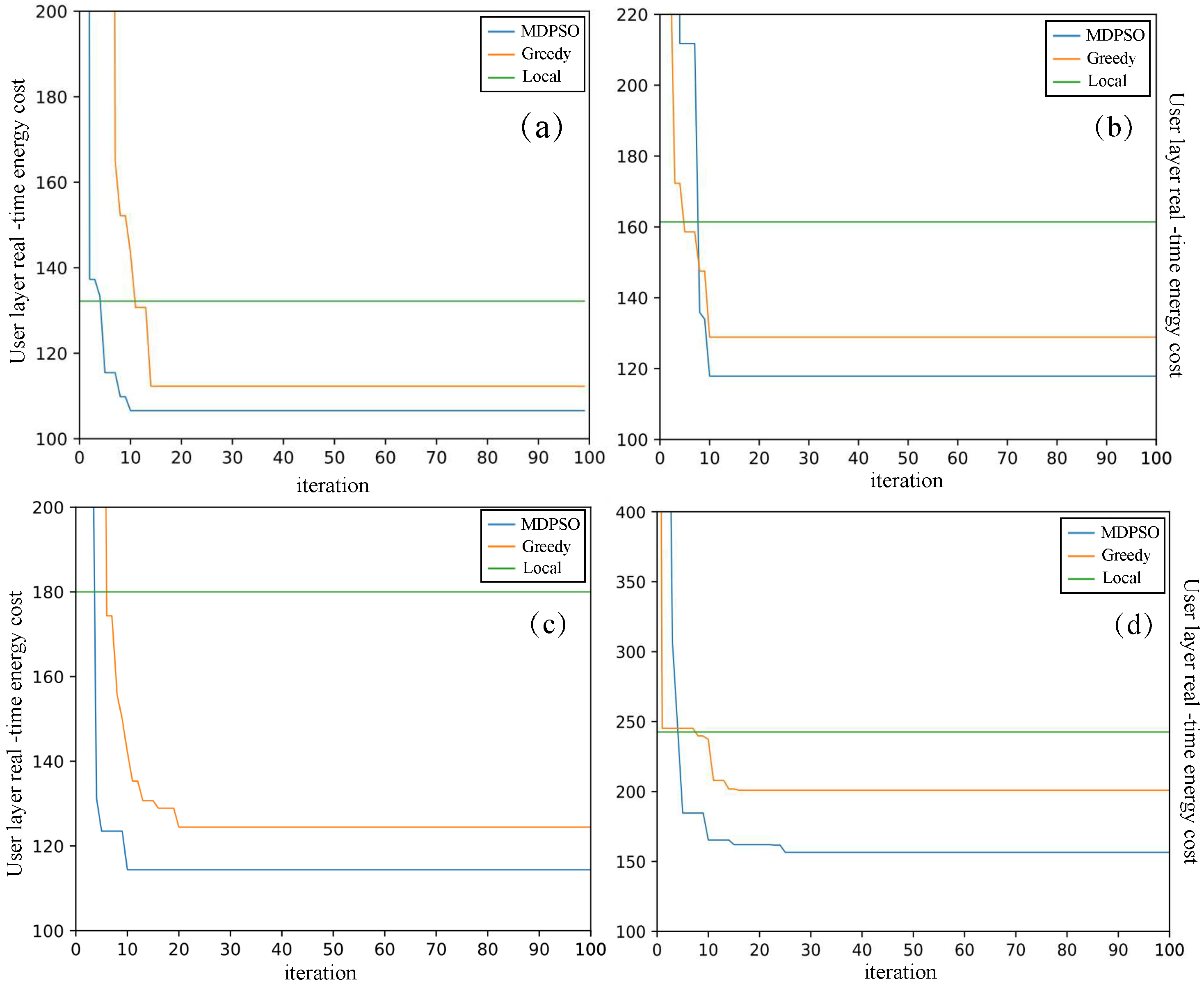
Firstly, the convergence analysis of the proposed algorithm is conducted. Figure 4 illustrates the instantaneous energy consumption obtained after iterations for both the MDPSO algorithm and the Greedy algorithm in the single-server scenario. The experiment is conducted with different MU counts ($N_d=15,25,35,45$) and a local MEC cache capacity of 2 GB. The horizontal axis represents the number of iterations for particles or algorithms, while the vertical axis represents the energy consumption of the MEC server. In the experiment, the dimension L of particles is set to 500, and the number of iterations i is 100.

The blue line represents the convergence curve of the MDPSO, while the orange line represents the Greedy algorithm. The green horizontal line, which remains constant throughout iterations, represents the energy consumption of local computation. Comparing the two algorithms, it is observed that both MDPSO and Greedy strategies converge within the first 40 rounds and can reduce user-level energy consumption by 18.75% to 41.17% compared to local computation. Moreover, MDPSO exhibits better convergence compared to the Greedy strategy, with an average reduction of 19.7% in user-level energy consumption per round. This indicates that the MDPSO algorithm can explore the solution space more comprehensively, avoiding local optima, and performs well when dealing with discrete vectors.

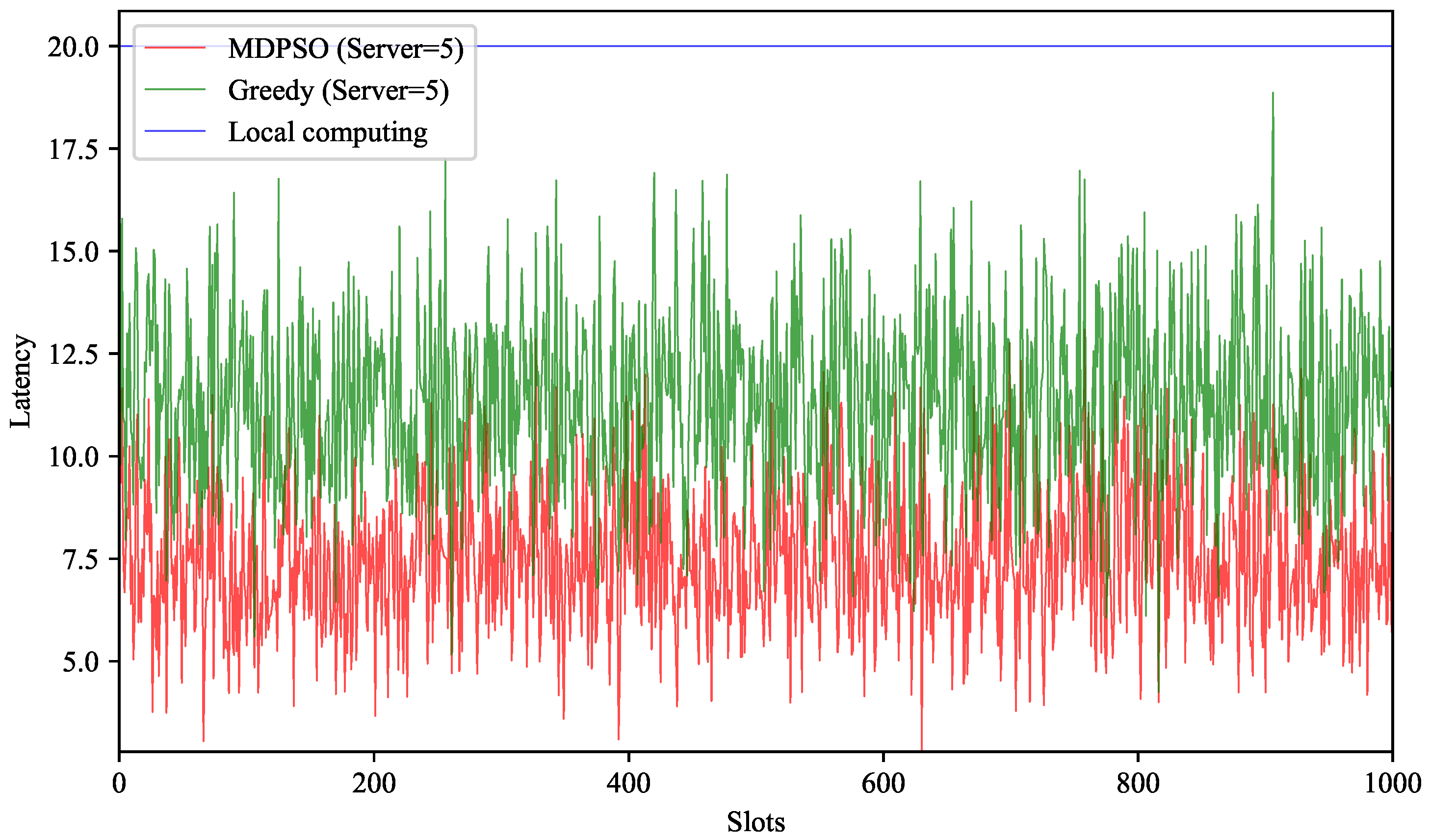
Figure 5 illustrates the average task completion time of user layer per time slot with a task latency constraint of $\tau =20$ ms. The red line represents the MDPSO algorithm with collaboration among five nodes, while the green line represents the Greedy offloading strategy with the same number of collaborating nodes. Since MUs can adopt DVFS to adjust the computational power of local devices and ensure timely task completion, the task completion time in each round remains stable at a maximum latency constraint of 20 ms. After running for 1000 time slots, the proposed algorithm outperforms others, with an average latency of 7.4 ms, while the Greedy strategy exhibits an average latency of 11.4 ms, both showing a decrease compared to the local computing. This implies that the proposed algorithm can converge to the optimal offloading strategy, thereby applying the cache-based offloading mode as much as possible, to reduce data transmission overhead for MUs.

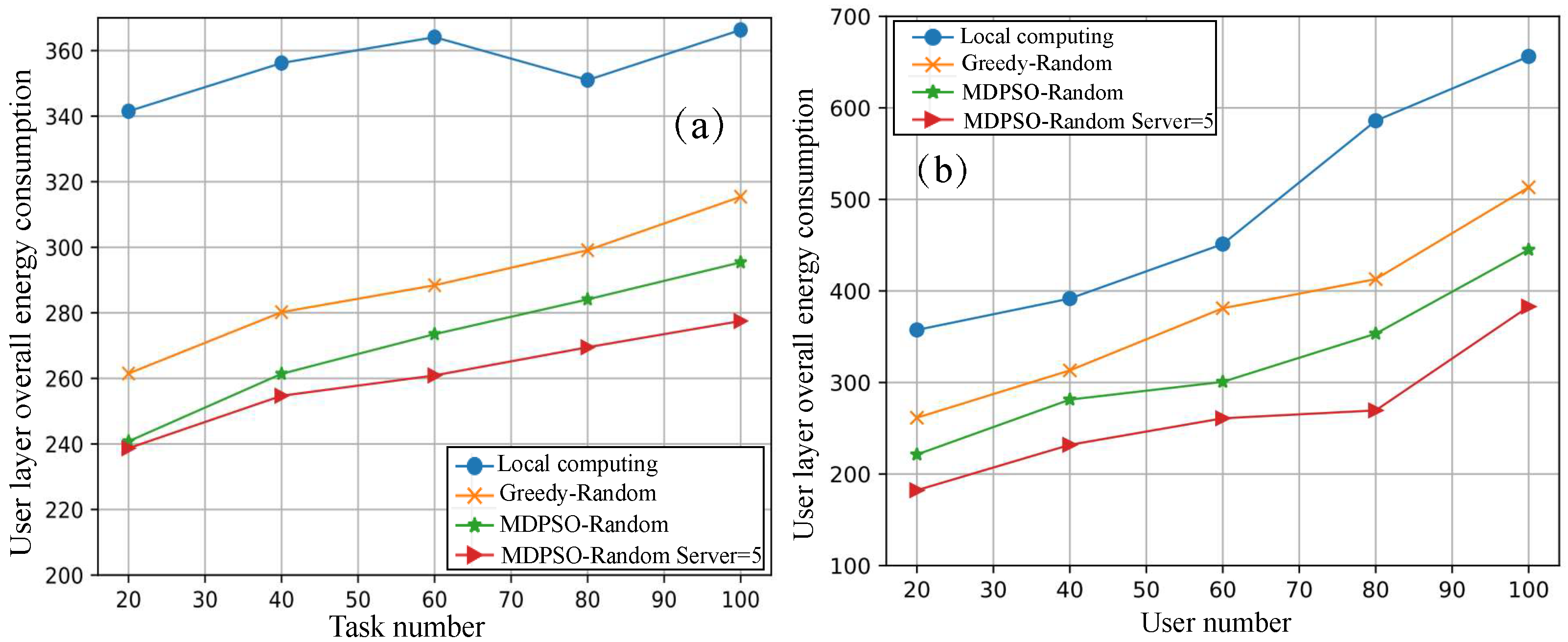
Figure 6 compares the energy consumption of local computation, Greedy-Random, MDPSO-Random, and MDPSO-Random with Cache Chord (CC)-assisted algorithms under different numbers of MUs and task richness conditions, using the default Zipf service request distribution function. In Figure 6a, the number of users covered by each MEC server is fixed at 5. Through the experiments, it is observed that, relative to local computation, the other three algorithms effectively reduce energy consumption overhead. In Figure 6a, the curve for local energy consumption remains relatively constant. This is because the energy consumption of local computation is only dependent on the number of tasks and FLOPs of tasks. The increase in the number of user types only poses challenges for cache-based algorithms. Moreover, through horizontal comparison, it is noted that the algorithm based on the cooperation of 5 distributed MEC servers with cache exhibits the best performance. This is attributed to the CC data-sharing mechanism, which allows users at any location to access resources across the entire MEC edge layer. This implies that the cache space linearly increases with the addition of servers in the CC network, thereby eliminating the need for users to transmit ${\theta }_k$ and resulting in a higher transmission of energy consumption.

Figure 7 compares the average energy consumption of a cluster of users under the collaboration of different numbers of MEC servers. As the number of MEC servers increases, the energy consumption in all cases shows a decrease and converges to the same value in all cases, because as the total number of server D increases, the cache pool storage is richer, which allows more requests to be converted from pure offloading to cache-based offloading until all MUs do not need to upload application data ${\omega }_k$. It can also be noticed that the slopes of the three energy consumption curves decrease gradually as the total number of tasks increases. The energy consumption curve decreases most rapidly when the total number of tasks is small ($N_d=100$) and converges at around 20 servers; the energy consumption curve of $N_d=100$ converges at $D=45$ because when the total number of tasks is larger, the servers also need to collaborate on a larger scale to make sure that the corresponding application data are stored.

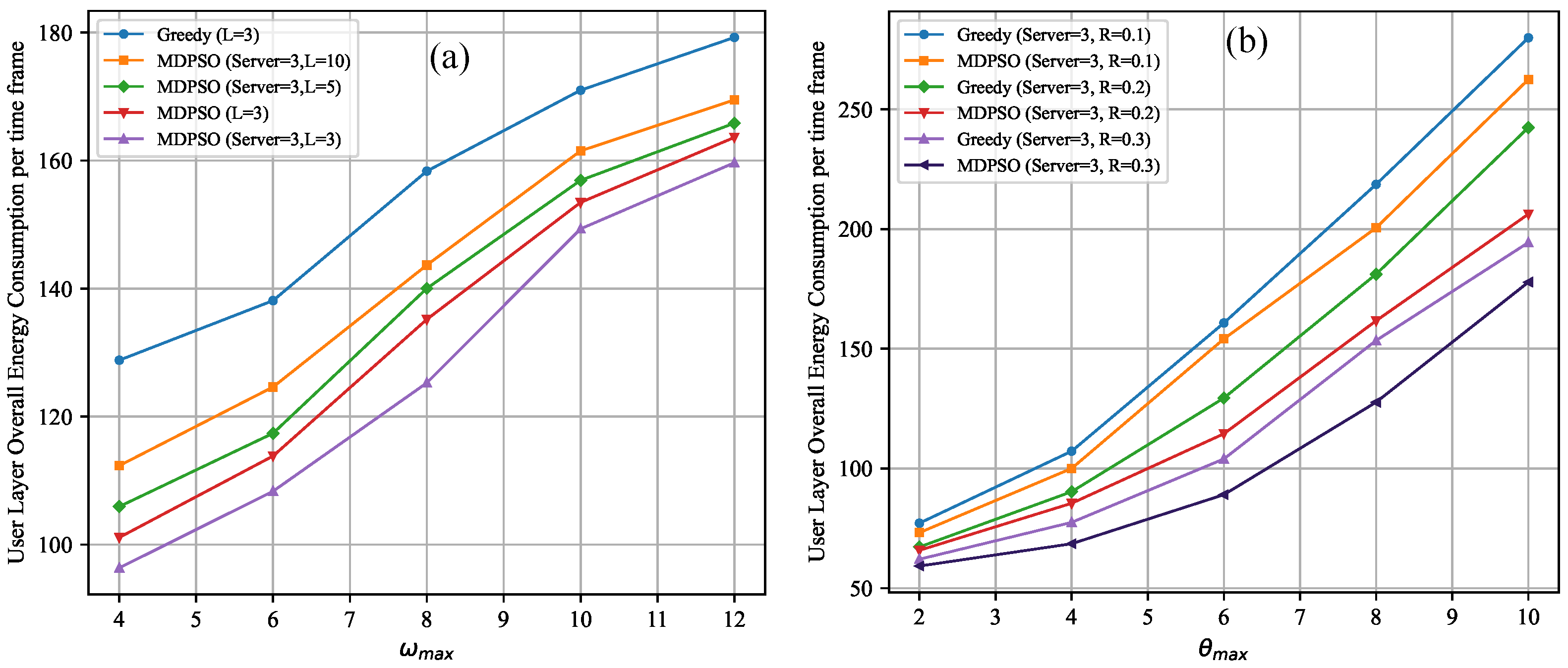
Figure 8 illustrates the average energy consumption of MUs per time slot under different Zipf parameters and various task attributes for MDPSO. As depicted in Figure 8a, it can be observed that with the increase in the maximum value of application data ${\omega }_{max}$, the average energy consumption of the Greedy algorithm and the MDPSO assisted by CC continues to rise. This is due to the increase in ${\omega }_{max}$, which increases the transmission overhead of tasks, thereby reducing the offloading benefits. The proposed algorithm can effectively reduce the average energy consumption by 10.9% to 25.17% compared to the Greedy offloading strategy. Additionally, under the same parameter conditions ($L=3$), MDPSO based on multi-server collaboration can reduce the average energy consumption by 7.89% to 4.7% compared to the single-node mode.

Observing Figure 8b, we can conclude that with the growth of ${\theta }_{max}$, the average energy consumption of all algorithms increases. Moreover, comparing the Greedy algorithm with the MDPSO algorithm based on multi-node collaboration, under the same Zipf R condition, MDPSO can reduce the average energy consumption by 2.1% to 16.8% compared to Greedy. Furthermore, with the increase in parameter R, the energy consumption also decreases. This is because parameter R is positively correlated with the probability that the MUs’ next stage service request is empty. A larger R means more MUs with empty requests at any time. Sparse service requests undoubtedly lead to reduced transmission energy consumption for MUs.

Figure 9a,b, respectively, explore the impact of the number of servers in the CC mechanism on the cache hit ratio from the perspectives of user count and service types. The cache hit ratio represents the ratio of the total number of accesses to the edge layer by users $C_s$ to the number of services successfully requested $C_h$, expressed as the following formula:

$$\mathrm{Cache}\mathrm{hit}\mathrm{ratio}=\frac{C_h}{C_s}$$

(48)

By vertically comparing Figure 9, it is evident that under the same conditions, as the number of MEC servers increases, the cache space grows linearly, leading to a significant improvement in the cache hit ratio $C_r$. Compared to a single server, when the number of servers is increased to 10, the cache hit ratio $C_r$ increases by $33.3\%$ to $42.7\%$. Moreover, when the number of users $N_d$ is 20 and the number of services $K<80$, the cache hit ratio achieved by the cooperation of 10 servers is consistently above 91%. This improvement is attributed to the Cache Chord mechanism overcoming the bottleneck imposed by the storage space limitation.

However, as the number of task types increases, the cache hit ratio decreases. This decline is due to the sparser distribution of user service requests as the task types increase. For individual MEC servers, the proportion of service data stored in the limited space of the local cache pool becomes relatively smaller compared to the overall request volume, leading to a decrease in $C_r$. Comparing the four models, it can be concluded that the Cache Chord mechanism effectively assists in computation offloading. Moreover, with the increase in node scale, higher benefits can be achieved.

6. Conclusions

This paper investigates how to provide higher-quality services to MUs while reducing user layer energy consumption in MEC networks. The DESCO network architecture is proposed to address this issue. In the DESCO network, a cache-sharing mechanism, Cache Chord, is conducted based on a geo-distributed edge server collaboration. Cache Chord utilizes consistent hashing to map servers and real-time applications into a circular logical topology. We also improved the IP routing algorithm to reduce computational complexity and designed an index update mechanism to ensure information synchronization among edge nodes. Furthermore, in addressing the bottleneck of channel allocation caused by concurrent requests from current users, the problem is formulated as a multi-player static game. After proving the existence of the Nash equilibrium point, the MDPSO algorithm is proposed to simulate user requests as particles, exploring the global optimal node in the solution space to provide users with the lowest energy consumption offloading strategy. Finally, the algorithm is compared with baseline algorithms, and the performance of the Cache Chord structure is tested at different scales.

Through simulation experiments, we have found that computation offloading assisted by the Cache Chord mechanism can significantly reduce user energy consumption overhead. It is foreseeable that with the increasing scale of added server nodes, energy consumption will be further reduced. However, this paper overlooks the fact that with the increase in server nodes, the transmission delay of the corresponding backhaul links will also increase, posing new challenges for performance optimization. Therefore, the next step will be to explore how larger node scales will affect service quality and consider deploying the protocol in a real network environment to test its performance.