Characterising Payload Entropy in Packet Flows—Baseline Entropy Analysis for Network Anomaly Detection

Abstract

The accurate and timely detection of cyber threats is critical to keeping our online economy and data safe. A key technique in early detection is the classification of unusual patterns of network behaviour, often hidden as low-frequency events within complex time-series packet flows. One of the ways in which such anomalies can be detected is to analyse the information entropy of the payload within individual packets, since changes in entropy can often indicate suspicious activity—such as whether session encryption has been compromised, or whether a plaintext channel has been co-opted as a covert channel. To decide whether activity is anomalous, we need to compare real-time entropy values with baseline values, and while the analysis of entropy in packet data is not particularly new, to the best of our knowledge, there are no published baselines for payload entropy across commonly used network services. We offer two contributions: (1) we analyse several large packet datasets to establish baseline payload information entropy values for standard network services, and (2) we present an efficient method for engineering entropy metrics from packet flows from real-time and offline packet data. Such entropy metrics can be included within feature subsets, thus making the feature set richer for subsequent analysis and machine learning applications.

1. Introduction

Packet level information entropy can reveal useful insights into the types of content being transported across data networks, and whether that content type is consistent with the communication channels and service types being used [1,2]. By comparing payload entropy with baseline values, we can ascertain—for example—whether security policy is being violated (e.g., an encrypted channel is being used covertly). To the best of our knowledge, there are no published baseline information entropy values for common network services, and, therefore, no way to easily compare deviations from ‘normal’. In this paper, we analyse several large packet datasets to establish baseline entropy for a broad range of network services. We also present an efficient method for recovering entropy during flow analysis on live or offline packet data, the results of which, when included as part of a broader feature subset, will considerably enhance the feature set for subsequent analysis and machine learning applications.

1.1. Background

Broadly, entropy is a measure of the state of disorder, randomness, or uncertainty in a system. Definitions span multiple scientific fields, and the concept of ‘order’ can be somewhat subjective. However, for the purpose of this work, we are concerned with information entropy. In terms of physics, for example, the configuration of the primordial universe has the lowest overall entropy since it is the most ordered and least likely state over a longer timeframe. We can consider entropy as the number of configurations of a system. It may also be viewed as a measure of the lack of information in a system. In the context of information theory, entropy was first described by Shannon in his seminal 1948 paper [3], which provides a mathematical framework to understand, measure, and optimise the transmission of information. Shannon formalised the concept of information entropy as a measure of the uncertainty associated with a set of possible outcomes: the higher the entropy, the more uncertain the outcomes.

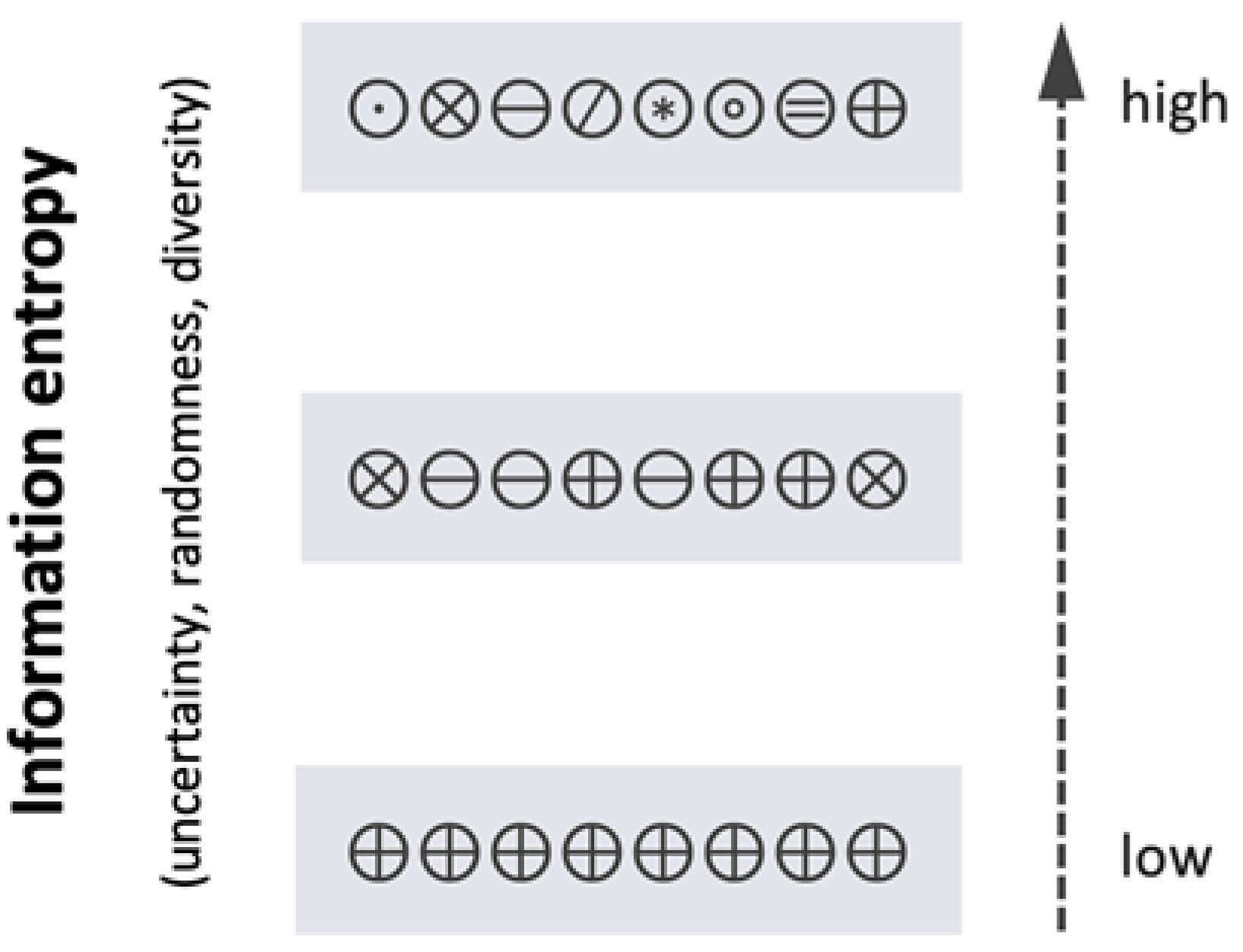
Practically, if we consider entropy in data, we are interested in the frequency distribution of symbols, taken from a finite symbol set. The higher the entropy, the greater the diversity in symbols. Maximum entropy occurs when the symbolic content of data is unpredictable, so for example, if a file or network byte stream has high entropy, it follows that any symbol (here, we typically equate a byte to a symbol) is almost equally likely to appear next (i.e., the data sequence is unpredictable, close to random); see Figure 1.

Shannon’s entropy [3,4]—sometimes referred to as information density, is a measurement of the optimal average length of a message, given a finite symbol set (an alphabet). The use of entropy to measure uncertainty in a series of events or data is a widely accepted statistical practice in information theory [3,4].

We can compute the entropy of a discrete random event x using the following formula:

$$H\left(X\right)=-\sum _{i-1}^{n}p\left(x_{i }\right){\log }_2\left(p\right(x_i\left)\right)$$

where H(X) is the information entropy of a random variable X, with a finite set of n symbols. This formula is effectively the weighted average uncertainty for each outcome xi, where each weight is the probability p(x_i). p(x_i) is the probability [0,1] of the occurrence of the ith outcome. Log base 2 is convenient to use since we are measuring entropy in bits (i.e., x ∈ {0,1}). The negative sign ensures non-negative entropy. In Section 3, we describe how we normalise entropy values to lie within the range of 0 to 8 for the purpose of our packet analysis.

1.2. Network Packet and Flow Datasets

Machine learning is a powerful tool in cybersecurity, particularly in its ability to detect anomalies, and cybersecurity researchers in network threat identification and intrusion detection are particularly interested in the analysis of large network packet and flow datasets. A survey of the composition of publicly available intrusion datasets is provided in [5].

Packet datasets are typically large, high-dimensional, time-series data, often containing tens of millions of discrete packet events. Due to memory constraints and temporal complexity, it is common to abstract packet data into lower-dimensional containers called flows. Flows capture the essential details of packet streams in a compact, extensible format, without the inherent complexity of raw packets [5]. Packet flows offer a convenient lower-dimension sample set with which to do cyber research.

A flow can be created using a simple tuple, to create a unique fingerprint with which to aggregate associated packets over time, based on the following attributes:

• Source and Destination IP Address;
• Source and Destination Port identifier;
• Protocol ID.

Flows can be stateful (for example, TCP flows have a definite lifecycle, controlled by state flags), with additional logic and timeouts required to capture the full lifecycle of a flow. Flows may also be directional (i.e., unidirectional, or bidirectional), and flows may be unicast, multicast, or broadcast (one-to-one, one-to-group, one-to-all). While flows are essentially unique at any instant, they may not be unique across time—based solely on the tuple—since some attributes are likely to be reused in the distant future. (For example, port numbers will eventually ‘wrap around’ once they reach a maximum bound—so large packet trace could contain two identical flows, but these are likely to be separated by a substantial time interval, unless there is a bug in the port allocation procedure).

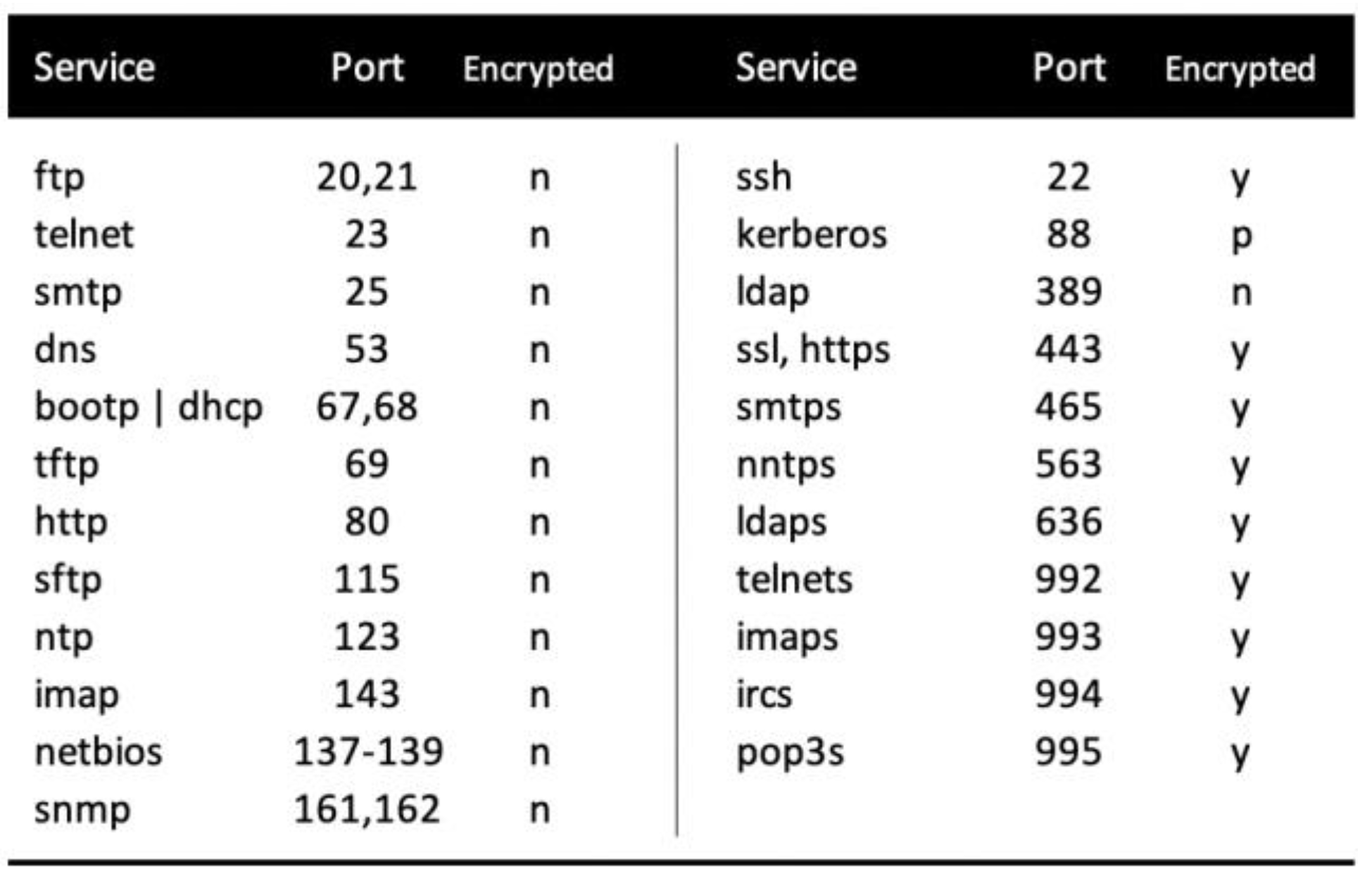
Modern public datasets used in network threat research often include high level flow summaries and metadata, but rarely include payload content in these summaries (notably, the UNB 2012 intrusion dataset did include some payload information encoded in Base 64; however, subsequent updates did not, due to the size implications). Since packet payload typically represents the largest contributor to packet size (typically, an order of magnitude larger than the protocol headers), it tends to be removed during the creation of flow datasets. Payload also adds complexity in that it requires reassembly and in-memory state handling across the lifecycle of a flow. Payload is often encrypted (see Figure 2), which means that many potentially useful features are not accessible. There are also potential privacy and legal concerns, given that payload may contain confidential, sensitive, or personal information [5]. For these reasons, we rarely see much information on packet payload within flow datasets and metadata summaries other than simple volumetric metrics. As such, we have very few insights of what the actual content of the data being transferred looks like, at any point in time, and this lack of visibility can impair the detection of anomalous and suspicious activity that might exploit this feature. Specifically, the omission of such metrics in flow and packet data may inhibit the detection of certain types of attacks, and as discussed in Section 2.

1.3. What Kind of Entropy Metrics Are Useful Network Packet Data

In the context of network packet data, a variety of entropy measurements can be taken and applied in the classification of network anomalies, based on the premise that deviation in entropy values from expected baselines can be indicators of specific threat vectors. For example, where synthetic attacks rely on simple script-based malware, features such as timing or address allocation may exhibit lower entropy (e.g., we might observe predictable packet intervals, payload sizes, port number allocations, etc.). This might, for example, be the case where malware contains simple data generating loops, and where events and data are allocated incrementally, at predictable intervals. Naturally, skilled malware creators will attempt to mask such characteristics by reducing predictability (for example, by introducing randomised timing, more sophisticated address and port allocation techniques, perturbations in content, etc.).

In practice, we can calculate entropy against several network features, including packet payload content, packet arrival times, IP addresses, and service or port identifiers, as well as changes in entropy across time. Cybersecurity researchers have extended these concepts to a range of use cases in malware detection and content classification. For instance, techniques have been developed to identify anomalies in binary files, as well as encrypted network traffic, to indicate the presence of malicious code. We discuss several implementations of entropy in anomaly detection, as described in the literature in Section 2.

Importantly, even where payload content is removed during flow creation, it is possible to extract useful information about payload composition based on symbolic predictability. Metrics such as information entropy [3,4] can provide insights into the nature of encapsulated payload data and may be used as an indicator for security threats from covert channels, data exfiltration, and protocol compromise.

There is a subtle distinction here worth pointing out regarding the use of packet and flow-level entropy metrics:

• At the discrete packet level, individual packets arrive at typically random intervals (on a large, busy, multiprotocol network with many active nodes, we can reasonably assume this at least appears to be the case in practice), intermingled with many other packets, denoting different services and conversations. At a packet level, the information entropy is effectively atomic, and we do not obtain a view of cumulative entropy over time, nor any changes in entropy over time.
• At a flow level, packets that are closely related over time can undergo stateful analysis as a discrete group. For example, if a user sends an email, there will typically be several related packets involved in the exchange in two directions, and this collection of packets is termed a packet flow. Information entropy at this level can be useful in providing an overall perspective of the content of payload and a per-packet perspective on any changes in entropy throughout the flow, by direction.

While there are times when individual packet entropy may be useful (for example, where real-time intervention is critical), ideally, we want to understand the cumulative entropy within packet payload, by direction, with the ability to identify any significant changes in entropy during the flow lifecycle.

1.4. Information Entropy Baselines for Network Services

Each packet traversing a network typically contains identifiers that associate that packet with a network service—for example, the File Transfer Protocol (FTP), where the payload of each packet usually represents a fragment of the content being transferred. Packet payload represents a rich source of high dimensional data, and techniques that examine this low-level information are termed Deep Packet Inspection (DPI). In the past, we enjoyed almost complete visibility of this content since older network services (such as HTTP) encoded content in plaintext (i.e., unencrypted). Today, networks are dominated by encrypted services, such as HTTPS, where payload is effectively treated as a ‘black-box’ (without resorting to technologies that can unpack the data in transit, such as SSL intercept), although, there remain some important legacy services that do not encrypt data, as shown in Figure 2.

We know that network services exhibit markedly different entropy profiles, since some are known to be plaintext, and some are partially or fully encrypted—as illustrated in Figure 2. This gives us some intuition on what level of information entropy to expect when analysing the content of network traffic. However, since there are no published baselines for service level information entropy, even if we dynamically compute payload entropy (e.g., within an active flow), there are no ‘ground truth’ values with which to compare. Baseline data can prove very useful in determining whether the characteristics of flow content are deviating significantly from expected bounds, and this may be a strong indicator of anomalous activity, such as a covert channel, compromised protocol, or even data theft—as discussed in Section 2.

1.5. Information Entropy Expression in Feature Subsets

Cybersecurity researchers using machine learning typically rely on small feature subsets with high predicted power to identify malicious behaviour (particularly in applications such as real-time anomaly detection). These features may be drawn from a broader pool of features provided with a dataset or may be engineered from the dataset by the researcher. The composition and correlation strengths across these feature sets often vary, depending on the type of threat and the deployment context; hence, the engineering of new features (particularly novel features) is an important area of research.

We described earlier that packet and flow datasets (particularly those publicly available [5]) typically lack entropy metrics for payload content in their associated metadata. This happens for several reasons, mainly due to payload being encrypted nowadays, and the scale and resource challenges in decomposing and reassembling high dimensional content types. In Section 3, we describe a methodology to enhance dataset flow metadata with information entropy features, and how we subsequently use that to calculate service level baseline information entropy values for various payload content types.

In the following section, we describe related work in characterising various entropy metrics, and discuss examples where entropy has been used in anomaly detection and content classification to assist in network analysis and cybersecurity research.

2. Related Work

Existing research demonstrates that information gain metrics, using techniques such as entropy, can be useful in detecting anomalous activity. Encrypted traffic tends to exhibit a very different entropy profile to unencrypted traffic (unencrypted but compressed data may also show high entropy, depending on the compression algorithm and underlying data); specifically, it tends to have much higher entropy values due to the induced unpredictability (randomness) of the data. Entropy has been widely used as a method to detect anomalous activity, and so intrusion detection, DDoS detection, and data exfiltration are of interest in research. A major challenge in detecting anomalies at the service layer (i.e., packet payload) is that there are no published ‘ground truth’ metrics on data composition with which to compare live results—unless the researcher is prepared to perform their own ‘ground truth’ analysis. Furthermore, publicly labelled intrusion datasets, frequently used in anomaly detection research, do not provide any useful metadata on payload composition other than size and flow rate metrics [5]. This effectively means that information on higher level service anomalies is largely hidden. One of the key contributions of this work is the publication of baseline payload entropy values across common network services, achieved by sampling normal (i.e., benign) network activity from multiple large packet flow datasets. This metadata can be used to compare deviations in live traffic characteristics. We would also suggest that payload entropy should be added to public intrusion dataset flow metadata, so that it can be employed to assist in anomaly detection and machine learning research.

Early work by [6] characterises the entropy of several common network activities, as shown in Figure 3. As discussed in [6], with standard cryptographic protocols (such as SSH, SSL, and HTTPS), it is feasible to characterise which parts of traffic should have high entropy after key exchange has taken place. Therefore, significant changes in entropy during a session may indicate malicious activity. During an OpenSSL or OpenSSH attack, entropy within an encrypted channel is likely to drop below expected levels as the session is perturbed; the authors of [6] suggest entropy scores would dip to approximately six bits per byte during such a compromise (i.e., entropy values of around six, where we would normally expect them to be closer to eight).

In [7], the authors use static analysis across large sample collections to detect compressed and encrypted malware, using entropy analysis to determine statistical variations in malware executables. In [8], the authors use methods that exploit structural file entropy variations to classify malware content. In [9], the authors use visual entropy graphs to identify distinct malware types. In [10], the authors propose a classifier to differentiate traffic content types (including text, image, audio, video, compressed, encrypted, and Base64-encoded content) using Support Vector Machine (SVM) on byte sequence entropy values.

Analysis of the DARPA2000 dataset in [11] lists the top five most important features as TCP SYN flag, destination port entropy, entropy of source port, UDP protocol occurrence, and packet volume. In [12], the authors describe how peer-to-peer Voice over IP (VOIP) sessions can be identified using entropy and speech codec properties with packet flows, based on payload lengths. In [13], the authors use graphical methods for detecting anomalous traffic, based on entropy estimators.

In [GU05], the authors propose an efficient behavioural-based anomaly detection technique by comparing the maximum entropy of network traffic against a baseline distribution, using a sliding window technique with fixed time slots. The method is applied generically across TCP and UDP traffic and is limited to only three features (based on protocol information and the destination port number). They are able to detect fast or slow deviations in entropy; for example, an increase in entropy during an SYN Flood. In [14], the authors analyse entropy changes over time in PTR RR (Resource Records (RR) used to link IP addresses with domain names) DNS traffic to detect spam bot activity. In [15], the authors build on the concepts outlined in [16], capturing network packets and applying relative entropy with an adaptive filter to dynamically assess whether a change in traffic entropy is normal or contains an anomaly. Here, the authors employ several features, including source and destination IP address, source and destination port, and the number of bytes and packets sent and received. In [17], the authors describe an entropy-based encrypted traffic classifier based on Shannon’s entropy, weighted entropy [18], and the use of a Support Vector Machine (SVM).

In [19], the authors propose a taxonomy for network covert channels based on entropy and channel properties, and suggest prevention techniques. More recently, in [20], the authors focus on the detection of Covert Storage Channels (CSCs) in TCP/IP traffic based on the relative entropy of the TCP flags (i.e., deviation in entropy from baseline flag behaviour). In [21], the authors describe entropy-based methods to predict the use of covert DNS tunnels, focussing on the detection of embedded protocols such as FTP and HTTP.

Cyber physical systems present a broad attack surface for adversaries [22], and there can be many active communication streams at any point in time. These channels can be blended into the victim’s environment and used for reconnaissance activities and data exfiltration. In [23], the authors use TCP payload entropy to detect real-time covert channels attacks on Cyber-Physical Systems (CPSs). In [24], the authors describe a flow analysis tool that provides application classification and intrusion detection based on payload features that characterise network flows, including deriving probability distributions of packet payloads generated by N–gram analysis [25].

Computing entropy in packet flows can be implemented by maintaining counters to keep track of the symbol distributions. However, this requires the flow state to be maintained over time (we describe this further in Section 3). This can be both computationally and memory intensive—particularly in large network backbones with many active endpoints, since flows may need to reside in memory for several minutes, possibly longer. For example, in [16], the authors state that their method requires constant memory and a computation time proportional to the traffic rate.

Where entropy is to be calculated in real time, a different approach is required. In [26], the authors offer a distributed approach to efficiently calculate conditional entropy to assist in detecting anomalies in wireless network streams by taking packet traces while an active threat is in progress. They propose a model based on the Hierarchical Sample Sketching (HSS) algorithm, looking at three features of the IEEE 802.11 header: frame length, duration/ID, and source MAC address (final 2-bytes), to compute conditional entropy.

3. Methodology

In this section, we discuss the methodology used to calculate both baseline values and the individual flow level entropy feature values.

3.1. Baseline Data Processing Methods

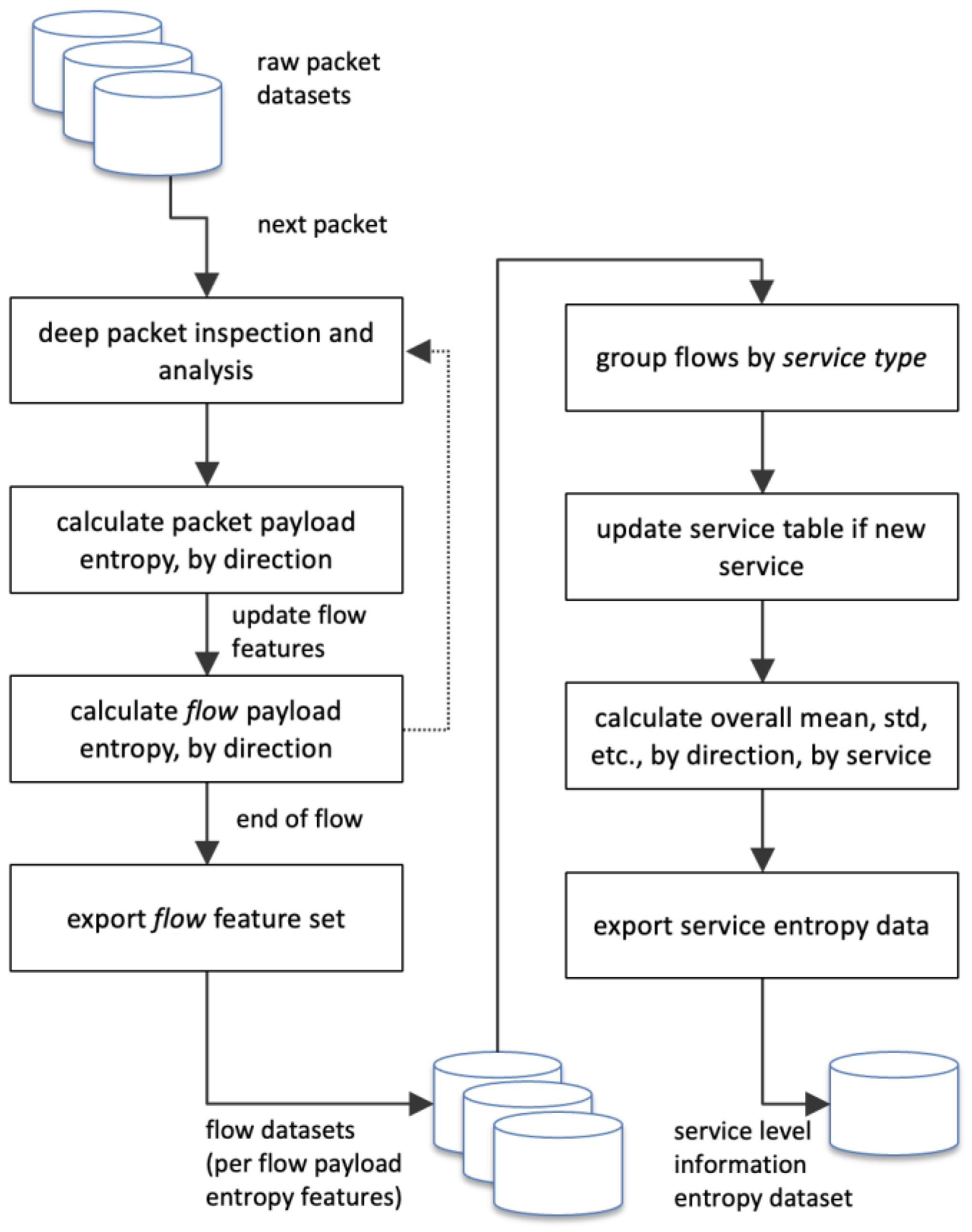
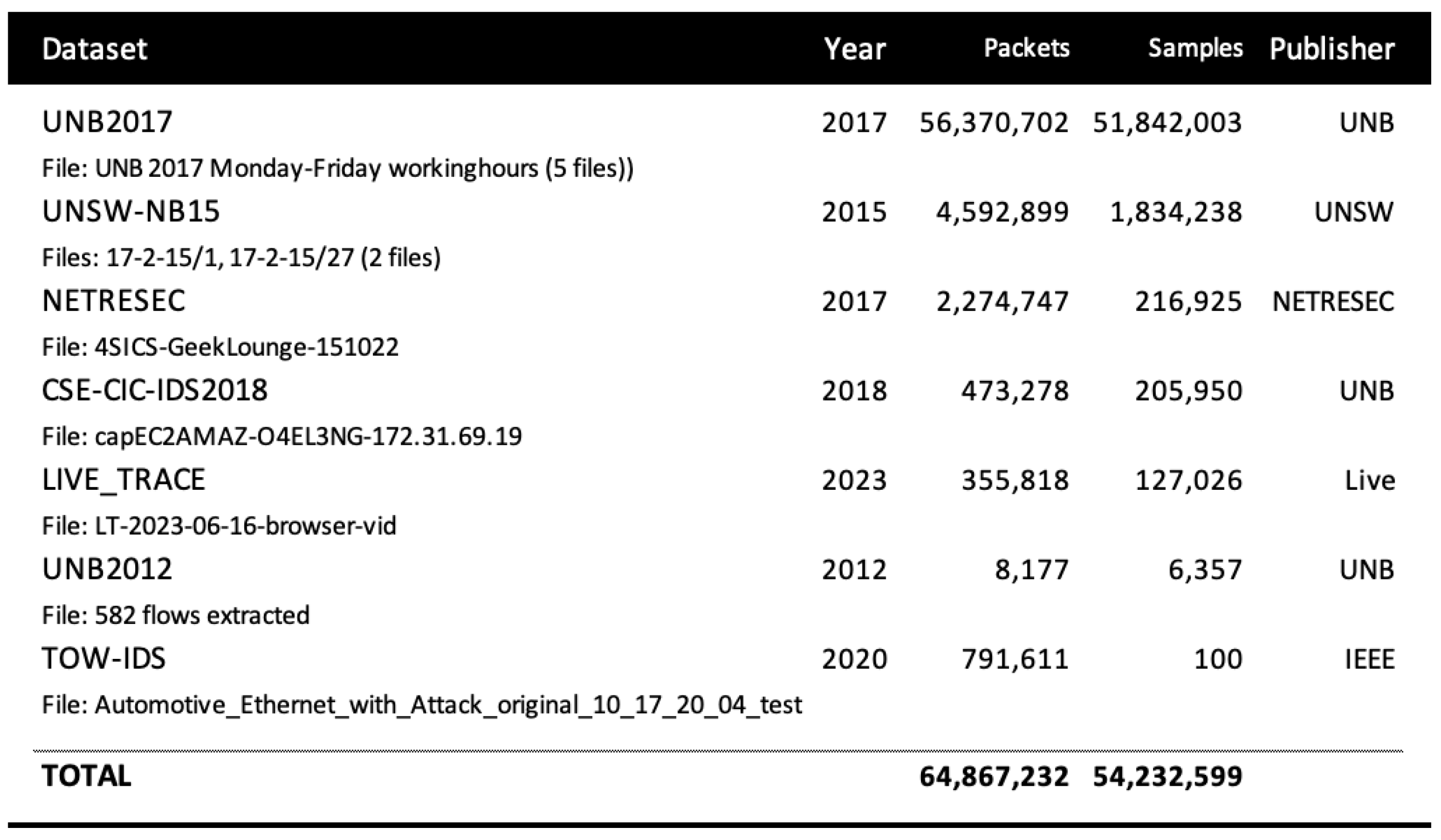
The methodology we used to analyse information entropy in packet traces and calculate service level baselines can be summarised in two phases, as illustrated in Figure 4. The first phase analyses a set of raw packet datasets (listed in Figure 5), calculating payload entropy per packet, grouping packets into flows, and calculating the final payload entropy per flow. The second phase takes the resulting flow datasets, grouping all flows by service type (i.e., based on TCP or UDP destination port), and calculates the service level baseline entropy features for all datasets.

Sample size is included in the analysis, since some services are more widely represented in the packet distributions than others (for example, in a typical enterprise network packet trace, we would expect to see a high percentage of web traffic and much less SSH traffic [5]).

3.2. Data Sources

As part of this research, detailed analysis was performed to characterise payload entropy values for a range of well-known and registered services averaged across a range of environments, as shown in Figure 4. Raw packet data were sourced from several widely used public sources (described in [5]) as well as recent live capture traces. Raw PCAP files were converted into flow records, with payload entropy reconstructed for common TCP and UDP protocols.

In total, over 54 million packets were sampled. Datasets were selected to avoid sources with known large distortions to ensure that values were statistically consistent across datasets (and where possible, labelled anomalies are excluded). Results were also weighted per service type with respect to sample size, so that the contribution of each packet trace is proportionate (i.e., small dataset samples containing outliers do not distort overall results). Where anomalies were labelled, we excluded these labelled events from the calculations—therefore, the estimates were for known ‘normal’ traffic.

3.3. Flow Information Entropy Calculation Methods

In our implementation we provided measures for characterising mean payload entropy in both flow directions (inbounds and outbound), as part of the feature engineering process. These features have been implemented in the GSYNX analysis suite, which will be made available at [GIT]. Since payload is typically fragmented over multiple packets, entropy may vary during the lifespan of the flow and will be summarised from multiple consecutive samples. For TCP, these content ‘fragments’ may represent encapsulated data and/or other protocol plus data. Our implementation was based on a modified Krichevsky–Trofimov (KT) estimator [27], which estimates the probability of each symbol in a particular symbol alphabet.

• A KT class was implemented as a bi-directional in-memory cache (a hash table of symbol frequencies, of capacity 256 since we are dealing with a byte encoded stream; each symbol is 8 bits wide, corresponding to 0–255) and held symbolic frequency data for the two payloads.
• The flow tuple was used to index the cache. Each flow effectively had a single cache entry, with statistics and state tracked for both flow directions.
• Cache entries were updated when each new packet was encountered. The updates were assigned to the associated flow record in the cache, or a new flow record was created, and those updates were applied.
• Cumulative flow entropy values were recalibrated per packet, per direction, based on the current payload symbol frequencies and the running payload length.
• Once a flow was finalised, the final payload information entropy values were calculated using the total length of the payload against the cumulative symbol frequencies per direction.

Even if a flow is not terminated correctly, a cumulative entropy value is maintained and exported during flow dataset creation. The final entropy value will be in the range of 0 to 8, for reasons described below.

3.4. Applying Shannon’s Entropy to Byte Content

When we apply Shannon’s method (described in Section 1) to text content, we assume that symbols may be encoded in 8 bit bytes. pPacket payload is generally viewed as an unstructured sequence of bytes, and this is a useful way to treat the data generically; for example, plaintext data in payload will often be decoded using the ASCII character set. Unicode text may be encoded in 8, 16, or 32 bit blocks, but again, for the purpose of this work we can use byte sequences since the internal encoding scheme may not be opaque. Since each bit has two possible values (0 or 1), the total number of possible combinations for a byte is 2⁸, or 256. This gives us a range of entropy values between 0 (low) and 8 (high).

• Where only one symbol is repeated, the symbol has a probability of 1, and hence, the formula is resolved to the following:

$$H=-{\log }_2\left(1\right)=0$$

• Where all symbols are used, each symbol has a probability of 1/256, and hence, the formula is resolved to the following:

$$\begin{gathered} H=-\sum _{i=1}^{256}\left({\displaystyle \frac{1}{256}}\right){\log }_2({\displaystyle \frac{1}{256}}) \\ =-256\left({\displaystyle \frac{1}{256}}\right){\log }_2\left({\displaystyle \frac{1}{256}}\right) \\ =-{\log }_2{\displaystyle \frac{1}{256}} \\ =8 \end{gathered}$$

This gives a low to high range of entropy values from 0 to 8, which is the range we applied in our analysis.

3.5. Flow Recovery Methods

Our analysis required the use of specially developed software called GSX [28] to perform flow recovery from large packet traces in pcap (PCAP—LibPCAP format specification available: (https://wiki.wireshark.org/Development/LibpcapFileFormat, 10 December 2024) format. GSX performs advanced flow recovery, including stateful reconstruction of TCP sessions, with additional feature engineering to calculate a broad variety of metrics, including features characterising payload (in this analysis, we focus primarily on TCP and UDP protocols). Payload entropy was calculated in both directions (outbound and inbound, with respect to the packet flow source; outbound meaning that the initiator of the flow is sending data to a remote entity. Here, source can be thought of as the end-point IP address).

Flow collection is also possible in real-time by using common network tools and hardware [29,30], using industry standard and extensible schemas, as provided with network flow standards such as IPFIX [31], and later versions of NetFlow. Depending on available resources, in-flight capture may differ, for example, by employing sampling and sliding window methods [32].

3.6. Implementation Challenges

This section highlights a number of challenges in efficient entropy calculations within the flow recovery process:

Language Sensitivity: Large packet traces may hold millions of packet events (see Figure 5), resulting in hundreds and thousands of flows [5]. Flow recovery is both memory and computationally expensive, and the time to produce an accurate flow dataset with a broad list of useful feature sets (e.g., 100 features) may take hours, depending on the implementation language and efficiency of the design. For example, an interpreted language such as python is likely to be an order of magnitude slower when compared with languages like Go, C, C++, or Rust.

Cache Size: Large packet traces may hold millions of packet events (see Figure 5), resulting in hundreds and thousands of flows [5]. Flow recovery is both memory and computationally expensive and is sensitive to the composition of the packet data and length of the trace. For example, with a short duration trace from a busy internet backbone, there may be tens of thousands of flows that never terminate within the lifetime of the trace—in which case all of these flows will need to be maintained in cache memory until the last packet is processed. Conversely, a longer packet trace from a typical enterprise network may contain many thousands of flows that terminate across the lifetime of the packet trace, and so the cache size will tend to grow to reach a steady state and then gradually shrink.

Entropy Calculation: to avoid multiple processing passes on the entire packet data, flow level information entropy analysis can be implemented within the flow recovery logic. As described earlier, by using the flow tuple as an index to a bidirectional hash table, symbol counts can be updated efficiently on a per packet basis. Each symbol type acts as a unique key to a current counter value. Changes in entropy are, therefore, detectable within the lifespan of the flow, by direction. We include additional measures of entropy variance by flow direction, which can be another useful indicator for major entropy deviations from baselines.

Real-time flow recovery: Flows can be recovered from offline packet datasets and archives. They can also be assembled in real time, using industry standards such as NetFlow [33,34] and IPFIX [31,35,36]. Since our primary interest is in recovering these features from well-known research datasets, we do not implement real-time recovery of payload entropy from live packet captures. Prototyping, however, suggests that using our implementation in a compiled language with controlled memory management (such as Rust or C++) is practical (real-time performance (without packet drop) will depend, to some extent, on how many other features are to be calculated alongside entropy, and the complexity of those calculations). It is also possible to avoid some of the time and memory complexities of flow recovery if we only want to record flow level payload entropy from live packet data by using simpler data structures, although protocol state handling is still required [28].

4. Analysis

In this section, we present our analysis on expected baseline entropy values across a broad range of common network services, together with our findings and some notes on applications.

4.1. Baseline Payload Information Entropy

The results of our analysis are shown in Figure 6. This table shows average entropy values for common network services, together with their overall mean, directional mean, and standard deviations In a small number of cases, only one flow direction is recorded, typically because such protocols are unidirectional or broadcast in nature. Note that the service list has been derived dynamically from the datasets cited in Section 3.2. For further information on specific port allocations and service definitions, see [37].

The table forms a consistent view of the expected ‘ground truth’ across a range of deployment contexts. As might be expected, services that are encrypted (such as SSH) tend to exhibit high entropy (close to 8.0), whereas plaintext services (such as DNS) tend to have low to mid-range entropy values. It is worth noting that entropy values close to zero are unlikely to be observed in real-world network traffic, since this would equate to embedding symbol sequences with very little variety (for example, by sending a block of text containing only repetitions of the symbol ‘x’), and even plaintext messages are likely to have entropy values in the range 3–4. 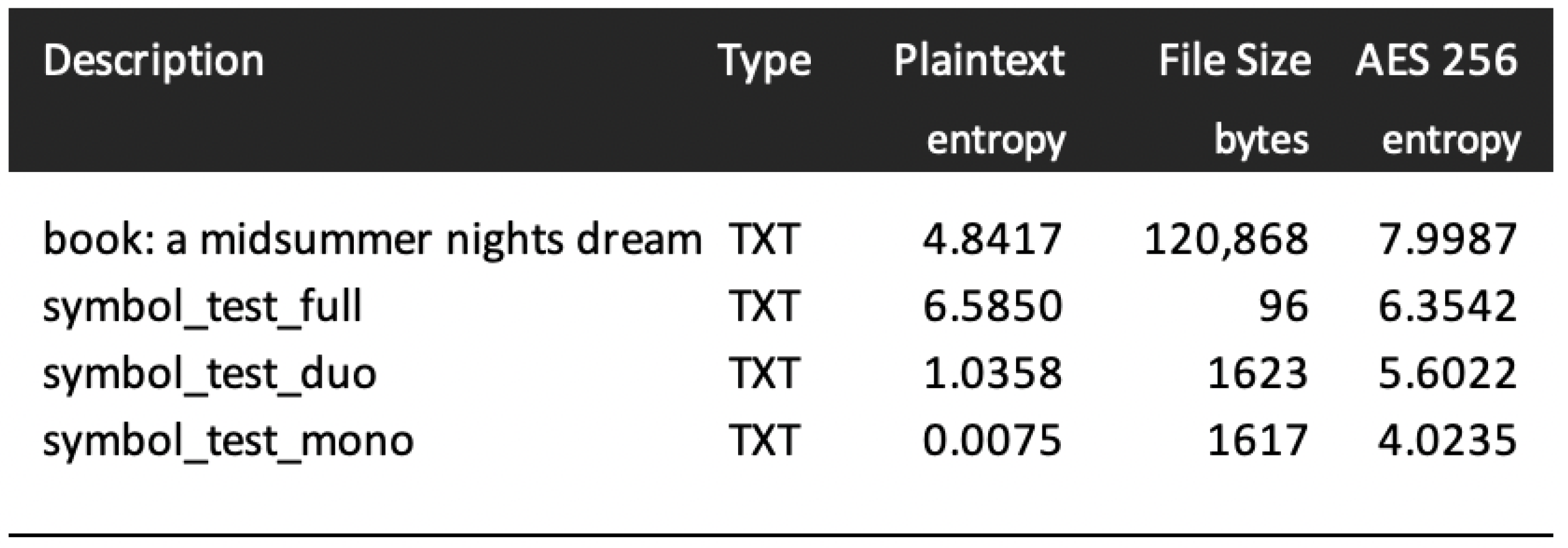This may not be immediately obvious and so in Figure 7, we show how low entropy values (close to zero) might be achieved by severely restricting the symbolic content artificially.

As noted earlier, the sample count indicates the number of packet level observations found in the data, and here we see a wide variation in the distribution frequency across the services represented. For example, web based flows (HTTPS and HTTP) dominate the dataset composition, whereas older protocols such as TFTP are less well represented. While sample size can be used as a rough analogue for confidence in these baseline estimates, we have excluded services that had extremely low representation.

We observed a strong consistency across many of the packet traces; however, it is worth noting that in practice, some services may exhibit deviation in entropy from baselines during normal activities, and this may depend on the context. For example, some services are specifically designed to encapsulate different types of file and media content that could vary markedly in composition and encoding (e.g., compressed video and audio content will tend to exhibit high entropy, whereas uncompressed files may exhibit medium-range entropy).

Also note that peer-to-peer protocols may also be encapsulated within protocols such as HTTP and HTTPS, and this can make it harder to characterise the true underlying properties of the content (without deeper payload inspection) as highlighted in [10]. t is also worth noting that system administrators sometimes change the port allocations to mask service usage or conform to strict firewall rules (this is common practice with protocols such as FTP and OpenVPN). It is, therefore, important to use appropriate domain expertise when performing analysis, with an understanding of the communication context.

Note that the standard deviation metrics are also presented in Figure 6, on a per service, per flow direction basis. For most of the services, we analysed the standard deviation sits typically below 2.0. Higher variance is more likely to be found in services that are used to encapsulate and transport a variety of content types, particularly where a service is normally unencrypted (e.g., web-based protocols such as HTTP, and file transfer protocols such as CIFS). This higher variance is likely to be attributable to the wide variety of content types encapsulated (some of which might be encrypted or compressed at source).

4.2. Interpreting Entropy Variations

Since baseline information entropy values are generally consistent across a range of deployment contexts, a deviation in entropy may be useful to indicate the type of content being transferred, and whether this is normal or anomalous behaviour. For example, if a user is uploading an encrypted file using FTP, we would anticipate a higher entropy value than the expected baseline (around 4.1) for a particular flow. If this transfer were to be an unknown external destination, then this might raise suspicion about the possibility of data exfiltration. Here again, some domain expertise can be valuable, coupled with local knowledge on user behaviour and the type of data being moved (for example, moving encrypted data over a plaintext channel such as FTP to a third party could be suspicious).

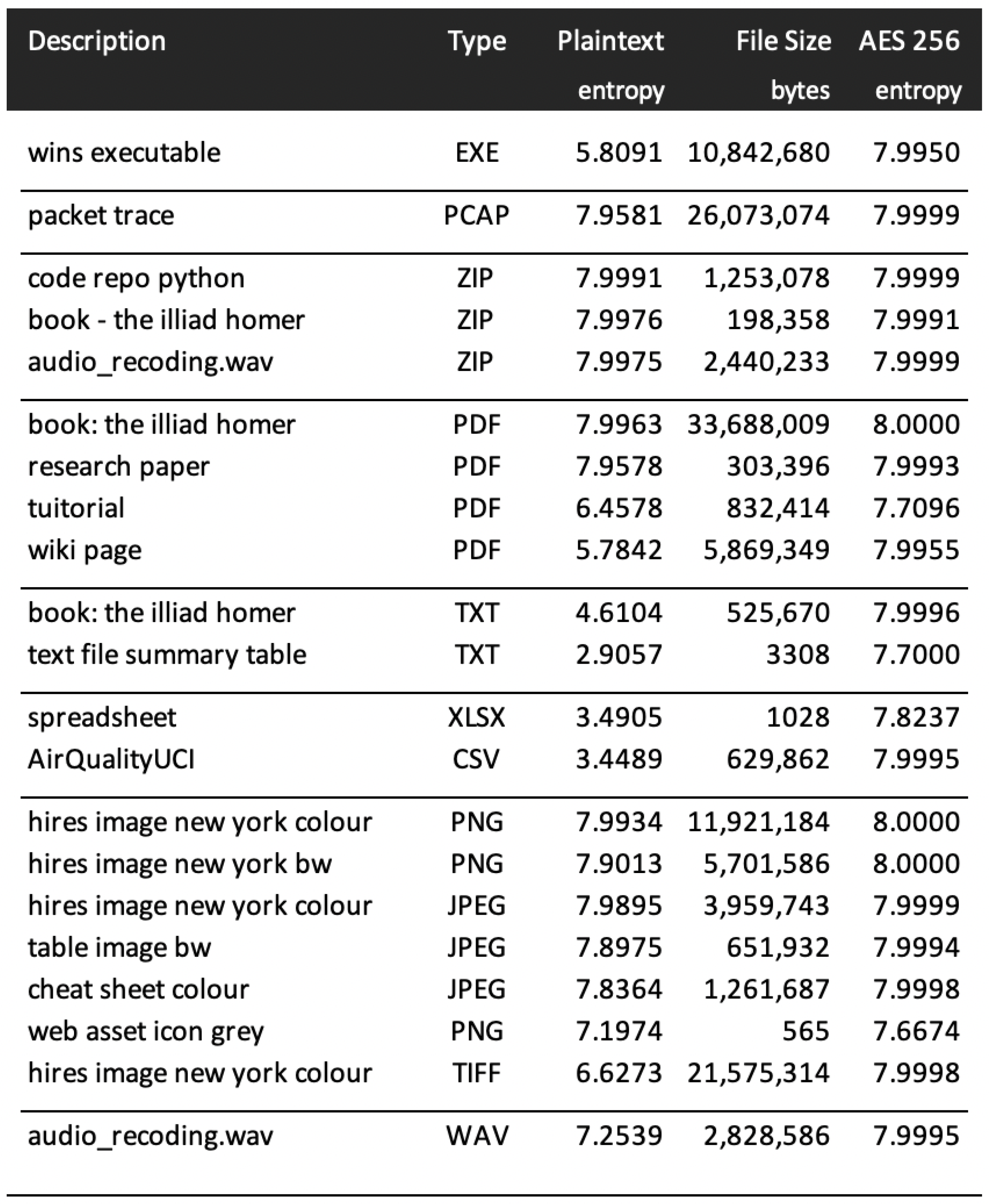
Embedded malware and executable files, often compressed, may also be an indicator of unusual content. For reference, several common types of file content have been analysed and their respected entropy values given in Figure 8, together with their post-encrypted entropies. Note that compressed content (here, we tested ZIP compression, although other comparable compression methods will present similar entropy results. The more efficient the compression method, the higher the entropy) exhibits entropy close to eight, as we might expect, due to symbol repetition compaction. In these tests, AES encryption was used with 256 byte keys, although other key sizes yielded similar entropy results. Domain expertise may be useful in determining whether a flow with very high entropy is likely to be encrypted or compressed—for example, by examining a flow to establish whether entropy is consistent throughout its lifespan.

To illustrate the relationship between entropy and symbolic variety more clearly, Figure 7 illustrates entropy values for three test files, plus an example of a well-known English text. The test files were constructed with increasing levels of symbolic variety, and we can clearly see corresponding changes in entropy. From this, and the examples in Figure 7, we can reasonably infer that typical written messages and content would be expected to have entropy in the mid-range (between three and five).

4.3. Applications

As mentioned earlier, it is possible to detect threats, even with encrypted traffic streams, where entropy deviates significantly from expected ranges, or changes during the lifespan of the session. Where content is being passed over a network, high entropy tends to indicate that data are either encrypted or compressed (in general, encryption tends to produce the highest entropy values compared with compression. Further, naive compression techniques may not achieve high entropy). Knowing this, we can analyse payload entropy dynamically and use this as an indicator for encrypted data streams, potentially identifying covert channels [38,39] and encapsulated malware. For example:

• Where a particular service is expected to encode content as plaintext (such as DNS), the detection of high entropy may indicate the presence of a covert channel, which could be used for data exfiltration.
• Unexpected plaintext on an encrypted channel may indicate a misconfiguration of the SSL/TLS encryption settings, or a security vulnerability in the system. For example, the Heartbleed vulnerability found in OpenSSL in 2014 is triggered when a malicious heartbeat message causes the SSL server to dump plaintext memory contents across the channel [40].
• On an encrypted channel (such as an SSH tunnel or an HTTPS session), after a connection is established (i.e., after key exchange), we would expect the entropy to sit close to eight bits per byte, once encrypted. Shifts in this value might indicate some form of compromise.
• Many legacy protocols still use ASCII encoded plain text encodings. If we detect a higher entropy than expected on a known plaintext channel, this may indicate an encrypted channel is being used to send covert messages or exfiltrate sensitive data (e.g., by using encrypted email, or DNS tunnels [21]).

4.4. Other Potential Uses of Entropy in Anomaly Detection

In the literature, there are studies citing the use of entropy in anomaly detection, and these methods might also be used to characterise and fingerprint a particular infrastructure. For example, entropy can be used to characterise the use of IP addresses, and TCP and UDP Port ranges. This may give valuable insights.

For example, we can use the same technique described in Section 3 to estimate entropy for features such as the following:

• Packet attributes over time;
• IP Addresses and IP Address Pairs;
• Port ID and Port ID Pairs;
• Timing intervals;
• Packet classification;
• Flow composition changes across time.

The entropy of a set number of attributes with packets can be tracked to assess changes in entropy over time, as described in [15].

Address and port number entropy (calculated individually or as flow pairs) may give some insights on whether the allocation process for such values appears to be synthetic (or has bugs in the implementation). Entropy in these identifiers may also be used to draw conclusions about the variety of endpoints and services within a packet trace or live network.

Timing (such as packet intervals) can also be a strong indicator of synthetic behaviour. For example, in a denial of service (DOS) attack or brute force password attack, regular packet intervals may be an indicator that the attack is scripted. Even where some randomness has been introduced by the adversary, it may be possible to infer a higher predictability than expected (for example, where a weak random number generator has been used).

Packets may be classified as encrypted on unencrypted using entropy estimates, for example, as described in [41]. This may be problematic if only the first packet payload is used (as in [41]), since early-stage protocol interactions (such as key exchange) may not reflect subsequent higher entropy values.

As discussed earlier, by measuring entropy deviations across the lifecycle of a flow, by flow direction, we may be able to indicate that a flow has been compromised (for example, during a masquerade attack, or where a particular encryption method has been subverted [6]).

Finally, we should keep in mind that skilled malware authors may attempt and hinder entropy-based detection by building synthetic randomness into malware, although it seems promising that weighted or conditional entropy could be deployed across several features to identify outliers.

5. Conclusions

In this paper, we provided baseline payload information entropy metrics across a broad range of common network services by analysing several widely used datasets in cybersecurity research. To the best of our knowledge, these data have not been published previously—at least not comprehensively. From our analysis, mean information entropy values for packet payload are generally consistent across a range of packet capture environments and illustrate the varying degrees of data protection provided by internet and enterprise services, with subtle differences in inbound and outbound directions. These metrics may be used to approximate ground truth for efficiently characterising encapsulated content, from which it should be feasible to help identify certain types of anomalous behaviour. While payload information entropy alone is insufficient to detect broader classes of suspicious behaviour, it can be useful to help identify unusual network behaviour, particularly when correlated with other features, such as flow direction, source and destination network addresses, destination port, timing, state flags, and complementary volumetric features, such as payload size and transfer rate.

6. Further Work

Since entropy features are rarely published in flow datasets, this represents an interesting area from which to perform additional intrusion and outlier detection research, particularly when combined with other features used to classify cyber threats. In future analyses, we intend to provide additional fine-grained metrics that further characterise entropy variance deviation and timing changes by flow direction and during a flow lifecycle to assist in detecting subtle compromises and man-in-the-middle (MIM) attacks. We also intend to extend the number of datasets analysed.