Abstract
Load balancing between required power demand and the available generation capacity is the main task of demand response for a smart grid. Matching between the objectives of users and utilities is the main gap that should be addressed in the demand response context. In this paper, a multi-user optimal load scheduling is proposed to benefit both utility companies and users. Different objectives are considered to form a multi-objective artificial hummingbird algorithm (MAHA). The cost of energy consumption, peak of load, and user inconvenience are the main objectives considered in this work. A hybrid multi-criteria decision making method is considered to select the dominance solutions. This approach is based on the removal effects of criteria (MERECs) and is utilized for deriving appropriate weights of various criteria. Next, the Vlse Kriterijumska Optimizacija Kompromisno Resenje (VIKOR) method is used to find the best solution of load scheduling from a set of Pareto front solutions produced by MAHA. Multiple pricing schemes are applied in this work, namely the time of use (ToU) and adaptive consumption level pricing scheme (ACLPS), to test the proposed system with regards to different pricing rates. Furthermore, non-cooperative and cooperative users’ working schemes are considered to overcome the issue of making a new peak load time through shifting the user load from the peak to off-peak period to realize minimum energy cost. The results demonstrate 81% cost savings for the proposed method with the cooperative mode while using ACLPS and 40% savings regarding ToU. Furthermore, the peak saving for the same mode of operation provides about 68% and 64% for ACLPs and ToU, respectively. The finding of this work has been validated against other related contributions to examine the significance of the proposed technique. The analyses in this research have concluded that the presented approach has realized a remarkable saving for the peak power intervals and energy cost while maintaining an acceptable range of the customer inconvenience level.
1. Introduction
The development strategies of human life provide a high level of urbanization that requires the inclusion of many new devices and applications [1]. These requirements draw a new energy demand request against the available generation capacity. Adding new generation capacity requires building new generation plants to support the required rising demand. However, building new traditional power generation plants leads to an increase in the greenhouse gasses (GHGs) that cause climate warming [2]. Renewable energy generation is one of the effective solutions for supporting high energy demand. However, high initial cost and intermittent supply are the drawbacks of depending on these sources [3]. Therefore, demand response (DR) is the compromising solution, which manages the available generation to support the required demand without adding new generation plants. DR works to manage the peak time energy demand (which is about 5% from the whole day times) and represents the high level of energy demand during the day. The development is basically relying on two factors, which are demand response pricing schemes and information and communication technologies (ICTs) that are based on the recent internet of things context. Accordingly, this provides the essential incentives to convert the current traditional power grid into a smart grid [4,5]. A smart grid with its effective networks and applications makes the end-users the key factor for managing the load profile (load scheduling (LS)). This in turn lowers the energy bill in reflection of the decrease in the peak load demand. LS helps to defer the flexible user peak load from the peak time with a high price rate to the off-peak time with a lower price rate. However, deferring the peak load to the off-peak leads to generating a new peak time slot that must increase the price rate. Accordingly, load synchronization or load smoothing is applied. In turn, this supports end-user load scheduling without making a new peak load. Therefore, cooperative load scheduling is the key factor of load management that makes many end-users work together to schedule the load for benefiting both users and the utility company by lowering the energy bill and peak load.
The available studies for load scheduling deal with cost and energy saving. However, these studies have the following issues: First, most studies have covered only one user of limited appliances [6,7,8,9,10,11,12]. These approaches may contribute to load and energy saving by using load scheduling but did not consider the load synchronization to prevent the generation of new peak load during load shifting. Second, combing many objectives is mostly converted into a single objective using the aggregated weighted-sum model [6,7,8,9,10,11,13,14,15,16]. Third, multi-criteria decision making has not been widely utilized in sorting the given Pareto front solutions [6,7,8,9,10,11,13,14,15,16,17].
Based on the previous research difficulties, the contributions of this work regarding load scheduling (LS) are listed as follows:
- First is a triple-objective LS, which utilizes dominant rank and is based on the artificial hummingbird algorithm (AHA) to realize end-user inconvenience, peak demand, and optimal cost. The given objectives are combined using multi-objective AHA (MAHA) to produce all sets of solutions with the considered criteria.
- A hybrid multi-criteria decision making technique is considered to select the dominance solutions. This method is based on the removal effect of criteria (MEREC) and used for deriving appropriate weights for various criteria. After that, the VIKOR method is applied to find the best solution of load scheduling among a set of solutions produced by AHA.
- Synchronized multi-user cooperative load scheduling (SMUCLS) is covered to overcome the issue of generating peak time caused by shifting user load away for minimum energy cost.
- ToU and the adaptive consumption level pricing scheme (ACLPS) are applied to validate the proposed system against different price rates.
2. Related Works
The current works on load management can be divided according to the number of considered users.
2.1. Single-User Load Management Systems
Different studies have addressed load scheduling for a single user with only two objectives. A dwarf mongoose optimization (DMO) and hybrid honey badger optimization (HBA) are used in [6] for applying the DR technique. The outcomes of the conducted simulations showed that the presented approach has managed to arrange the appliances according to the best applicable way. In [7], a peak shaving control strategy was proposed to optimally schedule the peak demand. A genetic algorithm is utilized to determine the required optimal inputs regarding the rule-based control method that in turn reduces the peak grid power. The outcomes show a reduction of 42.46%, 49.82%, 40.44%, and 33.1% in peak demand and 19.02%, 20.9%, 4.72%, and 0% in energy consumption, for case studies 1, 2, 3, and 4, respectively. A load shifting-based earth worm optimization algorithm (EWOA) and virulence optimization algorithm (VOA) were used in [8] to optimally change the time slots of shiftable devices. A ToU is considered as a dynamic pricing scheme. The VOA has managed to achieve 59% reduction in PAR of power consumption and is more reliable than other contestants. A residential load scheduling model in [9] is proposed that is based on user preference (UP) and cost efficiency (CE) and is targeted for demand response in a smart grid. The UP has been derived according to the load scheduling framework, whereas the CE is being modeled according to UP. The simulation outcomes have demonstrated a positive correlation between UP and CE. The authors of [10] presented a DR scheduling technique, which covers four residential building loads’ types. These four types are interruptible and deferrable loads, non-interruptible and deferrable loads, non-interruptible and nondeferrable loads, and air conditioning loads. A multi-objective optimization model that depends on nondominated sorting genetic model II is adapted to reduce the energy cost and inconvenience index. By adapting this approach, 25% of nocturnal peak load saving has been realized, while 10% of the daily power cost is minimized.
Other studies consider a single user with more than two objectives. The authors of [11] proposed a DR in a smart grid using the lens-oppositional duck pack algorithm (LODPA). The LODPA is influenced by both conventional DPA and lens-oppositional-based learning (LOBL). This in turn led to a minimization in both the electricity price and peak-to-average ratio (PAR) with maximum user comfort (UC). The analysis has demonstrated that the LODPA scheme shows better performance as compared to other approaches regarding different aspects. The evaluations showed that the LODPA model has accomplished a lower PAR of 2.10.
2.2. Multi-User Load Management Systems
Other contributions have been made regarding the multi-user load management context for only two objectives. In [12], the authors presented a multi-objective problem, which is determined as a mixed integer linear programming (MILP). The objective of this work is to provide an integration between an aggregator and demand response program to minimize the overall electricity cost. This led to enhancing the efficiency and supports an economic structure regarding the smart residential distribution context. The simulation outcomes showed that the peak-to-average ratio (PAR) is minimized from 2.6 to 2.22. The authors of [13] suggested an implicit demand flexibility paradigm regarding residential clients within practically high electricity prices during winter in Norway. The paper developed an econometric technique, which compares pre-crisis levels with demand. This has been achieved through managing some factors that impact electricity consumption. These factors are like outdoor temperature besides using an extensive data set, which maintains an hourly-based electricity demand statistic. The analyses indicate energy saving that reaches 11.4% while the peak hour minimization approaches 10.4%. In [17], the authors proposed a centralized DR scheduling model that utilizes fuzzy clustering in order to determine the heterogeneity of residents’ energy consumption. The proposed demand response scheduling model managed to minimize the energy cost by 10%. This helps to realize a low peaking-to-average ratio and manages to provide a satisfaction level for numerous residents’ power demands.
Other contributions have considered the multi-user concept for more than two objectives. In [14], a load scheduling model regarding a domestic area is presented, which addresses end-users’ preferences. The target of the proposed model is to minimize three objectives: peak load demand, energy cost, and end-user inconvenience. According to those three objectives, both end-users and utility companies will be able to change their reduction priority for one over another. Three multi-objective optimization models in this work have been applied, which are the normalized weighted-sum approach, compromise optimization, and preemptive optimization. The simulation analyses showed an enhanced performance when compared to three related approaches in the literature. A combination between the honey badger algorithm (HBA) and Mexican axolotl optimization (MAO) has been realized in [18]. The proposed hybrid approach is an energy management model that optimizes user energy consumption behavior to reduce each of the following: electricity costs, peak power consumption, and carbon emissions. The results indicate a carbon emissions minimization to 1.8 pounds and realize a minimum cost at 310 cents. In addition, it managed to gain a high load classification accuracy of 98.2%.
The authors of [15] developed a triple-objective load scheduling optimization problem (LSOP) that supports customer inconvenience, peak demand management, and optimal cost. According to the multi-objective context, a Henry gas solubility optimization (HGSO) model is utilized to solve LSOP. Multi-criteria decision making (MCDM) is used to sort the sets of optimal solutions. To compute the weights, an entropy weighting method (EWM) has been adapted and is based on multiple criteria that dominate LSOP. The sorted solutions are ranked depending on the technique for order of preference by similarity to ideal solution (TOPSIS). The provided model acquires an energy cost saving of 5.5%. Additionally, a 9.7% reduction to the peak demand is realized while non-cooperative users have turned into cooperatives.
A combined demand-side operational model has been studied in [16], which addresses five residential houses in South Africa. The study is based on two parts; the first one presents a power management scheme that composes a demand-side management scheme. The second part aims to reduce the client’s cost and minimizes the energy consumption regarding the grid side. The customers can achieve cost savings while the energy demand is minimized. This can be realized through efficiently schedule devices besides including a storage system and a dedicated photovoltaic under a ToU tariff. CO2 emissions and the joint influence of price have been investigated via devising a model in the second part of this work. The power drawn from the distribution part is reduced by 14% while the cost saving is 15.21%.
3. Mathematical Model
The considered objectives of multi-user load scheduling are cost (, user inconvenience (, and peak load (). The total cost of all users is given by the following [15,16]:
where is the index for instantaneous users for up to users, is the time index for the 24 h horizon, and is the indication for the user’s appliance for the overall count of . is the entire consumption of user for a given time slot for all available shiftable user loads of . is the price rate of energy consumption that is given from utility for a given time slot . is the optimal operation status ON/OFF of a given device within time slot for one user . is the time slot considered in the given model (15 min).
The second objective is the user inconvenience that considers the difference (late or advance) for the operation time of a user appliance between base (preferred user time operation) and optimal time operation. The user inconvenience can be expressed as
where and are the status of preferred and optimal user appliances’ operation time, respectively. The values of and are within [0, 1], where 1 indicates ON and 0 indicates OFF. To ensure that the optimal operation time is sufficient to complete their normal operation time, the following equation must be true:
where and are the beginning and ending optimal operation time for a given user appliance a. is the normal operational time for a given user’s appliance .
The third objective function is the peak load of user consumption, which can be given as below:
where is the total consumption of all users for all appliances within a given time slot .
4. Proposed Load Scheduling Model
In this section, the proposed artificial hummingbird algorithm (AHA) that is adapted to solve the load scheduling as a multi-objective optimization problem is presented. Furthermore, the multi-criteria weighting and the multi-criteria decision making models are highlighted in the next subsections.
4.1. Artificial Hummingbird Optimization Algorithm
AHA is represented as one of the bio-inspired optimization algorithms, which mimics the intelligent behavior of a hummingbird. AHA was found by Zhao et al. [19] in 2022 as a global optimization algorithm. The AHA includes three essential components, which are food sources, hummingbirds, and visit tables. The hummingbird chooses a suitable food source by evaluating nectar quality, the last time a source has been visited, and the nectar-refilling rate. In AHA, the food source is represented by an individual (solution) vector, while the nectar-refilling rate is considered by the fitness function of the optimization problem. It is worth mentioning that the highest nectar-refilling rate points to the leading fitness function value. In AHA, the position of a hummingbird and food source are the same because each hummingbird is assigned to a specific food source. The information about the food source of the position, nectar-refilling rate, and visit time are stored in the mind of a hummingbird. Moreover, the information is shared with other hummingbirds in the population. The time period since a hummingbird reached a food source represents the visit level (visit time). The visit level of every food source regarding various hummingbirds is registered into a visit table. The hummingbirds prefer visiting a food source with a high visit level, because it has a high nectar-refilling rate as compared to others. Thus, the visit table is used as a guide for hummingbirds to specify the appropriate food source. In each iteration, the visit levels in the visit table are updated for each food source.
The AHA comprises four main stages, namely, initialization, guided foraging, territorial foraging, and migration foraging. The stages will be discussed in detail in the following section. Figure 1 shows the general flow chart of the AHA algorithm.
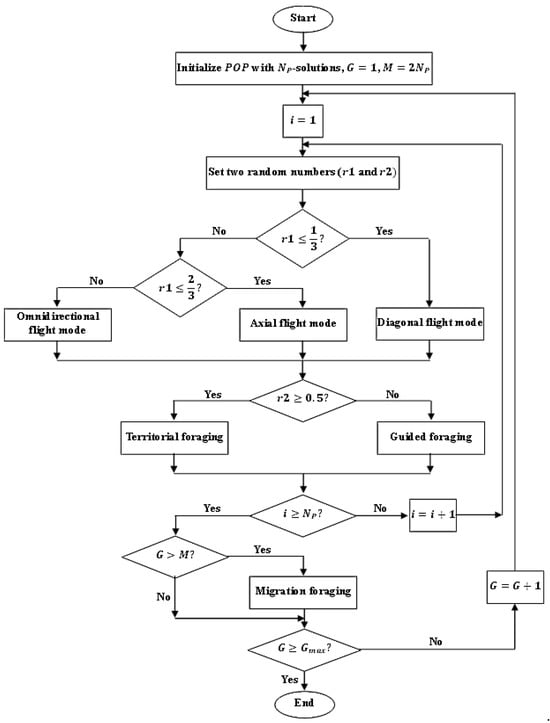
Figure 1.
AHA algorithm flowchart.
Initialization
Similar to other metaheuristic algorithms, the AHA uses the random distribution for initializing solutions of a population () within the search space of decision variables and is as follows [20]:
where is the initial value of decision variable of solution that refers to the food source position. are the lower and upper bounds of search space of decision variable of solution, respectively. is a random number, which is chosen within [0, 1]. In this stage, the visit table that includes the visit level of each food source is initialized by
where refers to the food source that has just been visited by hummingbird for iteration.
Flight modes
The hummingbird can use one of three different flight modes for flying towards the food sources. The flight modes are axial, diagonal, and omnidirectional. In the axial flight mode, the hummingbird flies on one coordinate axis. In the meantime, with the diagonal flight mode, the hummingbird flies on two coordinate axes. On the other hand, in the omnidirectional flight mode, the hummingbird flies in three coordinate axes. The choosing or switching between various flight modes is achieved by a directional switching vector. The axial, diagonal, and omnidirectional flight patterns for space can be presented, respectively, as follows [21]:
where is a random number between [0, 1]. is a function to generate a random integer within the interval [1, ], and is a random integer number belonging to the interval [1, ]. It is worth mentioning that switching among flight modes in a guided foraging or territorial foraging depends on a random number. When the random number () is less than 1/3, the diagonal flight mode is invoked. Meanwhile, the omnidirectional flight mode is invoked when the value of is greater than 2/3. Otherwise, the axial flight mode is used.
Guided foraging
The hummingbird tends to visit the food source that has the highest visit level (long unvisited time) and the highest nectar-refilling rate. When the food source is specified by the hummingbird, the last will fly toward the food source for feeding purposes. Flying towards the food source can be performed via one of the aforementioned three flight skills. After that, the candidate food source for iteration in the guided foraging case is derived based on the flight patterns’ vector and current or target food sources as follows:
where refers to the position of food source for iteration, and presents the position target food source, which the hummingbird needs to visit. refers to a guided factor with normal distribution within the interval (0, 1). is the candidate food source (solution). Thus, the current food source can be updated by using Equation (10). In the AHA model that is based on a single-objective optimization problem, a selection process is achieved between the current and updated food sources by comparing the fitness function ((·)) values of them as follows:
In each iteration, when the guided foraging is invoked to update the position of food source, the visit level of other food sources in the visit table is increased by 1, while the visit level regarding the target food source is set to 0.
In the multi-objective artificial hummingbird algorithm (MAHA) and to conduct the selection process, the dominance rank concept is used instead of Equation (11). In the dominance rank concept, an accumulative population () is created by combining the solutions of the population and the corresponding offspring solutions that were obtained in guided or territorial foraging steps. Thus, the dimension of will be . After initiating , a dominance rank index is calculated for every solution. The dominance rank index of a solution refers to the count of solutions that dominate the required solution besides one. Finally, the with dimensions for the next generation is updated by selecting the compromise solutions from . The compromise solutions are those that have the lowest dominance rank indices.
Territorial foraging
The hummingbird search on a new candidate food source is in the territorial area. The following formula is used for deriving a candidate solution corresponding to solution.
where refers to a territorial factor with a normal distribution within the interval (0, 1). Although the target food source is not used in Equation (12), the visit table is updated after performing the territorial foraging.
Migration foraging
When the hummingbirds frequently visit the same region of food sources, certainly the nectar in the food sources will be little. Therefore, the hummingbirds migrate to other distant food sources looking for nectar. The migration foraging is invoked when the iteration counter () exceeds the predetermined migration coefficient value. In migration foraging and the worst solutions, which have the worst fitness function values, it will be replaced with a randomly produced solution within the search space. The formula in Equation (5) is used in the migration foraging for replacing the worst solutions. It is worth mentioning that the visit level of the worst solutions in the visit table will be updated at the end of the migration foraging process.
Referring to AHA, besides the maximum number of iterations () and the population size () parameters, there is another parameter, which is the migration factor () that is used to execute the migration foraging. The migration factor is chosen to be twice the population size (i.e., ) [22].
In the guided foraging, the exploration is achieved at the early iterations, while in the later stage of iterations, the exploitation is achieved. The territorial foraging is devoted to exploitation, while the exploration is achieved in the migration foraging. The switching factor between the guided foraging and territorial foraging is a random number () between (0, 1). The guided foraging strategy is executed when the value is less than 0.5; otherwise, the territorial foraging strategy is invoked. The pseudo-code of MAHA is presented in Algorithm 1.
The time computational complexity of the proposed MAHA depends on the initialization, the evaluation of fitness functions (), the update of hummingbirds’ position, the population size (), the number of decision variables (), and the maximum number of iterations (). Thus, the overall computational complexity of MAHA can be presented by
| Algorithm 1. Pseudo-code of the proposed MAHA algorithm |
| Input: , , Output: Global minimum solution Initialization: For hummingbird from 1 to Do End For For food source from 1 to , Do If Then Else End If End For While Do For hummingbird from 1 to , Do If Then perform Equation (7) Else If Then perform Equation (7) Else Perform Equation (9) End If If Guided foraging: Then perform Equation (10) Specify If For food source from 1 to , Do End For For food source from 1 to , Do End For Else For food source from 1 to , Do End For End If Else Territorial foraging Perform Equation (12) If For food source from 1 to , Do End For For food source from 1 to , Do End For Else For food source from 1 to , Do End For End If End If End For Dominance rank Initiate 1 × 2 vector () to show the dominance rank value of every solution in . Set the 2 elements of to zero. For = 1 to 2 do For = 1 to (2 − 1) do If solution () is dominated by solution () where, then () = () + 1. End for End for Sort the elements of vector in ascending form. Sort the solutions in based on . Select the first solutions from to form the new population for next generation. Migration foraging If mod () = 0 Then perform Equation (5) For food source from 1 to , Do End For For food source from 1 to , Do End For End If End While |
4.2. MEREC-Weighting Method
In general, for evaluating and ranking a set of solutions that are dominated by a set of criteria and based on the MCDM method, four steps should be followed. These steps are (i) defining the criteria and alternatives of the problem, (ii) constructing the decision matrix that includes the performance of each alternative (solution) in terms of each criterion, (iii) computing the weights of each criterion, and (iv) evaluating and ranking the solutions according to the aggregate performance of them for all criteria [23]. Therefore, the weights of criteria play an essential role in evaluating the solutions within the MCDM problem.
However, there are three types of weighting methods, namely, subjective, objective, and hybrid, between the first and second types. The subjective weighting methods are represented as inefficient when the number of criteria is increased. Due to the preferences among the criteria with it being a mental task, which is achieved by the decision maker, the increasing in criteria leads to inaccuracy preferences among them. In the objective weighting method, the weights of criteria are computed by utilizing a specific computational step and based on the decision matrix. The hybrid weighting methods combine both subjective and objective methods.
The adopting weighting method (MEREC) in this proposed research represents one of the objective weighting methods. The MEREC-weighting method exploits the alternatives’ performance variation within the whole criteria for computing the weights of each criterion. The steps of the proposed MEREC-weighting method are depicted as follows [24].
Step 1: Constructing the decision matrix
The decision matrix () represents the corner stone in the MCDM process. The combines the performance () of alternative in terms of criterion. The dimension of is , where refers to the whole alternative count, and is the total number of criteria as presented below.
Step 2: Normalizing the decision matrix
A simple linear normalization strategy is used for normalizing each element in DM using Equation (15). The normalization process depends on the type of criterion, if it was beneficial or nonbeneficial. However, sets and refer to the beneficial and nonbeneficial criteria, respectively.
Step 3: Calculating the overall performance
In this step, the comprehensive performance of alternatives with equal criteria weights is computed by using a logarithmic measure as follows.
It is worth mentioning that the smaller values give greater values.
Step 4: Computing the overall performance with removing a criterion
Similar to Step 3, a logarithmic function is used for computing the overall performance with removing each criterion separately (). As a result of the current step, is obtained for each alternative considering the removal of criterion by
Step 5: Computing the aggregation of absolute deviations
The effect of canceling criterion () is computed as follows:
Step 6: Calculating the weights
In the last step, the weight of criterion () is calculated via utilizing the next equation.
4.3. VIKOR Method
Different MCDM models have been developed and used earlier in the literature regarding MCDM problems. Between these models is the VIKOR approach, which is derived from the Serbian name of “Vlse Kriterijumska Optimizacija Kompromisno Resenje” that means multi-criteria optimization and compromise solution. The VIKOR method was developed by Serbian citizen Opricovic and Tzeng in 2004 [25] as the MCDM method to solve decision problems dominated by non-commensurable and conflicting criteria. VIKOR is considered as one of the pivotal MCDM methods as it delivers a precise solution while maintaining computational simplicity [25]. It contains a record of the ranked compromised solutions that have been sorted according to the closeness degree of the ideal solution.
For the TOPSIS technique, VIKOR’s idea is based on determining negative and positive ideal solutions. Next, the finite solutions can be sorted according to two metrics: the closeness measure to one of the ideal solutions and afar from negative ideal one based on non-commensurable conflicting criteria. The construction of the decision matrix, which is notated by , is based on the assessment of ith alternative according to jth criterion function (). Dimensions of are , where refers to the number of alternatives and denotes the total number of attributes (criteria). Depending on the closeness measure to the ideal solution, the compromise ranking could be constructed. In MCDM, the compromise solution is considered as a feasible solution where here it is considered as the closest to the ideal solution. The VIKOR model is based on five stages that are illustrated as follows:
Stage 1: Finding best and worst evaluation values of all criteria
The best and the worst evaluation values regarding every criterion will be calculated, where . and values depend on the criterion type. Accordingly, if the criterion is useful (maximization), then and can be addressed as
Meanwhile, if the criterion is nonbeneficial (minimization), the worst and best values are described as follows:
Stage 2: Calculating regret and utility indices
The utility index () is calculated in this stage depending on normalized and weighted Manhattan distances of each alternative in order to find the column vector with dimensions as indicated below:
where is the weight of jth criterion. On the other hand, by relying on the weighted and normalized Chebyshev distance, the regret index is calculated and is represented as follows:
Stage 3: calculating comprehensive indicator
In step 3 of the VIKOR model, regarding the group utility function, there will be a comprehensive indicator that is called and is calculated according to the following formula:
where . is the strategy weight of the majority of attributes or the maximum group utility, where . The compromise ranking is selected with (consensus) or with (Veto) or with (majority group utility). Nevertheless, the value for is used by the majority of researchers in the literature [26].
Stage 4: Ranking alternatives
Three alternative-ranking lists are determined in this stage depending on sorting from minimum to maximum values.
Stage 5: Rank choice acceptance
According to values, all alternatives are sorted in ascending form. After that, the next conditions have to be evaluated to select the compromise solution (or solutions).
Condition 1 (C1): Acceptable advantage
To determine the satisfactory compromise solution, the next correlation is applied:
Here, are the alternatives, which comprise the first and second positions, correspondingly, while the ranking list is dependent on values. Meanwhile, indicates the count of alternatives.
Condition 2 (C2): Acceptable stability
Alternative should be ranked as the best by - and/or -ranked lists in order to guarantee the compromise solution stability regarding the decision making process.
The set of compromise solutions or the compromise solution may be addressed according to the previous conditions, which are listed in Table 1.

Table 1.
Compromise solutions according to list of satisfied conditions.
5. Experimental Results
The energy consumption profile data of customers in [16] are adopted in this work. These data are collected for five typical households; each household has seven appliances. The power rate and the operational time duration for each appliance of a given household are shown in Table 2. The preferred operation time for each appliance of given users (beginning and ending time ( and , respectively) are shown in Table 3. These preferred time operations for each appliance are indicated by the end-user, which is dependent on the preferred usage. For example, a microwave needs 6 min to complete its work during the preferred time of the first customer () from 06:00 to 21:00, while it needs about 8 min for finishing its work during 04:00–18:00 regarding the second user (). Two types of pricing rates are considered. A time of use (ToU) of [16] is utilized to realize a fair comparison, as shown in Table 4. The high price rate is in the peak time during two intervals, the first being 07:00–10:00 and the second being 18:00–20:00. Meanwhile, other time slots are considered as off-peak time with a lower price rate. The second price rate is the adaptive consumption level pricing strategy (ACLPS) that was discussed earlier in [27]. Seeking to separate the effect of high demanding users from maximizing the total pricing rate regarding other clients, ACLPS is set to handle different consumption levels for several time intervals. Accordingly, the consumption of any user will impact only their price rate. The pricing model has an acceptable high social fairness between different engaging users. ACLPS has been modified to be well matched with several time operations (peak, and off-peak) and consumption levels, as indicated in Table 4.

Table 2.
Time intervals and rated consumption power users’ profile [16].

Table 3.
Favorable operational time for users’ appliances [16].

Table 4.
Incentive rate and pricing [16].
In MAHA, the count of devices represents the number of decision variables. The population size (number of solutions) is set to be 30 for all scenarios. Meanwhile, the maximum number of iterations is represented as 100 based on extensive simulation attempts to obtain the optimal solution.
The optimal solutions of the Pareto front, which are produced by applying MAHA for the first and second users regarding both ToU and ACLPS pricing schemes, are tabulated in Appendix A (Table A1). It is worth mentioning that Table A1 includes 30 solutions related to the cost, inconvenience, and peak of power. According to Table A1, the minimum cost, inconvenience, and peak of the first and second users based on the ToU pricing scheme are (R7.618, 45 slots, 4310 W) and (R5.9438, 46 slots, and 2510 W), respectively. Meanwhile, the corresponding values based on the ACLPS pricing scheme are (R 0.6656, 40 slots, 2310 W) and (R 0.5268, 56 slots, and 2510 W). The ACLPS pricing scheme produces better results than ToU in terms of the cost, inconvenience, and peak of power for both the first and second users.
Table A2 illustrates the Pareto front of triple-objective function values for the third and fourth users according to ToU and ACLPS pricing schemes. The MAHA based on the ACLPS pricing scheme produces a minimum cost and peak for the third user, around R 0.7703 and 2510 W, respectively. On the other hand, the MAHA based on the ToU pricing scheme offers R 8.8058 and 2510 W. The minimum cost and peak can be obtained by the MAHA for the fourth user’s data set around R 8.5507 and 2110 W and R 0.5687 and 2110 W for ToU and ACLPS pricing schemes, respectively. According to Table A2, the ACLPS pricing scheme offers an enhancement in the cost and peak of power as compared to the ToU scheme for both the third and fourth users. In contrast, the ToU exhibits a little enhancement with inconvenience values compared to those obtained by the ACLPS pricing scheme for both the third and fourth users’ data set. In general, the ACLPS is still superior to the ToU pricing scheme for the first, second, third, and fourth users.
The optimal solutions produced by using the multi-objective optimization algorithm based on two different pricing schemes for the fifth user and all users combined together are tabulated in Table A3. For the fifth user case, the peak of power based on ACLPS and ToU pricing schemes is the same at 2110 W, while the cost was R 0.4970 and R 6.4792, respectively. Regarding all-users data set cases (cooperation mode), the ACLPS pricing scheme realizes advancement compared to ToU with minimum cost and peak values around R13.4078 and 4620 W, respectively. Furthermore, the ToU pricing scheme offers R 41.6497 and 5220 W for the cost and peak, respectively. The ToU exhibits a little advancement with the inconvenience compared to the ACLPS pricing scheme. According to Table A1, Table A2 and Table A3, MAHA based on the ACLPS pricing scheme converges to the optimal solution faster and candidate the Pareto front, which includes only two different solutions. This indicates that the proposed MAHA based on the ACLPS pricing scheme is a reliable, efficient, and powerful combination for solving load scheduling optimization problems.
After obtaining the optimal Pareto front solutions from the MAHA, the decision matrix of performance data is ready for deriving the appropriate weights by using the MEREC method. The next step is finding the best compromise solution by applying the VIKOR muti-criteria decision making method. As it has been mentioned earlier, the proposed weighting method derives the weights of cost, inconvenience, and peak criteria based on the decision matrix. Thus, the weights are affected by the Pareto front (decision matrix) of the MAHA. Table 5 tabulates the weights for the cost, inconvenience, and peak of power, respectively, for different pricing schemes. In the ACLPS pricing scheme, the cost has the highest weight corresponding to other criteria as highlighted within the third column of Table 5.

Table 5.
The weights of various criteria for different pricing schemes and data sets.
As stated previously, the number of alternatives equals the number of optimal solution sets (), which present as a Pareto front in the objective function space. Table 6 shows the acceptable advantage and acceptable stability conditions regarding the VIKOR model for different data sets of users based on the ToU and ACLPS pricing schemes. Referring to Table 6, the condition of the acceptable advantage has not been realized for various users in the ACLPS pricing scheme. Thus, the compromise solution will be a set of solutions. Meanwhile, the first and second conditions of VIKOR are achieved in the first, fourth, fifth, and all-users cases in the ToU pricing scheme. Therefore, there is one compromise solution that realizes equilibrium among the triple criteria. For the second and third users, the acceptable advantage has not been maintained in the ToU pricing scheme. Consequently, multiple sets of compromise solutions may offer comprising among the inconvenience, cost, and peak of power criteria according to the VIKOR method.

Table 6.
Acceptable advantage and acceptable stability of VIKOR model regarding pricing plans and various users.
Table 7 illustrates the criteria values of the compromise solutions for each user data set regarding both pricing schemes, which were obtained by the VIKOR method. The pairwise comparison of criteria values of ACLPS versus ToU for various users’ data set is tabulated in Table 8. According to Table 8, the ACLPS pricing scheme offers progress relative to ToU with the minimum cost, inconvenience, and peak of power values for the first and all-users data set. The ACLPS pricing scheme offers reduction as compared to the ToU in terms of the cost, inconvenience, and peak around 91%, 11%, and 46% for the first user, respectively. Meanwhile, they are 68%, 10%, and 12% for the all-users data set. In the second and fifth users’ data set, the ACLPS pricing scheme offers an enhancement in terms of cost as compared to the ToU with reduction around 91% and 92%, respectively. The ACLPS and ToU pricing schemes for the second, third, fourth, and fifth users realize the same peak of power values around 2510 W, 2510 W, 2110 W, and 2110 W, respectively. The inconvenience values obtained based on ACLPS for the second and fifth users were greater than those values achieved by the ToU pricing scheme. Finally, as compared to the ToU, the third and fourth users with the ACLPS have realized a cost reduction around 91% and 93%, respectively. Meanwhile, the inconvenience is decreased and increased around 5% and 7.5% for the third and fourth users, respectively.

Table 7.
Compromise solutions for various users’ cases and pricing schemes based on VIKOR method.

Table 8.
Percentage comparison of criteria values of ACLPS versus ToU for different users.
Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 depict different comparisons of load management prior to and after using the MAHA-MEREC-VIKOR to optimize the user load management of ToU and ACLPS regarding different users, with the non-cooperative (individual work) mode as mentioned above. These peak loads of different users’ profile for both ToU and ACLPS demonstrate the superiority of the proposed model as compared to the original or the user preferred operation time. For the first user as mentioned in Figure 2, the peak load for the ToU pricing rate is reduced from 5220 (before scheduling) to 4310 W (after scheduling), which is about 17% reduction. Furthermore, based on ACLPS, more peak reduction is gained and is around 55% (2310 W). For cost saving of the first user, the energy cost before scheduling is about R11.419 while after implementing an optimal scheduling, the cost reduces to R7.612 (about 33%) and R0.665 (about 94%) for ToU and ALCPS, respectively. ACLPS offers high-cost reduction compared to ToU, since ACLPS provides a lower-consumption user profile with higher cost reduction, whereas a high-energy-consumption user receives lower cost reduction. For the second user, the energy consumption is presented in Figure 3; the peak consumption for optimal energy consumption for both ToU and ACLPS is about 2510 W, while before scheduling, it is 4935 W (about 49% reduction). The cost saving of the second user is about 43% (from R10.453 to R5.9438) and 94% (from R10.453 to R 0.5268) for ToU and ACLPS, respectively. The energy consumption for the third, fourth, and fifth users for both pricing schemes are shown in Figure 4, Figure 5 and Figure 6, and the peak energy saving is 43%, 56%, and 38%, respectively. Moreover, the cost saving for the third, fourth, and fifth users based on ToU are 24%, 38%, and 38%, respectively. Based on ACLPS, the cost saving for the same users above are 93%, 95%, and 95%, respectively.
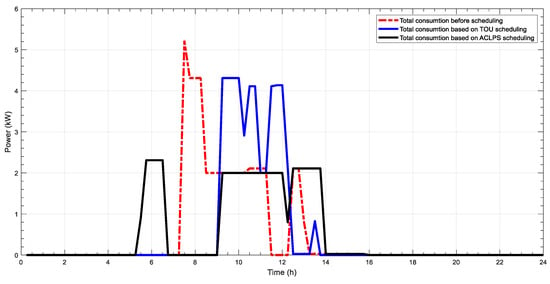
Figure 2.
Power consumption without and with scheduling for ToU and ACLPS for first user.
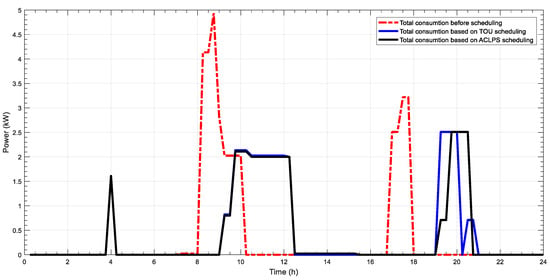
Figure 3.
Power consumption without and with scheduling for ToU and ACLPS for second user.
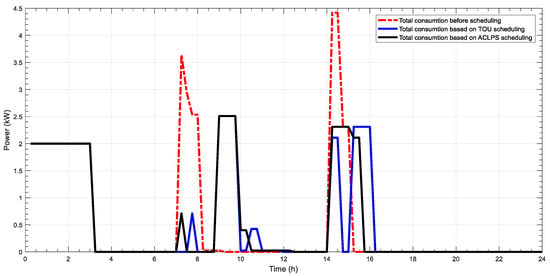
Figure 4.
Power consumption without and with scheduling for ToU and ACLPS for third user.
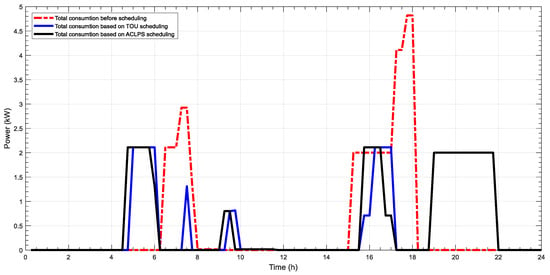
Figure 5.
Power consumption without and with scheduling for ToU and ACLPS for fourth user.
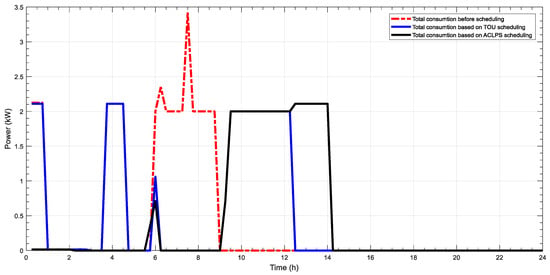
Figure 6.
Power consumption without and with scheduling for ToU and ACLPS for fifth user.
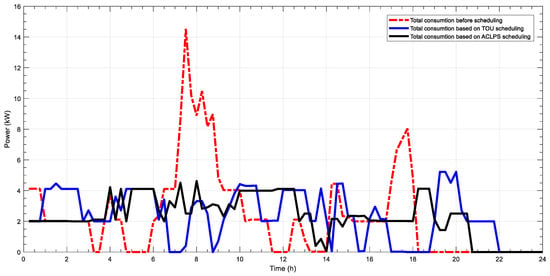
Figure 7.
Power consumption without and with scheduling for ToU and ACLPS for all users.
The synchronized multi-user cooperative load scheduling (SMUCLS) makes all users work together for optimal load scheduling. The results of the five users are presented in Figure 7; the peak consumption based on ToU is reduced from 14,525 to 5220 W for about 64% saving, while the cost saving is 40% (reduced from R70.233 to 41.649). For the ACLPS pricing rate, the peak energy consumption is reduced to 4620 W for around 68% peak saving while the cost saving becomes about 81% (R13.407).
ACLPS based on the proposed scheduling method (MAHA-MEREC-VIKOR) provides superior cost and peak reduction while maintaining the user’s preferences. Accordingly, both the utility company and users get benefited from the proposed scheduling method.
6. Validating the Proposed Load Scheduling Optimization Problem
Seeking to highlight the significance of the proposed scheduling approach, a comparison is formulated with the contribution in [16]. The data of the user energy consumption, pricing rate, and sampling time (15 min) are the same for both works. However, the work in [16] is considered with PV and batteries available for each user. Table 9 shows the comparison results for aggregated users’ peak consumption and energy cost saving. The cost saving based on ToU for [16] is about 15.21% and about 14% for peak saving. Moreover, regarding the developed model and with the same pricing rate, the results are 40% and 64% for cost and peak saving, respectively. Moreover, with the proposed approach, PV and the battery have not been considered, which in turn has provided less cost for users utilizing the proposed model. For the proposed load scheduling, the cost and energy saving based on the ACLPS pricing rate are 81% and 68%, respectively. According to the presented results, the proposed model provides higher energy and cost saving, which benefits both utility companies and users. This is achieved by reducing the required energy consumption for the utility company and through minimizing the cost regarding the user.

Table 9.
Comparison results with [16].
7. Conclusions
Multi-user load scheduling is presented for combining MAHA-MEREC-VIKOR methods to achieve the optimal cost, peak, and user inconvenience simultaneously. The proposed method realizes both cost and peak energy saving for the first, second, third, fourth, and fifth users, which are (33% and 17%), (43% and 49%), (24% and 43%), (38% and 56%), and (38% and 38%), respectively. With aggregated load consumption for all users (five users) based on ToU, the cost and peak savings are 40% and 64%, respectively. Regarding ACLPS, the cost and peak savings for the first, second, third, fourth, and fifth users are (94% and 55%), (94% and 49%), (93% and 43%), (95% and 56%), and (95% and 38%). Regarding all users and based on ACLPs, the cost and peak savings are 81% and 68%, respectively. Moreover, to highlight the significance of the proposed model, the results of the presented method are validated against other techniques published in recent contributions within the literature. According to the validation, the results of the proposed method provided superior cost and peak load saving. The importance of the proposed model was realized by saving the cost of energy for users and reducing the peak load for a utility company with an acceptable level of user inconvenience. Different pricing schemes were considered in this work to clearly present the effect of the price rate on the proposed method. Regarding future directions that are based on the proposed work, the allowance time period of ACLPS can be adaptive according to the user demand rather than constant value. Furthermore, the parameters of MAHA can be dynamically changed based on various objective functions. In addition, adding renewable energy sources to the user side provides more flexibility for demand management during peak periods.
Author Contributions
Conceptualization, H.T.H. and D.H.M.; methodology, H.T.H. and D.H.M.; software, H.T.H. and D.H.M.; validation, H.T.H. and D.H.M.; formal analysis, H.T.H., D.H.M. and Y.A.-N.; investigation, H.T.H. and Y.A.-N.; resources, G.G.S. and D.H.M.; data curation, H.T.H.; writing—original draft preparation, H.T.H. and D.H.M.; writing—review and editing, D.H.M. and Y.A.-N.; visualization, H.T.H. and G.G.S.; supervision, H.T.H. and D.H.M.; project administration, H.T.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank Mustansiriyah University (www.uomustansiriyah.edu.iq, accessed on 1 September 2024), Baghdad, Iraq, for its support in the present work.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Optimal solutions of 1st and 2nd users based on ToU and ACLPS pricing schemes.
Table A1.
Optimal solutions of 1st and 2nd users based on ToU and ACLPS pricing schemes.
| 1st User | 2nd User | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ToU | ACLPS | ToU | ACLPS | ||||||||
| Cost | I | Peak | Cost | I | Peak | Cost | I | Peak | Cost | I | Peak |
| 9.4450 | 63 | 6420 | 3.0310 | 62 | 5045 | 5.9438 | 54 | 2510 | 0.9720 | 31 | 3220 |
| 7.6185 | 45 | 4310 | 0.6656 | 40 | 2310 | 5.9438 | 49 | 2510 | 0.5268 | 56 | 2510 |
| 14.2658 | 44 | 4110 | 0.6656 | 40 | 2310 | 5.9438 | 54 | 2510 | 0.5268 | 56 | 2510 |
| 9.7235 | 50 | 4110 | 0.6656 | 40 | 2310 | 6.4827 | 85 | 4110 | 0.5268 | 56 | 2510 |
| 10.7026 | 85 | 4110 | 0.6656 | 40 | 2310 | 6.9498 | 84 | 2510 | 0.5268 | 56 | 2510 |
| 7.6185 | 95 | 4310 | 0.6656 | 40 | 2310 | 5.9438 | 92 | 2510 | 0.5268 | 56 | 2510 |
| 7.6485 | 95 | 6420 | 0.6656 | 40 | 2310 | 5.9438 | 56 | 3220 | 0.5268 | 56 | 2510 |
| 9.4151 | 76 | 6420 | 0.6656 | 40 | 2310 | 5.9438 | 96 | 2510 | 0.5268 | 56 | 2510 |
| 10.3927 | 50 | 4110 | 0.6656 | 40 | 2310 | 6.8480 | 108 | 2510 | 0.5268 | 56 | 2510 |
| 9.3118 | 65 | 4110 | 0.6656 | 40 | 2310 | 6.3689 | 93 | 3610 | 0.5268 | 56 | 2510 |
| 10.3852 | 68 | 4110 | 0.6656 | 40 | 2310 | 5.9438 | 84 | 2510 | 0.5268 | 56 | 2510 |
| 7.8910 | 87 | 4110 | 0.6656 | 40 | 2310 | 5.9438 | 71 | 2510 | 0.5268 | 56 | 2510 |
| 15.1760 | 83 | 2310 | 0.6656 | 40 | 2310 | 9.1626 | 52 | 2510 | 0.5268 | 56 | 2510 |
| 10.3852 | 57 | 4110 | 0.6656 | 40 | 2310 | 6.9648 | 87 | 2535 | 0.5268 | 56 | 2510 |
| 7.8910 | 89 | 4110 | 0.6656 | 40 | 2310 | 5.9438 | 53 | 2510 | 0.5268 | 56 | 2510 |
| 7.6185 | 63 | 4420 | 0.6656 | 40 | 2310 | 5.9438 | 53 | 2510 | 0.5268 | 56 | 2510 |
| 9.3193 | 56 | 4110 | 0.6656 | 40 | 2310 | 5.9438 | 52 | 2510 | 0.5268 | 56 | 2510 |
| 14.8047 | 96 | 2335 | 0.6656 | 40 | 2310 | 5.9438 | 53 | 2510 | 0.5268 | 56 | 2510 |
| 9.4151 | 89 | 4110 | 0.6656 | 40 | 2310 | 10.8453 | 36 | 2825 | 0.5268 | 56 | 2510 |
| 7.6185 | 52 | 4310 | 0.6656 | 40 | 2310 | 6.9648 | 90 | 2535 | 0.5268 | 56 | 2510 |
| 14.2059 | 61 | 3020 | 0.6656 | 40 | 2310 | 5.9438 | 106 | 2510 | 0.5268 | 56 | 2510 |
| 7.6185 | 56 | 4310 | 0.6656 | 40 | 2310 | 5.9438 | 47 | 2510 | 0.5268 | 56 | 2510 |
| 8.2174 | 76 | 4310 | 0.6656 | 40 | 2310 | 5.9438 | 49 | 2510 | 0.5268 | 56 | 2510 |
| 7.6634 | 78 | 4310 | 0.6656 | 40 | 2310 | 5.9438 | 50 | 2510 | 0.5268 | 56 | 2510 |
| 7.6185 | 63 | 4445 | 0.6656 | 40 | 2310 | 5.9438 | 97 | 2510 | 0.5268 | 56 | 2510 |
| 7.6634 | 92 | 4310 | 0.6656 | 40 | 2310 | 5.9438 | 50 | 2510 | 0.5268 | 56 | 2510 |
| 7.6185 | 62 | 4445 | 0.6656 | 40 | 2310 | 5.9438 | 50 | 2510 | 0.5268 | 56 | 2510 |
| 7.6185 | 70 | 4310 | 0.6656 | 40 | 2310 | 5.9438 | 49 | 2510 | 0.5268 | 56 | 2510 |
| 13.6070 | 113 | 2910 | 0.6656 | 40 | 2310 | 5.9438 | 50 | 2510 | 0.5268 | 56 | 2510 |
| 15.3632 | 55 | 4310 | 0.6656 | 40 | 2310 | 5.9438 | 46 | 2510 | 0.5268 | 56 | 2510 |

Table A2.
Optimal solutions of 3rd and 4th users based on ToU and ACLPS pricing schemes.
Table A2.
Optimal solutions of 3rd and 4th users based on ToU and ACLPS pricing schemes.
| 3rd User | 4th User | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ToU | ACLPS | ToU | ACLPS | ||||||||
| Cost | I | Peak | Cost | I | Peak | Cost | I | Peak | Cost | I | Peak |
| 8.5932 | 52 | 3220 | 1.4845 | 61 | 4420 | 8.1674 | 96 | 3420 | 1.6840 | 55 | 4110 |
| 11.0604 | 36 | 4420 | 0.7703 | 35 | 2510 | 8.5507 | 53 | 2110 | 0.5687 | 57 | 2110 |
| 8.7354 | 36 | 4420 | 0.7703 | 35 | 2510 | 8.1584 | 75 | 2710 | 0.5687 | 57 | 2110 |
| 8.5932 | 53 | 4420 | 0.7703 | 35 | 2510 | 9.4220 | 76 | 4110 | 0.5687 | 57 | 2110 |
| 10.8478 | 45 | 2510 | 0.7703 | 35 | 2510 | 8.1584 | 77 | 2710 | 0.5687 | 57 | 2110 |
| 8.5932 | 47 | 4420 | 0.7703 | 35 | 2510 | 8.1584 | 72 | 3420 | 0.5687 | 57 | 2110 |
| 9.3447 | 40 | 3245 | 0.7703 | 35 | 2510 | 8.1584 | 85 | 4820 | 0.5687 | 57 | 2110 |
| 8.8058 | 37 | 2510 | 0.7703 | 35 | 2510 | 8.1584 | 72 | 3420 | 0.5687 | 57 | 2110 |
| 9.5573 | 31 | 4420 | 0.7703 | 35 | 2510 | 8.1584 | 70 | 2820 | 0.5687 | 57 | 2110 |
| 8.8058 | 39 | 2510 | 0.7703 | 35 | 2510 | 8.5836 | 60 | 2110 | 0.5687 | 57 | 2110 |
| 10.8478 | 45 | 2510 | 0.7703 | 35 | 2510 | 12.8085 | 59 | 3420 | 0.5687 | 57 | 2110 |
| 8.5932 | 48 | 3220 | 0.7703 | 35 | 2510 | 8.3710 | 74 | 3420 | 0.5687 | 57 | 2110 |
| 8.5932 | 47 | 4420 | 0.7703 | 35 | 2510 | 10.8383 | 70 | 2110 | 0.5687 | 57 | 2110 |
| 8.8058 | 37 | 2510 | 0.7703 | 35 | 2510 | 8.1584 | 52 | 3420 | 0.5687 | 57 | 2110 |
| 8.5932 | 47 | 4420 | 0.7703 | 35 | 2510 | 8.5507 | 59 | 2110 | 0.5687 | 57 | 2110 |
| 10.8478 | 77 | 2510 | 0.7703 | 35 | 2510 | 9.8142 | 67 | 2110 | 0.5687 | 57 | 2110 |
| 10.3089 | 31 | 4420 | 0.7703 | 35 | 2510 | 8.7722 | 54 | 2710 | 0.5687 | 57 | 2110 |
| 8.5932 | 57 | 3220 | 0.7703 | 35 | 2510 | 8.7677 | 55 | 2710 | 0.5687 | 57 | 2110 |
| 8.5932 | 50 | 3220 | 0.7703 | 35 | 2510 | 8.7677 | 55 | 2710 | 0.5687 | 57 | 2110 |
| 8.8058 | 37 | 2510 | 0.7703 | 35 | 2510 | 9.2363 | 63 | 4110 | 0.5687 | 57 | 2110 |
| 9.3447 | 56 | 3220 | 0.7703 | 35 | 2510 | 8.1584 | 63 | 3420 | 0.5687 | 57 | 2110 |
| 8.8058 | 37 | 2510 | 0.7703 | 35 | 2510 | 8.7902 | 72 | 2710 | 0.5687 | 57 | 2110 |
| 9.3447 | 56 | 3220 | 0.7703 | 35 | 2510 | 8.6061 | 61 | 2710 | 0.5687 | 57 | 2110 |
| 8.8058 | 44 | 2510 | 0.7703 | 35 | 2510 | 8.5507 | 70 | 2710 | 0.5687 | 57 | 2110 |
| 8.8058 | 47 | 2510 | 0.7703 | 35 | 2510 | 11.0164 | 47 | 2710 | 0.5687 | 57 | 2110 |
| 8.7354 | 35 | 4420 | 0.7703 | 35 | 2510 | 9.4220 | 74 | 2110 | 0.5687 | 57 | 2110 |
| 8.8058 | 38 | 2510 | 0.7703 | 35 | 2510 | 9.6106 | 86 | 2110 | 0.5687 | 57 | 2110 |
| 8.8058 | 38 | 2510 | 0.7703 | 35 | 2510 | 8.1719 | 55 | 3420 | 0.5687 | 57 | 2110 |
| 8.8058 | 39 | 2510 | 0.7703 | 35 | 2510 | 9.4220 | 66 | 2710 | 0.5687 | 57 | 2110 |
| 8.8058 | 39 | 2510 | 0.7703 | 35 | 2510 | 8.1629 | 68 | 3420 | 0.5687 | 57 | 2110 |

Table A3.
The optimal solutions obtained by the MAHA by using ToU and ACLPS pricing schemes for the 5th and all users.
Table A3.
The optimal solutions obtained by the MAHA by using ToU and ACLPS pricing schemes for the 5th and all users.
| 5th User | All Users | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ToU | ACLPS | ToU | ACLPS | ||||||||
| Cost | I | P | Cost | I | P | Cost | I | P | Cost | I | P |
| 6.5974 | 111 | 2710 | 2.5094 | 164 | 4125 | 41.4820 | 368 | 6950 | 62.2565 | 359 | 9530 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.9267 | 365 | 6150 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 44.4344 | 304 | 6175 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.9267 | 353 | 6150 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 43.1513 | 466 | 6110 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.6422 | 389 | 6535 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 43.5166 | 396 | 6125 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.9267 | 372 | 6150 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 40.3876 | 393 | 7355 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 40.3876 | 393 | 7355 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.0524 | 432 | 6135 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.9177 | 421 | 8445 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 40.3876 | 395 | 7355 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.5150 | 369 | 6435 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 40.6107 | 391 | 6530 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.0524 | 425 | 6310 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.7755 | 386 | 6820 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.2919 | 394 | 6620 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.6497 | 358 | 5220 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 45.1200 | 420 | 6620 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 42.7127 | 367 | 6150 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 51.1385 | 324 | 8445 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.7755 | 385 | 6820 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 40.9550 | 393 | 6175 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.7755 | 387 | 6820 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.7755 | 386 | 6820 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 40.8502 | 361 | 6175 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 40.8502 | 371 | 6555 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 40.5778 | 374 | 6555 | 13.4078 | 321 | 4620 |
| 6.4792 | 31 | 2110 | 0.4970 | 116 | 2110 | 41.4820 | 369 | 6950 | 13.4078 | 321 | 4620 |
References
- Zheng, Z.; Shafique, M.; Luo, X.; Wang, S. A systematic review towards integrative energy management of smart grids and urban energy systems. Renew. Sustain. Energy Rev. 2024, 89, 114023. [Google Scholar] [CrossRef]
- Hui, H.; Ding, Y.; Shi, Q.; Li, F.; Song, Y.; Yan, J. 5G network-based Internet of Things for demand response in smart grid: A survey on application potential. Appl. Energy 2020, 257, 113972. [Google Scholar] [CrossRef]
- Alamir, N.; Kamel, S.; Megahed, T.F.; Hori, M.; Abdelkader, S.M. Developing Hybrid Demand Response Technique for Energy Management in Microgrid Based on Pelican Optimization Algorithm. Electr. Power Syst. Res. 2023, 214, 108905. [Google Scholar] [CrossRef]
- Shreenidhi, H.S.; Ramaiah, N.S. A two-stage deep convolutional model for demand response energy management system in IoT-enabled smart grid. Sustain. Energy Grids Netw. 2022, 30, 100630. [Google Scholar] [CrossRef]
- Rong, J.; Liu, W.; Jiang, F.; Cheng, Y.; Li, H.; Peng, J. Privacy-aware optimal load scheduling for energy management system of smart home. Sustain. Energy Grids Netw. 2023, 34, 101039. [Google Scholar] [CrossRef]
- Balavignesh, S.; Kumar, C.; Ueda, S.; Senjyu, T. Optimization-based optimal energy management system for smart home in smart grid. Energy Rep. 2023, 10, 3733–3756. [Google Scholar] [CrossRef]
- Hossain, J.; Saeed, N.; Manojkumar, R.; Marzband, M.; Sedraoui, K.; Al-Turki, Y. Optimal peak-shaving for dynamic demand response in smart Malaysian commercial buildings utilizing an efficient PV-BES system. Sustain. Cities Soc. 2024, 101, 105107. [Google Scholar] [CrossRef]
- Jasim, A.M.; Jasim, B.H.; Flah, A.; Bolshev, V.; Mihet-Popa, L. A new optimized demand management system for smart grid-based residential buildings adopting renewable and storage energies. Energy Rep. 2023, 9, 4018–4035. [Google Scholar] [CrossRef]
- Alghtani, A.H.; Tirth, V.; Algahtani, A. Lens-oppositional duck pack algorithm based smart home energy management system for demand response in smart grids. Sustain. Energy Technol. Assess. 2023, 56, 103112. [Google Scholar] [CrossRef]
- Jiang, X.; Wu, L. A Residential Load Scheduling Based on Cost Efficiency and Consumer’s Preference for Demand Response in Smart Grid. Electr. Power Syst. Res. 2020, 186, 106410. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Y.; He, R.; Liu, J.; Gao, M.; Zhang, L. Multi-objective residential load scheduling approach for demand response in smart grid. Sustain. Cities Soc. 2022, 76, 103530. [Google Scholar] [CrossRef]
- Muhsen, D.H.; Haider, H.T.; Al-Nidawi, Y.; Shayea, G.G. Operational Scheduling of Household Appliances by Using Triple-Objective Optimization Algorithm Integrated with Multi-Criteria Decision Making. Sustainability 2023, 15, 16589. [Google Scholar] [CrossRef]
- Jadhav, P.; More, D.; Salkuti, S.R. Smart residential distribution energy management system with integration of demand response and Aggregator. Clean. Responsible Consum. 2023, 9, 100115. [Google Scholar] [CrossRef]
- Fan, X.M.; Li, X.H.; Ding, Y.M.; He, J.; Zhao, M. Demand response scheduling algorithm for smart residential communities considering heterogeneous energy consumption. Energy Build. 2023, 279, 112691. [Google Scholar] [CrossRef]
- Yahia, Z.; Pradhan, A. Multi-objective optimization of household appliance scheduling problem considering consumer preference and peak load reduction. Sustain. Cities Soc. 2020, 55, 102058. [Google Scholar] [CrossRef]
- Setlhaolo, D.; Xia, X. Combined residential demand side management strategies with coordination and economic analysis. Int. J. Electr. Power Energy Syst. 2016, 79, 150–160. [Google Scholar] [CrossRef]
- Revathi, R.; Senthilnathan, N. Hybrid optimization approach for power scheduling with PV-battery system in smart grids. Energy 2024, 290, 130051. [Google Scholar] [CrossRef]
- Hofmann, M.; Lindberg, K.B. Residential demand response and dynamic electricity contracts with hourly prices: A study of Norwegian households during the 2021/22 energy crisis. Smart Energy 2024, 13, 100126. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Mirjalili, S. Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications. Comput. Methods Appl. Mech. Eng. 2022, 388, 114194. [Google Scholar] [CrossRef]
- Hamida, M.A.; El-Sehiemy, R.A.; Ginidi, A.R.; Elattar, E.; Shaheen, A.M. Parameter identification and state of charge estimation of Li-Ion batteries used in electric vehicles using artificial hummingbird optimizer. J. Energy Storage 2022, 51, 104535. [Google Scholar] [CrossRef]
- Fathy, A. A novel artificial hummingbird algorithm for integrating renewable based biomass distributed generators in radial distribution systems. Appl. Energy 2022, 323, 119605. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Hu, G.; Yang, M.S. An enhanced artificial hummingbird algorithm and its application in truss topology engineering optimization. Adv. Eng. Inform. 2022, 54, 101761. [Google Scholar] [CrossRef]
- Alfares, H.K.; Duffuaa, S.O. Simulation-Based Evaluation of Criteria Rank-Weighting Methods in Multi-Criteria Decision-Making. Int. J. Inf. Technol. Decis. Mak. 2015, 15, 43–61. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Determination of objective weights using a new method based on the removal effects of criteria (MEREC). Symmetry 2021, 13, 525. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Cristóbal, J.R.S. Multi-criteria decision-making in the selection of a renewable energy project in spain: The VIKOR method. Renew. Energy 2011, 36, 498–502. [Google Scholar] [CrossRef]
- Haider, H.T.; See, O.H.; Elmenreich, W. Residential demand response scheme based on adaptive consumption level pricing. Energy 2016, 113, 301–308. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).