EBBA: An Enhanced Binary Bat Algorithm Integrated with Chaos Theory and Lévy Flight for Feature Selection

Abstract

Feature selection can efficiently improve classification accuracy and reduce the dimension of datasets. However, feature selection is a challenging and complex task that requires a high-performance optimization algorithm. In this paper, we propose an enhanced binary bat algorithm (EBBA) which is originated from the conventional binary bat algorithm (BBA) as the learning algorithm in a wrapper-based feature selection model. First, we model the feature selection problem and then transfer it as a fitness function. Then, we propose an EBBA for solving the feature selection problem. In EBBA, we introduce the Lévy flight-based global search method, population diversity boosting method and chaos-based loudness method to improve the BA and make it more applicable to feature selection problems. Finally, the simulations are conducted to evaluate the proposed EBBA and the simulation results demonstrate that the proposed EBBA outmatches other comparison benchmarks. Moreover, we also illustrate the effectiveness of the proposed improved factors by tests.

1. Introduction

Communication networks, computers, and artificial intelligence technologies provide a vast array of tools and techniques to improve efficiency. With the development of these technologies and tools, huge amounts of data are generated, stored, and utilized [1]. For example, a large number of IoT devices monitor, sense, and generate continuous data from the edge [2]. In addition, operators retain large amounts of historical user data in various transaction and computing platforms. Then again, the generation of rich media data such as short videos and motion pictures also makes the amount of data in the network grow exponentially [3]. Machine learning can effectively use these data and learn rules and patterns from them to help people make predictions and decisions. Machine learning algorithms have been successfully applied to various fields of life, such as medicine, materials science, and physics. Specifically, machine learning algorithms can extract features from various types of data and use the features to train models for classification, regression, and clustering operations [4].

Despite the advantages of the mentioned machine learning algorithms in terms of effectiveness, wide application, and malleability, there are still some challenges and urgent issues that machine learning algorithms need to address. First, the training of machine learning algorithms is a time-consuming, computationally intensive, and energy-intensive process, which can lead to limited applications of machine learning algorithms [5]. Second, the training datasets of machine learning algorithms are derived from the features they extract, which are mostly extracted using automated tools and human experience, and have many repetitive, meaningless, or even misleading features [6]. These features can slow down the training process of machine learning algorithms even more and reduce the effectiveness of classification, clustering, and regression of machine learning algorithms. Therefore, the elimination of these useless and redundant features is important to improve the performance of machine learning algorithms and reduce their training consumption.

Feature selection is an effective means to solve the above problem. Feature selection can eliminate useless and redundant features in the dataset, thus reducing the number of features and improving the classification accuracy of machine learning algorithms. For a dataset with N features, there are $2^N$ feature selection schemes available, producing a combinatorial explosion. Therefore, selecting a subset of features with high classification accuracy and a low number of features can be regarded as an optimization problem. On the other hand, the feature selection problem is also proved to be an NP-hard problem. It is important to select and propose a suitable algorithm to solve the feature selection problem.

In general, feature selection methods can be classified into three categories, namely filter-based methods, wrapper-based methods, and embedded methods. Specifically, filter-based methods use a statistical measure that gives a score to the relevance of each feature in the dataset, by which the importance of the feature can be quantified. Subsequently, the decision-maker can set a threshold to remove features with scores below the threshold, thus achieving a reduction in the number of features. However, such methods do not consider the complementarity and mutual exclusivity among features, and therefore the classification accuracy obtained by the subset of features selected by such methods is low [7]. Embedded-based methods are a special kind of wrapper-based method, so they are not discussed in this paper. The wrapper-based methods introduce classifiers and learning algorithms. The learning algorithm continuously generates new feature subsets, while the classifier evaluates the generated feature subsets and selects the optimal one in continuous iterations [8]. In this type of method, the classification accuracy of feature selection is high but consumes more time due to the introduction of classifiers. On the other hand, this type of method has a great relationship with the performance of the learning algorithm.

Akin to some previous works [7,8,9], we aim to adopt the swarm intelligence algorithm as the learning algorithm in the wrapper-based feature selection method. Specifically, a swarm intelligence algorithm studies the complex behaviors of a swarm consisting of several simple agents. By iteratively updating the swarm, the agents will have a more powerful performance than before, so that the algorithm can provide a sub-optimal solution. Swarm intelligence has the benefits of high convergence and powerful solving ability. Moreover, swarm intelligence can also handle NP-hard problems such as feature selection. Thus, it can be seen as an effective method to overcome the challenges of feature selection. For instance, some well-known swarm intelligence, i.e., genetic algorithm (GA) [10], particle swarm optimization (PSO) [11], dragonfly algorithm (DA) [12], ant-lion optimizer (ALO) [13], and grey wolf optimizer (GWO) [14] has been applied in feature selection.

Bat algorithm (BA) and binary BA (BBA) are promising forms of swarm intelligence and have been demonstrated to be better than other algorithms in some applications due to their effectiveness and high performance. However, as suggested in no-free lunch (NFL) theory, there are no algorithms that can suitably solve all optimization problems. In addition, BA also has some shortcomings in solving feature selection problems. Thus, we aim to enhance the performance of BA for solving feature selection. The contributions of this work are summarized as follows:

• We show that the feature selection is a multi-objective optimization problem, and we present the decision variables and the optimization goals of the feature selection problem.
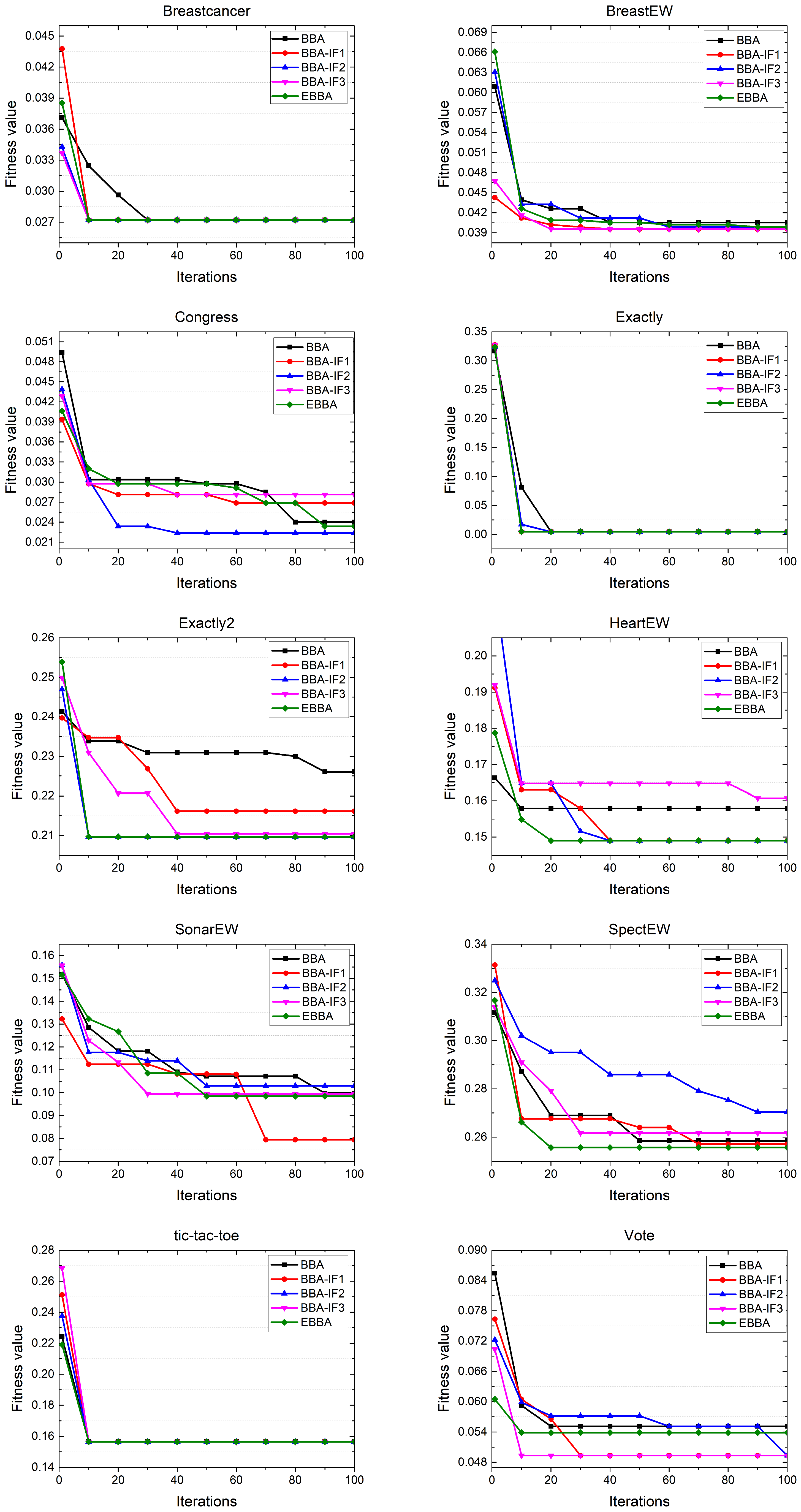
• We propose an enhanced binary BA (EBBA) for solving the feature selection problem. In EBBA, we propose Lévy flight-based global search method, which enables the algorithm to jump out of the local optimum. Moreover, we propose a population diversity boosting method so that the exploration capability of the algorithm can be further enhanced. In addition, we use a recently proposed chaotic mapping to assign values to the key parameter of the algorithm, thus enhancing the exploitation capability of the algorithm.
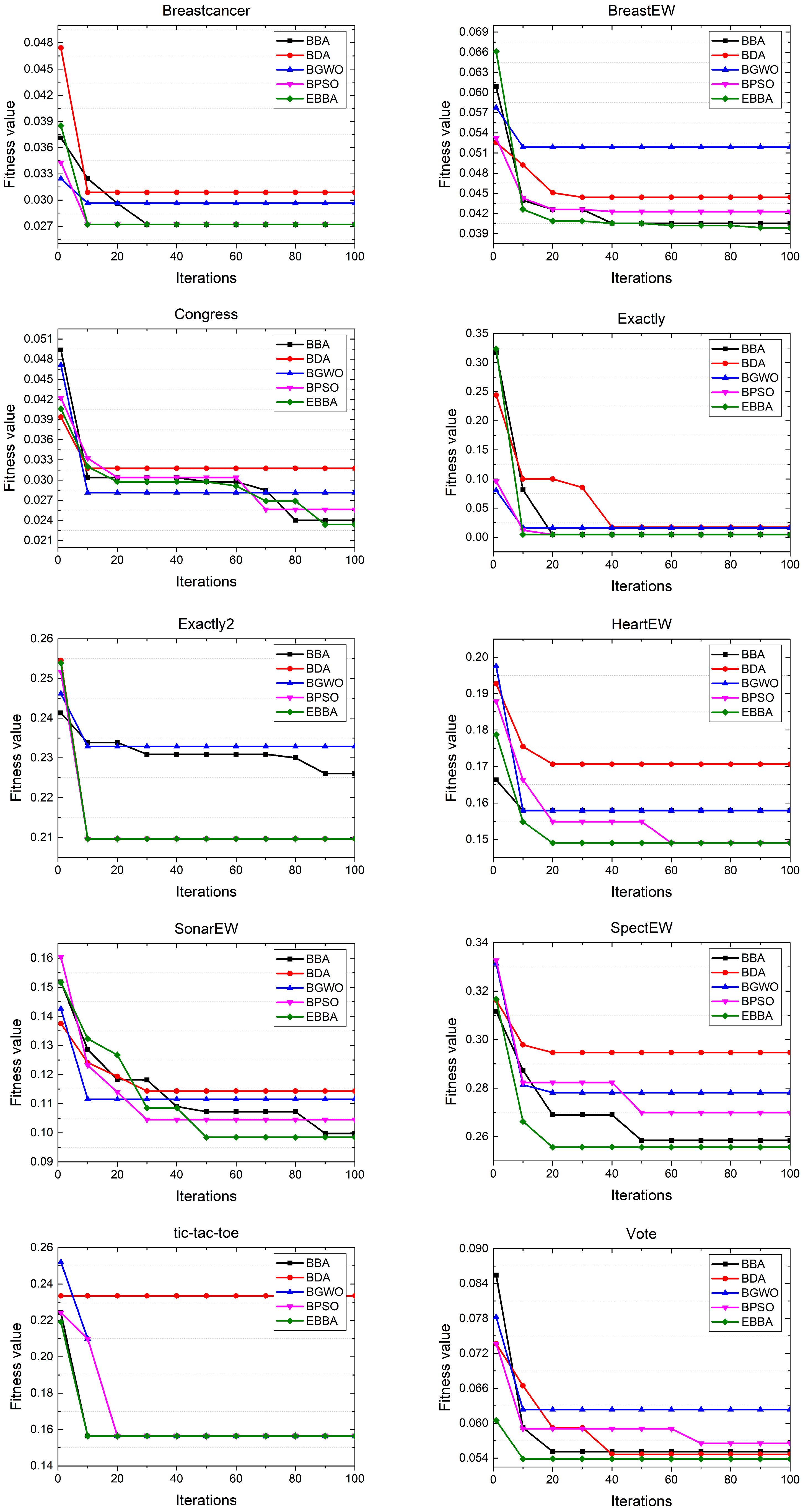
• Simulations are conducted based on open datasets of UC Irvine machine learning repository to verify the solving ability of the proposed EBBA. First, we introduce some benchmark algorithms for comparisons. Then, we show the effectiveness of the proposed improved factors.

The rest of this work is arranged as follows. Section 2 reviews some key related works about swarm intelligence algorithms and feature selection. Section 3 gives the model of feature selection. Section 4 proposes the EBBA and details the improved factors. Section 5 provides simulation results and Section 6 concludes this work.

2. Related Works

In this work, we aim to use one of the swarm intelligence algorithms, i.e., BA, to solve the feature selection problem, and thus some key related works are briefly introduced in this section.

2.1. Swarm Intelligence Algorithms

Swarm intelligence algorithms refer to evolutionary theory and swarm behavior. In the past few years, a large number of researchers have proposed various types of swarm intelligence algorithms to solve optimization problems in different domains.

First, some representative classical swarm intelligence algorithms are presented as follows. PSO is another representative swarm intelligence algorithm, which is inspired by the behavior of bird/fish populations. Moreover, artificial bee colony (ABC) [15], ant colony optimization (ACO) [16], etc., are also well-known swarm intelligence algorithms. Second, swarm intelligence algorithms also contain various types of bio-inspired algorithms. For example, Meng et al. [17] proposed a chicken swarm optimization (CSO) to solve optimization problems by simulating the rank order and the behavior of chickens (including roosters, hens, and chicks) in a flock. Yang et al. [18] proposed a BA and validated the performance of BA using eight nonlinear engineering optimization problems. Third, certain swarm intelligence algorithms were proposed inspired by various natural phenomena of the universe. Jiang et al. [19] proposed a new metaheuristic method, artificial raindrop algorithm (ARA), from natural rainfall phenomena and used it for the identification of unknown parameters of chaotic systems. Kaveh et al. [20] proposed a ray optimization (RO) based on Snell’s law of light refraction and the phenomenon of light refraction.

In summary, researchers have proposed a large number of effective swarm intelligence algorithms and applied them to various optimization problems. However, these algorithms are not necessarily applicable to all engineering fields. Accordingly, proposing an enhanced swarm intelligence algorithm version according to the characteristics of an optimization problem is a major challenge.

2.2. Ways of Feature Selection

There are several existing methods and ways have been proposed for the purpose of feature selection. First, some filter methods are widely used due to their simplicity and relatively high performance. For instance, some methods based on correlation criteria and mutual information are detailed in reference [21]. In this case, several effective filter-based algorithms including correlation-based feature selection (CFS) [22], fast correlation-based filter (FCBF) [23], wavelet power spectrum (Spectrum) [24], Information Gain (IG) [25], ReliefF [26], etc. Second, wrapper-based approaches are key methods in feature selection. This type of method can be categorized by the type of learning algorithms. For instance, exhaustive, random search and metaheuristic search methods. Due to their effectiveness, the metaheuristic search methods including swarm intelligence algorithms can be seen as the most popular methods [27]. Finally, there are several embedded methods. The main approach is to incorporate feature selection as part of the training process, e.g., [21,28].

2.3. Swarm Intelligence-Based Feature Selection

There are many swarm intelligence algorithms have been adopted or proposed as the learning algorithm in wrapper-based feature selection methods, and we review some key algorithms as follows.

Li et al. [29] proposed an improved binary GWO (IBGWO) algorithm for solving feature selection problems, in which an enhanced opposition-based learning (E-OBL) initialization and a local search strategy were proposed for improving the performance of the algorithm. Kale et al. [30] presented four different improved versions of the sine cosine algorithm (SCA), where the updating mechanism of SCA is the improvements and innovations. Ouadfel et al. [31] proposed a hybrid feature selection approach based on the ReliefF filter method and equilibrium optimizer (EO), which is composed of two phases and tested in some open datasets. Abdel-Basset et al. [14] proposed three variants of BGWO in addition to the standard variant, applying different transfer functions to tackle the feature selection problem. In [32], two different wrapper feature selection approaches were proposed based on farmland fertility algorithm (FFA), which denoted as BFFAS and BFFAG, and these methods are effective in solving feature selection problems. On the other hand, BA and some variants have been adopted for solving feature selection problems. Varma et al. [33] proposed a bat optimization algorithm for wrapper-based feature selection and conducted simulations based on the CICInvesAndMal2019 benchmark dataset. Naik et al. [34] proposed a feature selection method to identify the relevant subset of features for the machine-learning task using the wrapper approach via BA. Rodrigues et al. [35] presented a wrapper feature selection approach based on bat algorithm (BA) and optimum-path forest (OPF). In [36], the authors proposed an improved BPSO algorithm as an essential tool of pre-processing for solving classification problem, in which a new updating mechanism for calculating Pbest and Gbest were proposed. Moreover, the authors in [37] proposed a binary DA (BDA) and use it to solve the feature selection problems. Likewise, Nakamura et al. [38] proposed a binary version of the bat algorithm, i.e., BBA, and evaluate its performance in solving the feature selection problems. In addition, in [39], a new hybrid feature selection method was proposed by using the sine cosine algorithm (SCA) and genetic algorithm (GA), and the algorithm is used for solving feature selection problems. Furthermore, Nagpal et al. [40] proposed a feature selection method via binary gravitational search algorithms (BGSA) in medical datasets, in which they can reduce the number of features by an average of 66% and enhance the accuracy of prediction.

The aforementioned methods can solve feature selection problems in various applications. However, according to NFL theory, different swarm intelligence algorithms may have different performances in various applications. Therefore, the existing methods are insufficient to solve all feature selection problems, which motivates us to propose an EBBA to handle more feature selection problems in this work.

3. Feature Selection Model

As shown in [8,29,33], the feature selection problem can be seen as a binary optimization model, and in this section, we introduce it in details. Specifically, the main purpose of feature selection is to reduce the data dimension by retaining the most valuable features through feature selection methods. Thus, there are two possibilities for each feature, i.e., to be selected and to be discarded. Therefore, the feature selection problem can be regarded as an optimization problem with a binary solution space.

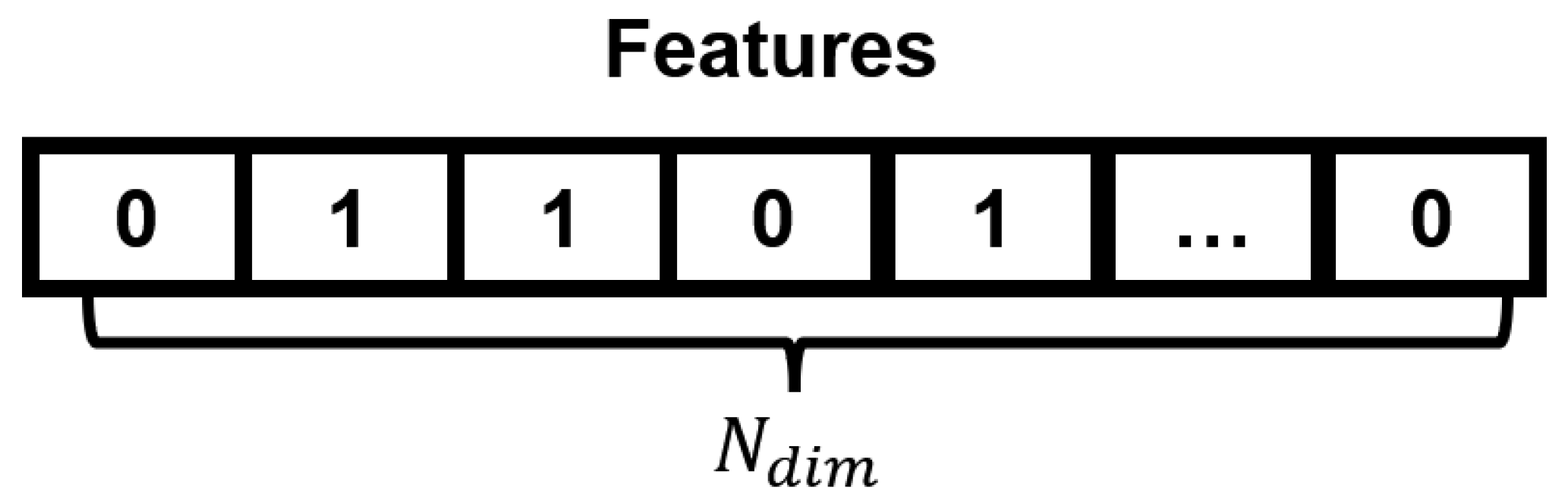
It is can be seen from Figure 1, the solution space of the considered feature selection problem is a binary. Each feature is represented by a binary number, and if that binary number is 1, it means that the feature is selected, and conversely, if that binary number is 0, it means that the feature is discarded. Thus, the feature selection of a dataset can be represented by a binary array as follow:

$$\left(\mathrm{Decision}\mathrm{variables}\right)X=[x_1,x_2,x_3,\cdots ,x_{N_{dim}}],$$

(1)

where $N_{dim}$ is the number of features, in other words, the dimension number of the dataset. Under this model, there are two main objectives of the feature selection, i.e., to reduce the classification error rate of the obtained feature subsets, and to reduce the feature number of feature subsets. Thus, the feature selection problem is a multi-objective problem in which the first objective can be expressed as follows:

$$\left(\mathrm{Objective}1\right)f_1=1-f_{acc},$$

(2)

where $f_{acc}$ is the classification accuracy of the obtained feature subsets. Note that we introduce the KNN as a classifier to evaluate the feature subsets and the reasons are analyzed in following section. Moreover, the second objective of this work is to reduce the feature number of feature subsets, which can be expressed as follows:

$$\left(\mathrm{Objective}2\right)f_2=\frac{N_{dim}^{\prime }}{N_{dim}},$$

(3)

where $N_{dim}^{\prime }$ is the feature number of the selected feature subsets. To simultaneously the aforementioned objectives, we introduce the fitness function as follows:

$$\left(\mathrm{Fitness}\mathrm{function}\right)f_{fit}=a\times f_1+b\times f_2,$$

(4)

where $a\in [0,1]$ and $b=1-a$ are constants that denote the weights of the two objectives $f_1$ and $f_2$, respectively. Specifically, we can increase a to obtain a higher classification accuracy or increase b to obtain a smaller dimensional feature subset.

4. Proposed Algorithm

Based on the aforementioned feature selection model, we can optimize the decision variables shown in Equation (1) to obtain a better fitness function shown in Equation (4). Accordingly, we propose an EBBA in this section for solving the feature selection problem.

4.1. Conventional BA

BA is a swarm intelligence algorithm for global optimization, which is inspired by the echolocation behavior of bats. Specifically, bats look for prey by flying at a random velocity $V_i$ at a random point $X_i$ with a fixed frequency $f_{min}$, changing wavelength l, and loudness $A_0$. Depending on the proximity of their target, these bats can autonomously modify the wavelength (in other words, frequency) of their generated pulses as well as the rate of pulse emission r in the range of $[0,1]$. The corresponding mathematical model of BA can be detailed as follows. In the tth iteration, the frequency $f_i$ of the the ith bat is expressed as follows.

$$f_i=f_{min}+(f_{max}-f_{min})\times \beta ,$$

(5)

where $f_{max}$ and $f_{min}$ are upper and lower bounds on the frequencies of all bats, respectively, and $\beta$ is a random number between $[0,1]$.

Moreover, the velocity of the ith bat $v_i$ can be modeled as follows:

$$V_i^t=V_i^{t-1}+(X_i^{t-1}-X^{*})f_i,$$

(6)

where $X^{*}$ is the bat with the highest fitness function value of the swarm.

In addition, the update method of the ith bat is shown as follows:

$$X_i^t=X_i^{t-1}+V_i^t,$$

(7)

where $X_i^t$ is the position of the ith bat in the tth iteration.

Furthermore, BA also enhances search ability through local random walks. Specifically, BA asks the best bat in the swarm to conduct a local search with a certain probability, which can be expressed as follows:

$$X^N=X^{*}+ϵ\times A^t,$$

(8)

where $X^N$ is the newly generated bat after the random walk, $A^t$ is the loudness of all bats in the t iteration, and $ϵ$ is a random variable that ranges $[-1,1]$.

Additionally, the loudness $A_i$ and the rate $r_i$ of pulse emission are also updated as the iterations proceed, which is shown as follows:

$$A_i^{t+1}=\alpha A_i^t,r_i^{t+1}=r_i^0[1-exp(-\gamma t)],$$

(9)

where $\alpha$ is a parameter that ranges from 0 to 1, and $\gamma >0$ is a parameter.

By using these mathematical models, the main steps of BA can be summarized as follows.

Step 1: Randomly generate population (bat swarm) $P=[X_1,X_2,\cdots ,X_{N_{pop}}]$, where $N_{pop}$ is the population size. Moreover, the velocity, pulse emissivity, and loudness of the bats are randomly generated. Then, the fitness values of all bats are calculated.

Step 2: Update the positions and velocities of bats by using Equations (5)–(9).

Step 3: A random number $N_{rand}$ between 0 and 1 is firstly generated, and then if $N_{rand}>r_i$, a random walk will be performed by using Equation (8) to generate a new individual $X^N$ around the current best individual $X^{*}$.

Step 4: Generate a random number $N_{rand}$ of $[0,1]$ again. If $N_{rand}<A_i$ and $f_{fit}\left(X^N\right)<f_{fit}\left(X_i\right)$, replace $X_i$ with $X^N$ and then update the loudness and pulse firing rate. If $f_{fit}\left(X^N\right)<f_{fit}\left(X^{*}\right)$, $X^N$ is used to replace $X^{*}$.

Step 5: Repeat steps 2–4 until the terminal condition is reached.

Step 6: Return $X^{*}$ as the final solution to the problem.

4.2. BBA

To make the BA can handle the binary solution space of the feature selection, Mirjalili et al. [41] introduce a binary operator. Specifically, the authors introduced a v-shape transfer function to map the continuous parameters into binary solution space, which can be expressed as follows:

$$V\left(v_{i,j}^t\right)=\left|\frac{2}{\pi }arctan\left(\frac{\pi }{2}{v}_{i,j}^t\right)\right|,$$

(10)

$$x_{i,j}^{t+1}=\left\{\begin{array}{cc}{\left(x_{i,j}^t\right)}^{-1}& \mathrm{if}\mathrm{rand}<V\left(v_{i,j}^{t+1}\right)\hfill \\ x_{i,j}^t& \mathrm{if}\mathrm{rand}\ge V{\left(v_{i,j}^{t+1}\right)}^{\prime }\hfill \end{array}\right.$$

(11)

where $x_{i,j}^t$ and $v_{i,j}^t$ indicate the position and velocity of ith individual at tth iteration in jth dimension, and ${\left(x_{i,j}^t\right)}^{-1}$ is the complement of $x_{i,j}^t$. As such, the BBA can handle and update the binary decision variable reasonably.

4.3. EBBA

Conventional BA may confront some key challenges in solving the feature selection problems. First, when dealing with the big solution space of feature selection problem, BA may lack exploration ability, which may make the algorithm fall in local optima. Second, the bats of the BA are guided by the best bat of the swarm, i.e., $X^{*}$, which means that the population diversity is lower for the large scale datasets. Third, the exploration and exploration abilities of BA should be further balanced. Finally, BA is proposed for continuous problems whereas the feature selection problems are with a binary solution space. Thus, these reasons motivate us to enhance BA for better feature selection performance. The main steps of the proposed EBBA are detailed in Algorithm 1, and the correspondingly improved factors are as follows:

Algorithm 1 EBBA

4.3.1. Lévy Flight-Based Global Search Method

Feature selection problems also are large-scale optimization problems since the dimension of some datasets is relatively large. In this case, the exploration ability of the optimization algorithm should be sufficient. However, the update of other bats in the swarm are determined by the best bat, and this mechanism will undoubtedly decrease the exploration ability of the algorithm. Thus, we introduce the Lévy flight to propose a global search method to improve the exploration ability of the algorithm. Specifically, a Lévy flight is a random walk in which the step-lengths have a Lévy distribution, a probability distribution that is heavy-tailed. By using the short-distance or long-distance searching alternately, the search scope can be extended.

First, mathematically, in each iteration, we generate a new bat according to the best bat $X^{*}$ and Lévy flight, which can be expressed as follows:

$$X^{new}=X^{*}+\alpha \oplus \mathrm{Lé}\mathrm{vy}\left(\lambda \right),$$

(12)

where $\alpha$ is a parameter and its value is often assigned according to applications. Moreover, Lévy flight is taken from the Lévy distribution, which can be expressed as follows:

$$\mathrm{Lé}\mathrm{vy}\left(\lambda \right)\sim u=t^{-\lambda }(1<\lambda <3),$$

(13)

Second, the newly generated bat $X^{new}$ is evaluated to obtain its fitness value, and then we compare the $X^{new}$ with the best bat $X^{*}$ based on their fitness function values. If the $X^{new}$ outmatches $X^{*}$, then $X^{*}=X^{new}$. By using this method, the best bat of the swarm is easy to jump out of local optima, thereby enhancing the exploration ability of EBBA.

4.3.2. Population Diversity Boosting Method

In BA, all the bats are guided by the best bat of the swarm, which may decrease the population diversity of the algorithm, thereby affecting the solving performance. In this case, we aim to propose a method for boosting population diversity. In bat swarm, the second best bat also is meaningful and with a strong value for guiding other bats. Thus, we use the second best bat $X^{**}$ to generate a part of new bats as follows:

$$X^{N2}=X^{**}+ϵ\times A^t,$$

(14)

where $X^{N2}$ is the newly generated bat and whether the method used is determined by a parameter $r^{\prime }$ which can be expressed as follows:

$$r_i^t{}^{\prime }=\frac{r_i^t}{2},$$

(15)

By using this method, the bat swarm is simultaneously guided by the best bat and the second-best bat, so that enhancing the population diversity of the algorithm.

4.3.3. Chaos-Based Loudness Method

The loudness in BA can determine the weights of exploitation and exploration abilities of the BA. However, the loudness update method of conventional BA is linear, which may be unsuitable for the feature selection. Thus, we introduce a novel fractional one dimensional chaotic map to update loudness [42], which can be expressed as follows:

$$A_i^t=C^t,$$

(16)

where $C^t$ is the tth dimension of the fractional one dimensional chaotic map, which can be expressed as follows:

$$C_{t+1}=f\left(C_t\right)=\left\{\begin{array}{cc}\frac{1}{C_t^2+\alpha }-\beta C_t\hfill & \mathrm{if}{C}_t\in \left[0,\frac{1}{\alpha }\right]\hfill \\ \frac{-1}{C_t^2+\alpha }-\beta C_t\hfill & \mathrm{if}{C}_t\in \left[\frac{-1}{\alpha },0\right)\hfill \end{array}\right.,$$

(17)

where $\alpha$ and $\beta$ are two real parameters, and they are assigned as 0.001 and 0.9 in this work, respectively. By using the high chaotic behavior of the method, the exploitation and exploration abilities of EBBA can be balanced.

4.3.4. Complexity Analysis of EBBA

The complexity of EBBA is analyzed in this part. In the proposed feature selection model, the most time-consuming step is the calculation of fitness function value since we introduce classifier, which is several orders of magnitude complex than other steps. In this case, other steps can be omitted. Accordingly, the complexity of EBBA is $\mathcal{O}(t_{max}·N_{pop})$ when the maximum number of iteration and population size are denoted as $t_{max}$ and $N_{pop}$, respectively.

5. Simulations

In this section, we conduct the simulations to evaluate the proposed EBBA. First, the datasets and setups are presented. Second, we compare the EBBA with some benchmark algorithms. Third, we illustrate the effectiveness of the improved factors.

5.1. Datasets and Setups

In this work, we introduce 10 typical UC Irvine Machine Learning Repository datasets. The main information of these datasets are shown in

Table 1. Datasets.

	Dataset	Number of Features	Number of Instance
1	Breastcancer	10	699
2	BreastEW	30	569
3	Congress	16	435
4	Exactly	13	1000
5	Exactly2	13	1000
6	HeartEW	13	270
7	SonarEW	60	208
8	SpectEW	22	267
9	tic-tac-toe	9	958
10	Vote	16	300

.

Moreover, the used CPU is 11th Gen Intel(R) Core(TM) i7-11700 @ 2.50 GHz and the RAM is 16 GB. We use python to implement the simulation codes and adopt KNN (k = 5). Note that we use KNN classifier since it is simple, easy and highly accurate, it is also insensitive to outliers and no data entry settings. Moreover, using a simple and relatively cheap classification algorithm in a wrapper approach can obtain a good feature subset that is also suitable for complex classification algorithms. In contrast, if an advanced classification algorithm is used for wrapper-based feature selection, the obtained feature subset will be failed for simple classification algorithms. The reason is that when using advanced classification algorithms, the learning algorithm of the wrapper approach (e.g., the proposed EBBA) will capture the characteristics of the classification algorithm instead of the relationship of different features. In addition, a and b in the fitness function are set to 0.99 and 0.01, respectively. Furthermore, In this paper, binary PSO (BPSO) [36], BGWO [43], BDA [37], and BBA [41] are introduced as the benchmarks, and the key parameters of these algorithms are shown in

Table 2. Key parameters of benchmark algorithms.

	Algorithm	Key Parameters
1	BPSO	$c1$ = 2, $c2$ = 2
2	BGWO	$\alpha$ = [2, 0]
3	BDA	w = [0.9, 0.4], s = [0.2, 0], a = [0.2, 0], c = [0.2, 0], f = [0.2, 0], e = [0, 0.1]
4	BBA	A = 0.25, $Q_{max}$ = 2, $Q_{min}$ = 0
5	EBBA	$Q_{max}$ = 2, $Q_{min}$ = 0

. Note that the population size and iteration number of EBBA and other benchmarks are set as 24 and 100, respectively. Additionally, to avoid the experiment’s random bias, each algorithm is performed 30 times independently in these selected datasets, as specified by the central limit theorem. What’s more, 80% of the instances are utilized for training, while the remaining 20% are used for testing [7,44,45]. Note that the classifier only provides feedback to the EBBA, which means that the overfitting affected by the division of the dataset will not have too much impact on the feature selection method based on the wrapper and swarm intelligence.

5.2. Simulation Results

Table 3. Optimization results achieved by various algorithms. (The best values are highlighted in bold).

		Accuracy	Feature #	Fitness Value	CPU Time
Breastcancer	BBA	0.9786	6.0000	0.0272	69.5141
	BDA	0.9767	5.8000	0.0289	68.7234
	BGWO	0.9767	6.5000	0.0296	75.3848
	BPSO	0.9786	6.0000	0.0272	69.2956
	EBBA	0.9786	6.0000	0.0272	60.9926
BreastEW	BBA	0.9613	6.6000	0.0405	73.3552
	BDA	0.9589	5.1667	0.0424	67.3963
	BGWO	0.9532	14.6667	0.0512	79.7631
	BPSO	0.9612	8.5000	0.0413	75.4869
	EBBA	0.9614	5.4333	0.0400	63.4576
Congress	BBA	0.9793	6.9000	0.0248	58.3419
	BDA	0.9743	5.1667	0.0287	55.9260
	BGWO	0.9750	8.8000	0.0303	61.5544
	BPSO	0.9785	6.7333	0.0255	59.3514
	EBBA	0.9793	6.4000	0.0245	49.2745
Exactly	BBA	1.0000	6.0000	0.0046	91.2861
	BDA	0.9197	6.6667	0.0846	100.3068
	BGWO	0.9040	8.0333	0.1012	116.4705
	BPSO	0.9999	6.0333	0.0048	103.6469
	EBBA	1.0000	6.0000	0.0046	88.3184
Exactly2	BBA	0.7854	2.2667	0.2142	86.8956
	BDA	0.7847	1.7667	0.2145	90.0558
	BGWO	0.7693	7.5333	0.2342	117.3080
	BPSO	0.7890	1.0667	0.2097	101.6048
	EBBA	0.7868	1.9667	0.2126	81.4770
HeartEW	BBA	0.8511	5.0333	0.1513	45.4301
	BDA	0.8391	4.9333	0.1631	44.0686
	BGWO	0.8357	6.6667	0.1678	45.2137
	BPSO	0.8527	5.0000	0.1497	44.8358
	EBBA	0.8520	5.0667	0.1504	39.0150
SonarEW	BBA	0.9100	27.3000	0.0937	49.9454
	BDA	0.9010	20.5000	0.1015	48.1458
	BGWO	0.8989	40.6667	0.1069	55.5145
	BPSO	0.9046	27.7333	0.0991	51.0521
	EBBA	0.9117	27.0667	0.0919	42.8189
SpectEW	BBA	0.7379	10.5000	0.2643	46.5456
	BDA	0.7185	8.9667	0.2827	44.8928
	BGWO	0.7219	14.3667	0.2819	47.5410
	BPSO	0.7335	10.5000	0.2687	46.3761
	EBBA	0.7407	10.7000	0.2615	38.4262
tic-tac-toe	BBA	0.8493	8.8667	0.1590	97.9119
	BDA	0.8099	7.1667	0.1962	97.8065
	BGWO	0.8465	8.8000	0.1618	91.4816
	BPSO	0.8521	9.0000	0.1564	88.2232
	EBBA	0.8521	9.0000	0.1564	84.4753
Vote	BBA	0.9519	5.2000	0.0509	46.4947
	BDA	0.9457	5.7667	0.0574	45.8363
	BGWO	0.9440	8.5333	0.0608	47.9505
	BPSO	0.9493	4.9000	0.0532	46.5221
	EBBA	0.9513	5.4000	0.0516	38.9119

shows the optimization results of the accuracy rate, number of selected features, fitness function values, and CPU times achieved by various algorithms. Note that the best values among all comparison algorithms are highlighted in bold font. As can be seen, the proposed EBBA achieves the best accuracy rate on 7 datasets and achieves the best of selected feature number on 2 datasets. More intuitively, the proposed EBBA achieves the best fitness function values on 9 datasets, which means that the proposed EBBA is with the best performance among all benchmark algorithms. The reason may be that we enhance the EBBA by improving its exploration ability and balancing its exploration and exploitation abilities, which make the EBBA more suitable for solving feature selection problems.

In addition, Figure 2 shows the convergence rates obtained by different benchmark algorithms during the solving processes. As can be seen, the proposed EBBA achieves the best curves on most datasets, which performs the best convergence ability among all the comparison algorithms.

On the other hand, we also evaluate the effectiveness of the proposed improved factors. Specifically, we combine the proposed Lévy flight-based global search method, population diversity boosting method, and chaos-based loudness method with conventional BBA, namely, EBBA-IF1, EBBA-IF2, and EBBA-IF3, respectively.

Table 4. Optimization results achieved by various EBBA versions. (The best values are highlighted in bold).

		Accuracy	Feature #	Fitness Value	CPU Time
Breastcancer	BBA	0.9786	6.0000	0.0272	69.5141
	BBA-IF1	0.9786	6.0000	0.0272	64.4441
	BBA-IF2	0.9786	6.0000	0.0272	67.0577
	BBA-IF3	0.9786	6.0000	0.0272	60.1375
	EBBA	0.9786	6.0000	0.0272	60.9926
BreastEW	BBA	0.9613	6.6000	0.0405	73.3552
	BBA-IF1	0.9613	5.2333	0.0400	65.2602
	BBA-IF2	0.9614	5.9000	0.0402	68.0782
	BBA-IF3	0.9611	5.4000	0.0403	63.0563
	EBBA	0.9614	5.4333	0.0400	63.4576
Congress	BBA	0.9793	6.9000	0.0248	58.3419
	BBA-IF1	0.9790	6.6667	0.0249	51.4119
	BBA-IF2	0.9783	6.2333	0.0253	54.6810
	BBA-IF3	0.9791	6.6667	0.0249	50.4441
	EBBA	0.9793	6.4000	0.0245	49.2745
Exactly	BBA	1.0000	6.0000	0.0046	91.2861
	BBA-IF1	1.0000	6.0000	0.0046	88.5090
	BBA-IF2	1.0000	6.0000	0.0046	92.2044
	BBA-IF3	1.0000	6.0000	0.0046	88.9417
	EBBA	1.0000	6.0000	0.0046	88.3184
Exactly2	BBA	0.7854	2.2667	0.2142	86.8956
	BBA-IF1	0.7859	2.0333	0.2136	81.4199
	BBA-IF2	0.7848	2.5333	0.2150	87.3399
	BBA-IF3	0.7848	2.4333	0.2149	84.0370
	EBBA	0.7868	1.9667	0.2126	81.4770
HeartEW	BBA	0.8511	5.0333	0.1513	45.4301
	BBA-IF1	0.8516	4.9000	0.1507	39.6087
	BBA-IF2	0.8521	5.1000	0.1503	40.7423
	BBA-IF3	0.8511	4.8333	0.1511	38.9901
	EBBA	0.8520	5.0667	0.1504	39.0150
SonarEW	BBA	0.9100	27.3000	0.0937	49.9454
	BBA-IF1	0.9097	27.0333	0.0939	42.1371
	BBA-IF2	0.9100	27.3000	0.0937	44.0751
	BBA-IF3	0.9105	26.7000	0.0931	41.8531
	EBBA	0.9117	27.0667	0.0919	42.8189
SpectEW	BBA	0.7379	10.5000	0.2643	46.5456
	BBA-IF1	0.7393	10.2333	0.2628	38.7934
	BBA-IF2	0.7393	10.2000	0.2628	40.4760
	BBA-IF3	0.7386	10.7000	0.2636	39.2009
	EBBA	0.7407	10.7000	0.2615	38.4262
tic-tac-toe	BBA	0.8493	8.8667	0.1590	97.9119
	BBA-IF1	0.8493	8.8667	0.1590	86.5623
	BBA-IF2	0.8521	9.0000	0.1564	89.9898
	BBA-IF3	0.8521	9.0000	0.1564	86.5650
	EBBA	0.8521	9.0000	0.1564	84.4753
Vote	BBA	0.9519	5.2000	0.0509	46.4947
	BBA-IF1	0.9518	5.3667	0.0511	39.7080
	BBA-IF2	0.9516	5.1000	0.0511	41.6823
	BBA-IF3	0.9513	5.4333	0.0516	40.1654
	EBBA	0.9513	5.4000	0.0516	38.9119

shows the optimization results of the accuracy rate, number of selected features, fitness function values, and CPU times achieved by various algorithms. Moreover, Figure 3 shows the convergence rates obtained by different EBBA versions during the solving processes. As can be seen, the EBBA, EBBA-IF1, EBBA-IF2, and EBBA-IF3 outperform conventional BBA, which means that the proposed improved factors are non-trivial and effective.

5.3. Performance Evaluation under Different Classifiers

In this section, we consider two other classification algorithms which are decision tree and random forest. Specifically, the decision tree is easy to understand and visualized, requires only little data preparation, whereas it may be easy to be overfitting. Likewise, random forest is also extremely accurate and not prone to overfitting, and can run effectively on large datasets with good noise immunity. Moreover, due to the complexity of the classification algorithms, validating the newly introduced two classifiers using all datasets is a huge and time-consuming task. Thus, we only consider using the dataset SpectEW as the experimental dataset since it has the middle dimension number of all datasets, which is representative. In addition, other settings are similar to that of the KNN-based method.

In this case,

Table 5. Optimization results obtained by different algorithms under decision tree. (The best values are highlighted in bold).

Algorithms	Accuracy	The Number of Features	Fitness Value
BBA	0.7312	7.9333	0.2683
BDA	0.7211	7.7333	0.2783
BGWO	0.7115	12.4000	0.2886
BPSO	0.7281	9.1667	0.2726
EBBA	0.7325	8.5333	0.2682

and

Table 6. Optimization results obtained by different algorithms under random forest. (The best values are highlighted in bold).

Algorithms	Accuracy	The Number of Features	Fitness Value
BBA	0.7247	8.9333	0.2766
BDA	0.7058	5.9333	0.2940
BGWO	0.7035	12.4333	0.2992
BPSO	0.7235	9.0667	0.2779
EBBA	0.7252	9.0667	0.2762

provide the simulation results obtained by different algorithms in terms of accuracy, the number of features and fitness function value under decision tree and random forest, respectively. As can be seen, the proposed EBBA also outperforms other comparison algorithms under other classification algorithms, which shows that the improved factors are effective even if the classification algorithm is changed. Thus, the proposed method has good performance in both maybe overfitting and non-overfitting cases.

6. Conclusions

In this paper, the feature selection problems which can enhance the classification and reduce data dimension are studied. First, we model the feature selection problem and then transfer it as a fitness function. Then, we propose an EBBA for solving the feature selection problem. In EBBA, we introduce Lévy flight-based global search method, population diversity boosting method and chaos-based loudness method to improve the BA and make it more applicable to feature selection problems. Finally, the simulations are conducted to evaluate the proposed EBBA and the simulation results demonstrate that the proposed EBBA outmatches other comparison benchmarks. Moreover, the non-trivial of the proposed improved factors is illustrated. In the future, we intend to use more realistic datasets to evaluate the proposed EBBA.