Stiffness Analysis to Predict the Spread Out of Fake Information
Abstract
:1. Introduction
2. Stiffness Analysis of the SIR Model for the Diffusion of Fake Information
- : potentially authoring the spreading of fake news;
- : the wide variety of authors highly active in posting fake information;
- : authors who are inactive to the spreading of fake news.
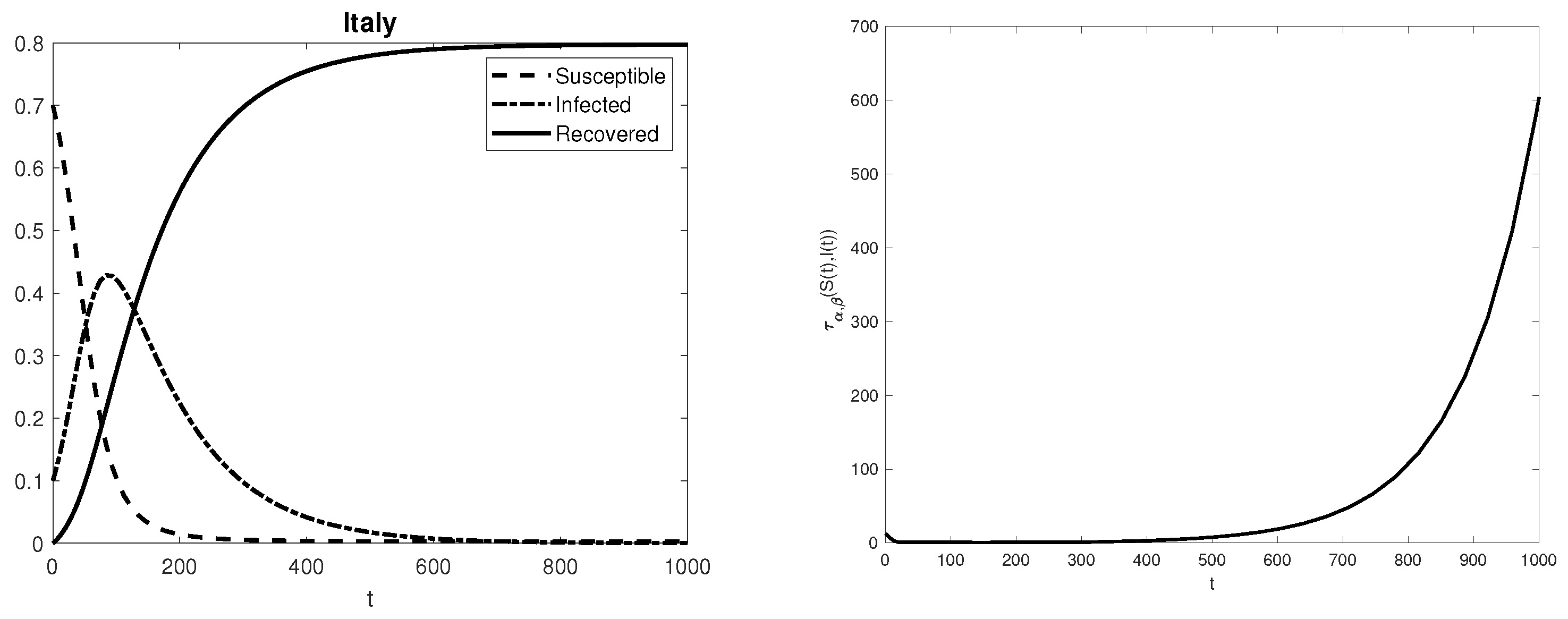
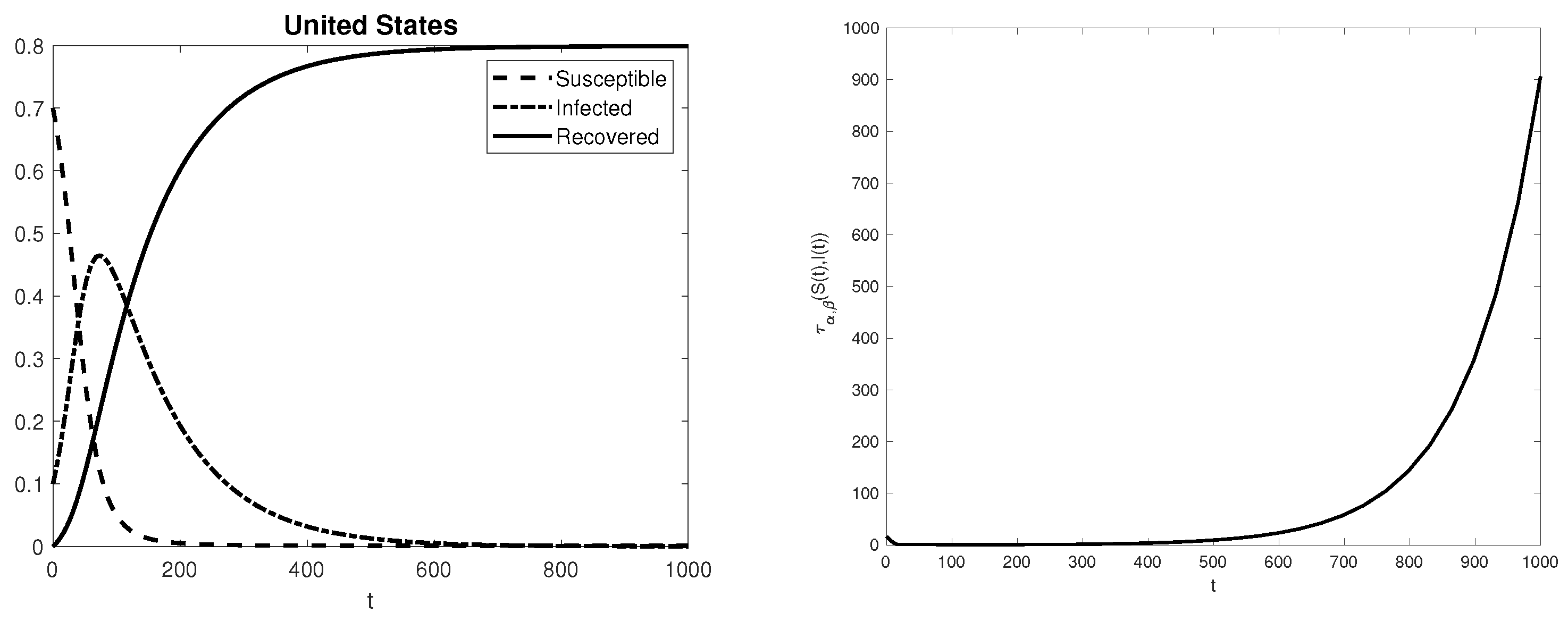
3. Numerical Experiments and Conclusions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allen, J.; Howland, B.; Mobius, M.; Rothschild, D.; Watts, D.J. Evaluating the fake news problem at the scale of the information ecosystem. Sci. Adv. 2020, 6, eaay3539. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berduygina, O.N.; Vladimirova, T.N.; Chernyaeva, E.V. Trends in the spread of fake news in mass media. Media Watch 2019, 10, 122–132. [Google Scholar] [CrossRef]
- Dentith, M.R.X. The Problem of Fake News. Public Reason. 2016, 8, 65–79. [Google Scholar]
- Gelfert, A. Fake News: A Definition. Inform. Log. 2018, 38, 84–117. [Google Scholar] [CrossRef]
- Guo, B.; Ding, Y.; Sun, Y.; Ma, S.; Li, K.; Yu, Z. The mass, fake news, and cognition security. Front. Comput. Sci. 2021, 15, 153806. [Google Scholar] [CrossRef]
- Guo, B.; Ding, Y.; Yao, L.; Liang, Y.; Yu, Z. The Future of False Information Detection on Social Media: New Perspectives and Trends. Acm Comput. Surv. 2020, 53, 3393880. [Google Scholar] [CrossRef]
- Kapantai, E.; Christopoulou, A.; Berberidis, C.; Peristeras, V. A systematic literature review on disinformation: Toward a unified taxonomical framework. New Media Soc. 2021, 23, 1301–1326. [Google Scholar] [CrossRef]
- Kelly, D. Evaluating the News: (Mis)Perceptions of Objectivity and Credibility. Political Behav. 2019, 41, 445–471. [Google Scholar] [CrossRef]
- O’Connor, C.; Weatherall, J.O. The Misinformation Age: How False Beliefs Spread; Yale University Press: New Haven, CT, USA, 2019. [Google Scholar]
- Peters, M.A.; Rider, S.; Hyvönen, M.; Besley, T. Post-Truth, Fake News: Viral Modernity Higher Education; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Reyes-Menendez, A.; Saura, J.R.; Filipe, F. Figure 1: Evolution of searches about fake news and fake reviews. PeerJ Comput. Sci. 2019, 5. [Google Scholar] [CrossRef]
- Reyes-Menendez, A.; Saura, J.R.; Filipe, F. The importance of behavioral data to identify online fake reviews for tourism businesses: A systematic review. PeerJ Comput. Sci. 2019, 5, e219. [Google Scholar] [CrossRef] [Green Version]
- Shin, J.; Jian, L.; Driscoll, K.; Bar, F. The diffusion of misinformation on social media: Temporal pattern, message, and source. Comput. Hum. Behav. 2018, 83, 278–287. [Google Scholar] [CrossRef]
- Tandoc, E.C.; Lim, D.; Ling, R. Diffusion of disinformation: How social media users respond to fake news and why. Journalism 2020, 21, 381–398. [Google Scholar] [CrossRef]
- Tandoc, E.C. The facts of fake news: A research review. Sociol. Compass 2019, 13, e12724. [Google Scholar] [CrossRef]
- Zannettou, S.; Sirivianos, M.; Blackburn, J.; Kourtellis, N. The web of false information: Rumors, fake news, hoaxes, clickbait, and various other shenanigans. J. Data Inf. Qual. 2019, 11, 10. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Ghorbani, A.A. An overview of online fake news: Characterization, detection, and discussion. Inf. Process. Manag. 2020, 57, 102025. [Google Scholar] [CrossRef]
- Zhou, X.; Zafarani, R. A Survey of Fake News: Fundamental Theories, Detection Methods, and Opportunities. ACM Comput. Surv. 2020, 1, 3395046. [Google Scholar]
- Giordano, G.; Mottola, S.; Paternoster, B. A short review of some mathematical methods to detect fake news. Int. Circ. Syst. Signal Process 2020, 14, 255–265. [Google Scholar]
- Mottola, S. Las Fake News Como fenóMeno Social. Análisis lingüíStico y Poder Persuasivo de Bulos en Italiano y Español. Discurso Soc. 2021, 14, 683–706. [Google Scholar]
- Fan, D.; Jiang, G.P.; Song, Y.R.; Li, Y.W. Novel fake news spreading model with similarity on PSO-based networks. Phys. A 2020, 549, 124319. [Google Scholar] [CrossRef]
- Khurana, P.; Kumar, D. Sir Model for Fake News Spreading Through Whatsapp. In Proceedings of the 3rd International Conference on Internet of Things and Connected Technologies, Jaipur, India, 26–27 March 2018. [Google Scholar] [CrossRef]
- Lotito, Q.F.; Zanella, D.; Casari, P. Realistic Aspects of Simulation Models for Fake News Epidemics over Social Networks. Future Internet 2021, 13, 76. [Google Scholar] [CrossRef]
- Mahmoud, H. A model for the spreading of fake news. J. Appl. Prob. 2020, 57, 332–342. [Google Scholar] [CrossRef]
- Murayama, T.; Wakamiya, S.; Aramaki, E.; Kobayashi, R. Modeling the spread of fake news on Twitter. PLoS ONE 2021, 16, E0250419. [Google Scholar] [CrossRef] [PubMed]
- Reyes-Menendez, A.; Saura, J.R.; Martinez-Navalon, J.G. The impact of e-WOM on hotels management reputation: Exploring tripadvisor review credibility with the ELM model. IEEE Access 2019, 7, 68868–68877. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhao, J.; Sano, Y.; Levy, O.; Takayasu, H.; Takayasu, M.; Li, D.; Wu, J.; Havlin, S. Fake news propagates differently from real news even at early stages of spreading. EPJ Data Sci. 2020, 9, 7. [Google Scholar] [CrossRef]
- Brody, D.C.; Meier, D.M. How to model fake news. arXiv 2018, arXiv:1809.00964. [Google Scholar]
- Brainard, J.; Hunter, P.R.; Hall, I.R. An agent-based model about the effects of fake news on a norovirus outbreak. Rev Epidemiol. Sante Publique 2020, 68, 99–107. [Google Scholar] [CrossRef] [Green Version]
- Kendall, D.G. Deterministic and stochastic epidemics in closed populations. In Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability: Contributions to Biology and Problems of Health; University of California: Berkeley, CA, USA, 1956; Volume 4, pp. 149–165. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. R. Soc. 1927, 115, 700–721. [Google Scholar]
- Ross, R. Ronald, An application of the theory of probabilities to the study of a priori pathometry-Part I. R. Soc. 1916, 92, 204–230. [Google Scholar] [CrossRef] [Green Version]
- Ross, R.; Hudson, H. An application of the theory of probabilities to the study of a priori pathometry-Part II. R. Soc. 1917, 93, 212–225. [Google Scholar]
- Ross, R.; Hudson, H. An application of the theory of probabilities to the study of a priori pathometry-Part III. R. Soc. 1917, 89, 225–240. [Google Scholar]
- Diekmann, O.; Heesterbeek, H.; Britton, T. Mathematical Tools for Understanding Infectious Disease Dynamics; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Elston, R.C.; Johnson, W.D. Basic Biostatistics for Geneticists and Epidemiologists: A Practical Approach; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Epstein, J.M. Nonlinear Dynamics, Mathematical Biology, and Social Science; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Ma, Z.; Li, J. Dynamical Modeling and Analysis of Epidemics; World Scientific: Singapore, 2009. [Google Scholar]
- Malchow, H.; Petrovskii, S.V.; Venturino, E. Spatiotemporal Patterns in Ecology and Epidemiology: Theory, Models, and Simulation; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Brauer, F.; Kribs, C. Dynamical Systems for Biological Modeling: An Introduction; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Chowell, G.; Hyman, J.M. Mathematical and Statistical Modeling for Emerging and Re-Emerging Infectious Diseases; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Chowell, G.; Hyman, J.M.; Bettencourt, L.M.A.; Castillo-Chavez, C. Mathematical and Statistical Estimation Approaches in Epidemiology; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Deters, J.; Aguiar, I.P.; Feuerborn, J. The Mathematics of Gossip. Codee J. 2019, 12, 7. [Google Scholar] [CrossRef]
- Shrivastava, G.; Kumar, P.; Ojha, R.P.; Srivastava, P.K.; Mohan, S.; Srivastava, G. Defensive Modeling of Fake News Through Online Social Networks. IEEE Trans. Comput. Soc. Syst. 2020, 7, 1159–1167. [Google Scholar] [CrossRef]
- United Nations Development Programme, Human Development Data Center. Available online: http://hdr.undp.org/en/data (accessed on 28 August 2021).
- The Ji Village News, Mathematical Modeling of Fake News. Available online: https://www.haidongji.com/2018/07/23/mathematical-modeling-of-fake-news/ (accessed on 28 August 2021).
- Wikipedia, List of Countries by Number of Internet Users. Available online: https://en.wikipedia.org/wiki/List_of_countries_by_number_of_Internet_users (accessed on 28 August 2021).
- Soroush, V.; Deb, R.; Sinan, A. The spread of true and false news online. Science 2018, 359, 1146–1151. [Google Scholar]
- Lambert, J.D. Numerical Methods for Ordinary Differential Systems; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Hutzenthaler, M.; Jentzen, A. Numerical approximations of stochastic differential equations with non-globally Lipschitz continuous coefficients. Mem. Am. Math. Soc. 2015, 236. [Google Scholar] [CrossRef]
- Aslam, N.; Alotaibi, I.U.K.F.S.; Aldaej, L.M.; Aldubaikil, A.K. Fake Detect: A Deep Learning Ensemble Model for Fake News Detection. Complexity 2021, 2021, 5557784. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F.; Zanzottera, P. A multiregional extension of the SIR model, with application to the COVID-19 spread in Italy. Math. Meth. Appl. Sci. 2021, 44, 4414–4427. [Google Scholar] [CrossRef] [PubMed]
- Burrage, K.; Cardone, A.; D’Ambrosio, R.; Paternoster, B. Numerical solution of time fractional diffusion systems. Appl. Numer. Math. 2017, 116, 82–94. [Google Scholar] [CrossRef] [Green Version]
- Conte, D.; D’Ambrosio, R.; Paternoster, B. Improved theta-methods for stochastic Volterra integral equations. Commun. Nonlinear Sci. Numer. Simul. 2021, 93, 105528. [Google Scholar] [CrossRef]
- D’Ambrosio, R.; Moccaldi, M.; Paternoster, B. Adapted numerical methods for advection-reaction-diffusion problems generating periodic wavefronts. Comput. Math. Appl. 2017, 74, 1029–1042. [Google Scholar] [CrossRef]
- D’Ambrosio, R.; Moccaldi, M.; Paternoster, B. Numerical preservation of long-term dynamics by stochastic two-step methods. Discr. Cont. Dyn. Syst. B 2018, 23, 2763–2773. [Google Scholar] [CrossRef] [Green Version]
- D’Ambrosio, R.; Scalone, C. On the numerical structure preservation of nonlinear damped stochastic oscillators. Numer. Algorithms 2021, 86, 933–952. [Google Scholar] [CrossRef]
- D’Ambrosio, R.; Scalone, C. Filon quadrature for stochastic oscillators driven by time-varying forces. Appl. Numer. Math. 2021, 169, 21–31. [Google Scholar] [CrossRef]
- Reyes-Menendez, A.; Saura, J.R.; Filipe, F. Marketing challenges in the MeToo era: Gaining business insights using an exploratory sentiment analysis. Heliyon 2020, 6, e03626. [Google Scholar] [CrossRef] [PubMed]
- Reyes-Menendez, A.; Saura, J.R.; Alvarez-Alonso, C. Understanding World Environment-Day user opinions in Twitter: A topic-based sentiment analysis approach. Int. J. Environ. Res. Public Health 2018, 15, 2537. [Google Scholar] [CrossRef] [Green Version]
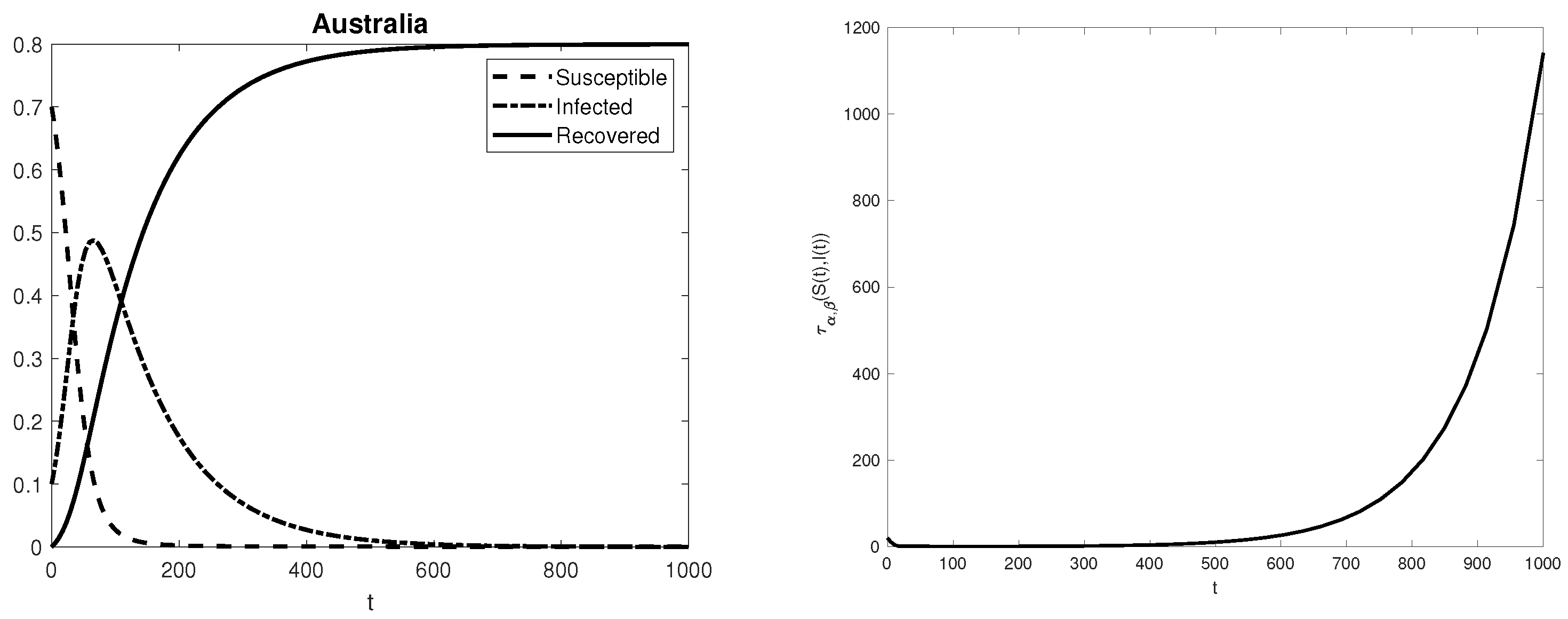
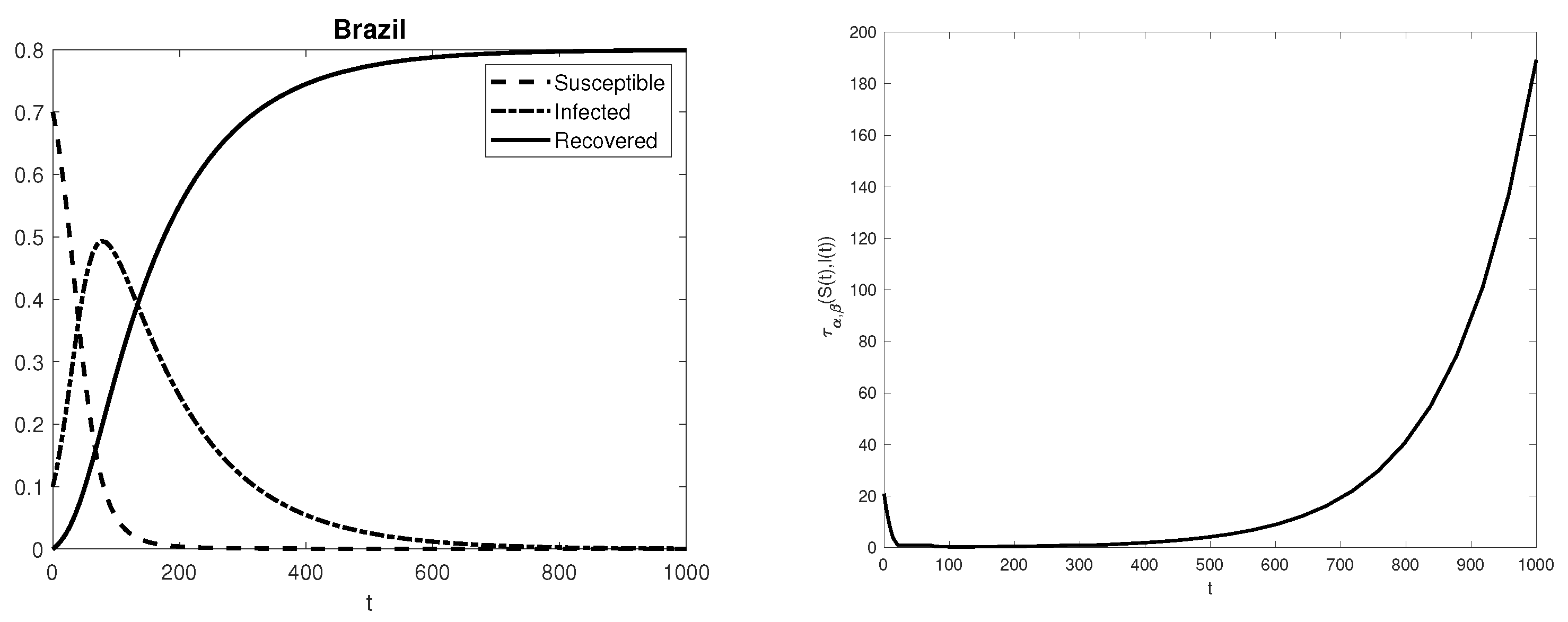
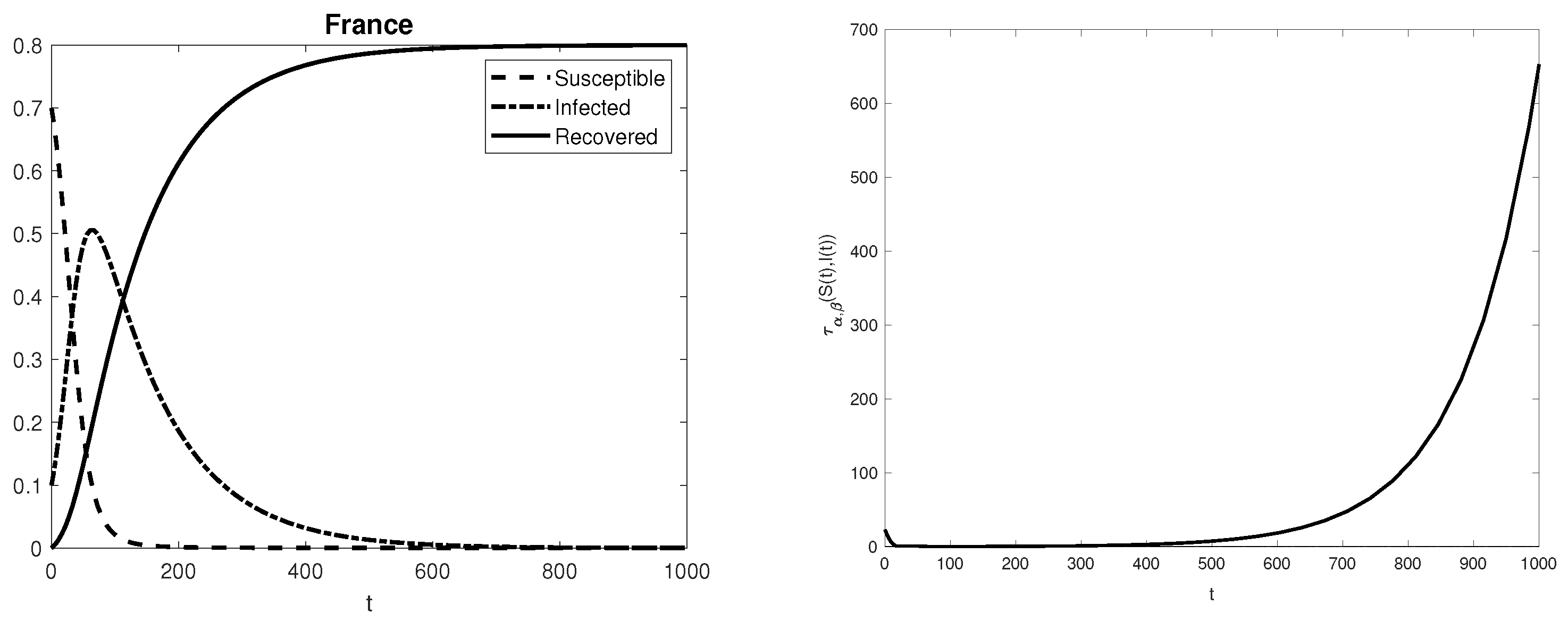
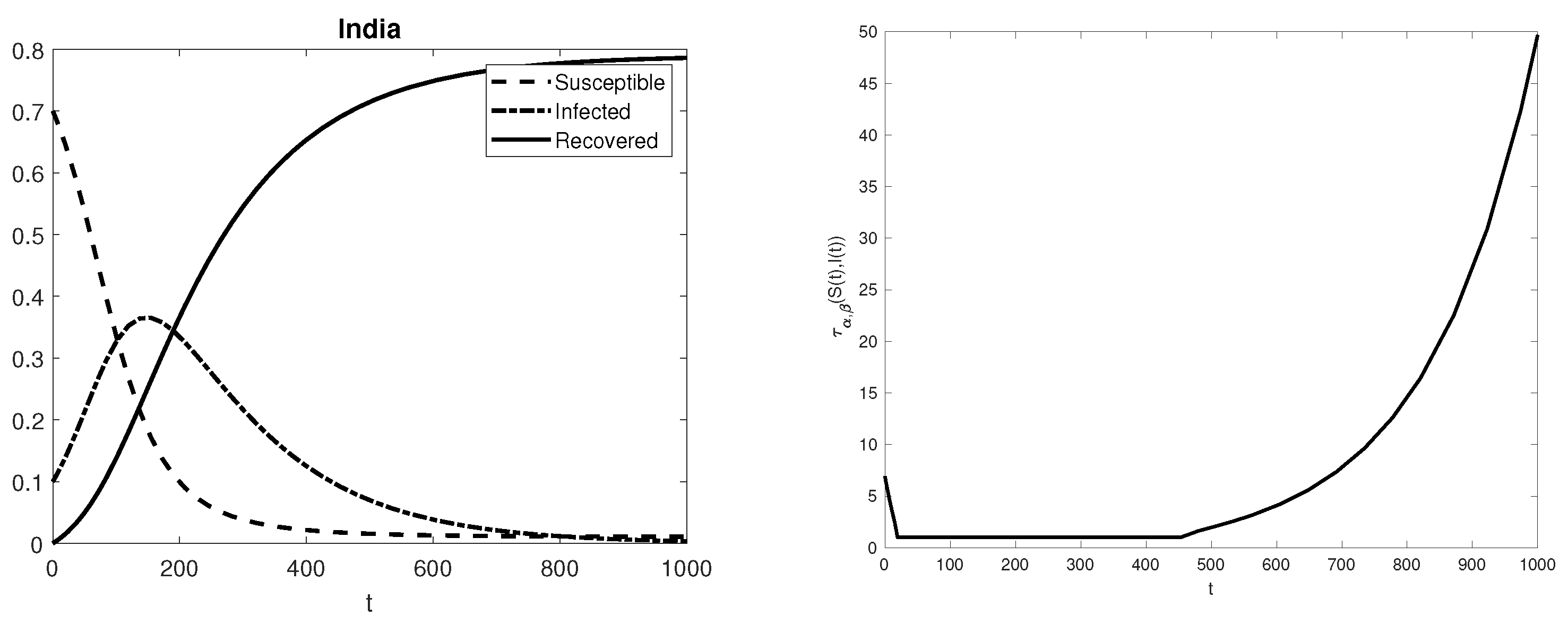


| Australia | 0.009 | 0.087 |
| Brazil | 0.008 | 0.072 |
| France | 0.009 | 0.089 |
| India | 0.006 | 0.035 |
| Italy | 0.009 | 0.061 |
| Mexico | 0.008 | 0.064 |
| Mozambique | 0.005 | 0.021 |
| United States | 0.009 | 0.075 |
| Australia | 20.03 |
| Brazil | 20.85 |
| France | 23.07 |
| India | 8.38 |
| Italy | 12.35 |
| Mexico | 17.13 |
| Mozambique | 4.39 |
| United States | 17.00 |
| Number of Time Units | |
|---|---|
| Australia | 66.15 |
| Brazil | 77.00 |
| France | 61.16 |
| India | 145.75 |
| Italy | 88.90 |
| Mexico | 87.02 |
| Mozambique | 234.40 |
| United States | 74.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Ambrosio, R.; Giordano, G.; Mottola, S.; Paternoster, B. Stiffness Analysis to Predict the Spread Out of Fake Information. Future Internet 2021, 13, 222. https://doi.org/10.3390/fi13090222
D’Ambrosio R, Giordano G, Mottola S, Paternoster B. Stiffness Analysis to Predict the Spread Out of Fake Information. Future Internet. 2021; 13(9):222. https://doi.org/10.3390/fi13090222
Chicago/Turabian StyleD’Ambrosio, Raffaele, Giuseppe Giordano, Serena Mottola, and Beatrice Paternoster. 2021. "Stiffness Analysis to Predict the Spread Out of Fake Information" Future Internet 13, no. 9: 222. https://doi.org/10.3390/fi13090222
APA StyleD’Ambrosio, R., Giordano, G., Mottola, S., & Paternoster, B. (2021). Stiffness Analysis to Predict the Spread Out of Fake Information. Future Internet, 13(9), 222. https://doi.org/10.3390/fi13090222







