Fast Flow Reconstruction via Robust Invertible n × n Convolution
Abstract
:1. Introduction
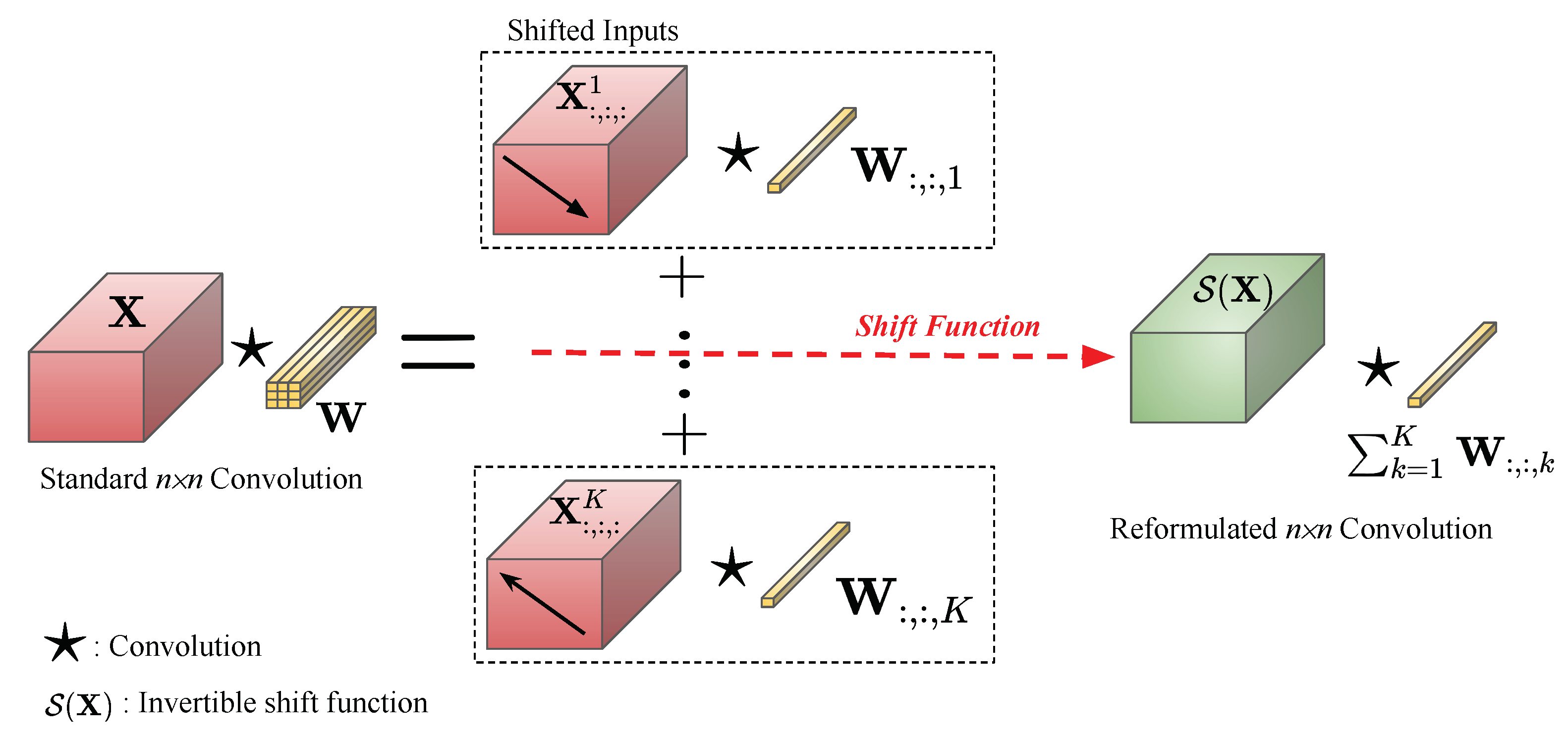
- Firstly, by analyzing the standard convolution layer, we reformulate its equation into a form such that, rather than shifting the kernels during the convolution process, shifting the input provides equivalent results.
- Secondly, we propose a novel invertible shift function that mathematically helps to reduce the computational cost of the standard convolution while keeping the range of the receptive fields. The determinant of the Jacobian matrix produced by this shift function can be computed efficiently.
- Thirdly, evaluations of several datasets on both objects and faces have shown the generalization of the proposed convolution using our proposed novel invertible shift function.
2. Related Work
3. Background
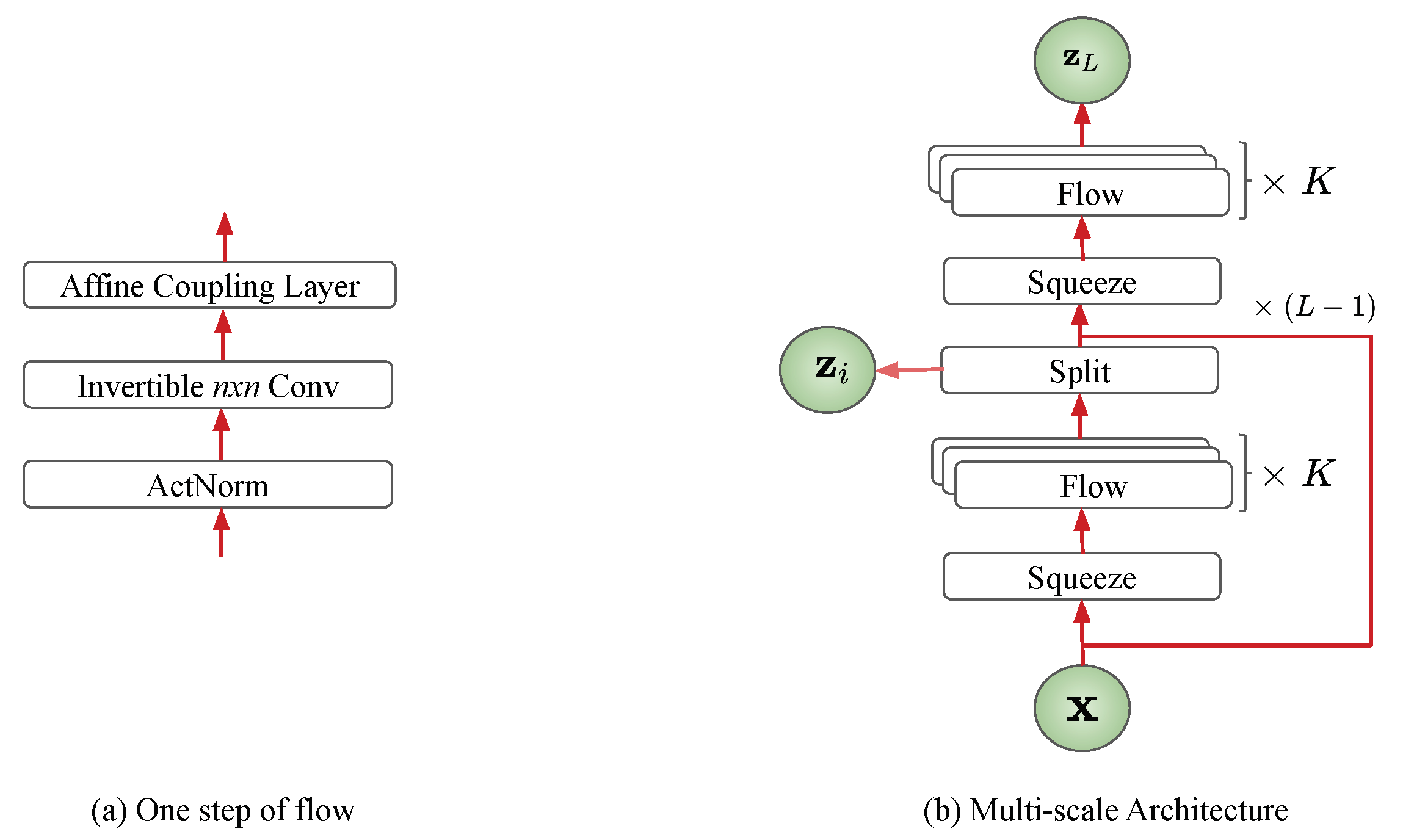
3.1. Flow-Based Generative Model
3.2. Standard Convolution
4. Invertible Convolution
4.1. Invertible Shift Function
4.2. Invertible Convolution
| Algorithm 1: Invertible Convolution |
| Input: An input |
| Result: An output of invertible convolution and the log Jacobian determinant |
| Initialize for the invertible shift function; |
| Initialize as a rotation matrix for the invertible convolution function; |
| logdet = 0.0; |
| The invertible shift function; |
| (Channel-wise operations); |
| The inverse will be ; |
| logdet = logdet + ; |
| The invertibleconvolution; |
| ; |
| The inverse will be ); |
| logdet = logdet + * H * W; |
| Return and logdet; |
5. Experiments
5.1. Quantitative Experiments
5.2. Qualitative Experiments
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Sun, S.; Pang, J.; Shi, J.; Yi, S.; Ouyang, W. FishNet: A Versatile Backbone for Image, Region, and Pixel Level Prediction. Available online: https://arxiv.org/abs/1901.03495 (accessed on 8 July 2021).
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In Lecture Notes in Computer Science Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 21–37. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Luu, K.; Seshadri, K.; Savvides, M.; Bui, T.; Suen, C. Contourlet Appearance Model for Facial Age Estimation. In Proceedings of the 2011 International Joint Conference on Biometrics (IJCB), Washington, DC, USA, 11–13 October 2011. [Google Scholar]
- Le, H.; Seshadri, K.; Luu, K.; Savvides, M. Facial Aging and Asymmetry Decomposition Based Approaches to Identification of Twins. Pattern Recognit. 2015, 48, 3843–3856. [Google Scholar] [CrossRef]
- Xu, F.; Luu, K.; Savvides, M. Spartans: Single-sample Periocular-based Alignment-robust Recognition Technique Applied to Non-frontal Scenarios. IEEE Trans. Image Process. 2015, 12, 4780–4795. [Google Scholar] [CrossRef]
- Xu, J.; Luu, K.; Savvides, M.; Bui, T.; Suen, C. Investigating Age Invariant Face Recognition Based on Periocular Biometrics. In Proceedings of the 2011 International Joint Conference on Biometrics (IJCB), Washington, DC, USA, 11–13 October 2011. [Google Scholar]
- Duong, C.; Quach, K.; Luu, K.; Le, H.K. Fine Tuning Age Estimation with Global and Local Facial Features. In Proceedings of the 36th International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- Luu, K.; Bui, T.K.; Suen, C. Age Estimation using Active Appearance Models and Support Vector Machine Regression. In Proceedings of the 2009 IEEE 3rd International Conference on Biometrics: Theory, Applications, and Systems, Washington, DC, USA, 28–30 September 2009. [Google Scholar]
- Luu, K.; Bui, T.; Suen, C. Kernel Spectral Regression of Perceived Age from Hybrid Facial Features. In Proceedings of the 2011 IEEE International Conference on Automatic Face and Gesture Recognition (FG), Santa Barbara, CA, USA, 21–25 March 2011. [Google Scholar]
- Chen, C.; Yang, W.; Wang, Y.; Ricanek, K.; Luu, K. Facial Feature Fusion and Model Selection for Age Estimation. In Proceedings of the 2011 IEEE International Conference on Automatic Face and Gesture Recognition (FG), Santa Barbara, CA, USA, 21–25 March 2011. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Luu, K.K., Jr.; Bui, T.; Suen, C. The Familial Face Database: A Longitudinal Study of Family-based Growth and Development on Face Recognition. In Proceedings of the Robust Biometrics: Understanding Science and Technology, Marriott Waikiki, HI, USA, 2–5 November 2008. [Google Scholar]
- Luu, K. Computer Approaches for Face Aging Problems. In Proceedings of the 23th Canadian Conference On Artificial Intelligence (CAI), Ottawa, ON, Canada, 31 May–2 June 2010. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Karras, T.; Aila, T.; Laine, S.; Lehtinen, J. Progressive growing of gans for improved quality, stability, and variation. arXiv 2017, arXiv:1710.10196. [Google Scholar]
- Duong, C.; Luu, K.; Quach, K.; Bui, T. Longitudinal Face Modeling via Temporal Deep Restricted Boltzmann Machines. In Proceedings of the 2016 IEEE Conference On Computer Vision And Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Duong, C.; Quach, K.; Luu, K.; Le, T.; Savvides, M. Temporal Non-volume Preserving Approach to Facial Age-Progression and Age-Invariant Face Recognition. In Proceedings of the 2017 IEEE International Conference On Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Mattia, F.D.; Galeone, P.; Simoni, M.D.; Ghelfi, E. A Survey on GANs for Anomaly Detection. arXiv 2019, arXiv:1906.11632. [Google Scholar]
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T.S. Generative image inpainting with contextual attention. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5505–5514. [Google Scholar]
- Karras, T.; Laine, S.; Aila, T. A style-based generator architecture for generative adversarial networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4401–4410. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Duong, C.; Luu, K.; Quach, K.; Nguyen, N.; Patterson, E.; Bui, T.; Le, N. Automatic Face Aging in Videos via Deep Reinforcement Learning. In Proceedings of the 2019 IEEE/CVF Conference On Computer Vision And Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Duong, C.; Luu, K.; Quach, K.; Bui, T. Deep Appearance Models: A Deep Boltzmann Machine Approach for Face Modeling. Int. J. Comput. Vis. 2019, 127, 437–455. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Dhariwal, P. Glow: Generative Flow with Invertible 1x1 Convolutions. In Advances in Neural Information Processing Systems 31; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; pp. 10215–10224. [Google Scholar]
- Kingma, D.P.; Salimans, T.; Jozefowicz, R.; Chen, X.; Sutskever, I.; Welling, M. Improved Variational Inference with Inverse Autoregressive Flow. In Advances in Neural Information Processing Systems 29; Lee, D.D., Sugiyama, M., Luxburg, U.V., Guyon, I., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2016; pp. 4743–4751. [Google Scholar]
- Dinh, L.; Krueger, D.; Bengio, Y. NICE: Non-linear Independent Components Estimation. arXiv 2015, arXiv:1410.8516. [Google Scholar]
- Dinh, L.; Sohl-Dickstein, J.; Bengio, S. Density estimation using Real NVP. In Proceedings of the 3rd International Conference on Learning Representations, ICLR, Toulon, France, 24–26 April 2017. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Advances in Neural Information Processing Systems 27; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2014; pp. 2672–2680. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Hoogeboom, E.; van den Berg, R.; Welling, M. Emerging Convolutions for Generative Normalizing Flows. arxiv 2019, arXiv:1901.11137. [Google Scholar]
- Papamakarios, G.; Murray, I.; Pavlakou, T. Masked Autoregressive Flow for Density Estimation. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 2335–2344. [Google Scholar]
- Behrmann, J.; Grathwohl, W.; Chen, R.T.Q.; Duvenaud, D.; Jacobsen, J.H. Invertible Residual Networks. In Proceedings of the 36th International Conference on Machine Learning, Beach, CA, USA, 10–15 June 2019; Chaudhuri, K., Salakhutdinov, R., Eds.; PMLR: Long Beach, CA, USA, 2019; Volume 97, pp. 573–582. [Google Scholar]
- Kim, H.; Papamakarios, G.; Mnih, A. The Lipschitz Constant of Self-Attention. arXiv 2021, arXiv:2006.04710. [Google Scholar]
- Chen, R.T.; Behrmann, J.; Duvenaud, D.; Jacobsen, J.H. Residual flows for invertible generative modeling. arXiv 2019, arXiv:1906.02735. [Google Scholar]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: http://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 8 July 2021).
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. Proceedings of Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Liu, Z.; Luo, P.; Wang, X.; Tang, X. Deep Learning Face Attributes in the Wild. Proceedings of International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Ho, J.; Chen, X.; Srinivas, A.; Duan, Y.; Abbeel, P. Flow++: Improving Flow-Based Generative Models with Variational Dequantization and Architecture Design. arXiv 2019, arXiv:1902.00275. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.U.; Polosukhin, I. Attention is All you Need. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Germain, M.; Gregor, K.; Murray, I.; Larochelle, H. MADE: Masked Autoencoder for Distribution Estimation. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; Bach, F., Blei, D., Eds.; PMLR: Lille, France, 2015; Volume 37, pp. 881–889. [Google Scholar]
- Truong, D.; Duong, C.N.; Luu, K.; Tran, M.; Le, N. Domain Generalization via Universal Non-volume Preserving Approach. In Proceedings of the 2020 17th Conference On Computer And Robot Vision (CRV), Ottawa, ON, Canada, 13–15 May 2020. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]



| Description | Function | Reverse Function | Log-Determinant |
|---|---|---|---|
| ActNorm [29] | |||
| Affine Coupling [32] | |||
| conv [29] | |||
| Our Shift Function |
| Models | CIFAR-10 | ImageNet 32 | ImageNet 64 |
|---|---|---|---|
| RealNVP | 3.49 | 4.28 | 3.98 |
| Glow | 3.35 | 4.09 | 3.81 |
| Emerging Conv | 3.34 | 4.09 | 3.81 |
| Ours | 3.50 | 3.96 | 3.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Truong, T.-D.; Duong, C.N.; Tran, M.-T.; Le, N.; Luu, K. Fast Flow Reconstruction via Robust Invertible n × n Convolution. Future Internet 2021, 13, 179. https://doi.org/10.3390/fi13070179
Truong T-D, Duong CN, Tran M-T, Le N, Luu K. Fast Flow Reconstruction via Robust Invertible n × n Convolution. Future Internet. 2021; 13(7):179. https://doi.org/10.3390/fi13070179
Chicago/Turabian StyleTruong, Thanh-Dat, Chi Nhan Duong, Minh-Triet Tran, Ngan Le, and Khoa Luu. 2021. "Fast Flow Reconstruction via Robust Invertible n × n Convolution" Future Internet 13, no. 7: 179. https://doi.org/10.3390/fi13070179
APA StyleTruong, T.-D., Duong, C. N., Tran, M.-T., Le, N., & Luu, K. (2021). Fast Flow Reconstruction via Robust Invertible n × n Convolution. Future Internet, 13(7), 179. https://doi.org/10.3390/fi13070179






