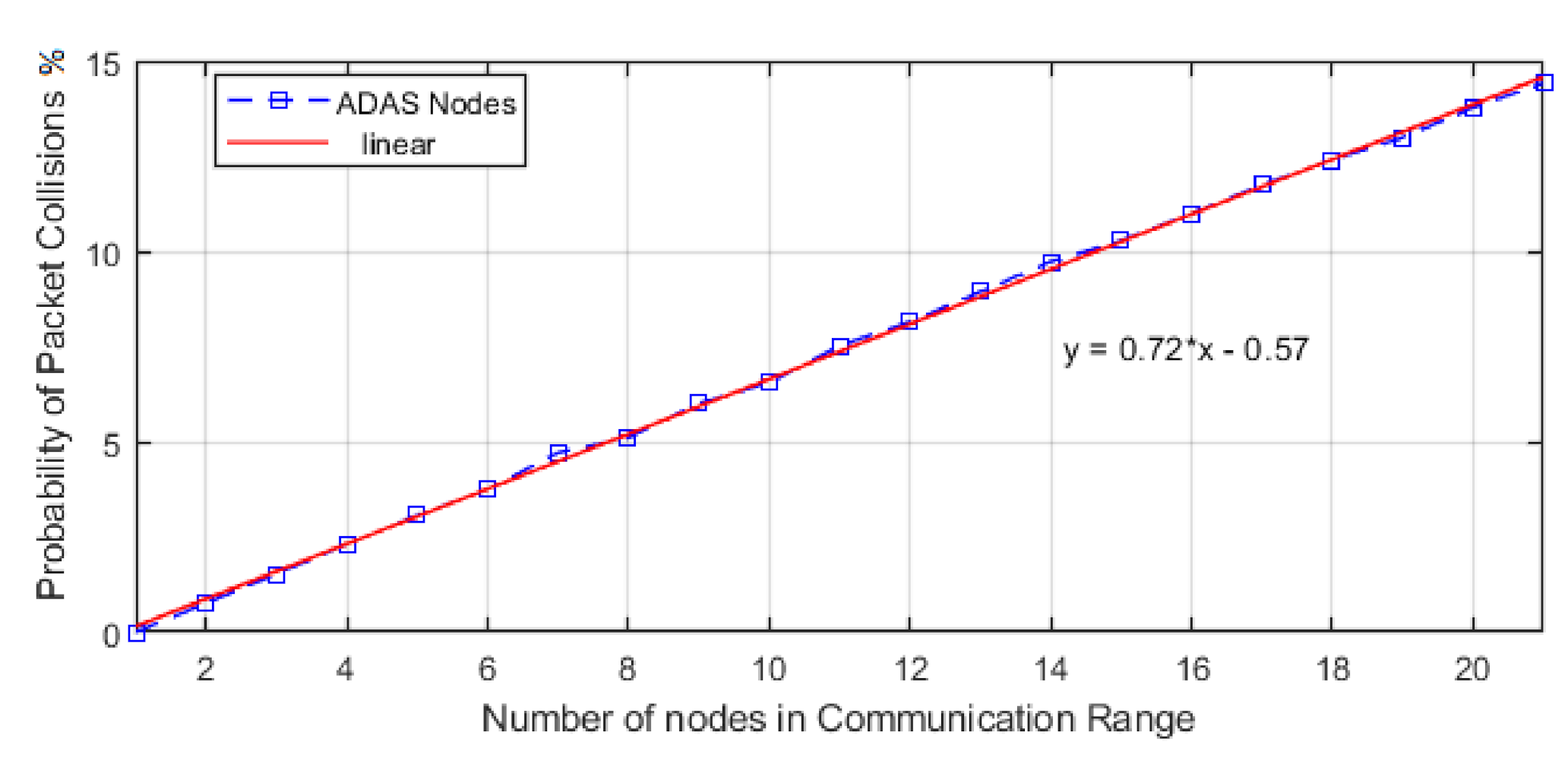
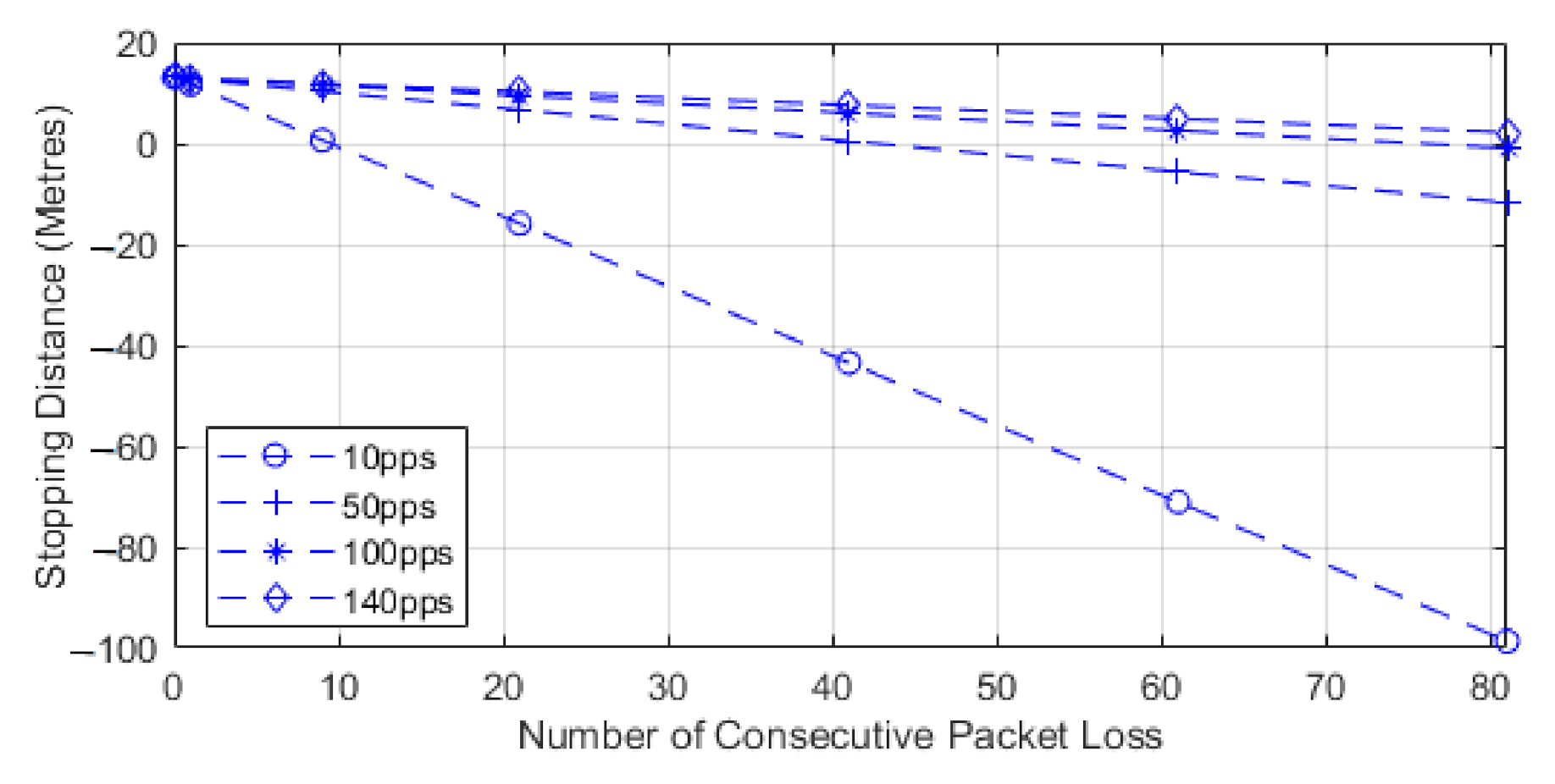
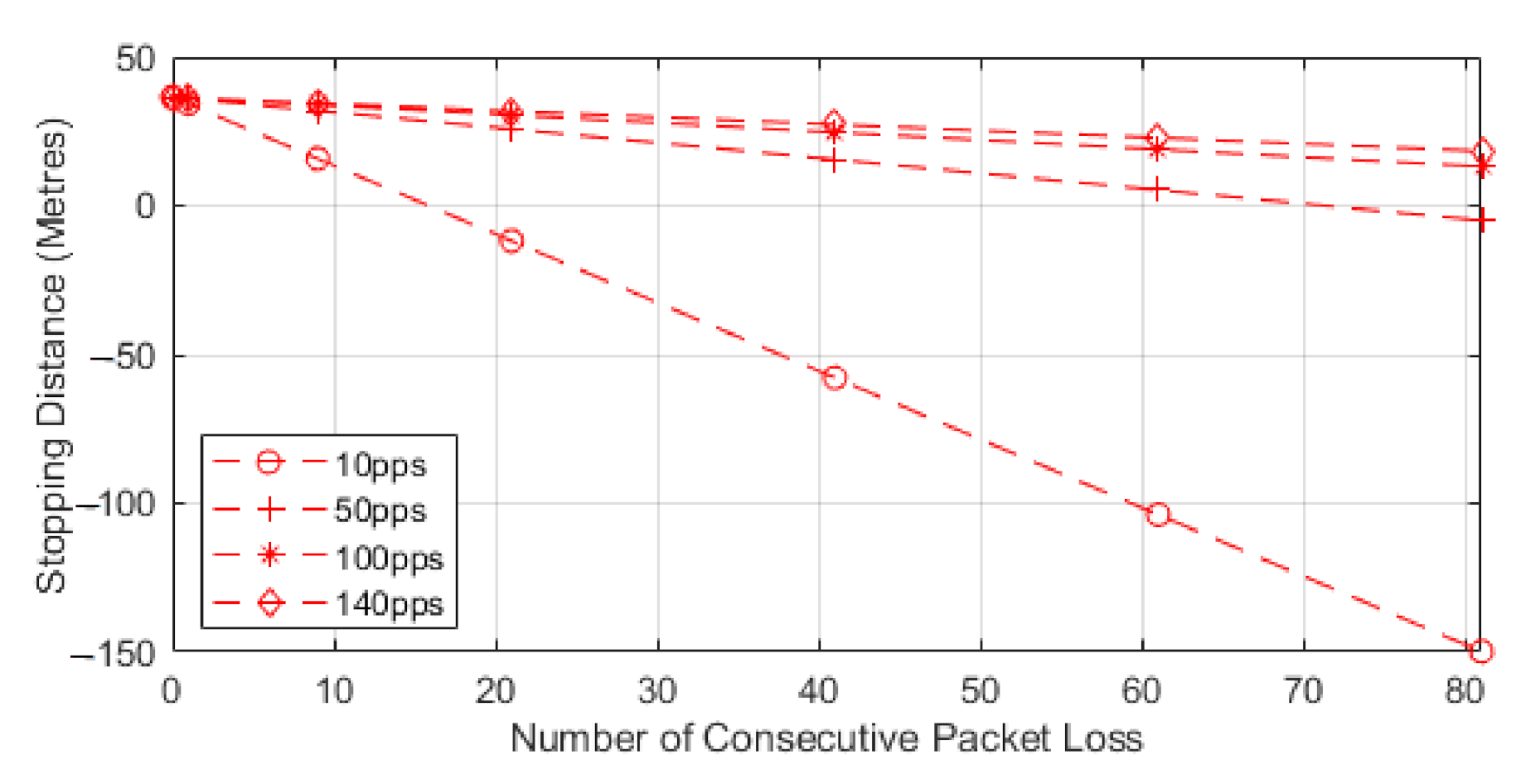
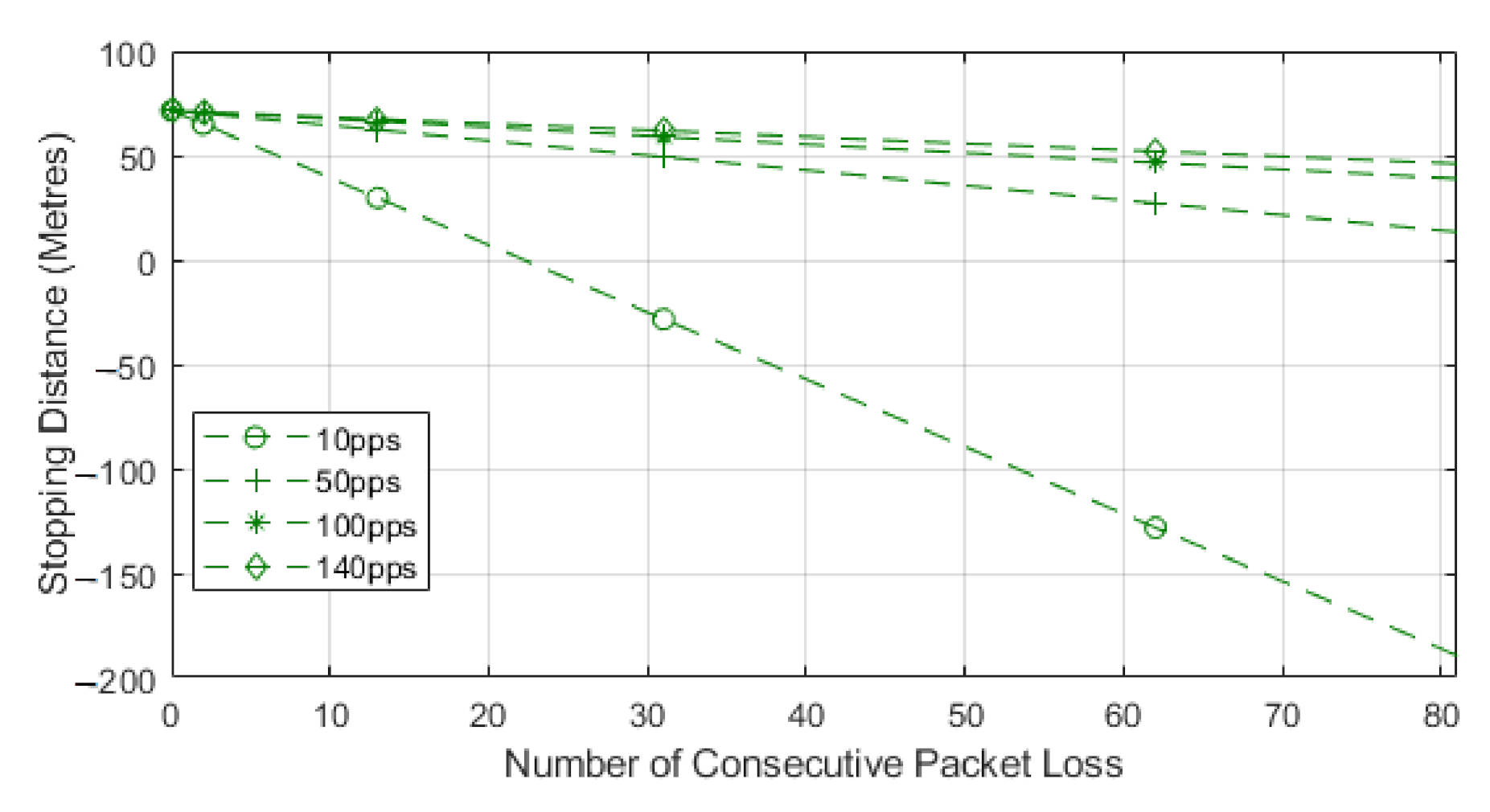
These different timings will be broken down in our results with the reaction time being substituted to our communication time. We also omit the Thinking Distance parameter as this would be an automatic braking system based on communication the driver of the vehicle would not be counted upon to react.
4.1. Stopping Distance
This section shows results on how the testbed could be used in collision avoidance, such as rear end collisions or emergency braking. This is based upon the latency finding of our experiments between sending and receiving nodes. Latency or information freshness is critical for CAVs as this is the speed at which the nodes are communicating information and is required to be 100 ms for standard BSM [
39,
40]. The latency that we monitored can be seen in
Figure 1, and this experiment was conducted by measuring processing time and calculating the propagation time. The equation that is used to calculate End to End processing time (
PT) is shown in Equation (1), and it shows the Time sent (
T) and Time received (
T) of a packet when transmitted through direct connection via SubMiniature version A (SMA) cable, which eliminates the propagation time. We then subtract the times from one another, leaving us with the processing time of both systems, which we assume is even on both sides. Then, we calculated the propagation time (
T) for each distance, and, because we are only using distances up to 100 m, the propagation is at most 33.4 micro seconds. We then add the two times to find total End to End Latency (
T). This latency, however, ignores the logical processing inside of the receiving device for reacting to the received packet, which would be negligible.
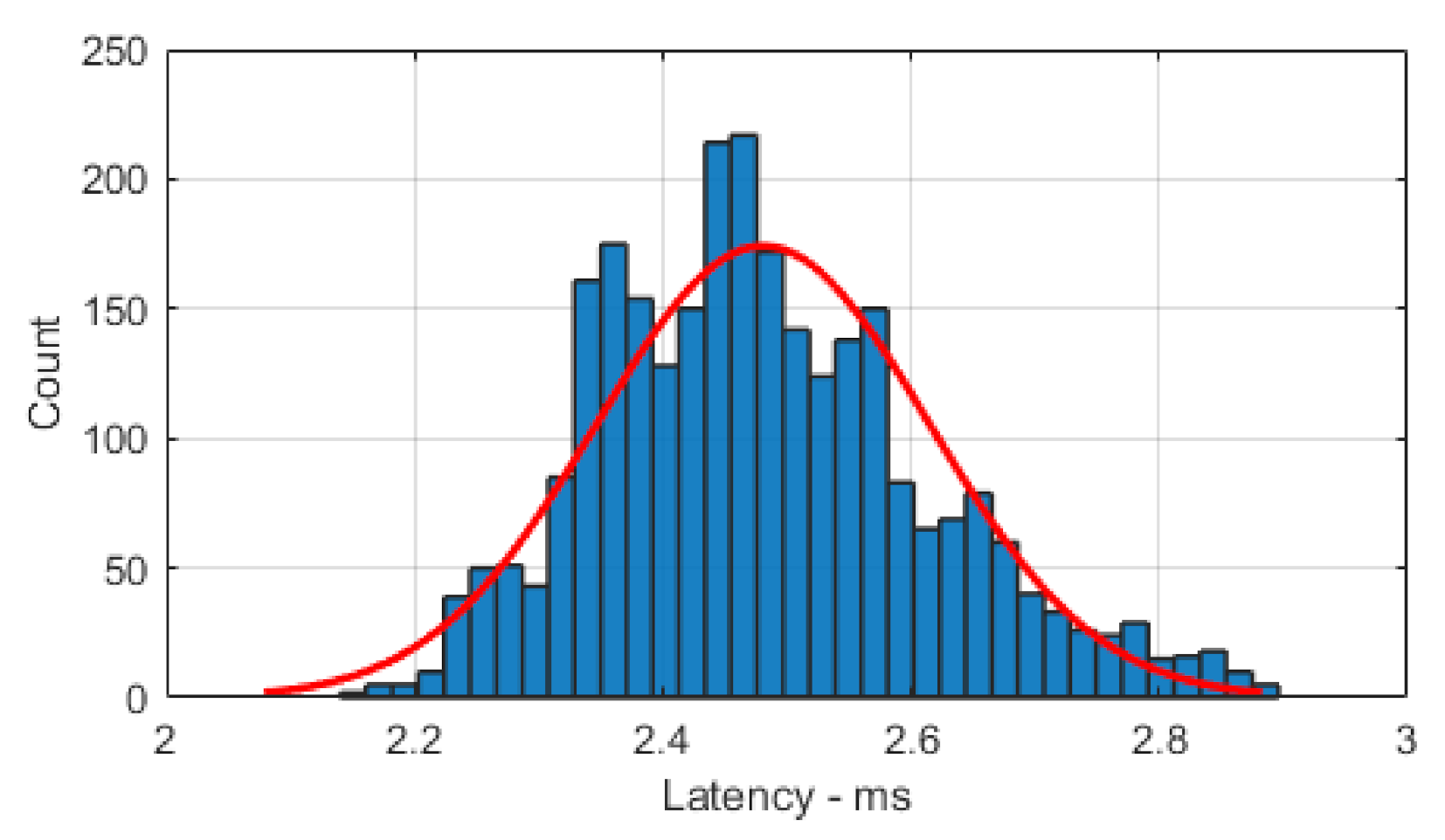
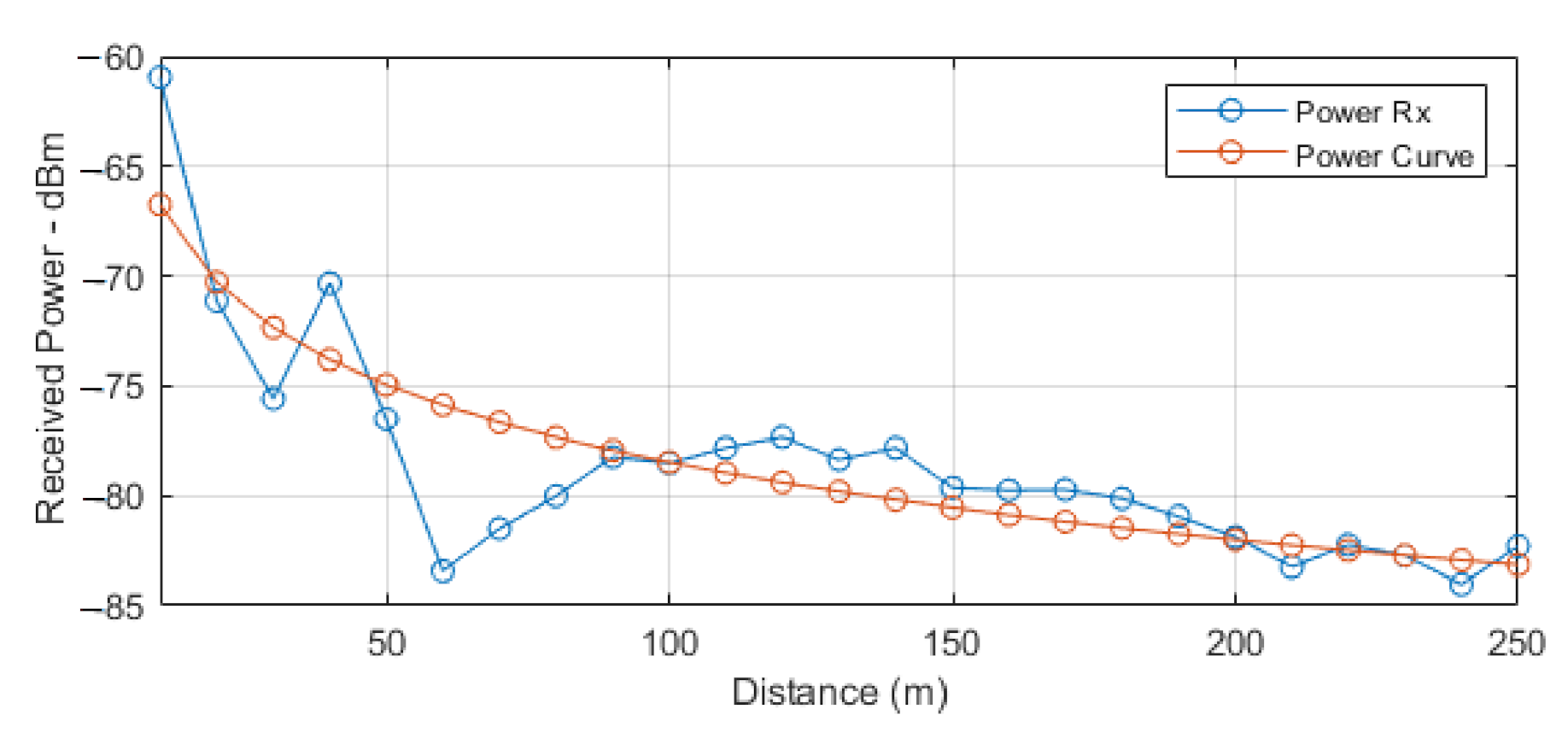
The results for latency can be seen in
Figure 1 and are the product of over 2000 samples. We found that the latency ranged between 2.1 and 2.9 ms with a mean of 2.48 ms, showing the latency is lower than expected for information freshness of 50 ms required for pre-crash sensing [
41].
To calculate the stopping distance (
DS), we chose to use two different methods available and used in the literature. The first equation shown in Equation (2) is the most commonly used formula used in physics to calculate braking distance (
DB); however, it is not based upon vehicle mass and assumes a rate of deceleration from 0 to max deceleration (maximum braking force) [
35,
36,
37,
38], where g is acceleration due to gravity (9.81 m/s
2),
V is velocity of vehicle, and u is the coefficient of friction. This equation is then used with an equation for thinking distance to calculate total stopping distance. Thinking distance (
DR) is calculated with the velocity (
V) and reaction time (
TR).
TR can also be represented in our case with
TE2E when using the testbed.
The coefficient of friction is a variable to describe the friction between the rubber tires of the vehicle and the road.
Table 1 shows some road examples that are based on weather and ground type, with the average coefficient values associated [
42]. In our experiments, we chose to use 0.8 as the coefficient of friction as this is the standard for normal dry road conditions for both asphalt and concrete.
The second equation shown in Equation (3) is used by many researchers, like in References [
42,
43,
44,
45], as this equation considers more in-depth variables concerning the type of car, road conditions, air conditions, and other parameters.
Table 2 details each component of Equation (3), along with the value we chose to use and the range of values that are typically used. This is then added to
DR, which is calculated in the same way as previously and leads to the total
DS.
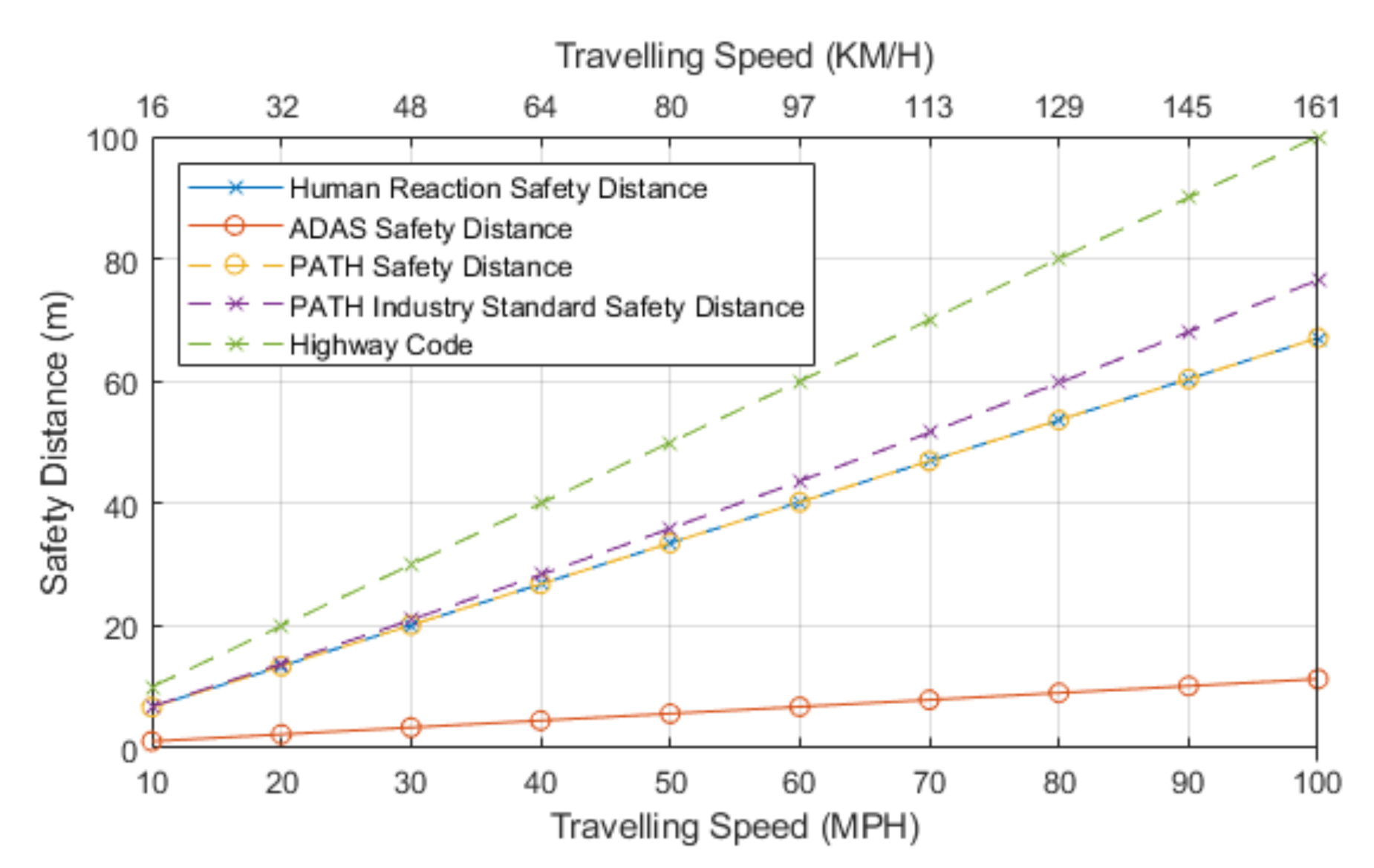
Using these equations, we predict the effect of using our maximum communication latency of 2.92 ms as the reaction time in place of the typical driver reaction time, which is suggested to be between 0.67 s and 2 s. The reaction time depends on driver state, such as age, driver experience, and state of mind. In this work, 1.5 s is chosen as the reaction time as this is the time reported by Brake to most accurately represent most drivers [
46].
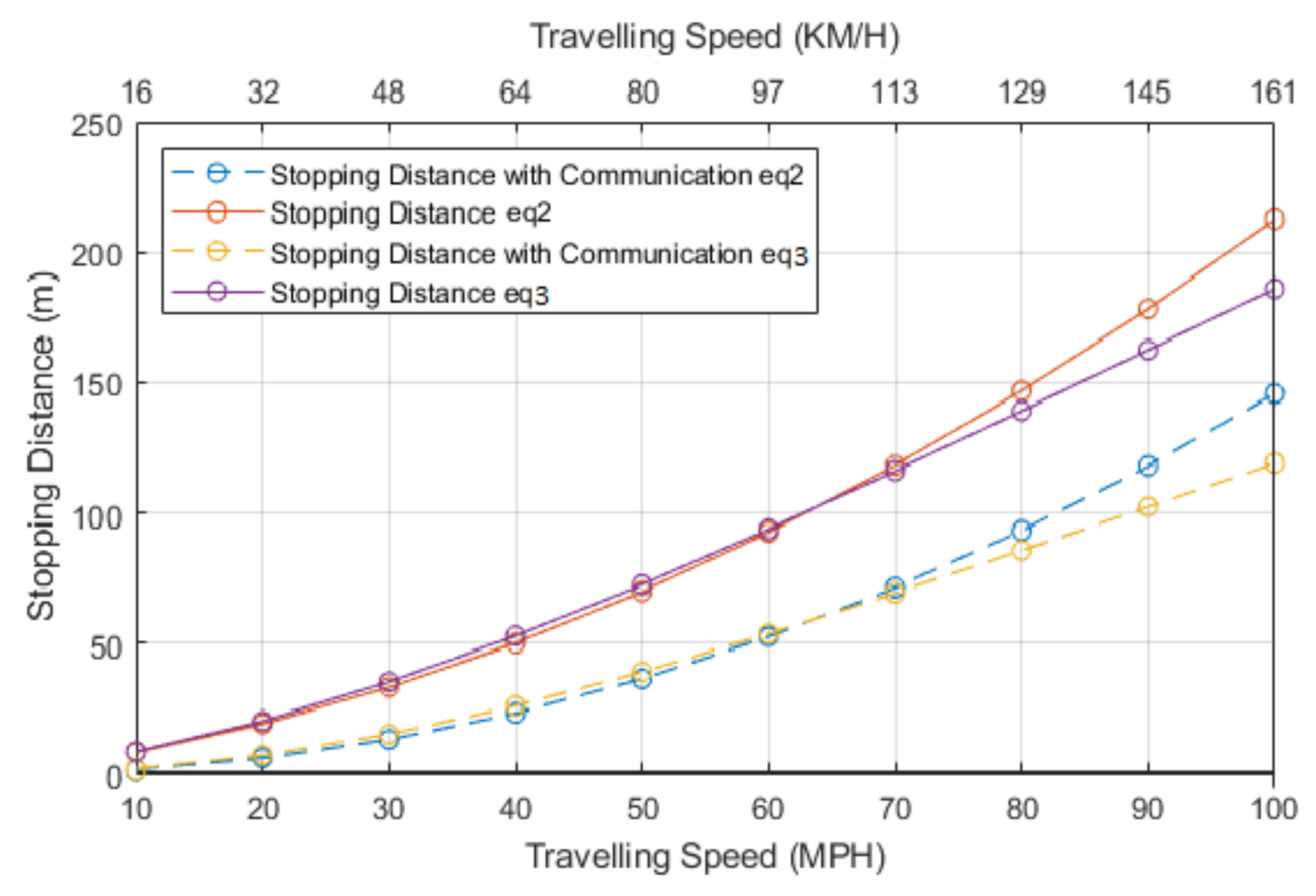
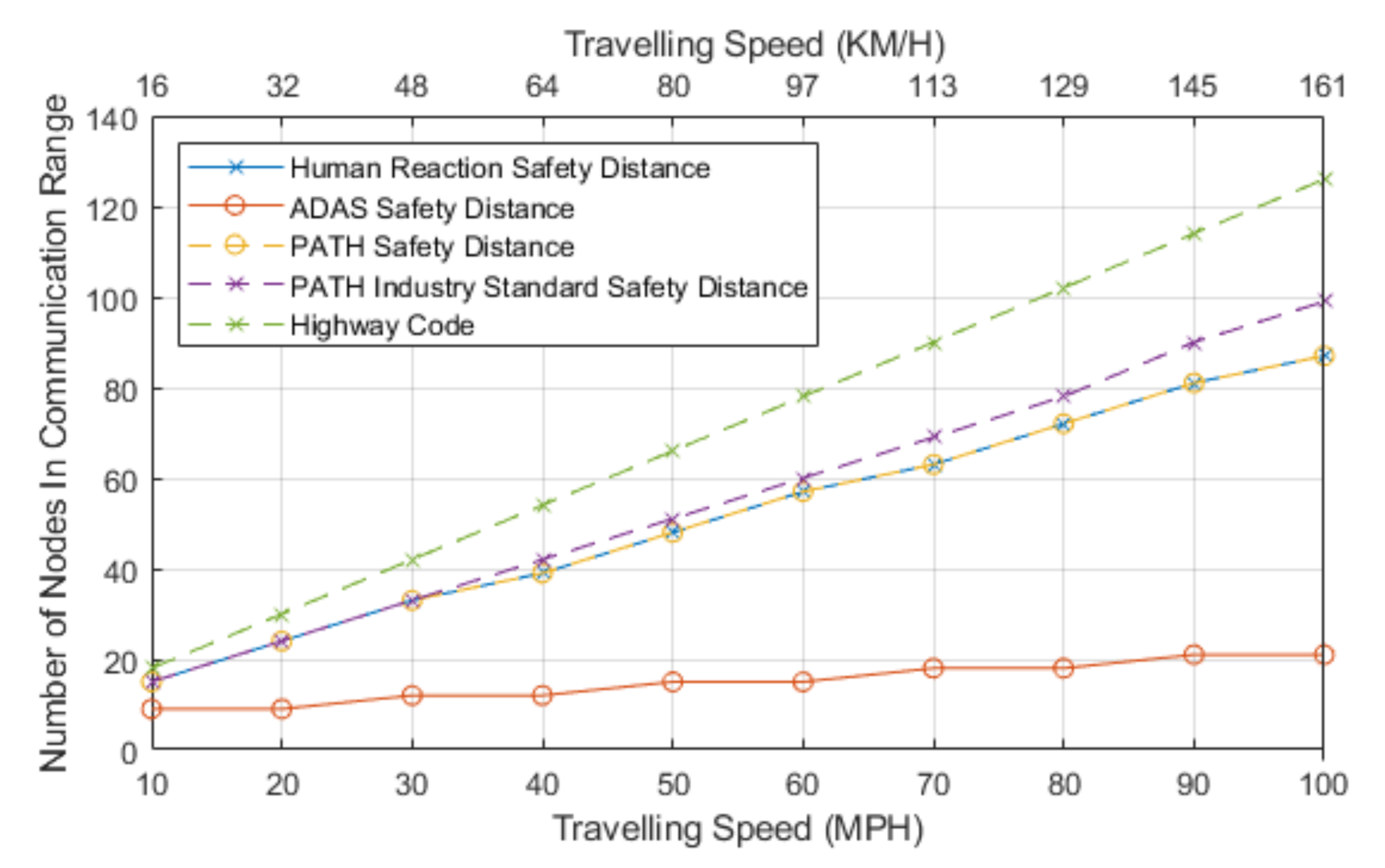
Figure 2 highlights the stopping distance reduction that could be observed when using communication-assisted systems or autonomous braking systems.
The results for this section show the difference between the stopping distance when using each method of measuring stopping distances, and they show the second has a slight reduction in distance needed. The second finding is that the reduction in distance is large when using the communication reaction time. This information can used in critical braking scenarios, such as debris on the road causing an emergency braking situation, a vehicle breaking down, a crash occurring, or sudden braking by the lead vehicle.
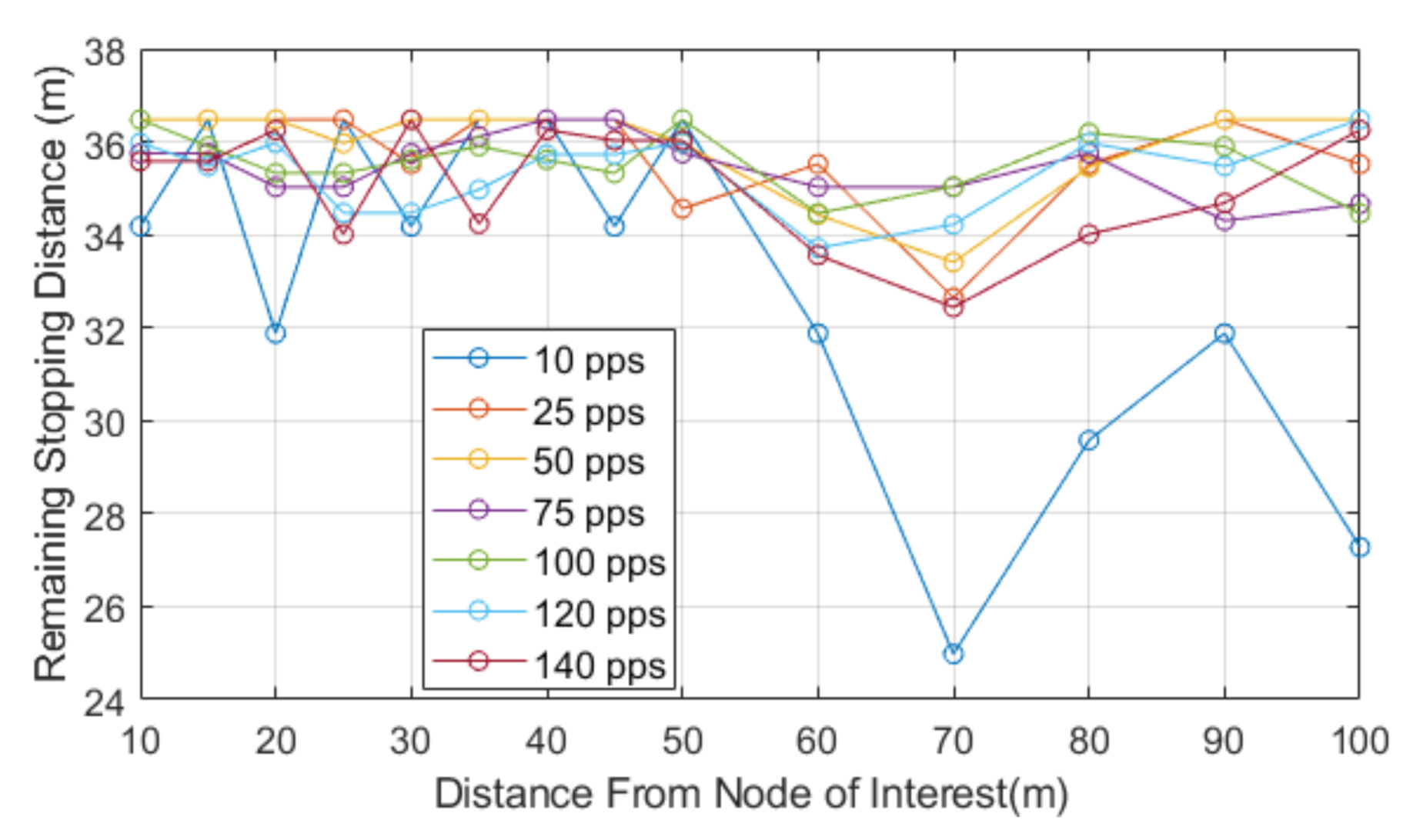
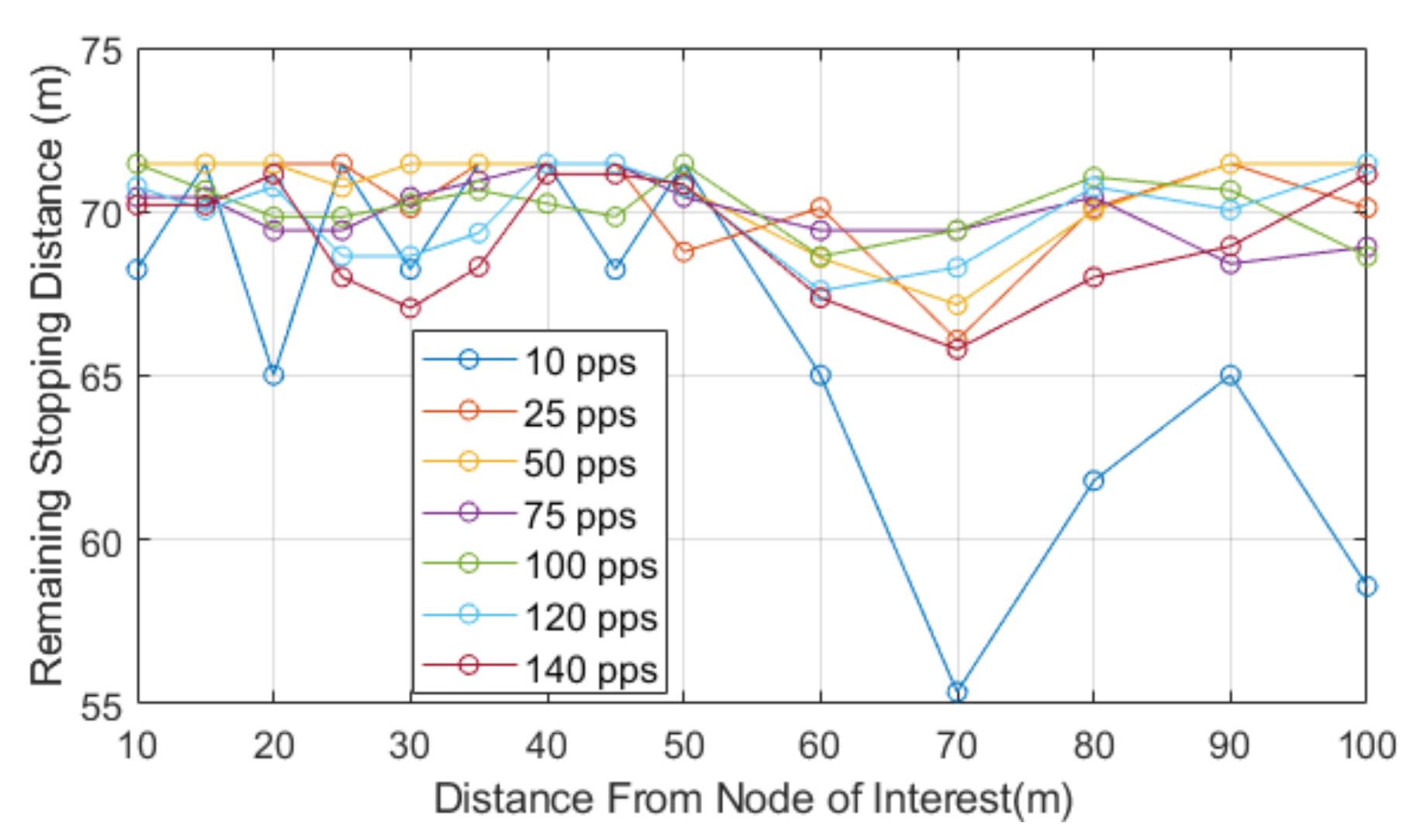
Table 3 shows the distance that can be saved at each distance with the use of communication-based reaction time when the consecutive losses are 0. This table also shows the percentage of distance that is saved and at its lowest is a decrease of over 30%.
Through the use of the two formulas, it can be seen that Equation (3) is more accurate showing the braking distances for any vehicle that is chosen. Our experiments used a small hatchback, but the equation can be altered to represent any vehicle necessary. For these reasons, this will be the method used in our experiments.
4.2. Theoretical Model for Consecutive Losses
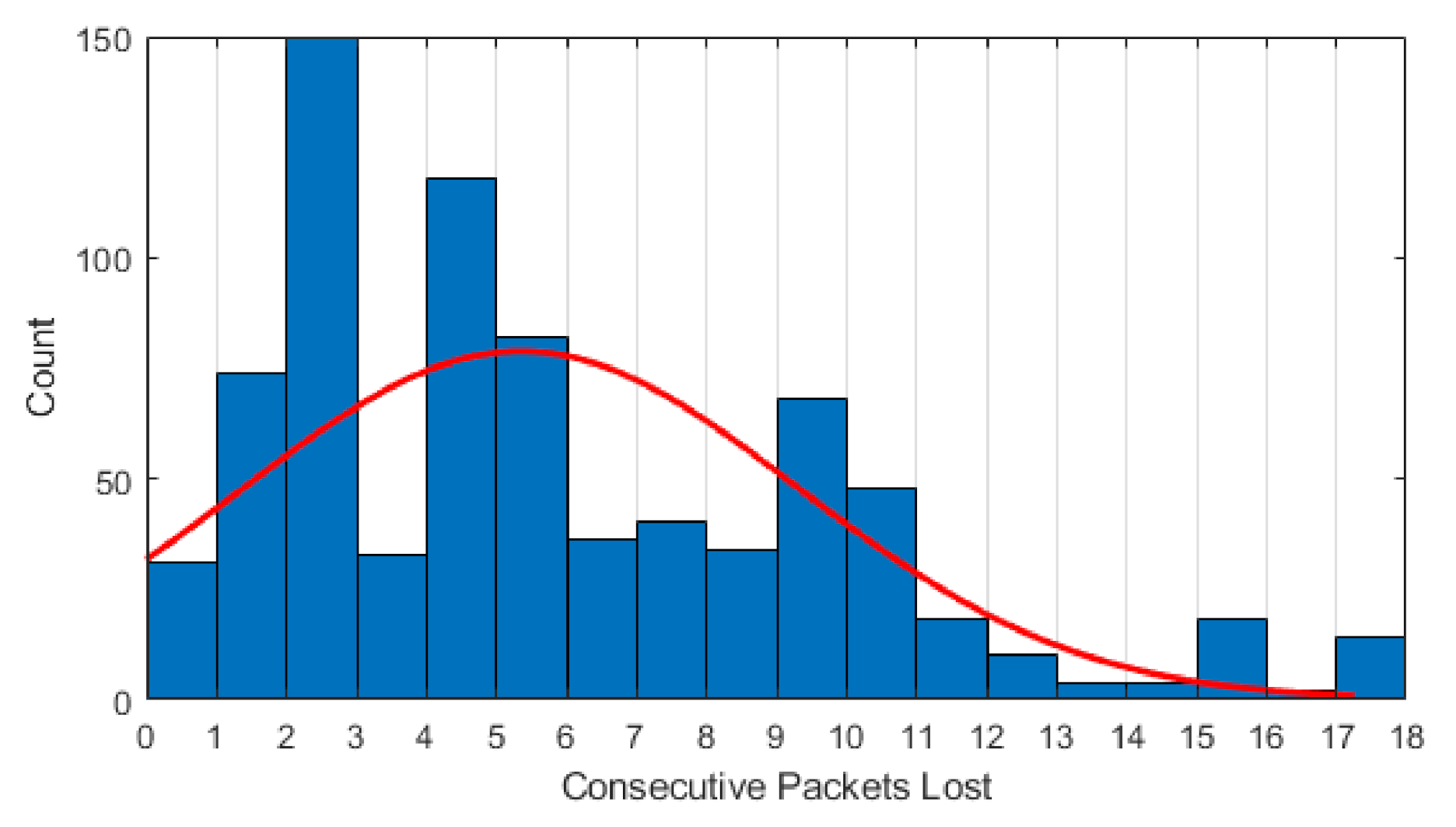
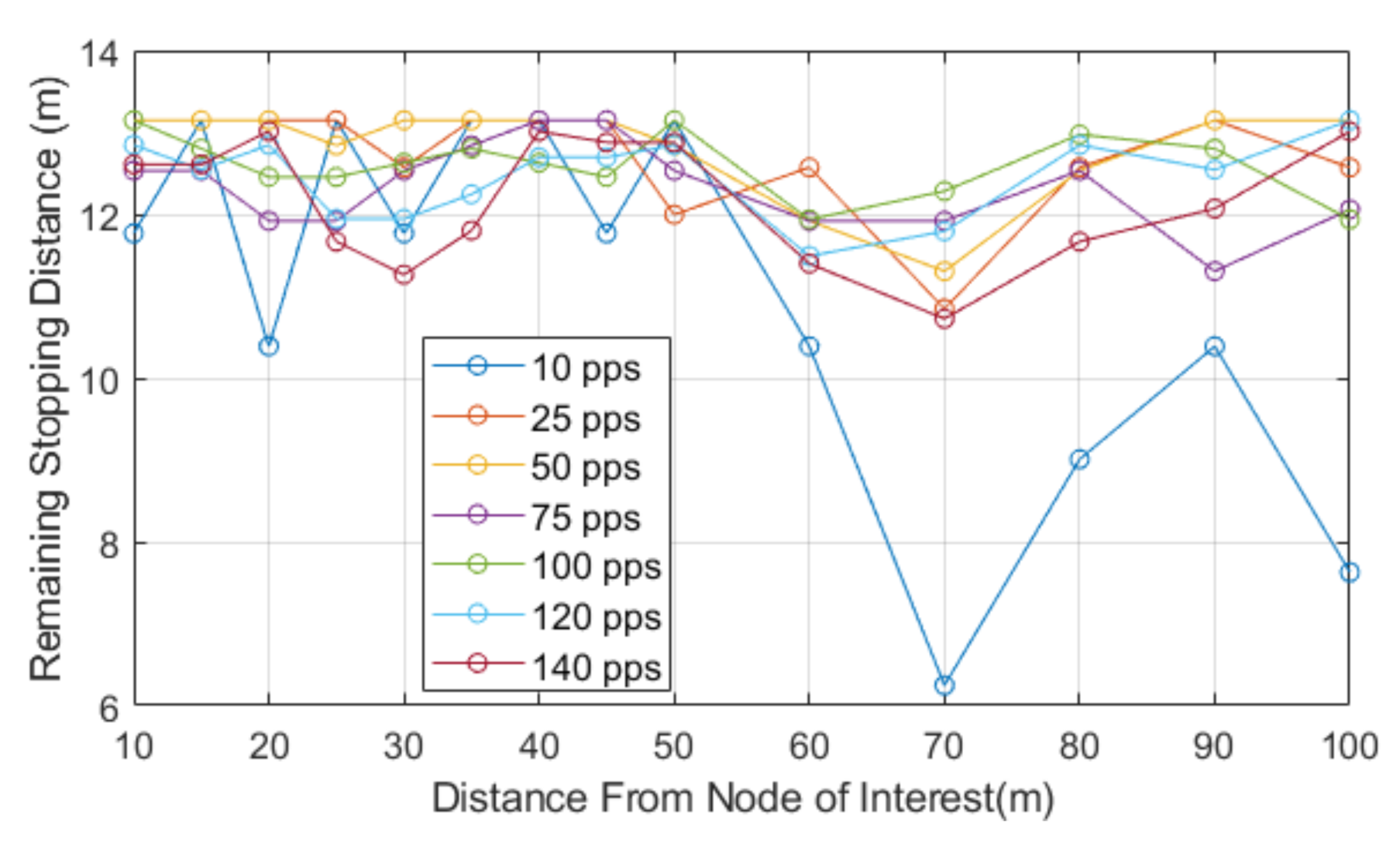
The following section outlines the main findings of the work, where the analysis is conducted as to multiple consecutive packet losses, and a model is designed and assessed to show impacts of consecutive losses. The losses we observed in our field tests, can be split into single losses or consecutive losses (burst losses). These types losses can occur due to circumstances, such as channel fluctuations, obstacles in the way, weather changes, or the hidden node problem. The use of UDP in our testbed means there is no acknowledgement of a packet being received, and this means that, if a packet is lost, the sender is not aware of this. UDP is the closest representation of a broadcast type communication used for CAMs/BSMs.
We believe this assists in identifying the reliability requirements for DSRC and highlights the importance of maintaining highly reliable systems. We have also chosen to monitor this over different data rates to analyze impacts by the Inter Packet Gap (IPG). The IPG will be abbreviated to T, which is the Packet Interval Time. The number of losses we chose to use will be shown later, but it will be stated that these losses are based upon real world field tests conducted.
We developed a model that shows the theoretical loss on the stopping distance that consecutive packet losses could have. This model is based upon the field work for stopping distance, along with an equation that calculates the loss of stopping distance per packet, which includes the packet sending interval. Equation (4) shows the model formula, and
Table 4 shows the parameter information.
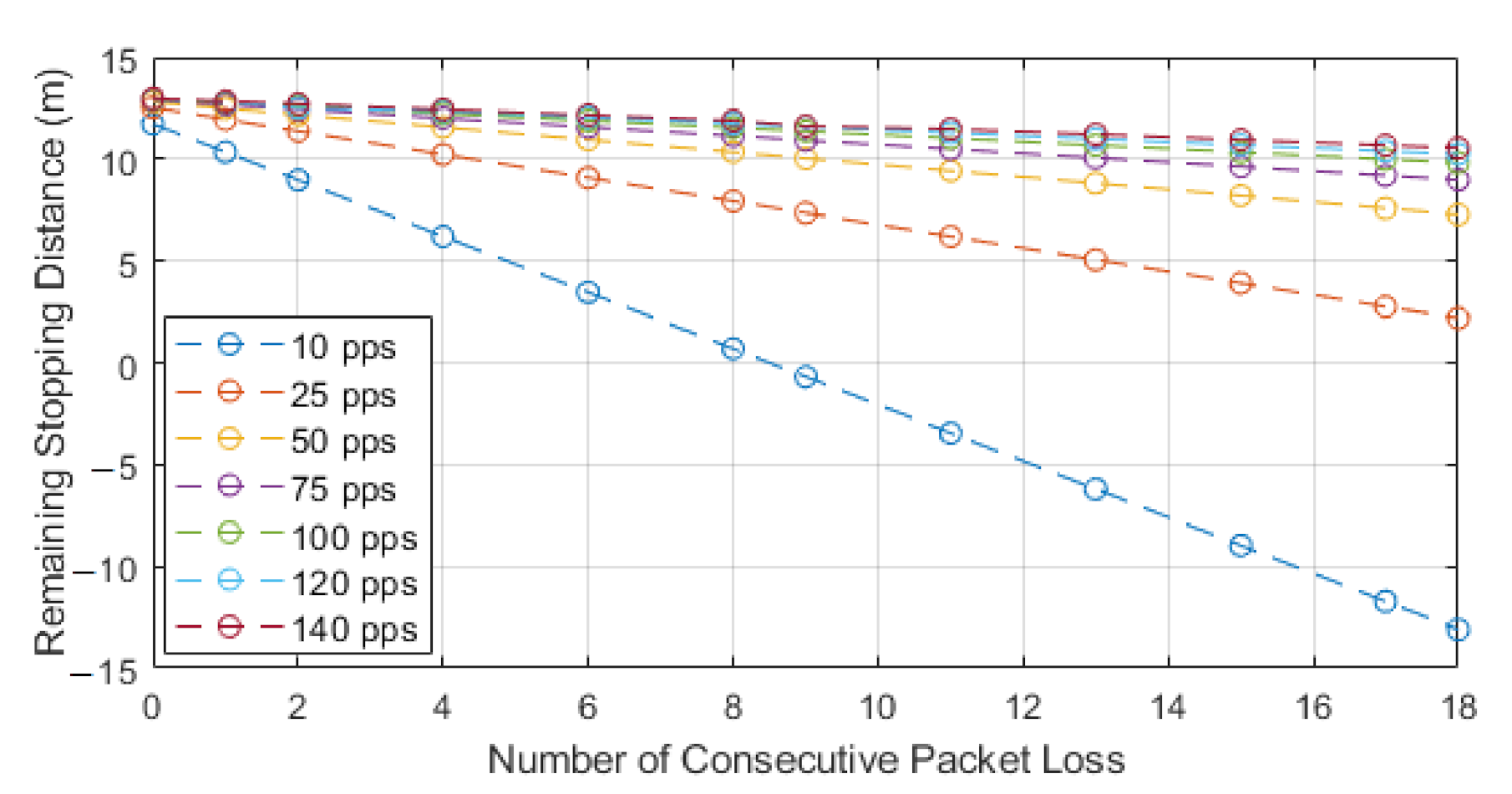
This initial model represented in Equation (4) does not consider the next packet after the burst loss being received and processed. This means that, after consecutive packet losses, no packet is successfully received, processed, and an action taken. This would be vital in autonomous systems, whereby the communication would be essential to maintaining adequate distances and awareness. For this an extra iteration of processing, round-trip time and packet interval would need to be included, which are used to represent the packet being received successfully, and this is shown in Equation (5).
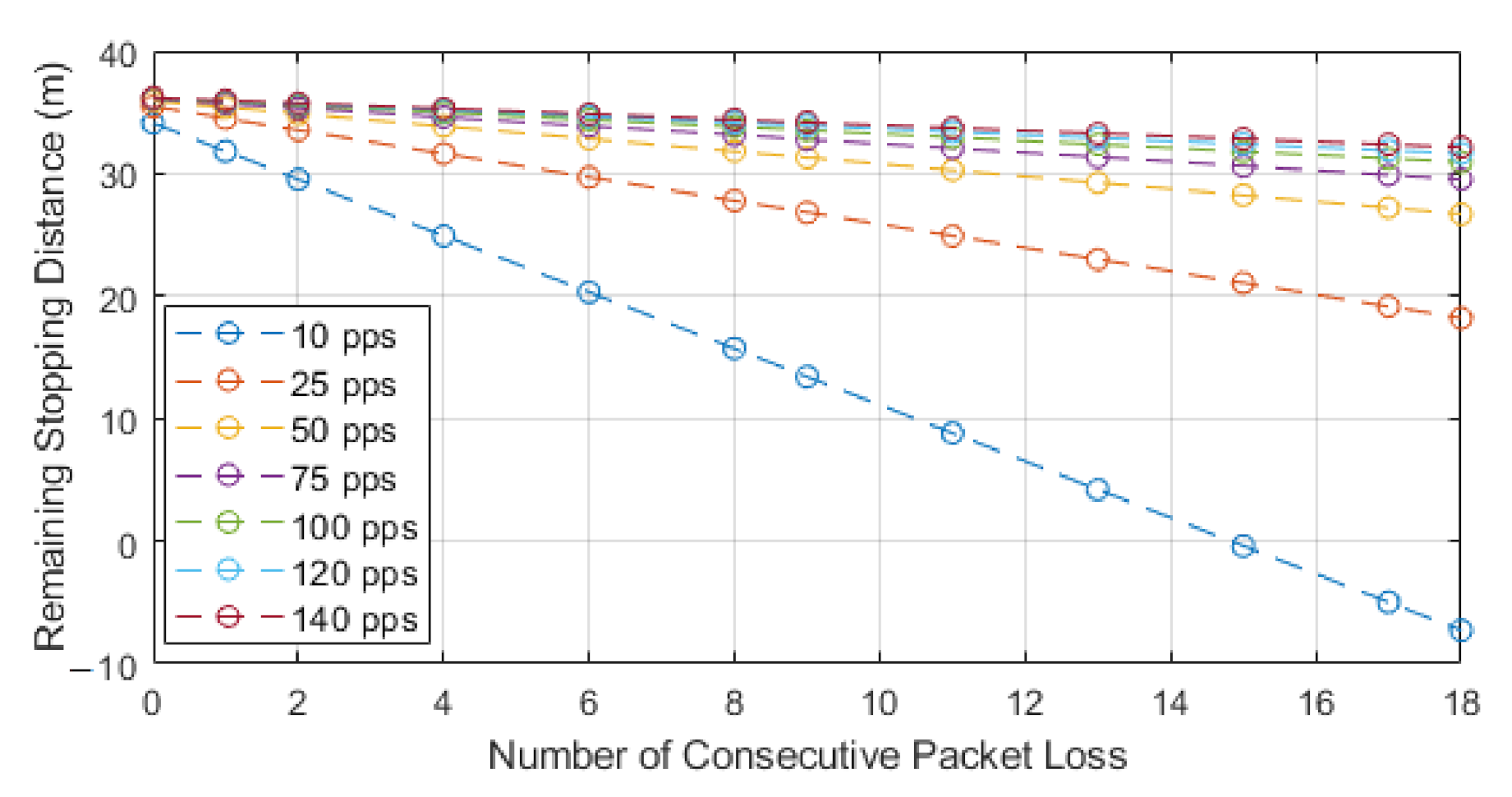
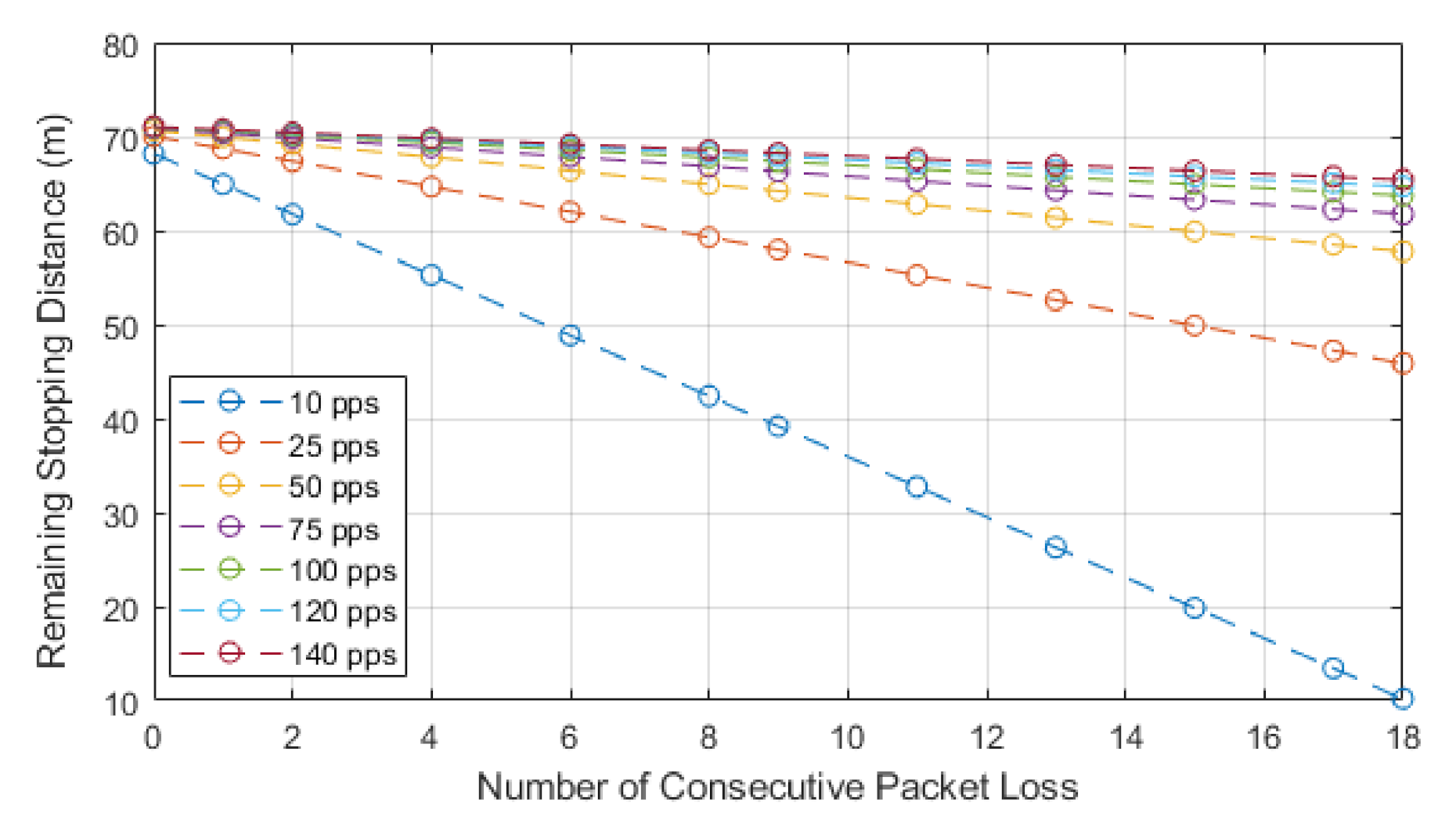
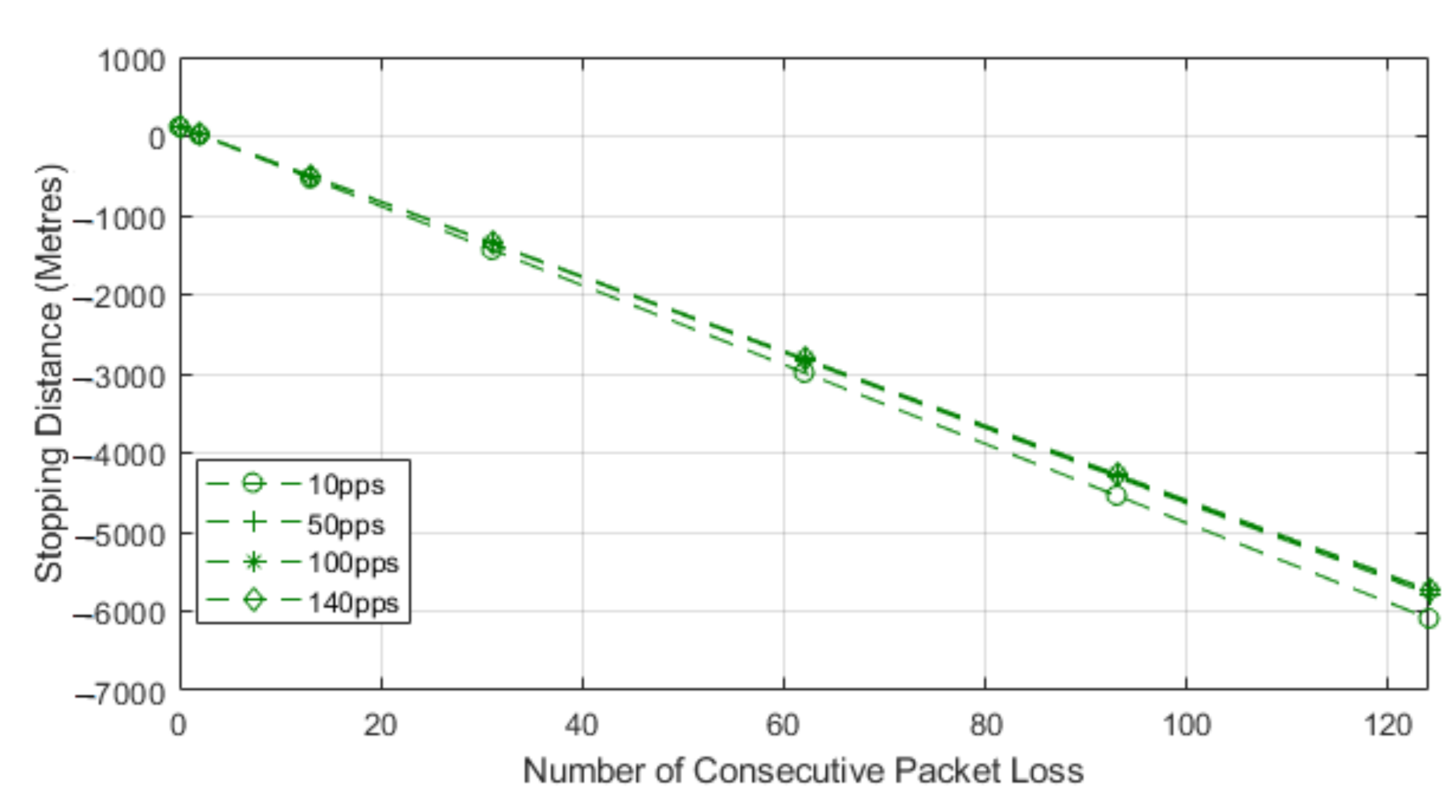
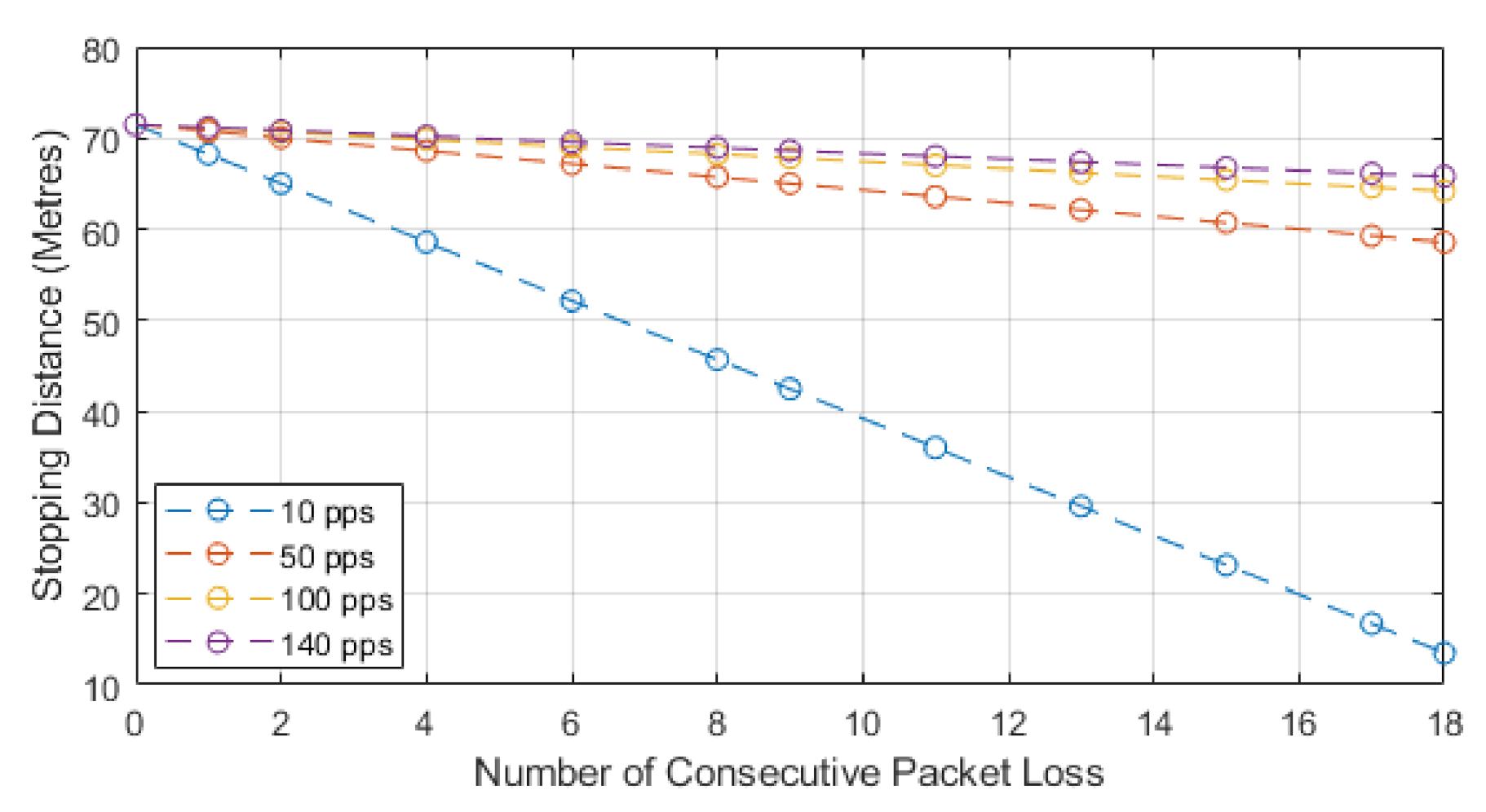
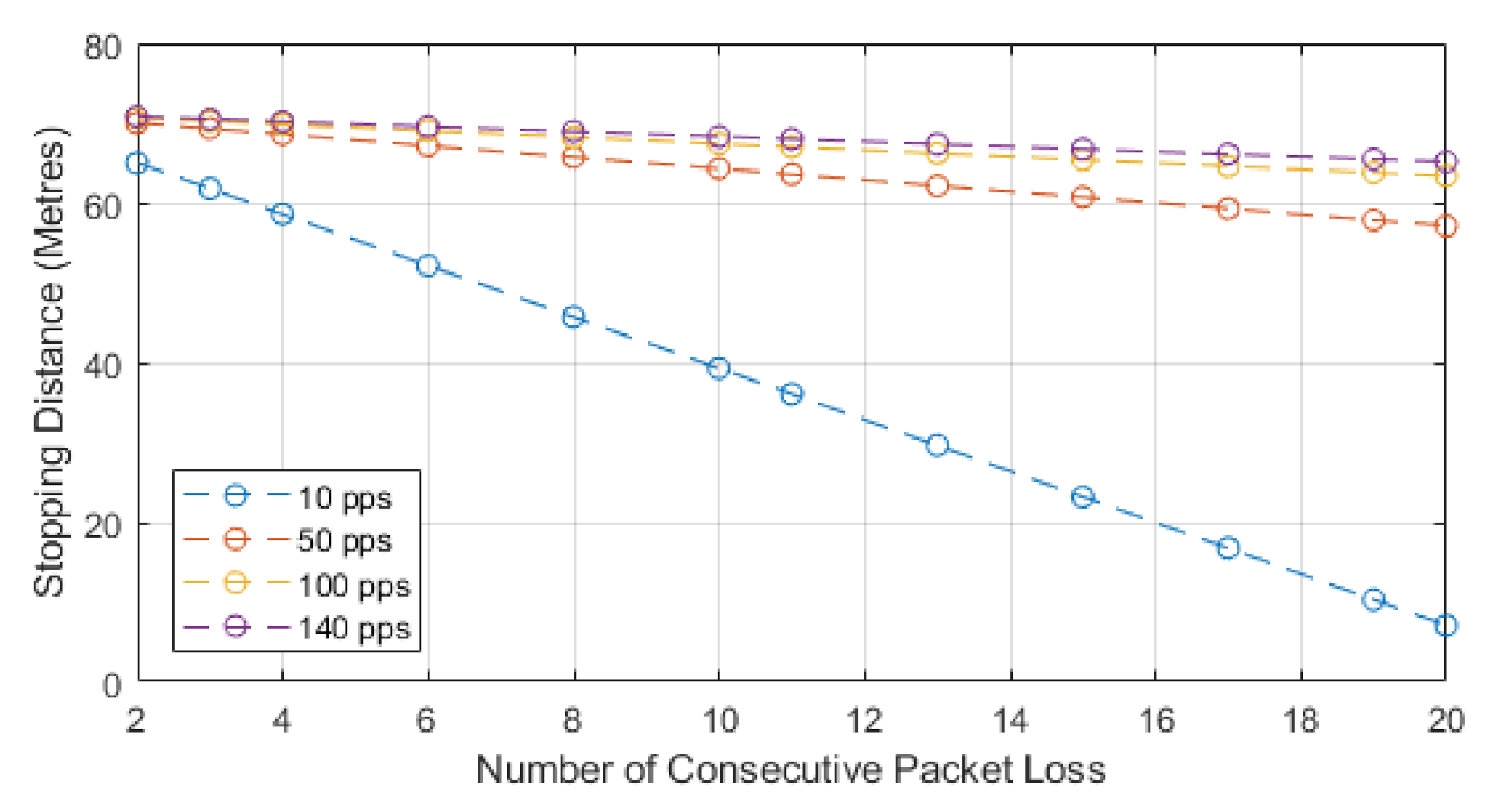
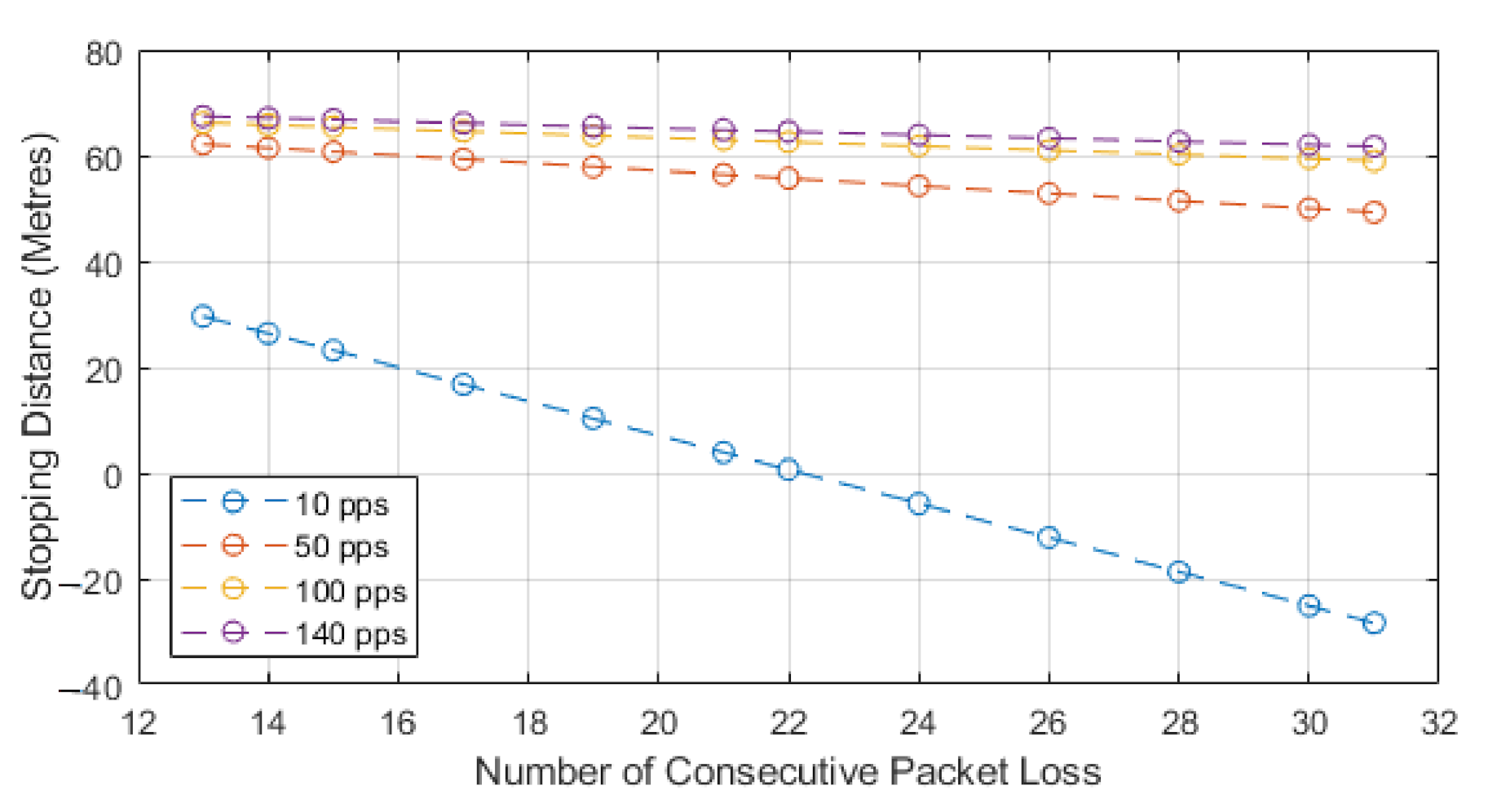
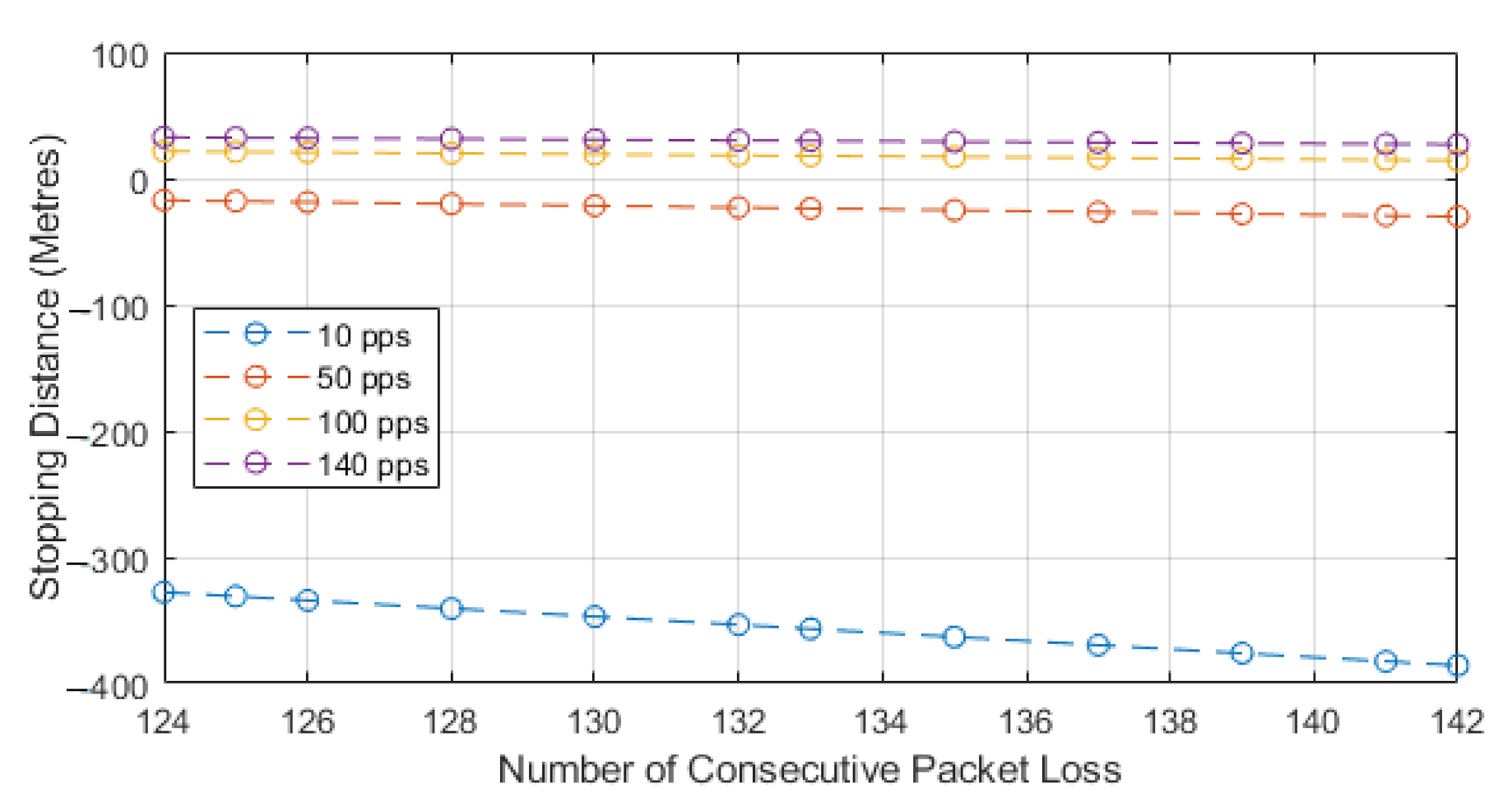
We chose to use the second model as this paper is focused on the impacts of how packet loss can alter the stopping distance when relying on communications, and this equation highlights that impact. The model works by utilizing Equation (3) to find the normalized stopping distance for a vehicle and then we subtract the distance lost via consecutive losses. The losses can be seen in the second part of Equation (5). The result of this equation will leave us with the distance remaining to a collision or stopping distance remaining. We know that, after losing the consecutive packets, the vehicle will still need to stop in order to show the full distance required to stop, and the Equation (5) sign could switch. This would then represent the stopping distance, plus the distance lost through consecutive loss, to leave us with total stopping distance. In our case, we are showing how lead and following autonomous vehicles communicate, with the following vehicle adhering to a communication-assisted stopping distance. We then analyze how this stopping distance is impacted with the addition of consecutive packet loss, and this is shown for different speeds and data rates. For our results, we show the stopping distance when 0 packets are lost, and we then show how the stopping distance is reduced with each consecutive loss. This highlights how the reduction in reliability leads to reduced stopping distance and, hence, a higher chance of collisions with the lead vehicle. As the reduction value reaches 0, we deem this to be the point at which lead and follow vehicle will be occupying the same space or that a collision may have occurred. We also show a negative value, which would mean the follow vehicle has gone past the lead vehicle, and this would be classified as a collision; we show this to identify the impact of reliability.