Interpretable Variational Graph Autoencoder with Noninformative Prior

Abstract

Variational graph autoencoder, which can encode structural information and attribute information in the graph into low-dimensional representations, has become a powerful method for studying graph-structured data. However, most existing methods based on variational (graph) autoencoder assume that the prior of latent variables obeys the standard normal distribution which encourages all nodes to gather around 0. That leads to the inability to fully utilize the latent space. Therefore, it becomes a challenge on how to choose a suitable prior without incorporating additional expert knowledge. Given this, we propose a novel noninformative prior-based interpretable variational graph autoencoder (NPIVGAE). Specifically, we exploit the noninformative prior as the prior distribution of latent variables. This prior enables the posterior distribution parameters to be almost learned from the sample data. Furthermore, we regard each dimension of a latent variable as the probability that the node belongs to each block, thereby improving the interpretability of the model. The correlation within and between blocks is described by a block–block correlation matrix. We compare our model with state-of-the-art methods on three real datasets, verifying its effectiveness and superiority.

1. Introduction

Many complex systems in real life, such as social networks (e.g., Facebook) and coauthor networks, can be abstracted into graph-structured data for analysis. The analysis results can be leveraged to guide practical applications, such as link prediction and personalized recommendation. The variational graph autoencoder (VGAE) proposed by Kipf and Welling [1], which extended the variational autoencoder (VAE) [2] from the field of Euclidean structure data (e.g., image) to that of non-Euclidean data (e.g., graph-structured data), is one of the commonly utilized methods for studying graph-structured data. It could capture the distribution of the samples through a two-layer graph convolutional network (GCN) [3] and reconstruct the graph structure through a decoder. In recent years, the variations of VAE and VGAE [4,5,6,7] have emerged in an endless stream, further improving the performance of the variational (graph) autoencoder on traditional machine learning tasks such as link prediction. Although VGAE has been widely applied and promoted, there are two urgent challenges to be solved:

How to set a reasonable prior without additional expert knowledge. VGAE and its variants assumed that the prior distribution of latent variables obeyed a simple standard normal distribution. Under this assumption, the Kullback–Leibler (KL) term in the objective function usually caused the posterior distribution to overfit the shape and parameters of the prior and encouraged samples to focus on the origin. Therefore, the phenomenon of Posterior Collapse [8] will occur. Two types of methods are proposed to handle the issue. The first is to improve the loss function of the variational (graph) autoencoder [9,10,11,12]. However, most of the methods were designed for Euclidean structure data based on the variational autoencoder. These methods are difficult to extend to graph-structured data since they are not arranged neatly, making it difficult to define the same convolution operation as image data. The second is to assume the latent variables follow a more complex prior or posterior distribution [13,14,15,16,17]. Unfortunately, these methods applied a more complex distribution as the prior for latent variables. In general, a more complex prior means more expert experience is involved. Thus, it is an arduous task to determine a suitable prior when we lack prior knowledge.

How to improve the interpretability of VGAE. Graph neural networks (GNNs) have achieved great success in processing graph-structured data in recent years. However, this type of methods is often a black box, which makes the learned low-dimensional representations unexplainable. For example, we cannot explain the meanings of the neural networks’ parameters when we want to convince people of the prediction results in the neural networks. Existing methods improved the interpretability of GNNs by analyzing and explaining the prediction results of the algorithms [18] or constructing an interpretable model [19]. However, the above methods made the node embeddings still black boxes because they did not point out the meanings of embeddings themselves, i.e., they could not explain the meaning of each dimension of the learned representations.

To cope with the above challenges, we propose a noninformative prior [20] based interpretable variational graph autoencoder called NPIVGAE, which utilizes the noninformative prior distribution as the prior of the latent variables. Such a prior is more reasonable, especially when we lack prior knowledge. It no longer forces the posterior distribution to tend to the standard normal distribution, so that almost all the posterior distribution parameters are learned from the sample data. In addition, we leverage a new perspective to understand the node representations to improve the interpretability of the model. Specifically, each dimension of the latent variables is regarded as the soft assignment probability that the node belongs to each community (also called block in the stochastic blockmodel). Meanwhile, the correlation within and between the blocks to which the nodes belong is described by a block–block correlation matrix. When reconstructing the link between two nodes in the graph, the representations of these two nodes and the correlation between the blocks to which two nodes belong are taken into account.

Our main contributions can be summarized as follows:

• We propose a novel noninformative prior-based variational graph autoencoder, giving the prior distribution of latent variables when we lack prior knowledge. Then we analyze the influence of the noninformative prior on the posterior and confirm that the posterior distribution is affected by the data itself instead of the prior knowledge, when we use noninformative prior.
• We improve the interpretability of the model by regarding each dimension of the node representations as the probability of which the node belongs to each block. When reconstructing the graph, we also consider the correlation within and between the blocks, which is described by a block–block correlation matrix.
• Substantial experiments performed on three real datasets verify the effectiveness of our model. Experimental results show that the proposed model significantly outperforms the graph autoencoder model and its variants.

2. Related Work

In this section, we summarize the variants of the variational (graph) autoencoder and methods to improve the interpretability of graph neural networks.

2.1. Extended Variational (Graph) Autoencoders

The variational (graph) autoencoder assumes that the latent variables’ prior is a standard normal distribution, which easily causes the posterior to collapse to the prior. Recently, many methods have been proposed to study the problem of posterior collapse. Some methods solve the problem by adding additional loss. For example, Yeung et al. [9] and Khan et al. [10] analyzed the activity of the hidden layer units and divided these units into multiple groups. In addition, they introduced a hidden variable to specify the group corresponding to each sample. Dieng et al. [11] introduced mutual information between a sample and a hidden variable in the loss function. Some others employ a more complex distribution to construct the prior of variational (graph) autoencoder. For instance, Abiri and Ohlsson [13] replaced the prior and posterior of latent variables with the multivariate Student’s t-distribution, which was regarded as weak information. Joo et al. [14] and Li et al. [15] applied a Dirichlet distribution as the prior. Tomczak and Welling [16] utilized pseudo-input to learn an approximate mixed posterior and utilize the posterior to construct a more flexible prior. Guo et al. [17] utilized Gaussian mixture distribution to construct a more complex prior and posterior distribution, for the reason that they were convinced the latent space might be multi-peak.

There are also some works with the idea of the noninformative prior distribution. Freitas et al. [21] were the first to apply the noninformative prior to neural networks and analyzed the advantage of this prior. Choong et al. [22] expanded [23] and proposed a variational graph autoencoder based on the community discovery task. They generalized the generation process of VGAE to the mixed Gaussian distribution by introducing a community assignment parameter. Moreover, they assumed that the noninformative prior of the community assignment parameter was a uniform distribution, i.e., the probability that a node belonged to each community was the same initially. Although the model improved community division performance, it could be utilized only for the community division task.

2.2. Interpretable Graph Neural Networks

Methods to improve the interpretability of GNNs can be roughly divided into two categories. The first is to analyze and explain the prediction results of the algorithm. For instance, Ying et al. [18] improved the explanation of GNNs by performing subsequent interpretations of the prediction results of node classification and graph classification tasks. Specifically, this method could identify a compact subgraph structure that played a vital role and a small part of the node features that played a crucial role in prediction. The second is to improve the interpretability of the model itself. Ma et al. [19] insisted that the formation of a node’s neighbors often depended on many factors, so they tried to identify and separate these potential factors. They performed convolution operations in different subspaces and then concatenated the results of each channel as node representations. The method that is similar to ours is the Deep Generative Latent Feature Relational Model (DGLFRM) proposed by Mehta et al. [24]. They combined the stochastic blockmodel [25] and GNNs to improve the efficiency of the model and the interpretability of latent variables. However, this model sets too many prior distributions to expand to large-scale networks.

3. Preliminaries

3.1. Noninformative Prior

Prior knowledge is usually acquired through historical laws or expert experience. In some probabilistic inference problems using Bayes methods, we may have some prior knowledge that can be easily expressed through prior distribution. In many practical cases, however, we may not know what form of prior should be adopted, or it is not easy to obtain prior distribution. For example, in the coin toss problem, we would generally judge that the probability of heads or tails is 50% before tossing. Nevertheless, when the coin material is not uniform, it is hard to obtain the prior probability distribution of heads.

In this case, we can use the noninformative prior [20] for inference and analysis. Frankly, the so-called noninformative prior does not mean that there is no information at all, but the information currently contained in the prior distribution is negligible for the sample data. This form of the prior distribution is designed to minimize the impact of prior on the posterior distribution [26], that is, the mean and variance of the posterior distribution are almost all learned from the input data. We will discuss this effect in detail in Section 4.6.

The Jeffrey’s prior mentioned in [27] can be used to determine the noninformative prior distribution of variables. This prior can ensure that the form of the prior does not change with the change of the parameter form (i.e., invariance). Jeffrey’s prior was generalized to the case of multidimensional parameters by using the square root of the Fisher information matrix determinant as the variables’ noninformative prior. The following is to derive the noninformative prior distribution when the variables follow a normal distribution.

Let $\mathbf{x}=(x_1,x_2,...,x_n)$ be a sample from the population X that obeys the normal distribution $\mathcal{N}(\mu ,\sigma )$, and its log likelihood function is:

$$l(\mu ,\sigma )=-\frac{1}{2}ln\left(2\pi \right)-nln\sigma -\frac{1}{2{\sigma }^2}\sum _{i=1}^n{(x_i-\mu )}^2.$$

(1)

Its Fisher information matrix is:

$$\begin{array}{c}I(\mu ,\sigma )=\left(\begin{array}{cc}E\left(-\frac{{\partial }^{2}l}{\partial {\mu }^2}\right)& E\left(-\frac{{\partial }^{2}l}{\partial \mu \partial \sigma }\right)\\ E\left(-\frac{{\partial }^{2}l}{\partial \mu \partial \sigma }\right)& E\left(-\frac{{\partial }^{2}l}{\partial {\sigma }^2}\right)\end{array}\right)=\left(\begin{array}{cc}n/\phantom{n{\sigma }^2}{\sigma }^2& 0\\ 0& 2n/\phantom{n{\sigma }^2}{\sigma }^2\end{array}\right)\hfill \end{array}.$$

(2)

$$detI(\mu ,\sigma )=2n^2{\sigma }^{-4}.$$

(3)

Hence, the noninformative prior of the normal distribution parameters $(\mu ,\sigma )$ is $h(\mu ,\sigma )\propto 1/\phantom{1{\sigma }^2}{\sigma }^2$.

4. The Proposed NPIVGAE

In this section, we first describe the framework of NPIVGAE and then introduce the model in details. Finally, we analyze the influence of the noninformative prior distribution on the posterior distribution.

4.1. Notations and Problem Formulation

An undirected attribute network $\mathbf{G}$ with n nodes can be denoted by an $n\times n$ adjacency matrix $\mathbf{A}$ and an $n\times m$ attribute matrix $\mathbf{X}$. Concerning $\mathbf{A}$, if there is an edge (also called a link) between node $v_i$ and node $v_j$, $a_{ij}=1$, otherwise $a_{ij}=0$. Set the diagonal elements of $\mathbf{A}$ to 1, namely, each node has an edge to itself. The attribute information of all nodes is contained in the attribute matrix $\mathbf{X}$, of which ${\mathbf{x}}_{\mathbf{i}}$ is the attribute of $v_i$ and m denotes the number of the features observed.

Given an attribute graph $\mathbf{G}$, we aim to learn a latent variable ${\mathbf{z}}_{\mathbf{i}}$ for node $v_i$, and ${\mathbf{z}}_{\mathbf{i}}$ can be explained. Specifically, we define the node representations as an $n\times d$ latent variables matrix $\mathbf{Z}$, where ${\mathbf{z}}_{\mathbf{i}}$ stands for the embedding of node $v_i$ and d is dimensions of latent variables. d is also the number of blocks in the attribute network $\mathbf{G}$. Each dimension of the embedding ${\mathbf{z}}_{\mathbf{i}}$ is regarded as the probability that the node $v_i$ belongs to each block. We also introduce a block–block correlation matrix $\Pi =({\pi }_{mn}{)}_{d\times d}$, where ${\pi }_{kl}$ affects the link between node $v_i$ and node $v_j$ belonging to block k and block l, respectively.

4.2. Framework

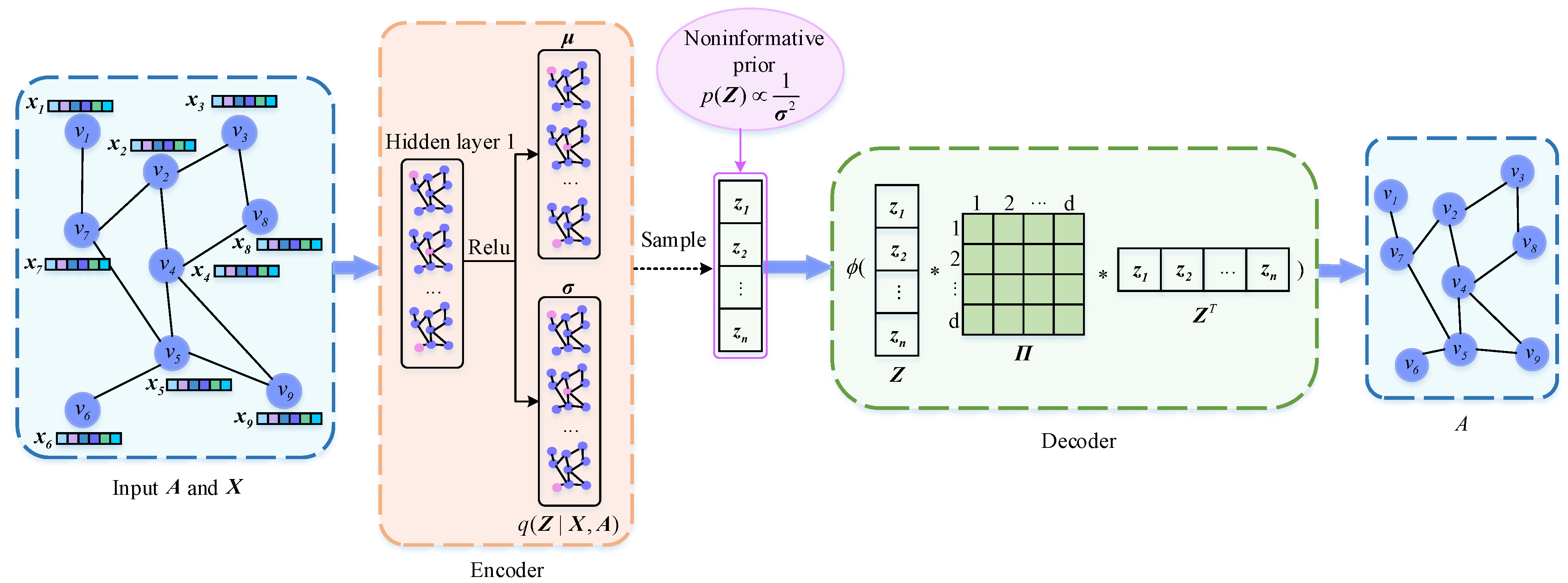
Figure 1 shows the overall framework of NPIVGAE, which mainly includes two parts: encoder and decoder. Firstly, we input the adjacency matrix $\mathbf{A}$ and the attribute matrix $\mathbf{X}$ to the encoder to obtain the mean and variance of the latent variables’ posterior and then sample to get $\mathbf{Z}$. Unlike VGAE, we introduce the noninformative prior probability as the prior of $\mathbf{Z}$ and leverage node embeddings as well as block–block correlation matrix to reconstruct the adjacency matrix. Finally, the loss function is calculated to update the parameters in reverse. Details of each section are described below.

4.3. Encoder

We leverage a two-layer GCN as the encoder to generate the parameters $\mathbf{\mu }$ and $\mathbf{\sigma }$ of the normal distribution:

$$\mathbf{\mu }=GC{N}_{\mathbf{\mu }}(\mathbf{X},\mathbf{A}),$$

(4)

$$log\mathbf{\sigma }=GC{N}_{\mathbf{\sigma }}(\mathbf{X},\mathbf{A}).$$

(5)

Here $\mathbf{\mu }$ is the matrix corresponding to ${\mathbf{\mu }}_i$ (the mean vector of node $v_i$’s embedding ${\mathbf{z}}_i$), and similarly, $log\mathbf{\sigma }$ is the matrix corresponding to ${\mathbf{\sigma }}_i$ (the standard deviation vector of node $v_i$’s embedding ${\mathbf{z}}_i$). The two-layer GCN is defined as $GCN(\mathbf{X},\mathbf{A})=\widehat{\mathbf{A}}\mathrm{ReLU}(\widehat{\mathbf{A}}\mathbf{X}{\mathbf{W}}_0){\mathbf{W}}_1$, $\mathrm{ReLU}(·)$ represents the Relu activation function, $\widehat{\mathbf{A}}={\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2}$ is the symmetric normalized matrix of the adjacency matrix $\mathbf{A}$. $GC{N}_{\mathbf{\mu }}(\mathbf{X},\mathbf{A})$ and $GC{N}_{\mathbf{\sigma }}(\mathbf{X},\mathbf{A})$ share the weights ${\mathbf{W}}_0$ of the first layer. The second layer weights of $GC{N}_{\mathbf{\mu }}(\mathbf{X},\mathbf{A})$ and $GC{N}_{\mathbf{\sigma }}(\mathbf{X},\mathbf{A})$ are ${\mathbf{W}}_1$ and ${\mathbf{W}}_2$ respectively. Then the latent variables are obtained by sampling $\mathcal{N}(\mathbf{\mu },\mathbf{\sigma })$. The specific process is as follows:

$$q\left(\mathbf{Z}|\mathbf{A},\mathbf{X}\right)={\prod }_{i=1}^{n}q\left({\mathbf{z}}_i\right|\mathbf{A},\mathbf{X}),$$

(6)

$$q\left({\mathbf{z}}_i\right|\mathbf{A},\mathbf{X})=\mathcal{N}\left({\mathbf{z}}_i\right|{\mathbf{\mu }}_i,diag\left({\mathbf{\sigma }}_i^2\right)).$$

(7)

4.4. Decoder

We regard each dimension of the latent representation ${\mathbf{z}}_i$ as the probability that the node belongs to each block. We allow each node to belong to overlapping blocks (communities), making each dimension of ${\mathbf{z}}_i$ interpretable. Then we introduce the block–block correlation matrix $\Pi$ to describe the relevance within and between blocks.

We reconstruct the adjacency matrix by considering the node embeddings and the correlation between the block to which node $v_i$ belongs and the block to which node $v_j$ belongs by the following equations:

$$p\left(\mathbf{A}\right|\mathbf{Z})={\prod }_{i=1}^n{\prod }_{j=1}^{n}p\left(a_{ij}|{\mathbf{z}}_i,{\mathbf{z}}_j\right),$$

(8)

$$p\left(a_{ij}=1|{\mathbf{z}}_i,{\mathbf{z}}_j,\Pi \right)=\varphi \left({{\mathbf{z}}_i}^T\Pi {\mathbf{z}}_j\right).$$

(9)

where $\varphi \left(·\right)$ represents the activation function. In (9), each value ${\pi }_{mn}$ in the block–block correlation matrix affects the probability of the link between node $v_i$ and node $v_j$, where node $v_i$ and node $v_j$ belong to block m and block n, respectively.

4.5. Loss Function

The proposed NPIVGAE takes the noninformative prior as the prior distribution of the latent variables $\mathbf{Z}$ to minimize the influence of the prior on the posterior. Since we still assume that the variational posterior $q\left(\mathbf{Z}\right|\mathbf{X},\mathbf{A})$ is a normal distribution $\mathcal{N}(\mathbf{\mu },\mathbf{\sigma })$, the corresponding noninformative prior is $p\left(\mathbf{Z}\right)\propto \frac{1}{{\mathbf{\sigma }}^2}$ (i.e., uniform distribution, which is regarded as noninformative) according to Section 3.1.

By minimizing the negative evidence lower bound (ELBO), we define the loss function of the noninformative prior-based interpretable variational graph autoencoder:

$$\begin{array}{c}\hfill \mathcal{L}=E_{\mathbf{Z}\sim q\left(\mathbf{Z}\right|\mathbf{X},\mathbf{A})}[log\frac{q\left(\mathbf{Z}\right|\mathbf{X},\mathbf{A})}{p\left(\mathbf{Z}\right)}]-E_{\mathbf{Z}\sim q\left(\mathbf{Z}\right|\mathbf{X},\mathbf{A})}[logp\left(\mathbf{A}\right|\mathbf{Z})].\end{array}$$

(10)

After deduction (please refer to Appendix A for the detailed derivation), we can get the final objective function:

$$\begin{array}{c}\hfill \mathcal{L}=\sum _{i=1}^n\sum _{j=1}^d(\log \frac{1}{\sqrt{2\pi }}+log{\sigma }_{ij}-\frac{1}{2})-\sum _{i=1}^n\sum _{j=1}^n{E}_{\mathbf{Z}\sim q\left(\mathbf{Z}\right|\mathbf{X},\mathbf{A})}[logp\left(a_{ij}\right|{\mathbf{z}}_i,{\mathbf{z}}_j,\Pi )].\end{array}$$

(11)

Our model exploits stochastic gradient descent to minimize the objective function and optimize the parameters. Like VGAE, the reparameterization trick is also leveraged for training in this paper to achieve the gradient update of the mean and variance.

4.6. The Influence of the Noninformative Prior on the Posterior

In Section 3.1, we mentioned that our purpose of designing the noninformative prior was to reduce the influence of the prior on the posterior. We take a single Gaussian variable $s\sim \mathcal{N}(\alpha ,\beta )$ as an example to analyze this effect. Assuming that the variance ${\beta }^2$ is known, we desire to get the solution of the mean $\alpha$ based on a set of t sample data $\mathbf{S}=\{{\mathrm{s}}_1,{\mathrm{s}}_2,\dots {\mathrm{s}}_t\}$ and set the conjugate prior distribution $p\left(\alpha \right)=\mathcal{N}({\alpha }_0,{\beta }_0^2)$. According to [20], the posterior probability of $\alpha$ is $p\left(\alpha \right|\mathbf{S})=\mathcal{N}\left(\alpha \right|{\alpha }_t,{\beta }_{\mathrm{t}}^2)$, of which ${\alpha }_{\mathrm{t}}=\frac{{\beta }^2}{t{\beta }_0^2+{\beta }^2}{\alpha }_0+\frac{t{\beta }_0^2}{t{\beta }_0^2+{\beta }^2}{\alpha }_L$ and $\frac{1}{{\beta }_{\mathrm{t}}^2}=\frac{1}{{\beta }_0^2}+\frac{t}{{\beta }^2}$. The ${\alpha }_L$ represents the maximum likelihood estimate of $\alpha$, and ${\alpha }_L=\frac{1}{t}{\sum }_{k=1}^t{s}_k$ is given by the sample data.

When ${\beta }_0^2$ in the prior distribution tends to infinity, the prior distribution $p\left(\alpha \right)$ becomes a uniform distribution, also regarded as a noninformative prior. At this time, the posterior mean is given by the maximum likelihood ${\alpha }_{\mathrm{t}}\approx {\alpha }_L$, and the variance is ${\beta }_{\mathrm{t}}^2=\frac{{\beta }^2}{t}$, i.e., ${\alpha }_t$ and ${\beta }_t$ have nothing to do with the prior parameters ${\alpha }_0$ and ${\beta }_0$. Thus, we can conclude that when the prior of the Gaussian distribution is selected as the noninformative prior, the prior can have the smallest impact on the posterior distribution, and the posterior parameters can be learned almost all from the sample data.

4.7. Algorithm and Complexity Analysis

The flow of our algorithm is demonstrated in Algorithm 1. First, we initialize the network parameters and the block–block correlation matrix $\Pi$. For each iteration, the mean and variance of the latent variables $\mathbf{Z}$ are obtained through step 4, and the noninformative prior of $\mathbf{Z}$ is obtained according to $p\left(\mathbf{Z}\right)\propto \frac{1}{{\mathbf{\sigma }}^2}$. Then sample $\mathbf{Z}$ according to (7). Finally, we calculate the objective function and use gradient descent to update the parameters $\mathbf{\mu }$, $\mathbf{\sigma }$, and $\Pi$.

In the following, we analyzed the time complexity of our model. In each iteration, it takes $O\left(dn\right)$ to calculate the d-dimensional vectors $\mathbf{\mu }$, $\mathbf{\sigma }$, and $\mathbf{Z}$, so the total time complexity is $O\left(Edn\right)$, where $d\ll n$ and E represents the number of iterations.

Algorithm 1 NPIVGAE.

Input:

The adjacency matrix $\mathbf{A}$ and the attribute matrix $\mathbf{X}$.

Hyperparameters: Number of iterations E, latent dimension d.

Output:

Latent variables $\mathbf{Z}$.

1: Initialize neural networks’ parameters and $\Pi$.

2: for $e=1$ to E do

3: for $i=1$ to n do

4:  Obtain the mean ${\mathbf{\mu }}_i$ and variance ${\mathbf{\sigma }}_i$ according to (4) and (5), respectively.

5:  Get the noninformative prior of ${\mathbf{z}}_i$ using $p\left({\mathbf{z}}_i\right)\propto \frac{1}{{\mathbf{\sigma }}_i^2}$.

6:  Sample to get the latent variable ${\mathbf{z}}_i$ through (7).

7: end for

8: Calculate the loss function $\mathcal{L}$ according to (11).

9: Update parameters $\mathbf{\mu }$, $\mathbf{\sigma }$, and $\Pi$ with back propagation.

10: end for

11: return $\mathbf{Z}$.

5. Experimental Results and Analysis

In this section, we assess the effectiveness of our model (NPIVGAE) on two classic downstream tasks: (i) link prediction and (ii) node classification. The processor used in the experiments is Intel(R) Core(TM) i5-9400 CPU @ 2.90 GHZ. The memory is 8G and the Windows version is WIN10. Our experiments are implemented with Python’s Tensorflow, and the version of Tensorflow is 1.12.0. The weights ${\mathbf{W}}_0$, ${\mathbf{W}}_1$, and ${\mathbf{W}}_2$ of the two-layer GCN are initialized to be uniform distribution using the random_uniform function in Tensorflow, and the weights are updated in the back propagation process. In order to show the effectiveness of using the noninformative prior, we design a variant of our model, namely NPVGAE. It employs $p\left(\mathbf{Z}\right)\propto {\mathbf{\sigma }}^{-2}$ as the noninformative prior of the hidden variables $\mathbf{Z}$ without introducing block–block correlation matrix $\Pi$.

5.1. Datasets

In this paper, we adopt three real datasets—Cora, Citeseer, and Pubmed [28]—for testing the performance of the proposed NPIVGAE and its variant. They all belong to citation networks. The statistics of the three datasets are depicted in

Table 1. Statistics of the datasets utilized in the experiments.

Datasets	# Nodes	# Links	# Features	# Lables
Cora	2708	5429	1433	7
Citeseer	3327	4732	3703	6
Pubmed	19717	44338	500	3

. A more detailed description is as follows:

Cora: The nodes in this dataset represent papers in the field of machine learning, the edges are the citation relationships of the papers, and the attributes represent the words contained in the paper. The labels indicate the classification of the papers, such as Neural_Networks and Rule_Learning.

Citeseer: In the Citeseer dataset, the meanings of nodes, edges, and attributes are the same as those in Cora. The labels are also the categories of the papers, such as agents and machine learning.

Pubmed: This dataset is made up of 19,717 papers related to diabetes, all of which are from the Pubmed database. Nodes represent papers, edges denote citation relationships, and attributes are words in the paper. All the papers are divided into 3 categories, namely (1) Diabetes Mellitus, Experimental, (2) Diabetes Mellitus Type I, and (3) Diabetes Mellitus Type II.

5.2. Baselines

We compare NPIVGAE and its variant NPVGAE with several state-of-the-art methods, including using a standard normal distribution as the prior and solving the posterior collapse problem.

• GAE [1] is a non-probabilistic graph autoencoder model, which reconstructs the adjacency matrix through the inner product of the node representations. It minimizes the reconstruction error to learn the parameters in the neural networks.
• VGAE [1] assumes that the latent variables follow a normal distribution. The mean and variance of latent variables are encoded by a two-layer GCN, and the structure is reconstructed by a decoder.
• ARGE [29] introduces an adversarially regularized term into the graph autoencoder. The adversarial module aims to discriminate whether the node embeddings come from the prior distribution or the graph encoder.
• ARVGE [29] realizes regularization and promotion of node embeddings by drawing an adversarial module into the variational graph autoencoder.
• EVGAE [10] divides the dimensions of the latent variables into multiple groups, called epitomes, and only penalizes one group each time. This method alleviates the posterior collapse problem by increasing the activity of the hidden units.

5.3. Link Prediction

5.3.1. Experimental Setup

Link prediction is one of the most common downstream tasks in network representation learning. It can recover missing links or predict possible links in the future by analyzing the given network structure. Consistent with VGAE, we also make use of 5% and 10% links as the validation set and test set, respectively, and randomly generate the same number of non-existent links. The purpose of using the validation set is to adjust the hyperparameters, and the remaining 85% of the links are employed for the training set. In the training process, we add $\Pi$ as a neural network parameter to the objective function and update it through backpropagation. Due to the relatively small scale of Cora and Citeseer datasets, we set weight_decay = 0.01 to prevent overfitting. We iterate 800 times to train sufficiently for the large scale of the Pubmed dataset. The number of hidden layer units and iteration times of three datasets of our model are described in

Table 2. Experimental settings for training.

Datasets	The Number of Neurons per Layer	The Number of Iterations
Cora	64-16	200
Citeseer	128-32	200
Pubmed	64-16	800

. We take advantage of Adam optimizer to optimize the parameters with a learning rate of 0.01.

We take the same experimental setup as our model for GAE and VGAE. As for ARGE, ARVGE, and EVGAE, we adopt the same setting as the original papers. We exploit the area under the ROC curve (AUC) and average precision (AP) to evaluate the performance of our model and other baselines. These are two evaluation indexes commonly employed in the link prediction task. The more the values of AUC and AP approach 1, the better the experimental results are. We ran each dataset five times and reported the average value to ensure the accuracy of the algorithm.

5.3.2. Results and Discussion

The experimental results are illustrated in

Table 3. Experimental results on the link prediction task. (*: outperforms 2nd-best with p-value < 0.01).

Method	Cora		Citeseer		Pubmed
	AUC	AP	AUC	AP	AUC	AP
GAE	91.00 ± 0.02	92.00 ± 0.03	91.70 ± 0.13	93.23 ± 0.12	96.18 ± 0.01	96.43 ± 0.02
VGAE	91.40 ± 0.01	92.60 ± 0.01	91.37 ± 0.44	92.77 ± 0.17	96.61 ± 0.02	96.88 ± 0.06
ARGE	91.98 ± 0.01	93.20 ± 0.01	92.73 ± 0.01	93.00 ± 0.01	96.80 ± 0.00	97.10 ± 0.00
ARVGE	92.40 ± 0.01	92.60 ± 0.01	92.65 ± 0.01	93.42 ± 0.01	96.50 ± 0.00	96.80 ± 0.00
EVGAE	* 92.96 ± 0.02	93.58 ± 0.03	91.55 ± 0.03	93.24 ± 0.02	96.80 ± 0.01	96.91 ± 0.02
NPVGAE	92.45 ± 0.01	* 93.73 ± 0.05	92.15 ± 0.16	94.15 ± 0.15	* 96.92 ± 0.06	* 97.16 ± 0.03
NPIVGAE	91.46 ± 1.58	91.08 ± 1.84	* 93.66 ± 0.47	94.31 ± 0.08	96.79 ± 0.03	97.11 ± 0.01

, and the best results are shown in bold. It can be concluded from the experimental results that the proposed NPIVGAE and its variant NPVGAE achieve the best results on almost all datasets. For example, AUC exceeds 93% and AP reaches 94% on the Citeseer dataset, while ARVGE only reaches 92% and 93%, respectively. The reason may be that ARVGE employs a discriminator to make the latent variables more inclined to the prior given manually. This prior may be unreasonable so that ARVGE cannot learn the characteristics of the sample data well. Our variant NPVGAE performs better than other baselines on the Cora’s AP as well as Pubmed’s AUC and AP, proving that the noninformative prior we introduced plays a critical role. We do not give a strong prior assumption to the model so that almost all parameters of the posterior distribution are learned from the sample data. NPIVGAE achieves better results than NPVGAE on the Citeseer dataset. That proves the effectiveness of combining the block–block correlation matrix. To sum up, the two components of the noninformative prior and the block–block correlation matrix can help improve the performance of the model. The noninformative prior module contributes most to the performance of the overall model NPIVGAE.

5.4. Semi-Supervised Node Classification

We evaluate the effectiveness of our model on the semi-supervised node classification task. Let ${\mathbf{y}}_i=\{y_1,y_2,\cdots y_l\}$ denote the true label vector of node $v_i$, where l is the number of categories. The learned embeddings are concatenated into a fully connected layer. The outputs of this layer are employed as the predicted label vectors ${{\mathbf{y}}_i}^{\prime }$ (the length of the outputs is the number of categories l). We apply the cross-entropy loss function in (12) to calculate the loss between the predicted label and the true label of each node and optimize it through the Adam optimizer.

$$\begin{array}{c}\hfill L({\mathbf{y}}_i,{{\mathbf{y}}_i}^{\prime })=-\sum _d({\mathbf{y}}_{i}log{{\mathbf{y}}_i}^{\prime }+(1-{\mathbf{y}}_i)log(1-{{\mathbf{y}}_i}^{\prime })).\end{array}$$

(12)

5.4.1. Experimental Setup

Following [28], we randomly selected 5, 10, and 20 labels per class to train. For the Cora dataset, for example, there are 7 classes, and we select 5 labels randomly for each class. Hence, there are 35 labels for semi-supervised training in all. We randomly divide the dataset into training, validation, and test sets at each iteration. It can provide more robust performance when the dataset is randomly divided. In the experiment, the encoder of our model (NPIVGAE) contains a two-layer GCN with 32 and 16 hidden units in the first and second layers, respectively, and so does that of NPVGAE. The NPIVGAE and NPVGAE, together with other baselines, are trained 50 iterations, and the learning rate is set to 0.01. We took the average results of 10 runs as a report.

5.4.2. Experimental Results and Analysis

The classification results on the Cora, Citeseer, and Pubmed datasets are shown in

Table 4. The prediction accuracy (percentage of labels correctly predicted) on the Cora dataset. Asterisks indicate that the optimal algorithm outperforms 2nd-best with p-value < 0.01.

Method	5 Labels	10 Labels	20 Labels
GAE	77.6	79.6	79.2
VGAE	77.9	79.0	81.6
ARGE	70.7	71.9	72
ARVGE	72.4	72.2	73.6
EVGAE	60.5	62.4	66.3
NPVGAE	79.2	79.9	82.2
NPIVGAE	* 81.8	* 82.0	83.1

,

Table 5. The prediction accuracy (percentage of labels correctly predicted) on the Citeseer dataset. Asterisks indicate that the optimal algorithm outperforms 2nd-best with p-value < 0.01.

Method	5 Labels	10 Labels	20 Labels
GAE	61.6	60.5	63.0
VGAE	63.6	65.7	66.7
ARGE	52.5	56.7	60.1
ARVGE	55	56.5	59.4
EVGAE	33.2	35.4	45.1
NPVGAE	67.8	65.5	67.1
NPIVGAE	* 69.9	* 69.3	* 69.0

,

Table 6. The prediction accuracy (percentage of labels correctly predicted) on the Pubmed dataset. Asterisks indicate that the optimal algorithm outperforms 2nd-best with p-value < 0.01.

Method	5 Labels	10 Labels	20 Labels
GAE	79.6	80.0	80.5
VGAE	79.4	79.8	80.4
ARGE	73.4	75	75.5
ARVGE	74.1	75.9	73.4
EVGAE	65.5	70.8	71.8
NPVGAE	81.6	81.4	* 82.6
NPIVGAE	81.8	* 82.6	81.9

, respectively. When the number of labels applied for training is relatively small (e.g., each class can only obtain 5 or 10 labels), the effect of promotion is particularly obvious. In comparison with the baselines, NPIVGAE and its variant has achieved excellent results on all datasets. The prediction accuracy of NPIVGAE on the Cora dataset has reached more than 81%, as depicted in Table 4. The indicators of NPIVGAE on the Citeseer dataset also exceed 69%, while the results of other baselines are relatively poor, as displayed in Table 5. It demonstrates that the NPIVGAE we proposed can learn the information in the graph so effectively that it achieves better performance.

5.5. Efficiency Evaluation

In this section, we analyze the running time of our model to prove the efficiency of the neural network-based model. Then we graphically demonstrated the learning process of NPIVGAE to prove that there is no overfitting.

We selected two methods that did not use neural networks (i.e., LINE (Large-scale Information Network Embedding) [30] and TADW (text-associated DeepWalk) [31]) for comparison. LINE embeds a large-scale information network into a low-dimensional vector space while retaining the first-order and second-order similarities. TADW is a matrix factorization method that combines network structure and text features to obtain a better network representation. We conducted experiments on the semi-supervised node classification task with the Cora and Citeseer datasets as examples. To be fair, both TADW and our model NPIVGAE were iterated 50 times. 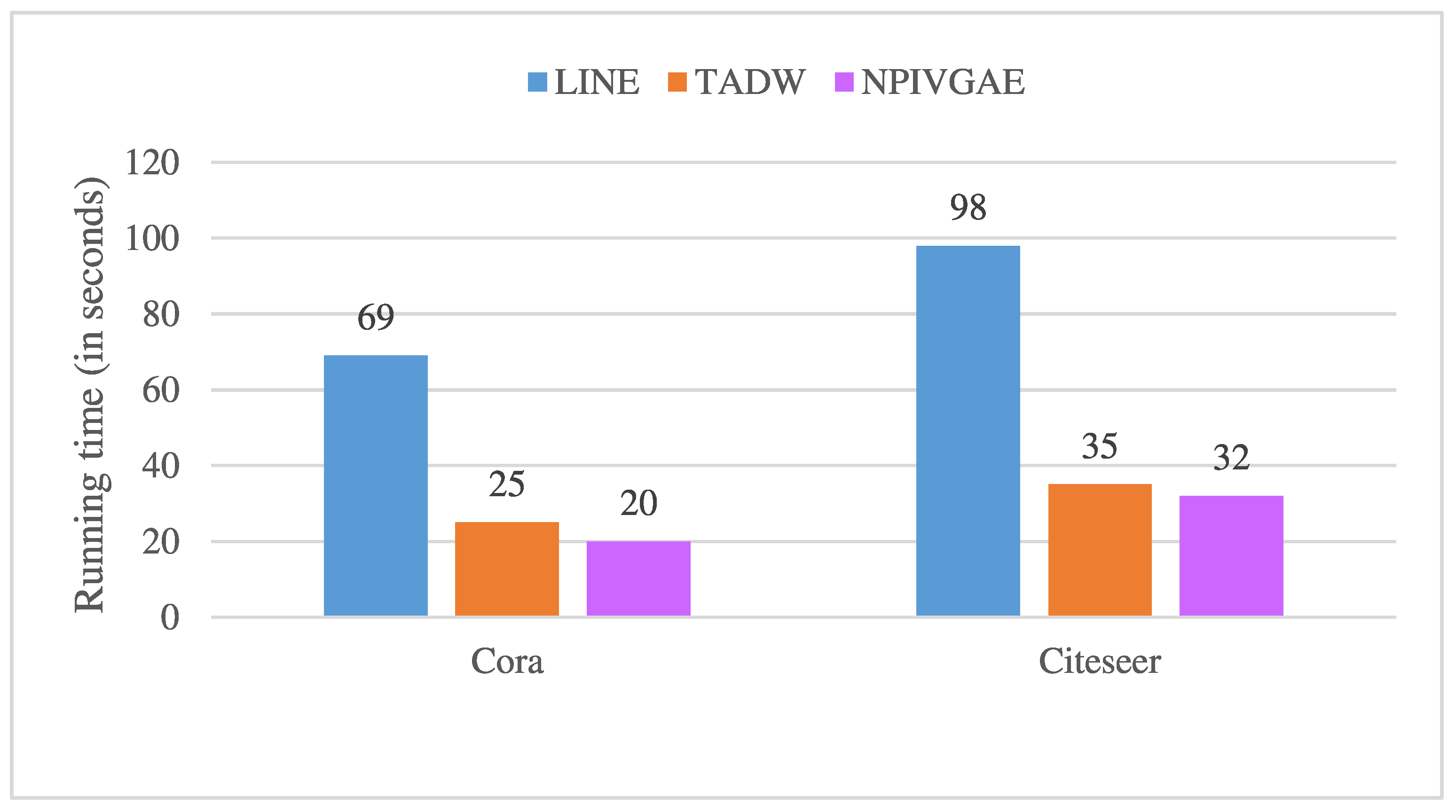We report the running time in Figure 2. From Figure 2, we know that NPIVGAE and TADW are significantly faster than LINE, and NPIVGAE is slightly faster than TADW. In addition, our model was compared with LINE and TADW on time complexity. LINE and TADW have relatively high time complexity, as shown in

Table 7. The time complexity of LINE, TADW, and NPIVGAE. K is the number of negative samples, $\left|C\right|$ is the number of edges. $NZ(·)$ indicates the number of non-zero items and $\mathbf{M}$ represents a certain relationship matrix.

	LINE	TADW	NPIVGAE
Time complexity	$O\left(dK\left|C\right|\right)$	$O(n^2+NZ\left(\mathit{M}\right)d+n{d}^2)$	$O\left(Edn\right)$

. TADW requires expensive matrix operations, such as SVD decomposition, which limits the ability of TADW to process large-scale data. In contrast, our model NPIVGAE has higher efficiency while guaranteeing accuracy.

Figure 3 shows the learning process of our model in the link prediction task. Our model was iterated 200 times, and the AUC and AP of the training and validation sets are displayed in Figure 3. The horizontal axis is the number of iterations, and the vertical axis is the accuracy of AUC and AP. We can see that the training and validation accuracy of the model rose sharply in the first 20 iterations, and then gradually slowed down and converged. As mentioned in Section 5.3.1, we set the weight decay parameter to 0.01 in the experiment since the Cora and Citeseer datasets are relatively small. NPIVGAE performed well on training, validation, and test sets, proving that the strategy we adopted successfully prevented overfitting.

5.6. Visualization

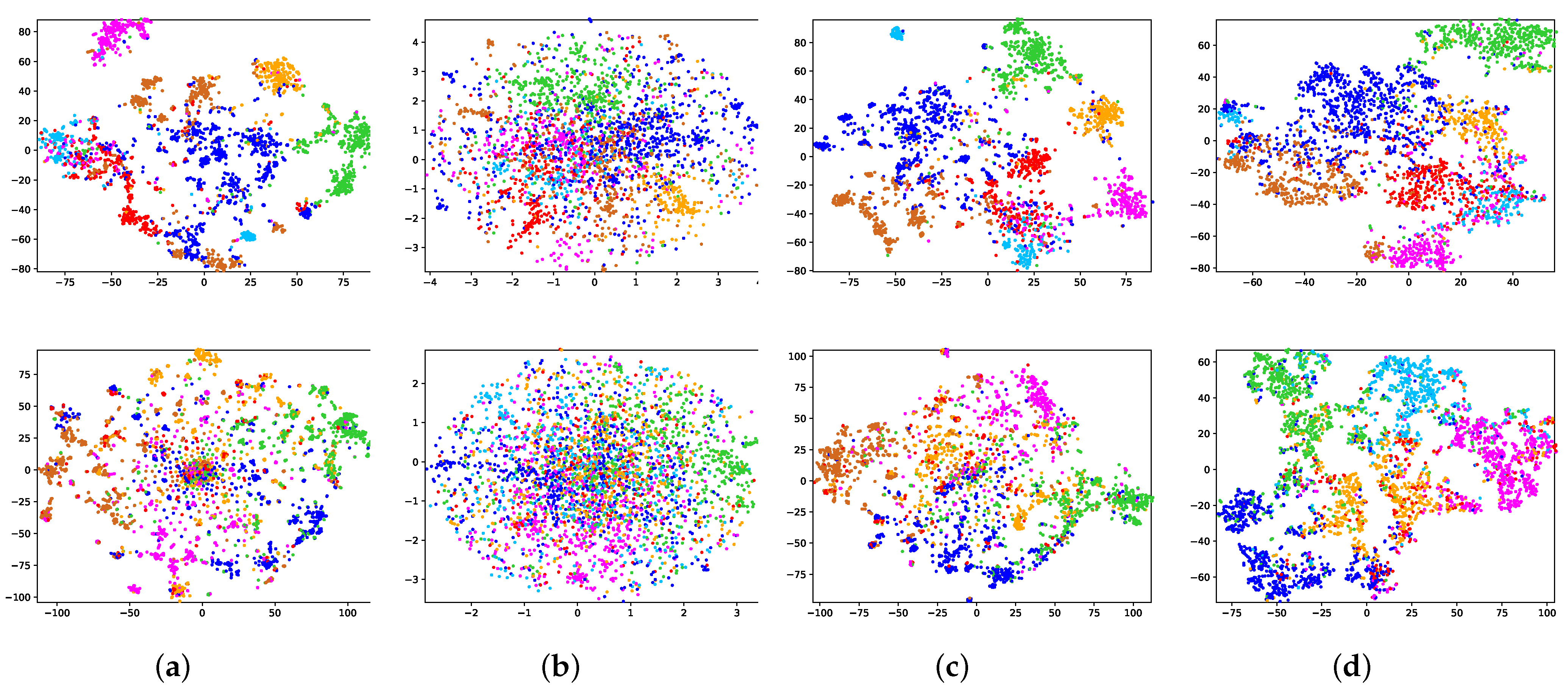
For the purpose of displaying the experimental results more intuitively, t-SNE [32] is applied to visualize the embeddings of the nodes. We paint nodes according to their true labels, and the nodes belonging to the same category will be painted in the same color. From the second row of Figure 4a, we can clearly see that the classic VGAE (i.e., assuming that the prior is a standard normal distribution) cannot distinguish different categories of nodes in the latent space. This is because the standard normal distribution prior will encourage the centers of all categories to approach the origin, resulting in the inability to make full use of the latent space. Similar problems also exist in EVGAE and ARVGE, the second row of Figure 4b,c is more obvious. However, the ideal prior should have as little impact as possible on the posterior distribution and encourage the posterior distribution to learn parameters from the input data. The NPIVGAE we put forward can make full use of the latent space to learn the node representations while distinguishing categories relatively well as shown in Figure 4d.

6. Discussion

We propose a general variational graph autoencoder framework based on noninformative prior to address the posterior collapse issue, and it can learn a more realistic posterior through sample data. In the meantime, we show the latent variables of our model can be understood as block memberships, which improves interpretability. A block–block correlation matrix is introduced to describe the relevance within and between blocks. We consider the node embeddings and the relevance between the communities to which the nodes belong to reconstruct the links in the graph. We tested the proposed model (NPIVGAE) on link prediction and semi-supervised node classification tasks, and it achieves better results than other baselines. Our model also has certain limitations. When learning the node representations in a complex network, it does not consider the node importance, which is usually measured by node degree (the number of edges connected to a node). According to previous studies [33], a high-degree node tends to impact network structure and function significantly. A possible promotion in the future is to consider the importance of each node and introduce degree correction [34] to further improve the efficiency of the model.