A Middleware-Based Approach for Multi-Scale Mobility Simulation
Abstract
1. Introduction
2. Literature Review
2.1. Scales in Mobility Simulations
2.2. Simulations Validity
- either the corrector simulation uses more relevant data than the second simulation,
- or the corrector simulation was validated and the second one wasn’t, or was validated with a lower .
2.3. Simulation Scales
- Macroscopic scale: this scale uses traffic flows and only aggregate variables such as vehicle density and average speed over an arc of the network. Lateral movements such as lane changes are not modeled.
- Mesoscopic scale: This scale also works with traffic flows but also uses probability functions to determine the possibility of a vehicle at a certain position, a certain time, and a certain speed.
- The microscopic scale: This scale represents individual vehicles with their own trajectory and speed. The behavior of the vehicles is modeled by a car-following model or by a cellular transmission model.
- Picoscopic scale: This scale represents individual vehicles with their own trajectory and speed. In contrast to the microscopic scale, the speed and trajectory of a vehicle are in two dimensions, on the road axis and laterally. In the most detailed models, the vehicle and the driver are two separate entities interacting with each other.
- The representation of the travelers (noted ). Three main modalities are defined for this scale: individual representation (called microscopic by abuse of language), representation by groups of individuals (called mesoscopic), and representation by flow (called macroscopic).
- Space (noted ). Several modalities are possible for this dimension. We could refer to the levels of detail of the OGC CityGML standard [33], for which the authors in [34] specify for transportation modeling. However, mobility simulations rarely explicitly refer to the CityGML standard, so we decide to refer instead to two main modalities used in simulation and traffic assignment, following the existing layers in commercial maps: either a very detailed representation of networks (including small streets and directional restrictions, i.e., one-way restrictions, turning bans, etc.), or an aggregated representation, which represent only the main traffic axes.
- Time (noted ). We identify three main modalities corresponding to the orders of magnitude of the represented time dimension. The order of seconds corresponds to very detailed mobility simulations, the order of minutes corresponds to dynamic traffic assignment models, and the order of hours corresponds to static assignment models (considering stationary time, usually referring to peak hours).
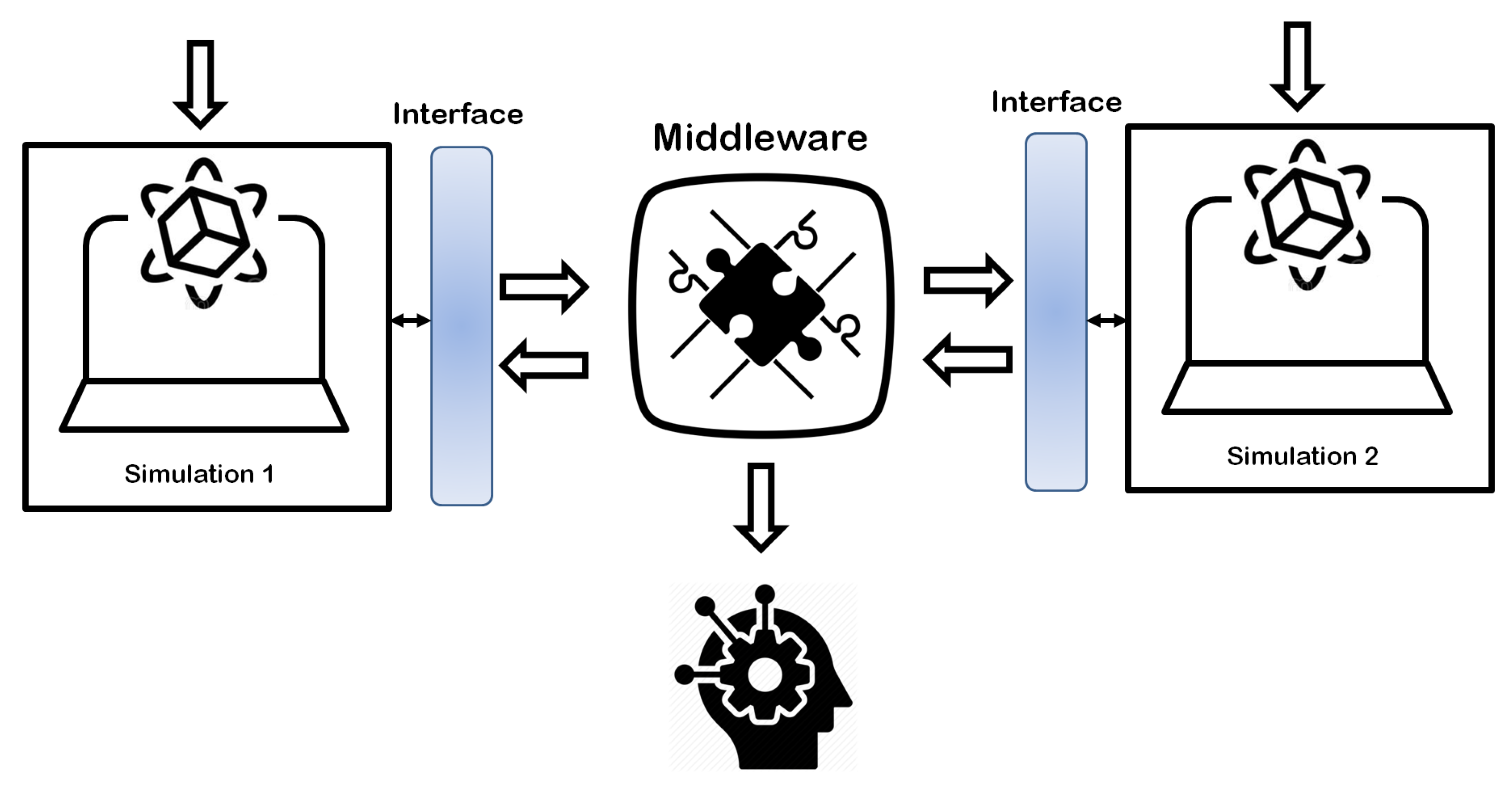
3. The Model
3.1. Dynamic Inputs
3.2. Model Components
- the generic input parameters that are considered by the middleware, with the origin–destination matrix and G the transportation graph.
- are all the other input parameters that are specific to each simulation (e.g., drivers’ aggressiveness for a microscopic simulation). These parameters will be omitted in the remainder of the presentation, since the middleware does not consider them.
- y the simulation’s output , which shows the successive states of G, and the remaining demand through time.
- Demand management ( function). This function defines how the origins and destinations of travelers in are handled.
- The assignment (function ). Given a request, the assignment consists of determining the path travelers will take. Each simulation may have its own method of assigning travelers and the paths determined may be different from one simulation to another. The simulations usually look for a Wardrop’s equilibrium situation where no traveler would gain from changing his currently chosen itinerary [36].
- Travel times (function ). The travel time indicates the time it takes travelers to travel, with a certain speed, through each arc of the route to which they are assigned.
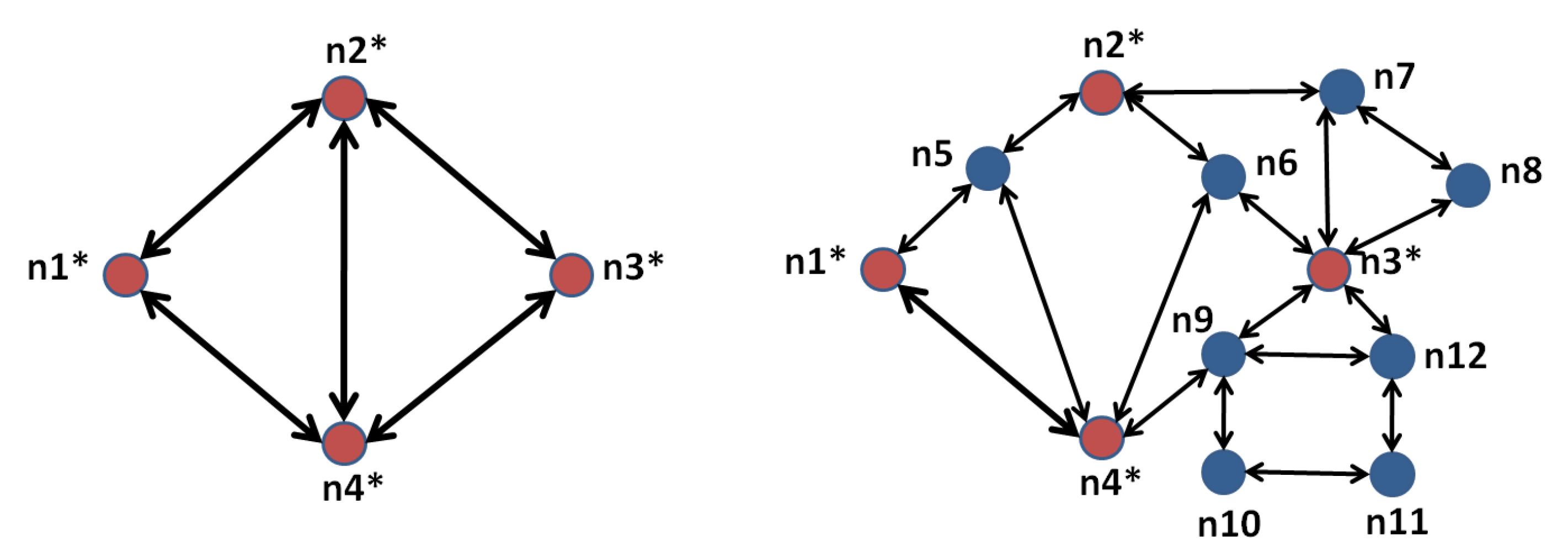
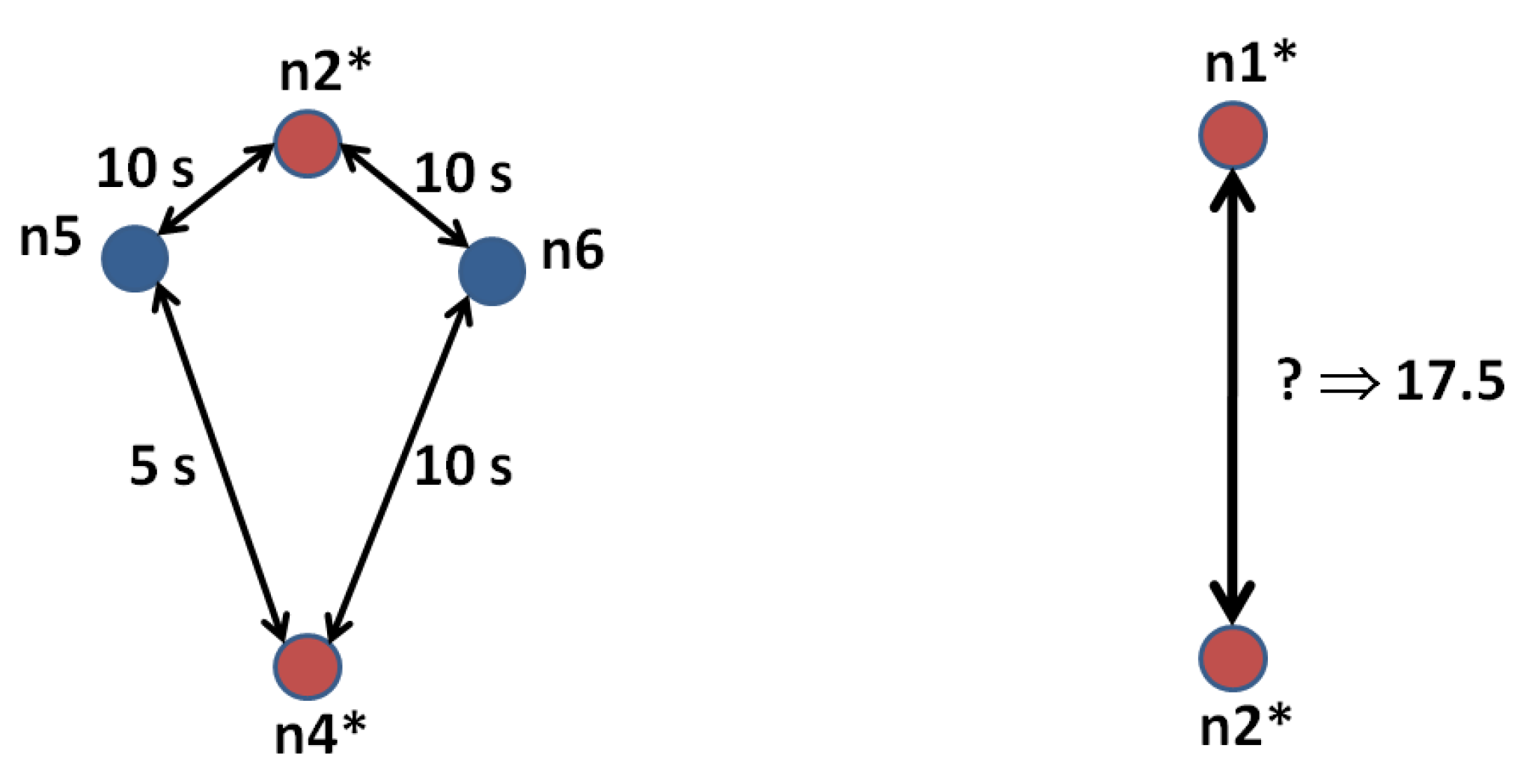
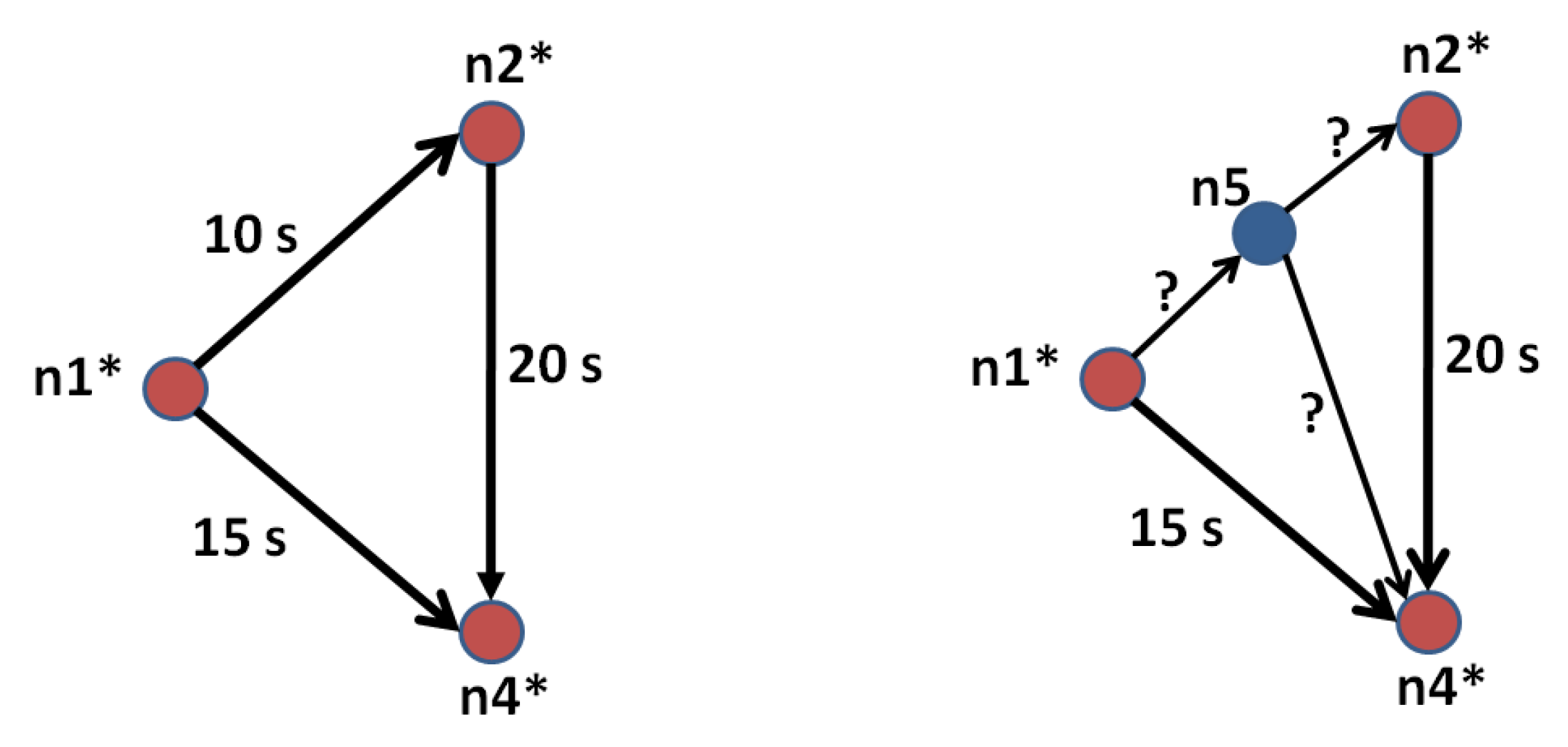
3.3. Synchronizing Simulations (The Time Dimension): The Operator ∘
- the demand (the portion of that is being simulated at the moment ),
- the route that these travelers will take from their origin to their destination.
3.4. Composing the Representations of Travelers: The • Operator
- For each vehicle, a function of its position x is defined: if the vehicle is present in x, then the function returns a positive constant, 0 otherwise.
- Next, all previously defined functions are summed to create a new function. This new function thus returns a positive constant for each x position where a vehicle is present, 0 if no vehicle is present. This function is called .
- Finally, if the cells of the model are spaced by , we obtain the density of traffic on the parts of the arc, necessary for the macroscopic model with the following function:
3.5. Composing Spatial Representations: The ⋄ Operator
3.6. Composing Processes: The ⊕ Operator
3.6.1. Composing Travel Times- Functions
3.6.2. Composing Demand: Functions
3.6.3. Composing Assignment: Functions
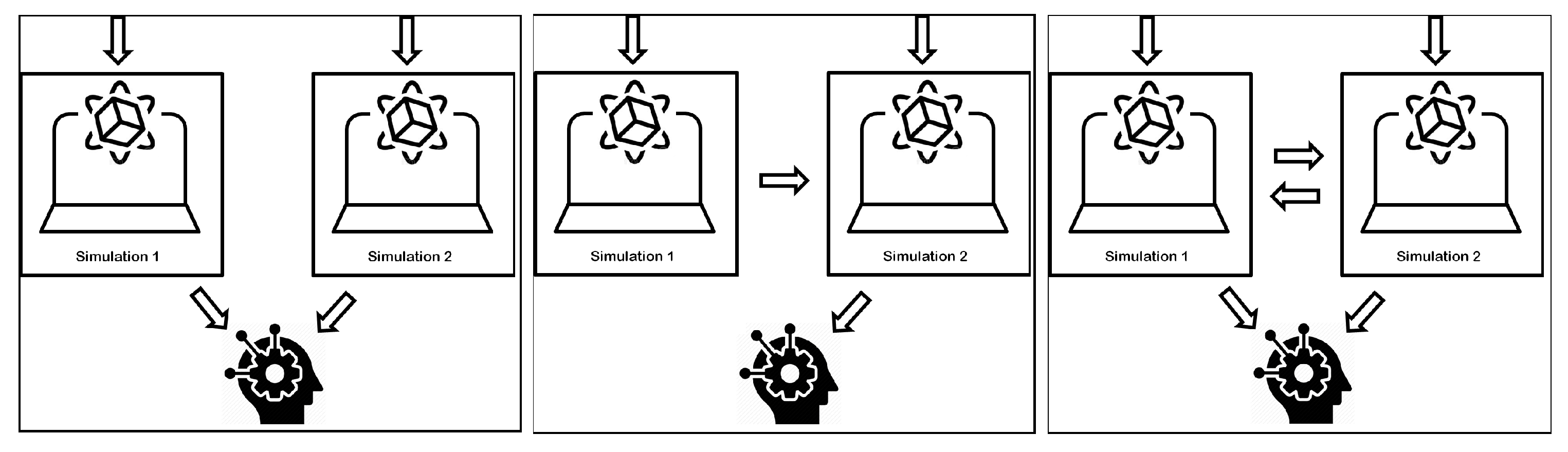
4. Inter-Dependency between Simulations
4.1. Cases 3 and 8
| Algorithm 1 D-AM algorithm. |
| Require:; , |
| Ensure: |
| (1) |
| (2) |
| (3) |
| whiledo |
| (4) execute and save its demand in |
| (5) execute with the demand and save the resulting in |
| (6) execute again with and save its demand in |
| end while |
| (7) Return |
4.2. Cases 4 and 7
| Algorithm 2 A-DM algorithm. |
| Require:; , |
| Ensure: |
| (1) |
| (2) |
| (3) |
| whiledo |
| (4) execute and save its demand in |
| (5) execute with the demand and save the resulting in |
| (6) execute again with and save its demand in |
| end while |
| (7) Return |
4.3. Cases 5 and 6
| Algorithm 3 M-DA algorithm. |
| Require:; , |
| Ensure: |
| (1) |
| (2) |
| (3) |
| whiledo |
| (4) execute and save its demand in |
| (5) execute with the demand and save the resulting |
| (6) execute again with and save its demand in |
| end while |
| (7) Return |
5. Experiments and Results
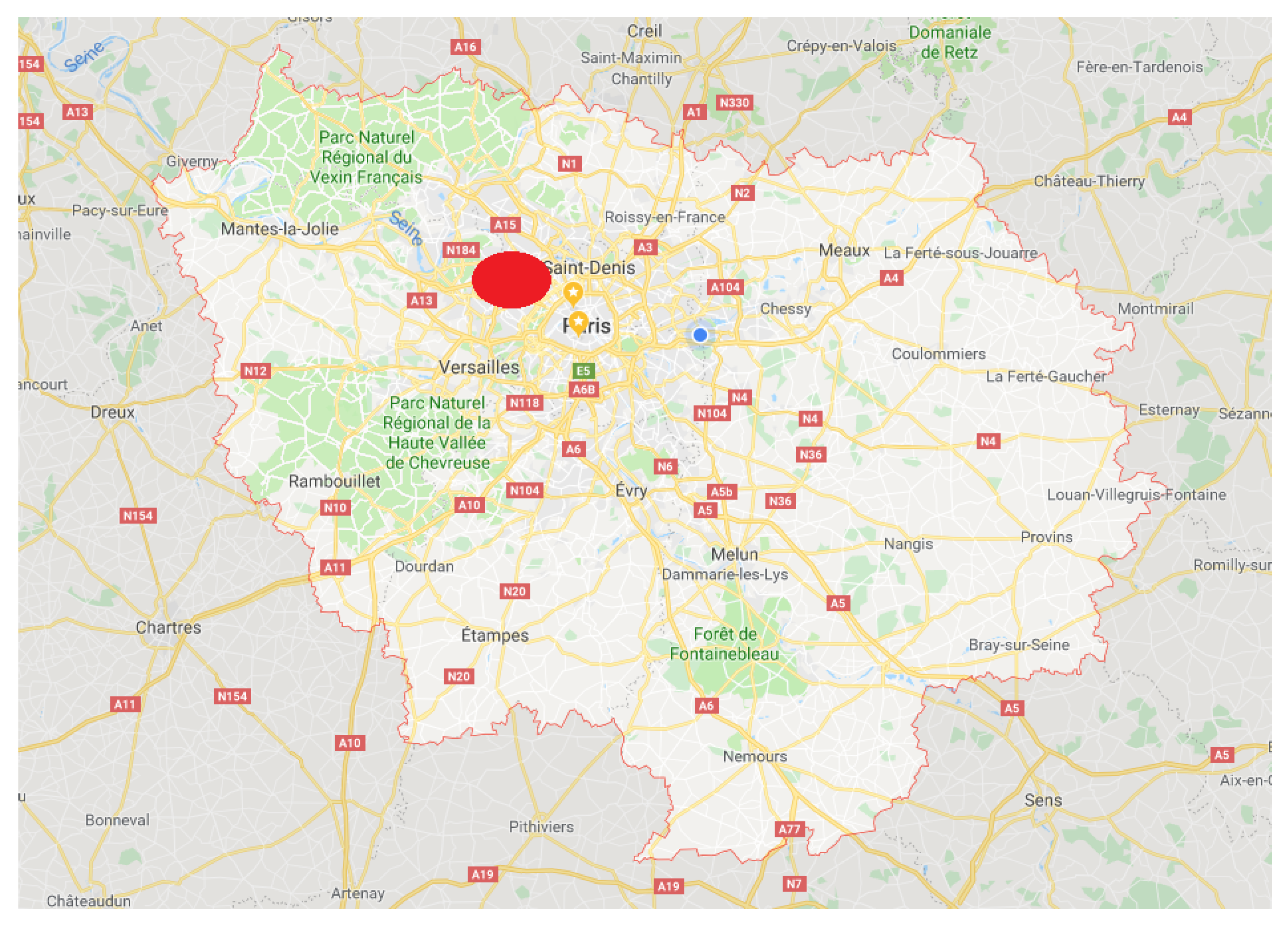
5.1. Case Study
5.2. Middleware Implementation
- The representation of travelers (flows, groups, or individual).
- The length of a simulation time step in seconds.
- The considered transportation network (following a defined XSD schema).
- the functions that are considered valid for each simulation (Assign, Demand, and Move).
5.3. Setup
- The first simulation is implemented in Java, and operates with traveler flows, on an aggregated network and with a time step of 10 min. It assigns travelers’ flows on the shortest route at Wardrop’s equilibrium using the transfer-and-equalize method [41]. The input of the simulation is:
- The temporized origin–destination matrix on a region scale. These data are based on a National survey [42].
- The aggregated network of the region (main streets only).
Its output is the valuated graph every ten minutes. - The second simulation is implemented in Java, works with agents representing individual travelers, on a very detailed network and with a time step of 20 s. It assigns travelers using a K-shortest path algorithm [43]. This simulation uses a car-following model for travelers movements (Simplified Gipp Model from [44]). The inputs of this simulation are:
- The temporized origin–destination matrix on the local scale. To obtain a matrix that is not too different from the regional matrix, we use the method described in [38] to infer a local matrix from a regional one. Then, we introduce some noise, by randomly multiplying the number of travelers in the matrix by a number in .
- The detailed network of the local area.
5.4. Hypotheses
5.5. Scenarios
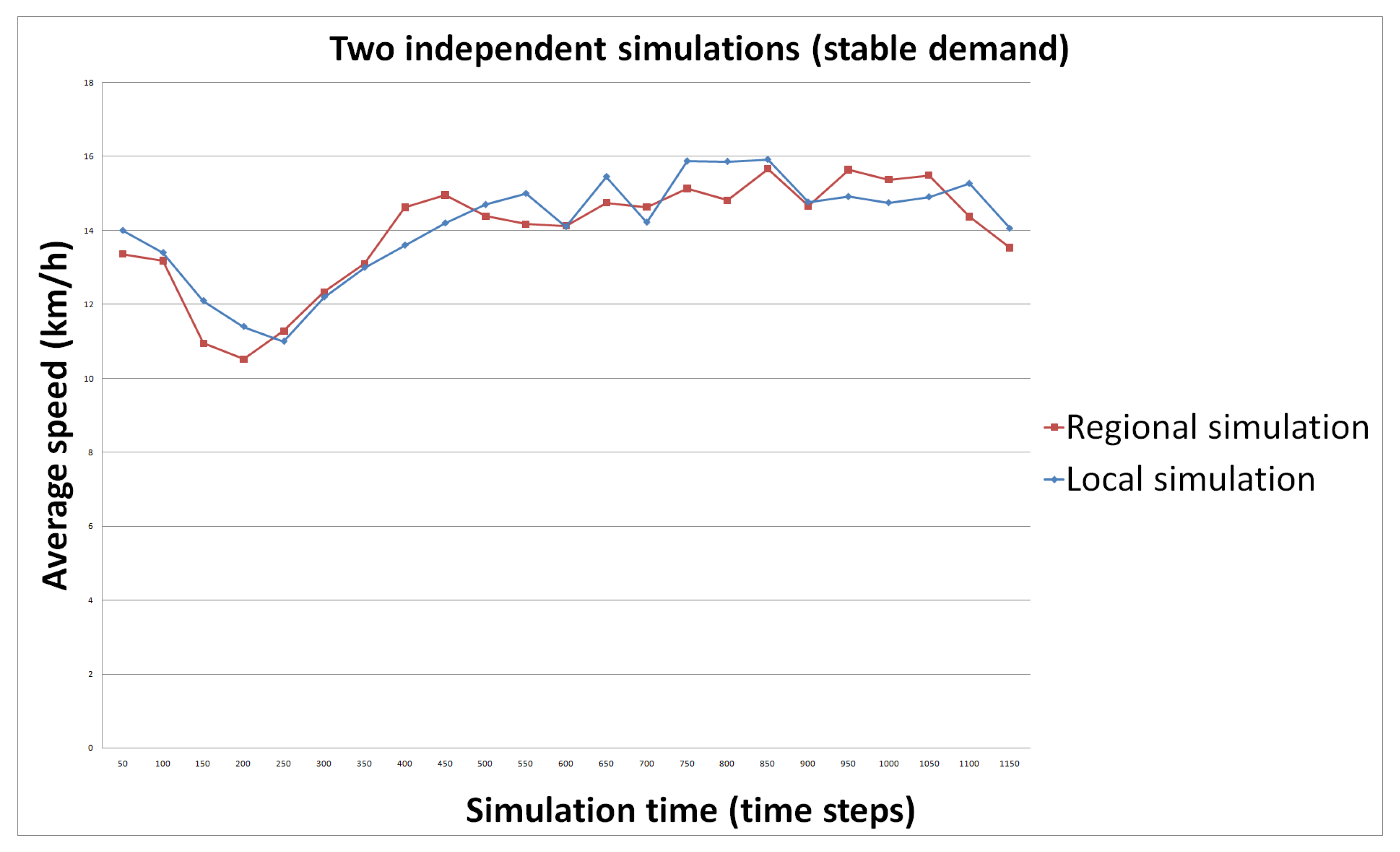
- S1: we use each simulation independently. The demand is stable. To have a stable demand, we distribute the number of origin–destination equally over the available time slots in both regional and local origin–destination matrices.
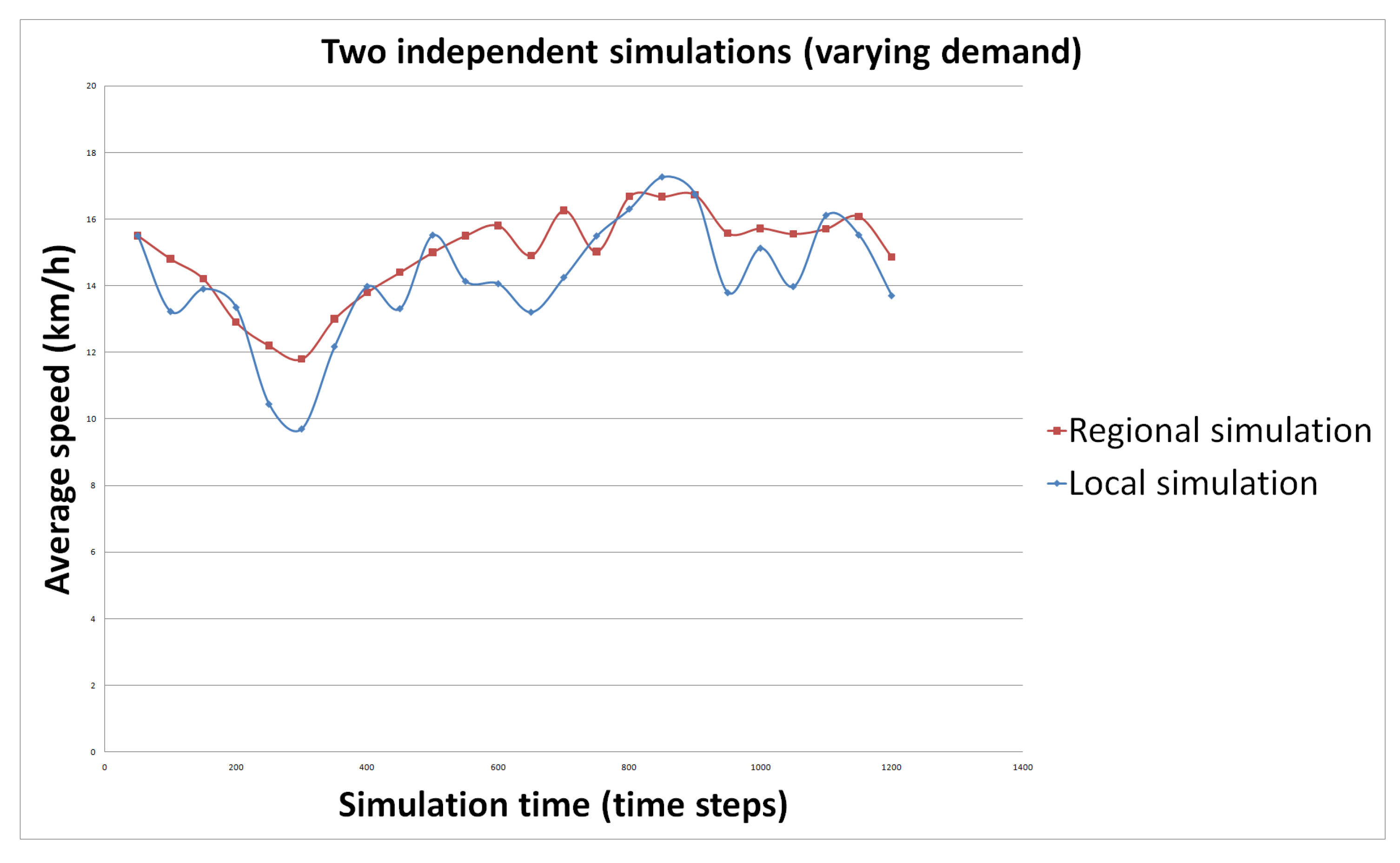
- S2: we use each simulation independently. The demand is variable (we use the original origin–destination matrices).
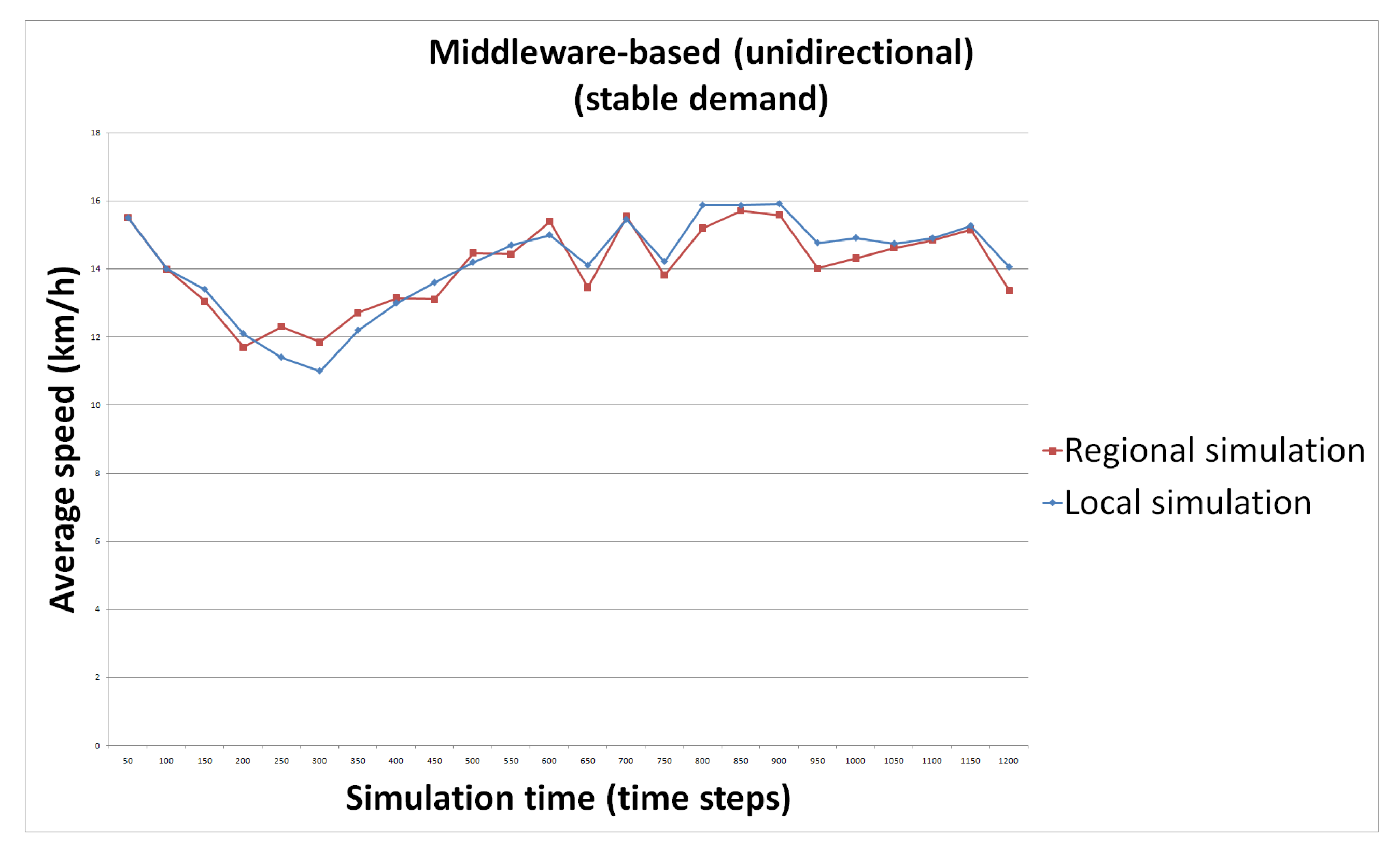
- S3: we use the simulations interacting via the middleware. The interaction is unidirectional, meaning that a time step is not executed twice as defined in Section 4. Demand is stable.
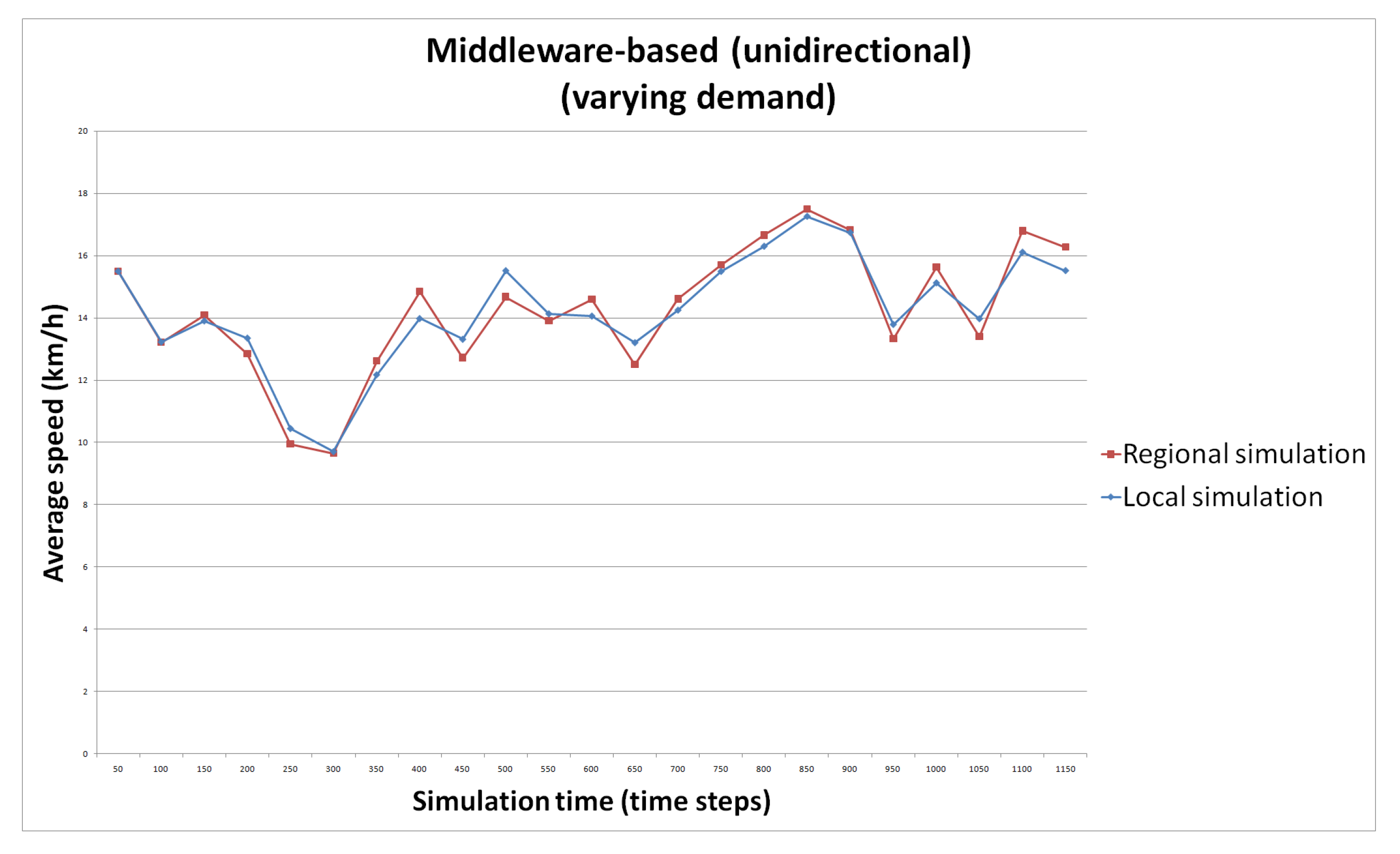
- S4: we use the simulations interacting via the middleware. The interaction is unidirectional, meaning that a time step is not executed twice as defined in Section 4. Demand is variable.
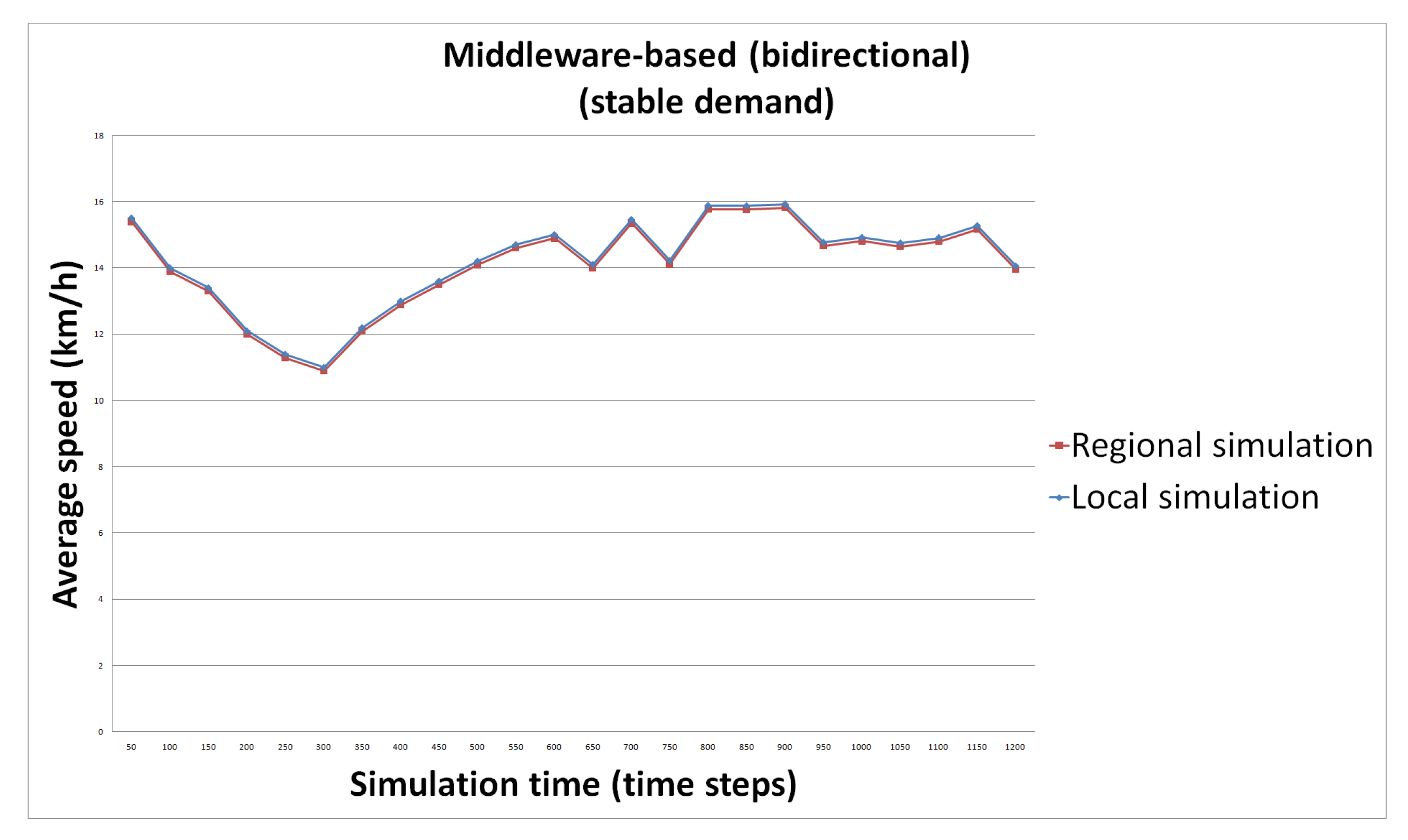
- S5: we use the simulations interacting via the middleware. The interaction is bidirectional, meaning that a time step is executed twice as defined in Section 4. Demand is stable.
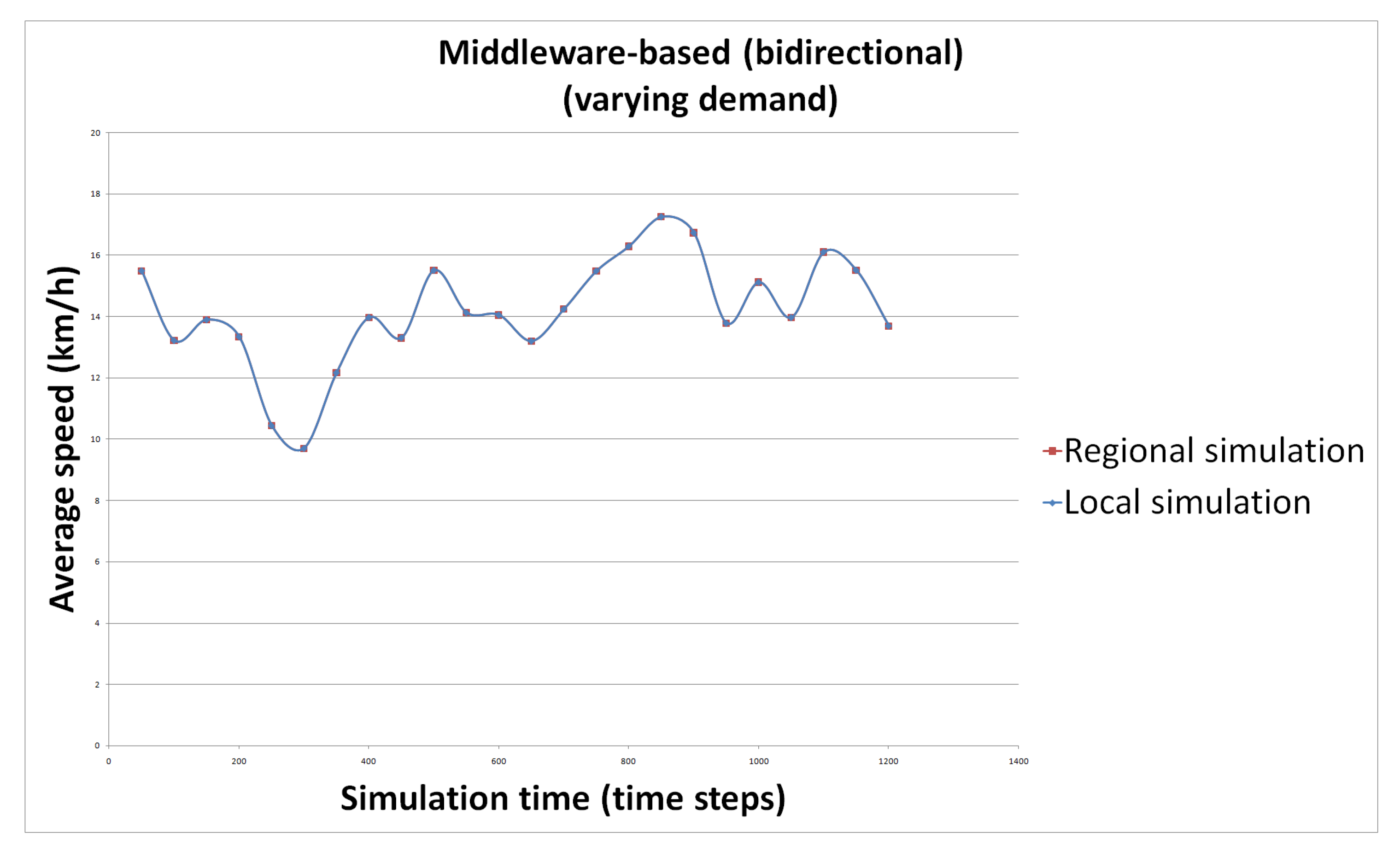
- S6: we use the simulations interacting via the middleware. The interaction is bidirectional, meaning that a time step is executed twice as defined in Section 4. Demand is variable.
5.6. Results
5.6.1. Hypothesis 1
5.6.2. Hypothesis 2
5.6.3. Hypothesis 3
5.6.4. Hypothesis 4
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nipa, T.J.; Kermanshachi, S.; Ramaji, I. Comparative analysis of strengths and limitations of infrastructure resilience measurement methods. In Proceedings of the 7th CSCE International Construction Specialty Conference (ICSC), Laval, QC, Canada, 12–15 June 2019; pp. 12–15. [Google Scholar]
- Ortega, F.A.; Pozo, M.A.; Puerto, J. On-line timetable rescheduling in a transit line. Transp. Sci. 2018, 52, 1106–1121. [Google Scholar] [CrossRef]
- Gan, H.; Ye, X. Will commute drivers switch to park-and-ride under the influence of multimodal traveler information? A stated preference investigation. Transp. Res. Part Traffic Psychol. Behav. 2018, 56, 354–361. [Google Scholar] [CrossRef]
- Bhattacharya, D.; Painho, M.; Mishra, S.; Gupta, A. Mobile traffic alert and tourist route guidance system design using geospatial data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 11–18. [Google Scholar] [CrossRef]
- Nourinejad, M.; Roorda, M.J. Impact of hourly parking pricing on travel demand. Transp. Res. Part Policy Pract. 2017, 98, 28–45. [Google Scholar] [CrossRef]
- D’Ariano, A. Innovative decision support system for railway traffic control. IEEE Intell. Transp. Syst. Mag. 2009, 1, 8–16. [Google Scholar] [CrossRef]
- Toahchoodee, M.; Ray, I.; Anastasakis, K.; Georg, G.; Bordbar, B. Ensuring spatio-temporal access control for real-world applications. In Proceedings of the 14th ACM Symposium on Access Control Models and Technologies, Stresa, Italy, 3–5 June 2009; pp. 13–22. [Google Scholar]
- Zargayouna, M.; Othman, A.; Scemama, G.; Zeddini, B. Multiagent Simulation of Real-Time Passenger Information on Transit Networks. IEEE Intell. Transp. Syst. Mag. 2020, 12, 50–63. [Google Scholar] [CrossRef]
- Crociani, L.; Lämmel, G.; Vizzari, G. Multi-scale simulation for crowd management: A case study in an urban scenario. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, Singapore, 9–13 May 2016; pp. 147–162. [Google Scholar]
- Zia, K.; Farrahi, K.; Riener, A.; Ferscha, A. An agent-based parallel geo-simulation of urban mobility during city-scale evacuation. Simulation 2013, 89, 1184–1214. [Google Scholar] [CrossRef]
- Mastio, M.; Zargayouna, M.; Scemama, G.; Rana, O. Distributed agent-based traffic simulations. IEEE Intell. Transp. Syst. Mag. 2018, 10, 145–156. [Google Scholar] [CrossRef]
- Anagnostopoulos, D. A methodological approach for model validation in faster than real-time simulation. Simul. Model. Pract. Theory 2002, 10, 121–139. [Google Scholar] [CrossRef]
- Hsu, C.; Lian, F.; Huang, C. A Systematic Spatiotemporal Modeling Framework for Characterizing Traffic Dynamics Using Hierarchical Gaussian Mixture Modeling and Entropy Analysis. IEEE Syst. J. 2014, 8, 1129–1138. [Google Scholar]
- Holmgren, J.; Ramstedt, L.; Davidsson, P.; Edwards, H.; Persson, J.A. Combining macro-level and agent-based modeling for improved freight transport analysis. Procedia Comput. Sci. 2014, 32, 380–387. [Google Scholar] [CrossRef][Green Version]
- Fellendorf, M.; Vortisch, P. Microscopic traffic flow simulator VISSIM. In Fundamentals of Traffic Simulation; Springer: New York, NY, USA, 2010; pp. 63–93. [Google Scholar]
- Vliet, D.V. The Saturn Users Manual; Institute for Transportation Studies: Leeds, UK, 1998. [Google Scholar]
- Montero, L.; Codina, E.; Barceló, J.; Barceló, P. Combining macroscopic and microscopic approaches for transportation planning and design of road networks. In Proceedings of the 19 th ARRB Transport Research Conference, Sydney, Australia, 7–11 December 1998; pp. 93–108. [Google Scholar]
- Barceló, J.; Casas, J. Dynamic network simulation with AIMSUN. In Simulation Approaches in Transportation Analysis; Springer: New York, NY, USA, 2005; pp. 57–98. [Google Scholar]
- Sewall, J.; Wilkie, D.; Lin, M.C. Interactive hybrid simulation of large-scale traffic. ACM Trans. Graph. 2011, 30, 135. [Google Scholar] [CrossRef]
- Gaud, N.; Galland, S.; Gechter, F.; Hilaire, V.; Koukam, A. Holonic multilevel simulation of complex systems: Application to real-time pedestrians simulation in virtual urban environment. Simul. Model. Pract. Theory 2008, 16, 1659–1676. [Google Scholar] [CrossRef]
- Haman, I.T.; Kamla, V.C.; Galland, S.; Kamgang, J.C. Towards an multilevel agent-based model for traffic simulation. Procedia Comput. Sci. 2017, 109, 887–892. [Google Scholar] [CrossRef]
- Navarro, L.; Flacher, F.; Corruble, V. Dynamic level of detail for large scale agent-based urban simulations. In Proceedings of the 10th International Conference on Autonomous Agents and Multiagent Systems-Volume 2, Taipei, Taiwan, 2–6 May 2011; pp. 701–708. [Google Scholar]
- Navarro, L.; Corruble, V.; Flacher, F.; Zucker, J.D. A flexible approach to multi-level agent-based simulation with the mesoscopic representation. In Proceedings of the 2013 International Conference on Autonomous Agents and Multi-Agent Systems, Saint Paul, MN, USA, 6–10 May 2013; pp. 159–166. [Google Scholar]
- Biedermann, D.H.; Kielar, P.M.; Handel, O.; Borrmann, A. Towards TransiTUM: A generic framework for multiscale coupling of pedestrian simulation models based on transition zones. Transp. Res. Procedia 2014, 2, 495–500. [Google Scholar] [CrossRef][Green Version]
- Joueiai, M.; Van Lint, H.; Hoogendoom, S.P. Multiscale traffic flow modeling in mixed networks. Transp. Res. Rec. 2014, 2421, 142–150. [Google Scholar] [CrossRef]
- Bishop, T.A.; Karne, R.K. A Survey of Middleware. In Proceedings of the ISCA 18th International Conference Computers and Their Applications, Honolulu, HI, USA, 26–28 March 2003; ISCA 2003. pp. 254–258. [Google Scholar]
- Klügl, F. A validation methodology for agent-based simulations. In Proceedings of the 2008 ACM Symposium on Applied Computing, Fortaleza, Brazil, 16–20 March 2008; pp. 39–43. [Google Scholar]
- Balci, O. Validation, verification, and testing techniques throughout the life cycle of a simulation study. Ann. Oper. Res. 1994, 53, 121–173. [Google Scholar] [CrossRef]
- Law, A.M. How to build valid and credible simulation models. In Proceedings of the Winter Simulation Conference, Orlando, FL, USA, 4–7 December 2005. [Google Scholar]
- Bayarri, M.; Berger, J.O.; Molina, G.; Rouphail, N.M.; Sacks, J. Assessing uncertainties in traffic simulation: A key component in model calibration and validation. Transp. Res. Rec. 2004, 1876, 32–40. [Google Scholar] [CrossRef]
- Ni, D. Multiscale modeling of traffic flow. Math. Aeterna 2011, 1, 27–54. [Google Scholar]
- Bourrel, E.; Lesort, J.B. Mixing microscopic and macroscopic representations of traffic flow: Hybrid model based on Lighthill–Whitham–Richards theory. Transp. Res. Rec. 2003, 1852, 193–200. [Google Scholar] [CrossRef]
- Gröger, G.; Kolbe, T.H.; Nagel, C.; Häfele, K.H. OGC City Geography Markup Language (CityGML) Encoding Standard; Technical Report; Open Geospatial Consortium: Wayland, MA, USA, 2012. [Google Scholar]
- Beil, C.; Kolbe, T.H. CityGML and the streets of New York-A proposal for detailed street space modelling. In Proceedings of the 12th International 3D GeoInfo Conference 2017, Melbourne, Australia, 26–27 October 2017; pp. 9–16. [Google Scholar]
- Lok, L.; Brent, R. Automatic generation of cellular reaction networks with Moleculizer 1.0. Nat. Biotechnol. 2005, 23, 131–136. [Google Scholar] [CrossRef] [PubMed]
- Szeto, W.; Wong, S. Dynamic traffic assignment: Model classifications and recent advances in travel choice principles. Cent. Eur. J. Eng. 2012, 2, 1–18. [Google Scholar] [CrossRef]
- Connors, R.D.; Watling, D.P. Assessing the demand vulnerability of equilibrium traffic networks via network aggregation. Netw. Spat. Econ. 2015, 15, 367–395. [Google Scholar] [CrossRef]
- Ksontini, F.; Zargayouna, M.; Scemama, G.; Leroy, B. Building a Realistic Data Environment for Multiagent Mobility Simulation. In Agent and Multi-Agent Systems: Technologies and Applications; Springer: New York, NY, USA, 2016; pp. 57–67. [Google Scholar]
- Raju, N.; Arkatkar, S.; Joshi, G. Evaluating performance of selected vehicle following models using trajectory data under mixed traffic conditions. J. Intell. Transp. Syst. 2019, 24, 617–634. [Google Scholar] [CrossRef]
- Szeto, W.Y. Dynamic modeling for intelligent transportation system applications. J. Intell. Transp. Syst. 2014, 18, 323–326. [Google Scholar] [CrossRef]
- Leurent, F. The theory and practice of a dual criteria assignment model with a continuously distributed value-of-time. In Proceedings of the Transportation and Traffic Theory Proceedings of the ISTTT Conference, Lyon, France, 24–26 July 1996; pp. 455–477. [Google Scholar]
- INSEE. Enquête Globale Transport. 2010. Available online: http://www.omnil.fr/IMG/pdf/-4.pdf (accessed on 19 January 2021).
- Eppstein, D. Finding the k shortest paths. SIAM J. Comput. 1998, 28, 652–673. [Google Scholar] [CrossRef]
- Treiber, M.; Kesting, A. Traffic flow dynamics. In Traffic Flow Dynamics: Data, Models and Simulation; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Behrisch, M.; Bieker, L.; Erdmann, J.; Krajzewicz, D. SUMO- Simulation of Urban MObility—An Overview. In Proceedings of the Third International Conference on Advances in System Simulation, Barcelona, Spain, 23–28 October 2011; pp. 55–60. [Google Scholar]
- Maciejewski, M.; Nagel, K. Towards Multi-agent Simulation of the Dynamic Vehicle Routing Problem in MATSim. In Proceedings of the 9th International Conference on Parallel Processing and Applied Mathematics, Naleczow, Poland, 9–12 September 2012; pp. 551–560. [Google Scholar]
| # | ’s Valid Function (s) | ’s Valid Function (s) | Inter-Dependency? |
|---|---|---|---|
| 1 | Demand, Assign, Move | - | × |
| 2 | - | Demand, Assign, Move | × |
| 3 | Demand | Assign, Move | √ |
| 4 | Assign | Demand, Move | √ |
| 5 | Move | Demand, Assign | √ |
| 6 | Demand, Assign | Move | √ |
| 7 | Demand, Move | Assign | √ |
| 8 | Assign, Move | Demand | √ |
| Scenario | Regional Simulation | Local Simulation | Composition |
|---|---|---|---|
| 1 | 1100 | 3200 | - |
| 2 | 1532 | 3840 | - |
| 3 | - | - | 4945 |
| 4 | - | - | 6340 |
| 5 | - | - | 12,840 |
| 6 | - | - | 18,017 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boulet, X.; Zargayouna, M.; Scemama, G.; Leurent, F. A Middleware-Based Approach for Multi-Scale Mobility Simulation. Future Internet 2021, 13, 22. https://doi.org/10.3390/fi13020022
Boulet X, Zargayouna M, Scemama G, Leurent F. A Middleware-Based Approach for Multi-Scale Mobility Simulation. Future Internet. 2021; 13(2):22. https://doi.org/10.3390/fi13020022
Chicago/Turabian StyleBoulet, Xavier, Mahdi Zargayouna, Gérard Scemama, and Fabien Leurent. 2021. "A Middleware-Based Approach for Multi-Scale Mobility Simulation" Future Internet 13, no. 2: 22. https://doi.org/10.3390/fi13020022
APA StyleBoulet, X., Zargayouna, M., Scemama, G., & Leurent, F. (2021). A Middleware-Based Approach for Multi-Scale Mobility Simulation. Future Internet, 13(2), 22. https://doi.org/10.3390/fi13020022





