Abstract
Satellite–terrestrial integrated networks (STINs) are regarded as a promising solution to meeting the demands of global high-speed seamless network access in the future. Software-defined networking and network function virtualization (SDN/NFV) are two complementary technologies that can be used to ensure that the heterogeneous resources in STINs can be easily managed and deployed. Considering the dual mobility of satellites and ubiquitous users, along with the dynamic requirements of user requests and network resource states, it is challenging to maintain service continuity and high QoE performance in STINs. Thus, we investigate the service migration and reconfiguration scheme, which are of great significance to the guarantee of continuous service provisioning. Specifically, this paper proposes a dynamic service reconfiguration method that can support flexible service configurations on integrated networks, including LEO satellites and ground nodes. We first model the migration cost as an extra delay incurred by service migration and reconfiguration and then formulate the selection processes of the location and migration paths of virtual network functions (VNFs) as an integer linear programming (ILP) optimization problem. Then, we propose a fuzzy logic and quantum genetic algorithm (FQGA) to obtain an approximate optimal solution that can accelerate the solving process efficiently with the benefits of the high-performance computing capacity of QGA. The simulation results validate the effectiveness and improved performance of the scheme proposed in this paper.
1. Introduction
With the rapid development of micro satellite systems and internet technology, integrating terrestrial networks and satellite networks that are able to cover multiple natural environments, such as space, air, earth, maritime, and deep space environments, and that can provide seamless high-speed network access, satellite–terrestrial integrated networks (STINs) have gradually become one of the most important research fields in the current industry and academic community [1]. The combination of emerging network technologies, such as SDN/NFV [2], 5G [3], edge computing [4], and the Internet of Things [5], also ensure that STINs are efficient and have convenient management and control abilities as well as flexible and expandable network service support [6]. Under the STIN architecture, differentiated independent network slices are provided according to a user’s actual traffic demands and service requirements, or corresponding Virtual Network Functions (VNFs) are deployed. These aim to use limited network resources or service resources in order to meet the diverse traffic and service requirements of different users as well as to obtain a better network resource configuration and better service experience. However, the dynamic network topology of the STIN itself, as well as the changes in user traffic requests and task requirements, mean that one-time resource deployment and optimization strategies are no longer able to adapt to the dynamic network states, resulting in the deterioration of network performance, the decline of user service quality experience, the increase in network operation, and maintenance costs, etc.
The main reasons for the dynamics that are observed in STINs are the dual mobility of satellites and mobile users with varying requirements. For example, when the LEO satellites offering on-board services move out of the reachable range, the on-board services need to migrate to another satellite that is moving into range. Additionally, users change their access location and network requests along with the real-time tasks and the deployed service may not be able to meet the changing request, so it also needs to be reconfigured. That is, when facing the dynamics caused by user or node mobility that may seriously affect service traffic transmission or service deployment quality, it is necessary to find new adjustment methods to maintain the continuity and quality assurance of traffic transmission and service provisioning.
Thus, we need to design a new adjustment method that is able to manage service migration and reconfiguration in STINs and that is able to alleviate problems of load imbalance, degradation, or service quality interruptions to a certain extent [7]. Specifically, the proposed method migrates and deploys the VNFs on the original service node to a new service node that has more sufficient resources or more reasonable paths. Then, the service traffic would be guided according to the new location and would be transmitted by the new service path. Differently to the general network framework of mobile networks, the dual mobility and high dynamics of STINs increase the difficulty of solving the above problem [8].
Therefore, we focus on the service migration and reconfiguration caused by the dual mobility and dynamics under the STIN architecture, and the main contributions are as follows:
- Considering the dual mobility and high dynamics of STINs, we propose a detailed system model and problem statement for service migration in STINs, and the migration location and path selection problem is modeled and formulated as a classic integer linear programming (ILP) problem.
- To achieve the optimal objective efficiently, we propose a novel fuzzy logic quantum genetic algorithm-based dynamic service migration and reconfiguration (FQGA-SR) method that uses its quantum coding and parallel computing advantages to solve the optimization problem.
- Finally, the effectiveness and efficiency of the proposed algorithm are verified through simulation experiments. The proposed FQGA-SR can speed up the convergence and can better outperform the other three methods used in our scenarios in terms of various important service migration metrics.
The rest of this paper is organized as follows. In Section 2, we summarize previous studies that are related to the present topic, and in Section 3 we then present descriptions of service migration and reconfiguration problems as well as the network modeling and optimal objective formulation used in STINs. In Section 4, the FQGA-SR migration and reconfiguration algorithm is proposed with detailed basic steps and descriptions. Finally, simulations are presented in Section 5, which is followed by the conclusion and plans for future steps in Section 6.
2. Related Works
2.1. Service Migration in Mobile Edge Networks
At present, there are many well executed, relevant studies in the fields of mobile edge networks, the Internet of things, fog computing, and in the multi-source heterogeneous and dynamic STIN, its research is still in the start-up stage. As an example, in [9], the service migration problem in mobile edge computing networks is formulated as a Markov decision process (MDP). The work in [10] models the VNFs migration problem as an integrated linear programming (ILP) problem and proposed a greedy algorithm to minimize the migration cost while satisfying the computing and network resource capacity constraints. The mobile edge computing scenario service migration cost is studied in [11]. In this work, they take into account the service migration revenue and total cost of service at the same time and design a dynamic service migration algorithm based on deep reinforcement learning. On the premise of guaranteed service continuity and quality of service, this algorithm is used to optimize the service migration cost and total cost of network operation. In [12], the researchers study the service migration of a mobile backhaul network in fog computing scenarios. In order to meet the continuous network service demands of mobile terminal users with high capacity and low delay, a delay-awareness bandwidth slicing technique is proposed to address the service migration traffic limitation problem and to optimize the network performance of high-priority migration traffic. This study highlights the priority setting of migrating traffic and non-migrating traffic to optimize the traffic transmission efficiency of service migration. In [13], service migration in mobile edge networks is modelled as a reinforcement-learning model to optimize the service migration strategy and communication strategy in order to improve long-term efficiency. Simulation results show that the proposed method based on reinforcement learning has better results than the Q-learning method and the Deep Q-learning network method. The work in [14] proposed a service migration optimization algorithm based on machine learning, taking network delay and energy consumption as optimization targets while considering the changes of network bandwidth and mobile terminal energy. The work in [15] proposed an online multi-user service migration optimization algorithm based on Lyapunov to solve the service migration problem in multi-user vehicle scenarios without considering vehicle trajectory predictions. Considering the mobility of fog nodes, the work in [16] studied the deployment of application components in NFV-based hybrid cloud–fog computing system and proposed a component deployment algorithm based on Tabu search to find the optimal deployment strategy. Nevertheless, the mobility issue studied in this work is the increasing or decreasing of the number of connected nodes, rather than the mobility model.
The application scenarios of the works mentioned above have several similarities with the STINs, such as multi-source heterogeneous network architecture and the mobility of mobile users. However, the mobility of satellites trigger the structure and network state changes of the STINs, while the network sides of 5G, mobile edge network, and the IoT are fixed, which makes it different to studies of the service migration problem in STINs.
2.2. Service Migration in STINs
At present, researchers have made some achievements in the studies on the service migration and reconfiguration of STINs. In [17], the geographic migration model of computing resources in the scenario of satellite intelligent urban vehicle networking is established. The road states and vehicle states are known through fog nodes, and a vehicle route selection scheme based on resource pricing is proposed. Its main innovations are that of regarding the moving vehicles as computing resources and proposing the pricing strategy algorithm under diverse demand conditions, while the computational efficiency of the migration strategy is slightly insufficient. The work in [18] proposes a space-based edge cloud service on orbit service architecture, which can carry out service migration dynamically according to the real-time uplink and downlink traffic changes. Aiming at optimizing the migration node delay and energy consumption, a space-based edge cloud service migration model is established and verified by simulation. However, the object and scope of service migration are merely for satellite nodes and their on-orbit services, and the migration between satellite and ground nodes is not considered. The work in [19] studied dynamic resource allocation and reconfiguration of communication services in the space–time network scenario, modelling the on-board user resource allocation problem as a multi-period generalized allocation problem, and proposed a deep Q-learning control framework to optimize resource allocation and reconfiguration. Considering the dynamics of the Internet of vehicles scenario, [20] studied the online dynamic VNF mapping and scheduling problem in the Internet of vehicles scenario of space–time cooperation, and proposed two VNF mapping and rescheduling algorithms based on Tabu search algorithm, which can effectively obtain the approximate optimal VNF migration scheme. In the 5G heterogenous scenario, the work in [21] focuses on the power control problem in 5G heterogeneous cells, proposes a novel deep reinforcement learning (DRL) scheme, which can efficiently configurate the cells power to gratify the user demand. In [22], the resource allocation problem in multi-cell networks was studied, a deep neural network for training the allocation model was proposed, and simulation results show the accuracy of its allocation method.
It seems that the DRL algorithms continually interact with environments to obtain the optimal solution, and, for the most part, performed well in large scale optimal problems such as resources allocation in 5G multi-cell networks or mobile edge networks, whose user side is mobile, while the network side is fixed and possesses ample computing capacity. However, while the necessary and frequent interaction of DRL may lead to more consumption of communication and computing resources, it is still worth discussing whether it is suitable for the STINs scenario with limited on-board resources and longer communication delay.
Although some researchers have studied the service migration and reconfiguration of STINs and similar network architectures from various perspectives, their pertinence and optimization effect are slightly insufficient and required further discussing. Especially since there is a high dynamicity coupled with dual mobility both in the network side and the user side of STINs, which makes it challenging to obtain an efficient service migration and reconfiguration method. The quantum computing algorithms have higher computational efficiency than other iterative-based algorithms, since the superposition coding manner of quantum computing supports parallel computing capability [23]. Thus, in this work, a novel optimal method FQGA-SR with STIN model is proposed, so as to achieve higher computational efficiency and better performances in service migration and reconfiguration problems.
3. Problem Descriptions
3.1. Problem Statement of Service Migration in STINs
Figure 1 shows the service migration and reconfiguration process of STINs. The basic architecture of a STIN is a three-layer network structure composed of a satellite network, a high-altitude platform (HAP), and a terrestrial network, as well as a two-layer control structure composed of a ground management control center (GMCC) and GEO satellite controller. Assuming that LEO satellite edge nodes and ground edge nodes have certain computing and storage resources, they can carry a variety of VNFs according to the deployment strategy, and can provide users with high-speed network access, edge computing service, data relay, and backhaul capabilities. At the same time, both UAV nodes and satellite nodes have communication relay and backhaul capabilities. Due to the limitations of energy and load, UAV nodes are not considered as edge nodes in this paper, but only work as data relay and forwarding functions. The satellite nodes in the satellite network layer are connected with each other by directional wireless communication links and can afford high-speed data transmission.
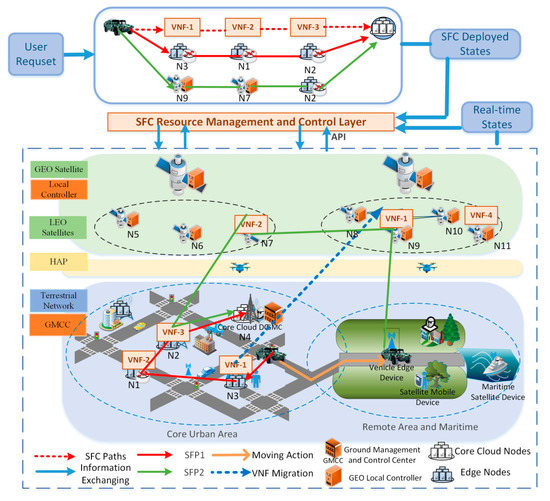
Figure 1.
Service migration and reconfiguration process in satellite–terrestrial integration networks.
The upper part of Figure 1 shows the basic process of a service request made by a STIN user. At present, the object of service provisioning is mobile vehicle end users. Vehicle users drive from core urban areas to remote areas. At present, the service function chains (SFCs) required by the vehicle users are sequential virtual network functions (VNFs), as an example, VNF-1, VNF-2, and VNF-3.
Before the vehicle user moves, there is a nearby access point of a ground edge node N3, and it can provide sufficient edge computing capability and service support. The data flow initiates from the source node N3 and reaches the destination node N4 through the service function path (SPF) of the SPF1 (N3-N1-N2), while the VNF-1, VNF-2, and VNF-3 are deployed at nodes N3, N1, and N2.
After the vehicle user moves to the remote area, it loses the access point and service support from the ground edge node. The management and control plane run the service migration and reconfiguration algorithm to obtain the optimal migration location and migration path according to the real-time network states and vehicle user service request. For example, VNF-1 on ground edge node N3 is migrated to satellite edge node N9, VNF-2 on N1 is migrated to satellite edge node N7, while the migration path is the shortest path. Furthermore, the data flow of the migrated user’s vehicle reaches the destination node N4 through the new path SFP2 (N9-N7-N2), so as to satisfy the requirement of vehicle users and maintains the continuity and reliability of communication and service.
As mentioned above, the key contribution of this paper is to find the appropriate migration location for VNF through service migration and reconfiguration algorithms, and solve the optimal migration strategy with specific objectives and constraints of the STIN system.
3.2. Workflow of Service Migration and Reconfiguration
The service migration and reconfiguration process of the STIN can be divided into two main steps, the migration awareness stage and the execution stage. The flowchart is shown in Figure 2.
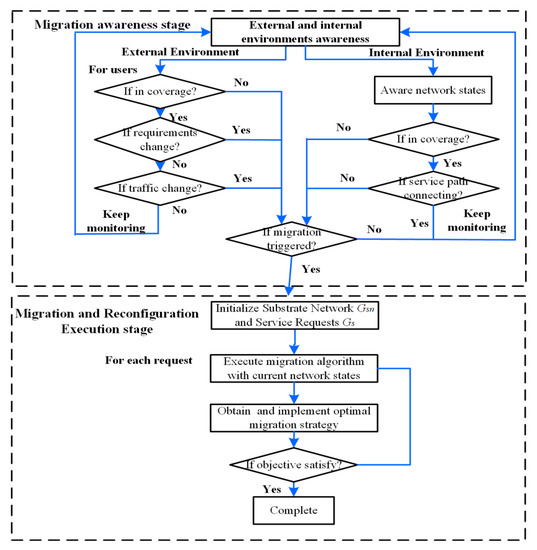
Figure 2.
Flowchart of service migration and reconfiguration.
- (1)
- Migration awareness stage
Due to the periodic movement of satellite nodes in the STIN and the mobility of users, both satellite edge nodes and ground edge nodes may experience service migration and reconfiguration. First, the global states awareness ability of SDN/NFV is used to obtain external and internal environmental states of the current STIN system as well as the previous services that are already deployed, subsequently it decides whether the service migration is triggered. If the trigger event occurs, the next stage of the algorithm is execution. If not, there is sustained monitoring as before.
- (2)
- Migration and reconfiguration execution stage
The second stage mainly uses the service migration reconfiguration algorithm proposed to calculate the new migration location for the services to be migrated, and optimizes the migration path to meet the reconfiguration requirements with minimizing cost as the optimal objective.
The service migration strategy is decided by the migration and reconfiguration algorithm, which is running on the control nodes in the STIN, usually on a GMCC or GEO controller. Additionally, it determines whether the migration needs to be started in the current network state. If so, the optimal migration strategy is determined, including the target location of the migration node, the optimal migration path, and the resource reconfiguration scheme. Once the corresponding satellite nodes have received the determined migration strategy, it will execute the migrate action that is moving the VNF to the target location through the optimal migration path. Those migration processes may lead to extra delays, including the transmission delay of migrating the VNF and the propagation delay of the migration path. Furthermore, the extra delay would affect the end-to-end delay of the network users, for which it is important to design an effective service migration optimal algorithm that can minimize the negative impact of migration.
Additionally, in the process of migration, the data synchronization function of the GEO satellite is used to save data to ensure the continuity of service and data consistency.
3.3. Network Models
Assuming that the number of ground edge nodes and satellite edge nodes in the current STIN is known and fixed, network users and satellite nodes can move with time, and the connection states and resource states among each node and links can be obtained through the SDN/NFV global states collecting ability, that is, the network topology states and network resource states can be known at any time.
- (1)
- Substrate network model
The substrate network in the STIN is modeled as a time-varying weighted undirected graph , where is the substrate node set composed of ground edge nodes and satellite edge nodes in the STIN, is the substrate link between substrate nodes, represents the attributes of substrate nodes, while is the attributes of the substrate links. The substrate node attributes include the node type , physical location , and CPU capacity . The substrate link attributes include physical distance , and bandwidth capacity . The VNFs deployed on the same node share the resource capacity of the node, the bandwidth capacity of the link is also shared through multiple service paths of the same substrate link.
- (2)
- Service request
Suppose there is a given set of virtual network service requests , which is a time-varying weighted digraph . For each service request , is the th ordered VNF sequence of , is the th VNF in the current service request, and is the virtual link between these VNFs. refers to the node attributes corresponding to the VNFs, including the network function type of the current VNF. represents the required node resources, is a Boolean variable of a VNF deployed location, while indicates VNF is deployed on the substrate node , and means it is not deployed in that location. refers to the link attributes between the VNFs, including the bandwidth resources required by the link, and a Boolean variable of mapping relationship, while indicates the virtual link is a mapping on the substrate link otherwise it is not.
In particular, the deployment states of service requests and the usage of substrate network resources alter with time. The network states at current can be obtained by using the SDN/NFV centralized control function. The quantity of user service requests that each edge node can carry is relevant to the number of remaining resources and specific user requests. In order to describe the problem easily and clearly the main notation and its definition are as shown in Table 1.

Table 1.
Main notation and definition.
3.4. Optimal Objective
In order to obtain the optimal location and migration path of service migration, the selection of service target location and migration path optimization are modeled as an ILP model for network shortest path optimization. Considering that the user end-to-end delay in STINs is one of the most important performance indicators affecting the service experience, and the service migration will generate extra delay based on the original end-to-end delay, this needs to be considered as the migration cost.
Therefore, the optimization objective of service migration and reconfiguration in STINs is defined as minimizing end-to-end delay and migration cost while ensuring service continuity. The following gives the formal definition of end-to-end delay and migration cost, as well as the optimization objectives and constraints of service migration and reconfiguration.
- (1)
- End-to-end delay
The end-to-end delay is calculated as the delay generated when the user service request reaches the edge access point and the user data is transmitted through the network and successively through the node where the service function is located in the service path to complete all service functions. This mainly includes three parts of propagation delay , transmission delay , and processing delay , which can be expressed as Equation (1):
Among them, the propagation delay is mainly related to the physical distance of satellite–terrestrial and inter-satellite links, which can be expressed as Equation (2):
where and represent two adjacent VNF nodes in the service request, and c is the speed of light.
The transmission delay is mainly related to the amount of data transmitted and the bandwidth of satellite–terrestrial and inter-satellite links, which can be expressed as Equation (3):
Processing delay is mainly related to the amount of data transmitted and the computing ability provided by the edge node hosting the service. It can be expressed as Equation (4):
- (2)
- Migration Cost
The migration cost refers to extra operation cost and overhead caused by the migration in the course of the service migration of the STIN. Since our study concentrates on the service migration caused by the mobility of users and satellite nodes, only a single VNF is considered here. For each service migration, the migration cost mainly includes the cost of instantiating a new VNF at the migration node and the extra delay caused by migration path selection. The more routing nodes the service migration passes through and the more inadequate the available bandwidth of the path, the higher the migration cost and the longer the service interruption time caused by the migration, which is not conducive to the user service experience. At the same time, the nodes passing through the migration path can be replaced by the number of routing hops, and the migration cost can be measured by the extra propagation delay caused by the number of migration path hops and the extra transmission delay related to the bandwidth of the migration path. Since the cost of instantiating a new VNF is independent of the migration location, only the extra delay is considered, so the migration cost is dwindled. The migration cost can be expressed as Equation (5):
where represents the number of routing hops between VNF nodes and , and and represent the extra propagation delay and transmission delay generated by each hop. Since the forwarding node will not process packets during migration, it will not increase extra forwarding processing delay.
4. Algorithm Design and Description
Considering the dynamics and mobility of satellite nodes and users, the solution space of the service migration and reconfiguration optimization problem is large. Many traditional solutions, such as the classical exact solution, heuristic solution, and meta heuristic solution algorithms, have limitations to a certain extent, and are not suitable for large-scale discrete-state space problems [23]. The classical genetic algorithm is a random heuristic search algorithm. Compared with the accurate solution algorithm, the algorithm has higher efficiency and the crossover and mutation steps are random, which can avoid the algorithm falling into local optimization to a certain extent, but a randomness setting that is too high will increase the solution space and reduce the solution efficiency. Based on the classical genetic algorithm, the quantum genetic algorithm (QGA) applies the advantages of quantum superposition states in the quantum algorithm which can be calculated in parallel to accelerate the solution process to the population coding mode and the evolution strategy, and further improves the original solution efficiency and global optimization ability of the genetic algorithm. Moreover, it can make up for the defects of a solution space that is too large and difficult solutions caused by the randomness of chromosome combination crossover and mutation, and it has shown good performance. It can quickly obtain the global optimal solution in a small population size.
Therefore, we combine quantum machine learning with traditional algorithms, and propose a service migration optimization algorithm based on fuzzy logic (FL) and QGA. Firstly, the basic steps of the proposed algorithm are described in detail, and the pseudo code of the algorithm is given.
4.1. Problem Formulation
First, we formulate the service migration and reconfiguration problem in STINs based on the network models and optimal objectives in Section 3. Considering the service experience and operation cost of network users, we regard minimizing end-to-end delay and migration cost as our optimal objective, it can be expressed as:
Equation (6) is the objective function of the optimization problem, which aims to obtain the optimal migration location and migration path with the minimum end-to-end delay and migration cost, where and are the correction coefficients of end-to-end delay and migration costs , which are used to dynamically adjust the different requirements of different services for delay and migration costs. In this paper, the migration cost is modeled as extra delay generated by the migration process, for which we should assign the value of and as 0.5 and 0.5, respectively. Once the migration costs are modeled as other factors, for example, the joint consumptions of computing resource and bandwidth resource. The value of and should be assigned by the service request at present, for example, and for the resources-awareness service request. Equations (7)–(12) are constraints, which mainly consider the balance between the resource constraints of the substrate network and the demand for service migration; Equation (7), (8) ensures that a service migration node and link can only mapped to one substrate node and link at most; Equation (9) ensures that the computing resource demand of the service migration node does not exceed the computing resource capacity of the mapped substrate node; Equation (10) ensures that the bandwidth resource demand of the service migration link does not exceed the bandwidth resource capacity of the mapped substrate link; Equation (11) uses Boolean variables to indicate whether the substrate node is selected as the current service deployment node, 1 means deployed, 0 means its not; Equation (12) is the same as above, which represents whether the substrate link is selected as the service request virtual link. The value 1 means mapped, and 0 means its not.
4.2. Basic Steps of FQGA-SR
The basic steps of the service migration and reconfiguration algorithm based on fuzzy quantum genetic algorithm (FQGA-SR) are as follows:
- (1)
- Establish the shortest path matrix :
Firstly, the input matrix of FQGA-SR is established, which is used to represent the association relationship between any two substrate nodes in the substrate network Gsn, the th row and th column of the matrix represent the minimum delay between node and node of deployed SFCs. The matrix can be obtained by calculating the shortest path between two nodes using the k-Dijkstra algorithm.
- (2)
- FQGA-SR algorithm initialization:
The population and individuals are initialized, and the number of observation sequences is set as , the qubit probability space is , the coding length of the chromosome qubit is , and the population size is . The initial population and individuals are constructed by quantum bit coding, and the chromosomes are expressed in the form of quantum superposition state, which can greatly improve the diversity of population genotypes on the premise of maintaining the population size.
Let represent the th generation of the subpopulation, in which the individual is initialed by Equation (13), and each qubit may be in ,, with their entangled states between and , i.e., , where and are the complex coefficient representing the probability amplitude of qubits. In the above quantum bit coding model, the th qubits represent the substrate node states carrying VNF , i.e., represents that node does not carry VNF, and represents the node carried VNF . In the initialization phase, let all qubits have the same state, that is .
- (3)
- Subpopulation evolution:
The FL algorithm fuzzies the discrete data in the form of membership degree and can define the discrete probability function with a single fuzzy set, so as to obtain more accurate output results efficiently. Therefore, using the FL algorithm to describe the population and individuals of quantum bit coding with probability amplitude is helpful to obtain the evolution of optimized subpopulation. Let represent the ratio between the number of in the subpopulation and the qubits coding length , which can be expressed as Equation (14):
Fitness function can be expressed as: , where the refers to the optimal objective, that is, to minimize end-to-end delay and migration cost. The fitness function definition , which is used to measure the current closely related to fitness function, can be expressed as Equation (15):
where is the highest value of the fitness function. Taking and quantified as and , where the range is [0, 1]. By inputting and into the quantum rotation the gate phase is obtained along with mutation probability .
- (4)
- Adaptive adjustment strategy of quantum rotation gate and mutation:
The chromosome update is realized by quantum rotation gate phase transformation and mutation operation, which makes the algorithm possess the ability of expansion and exploration, so as to ensure the rapid convergence of the algorithm. By adjusting the phase of the quantum rotation gate and mutation probability , it can adjust the value of and . Assuming is a positive real number, if and , it represents that the fitness of the current individual is better than the highest fitness value . At this time, FL is used to increase and , in order to increase the value of , while if and , it represents that the fitness of the current individual, , is lower than the optimal fitness value . Then, the FL algorithm is used to adjust the and respectively, which means decreasing the while increasing , so as to reduce the value of .
- (5)
- Quantum mutation operation:
Applying quantum rotation gate to quantum mutation operation can effectively avoid converging into local optimum. Then, according to the mutation probability , the chromosome coding is selected, and some qubits are randomly selected. If , then the qubits of an individual are selected to transform the quantum gate and exchange the two quantum probability amplitudes of the qubits. Otherwise, is selected, and its quantum probability amplitude is exchanged.
4.3. Algorithm Description
According to the basic steps of the FQGA-SR algorithm, taking the substrate network , migration requirements , chromosome qubit coding length K, and population size M as the output, the FQGA algorithm can be used to obtain the optimal migration strategy , where represents the VNF state of the node after service migration and is where the VNF department is deployed on the substrate node .
For ease of understanding, the pseudo code of the main steps of FQGA-SR algorithm is shown in Table 2. The algorithm divides the service migration problem into two parts: the migration node selection stage and the shortest migration path selection stage. Among them, line 3 is used to obtain the shortest path matrix , line 4 is used to initialize the model parameters of FQGA, lines 5–9 are the population evolution process, and lines 10–13 are the mutation process of FQGA.

Table 2.
FQGA-SR Algorithm Description.
In addition, combined with the computing power of the cloud computing center and edge nodes of the ground management control center, the migration strategy optimization algorithm based on FQGA runs on the control plane of the STIN to collect the whole network state information in real time through the GEO satellite controller. It can quickly and effectively obtain the optimal migration decision, realize VNF migration, and reallocate network resources for the migrating nodes and related links, to complete the service migration and refactoring steps.
5. Simulation Experiment and Analysis
5.1. Parameter Setting
In order to evaluate the effectiveness and performance of the proposed algorithm in the service migration optimization problem of STINs, a simulation platform is established. The simulation experiment runs on the host of Intel Core i7-10710u CPU @ 3.3 GHz and 16GB Ram. The joint simulation experiment of MATLAB 2018b and STK 11 is used to simulate the satellite constellation networking and terrestrial network connection states information.
As shown in Table 3, the satellite network operation in the STIN is simulated through STK and MATLAB joint simulation, so as to obtain the visibility of satellite nodes at all times, the sustainable time of satellite–terrestrial and inter-satellite links, and the satellite connecting to ground nodes. Assuming the SFC reconfiguration scenario is under the STIN architecture. The service migration simulation parameter settings are shown in Table 3, which is adjusted on the basis of work [24]. We set 1 core cloud node, 15 ground edge nodes (MEC nodes), and 3 LEO satellite edge nodes (Leo nodes). The satellite–terrestrial, inter-satellite, and ground link connections change with the operation of the LEO satellite nodes.

Table 3.
Simulation parameters of service migration.
Assume the SFCs arriving per unit of time follows a Possion distribution, which has arriving rate in range of [0.05, 0.2], each SFC contains [2,6] VNFs, the live time is [30, 80] ms, and the processing delay generated by each VNF is [120, 200] ns. The above simulation parameters obey the random distribution of their respective value ranges. The experimental results are averaged by 10 repeated experiments.
5.2. Result Analysis
Considering the four performance indicators of algorithm convergence, end-to-end delay, service reconfiguration success rate, and algorithm running time, the proposed service migration reconfiguration method based on the fuzzy quantum genetic algorithm (FQGA-SR) is compared with the SEC-SM algorithm [14], TS-MAPSCH algorithm [16], and MGA algorithm [13] to prove the effectiveness and performance of the proposed algorithm.
From the comparison of algorithm convergence in Figure 3, it can be seen that the proposed FQGA-SR algorithm converges to a stable state at the fastest speed and tends to be stable when the number of iterations reaches about 58. The speed of the TS-MAPSCH and SEC-SM algorithms is second, both tend to be stable when the number of iterations is about 200. The convergence speed of the MGA algorithm is slow and converges at about 280. At the same time, the proposed FQGA-SR algorithm and TS-MAPSCH algorithm perform well in the optimization results of end-to-end total delay. The FQGA-SR algorithm introduces quantum chromosome coding and quantum crossover processes, which greatly improves the computational efficiency, so the solution effect is the best. The MGA algorithm adopts the traditional chromosome coding method, which is difficult to solve in the dynamic network demand and large-scale problem space. In order to avoid converging to the local optimum, it needs to sacrifice the solution speed to improve the solution accuracy, so the convergence speed is slow.
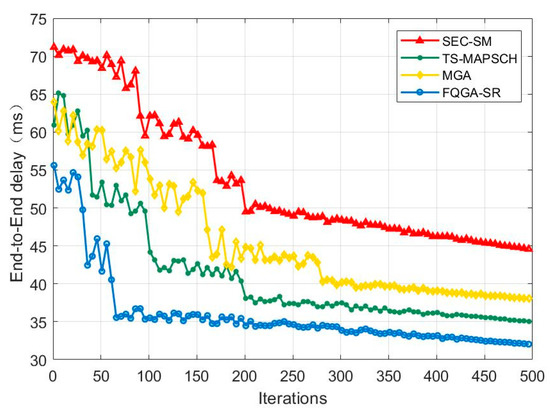
Figure 3.
Comparison of algorithm convergence.
Figure 4 shows the change of end-to-end delay with the number of service requests under different traffic load states, in which Figure 4a,b show the states of 60% and 90% traffic load, respectively. It can be seen that the optimization results obtained by the proposed FQGA-SR algorithm are superior to the MAG algorithm, TS-MAPSCH algorithm, and SEC-SM algorithm. Among them, the convergence speed of the MGA algorithm based on the genetic algorithm is slightly slower, so the fluctuation range is slightly larger than that of other algorithms. The node selection of the SEC-SM algorithm mainly depends on the shortest path algorithm and does not fully consider the resource state, so the end-to-end delay performance of deployment results is less efficient. Overall, with the increase in the number of service requests, the remaining resources in the network continue to decrease. The deployment and migration of subsequent service requests are affected to a certain extent, and the value of end-to-end delay increases slightly. Comparing with Figure 4a,b, when the traffic load reaches 90%, the remaining available resources in the network are less, and the choice of nodes and links that can be migrated and deployed is less, so the end-to-end delay increases relatively as a whole.
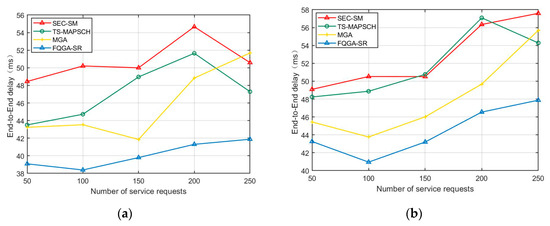
Figure 4.
Comparison of end-to-end delay: (a) traffic load of 60%; (b) traffic load of 90%.
Figure 5a,b shows the service reconfiguration request arrival rates, respectively and , and the service reconfiguration success rate changes with the number of reconfiguration requests. Taking Figure 5a as an example, it can be seen that the overall performance of the FQGA-SR algorithm is the best. When the reconfiguration request reaches 250 it can still maintain the service reconfiguration success rate of 0.847. The second is the MGA algorithm, the third is the TS-MAPSCH algorithm, and the last one is the SEC-SM algorithm, with a success rate of only 0.765. The reason is that the proposed FQGA-SR algorithm fully considers the node mobility and the current network topology state, so it can better make the migration and reconfiguration decision. The MGA algorithm and TS-MAPSCH algorithm belong to heuristic algorithms, while the SEC-SM algorithm mainly considers the traffic change and has no obvious perception of the change of network topology state, so the effect is poor.
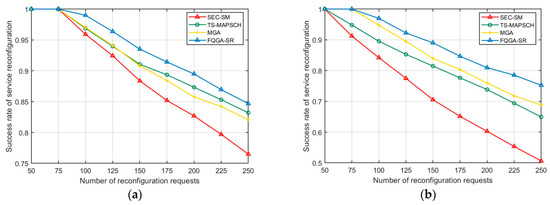
Figure 5.
Comparison of the success rate of service reconfiguration: (a) arrival rate of service reconfiguration requests ; (b) arrival rate of service reconfiguration requests .
Comparing (a) and (b) in Figure 5, the success rate of service reconfiguration of the four algorithms decreases, while the request arrival rate increases to , and the performance of the MGA algorithm is slightly better than that of the TS-MAPSCH algorithm. The reason for the decline in reconfiguration success rate is that the migration reconfiguration algorithm may face the condition that nodes and links are occupied and computing and bandwidth resources have not been released when tackling service requests with high arrival density, so its reconfiguration success rate is low. The performance of the MGA algorithm is slightly better because the global solution ability and efficiency of the MGA algorithm based on the genetic algorithm are slightly better than the TS-MAPSCH algorithm based on the Tabu algorithm.
Figure 6 shows the algorithm running time under different traffic loads. With the gradual increase in traffic load, the running time of each algorithm also increases. The simulation is set between 40–90% of the traffic load. Obviously, the average running time of the proposed FQGA-SR algorithm is much lower than the MGA algorithm, the TS-MAPSCH algorithm and the SEC-SM algorithm. Taking 90% load as an example, the average running time of the FQGA-SR algorithm is 2.27 s, the MGA algorithm is 4.38 s, the TS-MAPSCH algorithm is 5.15 s, and SEC-SM algorithm is 6.89s. Compared with the latter three algorithms, the running time of the former is increased by 48%, 55%, and 67%, respectively. As the FQGA-SR algorithm uses the quantum superposition principle to accelerate the calculation and can quickly decide the migration and reconfiguration scheme, the calculation efficiency is much higher than the other three algorithms. The calculation efficiency of the MGA algorithm is higher than the other two algorithms when the solution space is large, but the solution obtained at this time may not be the global optimal solution.
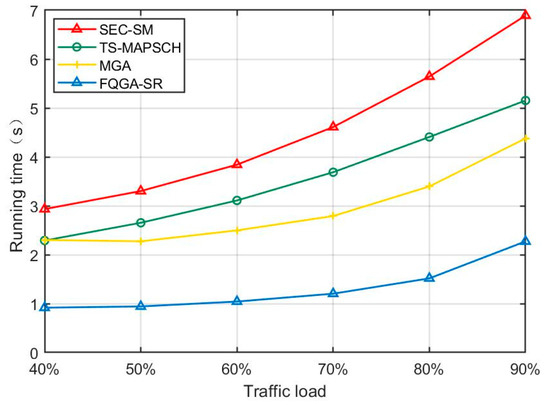
Figure 6.
Comparison of algorithm running time.
6. Conclusions
This paper provides a novel dynamic service migration and reconfiguration method to improve the service provisioning quality in STINs. Since the dynamics of user demand and the mobility of network topology in STINs, and the difficulty of solving this kind of large-scale formulated problem, we design a joint optimization model to minimize the end-to-end delay and migration cost in the service migration problem, and solve the problem using fuzzy logic combined with the quantum genetic algorithm, which can provide efficient and paralleled computing capability in solving the optimization problem. Simulation results reveal that the proposed algorithm has good performance in convergence, effectiveness, and network performances, and the impacts of different parameters also have been analyzed. The models provided in this paper could help researchers to improve their service provision schemes in STINs studies, and could also help the service providers of STINs to adjust their resource allocation scheme, in order to improve the resource utilization of STINs.
As future work, we will explore the lightweight framework of the deep reinforcement learning approach that is suitable for the communication scenario in the urban area of STINs, which could significantly enhance the performance of the service deployment scheme or resource allocation method in STINs.
Author Contributions
Conceptualization, W.Q. and Y.L. (Yu Lu); methodology, W.Q.; software, W.Q.; validation, H.L. and Y.L. (Yicen Liu); formal analysis, H.L.; investigation, W.Q. and H.L.; resources, Y.L. (Yu Lu); data curation, Y.L. (Yicen Liu) and L.M.; writing—original draft preparation, W.Q.; writing—review and editing, W.Q. and L.M.; funding acquisition, Y.L. (Yu Lu). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the “National Natural Science Foundation of China, grant number 62071483” and the “Military Science Research Project, grant number LJ20202C020344”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dogra, A.; Jha, R.K.; Jain, S. A Survey on Beyond 5G Network With the Advent of 6G: Architecture and Emerging Technologies. IEEE Access 2021, 9, 67512–67547. [Google Scholar] [CrossRef]
- Ferrús, R.; Koumaras, H.; Sallent, O.; Agapiou, G.; Rasheed, T.; Kourtis, M.A.; Boustie, C.; Gélard, P.; Ahmed, T. SDN/NFV-enabled satellite communications networks: Opportunities, scenarios and challenges. Phys. Commun. 2016, 18, 95–112. [Google Scholar] [CrossRef] [Green Version]
- Boero, L.; Bruschi, R.; Davoli, F.; Marchese, M.; Patrone, F. Satellite Networking Integration in the 5G Ecosystem: Research Trends and Open Challenges. IEEE Netw. 2018, 32, 9–15. [Google Scholar] [CrossRef]
- Mao, Y.; You, C.; Zhang, J.; Huang, K.; Letaief, K.B. A Survey on Mobile Edge Computing: The Communication Perspective. IEEE Commun. Surv. Tutor. 2017, 19, 2322–2358. [Google Scholar] [CrossRef] [Green Version]
- Araniti, G.; Genovese, G.; Iera, A.; Molinaro, A.; Pizzi, S. Virtualizing Nanosatellites in SDN/NFV Enabled Ground Segments to Enhance Service Orchestration. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Tang, Q.; Xie, R.; Yu, F.R.; Huang, T.; Liu, Y. Decentralized Computation Offloading in IoT Fog Computing System With Energy Harvesting: A Dec-POMDP Approach. IEEE Internet Things J. 2020, 7, 4898–4911. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, G.; Fu, X.; Yahyapour, R. A Survey on Virtual Machine Migration: Challenges, Techniques, and Open Issues. IEEE Commun. Surv. Tutor. 2018, 20, 1206–1243. [Google Scholar] [CrossRef]
- Sheng, M.; Zhou, D.; Liu, R.; Wang, Y.; Li, J. Resource Mobility in Space Information Networks: Opportunities, Challenges, and Approaches. IEEE Netw. 2019, 33, 128–135. [Google Scholar] [CrossRef]
- Wang, S.; Urgaonkar, R.; Zafer, M.; He, T.; Chan, K.; Leung, K.K. Dynamic Service Migration in Mobile Edge Computing Based on Markov Decision Process. IEEE/ACM Trans. Netw. 2019, 27, 1272–1288. [Google Scholar] [CrossRef] [Green Version]
- Shoura, F.; Gharaibeh, A.; Alouneh, S. Optimization of Migration Cost for Network Function Virtualization Replacement. In Proceedings of the 2020 21st International Arab Conference on Information Technology (ACIT), Giza, Egypt, 28–30 November 2020; pp. 1–7. [Google Scholar]
- Wang, H.; Li, Y.; Zhou, A.; Guo, Y.; Wang, S. Service migration in mobile edge computing: A deep reinforcement learning approach. Int. J. Commun. Syst. 2020. [Google Scholar] [CrossRef]
- Li, J.; Shen, X.; Chen, L.; Ou, J.; Wosinska, L.; Chen, J. Delay-aware bandwidth slicing for service migration in mobile backhaul networks. IEEE/OSA J. Opt. Commun. Netw. 2019, 11, B1–B9. [Google Scholar] [CrossRef]
- Gao, Z.; Jiao, Q.; Xiao, K.; Wang, Q.; Mo, Z.; Yang, Y. Deep Reinforcement Learning Based Service Migration Strategy for Edge Computing. In Proceedings of the 2019 IEEE International Conference on Service-Oriented System Engineering (SOSE), San Francisco, CA, USA, 4–9 April 2019; pp. 116–1165. [Google Scholar]
- Cheng, Y.; Li, X. A Compute-intensive Service Migration Strategy Based on Deep Reinforcement Learning Algorithm. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; pp. 1385–1388. [Google Scholar]
- Ge, S.; Wang, W.; Zhang, C.; Zhou, X.; Zhao, Q. Multi-user Service Migration for Mobile Edge Computing Empowered Connected and Autonomous Vehicles. In Algorithms and Architectures for Parallel Processing; Springer: Cham, Switzerland, 2020; pp. 306–320. [Google Scholar]
- Mouradian, C.; Kianpisheh, S.; Abu-Lebdeh, M.; Ebrahimnezhad, F.; Jahromi, N.T.; Glitho, R.H. Application Component Placement in NFV-Based Hybrid Cloud/Fog Systems With Mobile Fog Nodes. IEEE J. Sel. Areas Commun. 2019, 37, 1130–1143. [Google Scholar] [CrossRef] [Green Version]
- Liao, S.; Dong, M.; Ota, K.; Wu, J.; Li, J.; Ye, T. Vehicle Mobility-Based Geographical Migration of Fog Resource for Satellite-Enabled Smart Cities. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Han, H.; Wang, H.; Cao, S. Space Edge Cloud Enabling Service Migration for On-Orbit Service. In Proceedings of the 2020 12th International Conference on Communication Software and Networks (ICCSN), Chongqing, China, 12–15 June 2020; pp. 233–239. [Google Scholar]
- Varasteh, A.; Frutuoso, H.S.; He, M.; Kellerer, W.; Mas-Machuca, C. Figo: Mobility-Aware In-Flight Service Assignment and Reconfiguration with Deep Q-Learning. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–7. [Google Scholar]
- Li, J.; Shi, W.; Wu, H.; Zhang, S.; Shen, X. Cost-Aware Dynamic SFC Mapping and Scheduling in SDN/NFV-Enabled Space-Air-Ground Integrated Networks for Internet of Vehicles. IEEE Internet Things J. 2021. [Google Scholar] [CrossRef]
- Giannopoulos, A.; Spantideas, S.; Tsinos, C.; Trakadas, P. Power Control in 5G Heterogeneous Cells Considering User Demands Using Deep Reinforcement Learning. In Artificial Intelligence Applications and Innovations; Springer: Cham, Switzerland, 2021; pp. 95–105. [Google Scholar]
- Ahmed, K.I.; Tabassum, H.; Hossain, E. Deep Learning for Radio Resource Allocation in Multi-Cell Networks. IEEE Netw. 2019, 33, 188–195. [Google Scholar] [CrossRef] [Green Version]
- Qiao, W.; Liu, Y.; Lu, Y.; Li, X.; Yan, J.; Yao, Z. A Novel Approach for Service Function Chain Embedding in Cloud Datacenter Networks. IEEE Commun. Lett. 2021, 25, 1134–1138. [Google Scholar] [CrossRef]
- Wang, G.; Zhou, S.; Zhang, S.; Niu, Z.; Shen, X. SFC-Based Service Provisioning for Reconfigurable Space-Air-Ground Integrated Networks. IEEE J. Sel. Areas Commun. 2020, 38, 1478–1489. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).