Adaptive Allocation Algorithm for Multi-Radio Multi-Channel Wireless Mesh Networks
Abstract
1. Introduction
2. Related Work
3. Mathematical Formulation of Adaptive Channel Allocation Problem
3.1. Assumptions
3.2. Notations
3.3. Network Mathematical Model
- The total number of NICs over the network should not exceed .
- The output number of assigned NICs for should be at least one. Suppose it will be ; therefore, where .
- Each link should be assigned to a channel , where .
- The maximum number of assigned channels is k.
- The chosen channel for the link at both APs’ NIC must be the same .
- The number of channels assigned to the links adjacent to must be or less.
3.4. The Outputs
- The number of NICs assigned to , .
- The channel between the two APs and , .
3.5. The Problem Formalization
4. Adaptive Channel Allocation Algorithm
4.1. The Initial Channel Allocation
4.1.1. NIC Deploying Stage
- NIC Initialization
- (i)
- Compute the load per AP from link traffic :
- (ii)
- Allocate one NIC to every AP: as a default.
- (iii)
- Assign the traffic for each NIC by:
- (iv)
- Set the number the allocated NICs: AN = N.
- NIC Deployment
- (i)
- Add one NIC to an AP (suppose ) where reaches the maximum load while maintaining . After that, and .
- (ii)
- Stop the phase if or the physical constraint () is reached for every AP.
- (iii)
- Recalculate the traffic:
- (iv)
- Return to step (i).
4.1.2. The Fixed Channel Allocation
- Compute the collision for the traffic:
- Arrange the links according to the collision in a descending order.
- Allocate to the most crowded link, let be the first link, and assign to both ’s first NIC and ’s first NIC.
- Allocate the links’ channel according to the following filtration steps:
- (a)
- Mandatory channel allocation:
- (i)
- Allocate to link if both and have NICs allocated to . If there are two or more such for both and , select the channel that minimizes without consideration to un-allocated links.
- (ii)
- If has only one NIC allocated with , and has no channel, then the link is allocated and one ’s NIC allocates to the same channel.
- (b)
- Variety channel allocation:
- (i)
- For each link , and have both un-allocated NICs, then select that minimizes without consideration to un-allocated links.
- (ii)
- if and have two or more NICs in allocated channels , then the link is allocated to minimize without consideration to un-allocated links.
- (c)
- Priority channel allocation change: If and are allocated to and sequentially and and is not an allocated channel, then the channel allocation priority for that link is increased. Return to step 2 after multiplying by a constant number greater than one.
- (d)
- Manage un-utilized NICs: After the completion of channel allocation for every link in the network, if there are unused NICs, these NICs are switched to other APs with the maintenance of the constraints, and then return to step 2.
4.2. The Adaptive Channel Allocation
Decision Function
- Step (1)
- We begin by calculating the traffic of GW’s links, where these links are assigned the same channel p, :where is the group of links adjacent to the GW, and is the channel assigned to .
- Step (2)
- We compute the decision factor:
5. Simulation Module Implementation
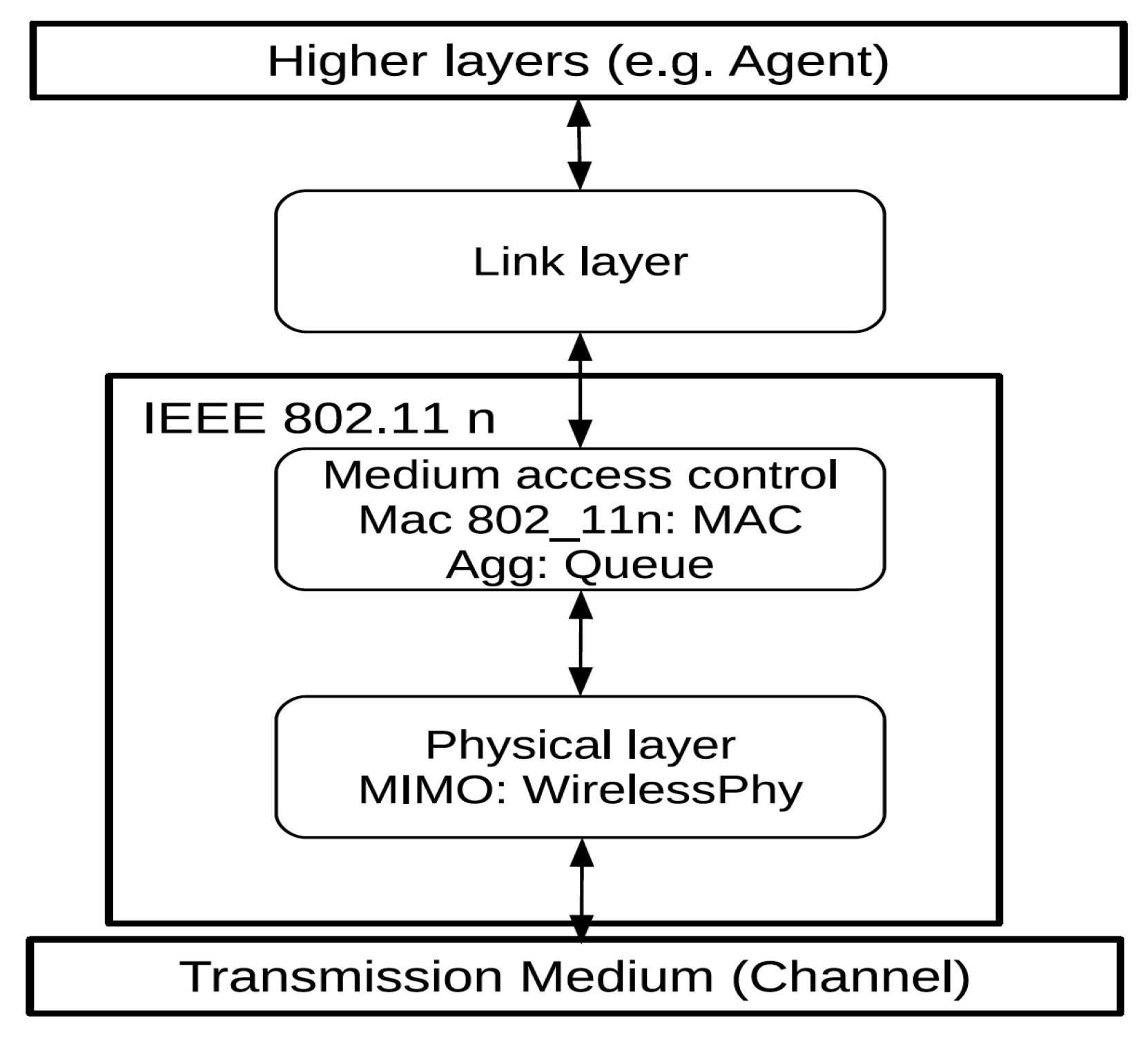
5.1. Modified NS-2 Simulator for IEEE802.11n
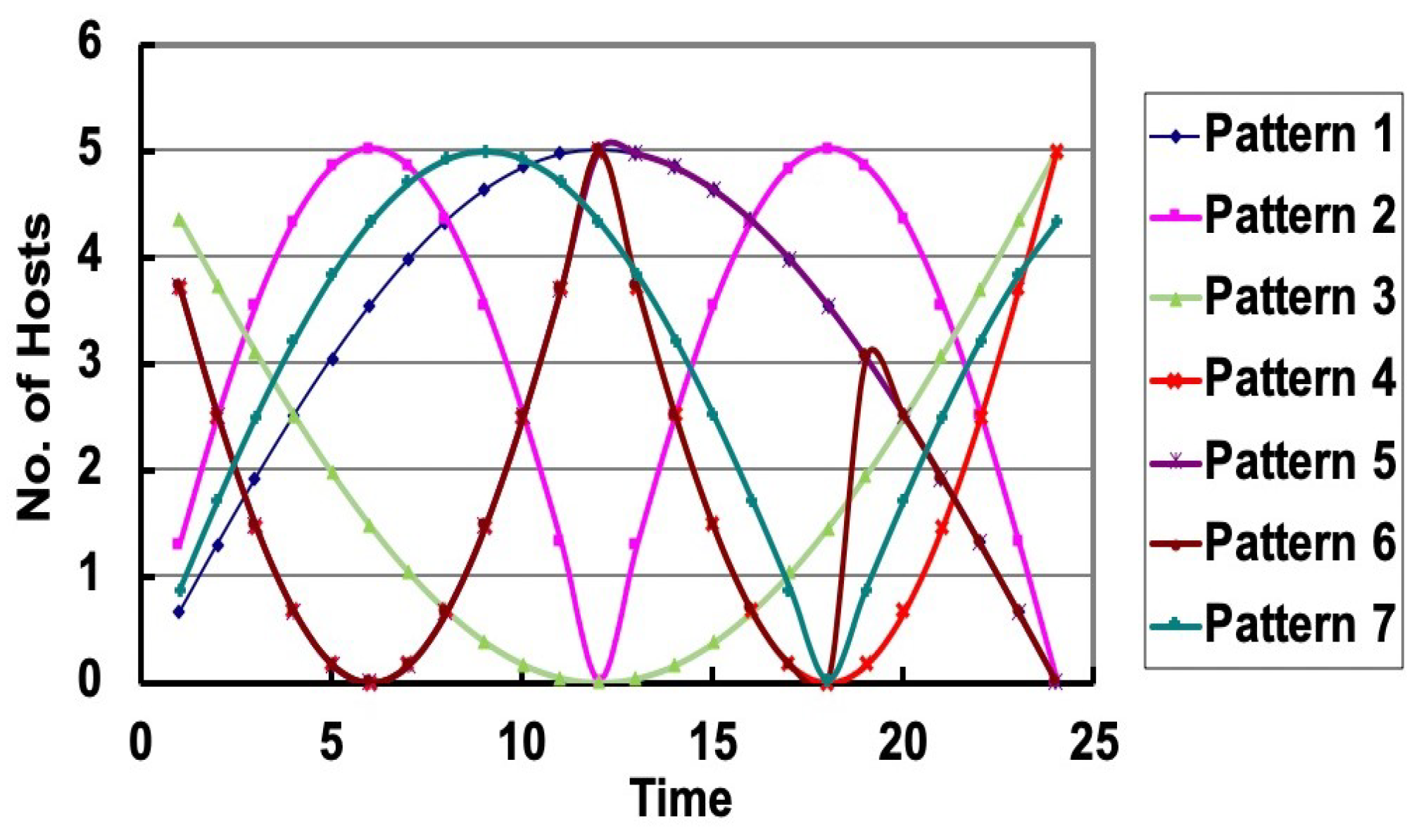
5.2. Simulation Instances
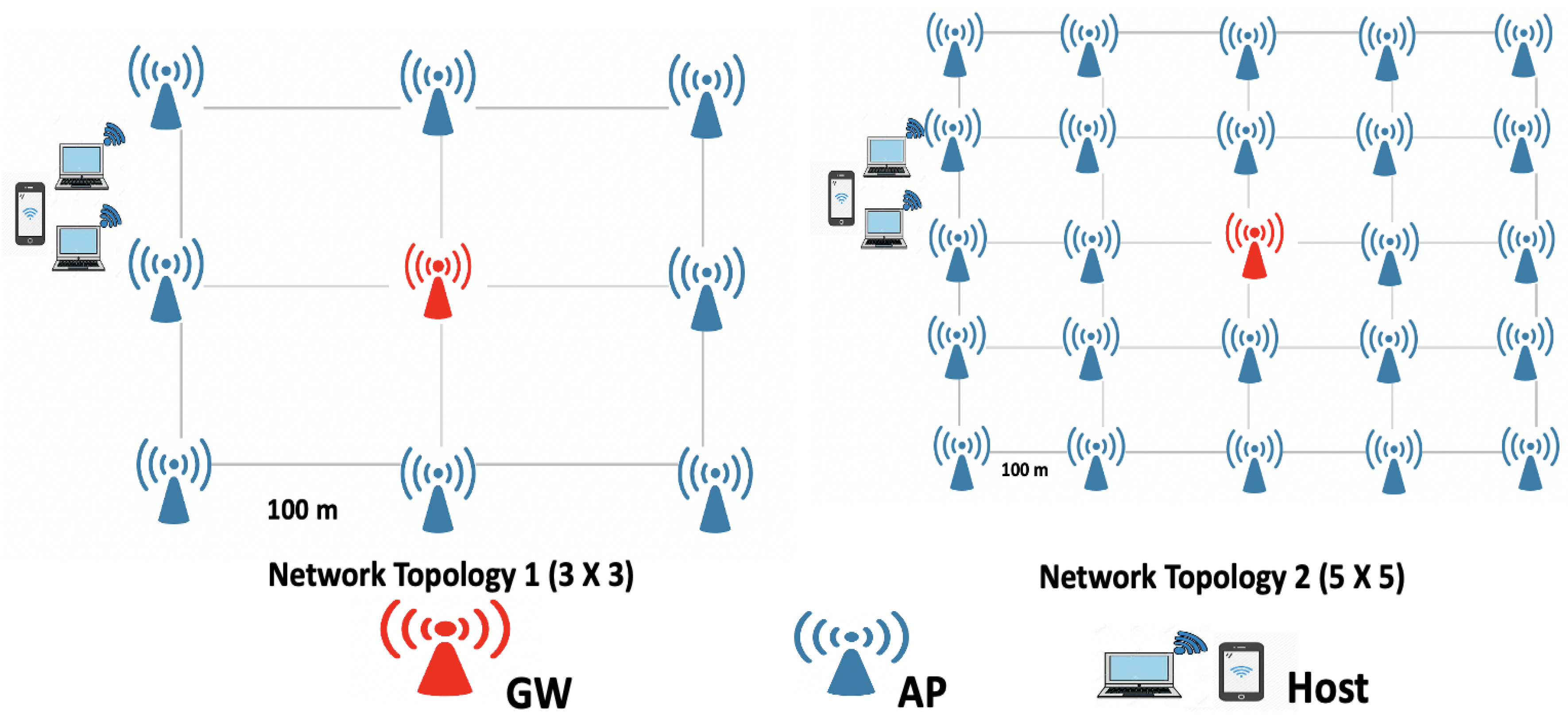
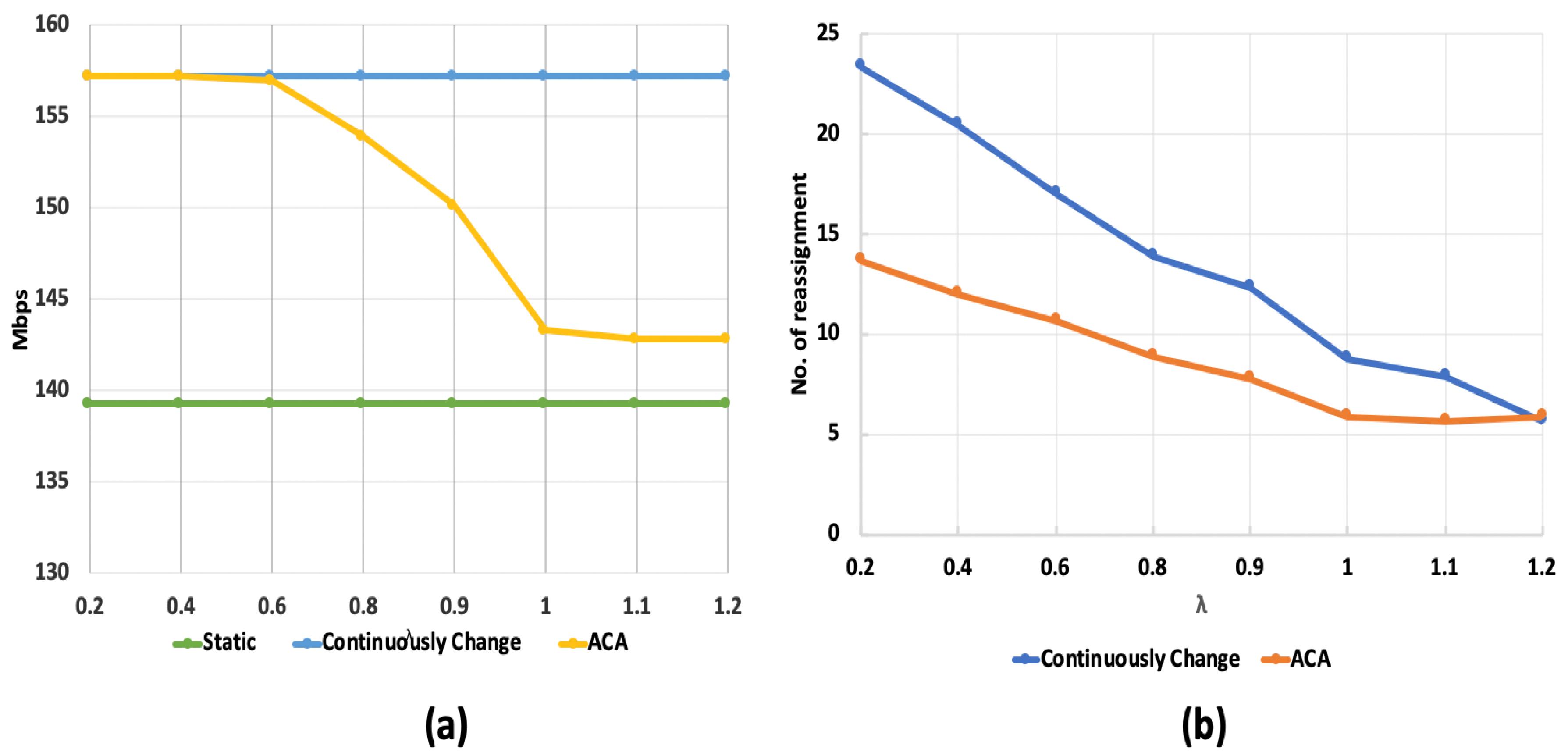
5.3. Network Topology 1 Simulation Results
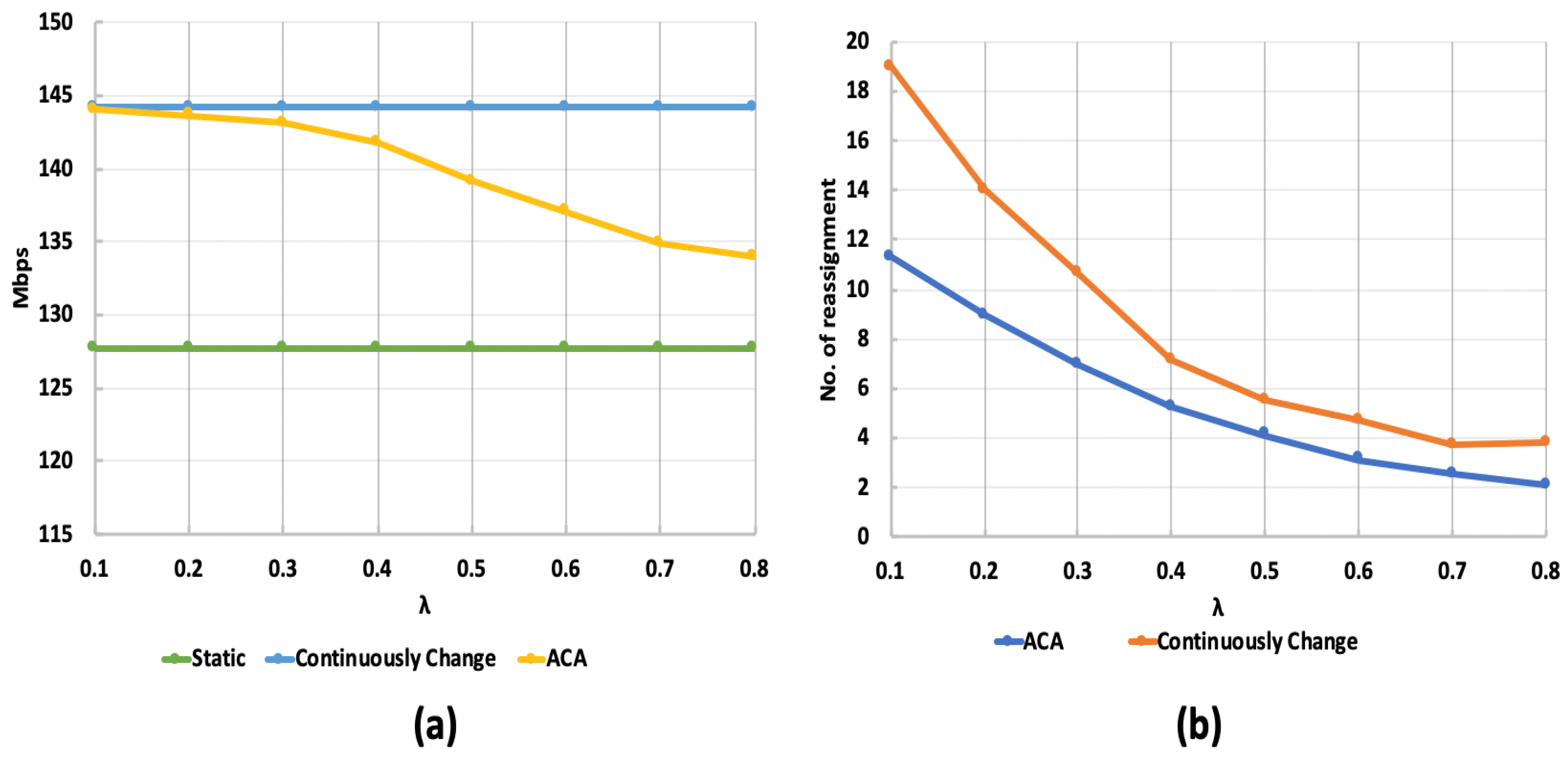
5.3.1. Case 1
5.3.2. Case 2
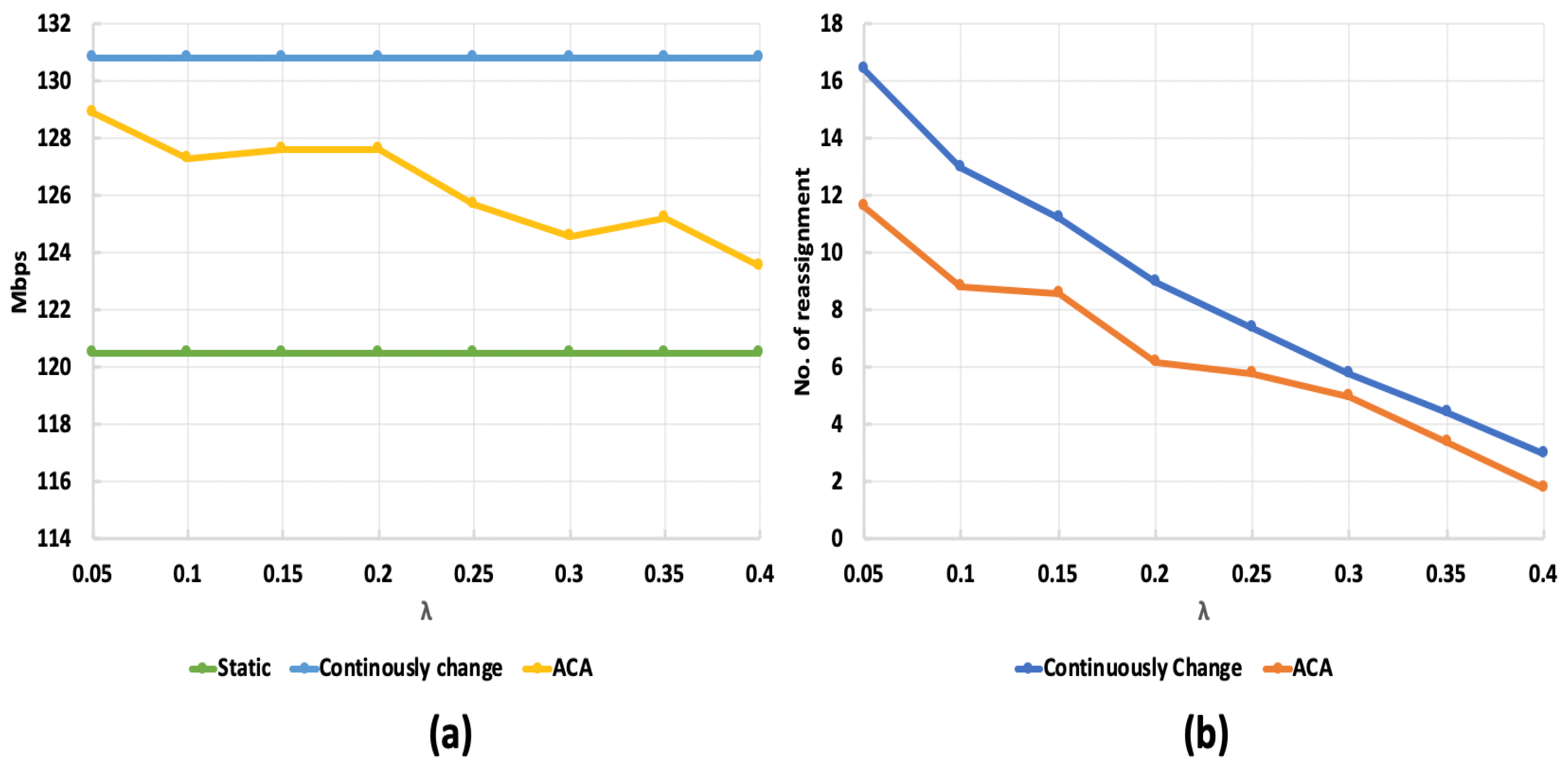
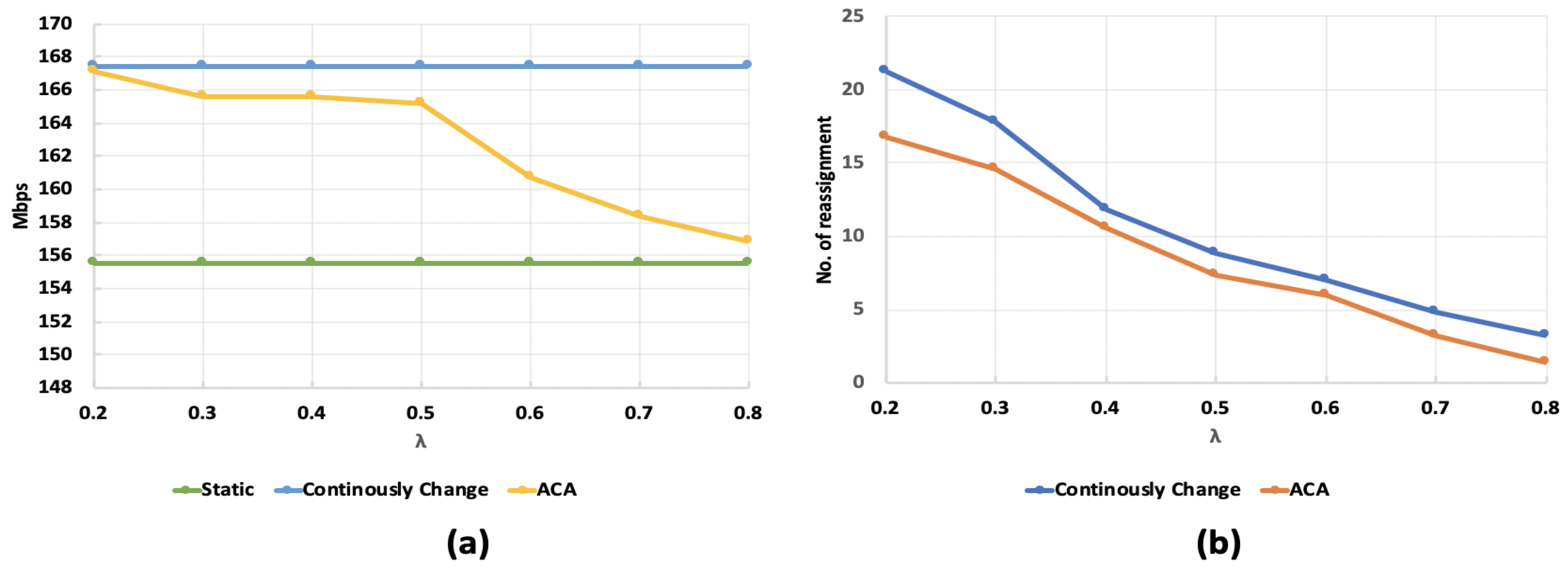
5.4. Network Topology 2 Simulation Results
5.4.1. Case 1
5.4.2. Case 2
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FCA | Fixed Channel Allocation |
| ACA | Adaptive Channel Allocation |
| GW | Gateway |
| NIC | Network Interface Card |
References
- Huo, Y.; Dong, X.; Xu, W.; Yuen, M. Enabling Multi-Functional 5G and Beyond User Equipment: A Survey and Tutorial. IEEE Access 2019, 7, 116975–117008. [Google Scholar] [CrossRef]
- Misra, S.; Misra, S.C.; Zhang, I. Guide to Wireless Mesh Networks; Springer: London, UK, 2010; pp. 119–147. [Google Scholar]
- Funabiki, N. Wireless Mesh Networks; InTech: Rijeka, Croatia, 2011. [Google Scholar]
- Al-rimy, B.A.S.; Kamat, M.; Ghaleb, F.A.; Rohani, M.F.; Razak, S.A.; Shah, M.A. A User Mobility-Aware Fair Channel Assignment Scheme for Wireless Mesh Network. Lect. Notes Electr. Eng. 2020, 603, 531–541. [Google Scholar]
- Santos, R.; Ogawa, H.; Tran, G.K.; Sakaguchi, K.; Kassler, A. Turning the Knobs on OpenFlow-Based Resiliency in mmWave Small Cell Meshed Networks. In Proceedings of the 2017 IEEE Globecom Workshops (GC Wkshps), Singapore, 4–8 December 2017; pp. 1–5. [Google Scholar]
- Burbank, J.L.; Andrusenko, J.; Everett, J.S.; Kasch, W.T.M. Wireless Networking Understanding Internetworking Challenges; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Chew, C.C.; Funabiki, N.; Fujita, S. Extensions of active access-point selection algorithm for wireless mesh networks using IEEE802.11ac protocol. In Proceedings of the 2014 2nd International Symposium on Computing and Networking, Shizuoka, Japan, 10–12 December 2014; pp. 310–314. [Google Scholar]
- Farag, T.; Funabiki, N.; Hassan, W. An Extension of Access-Point Allocation Algorithm for Adapting Link Speed Change in Wireless Mesh Network. IEICE Tech. Rep. 2013, 113, 137–142. [Google Scholar]
- Farag, T.; Funabiki, N.; Hassan, W. A Study of Access-Point Allocation Algorithm for Scalable Wireless Mesh Networks in Indoor Environments. IEICE Tech. Rep. 2014, 114, 1–6. [Google Scholar]
- Chew, C.C.; Funabiki, N.; Nakanishi, T. Throughput Measurements Using IEEE 802.11ac Devices for High-Speed Wireless Networks. IEICE Tech. Rep. Signal Process. 2014, 113, 23–28. [Google Scholar]
- Farag, T.; Funabiki, N.; Nakanishi, T. An access point allocation algorithm for indoor environments in wireless mesh networks. IEICE Trans. Commun. 2009, 92, 784–793. [Google Scholar] [CrossRef]
- Si, W.; Selvakennedy, S.; Zomaya, A.Y. An overview of Channel Assignment methods for multi-radio multi-channel wireless mesh networks. J. Parallel Distrib. Comput. 2010, 70, 505–524. [Google Scholar] [CrossRef]
- Hassan, W.; Funabiki, N.; Islam, M.E.; Farag, T. Throughput Evaluations Using NS-2 for Access-Point Aggregation Algorithm in IEEE802.11n Wireless LANs. IEICE Tech. Rep. Inf. Netw. 2014, 114, 25–30. [Google Scholar]
- Wang, J.; Shi, W.; Cui, K.; Jin, F.; Li, Y. Partially overlapped channel assignment for multi-channel multi-radio wireless mesh networks. EURASIP J. Wirel. Commun. Netw. 2015, 2015, 1–12. [Google Scholar] [CrossRef]
- Beheshtifard, Z.; Meybodi, M.R. An adaptive channel assignment in wireless mesh network: The learning automata approach. Comput. Electr. Eng. 2018, 72, 79–91. [Google Scholar] [CrossRef]
- Iqbal, S.; Abdullah, A.H.; Ahsan, F.; Qureshi, K.N. Critical link identification and prioritization using Bayesian theorem for dynamic channel assignment in wireless mesh networks. Wirel. Netw. 2018, 24, 2685–2697. [Google Scholar] [CrossRef]
- Bokhari, F.; Zrub, G. Partially Overlapping Channel Assignments in Wireless Mesh Networks. In Wireless Mesh Networks—Efficient Link Scheduling, Channel Assignment and Network Planning Strategies; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Tanigawa, Y.; Teramura, T.; Tode, H. Adaptive Channel Selection Control Equalizing Sojourn Time of Sending Uplink and Downlink Flows in Wireless Access Networks. In Proceedings of the 2019 IEEE International Conference on Consumer Electronics, Yilan, Taiwan, 20–22 May 2019. [Google Scholar]
- Huo, Y.; Dong, X.; Lu, T.; Xu, W.; Yuen, M. Distributed and Multilayer UAV Networks for Next-Generation Wireless Communication and Power Transfer: A Feasibility Study. IEEE Int. Things J. 2019, 6, 7103–7115. [Google Scholar] [CrossRef]
- Subramanian, A.P.; Gupta, H.; Das, S.R.; Cao, J. Minimum Interference Channel Assignment in Multiradio Wireless Mesh Networks. IEEE Trans. Mob. Comput. 2008, 7, 1459–1473. [Google Scholar] [CrossRef]
- Yoshihiro, T.; Noi, T. Collision-Free Channel Assignment Is Possible in EEE802.11-Based Wireless Mesh Networks. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Tian, Y.; Yoshihiro, T. Traffic-Demand-Aware Collision-Free Channel Assignment for Multi-Channel Multi-Radio Wireless Mesh Networks. IEEE Access 2020, 8, 120712–120723. [Google Scholar] [CrossRef]
- Yin, H.; Alamouti, S. OFDMA: A broadband wireless access technology. In Proceedings of the 2006 IEEE Sarnoff Symp, Princeton, NJ, USA, 27–28 March 2006. [Google Scholar]
- Meyers, M. CompTIA Network+ All-In-One Exam Guide; Exam N10-006; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Lammle, T. CCNA Routing and Switching Complete Study Guide; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Hamida, E.B.; Chelius, G.; Fleury, E. Revisiting neighbor discovery with interferences consideration. In Proceedings of the 3rd ACM International Workshop on Performance Evaluation of Wireless Ad Hoc, Sensor and Ubiquitous Networks, Torremolinos, Spain, 6 October 2006; pp. 74–81. [Google Scholar]
- The Network Simulator, NS–2. 1982. Available online: www.isi.edu/nsnam/ns/ (accessed on 2 July 2020).
- Wang, C.Y.; Wei, H.Y. IEEE 802.11n MAC enhancement and performance evaluation. Mob. Netw. Appl. 2009, 14, 760–771. [Google Scholar] [CrossRef]
| Symbol | Definition |
|---|---|
| link between the access point (AP) and | |
| NOC | non-overlapped channels |
| F | interference matrix between links |
| expected throughput between and | |
| C | the matrix of interfered channels |
| the maximum number of network interface cards (NICs) that can be allowed to | |
| the output assigned number of NICs to | |
| the assigned channel to | |
| maximum number of hosts per one NIC | |
| total interference of gateway (GW) adjacent links | |
| number of channel re-allocations |
| Contention window_Min | 15 |
| Contention window_Max | 1023 |
| Time Slot | 9 s |
| Short Interframe Space | 16 s |
| DCF Interframe Space | 34 s |
| Preamble Length | 16 s |
| Physical Layer Convergence Protocol Header | 48 bits |
| Physical Layer Convergence Protocol Rate | 6 Mbps |
| Basic Data Rate | 54 Mbps |
| Data Rate | 300 Mbps |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, W.; Farag, T. Adaptive Allocation Algorithm for Multi-Radio Multi-Channel Wireless Mesh Networks. Future Internet 2020, 12, 127. https://doi.org/10.3390/fi12080127
Hassan W, Farag T. Adaptive Allocation Algorithm for Multi-Radio Multi-Channel Wireless Mesh Networks. Future Internet. 2020; 12(8):127. https://doi.org/10.3390/fi12080127
Chicago/Turabian StyleHassan, Walaa, and Tamer Farag. 2020. "Adaptive Allocation Algorithm for Multi-Radio Multi-Channel Wireless Mesh Networks" Future Internet 12, no. 8: 127. https://doi.org/10.3390/fi12080127
APA StyleHassan, W., & Farag, T. (2020). Adaptive Allocation Algorithm for Multi-Radio Multi-Channel Wireless Mesh Networks. Future Internet, 12(8), 127. https://doi.org/10.3390/fi12080127






