Dynamic Group Recommendation Based on the Attention Mechanism
Abstract
1. Introduction
- This paper proposes a method for constructing potential groups based on the density peak clustering algorithm. The original density peak clustering algorithm is improved to construct highly similar user sets and realize group division. Improve group recommendation performance.
- Construct the AMGR (attention mechanism group recommended) model and use the neural attention network to dynamically fuse the weight of user preferences within the group to implement group recommendation.
- We have conducted experiments on a public data set. The experimental results show that the attention network can dynamically capture the overall decision-making process of the group, and the more alike the users in the group are, the better the group recommendation effect will be.
2. Related Work
2.1. Group Division
2.2. Group Recommended
3. Methods
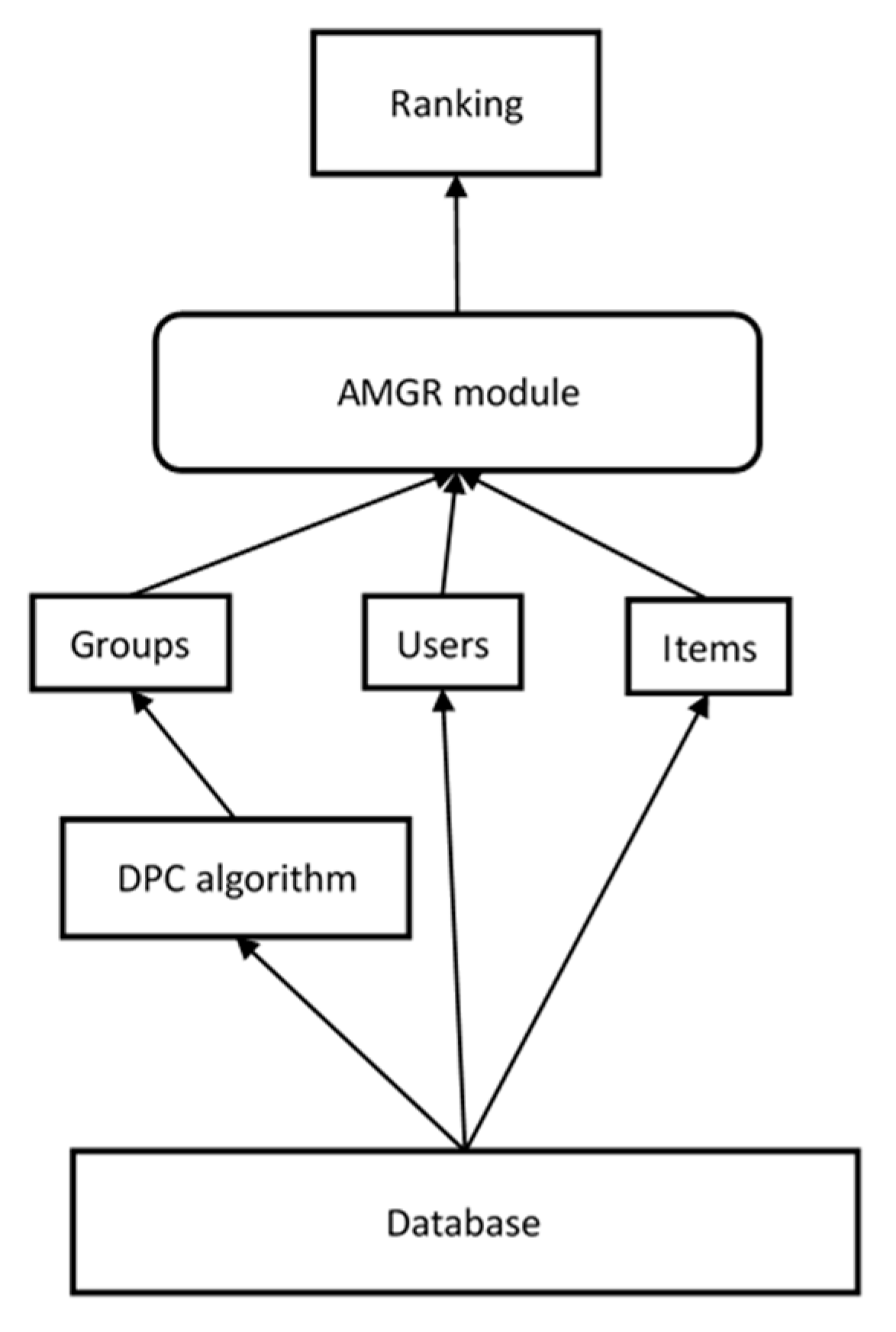
3.1. Overview of the Group Recommended
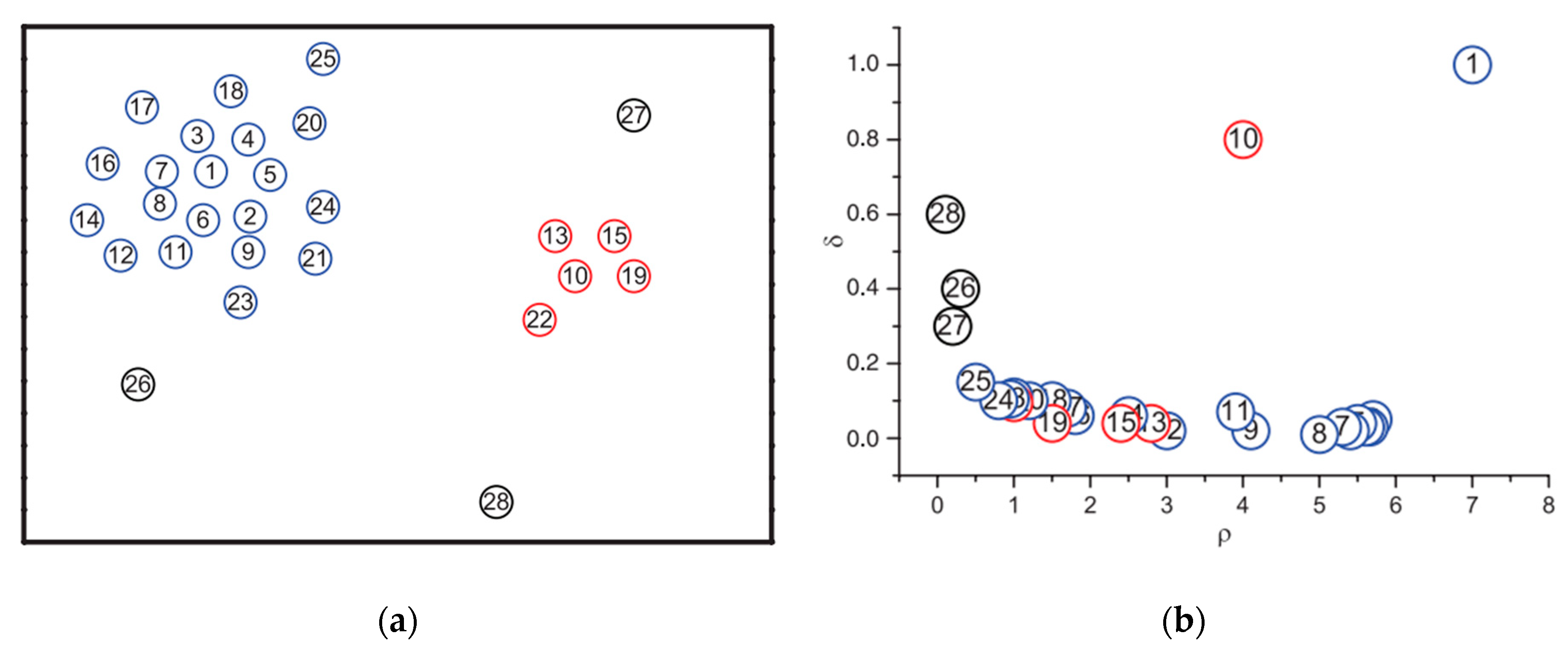
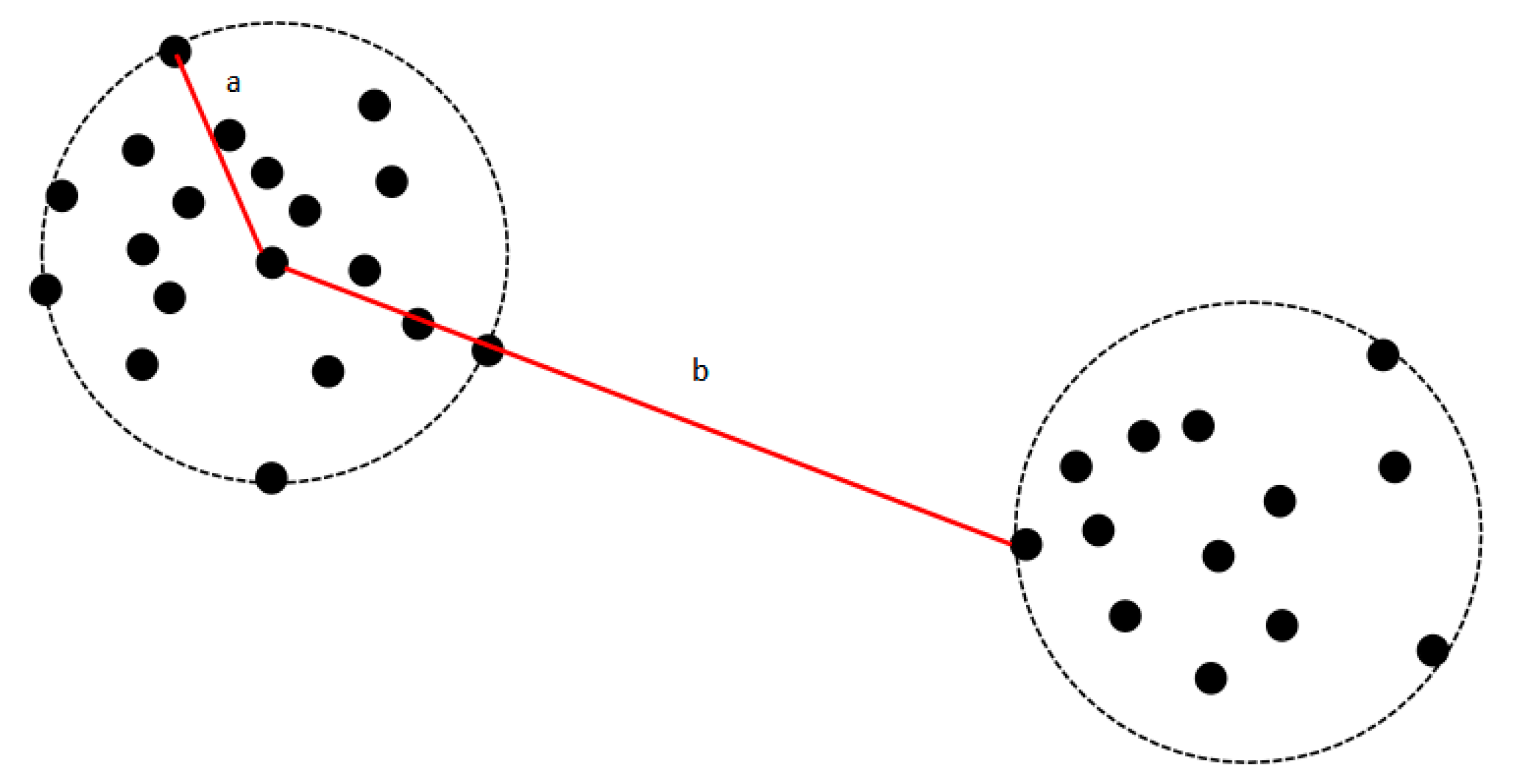
3.2. Density Peak Clustering Algorithm
3.3. Improvement
3.4. Group Recommendation Method
3.4.1. Problem Formulation
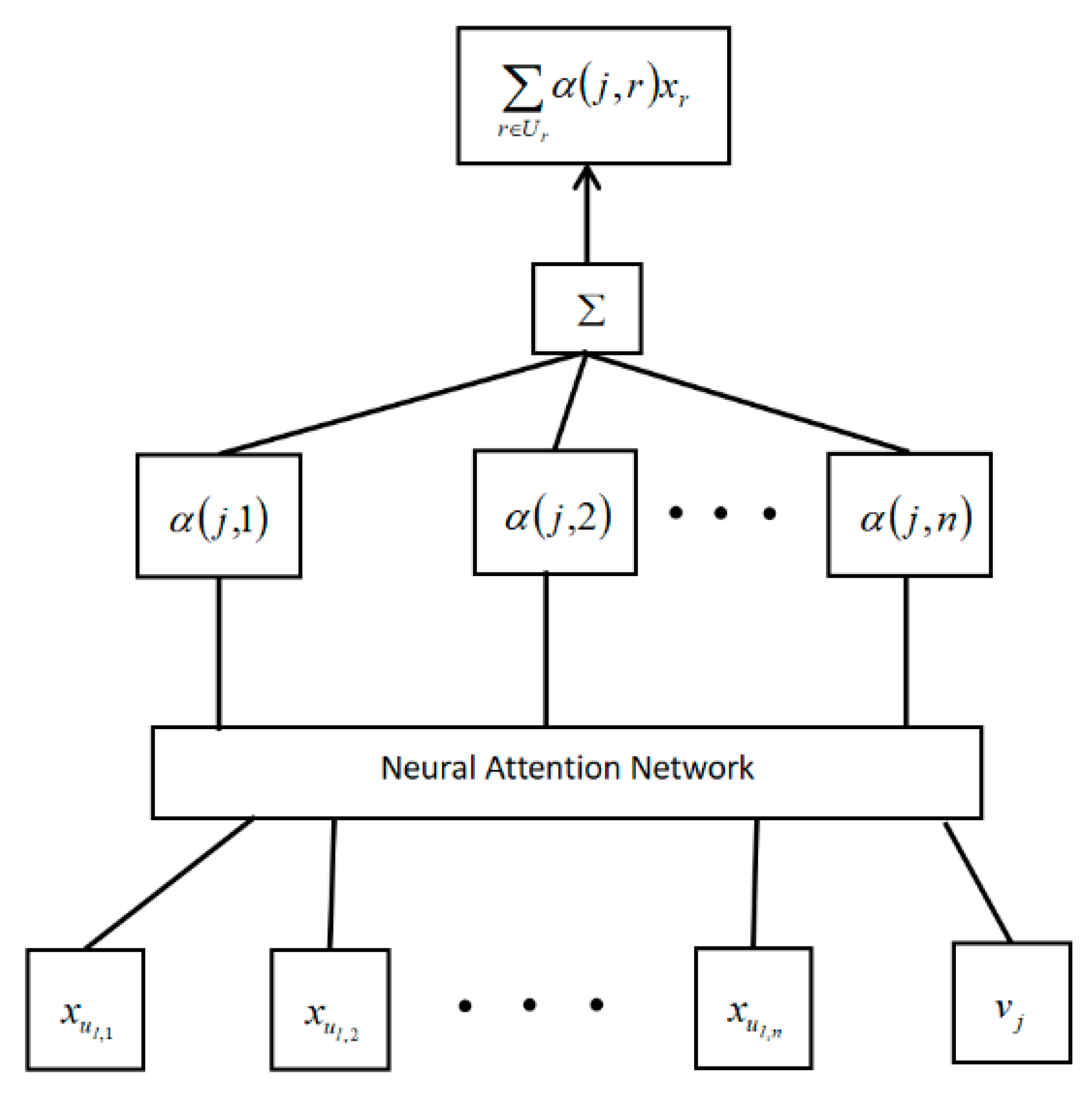
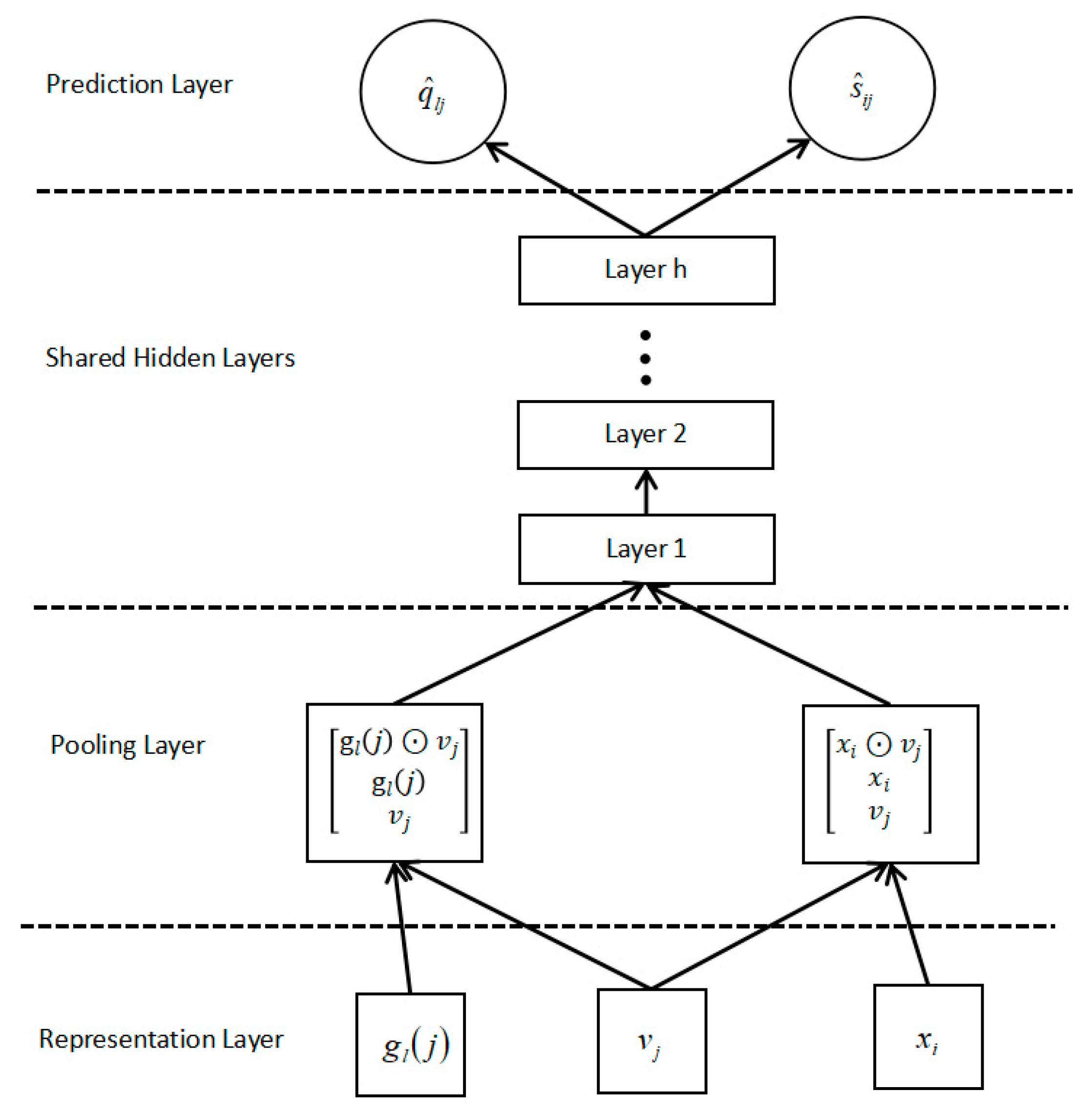
3.4.2. Attention Mechanism Model
3.4.3. Predicted Score
3.4.4. Objective Function
4. Experiments and Analysis
4.1. Experimental Settings
4.1.1. Dataset
4.1.2. Evaluation
4.1.3. Baselines
4.1.4. Parameter Setting
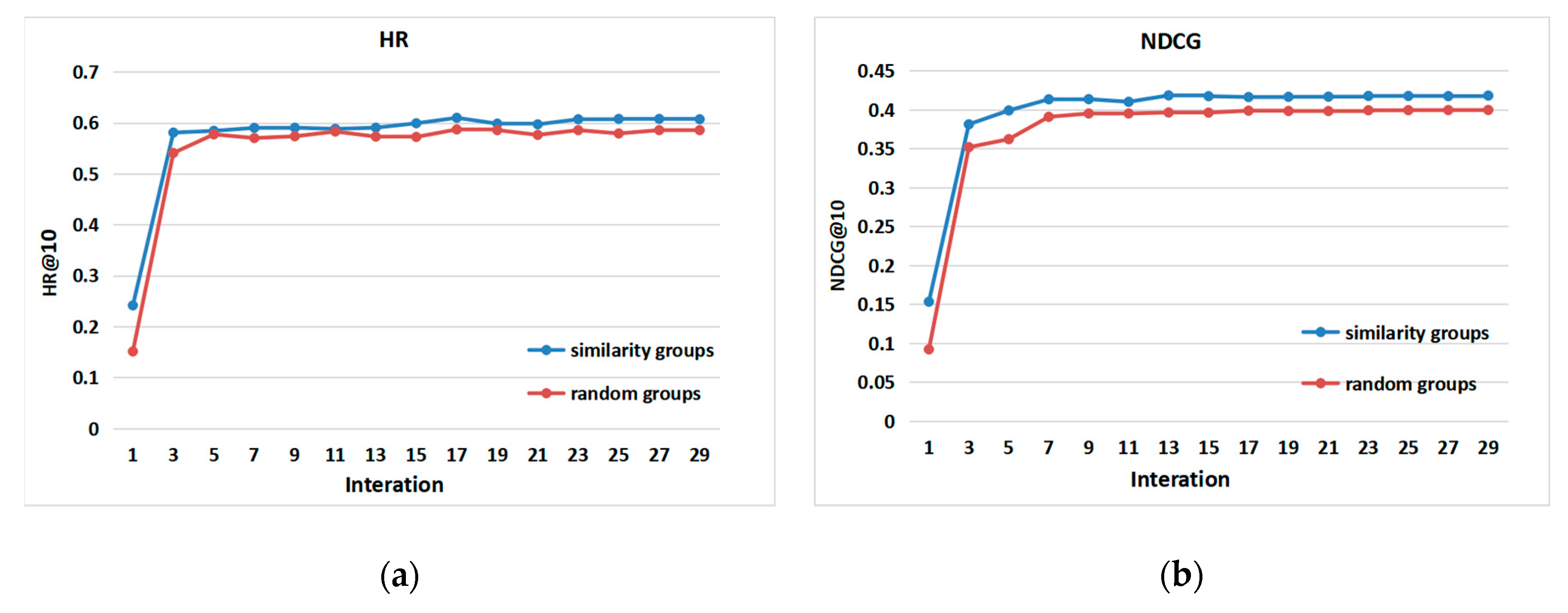
4.2. Effect of Group Recommendations (RQ1)
4.3. Overall Performance Comparison (RQ2)
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, Z.; Wu, B.; Zheng, K.; Wang, X.; Lei, L. A survey of collaborative filtering-based recommender systems for mobile Internet applications. IEEE Access 2016, 4, 3273–3287. [Google Scholar] [CrossRef]
- Wei, J.; He, J.; Chen, K.; Zhou, Y.; Tang, Z. Collaborative filtering and deep learning based recommendation system for cold start items. Expert Syst. Appl. 2017, 69, 29–39. [Google Scholar] [CrossRef]
- Balakrishnan, J.; Cheng, C.H.; Wong, K.F.; Woo, K.H. Product recommendation algorithms in the age of omnichannel retailing—An intuitive clustering approach. Comput. Ind. Eng. 2018, 115, 459–470. [Google Scholar] [CrossRef]
- Thanh, N.D.; Ali, M. A novel clustering algorithm in a neutrosophic recommender system for medical diagnosis. Cogn. Comput. 2017, 9, 526–544. [Google Scholar] [CrossRef]
- Kim, J.K.; Kim, H.K.; Oh, H.Y.; Ryu, Y.U. A group recommendation system for online communities. Int. J. Inf. Manag. 2010, 30, 212–219. [Google Scholar] [CrossRef]
- Cao, D.; He, X.; Miao, L.; An, Y.; Yang, C.; Hong, R. Attentive group recommendation. In Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 645–654. [Google Scholar]
- Xia, B.; Li, Y.; Li, Q.; Li, T. Attention-based recurrent neural network for location recommendation. In Proceedings of the 12th International Conference on Intelligent Systems and Knowledge Engineering (ISKE), Nanjing, China, 24–26 November 2017; pp. 1–6. [Google Scholar]
- Boley, D.; Gini, M.; Gross, R.; Han, E.-H.S.; Hastings, K.; Karypis, G.; Kumar, V.; Mobasher, B.; Moore, J. Partitioning-based clustering for web document categorization. Decis. Support Syst. 1999, 27, 329–341. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, Z.; Mao, J.; Ou, L. The study of parallel k-means algorithm. In Proceedings of the 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 5868–5871. [Google Scholar]
- Mirzaei, A.; Rahmati, M. A novel hierarchical-clustering-combination scheme based on fuzzy-similarity relations. IEEE Trans. Fuzzy Syst. 2009, 18, 27–39. [Google Scholar] [CrossRef]
- Handy, M.; Haase, M.; Timmermann, D. Low energy adaptive clustering hierarchy with deterministic cluster-head selection. In Proceedings of the 4th International Workshop on Mobile and Wireless Communications Network, Stockholm, Sweden, 9–11 September 2002; pp. 368–372. [Google Scholar]
- Wang, X.F.; Huang, D.S. A novel density-based clustering framework by using level set method. IEEE Trans. Knowl. Data Eng. 2009, 21, 1515–1531. [Google Scholar] [CrossRef]
- Kriegel, H.P.; Kröger, P.; Sander, J.; Zimek, A. Density-based clustering. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 231–240. [Google Scholar] [CrossRef]
- Grabusts, P.; Borisov, A. Using grid-clustering methods in data classification. In Proceedings of the International Conference on Parallel Computing in Electrical Engineering, Warsaw, Poland, 22–25 September 2002; pp. 425–426. [Google Scholar]
- Mann, A.K.; Kaur, N. Survey paper on clustering techniques. Int. J. Sci. Eng. Technol. Res. 2013, 2, 803–806. [Google Scholar]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 7, 881–892. [Google Scholar] [CrossRef]
- Le, T.; Le Son, H.; Vo, M.; Lee, M.; Baik, S. A cluster-based boosting algorithm for bankruptcy prediction in a highly imbalanced dataset. Symmetry 2018, 10, 250. [Google Scholar] [CrossRef]
- Naresh, V.R.K.; Gope, D.; Lipasti, M.H. The CURE: Cluster Communication Using Registers. ACM Trans. Embed. Comput. Syst. 2017, 16, 124. [Google Scholar] [CrossRef]
- Müllner, D. Fastcluster: Fast hierarchical, agglomerative clustering routines for R and Python. J. Stat. Softw. 2013, 53, 1–18. [Google Scholar] [CrossRef]
- Bryant, A.; Cios, K. RNN-DBSCAN: A density-based clustering algorithm using reverse nearest neighbor density estimates. IEEE Trans. Knowl. Data Eng. 2018, 30, 1109–1121. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [PubMed]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 8, 30–37. [Google Scholar] [CrossRef]
- Su, X.; Khoshgoftaar, T.M. A survey of collaborative filtering techniques. Adv. Artif. Intell. 2009, 2009, 421425. [Google Scholar] [CrossRef]
- Baskin, J.P.; Krishnamurthi, S. Preference aggregation in group recommender systems for committee decision-making. In Proceedings of the Third ACM Conference on Recommender Systems, New York, NY, USA, 22–25 October 2009; pp. 337–340. [Google Scholar]
- Baltrunas, L.; Makcinskas, T.; Ricci, F. Group recommendations with rank aggregation and collaborative filtering. In Proceedings of the Fourth ACM Conference on Recommender Systems, Barcelona, Spain, 26–30 September 2010. [Google Scholar]
- Berkovsky, S.; Freyne, J. Group-based recipe recommendations: Analysis of data aggregation strategies. In Proceedings of the Fourth ACM Conference on Recommender Systems, Barcelona, Spain, 26–30 September 2010; pp. 111–118. [Google Scholar]
- Amer-Yahia, S.; Roy, S.B.; Chawlat, A.; Das, G.; Yu, C. Group recommendation: Semantics and efficiency. Proc. VLDB Endow. 2009, 2, 754–765. [Google Scholar] [CrossRef]
- Boratto, L.; Carta, S. State-of-the-art in group recommendation and new approaches for automatic identification of groups. In Information Retrieval and Mining in Distributed Environments; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–20. [Google Scholar]
- Liu, X.; Tian, Y.; Ye, M.; Lee, W.C. Exploring personal impact for group recommendation. In Proceedings of the 21st ACM International Conference on Information and Knowledge Management, Maui, HI, USA, 29 October–2 November 2012; pp. 674–683. [Google Scholar]
- Yuan, Q.; Cong, G.; Lin, C.Y. COM: A generative model for group recommendation. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–28 August 2014; pp. 163–172. [Google Scholar]
- Ma, H.; Yang, H.; Lyu, M.R.; King, I. Sorec: Social recommendation using probabilistic matrix factorization. In Proceedings of the 17th ACM Conference on Information and Knowledge Management, Napa Valley, CA, USA, 26–30 October 2008; pp. 931–940. [Google Scholar]
- Karatzoglou, A.; Hidasi, B. Deep learning for recommender systems. In Proceedings of the Eleventh ACM Conference on Recommender Systems, Como, Italy, 23–31 August 2017; pp. 396–397. [Google Scholar]
- Zhang, S.; Yao, L.; Sun, A.; Tay, Y. Deep learning based recommender system: A survey and new perspectives. ACM Comput. Surv. 2019, 52, 5. [Google Scholar] [CrossRef]
- He, X.; Liao, L.; Zhang, H.; Nie, L.; Hu, X.; Chua, T.S. Neural collaborative filtering. In Proceedings of the 26th International Conference on World Wide Web, International World Wide Web, Perth, Australia, 3–7 April 2017; pp. 173–182. [Google Scholar]
- Chang, H.; Yeung, D.Y. Robust path-based spectral clustering. Pattern Recog. 2008, 4, 191–203. [Google Scholar] [CrossRef]
- Xiao, J.; Ye, H.; He, X.; Zhang, H.; Wu, F.; Chua, T.S. Attentional factorization machines: Learning the weight of feature interactions via attention networks. arXiv 2017, arXiv:1708.04617. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NE, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Chen, J.; Zhang, H.; He, X.; Nie, L.; Liu, W.; Chua, T.-S. Attentive collaborative filtering: Multimedia recommendation with item-and component-level attention. In Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval, Tokyo, Japan, 7–11 August 2017; pp. 335–344. [Google Scholar]
- Wang, X.; He, X.; Nie, L.; Chua, T.S. Item silk road: Recommending items from information domains to social users. In Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval, Tokyo, Japan, 7–11 August 2017; pp. 185–194. [Google Scholar]
| Methods | User | Group | ||
|---|---|---|---|---|
| HR@5 | NDCG@5 | HR@5 | NDCG@5 | |
| Popularity | 0.3725 | 0.2654 | 0.3494 | 0.2375 |
| COM | - | - | 0.4890 | 0.3310 |
| AVG (NCF) | - | - | 0.4793 | 0.3365 |
| LM (NCF) | - | - | 0.4703 | 0.3335 |
| MP (NCF) | - | - | 0.4564 | 0.3257 |
| MGR | 0.5047 | 0.3762 | 0.4981 | 0.3419 |
| AMGR | 0.5218 | 0.3803 | 0.4993 | 0.3502 |
| Methods | User | Group | ||
|---|---|---|---|---|
| HR@10 | NDCG@10 | HR@10 | NDCG@10 | |
| Popularity | 0.4246 | 0.2338 | 0.4013 | 0.2079 |
| COM | - | - | 0.5898 | 0.3957 |
| AVG (NCF) | - | - | 0.5896 | 0.3994 |
| LM (NCF) | - | - | 0.5907 | 0.4061 |
| MP (NCF) | - | - | 0.5896 | 0.3943 |
| MGR | 0.6103 | 0.4162 | 0.5908 | 0.4019 |
| AMGR | 0.6262 | 0.4243 | 0.6076 | 0.4180 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Ding, Y.; Sun, J.; Zhao, K.; Chen, Y. Dynamic Group Recommendation Based on the Attention Mechanism. Future Internet 2019, 11, 198. https://doi.org/10.3390/fi11090198
Xu H, Ding Y, Sun J, Zhao K, Chen Y. Dynamic Group Recommendation Based on the Attention Mechanism. Future Internet. 2019; 11(9):198. https://doi.org/10.3390/fi11090198
Chicago/Turabian StyleXu, Haiyan, Yanhui Ding, Jing Sun, Kun Zhao, and Yuanjian Chen. 2019. "Dynamic Group Recommendation Based on the Attention Mechanism" Future Internet 11, no. 9: 198. https://doi.org/10.3390/fi11090198
APA StyleXu, H., Ding, Y., Sun, J., Zhao, K., & Chen, Y. (2019). Dynamic Group Recommendation Based on the Attention Mechanism. Future Internet, 11(9), 198. https://doi.org/10.3390/fi11090198





