Scheduling for Multi-User Multi-Input Multi-Output Wireless Networks with Priorities and Deadlines
Abstract
1. Introduction
2. System Model
2.1. Queuing Model
- A refers to the inter-arrival time of the renewal process.
- B refers to the random process of service time required by the packets.
- C refers to the number of servers.
- D refers to the deadline random process.
- P refers to the priority or reward random process.
- A1
- The pair is a renewal reward process.
- A2
- Packets’ deadlines are measured with respect to the end of transmission.
- A3
- The reward is obtained only if packets arrived on time (hard real-time system requirements).
- A4
- , , and are known upon arrival of to the queue.
- A5
- The scheduling policy is non-preemptive, and forcing idle time is not allowed.
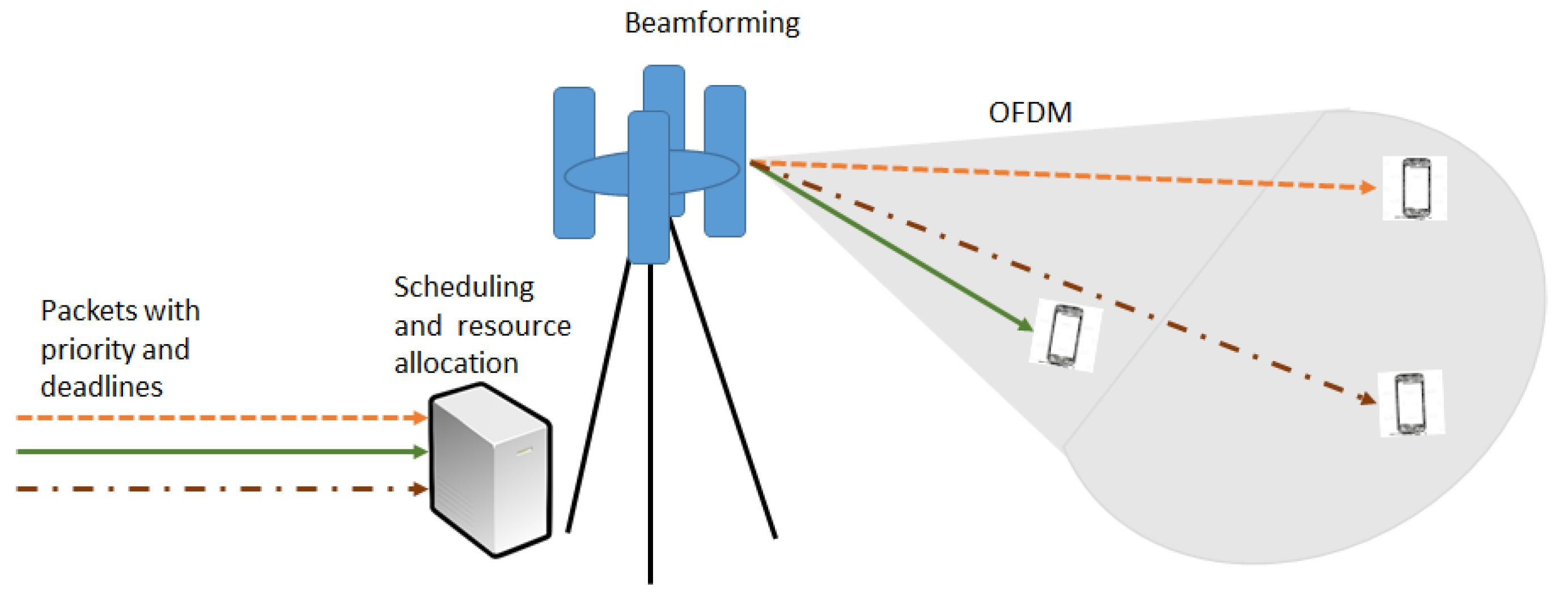
2.2. ZF Beamforming for MU-MIMO Wireless Networks
- A6
- The AP has perfect Channel State Information (CSI).
- A7
- Transmitted data symbols () are uncorrelated
- A8
- The power allocated to each user is constant. To simplify notation, we assume that the same power is allocated to all users, i.e., and .
2.3. Combining Scheduling and Beamforming
- A9
- Each packet is addressed to a specific MS (multicasting will be considered in an extension of this work).
- A10
- is known upon arrival of to the queue.
- A11
- Channel coherence time is longer than the packet service time.
- A12
- The queuing model is where .
- E1
- The packet arrives at the system.
- E2
- The beginning of packet transmission.
- E3
- The end of packet transmission.
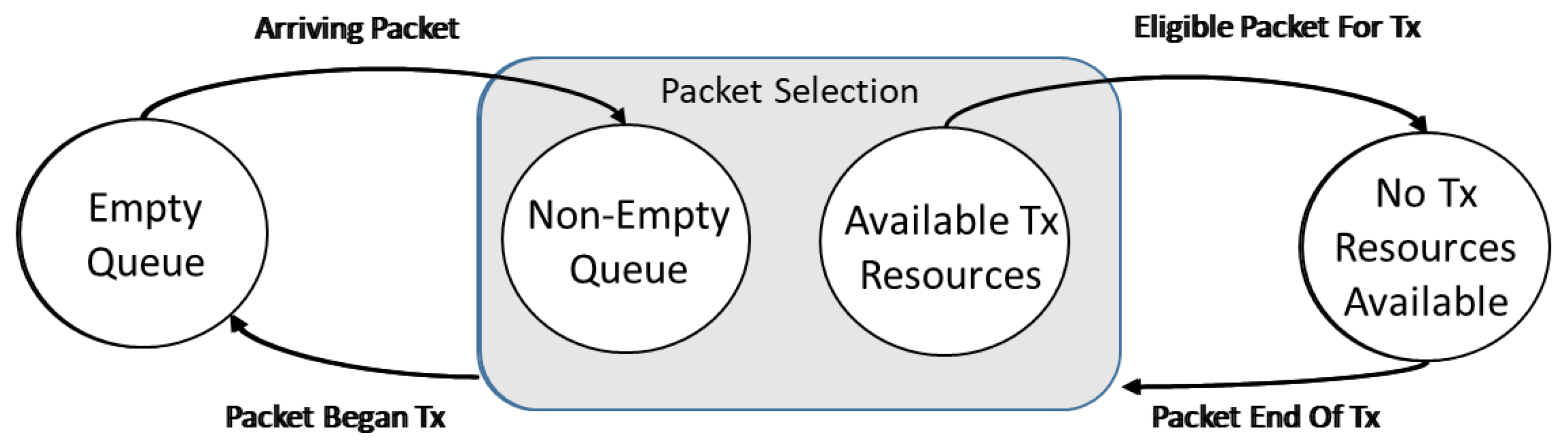
3. RPS Scheduling Policy
- M1
- New packet insertion into the arrival queue, Algorithm 1.
- M2
- Selection of the packet for transmission in case there is an eligible packet and there are available transmission resources, Algorithm 2.
- M3
- Precoder update for additional new packet transmission, Algorithm 3.
- M4
- Precoder downdate for a packet that ended its transmission, Algorithm 4.
| Algorithm 1 New packet queue insertion. |
Let be the packet that arrives at the system at time .
|
| Algorithm 2 Select new packet for transmission. |
Let be the channel matrix in the previous stage, and let be the arrival queue at the current time. Let , and be the channel vector, the length, and the deadline of the packet, which is in the position in queue . Let be the actual time as defined by the index time t. Let K be the packet selection window size.
|
| Algorithm 3 Precoder update. |
|
| Algorithm 4 Precoder downdate. |
|
Computational Complexity of RPS
- Complexity of processing a new packet.
- Selection of a transmitted packet.
- Transmission complexity.
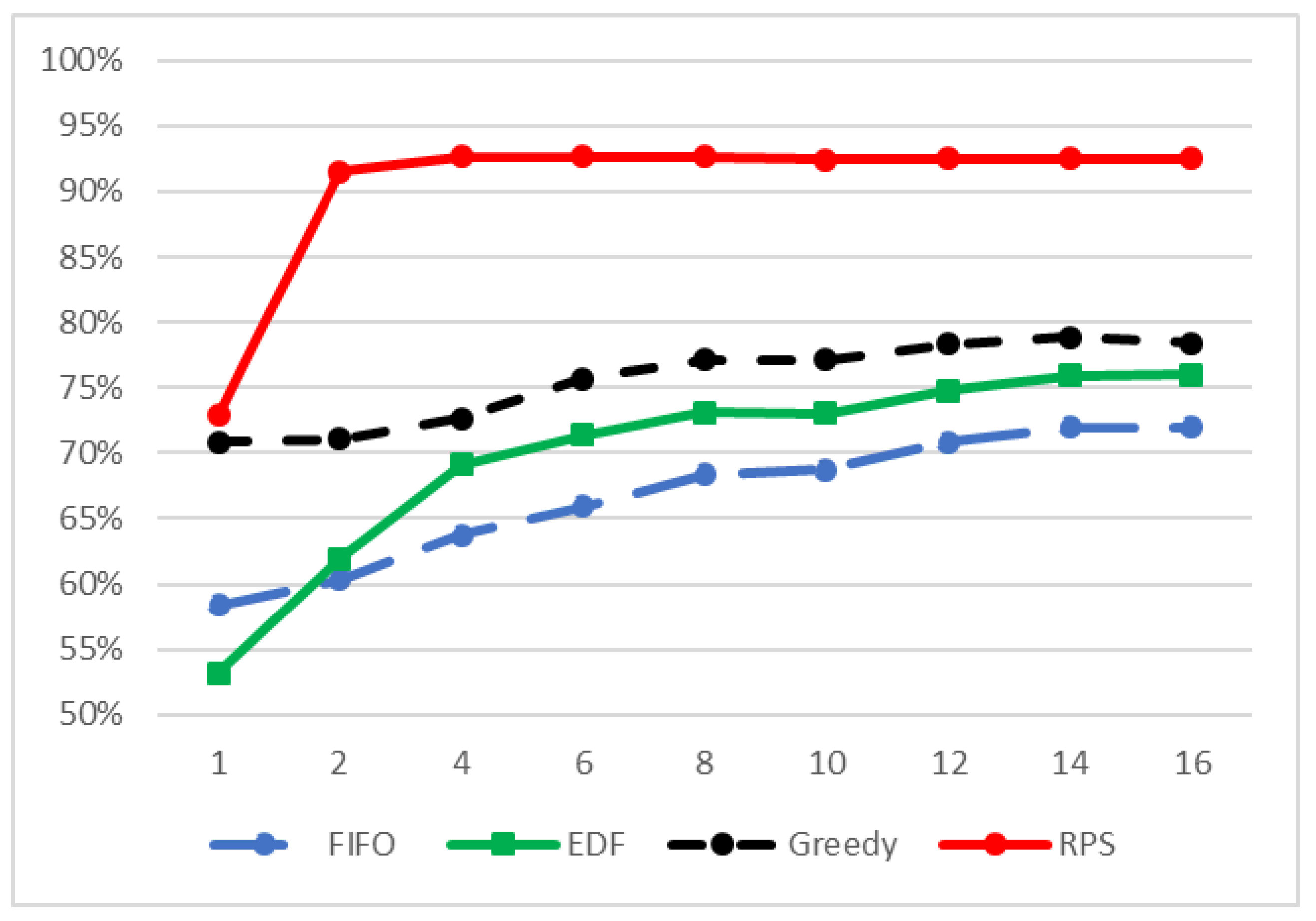
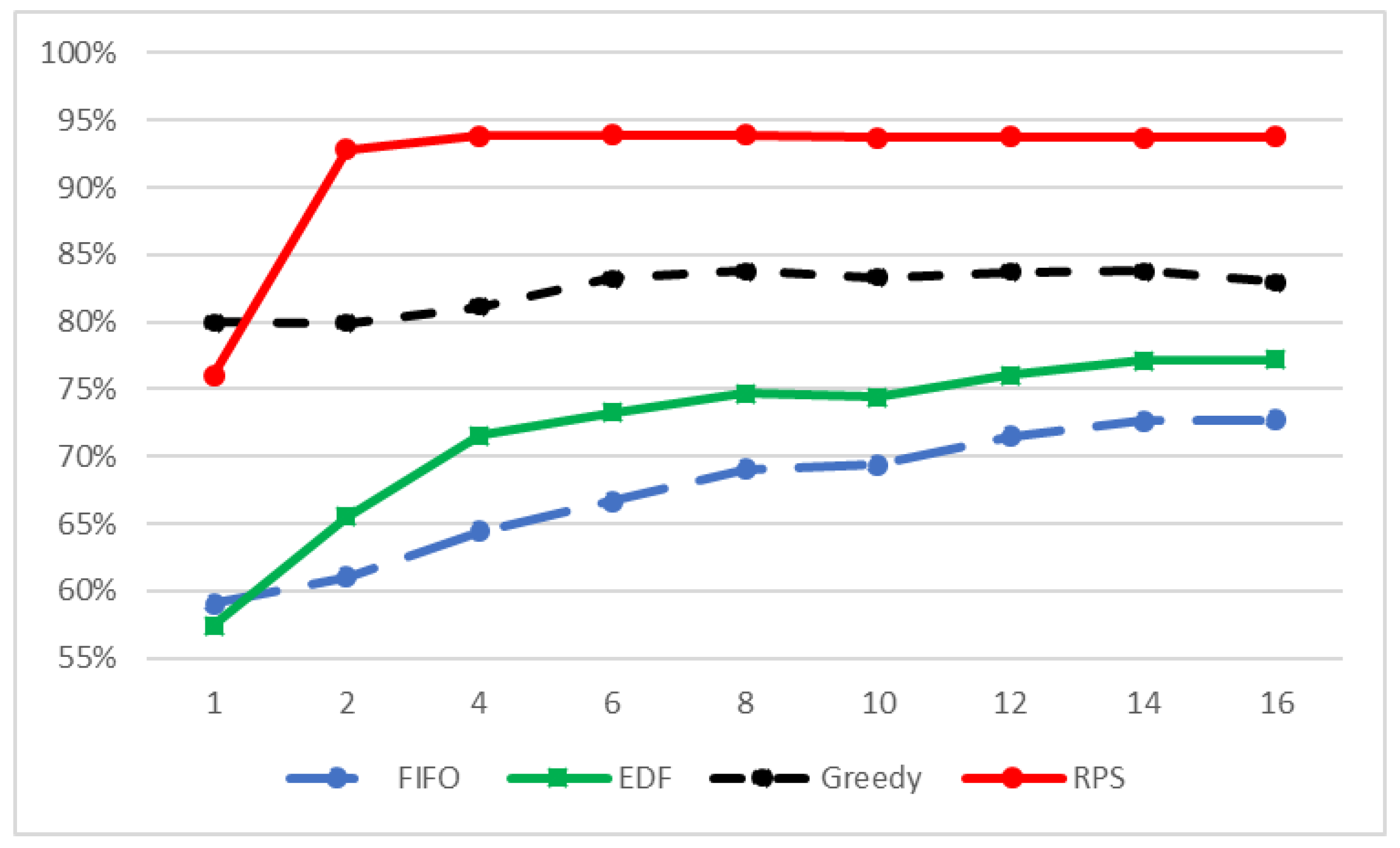
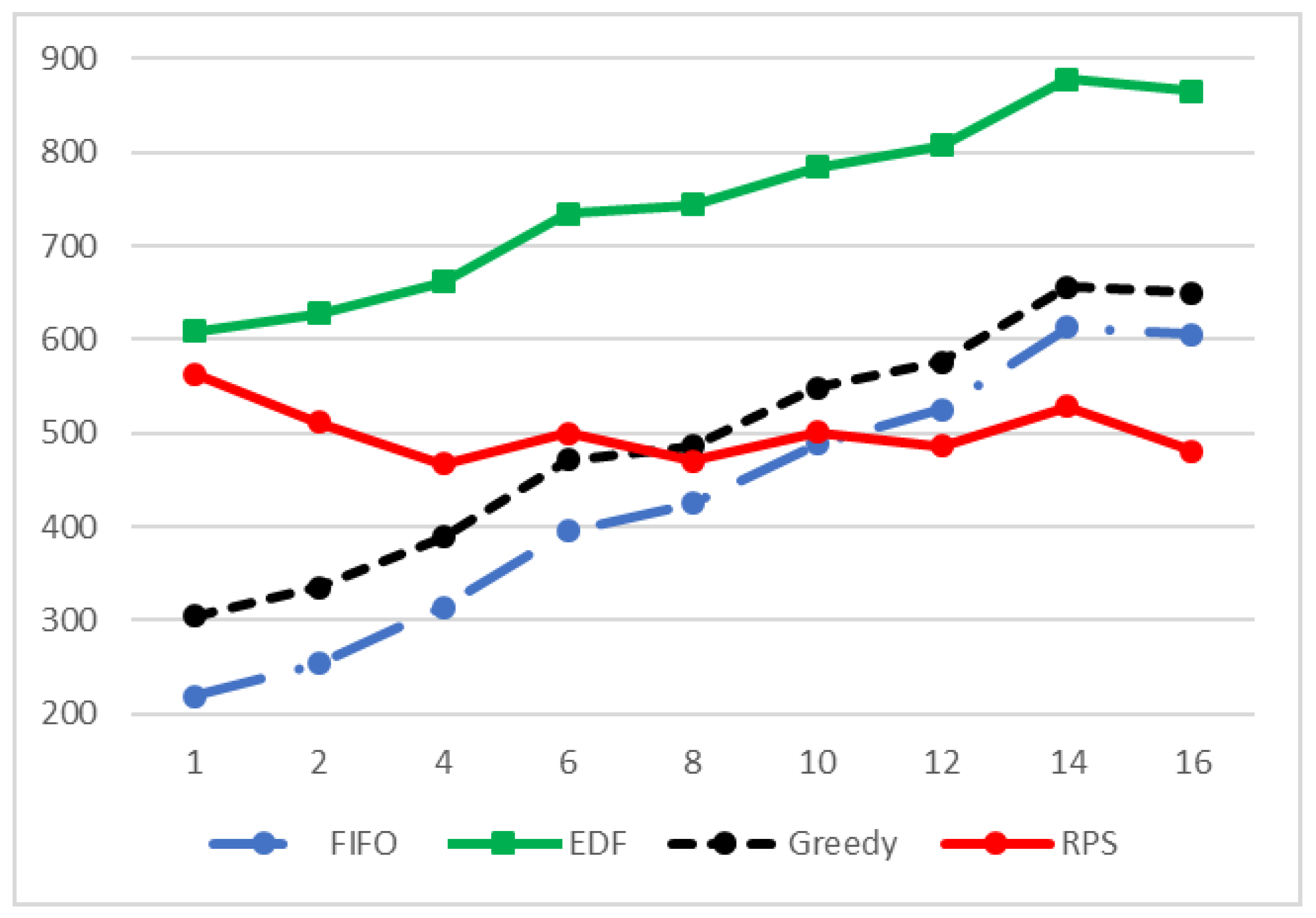
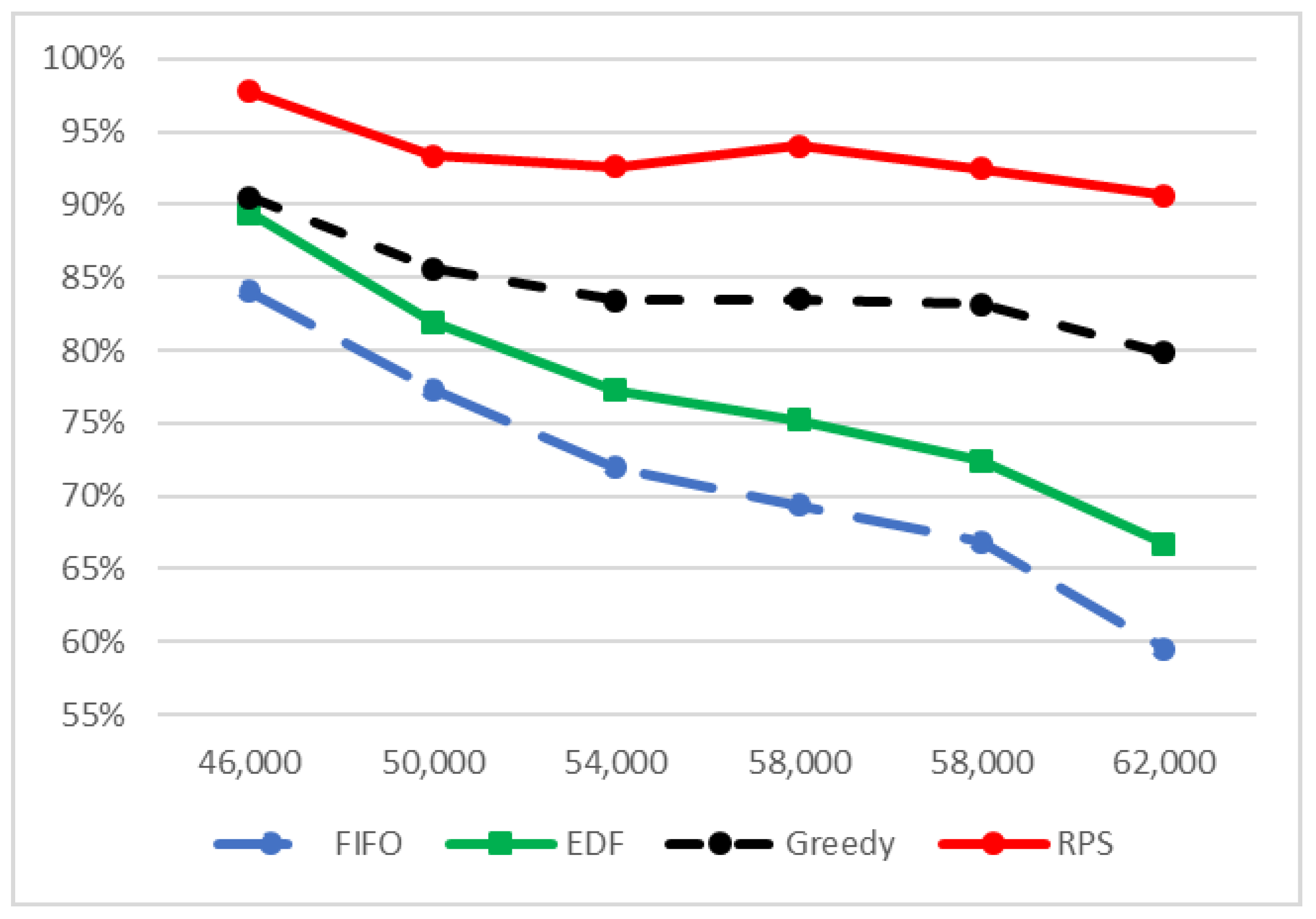
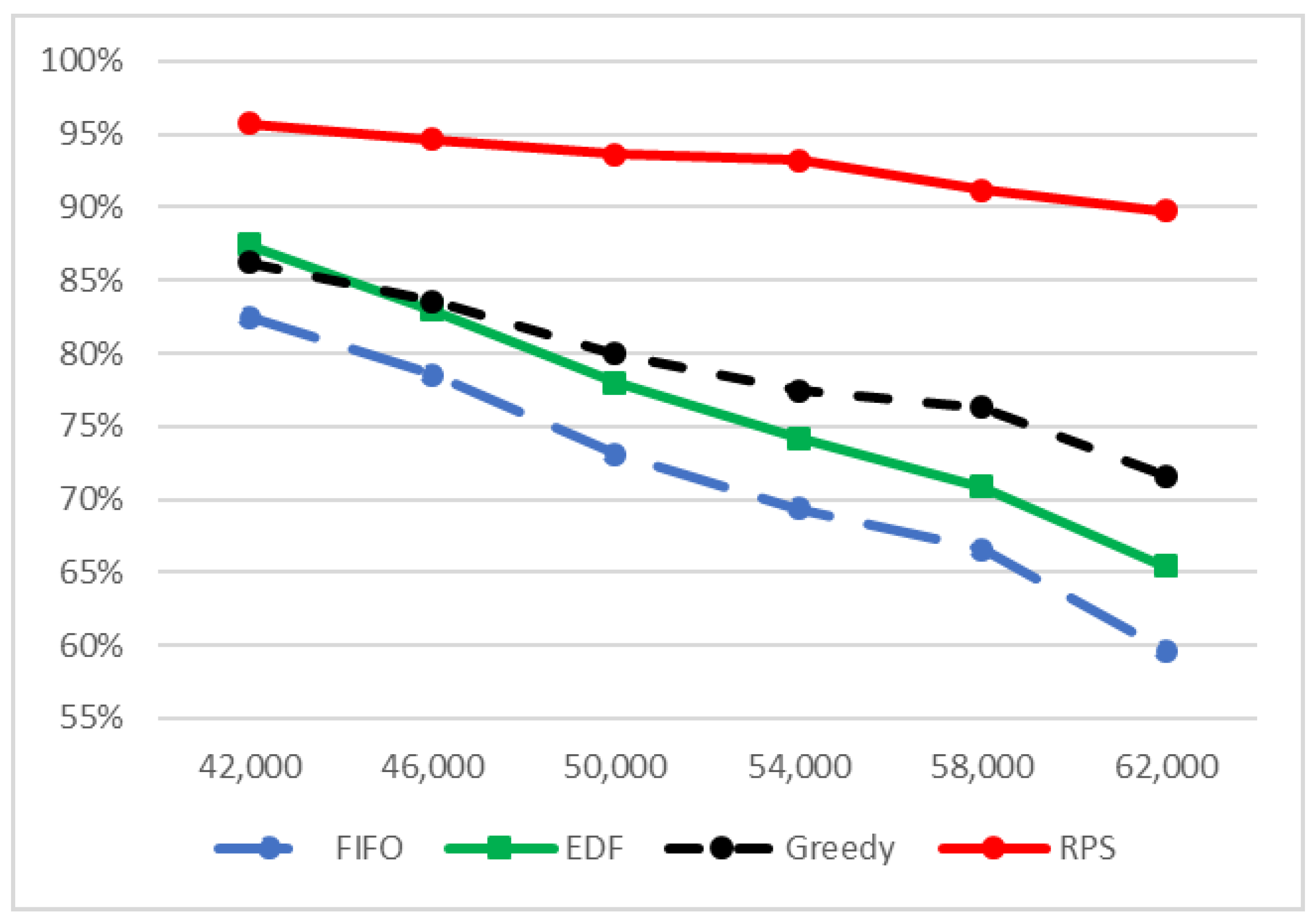
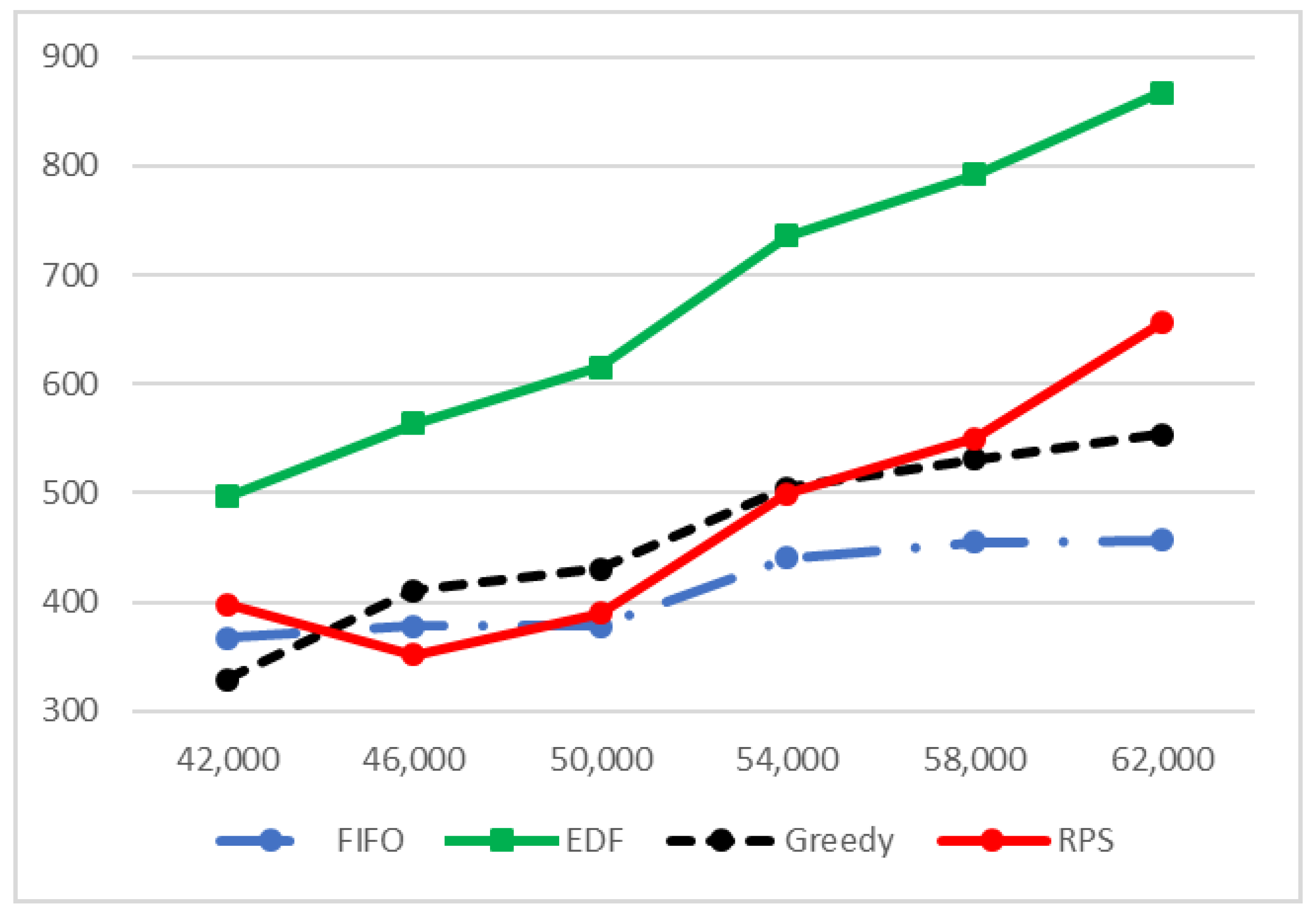
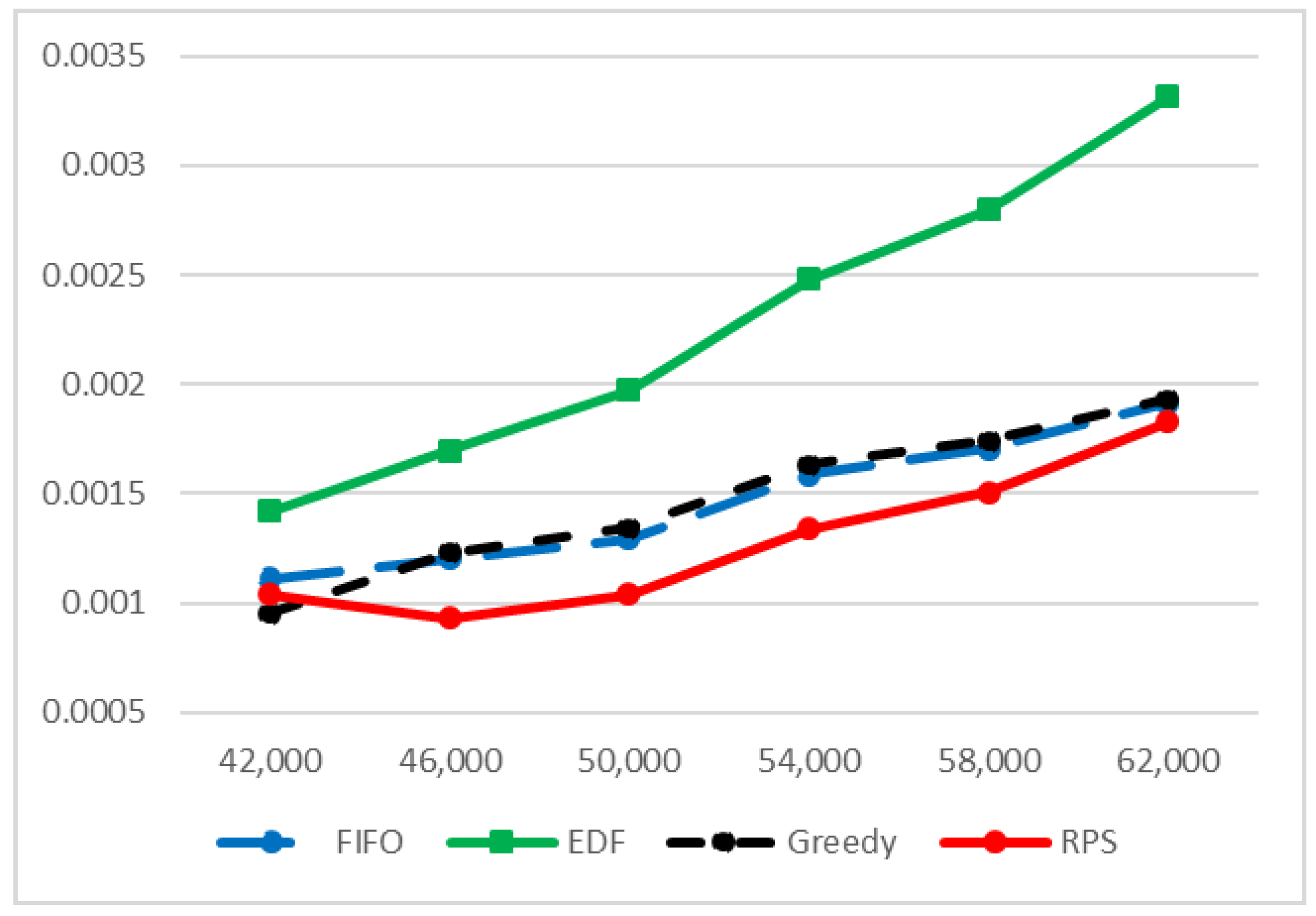
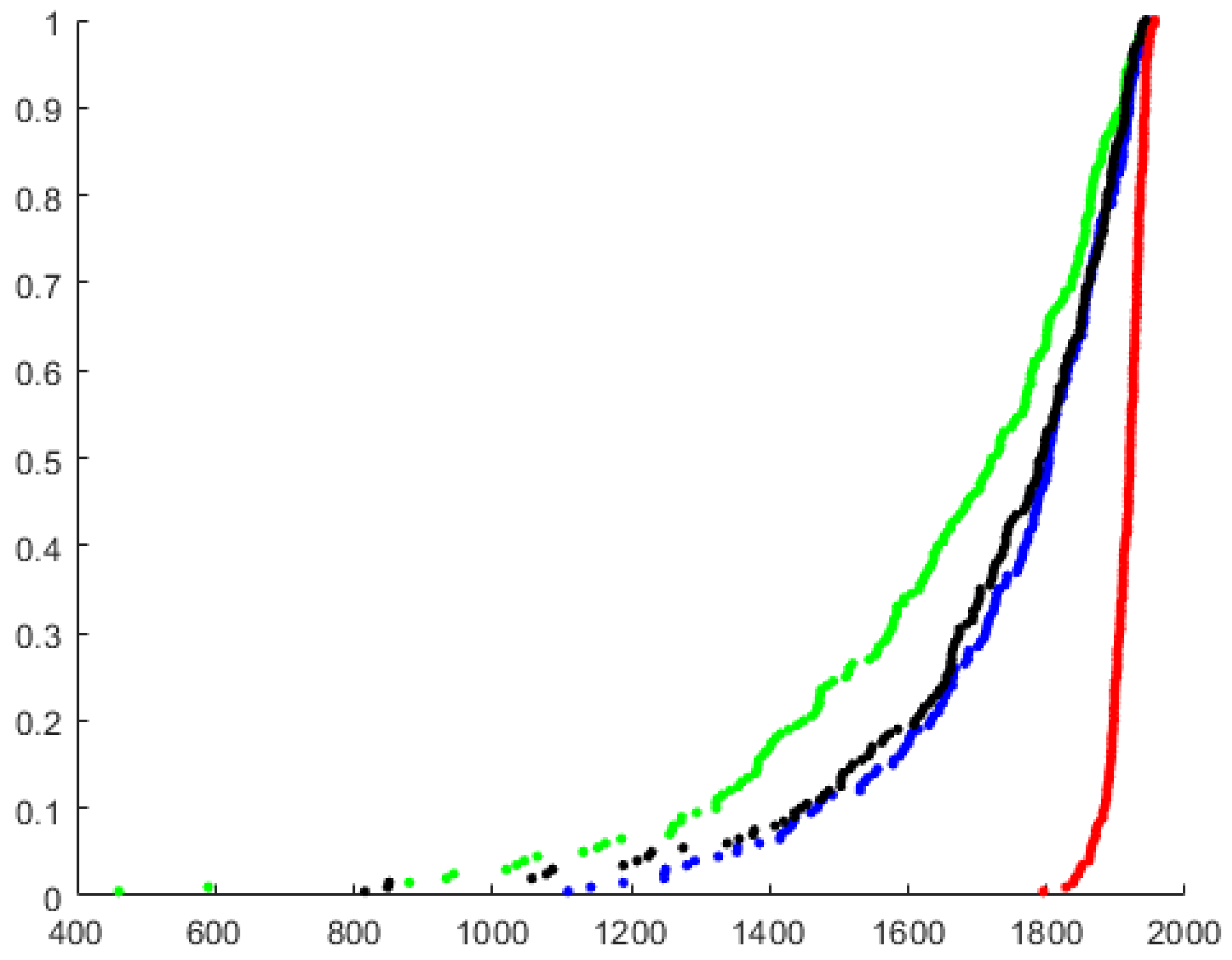
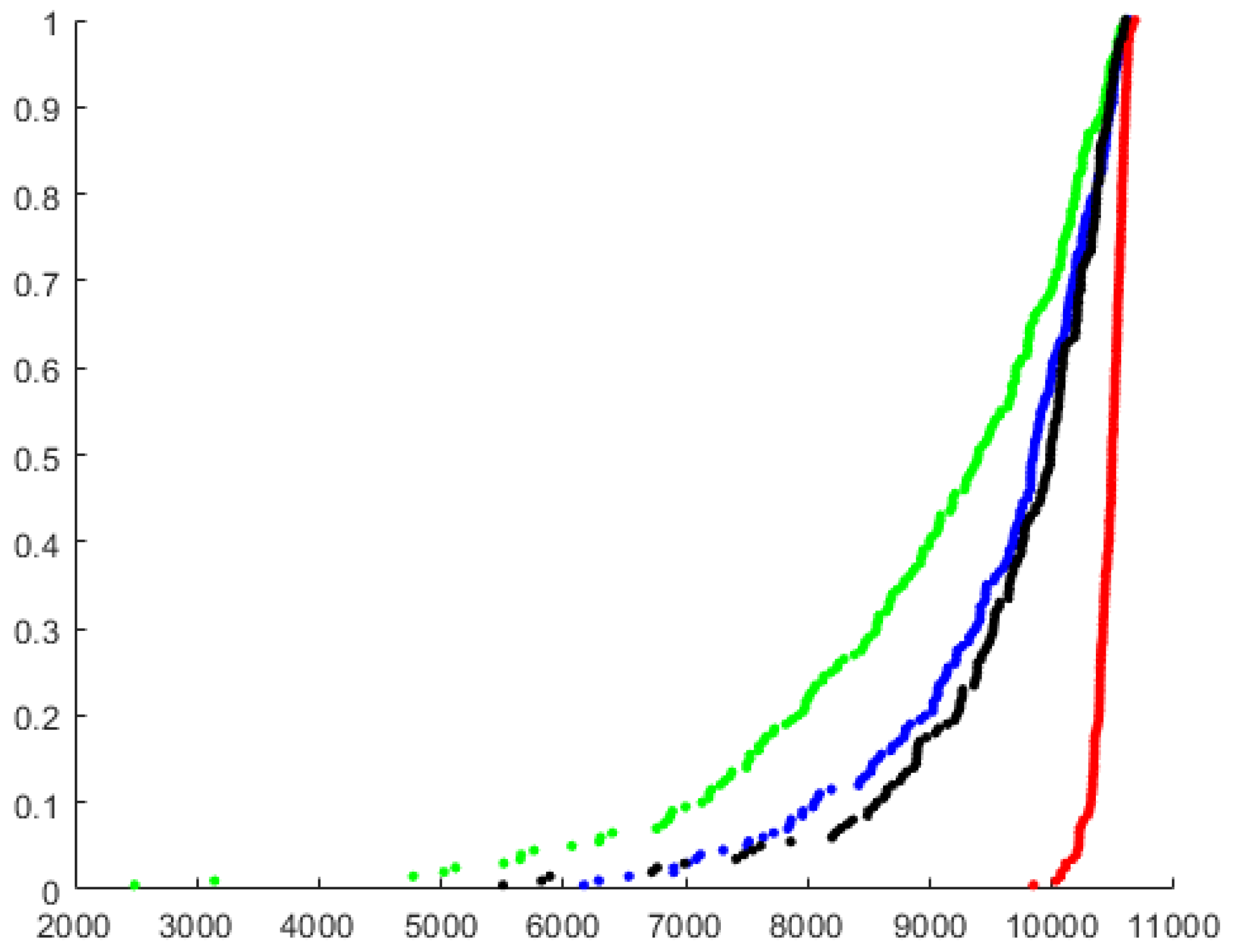
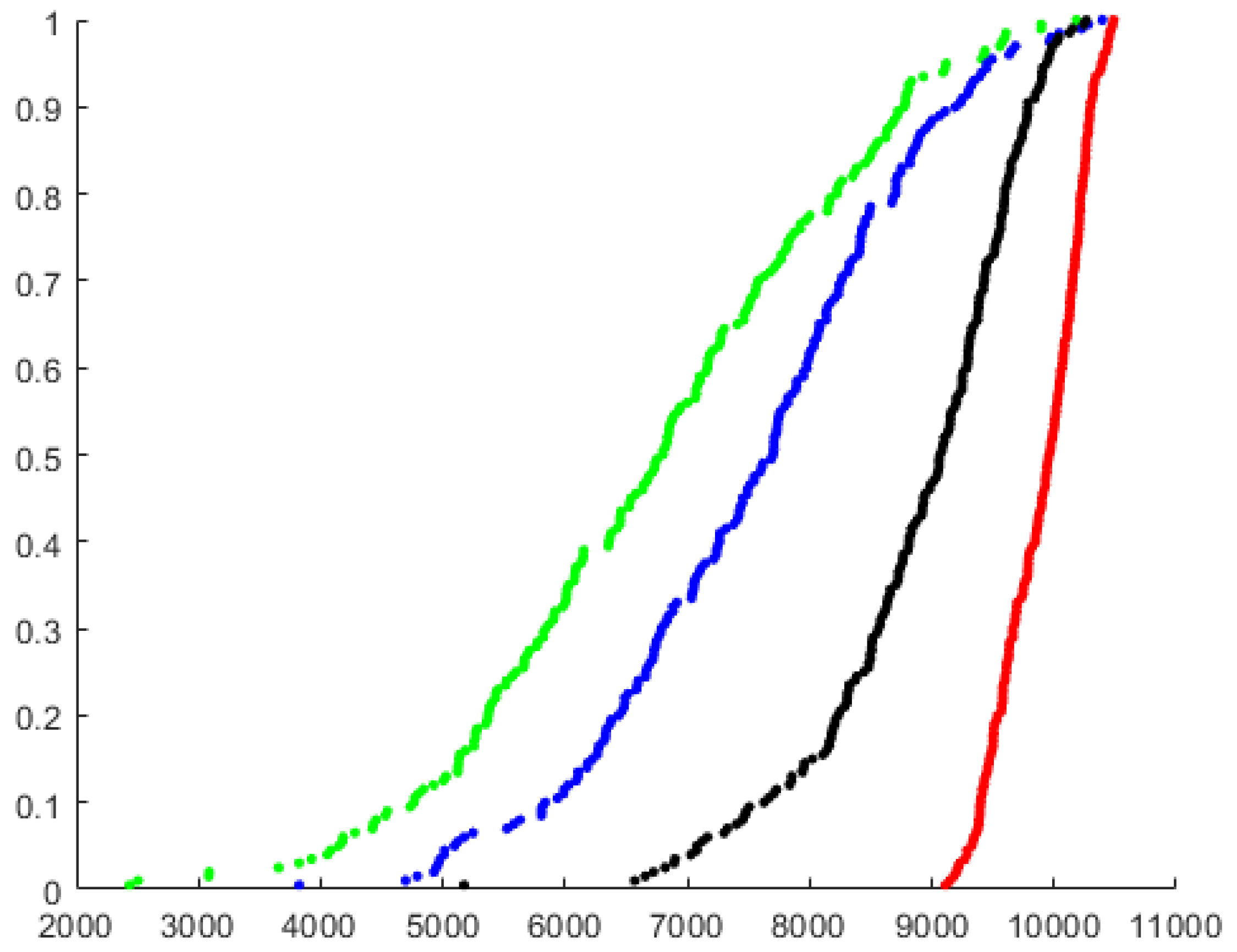
4. Simulations
- The arrival-time process was exponentially distributed with 42,000, 46,000, 50,200, 54,400, 58,000 and .
- The packets size was set to be similar to the Internet packet size distribution [53]. Forty percent were short packets with a length of 64 bytes; were long packets with a length of 1500 bytes. The length of the rest of the packets (medium packets) was uniformly distributed between the short and the long packet lengths .
- The deadline was exponentially distributed with from the arrival to the end of service.
- The reward was an integer that was distributed according to packet length. Short packets’ reward was uniformly distributed . Long packets’ reward was uniformly distributed , and medium packets’ reward was uniformly distributed .
- The destination of the packet was distributed uniformly between the MSs .
- Packets whose deadline expired were removed from the arrival queue.
- Packets with less than a 1-Kpbs rate did not begin transmission.
- Packets were selected only from a window of K packets at the prefix of the queue.
- All scheduling policies used ZFBF with a sequential insertion approach.
- Matrices and were downdated after packets ended their transmission.
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Terms | |
| AP | Access Point |
| AWGN | Additive White Gaussian Noise |
| BC | Broadcast Channel |
| C-RAN | Cloud Radio Access Network |
| DPC | Dirty Paper Coding |
| EDF | Earliest Deadline First |
| GBC | Gaussian Broadcast Channel |
| LOS | Line Of Sight |
| MIMO | Multiple Input Multiple Output |
| MISO | Multiple Input Single Output |
| MS | Mobile Station |
| MCS | Modulation and Coding Scheme |
| MU | Multi User |
| MU-MIMO | Multi User MIMO |
| OFDM | Orthogonal Frequency-Division Multiplexing |
| PG | Packet Generator |
| QoS | Quality of Service |
| QSI | Queue State Information |
| PR | Policy Runner |
| RPS | Reward Per Second |
| SINR | Signal-to-Interference plus Noise Ratio |
| SDN | Software-Defined Network |
| SNR | Signal-to-Noise Ratio |
| WLAN | Wireless Local Area Network |
| ZFBF | Zero Forcing Beam Forming |
| Notations | |
| Arrival random variable | |
| Packet length random variable | |
| C | Number of servers |
| Deadline random variable | |
| A packet that arrived at time . | |
| Reward or priority random variable | |
| The time of the arrival | |
| K | Defines the queue prefix size for eligible packets (window size) |
| M | The number of antennas |
| N | The number of mobile stations |
| The channel state information | |
| The conjugate transpose of matrix H | |
| A lower triangular matrix | |
| The transmission power | |
| An orthogonal matrix | |
| An upper triangular matrix | |
| The beamforming matrix | |
| A vector presenting the transmitted signal | |
| A vector presenting the received signal at the MS | |
| A vector presenting the AWGN |
References
- Corson, M.S.; Laroia, R.; Li, J.; Park, V.; Richardson, T.; Tsirtsis, G. Toward proximity-aware internetworking. IEEE Wirel. Commun. 2010, 17, 26–33. [Google Scholar] [CrossRef]
- Maeder, A.; Rost, P.; Staehle, D. The challenge of M2M communications for the cellular radio access network. In Proceedings of the 11th Würzburg Workshop IP Joint ITG ITC Euro-NF Workshop Vis. Future Gener. Netw. (EuroView), Würzburg, Germany, 1–2 August 2011; pp. 1–2. [Google Scholar]
- Cisco, V. Cisco Visual Networking Index: Forecast and Trends, 2017–2022. Available online: https://www.cisco.com/c/en/us/solutions/collateral/service-provider/visual-networking-index-vni/white-paper-c11-741490.html (accessed on 5 August 2019).
- Huang, X.; Xue, G.; Yu, R.; Leng, S. Joint scheduling and beamforming coordination in cloud radio access networks with QoS guarantees. IEEE Trans. Veh. Technol. 2015, 65, 5449–5460. [Google Scholar] [CrossRef]
- Nam, J.; Adhikary, A.; Ahn, J.Y.; Caire, G. Joint spatial division and multiplexing: Opportunistic beamforming, user grouping and simplified downlink scheduling. IEEE J. Sel. Top. Signal Process. 2014, 8, 876–890. [Google Scholar] [CrossRef]
- Eramo, V.; Lavacca, F.G.; Catena, T.; Polverini, M.; Cianfrani, A. Effectiveness of Segment Routing Technology in Reducing the Bandwidth and Cloud Resources Provisioning Times in Network Function Virtualization Architectures. Future Internet 2019, 11, 71. [Google Scholar] [CrossRef]
- Kobayashi, M.; Caire, G. Joint beamforming and scheduling for a MIMO downlink with random arrivals. In Proceedings of the 2006 IEEE International Symposium on Information Theory, Seattle, WA, USA, 9–14 July 2006; pp. 1442–1446. [Google Scholar]
- Sun, K.; Wang, Y.; Wang, T.; Chen, Z.; Hu, G. Joint channel-aware and queue-aware scheduling algorithm for multi-User MIMO-OFDMA Systems with downlink beamforming. In Proceedings of the 2008 IEEE 68th Vehicular Technology Conference, Calgary, AB, Canada, 21–24 September 2008; pp. 1–5. [Google Scholar]
- Matskani, E.; Sidiropoulos, N.D.; Luo, Z.Q.; Tassiulas, L. Convex approximation techniques for joint multiuser downlink beamforming and admission control. IEEE Trans. Wirel. Commun. 2008, 7, 2682–2693. [Google Scholar] [CrossRef]
- Costa, M. Writing on dirty paper (corresp.). IEEE Trans. Inf. Theory 1983, 29, 439–441. [Google Scholar] [CrossRef]
- Wiesel, A.; Eldar, Y.C.; Shamai, S. Zero-forcing precoding and generalized inverses. IEEE Trans. Signal Process. 2008, 56, 4409–4418. [Google Scholar] [CrossRef]
- Yoo, T.; Goldsmith, A. Optimality of zero-forcing beamforming with multiuser diversity. In Proceedings of the IEEE International Conference on Communications ICC 2005, Seoul, South Korea, 16–20 May 2005; Volume 1, pp. 542–546. [Google Scholar]
- Yoo, T.; Goldsmith, A. On the optimality of multiantenna broadcast scheduling using zero-forcing beamforming. IEEE J. Sel. Areas Commun. 2006, 24, 528–541. [Google Scholar]
- Dimic, G.; Sidiropoulos, N.D. On downlink beamforming with greedy user selection: Performance analysis and a simple new algorithm. IEEE Trans. Signal Process. 2005, 53, 3857–3868. [Google Scholar] [CrossRef]
- Kountouris, M.; de Francisco, R.; Gesbert, D.; Slock, D.T.; Salzer, T. Low complexity scheduling and beamforming for multiuser MIMO systems. In Proceedings of the 2006 IEEE 7th Workshop on Signal Processing Advances in Wireless Communications, Cannes, France, 2–5 July 2006; pp. 1–5. [Google Scholar]
- Karipidis, E.; Sidiropoulos, N.D.; Luo, Z.Q. Quality of service and max-min fair transmit beamforming to multiple cochannel multicast groups. IEEE Trans. Signal Process. 2008, 56, 1268–1279. [Google Scholar] [CrossRef]
- Huang, K.; Andrews, J.G.; Heath, R.W., Jr. Performance of orthogonal beamforming for SDMA with limited feedback. IEEE Trans. Veh. Technol. 2008, 58, 152–164. [Google Scholar] [CrossRef]
- Castaneda, E.; Silva, A.; Gameiro, A.; Kountouris, M. An overview on resource allocation techniques for multi-user MIMO systems. IEEE Commun. Surv. Tutorials 2016, 19, 239–284. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, Y.; Jing, Y.; Jin, S.; Yang, L. Sum-rate analysis for massive MIMO downlink with joint statistical beamforming and user scheduling. IEEE Trans. Wirel. Commun. 2017, 16, 2181–2194. [Google Scholar] [CrossRef]
- Pun, M.O.; Koivunen, V.; Poor, H.V. Performance analysis of joint opportunistic scheduling and receiver design for MIMO-SDMA downlink systems. IEEE Trans. Commun. 2010, 59, 268–280. [Google Scholar] [CrossRef]
- Katsinis, G.; Tsiropoulou, E.; Papavassiliou, S. Multicell interference management in device to device underlay cellular networks. Future Internet 2017, 9, 44. [Google Scholar] [CrossRef]
- Zafaruddin, S.M.; Bistritz, I.; Leshem, A.; Niyato, D. Multiagent Autonomous Learning for Distributed Channel Allocation in Wireless Networks. Available online: http://www.eng.biu.ac.il/leshema/files/2019/05/Multiagent-Autonomous-Learning-for-Distributed.pdf (accessed on 5 August 2019).
- Bertsekas, D.P.; Gallager, R.G.; Humblet, P. Data networks; Prentice-Hall International New Jersey: Upper Saddle River, NJ, USA, 1992; Volume 2. [Google Scholar]
- Stankovic, J.A.; Spuri, M.; Di Natale, M.; Buttazzo, G.C. Implications of classical scheduling results for real-time systems. Computer 1995, 28, 16–25. [Google Scholar] [CrossRef]
- Stankovic, J.A.; Spuri, M.; Ramamritham, K.; Buttazzo, G.C. Deadline Scheduling for Real-Time Systems: EDF and Related Algorithms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 460. [Google Scholar]
- Srikant, R.; Ying, L. Communication Networks: An Optimization, Control, and Stochastic Networks Perspective; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Panwar, S.S.; Towsley, D.; Wolf, J.K. Optimal scheduling policies for a class of queues with customer deadlines to the beginning of service. J. ACM (JACM) 1988, 35, 832–844. [Google Scholar] [CrossRef]
- Bhattacharya, P.P.; Ephremides, A. Optimal scheduling with strict deadlines. IEEE Trans. Autom. Control 1989, 34, 721–728. [Google Scholar] [CrossRef]
- Towsley, D.; Panwar, S. Optimality of the Stochastic Earliest Deadline Policy for the G/M/c Queue Serving Customers with Deadlines. Available online: https://pdfs.semanticscholar.org/cb01/08dca4ded7afd18e1bbbc950617749473c11.pdf (accessed on 5 August 2019).
- Cohen, R.; Katzir, L. Scheduling of voice packets in a low-bandwidth shared medium access network. IEEE/ACM Trans. Netw. (TON) 2007, 15, 932–943. [Google Scholar] [CrossRef][Green Version]
- Brucker, P.; Brucker, P. Scheduling Algorithms; Springer: Berlin/Heidelberg, Germany, 2007; Volume 3. [Google Scholar]
- Raviv, L.; Leshem, A. Maximizing service reward for queues with deadlines. IEEE/ACM Trans. Netw. 2018, 26, 2296–2308. [Google Scholar] [CrossRef]
- Grimmett, G.; Stirzaker, D. Probability and Random Processes; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Peha, J.M.; Tobagi, F.A. Cost-based scheduling and dropping algorithms to support integrated services. IEEE Trans. Commun. 1996, 44, 192–202. [Google Scholar] [CrossRef][Green Version]
- Atar, R.; Giat, C.; Shimkin, N. The cμ/θ rule for many-server queues with abandonment. Oper. Res. 2010, 58, 1427–1439. [Google Scholar] [CrossRef]
- Ayesta, U.; Jacko, P.; Novak, V. A nearly-optimal index rule for scheduling of users with abandonment. In Proceedings of the 2011 IEEE INFOCOM, Shanghai, China, 10–15 April 2011; pp. 2849–2857. [Google Scholar]
- Yu, Z.; Xu, Y.; Tong, L. Deadline scheduling as restless bandits. In Proceedings of the 2016 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 27–30 September 2016; pp. 733–737. [Google Scholar]
- Mangold, S.; Choi, S.; May, P.; Klein, O.; Hiertz, G.; Stibor, L. IEEE 802.11 e wireless LAN for quality of service. Proc. Eur. Wirel. 2002, 2, 32–39. [Google Scholar]
- Hadar, I.; Raviv, L.; Leshem, A. Scheduling For 5G Cellular Networks With Priority And Deadline Constraints. In Proceedings of the 2018 IEEE International Conference on the Science of Electrical Engineering in Israel (ICSEE), Eilat, Israel, 12–14 December 2018; pp. 1–5. [Google Scholar]
- Bejarano, O.; Knightly, E.W.; Park, M. IEEE 802.11 ac: From channelization to multi-user MIMO. IEEE Commun. Mag. 2013, 51, 84–90. [Google Scholar] [CrossRef]
- Perahia, E.; Gong, M.X. Gigabit wireless LANs: An overview of IEEE 802.11 ac and 802.11 ad. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2011, 15, 23–33. [Google Scholar] [CrossRef]
- Bellalta, B.; Barcelo, J.; Staehle, D.; Vinel, A.; Oliver, M. On the performance of packet aggregation in IEEE 802.11 ac MU-MIMO WLANs. IEEE Commun. Lett. 2012, 16, 1588–1591. [Google Scholar] [CrossRef]
- Perahia, E.; Cordeiro, C.; Park, M.; Yang, L.L. IEEE 802.11 ad: Defining the next generation multi-Gbps Wi-Fi. In Proceedings of the 2010 7th IEEE Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 9–12 January 2010; pp. 1–5. [Google Scholar]
- Nitsche, T.; Cordeiro, C.; Flores, A.B.; Knightly, E.W.; Perahia, E.; Widmer, J.C. IEEE 802.11 ad: Directional 60 GHz communication for multi-Gigabit-per-second Wi-Fi. IEEE Commun. Mag. 2014, 52, 132–141. [Google Scholar] [CrossRef]
- Ghasempour, Y.; Knightly, E.W. Decoupling beam steering and user selection for scaling multi-user 60 ghz wlans. In Proceedings of the 18th ACM International Symposium on Mobile Ad Hoc Networking and Computing, Chennai, India, 10–14 July 2017; p. 10. [Google Scholar]
- Kendall, D.G. Stochastic processes occurring in the theory of queues and their analysis by the method of the embedded Markov chain. Ann. Math. Stat. 1953, 24, 338–354. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Viswanathan, H.; Venkatesan, S.; Huang, H. Downlink capacity evaluation of cellular networks with known-interference cancellation. IEEE J. Sel. Areas Commun. 2003, 21, 802–811. [Google Scholar] [CrossRef]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Gill, P.E.; Golub, G.H.; Murray, W.; Saunders, M.A. Methods for modifying matrix factorizations. Math. Comput. 1974, 28, 505–535. [Google Scholar] [CrossRef]
- Bojanczyk, A.; Brent, R.; De Hoog, F. QR factorization of Toeplitz matrices. Numer. Math. 1986, 49, 81–94. [Google Scholar] [CrossRef]
- Yoo, K.; Park, H. Accurate downdating of a modified Gram-Schmidt QR decomposition. BIT Numer. Math. 1996, 36, 166–181. [Google Scholar] [CrossRef]
- Sinha, R.; Papadopoulos, C.; Heidemann, J. Internet Packet Size Distributions: Some Observations; Tech. Rep. ISI-TR-2007-643; USC/Information Sciences Institute: Marina Del Rey, CA, USA, 2007. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raviv, L.-o.; Leshem, A. Scheduling for Multi-User Multi-Input Multi-Output Wireless Networks with Priorities and Deadlines. Future Internet 2019, 11, 172. https://doi.org/10.3390/fi11080172
Raviv L-o, Leshem A. Scheduling for Multi-User Multi-Input Multi-Output Wireless Networks with Priorities and Deadlines. Future Internet. 2019; 11(8):172. https://doi.org/10.3390/fi11080172
Chicago/Turabian StyleRaviv, Li-on, and Amir Leshem. 2019. "Scheduling for Multi-User Multi-Input Multi-Output Wireless Networks with Priorities and Deadlines" Future Internet 11, no. 8: 172. https://doi.org/10.3390/fi11080172
APA StyleRaviv, L.-o., & Leshem, A. (2019). Scheduling for Multi-User Multi-Input Multi-Output Wireless Networks with Priorities and Deadlines. Future Internet, 11(8), 172. https://doi.org/10.3390/fi11080172




