Energy-Efficient Multi-User Routing in a Software-Defined Multi-Hop Wireless Network

Abstract

Software-defined networking (SDN) is an innovative architecture that designs a logical controller to manage and program the network based on the global view, providing more efficient management, better performance, and higher flexibility for the network. Therefore, applying the SDN concept in a multi-hop wireless network (MWN) has been proposed and extensively studied to overcome the challenges of MWN. In this paper, we propose an energy-efficient global routing algorithm for a software-defined multi-hop wireless network (SDMWN), which is able to get transmission paths for several users at the same time to minimize the global energy consumption with the premise of satisfying the QoS required by users. To this end, we firstly propose a Lagrange relaxation-based aggregated cost (LARAC) and K-Dijkstra combined algorithm to get the top K energy-minimum paths that satisfy the QoS in polynomial time. Then, we combine the alternative paths of each user obtained by K-LARAC and propose an improved genetic algorithm to solve the global routing strategy. The simulation results show that the proposed K-LARAC and genetic algorithm combined method has the ability to obtain an approximate optimal solution with lower time cost.

1. Introduction

With the increasing scale and complexity of networks, people’s requirements for the quality of network service are increasing. During data transmission, we need to not only develop a transmission strategy for multiple users at the same time, but also provide better QoS service and a wider transmission range. Traditional wireless networks allow nodes to exchange data directly within the transmission range, but this approach is severely limited by distance. As mobile communication technology develops rapidly, the utilization of mobile devices becomes more widespread and novel mobile applications emerge continuously. In order to solve the problem of traditional networks, a multi-hop wireless network (MWN) architecture has been proposed to reasonably utilize the idle resources of the mobile devices to process and forward data, thus extending the coverage of the network. In a multi-hop wireless network, the node forwards the data packet to the destination through the intermediate mobile nodes in a multi-hop manner, so MWN belongs to the infrastructure-less networks [1].

Unfortunately, although MWN provides a wider transmission range for data transmission technology, it still faces some crucial problems [2,3,4]. Firstly, since nodes can move arbitrarily, the network topology is always changing while the flexibility of the network is increasing. Therefore, the location of nodes should be acquired in real time to complete data forwarding. Secondly, MWN is self-organizing and distributed, resulting in that nodes only store a local network topology. In the absence of central control, it is difficult to modify the network topology dynamically and develop the global optimal data transmission strategy. Finally, since MWN is composed of battery-powered mobile nodes, we should consider the specific energy consumption of nodes and ensure that they do not lose too much power, so as to extend the life of the network. Moreover, without any central control, managing the energy consumption of the network is arduous.

Recently, the development of software-defined network (SDN) technology has brought new solutions to these problems [5,6]. The main idea of SDN is to separate data and control by separating the data plane and control plane [7]. Data routing and network traffic can be controlled by programming in a logical centralized controller, which centralizes decentralized routing information. Therefore, the SDN architecture can be applied to a multi-hop wireless network to compensate for the lack of centralized control, namely a software-defined multi-hop wireless network (SDMWN) [8]. In SDMWN, the SDN controller is responsible for centralized management of wireless nodes. Once the network topology changes, users can design the routing algorithm in the controller on the basis of their needs to implement the data transmission. The software-defined multi-hop wireless network has the following advantages [9]:

$\mathbf{Node}\mathbf{mobility}\mathbf{management}$: Mobility management means that once mobile nodes move, it is necessary to obtain the real-time location of the nodes and update the network topology in time. SDMWN adds centralized management to MWN, in which each node sends its location information to the logical centralized controller in real time. The logical centralized controller can get the global view of the network and dynamically adjust the current routing strategy.

$\mathbf{Energy}$: In SDMWN, all routing strategies are decided by the logical centralized controller. Nodes in the network only receive and transmit data, which reduces the energy consumption of mobile devices.

$\mathbf{Quality}\mathbf{of}\mathbf{service}$: Real time is the most significant feature of SDMWN. Nodes periodically send their current state to the logical centralized controller, such as energy remaining, network bandwidth and delay, etc. Then, the controller makes corresponding routing adjustments according to the collected information, so that the whole network can provide better service.

In the SDMWN model, the routing strategy is designed in the logical control layer and sent to each node by the controller to complete the deployment of the entire data transmission layer. The SDMWN allows the packet switches to have a centralized interface, like OpenFlow, to provide a real-time QoS assurance of certainty [10]. During the data transmission, the nodes transmit the current residual energy and other information back to the logical centralized controller without delay. Subsequently, the controller draws a new global network topology and adjusts the routing to get the shortest path of the next transmission process.

In this paper, we focus on the balance between transmission time and energy consumption, based on the energy model and delay model, which are suitable for practical application, aiming at studying the routing of providing data transmission for multiple users in the context of SDMWN. It is different from the previous research on the QoS minimum cost routing for a single user. In this paper, not only the routing algorithm conforming to constraints should be developed for multiple users, but also the global energy consumption of all users should be optimized, which is more consistent with the application scenarios. Therefore, the routing algorithm is designed for multiple users to minimize the total energy consumption of all transmission paths. In the proposed algorithm, users must specify their destinations, the size of data, and the maximum delay they can accept. To avoid transmission queuing and reduce transmission failures, we assume that the intermediate nodes do not transfer data for multiple users repeatedly.

Hence, the technology of this paper is as follows: In the first place, the Lagrange relaxation-based aggregated cost (LARAC) is adopted to aggregate delay and energy consumption variables. The LARAC algorithm is based on the Lagrange relaxation technique, which allows the routing problem to be solved in polynomial time. Then, owing to our goal being to solve simultaneously the problem of global minimum energy consumption and no duplicate nodes in the paths, the above conditions may not be satisfied when all users choose the optimal path. Therefore, combining the LARAC algorithm with K-Dijkstra, we develop the K-LARAC algorithm to find the alternative path set for each user. Finally, we map the alternative paths to chromosomes in the genetic algorithm (GA) and use it to quickly find the routing scheme that meets the global minimum energy consumption and does not have duplicate intermediate nodes. Simulation results show that the proposed global routing can not only be solved in polynomial time, but also obtain approximate optimal solutions, in which the validity of the algorithm is further demonstrated.

This paper is organized as follows: the related work is introduced in Section 2. In Section 3, we introduce the system model, including the network model, energy model, and delay model. In Section 4, the expression of global energy consumption minimization under constraint conditions and the optimization algorithm to solve the problem are introduced. Section 5 shows the simulation results, and Section 6 gives the conclusions.

2. Related Work

As a new network architecture model, SDMWN is the background of many research works. One of the most popular topics is centralized routing protocols, which use the global view of the network to develop better routing strategies. In [11], Wang et al. proposed a SDN-based multi-path routing protocol for MWN, which provides a disjoint multi-path for users according to hops and the residual energy of nodes. Compared with the conventional algorithms, it not only reduces the end-to-end delay, but also prolongs the nodes’ life time. Besides, in order to solve the problem of load balancing or congestion control, a number of research works [12,13] proposed some centralized SDN routing protocols in MWN. From [14], we know that the SDN-based traffic aware protocol (SDN-TAP) is an algorithm for monitoring the channel activity of intermediate nodes. Once the potential congestion is found, an alert will be sent to the SDN controller immediately, and the controller will call the load balancing algorithm to find a backup path. In most cases, SDN-TAP handles congestion quickly to reduce the packet loss rate and average end-to-end delay. The work in [15] presented an integrated approach based on the SDN concept to ensure efficient and reliable transmission in flow-aware networks. Even if network failures occur, the SDN controller can still provide solutions to solve congestion quickly based on traffic prediction. More importantly, congestion processing has a clear priority, which can ensure that high-priority transmission tasks get better quality of service. From [16,17,18], we know that task allocation for multiple running applications is also an important research field in SDMWN. In [19], Tomovic and Radusinovic proposed an algorithm to assign tasks on the basis of the location and residual energy of nodes and deployed it in a centralized controller. It not only balanced the energy consumption in the network, but also boosted the success rate of the task arrangement. Therefore, SDMWN is used widely as an emerging network architecture, which provides an excellent experimental background for the research.

In terms of routing strategies, due to the increasing demands for network quality of service, QoS routing has become the focus of current network research. According to the underlying routing strategy, the classical algorithms used in unicast QoS routing can be summarized as priority queue, Bellman–Ford, Lagrange relaxation, and so on [20]. Moreover, there are three kinds of QoS metrics for the link value: additive, multiplicative, and concave metrics, which are determined by the research object. For example, calculating the link delay is an additive metric that adds values together. Generally, the calculations of the packet loss rate and bandwidth are multiplicative and concave metrics, respectively. Accordingly, there is a difference in the QoS objectives, and the routing types are different. As far as the main content of this paper is concerned, the transmission request of each user can be regarded as the research on the minimum cost routing path of QoS constraints, i.e., the delay-constrained least-cost (DCLC) routing algorithm. The DCLC algorithm takes energy consumption as the cost and delay as the constraint, which belongs to the additive metric. In [21], it has been proven that this routing problem is NP-hard. Consequently, it is inevitable but worthwhile to sacrifice part of the time for lower costs until an acceptable balance is reached. In order to find a feasible solution in polynomial time, many people have studied this problem.

In [22], an optimization method for QoS disjoint multi-path routing that meets the multiple constraints was proposed. Firstly, the analytic hierarchy process (AHP) is used to calculate the weights of multiple constraints, so that the multiple objectives can be converted into a single objective, which is a common method to simplify the multi-constraint problem. Then, in order to achieve load balance and reliable transmission service, the author used an improved heuristic search algorithm to select disjoint paths and backup paths. The multi-objective optimization problem can also be solved by many other methods. For example, in [23], Salama et al. proposed to solve DCLC problems with the knowledge of the least-cost (LC) tree and the least-delay (LD) tree that can reach the destination. This is a simple distributed heuristic solution called the delay constrained unicast routing (DCUR) algorithm. At each node, this algorithm builds the path node by node and makes a choice between the LC path and LD path according to the current delay. If it satisfies the constraint, we select the LC edge to add to the path, otherwise we add the LD edge. If a loop occurs, the algorithm will go back to the node that selected the LC path and select the LD edge instead. Backtracking guarantees loop elimination and the integrity of the algorithm, but it is not optimal. In [24], a new Lagrangian based on minimum cost QoS routing algorithm (MCQRA) for SDMWN was proposed to find the path more effective at a lowering the cost and meeting the requirements of QoS. Despite the above research works having different solutions to multi-objective problems, they can find a path to meet the requirements of QoS at a lower cost. However, all the studies only focused on a single user. In practical application scenarios, multiple users often submit service requests at the same time and need to use the same range of network resources for data transmission.

At present, there are not many related works on global minimization routing designed for multiple users, and these works have achieved different purposes by considering diverse system models, optimization parameters, and methods. To our best knowledge, there is little work to consider energy-efficient multi-user routing in SDMWN. After all, mobile devices are widely used, and their transmission capabilities cannot be ignored. It is of great significance to design routing algorithms in this scenario. Accordingly, aiming at the multi-user routing problem of SDMWN, a global energy minimization algorithm with delay constraints is proposed. In addition, considering the congestion control problem, we assume that each intermediate node only provides transmission service for one user to avoid queuing delay effectively.

3. System Model

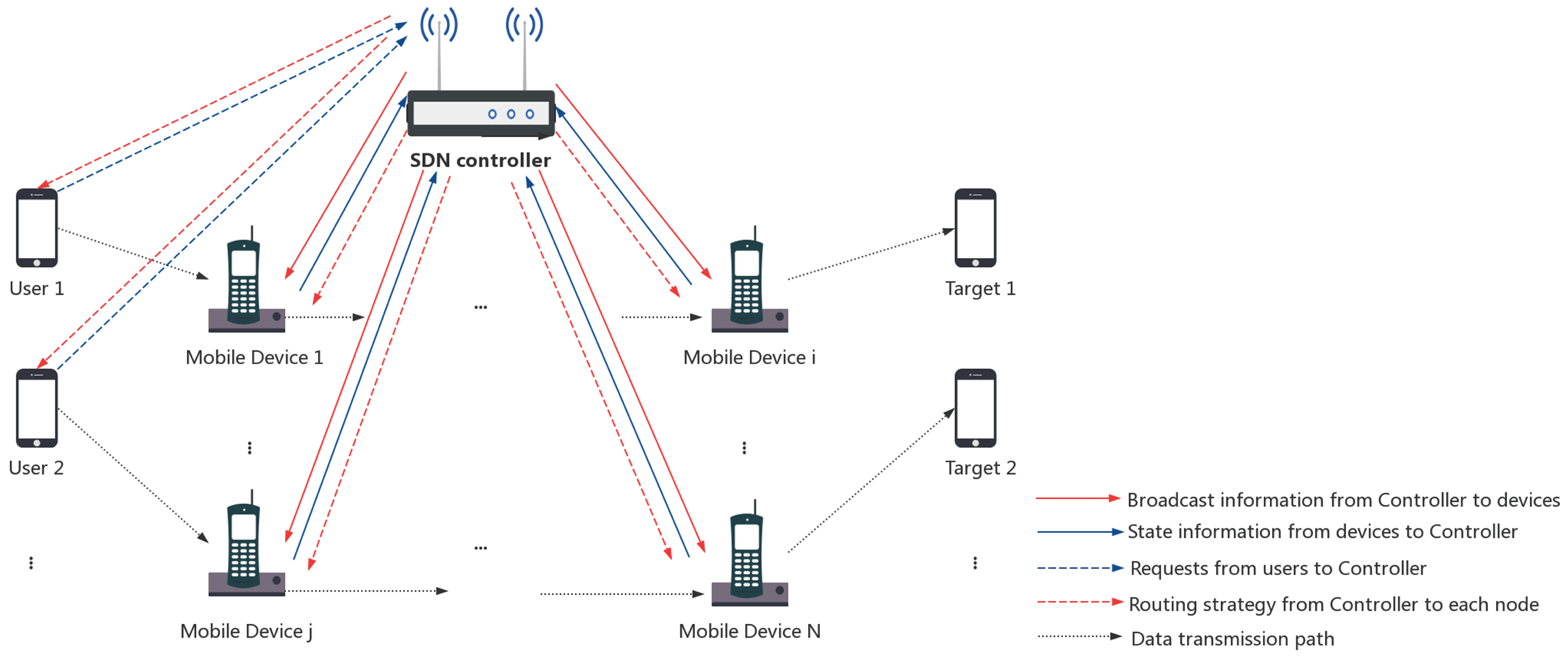
This paper considers a QoS routing algorithm with multiple users, supposing that there are one SDN controller, some users, and N mobile devices with transmission capabilities. The SDN controller can periodically obtain information from mobile devices and optimize the routing in line with the global view of the network. Mobile devices refer to heterogeneous mobile wireless nodes such as smartphones, laptops, vehicles, sensors, and so on. Besides, these devices not only receive the broadcast information from the controller, but also return their own real-time state. The system architecture is shown in Figure 1, and the specific description is as below.

• The SDN controller broadcasts information to each node, and these nodes form the backward paths to the controller based on the broadcast path;
• The state information of each node is sent to the SDN controller along the backward path. Then, the controller establishes the network topology according to the received information (residual energy, location);
• Before the users plan to send data to the target nodes, they shall send the transmission requests to the SDN controller;
• According to the global view and routing algorithm, the SDN controller calculates the transmission paths for multiple users at the same time and then sends them to each node;
• Users send data to target nodes in terms of routing information.

3.1. Network Model

This paper defines the topology of the data network as the weighted graph. For a given graph $G=(V,E)$ with two distinct vertices $s,t\in V$, V represents the mobile device and E represents a collection of network links. For a routing algorithm, we call the metrics that need to be optimized (or minimized) the costs. Meanwhile, the metrics that must be kept below the prescribed boundaries are called constraints. On the basis of this, the cost is $energy\left(e\right)$, the constraint is $delay\left(e\right)\le D$, and these two variables are set as edge weights. Then, we calculate M paths from M source points to their respective target nodes, so that the time delay of these M paths is no higher than their respective delay constraints $D_i$ and the total energy consumption is minimal. In order to solve the practical problem, the data of the network topology are stored in two-dimensional matrices, including the energy consumption matrix $Weigh{t}_e$ and the delay matrix $Weigh{t}_d$. In the matrix, if there is an edge between two nodes, the corresponding value is denoted as the weight; if there is no edge, set it to ∞. Before routing algorithms are executed, each edge (link) in the network graph is given a cost and a QoS metric. During the design of the routing strategy, we suppose that the information of the network topology remains the same. After the network topology is established, the following weight models are given to calculate the energy consumption and delay between any two points.

3.2. Energy Model

In the SDMWN architecture, in addition to location information, mobile devices also set the following parameters: transmission power, receiving power, channel state, etc. [25]. The processing rate for each mobile device according to the Shannon–Hartley formula is presented:

$$S_{i,j}^m=B^m\ast log(1+\frac{p^m{h}^m}{{\sigma }^2{d}_{i,j}})i,j=1,2,3,\dots ,N$$

(1)

where $d_{i,j}$ denotes the distance between node $V_i$ and node $V_j$. $B^m$ and ${\sigma }^2$ denote the system bandwidth and noise power at the mobile devices, respectively. $p^m$ denotes the transmission power, and $h^m$ is the channel power gain of mobile device m. When $m=i$, this formula represents the sending data rate; or when $m=j$, $S_{i,j}^m$ is the receiving data rate. Consequently, the transmission time on this link can be given by:

$$T_{i,j}^m=\frac{I_{i,j}}{S_{i,j}^m}i,j=1,2,3,\dots ,N$$

(2)

and also the energy consumption of the mobile device can be given by:

$$E_{i,j}^m=p^m\frac{I_{i,j}}{S_{i,j}^m}i,j=1,2,3,\dots ,N$$

(3)

In this study, both sending and receiving energy consumption adopt the above model. When it denotes the sending energy consumption, the bandwidth and the power are the parameters of the sending device; when it indicates the receiving energy consumption, we use the channel state information of the receiving node to calculate. According to the actual application, the energy consumption weight between any two points in the network topology is the sum of the sending and the receiving energy consumption.

3.3. Delay Model

The time delay of links generally consists of propagation delay, transmission delay, and queuing delay. Propagation delay is determined by link length, namely the physical distance between two points. The capacity of the bottleneck link on the path has a significant impact on the transmission delay. The queuing delay is related to the load of the network and the burst of information flow. In this paper, the link delay only considers the propagation delay and the transmission delay, where the transmission delay is calculated according to Formula (2). The propagation delay is defined as follows:

$$t_{i,j}=\frac{d_{i,j}}{v}i,j=1,2,3\dots N$$

(4)

where v denotes the propagation rate of packets on the channel; to simplify the analysis, we assume that the value between any two devices is a constant. Therefore, the delay model can be expressed as follows:

$$T_{i,j}^{total}=\frac{I_{i,j}}{S_{i,j}^i}+\frac{I_{i,j}}{S_{i,j}^j}+\frac{d_{i,j}}{v}i,j=1,2,3\dots N$$

(5)

Here, assuming that the size of transmitted packets is $I=500$ KB, we can obtain the network topology with 25 nodes as shown in Figure 2. Moreover, energy consumption and delay between two points are recorded on each link.

4. Strategy of Communication Path Selection

The paper studies the routing under the SDMWN environment, in order to get transmission paths for several users at the same time to minimize the global energy consumption with the premise of satisfying the QoS. In addition, the routing algorithm requires each mobile device to provide only one user with transmission service. Hence, if each user directly chooses the delay constrained least cost path, it may not satisfy the condition that the node has no duplication. In this section, we firstly introduce the LARAC algorithm, which can solve the delay constrained least cost path problem in polynomial time. Then, by integrating LARAC and K-Dijkstra, we propose a K-LARAC algorithm to get the top K energy-minimum paths that satisfy the QoS as the alternative path set for each user. Afterward, an improved genetic algorithm is used to select the paths from each set to obtain the routing strategy. According to the solving process, the pseudocode of the method can be describe indetail in Algorithm 1:

Algorithm 1 K-LARAC and Genetic Algorithm (KLG)

Input:  A graph $G=(V,E)$, each edge e with energy consumption $c\left(e\right)$ and delay $d\left(e\right)$, a given delay constraint $D_i\in Z^{+}$, $i=1,2,\dots ,M$. Output:  Global c-minimal paths between the nodes $s_i$ and $t_i$.

1: procedure KLG ($s_i$, $t_i$, c, d, ${\Delta }_{delay}$) 2:       repeat 3:             $S_i$ = K-LARAC ($s_i$, $t_i$, c, d, ${\Delta }_{delay}$) 4:              $i=i+1$ 5:       until $i=M$ 6:       result = GA ($S_1$, $S_2$, …, $S_M$, c) 7: end procedure

In the pseudocode of the method, M denotes the number of users, and $S_i$ is the alternative path set for user i. Therefore, the rest of this section introduces LARAC, K-LARAC, and the genetic algorithm in turn.

4.1. Lagrange Relaxation-Based Aggregated Cost

The optimal algorithm, as the name implies, always finds the optimal path with cost $z_{opt}$. Since the DCLC problem is NP-hard, it cannot find the optimal solution in polynomial time. If the algorithm always finds a feasible solution (if it exists), then the algorithm is said to be complete. Completeness does not imply optimality, but it is acceptable. In this paper, the LARAC algorithm is selected as the main routing algorithm, because it has the following properties [26]:

• In the network topology, as long as the target path can be obtained, the path always satisfies the delay constraint.
• The algorithm can be solved in polynomial time.
• It is impossible to provide general theoretical guarantees for finding the optimal cost path, but the algorithm gives the lower bound of the optimal cost. The difference between the two is within the acceptable range, so as to ensure the high quality of the result.
• The algorithm not only applies to a single QoS constraint, but also can be extended to study multiple QoS requirements.

4.1.1. Problem Formulation

With the analysis of the problem and the construction of the parameter model, the routing of a single user is described formally as follows:

$$min\{e\left(p\right):p\in P(s,t)andd\left(p\right)\le {\Delta }_{delay}\}$$

(6)

The problem is a typical NP-hard problem, and P (s, t) is the set of paths from the source node s to the destination node t. Unless P = NP, the optimal solution cannot be obtained in polynomial time under the existing constraint. In this case, we can try to get the maximum lower bound of all the solutions and find an approximate solution path that satisfies the constraint. Lagrangian relaxation is a common method to calculate the lower bound, which can be used to find the optimal parameter between two variables. The proportion of energy consumption and delay in the aggregate cost is adjusted on the basis of the residual time, which greatly reduces the difficulty of solving the problem and makes it possible to find the optimal solution in polynomial time after reducing some constraints.

Therefore, Lagrange relaxation-based aggregated cost (LARAC) is proposed, and this algorithm uses parameter $\lambda$ to aggregate energy and delay: $C_{\lambda }=c+\lambda ·d$. For a given $\lambda$, we can easily calculate the minimal path $\left(p_{\lambda }\right)$. If $\lambda$ = 0 and $d\left(p_{\lambda }\right)\le {\Delta }_{delay}$, we find an optimal solution for the original problem. If $d\left(p_{\lambda }\right)>{\Delta }_{delay}$, we must increase $\lambda$, which increases the weight of delay in the aggregate cost and penalizes the infeasibility of the solution. By adjusting $\lambda$, the time delay is reduced, while the energy consumption is increased until the delay constraint is satisfied. According to the brief analysis of the algorithm, the most vital step to obtain the optimal solution under constraints is to calculate the value of $\lambda$. Hereby, the next step is to introduce the process of solving $\lambda$. Above all, the original problem can be described as:

$$E=min\left\{e\right(p):p\in P(s,t\left)\right\}$$

(7)

$$s.t.d\left(p\right)\le {\Delta }_{delay}$$

(8)

The main idea of the Lagrangian relaxation algorithm is to build a function with $\lambda$, which is a parameter for the control constraints of the original problem. Hence, for a given $\lambda \ge 0$, the Lagrange relaxation of $\lambda$ is defined as:

$$L\left(\lambda \right)=min\{e\left(p\right):p\in P(s,t)\}+\lambda (d\left(p\right)-{\Delta }_{delay})$$

(9)

Let $p^{\ast }$ denote an optimal solution of Formula (6), then we can get Formula (9) $\le c\left(p^{\ast }\right)$. A feasible solution that satisfies Formula (8) naturally satisfies Formula (9), which indicates that Lagrangian relaxation is the lower bound of the original problem. We need to maximize the function $L\left(\lambda \right)$ by solving the following formula:

$$L^{\ast }=maxL\left(\lambda \right)$$

(10)

On account of the fact that solving the dual problem does not necessarily optimally solve the primal problem, we say that there is a duality gap. What we get is the boundary of the solution; this means how far away the optimal solution is. Formula (9) is known as the Lagrangian dual of the original problem, and we can use it to obtain an approximate optimal value, which is the lower limit of the path with the lowest energy consumption under the constraints. The key issue in solving this problem is how to search for the optimal $\lambda$ and set the appropriate termination conditions.

4.1.2. Algorithm Description

In the LARAC algorithm, $Dijkstra(s,t,c)$, $Dijkstra(s,t,d)$ and $Dijkstra(s,t,c_{\lambda })$ denote, respectively, Dijkstra’s shortest path algorithm using link costs, link delays, and aggregated link costs with respect to the multiplier $\lambda$.

In the process of solving the target path, the first step is to set $\lambda =0$ and use the algorithm to calculate the shortest path $p_c$ of the original cost c. Once the found path meets the delay constraint, the algorithm terminates with the success of finding the optimal solution. If not, the algorithm saves and records the path $p_c$ as the best path that does not satisfy ${\Delta }_{delay}$. In order to check whether there is an appropriate solution, the shortest path $p_d$ of the delay d is calculated. If the obtained path exceeds ${\Delta }_{delay}$, there is no suitable path from s to t that satisfies the delay requirement, and the algorithm stops with failure. Otherwise, it indicates that a feasible solution exists, and we store the path $p_d$.

The steps of the path selection algorithm under the delay constraint are introduced indetail in Algorithm 2:

Algorithm 2 Lagrange Relaxation based Aggregated Cost

Input:  A graph $G=(V,E)$, each edge e with energy consumption $c\left(e\right)$ and delay $d\left(e\right)$, a given delay constraint $D\in Z^{+}$. Output:  A c-minimal path between the nodes s and t.

1: procedure LARAC (s, t, c, d, ${\Delta }_{delay}$)   2:       $p_c$ = Dijkstra(s, t, c)   3:       if $d\left(p_c\right)\le {\Delta }_{delay}$ then   4:             return $p_c$   5:       end if   6:       $p_d$ = Dijkstra(s, t, d)   7:       if $d\left(p_d\right)>{\Delta }_{delay}$ then   8:             return “There is no solution”   9:       end if 10:       loop 11:             $\lambda =\frac{c\left(p_c\right)-c\left(p_d\right)}{d\left(p_d\right)-d\left(p_c\right)}$ 12:             r = Dijkstra(s, t, $c_{\lambda }$) 13:             if $c_{\lambda }\left(r\right)=c_{\lambda }\left(p_c\right)$ then 14:                  return $p_d$ 15:             else if $d\left(r\right)\le {\Delta }_{delay}$ then 16:                  $p_d=r$ 17:             else 18:                  $p_c=r$ 19:             end if 20:       end loop 21: end procedure

Next, we need to calculate $\lambda$ from Formula (10) and get the aggregated cost $c_{\lambda }$. With this value of $\lambda$, we can find a new $c_{\lambda }$-minimal path r. By comparison, if $c_{\lambda }\left(r\right)=c_{\lambda }\left(p_c\right)=c_{\lambda }\left(p_d\right)$, we will obtain the optimal $\lambda$ as proven in [27]. Otherwise, set r as the new $p_c$ or $p_d$ according to whether r is infeasible or feasible.

$$\lambda =\frac{c\left(p_c\right)-c\left(p_d\right)}{d\left(p_d\right)-d\left(p_c\right)}$$

(11)

4.2. K-LARAC Algorithm for Multiple Shortest Paths under Constraints

In order to get the alternative path set for each user, we combine the LARAC algorithm with K-Dijkstra to develop the K-LARAC algorithm to obtain the top K energy-minimum paths that can meet the delay constraints between nodes.

As is known to all, multi-path induction is an extension of the shortest path problem, which can generate corresponding subgraphs by deleting edges. The K-shortest-paths algorithm of Dijkstra can be called recursively to find K paths from the origin to the sink. In addition, the method based on the first $K-1$ shortest paths and its adjacent points is also feasible. However, these algorithms do not utilize the information of shortest paths between the starting point and the ending point, so the efficiency of searching K paths is low. In this paper, edges in the shortest path are deleted successively, and then, the LARAC algorithm is called to get the paths to meet the requirements.

The algorithm for solving K-shortest-paths with constraints between two points is composed of the following steps:

• Use the LARAC algorithm to find the shortest path from the starting point $\left(SourceVertex\right)$ to the ending point $\left(DestinationVertex\right)$, and this path is denoted as the first short path (FSP). Then, the number of nodes in the path is calculated as $n=length\left(FSP\right)$, which shows that the number of edges in the shortest path is $n-1$.
• Delete the last edge in the shortest path, that is set $Energy\left(P\right(n-1),P(n\left)\right)=inf$. Then, the LARAC algorithm is called again to find the new shortest path that meets the delay constraint. If the path exists, it is saved and recorded as $ks{p}_i$; where $Energy$ is a two-dimensional matrix storing the energy consumption model to record the current network topology and $ks{p}_i$ represents the a sub-optimal path i.
• Delete the second-to-last edge in the shortest path, that is set $Energy\left(P\right(n-2),P(n-1\left)\right)=inf$, and do the same as above to find the new shortest path. If the path exists, we save it.
• By analogy, until the first edge is deleted, $(n-1)$ paths that satisfy the delay constraint can be obtained.
• The paths are sorted in accordance with the energy consumption value from small to large, and the top K paths are selected as the alternative paths between the node pairs.

At this point, we have the K-shortest paths of a user. Next, the K-LARAC algorithm is used to find the alternative path sets for M users, that is M alternative path sets can be obtained. The alternative path set of user i can be represented as follows:

$$S_i=\{p_i^1,p_i^2,\dots ,p_i^K\}i=1,2,\dots ,M$$

(12)

where $p_i^1$, $p_i^2$, and $p_i^K$ all meet the constraint $D_i$ of user i, and the corresponding energy consumption values of these paths are from small to large. Since our purpose is to solve the global routing strategy of minimum energy consumption for multiple users, the next step is to choose one path from each user’s alternative path set to form a routing scheme that cannot only achieve the minimum energy consumption, but also ensure that there are no repeated nodes in each path.

4.3. Combinatorial Optimization Based on the Genetic Algorithm

With the increment of the scale of the problem, the search space of the combinatorial optimization problem increases sharply. Sometimes, it is difficult to find the optimal solution by the enumeration method. For this reason, people use the genetic algorithm to solve these complex problems, in order to find a satisfactory solution instead of the optimal solution. This paper assumes that the intermediate nodes do not repeatedly provide service for multiple users, in other words, which is the constraint in the combinatorial optimization problem. Therefore, we choose the heuristic genetic algorithm to obtain the routing that meets the conditions and introduce the constraint as penalty into the fitness calculation. On the one hand, the heuristic genetic algorithm can automatically acquire and accumulate knowledge about search space in the search process, and self-adaptively control the search process to obtain the optimal solution. On the other hand, this algorithm does not require continuity or differentiability for objective functions or constraints, as long as the problem is computable. According to the analysis of the combinatorial optimization problem, the problem belongs to integer programming. Therefore, compared with the particle swarm optimization algorithm, the heuristic genetic algorithm is more suitable for our needs.

According to the analysis, the genetic algorithm can be used to optimize the combination of alternative path sets for a large number of users, which is in line with practical application scenarios. The algorithm mainly contains the following concepts [28].

Genes and chromosomes: In the process of solving a practical problem, the first step is to build a mathematical model, that is we map the origin problem to a mathematical problem. The possible solution of the problem is a “chromosome”, which consists of several elements, and each of them is called a “gene” of a chromosome. In this experiment, each chromosome is composed of M genes, which correspond to M users. By setting different values for each gene, the path in the user’s alternative path set is selected for combination. To this end, we describe the problem as follows:

$$min\{c\left(p_1^i\right)+c(p_2^j)+\cdots +c\left(p_M^l\right)\}i,j,l=1,2,\cdots ,K$$

(13)

$$s.t.V_i\ne V_j,\forall V_i,V_j\in p_1^i,p_2^j\cdots ,p_M^l$$

(14)

where K represents the number of paths in each user’s alternative path set and i, j, and l are the superscripts to the paths in this set.

The fitness function is used to measure the quality of a chromosome, namely whether the corresponding solution of the chromosome matches the search criteria. The algorithm carries out n iterations in the running process, and each iteration will generate a number of chromosomes. Then, we use the fitness function to calculate the fitness of each chromosome, eliminate the chromosome with low fitness, and keep the chromosome with high fitness for the next iteration. Since the routing requires no repeat nodes of paths, the fitness function can be divided into two parts: the total cost and the penalty for the infeasible solution. The total cost can be calculated by the energy consumption. Firstly, the energy consumption of the kth routing scheme can be expressed as follows:

$$v_k=c^k\left(p_1^i\right)+c^k(p_2^j)+\cdots +c^k\left(p_M^l\right)i,j,l=1,2,\cdots ,K$$

(15)

Then, the cost of the routing scheme $v_k$ is:

$$f\left(v_k\right)=v_k$$

(16)

For the penalty of the infeasible solution, it should be related to the number of repeated nodes. Let the number of repeated nodes in the combined path be m, then the penalty item can be recorded as $g_k$ and calculated as follows:

$$g_k=\left\{\begin{array}{c}\hfill a,m=0\\ \hfill m\ast n,m\ne 0\end{array}\right.$$

(17)

where n represents the evolution algebra and a is a constant. On the basis of the objective function and penalty function, the fitness of chromosomes can be calculated in the following formula, and $popSize$ denotes the size of the current population:

$$eval\left(v_k\right)=\frac{1}{f\left(v_k\right)·g_k}k=1,2,\cdots ,popSize$$

(18)

Crossover is the process of generating new chromosomes, which involves taking two chromosomes from the previous generation, cutting them off at one point, and stitching them together to form a new chromosome. Among them, the selection of the parent chromosome is not random. Here, the roulette method is adopted for crossing. The fitness probability of each chromosome is calculated by Formula (18), and the chromosome with a larger value is more easily selected.

$$selectionProbability\left(v_k\right)=\frac{eval\left(v_k\right)}{\sum eval\left(v_k\right)}k=1,2,\cdots ,popSize$$

(19)

Mutation: A number of genes need to be selected randomly from the newly-generated chromosome and their values modified. In this way, new genes can be introduced into the existing chromosomes to break through the limitation of the current search and avoid falling into the local optimal solution, which is more conducive to the algorithm finding the global optimal solution. The value of the gene should change in the solution domain to ensure that the mutated chromosome still has the corresponding routing scheme.

Reproduction: The chromosome with higher fitness can be copied directly, which can preserve the excellent chromosome of the previous generation and accelerate the process of searching for the optimal solution.

In addition, the genetic algorithm is better every time it evolves, but it needs to find a balance between the accuracy of the results and the efficiency of execution in practical applications. Therefore, the algorithm can be stopped by limiting the number of evolutions $\left(S\right)$ or the error range of the solution $\left(\sigma \right)$. We take K alternative paths of each user as the input of the genetic algorithm and iterate according to the algorithm flow, so as to obtain the path combination with the global minimum energy consumption that meets the constraints.

5. Experimental Results and Evaluation

In this section, we present the simulations to verify the routing algorithm with minimum global energy consumption under the constraints and evaluate the performance of the proposed algorithm.

Firstly, we give the universal parameter settings for the simulations. For the energy model, we set noise power ${\sigma }^2=10e-9$ and system bandwidth $B=1$ MHZ. The distance between mobile devices follows the uniform distribution with $d_{i,j}$ ∈ [10,20] m. The channel power gain between mobile devices is modeled as $h_i^m$ = ${10}^{-3}{d}_i^{-\alpha }$${\varphi }_i$, where ${\varphi }_i$ represents the short-term fading, which is assumed to be an exponentially-distributed random variable, and $\alpha$ denotes the path-loss exponent and here is set $\alpha =2$.

The settings are used in the simulations in the following subsections unless specified otherwise. To avoid occasionality, the simulations are repeated 100 times for each variable value and we average the result, but the other unfixed parameters are randomly selected according to the above settings every time to simulate the real environment.

5.1. Time Complexity Analysis

Dijkstra is a typical shortest path algorithm, and the complexity of simple Dijkstra is $O\left(n^2\right)$. When solving the single source shortest path in the non-negative weight topology, the running speed outperforms Bellman–Ford (BF), Floyd, and shortest path faster algorithm (SPFA). So do the stability issues. Therefore, we chose LARAC based on Dijkstra as the main algorithm to ensure low time complexity. The simulation in this section is to verify the time complexity of the proposed algorithm in solving multi-user routing problems. For this purpose, we provide three experiments for comparison:

• The proposed algorithm, which combines K-LARAC with the genetic algorithm for path searching, called KLG.
• The K-LARAC algorithm and the full combination algorithm are used to compare the performance of the genetic algorithm.
• The delay-constrained Bellman–Ford (DCBF) algorithm based on Bellman–Ford and the genetic algorithm are used to verify the advantage of K-LARAC.

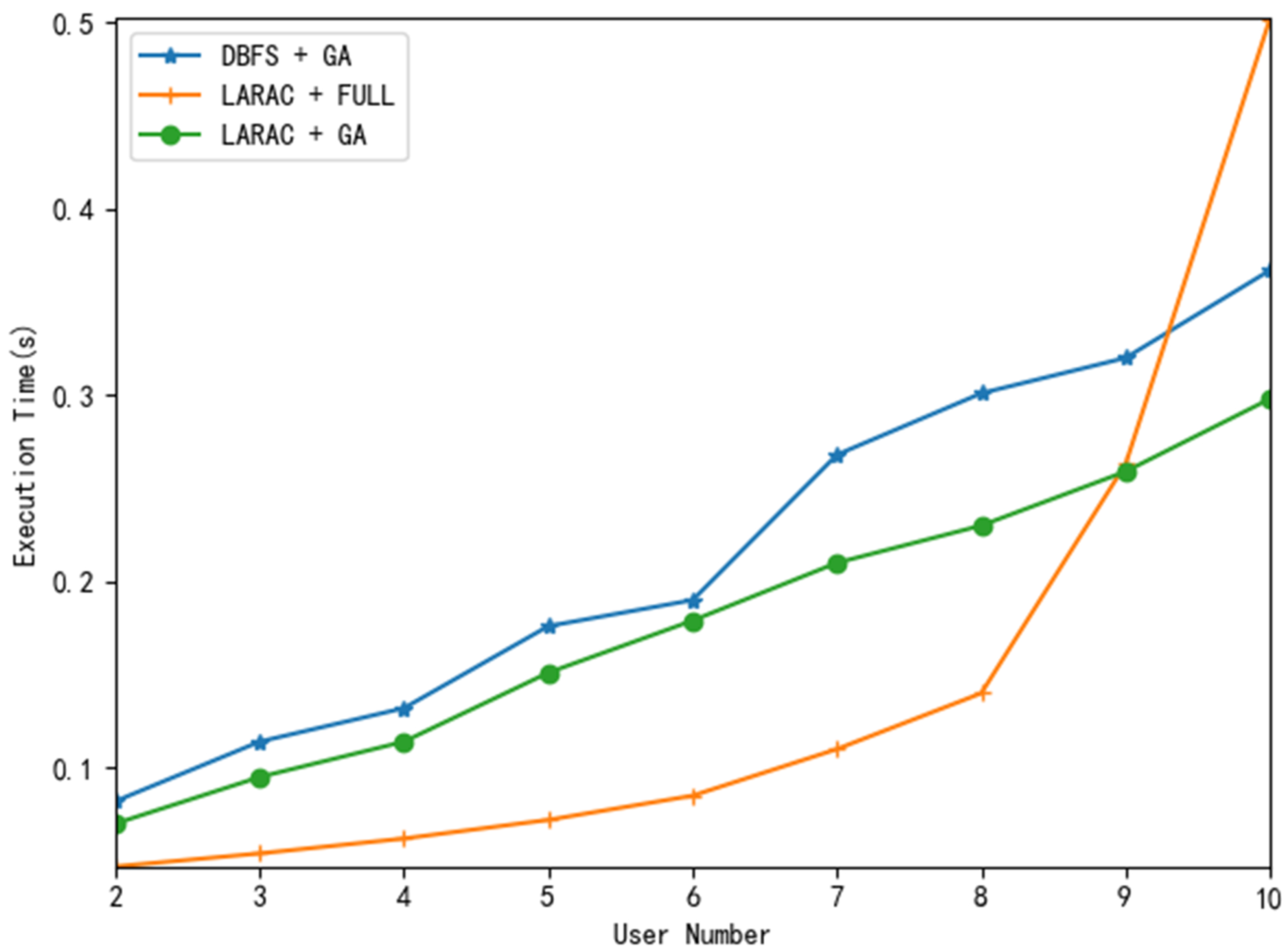
Since the DCBF algorithm needs to compare all the paths that are not larger than the upper limit of delay, we retain the paths that meet the conditions in the search process and rank them from small to large according to energy consumption. By adjusting the number of users, we observe the changes of execution time when they are dealt with by the three methods respectively. Suppose the number of user devices $M=10$ and target devices $T=10$, several intermediate transmission devices, and the number of alternative paths per user $K=3$. In order to ensure the experimental results, we simulated 100 times for each input size, and the results are shown in Figure 3.

By comparing the above experimental results, we know that the full combination can get the optimal solution, but with the increase of the number of users, the time overhead will increase exponentially. At the same time, the processing speed of KLG is also better than the combination of DCBF and the genetic algorithm. This is due to the fact that the average computing time of the genetic algorithm to find the optimal solution does not exceed the square of the scale of the problem, and the full combination needs to traverse $K^M$ solutions. Specifically, we know that the complexity of the Lagrangian relaxation method is $O\left(m^{m}lo{g}^{4}m\right)$ from [29], where m denotes the number of edges. Let the average number of edges in FSP be q. Then, finding the K-shortest-paths is by deleting the edges, and the LARAC algorithm is used q times, so the time complexity of K-LARAC is $O\left(q{m}^{2}lo{g}^{4}m\right)$. The time complexity of getting the alternative path set of M users by K-LARAC is $O\left(Mq{m}^{2}lo{g}^{4}m\right)$. Meanwhile, the average computing time of GA is no more than $O\left(n^2\right)$, where n refers to the scale of the problem, and it is related to the number of users M. Therefore, the time complexity of the KLG algorithm is $O(Mq{m}^{2}lo{g}^{4}m+n^2)$, that is the simplified form is $O\left(M{m}^{2}lo{g}^{4}m\right)$. For the DCLC problem, LARAC processes adjacent nodes step by step from the source point, while constrained Bellman–Ford (CBF) always starts from the source point and has repetitive operations. As you can see, the LARAC algorithm is more efficient and does not repeat processing nodes. Therefore, through cross-validation, we observe that the KLG algorithm can complete the path combination in a relatively short time. Next, we need to verify the accuracy of the algorithm.

5.2. Performance Analysis

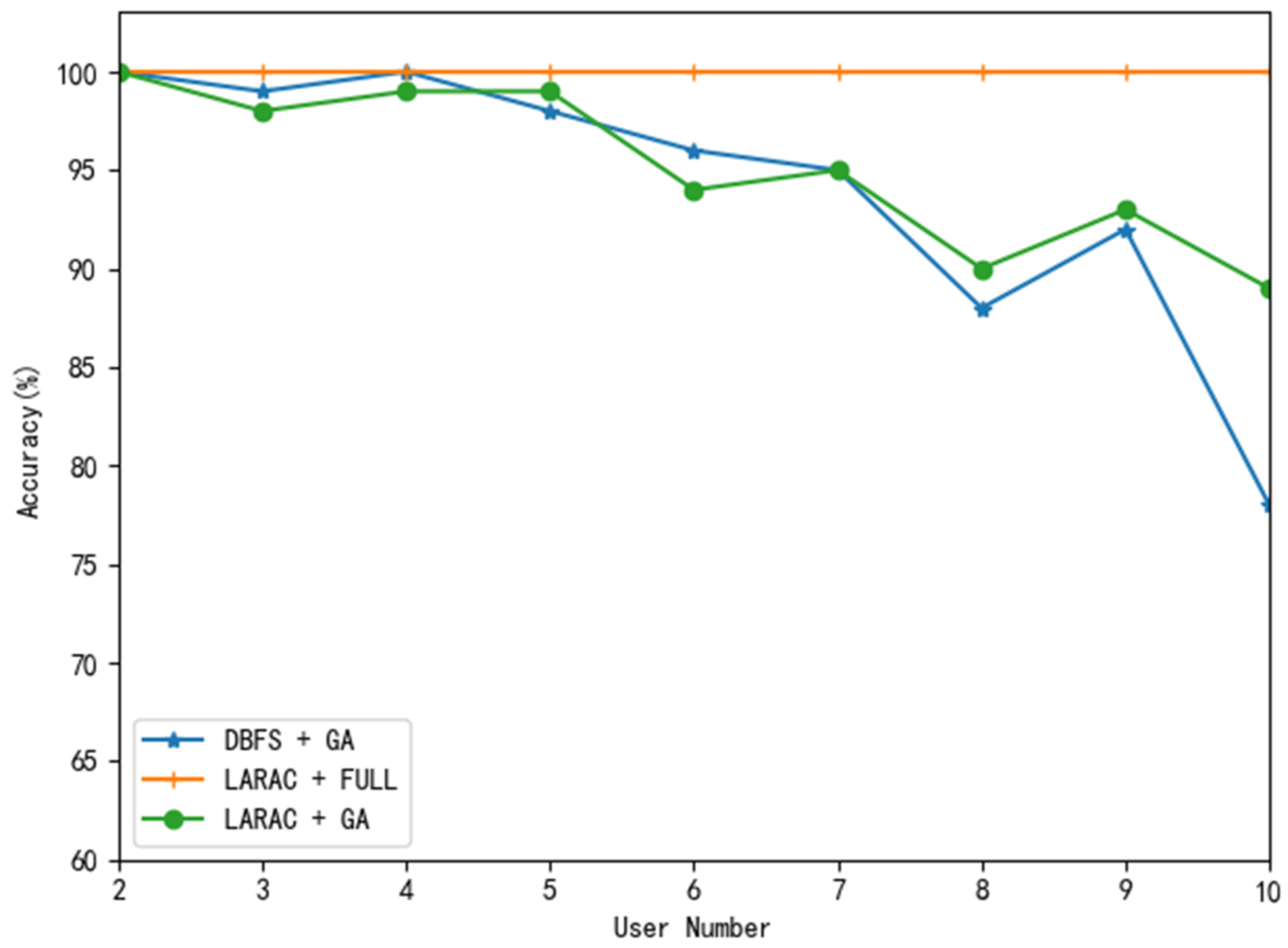
The simulation in this section aims to verify the accuracy of the proposed multi-user routing algorithm. From [30], although there is a duality gap in the LARAC algorithm, this method can give the lower bound of the theoretical optimal solution in polynomial time. In order to prove the good quality of the result, we still use the above methods to compare. The simulation results can be seen in Figure 4.

From the result in Figure 4, we have the observation that the accuracy decreases with the user number increasing, no matter which optimization is adopted, but the proposed KLG still has advantages. Specifically, the accuracy of KLG was still about 90% when the number of users was larger, indicating that KLG has the ability to adjust to larger tasks. As the number of users increases, the number of alternative path sets also increases, which increases the difficulty of solving the optimal combination solution. The improved GA is suitable for finding a satisfactory solution in complex solution space. DCBF selects K-paths with the least energy consumption from all the paths that satisfy the constraints as the alternative path set. It causes the difference of energy consumption between the paths to be slight, so that the local optimal solution is closer to the global optimal solution, and it is more likely to fall into the local optimum to result in a decrease in accuracy. Next, the relationship between total energy consumption and the number of requesting users is simulated to prove that the difference between the solution obtained by KLG and the optimal solution is small. Our results are shown in Figure 5.

Observing the results of the three methods in Figure 5, the total energy consumption increases with the number of requesting users, which is in line with the actual application scenario. As can be seen from the curve in the line graph, when the number of requesting users is small, the search space of the solution is small, and the energy consumption value is almost the same. However, when the number of requesting users increases, the solution space becomes larger, and the accuracy of the solution is lower. Our KLG proposed cannot solve the optimal value accurately, but the error is small compared with the full combination and better than the combination of DCBF and the genetic algorithm. This proves that the proposed KLG can obtain an approximate optimal solution at a lower time cost.

6. Conclusions

With the development of SDN technology and the improvement of service quality, more and more attention has been paid to the construction of constrained SDN path pre-planning. Besides, mobile devices are widely applied, and wireless multi-hop networks are also known as a research hotspot. The combination of the two points provides a favorable network environment for multiple users to transmit data. This paper mainly studies the data transmission path with the lowest global energy consumption for multiple users under the delay constraint.

In this paper, the network model was established by Shannon’s theorem to simulate the routing and links. The energy consumption matrix and time delay matrix were obtained from the initial topology and edge weight dataset. Next, the alternative paths between two points were selected by the K-LARAC algorithm. In the end, the alternative paths of each user were combined by the improved GA to develop the routing strategy that satisfied the global minimum energy consumption and ensured that each intermediate node could only forward data once.

For the QoS routing optimization problem based on SDMWN, it will take much time from theoretical research to technical implementation and practical application, particularly for the research of multi-user service in a large-scale network topology. From now on, the study of the QoS routing algorithm will focus on low computational complexity and high precision in order to better plan the path.