Intelligent Dynamic Data Offloading in a Competitive Mobile Edge Computing Market
Abstract
:1. Introduction
1.1. Related Work
1.2. Contributions and Outline
- The monetary-based pricing of the MEC servers’ computing services, the offered discount to the end-users, the total end-users’ offloaded workload, and the cost of the MEC servers to process the workload are considered towards formulating representative welfare functions for the MEC servers, creating a multi-server competitive computing market. In addition, the end-users’ perceived satisfaction from executing their tasks to the MEC servers is captured in holistic utility functions, while considering the corresponding cost that the end-users have to pay in order to enjoy the requested services (Section 2).
- A reinforcement learning framework is included within the SDN controller’s functionalities towards implementing the MEC server selection by the end-users to offload their data for further processing. The theory of stochastic learning automata is adopted, where the end-users are represented as stochastic agents at the SDN controller, learning the best MEC server selection based on their previous actions and the reaction of the MEC environment. Each MEC server is characterized by a reputation score, which acts as a reward probability to the MEC server selection process. The reputation score captures the discount offered by the MEC server, its congestion in terms of serving end-users’ computing tasks, its penetration in terms of serving the end-users’ computing demands, and its announced pricing for its computing services (Section 3).
- Following the reinforcement learning-based MEC server selection by the end-users, a two-layer optimization problem is formulated and solved aiming at maximizing the MEC servers’ profit and also maximizing the perceived satisfaction by the end-users. The end-users’ maximization problem of their satisfaction is addressed at the first stage as a non-cooperative game among the end-users, who practically aim at maximizing their personal utility function. A Nash Equilibrium (NE) point is determined, which expresses the optimal amount of offloading data for each end-user. At the second stage of the joint optimization problem, given the end-users’ offloaded data, an optimization problem of each MEC server’s profit (as expressed by its welfare function) is formulated and solved by the MEC servers (Section 4).
- An iterative and low-complexity algorithm is introduced to implement the MEC server selection process based on reinforcement learning and determine the optimal MEC servers’ computing services’ monetary pricing and end-users’ optimal data offloading based on game-theoretic and optimization techniques (Section 5).
- A series of detailed simulation experiments are performed to evaluate the performance and inherent attributes of the proposed framework. Furthermore, a comparative study demonstrates its superiority and benefits compared to other relevant alternative strategies (Section 6).
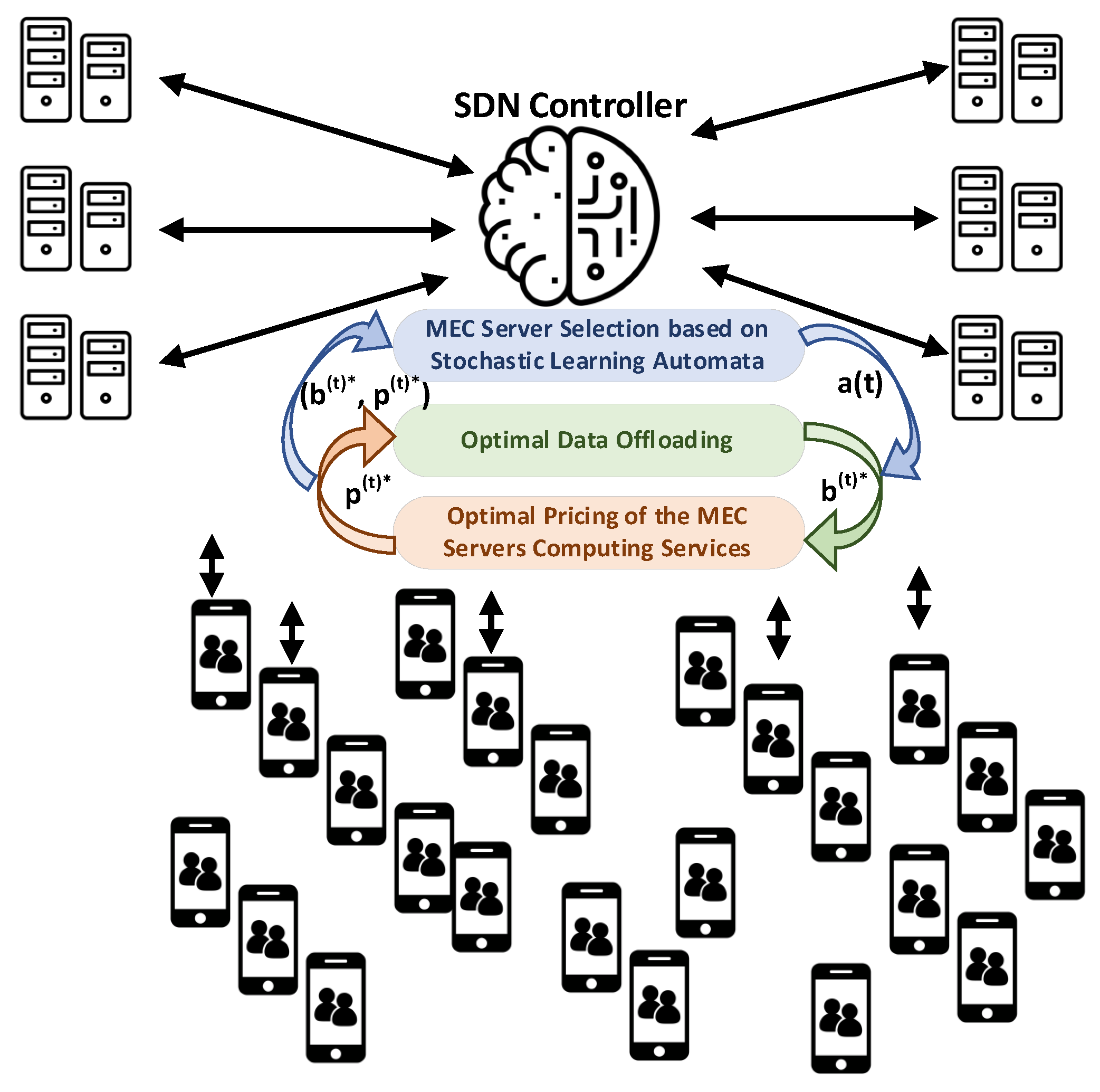
2. SDN-Powered Mobile Edge Computing
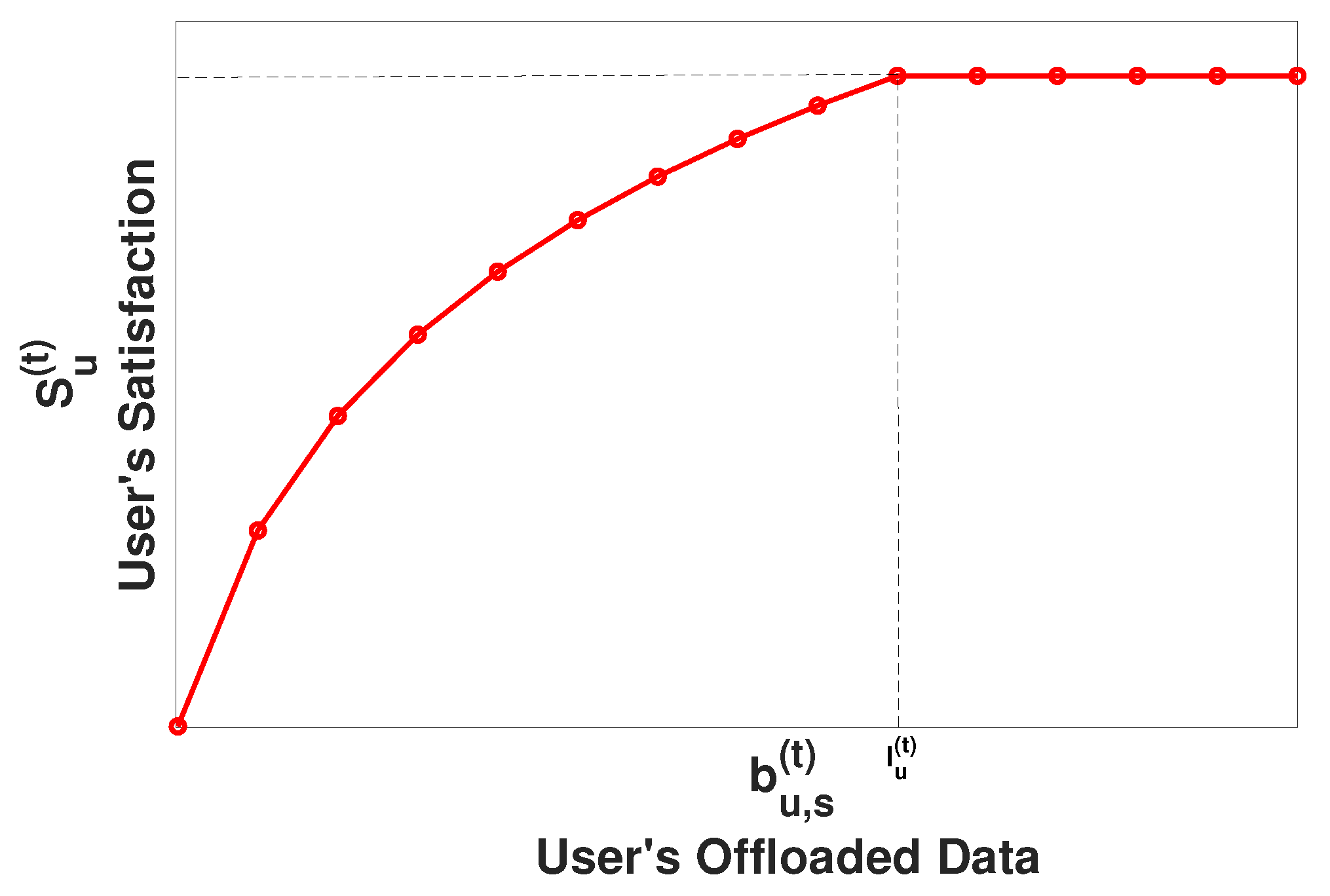
2.1. End-User Utility Function
2.2. Mobile Edge Computing Server Characteristics and Profit
3. MEC as a Learning System
4. Autonomous Data Offloading and Price Setting
4.1. Problem Formulation
4.2. Optimal Data Offloading
- Positivity ;
- Monotonicity: if , then ; and
- Scalability: for all , .
4.3. Optimal Pricing of the MEC Servers Computing Services
5. Data Offloading and MEC Server Selection (DO-MECS) Algorithm
6. Results
6.1. Operation of the DO-MECS Framework
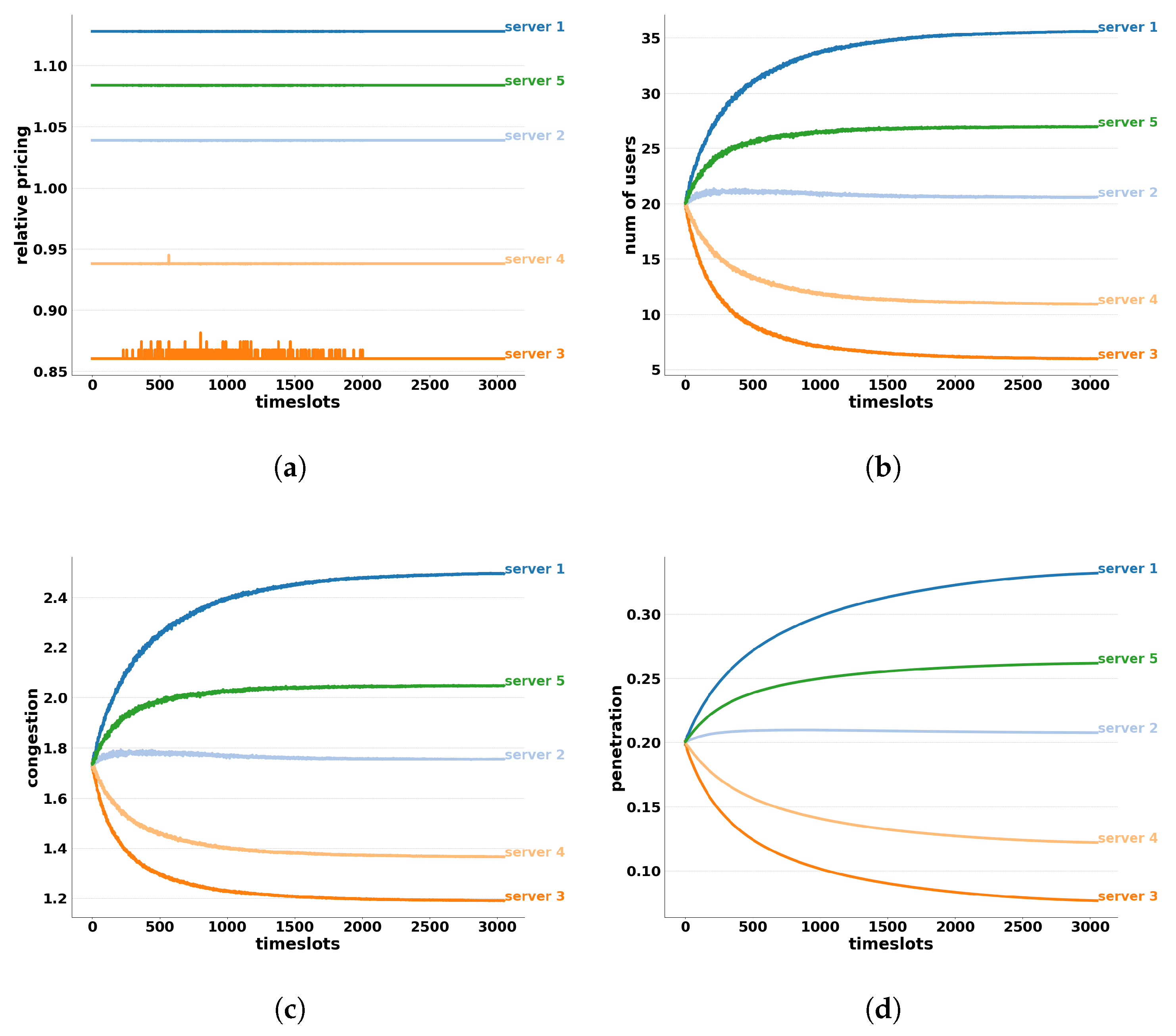
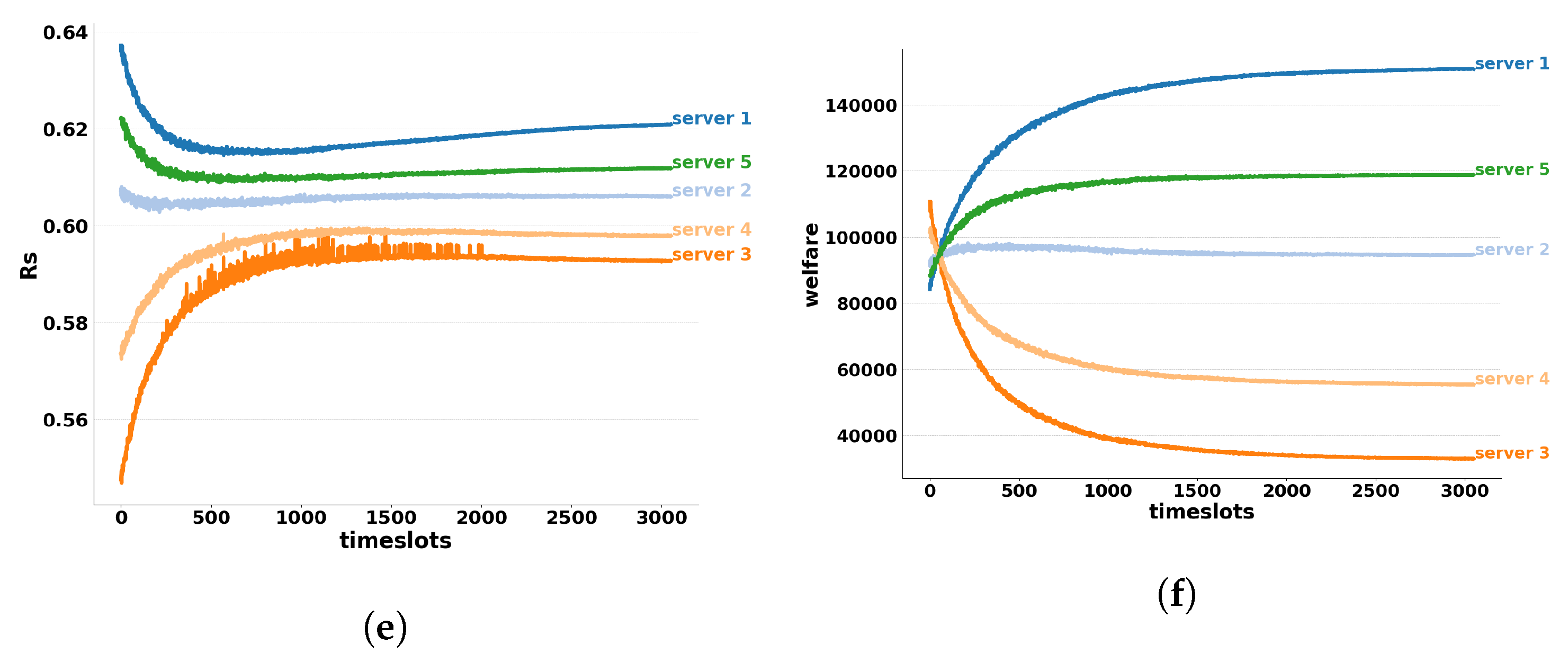
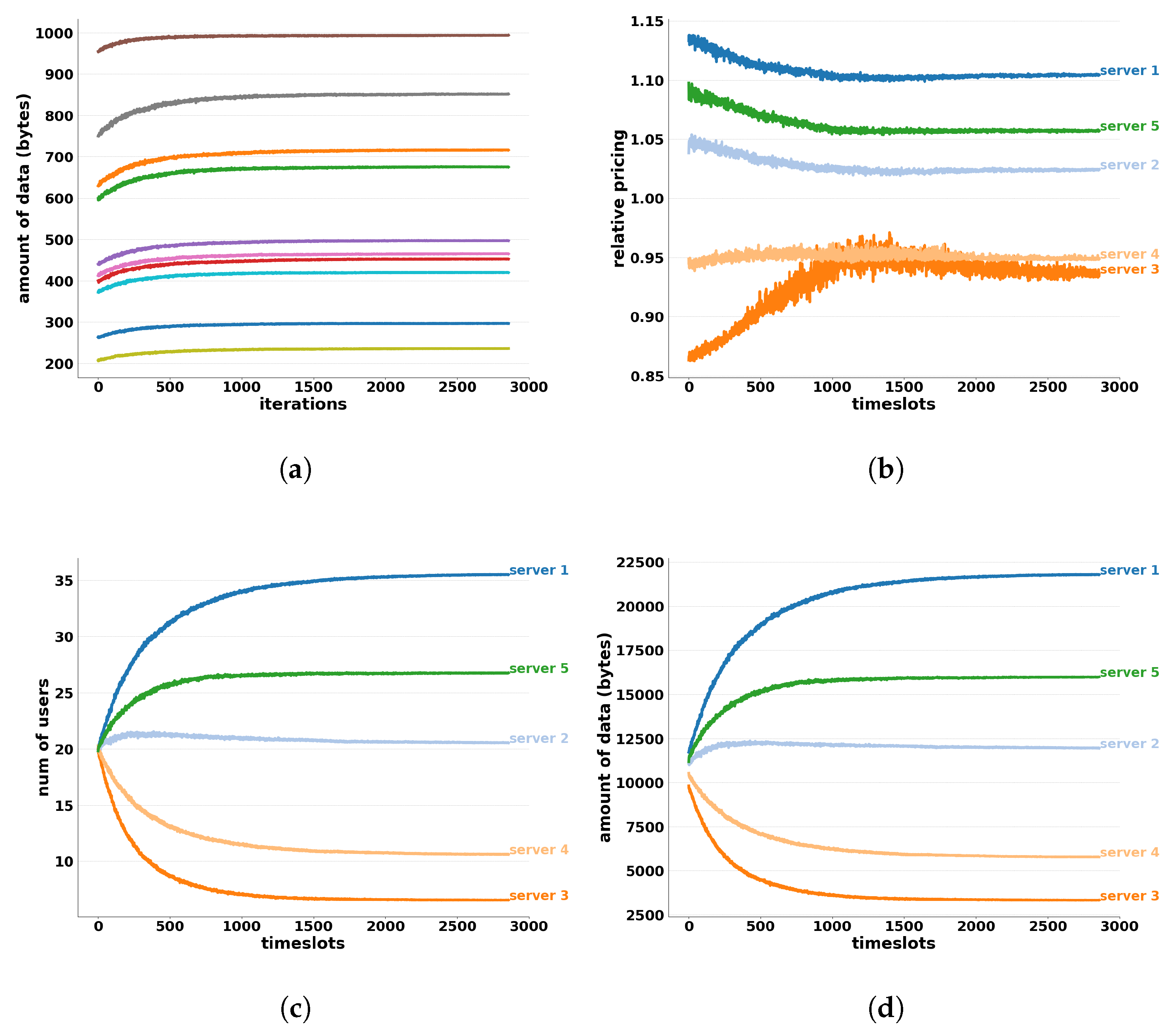
6.1.1. Homogeneous End-Users
6.1.2. Heterogeneous End-Users
6.2. Comparative Evaluation
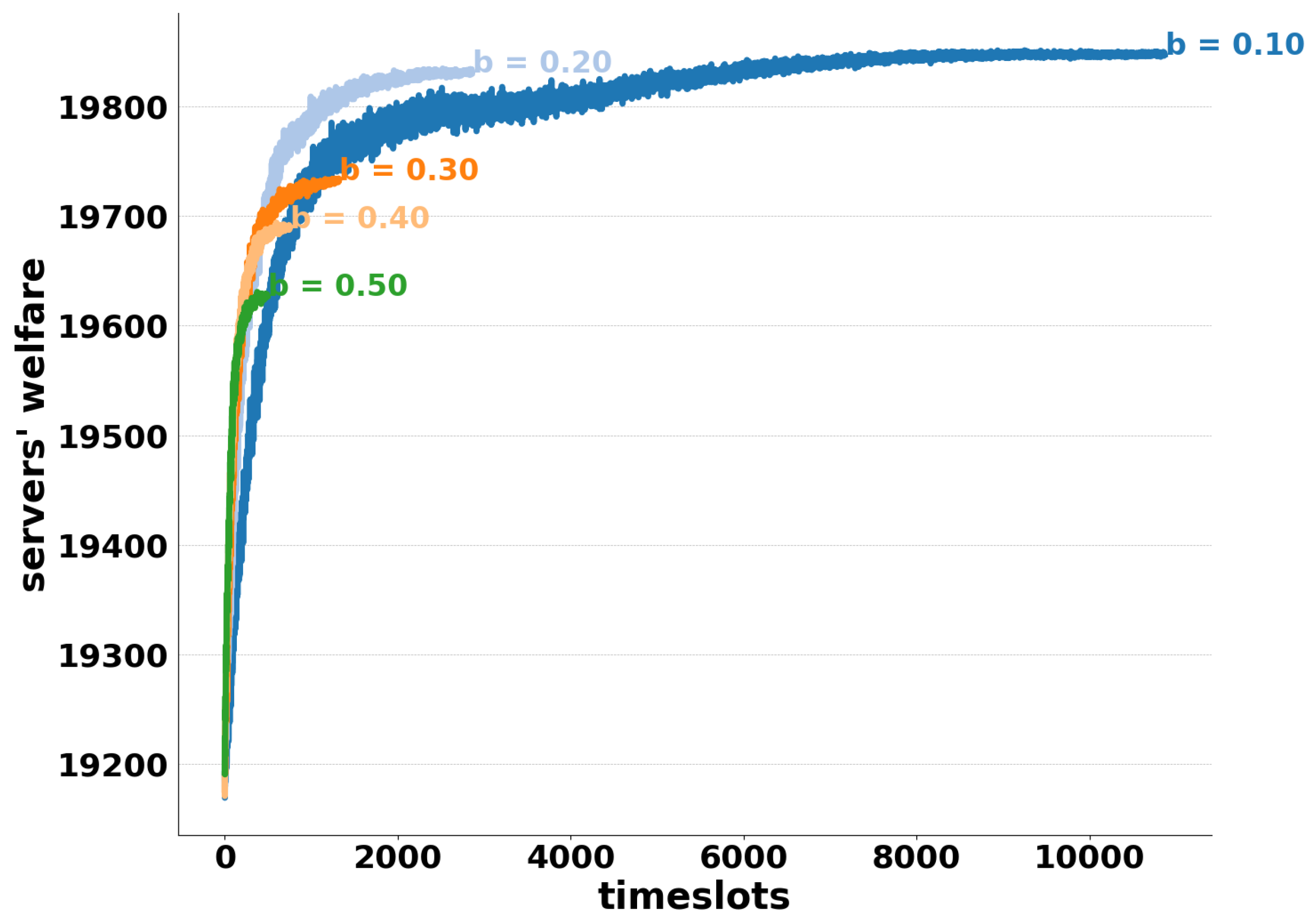
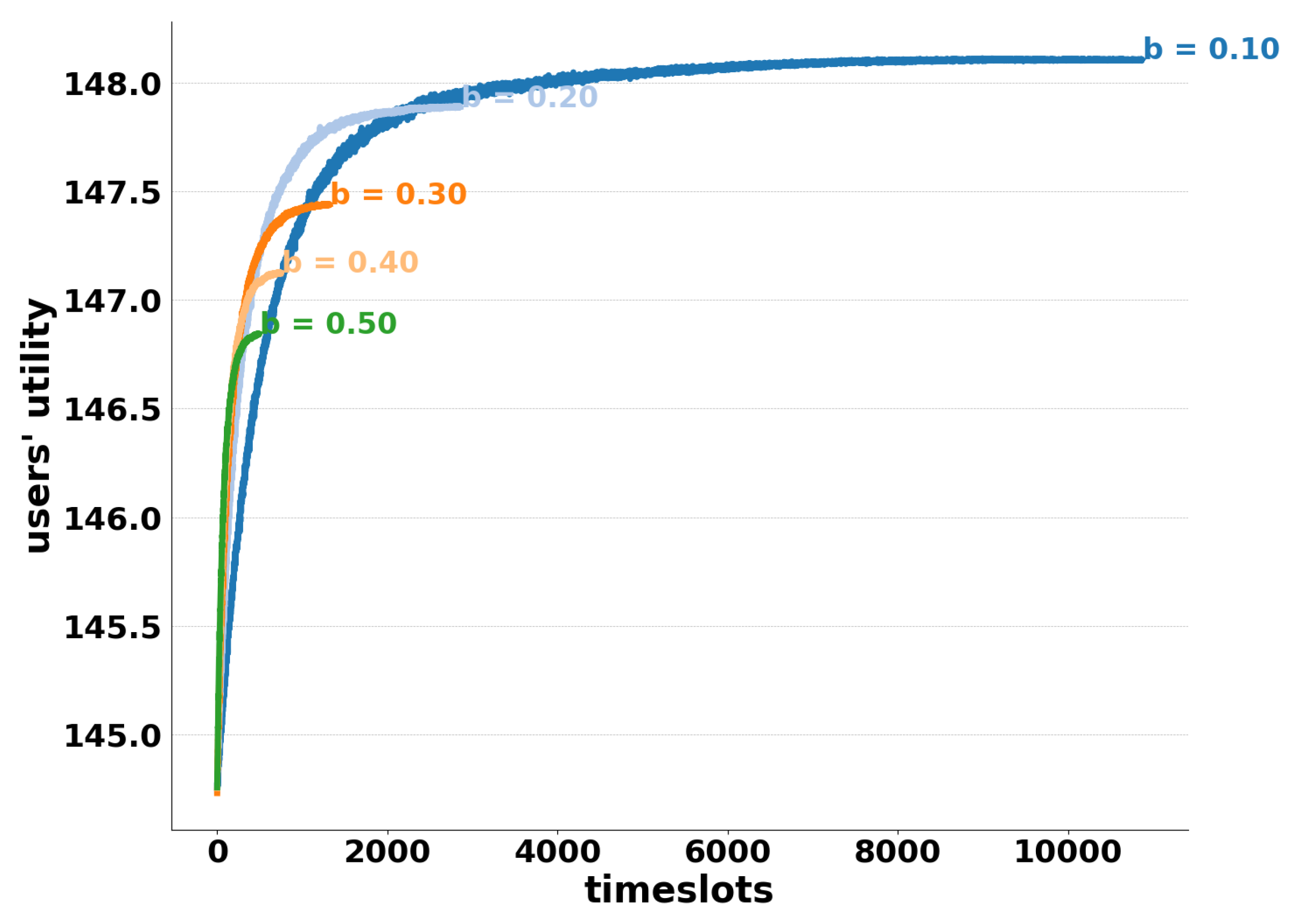
6.2.1. Different Learning Rates
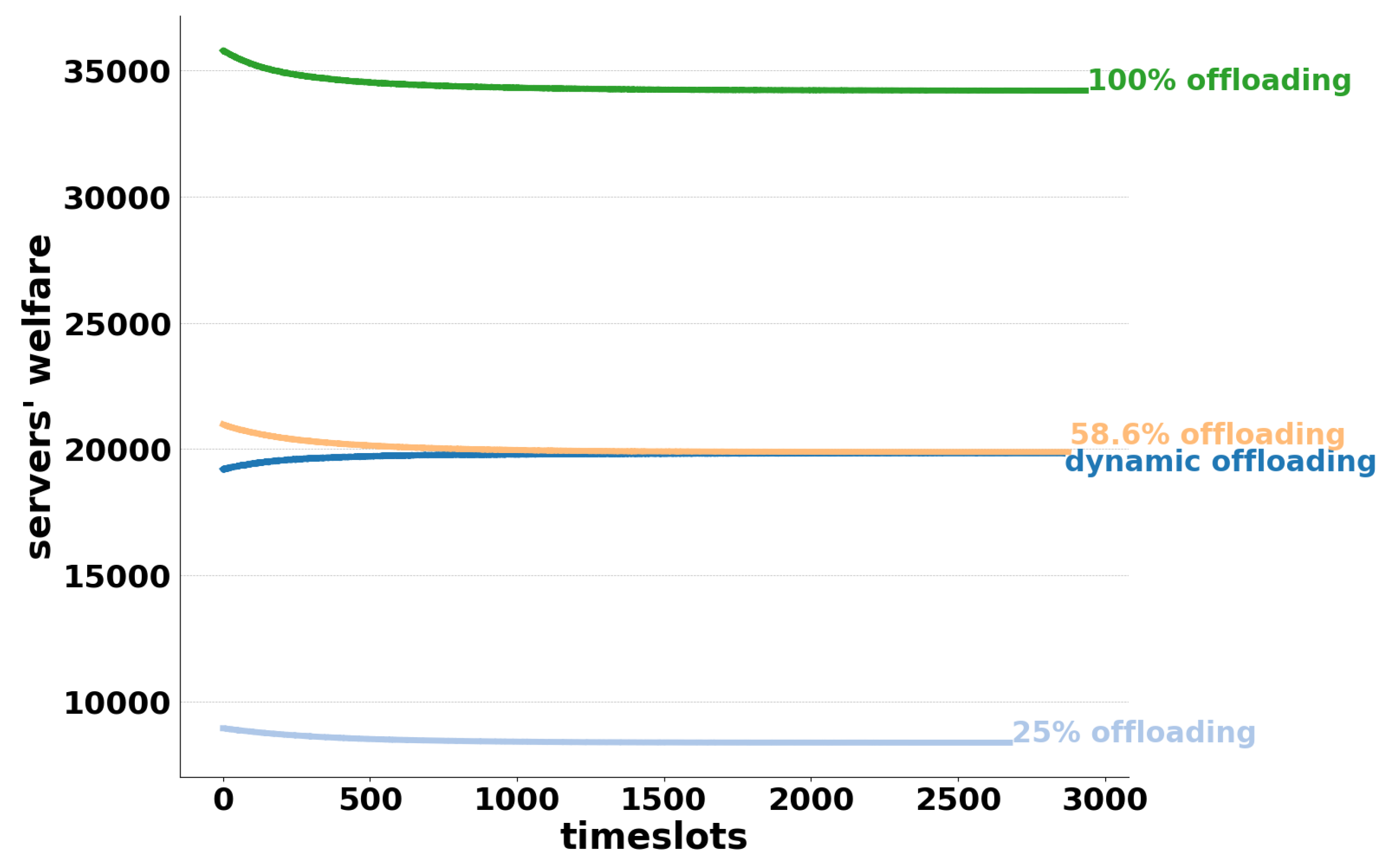
6.2.2. Different Offloading Mechanisms
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barbarossa, S.; Sardellitti, S.; Di Lorenzo, P. Joint allocation of computation and communication resources in multiuser mobile cloud computing. In Proceedings of the IEEE 14th Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Darmstadt, Germany, 16–19 July 2013; pp. 26–30. [Google Scholar]
- Mao, Y.; Zhang, J.; Song, S.; Letaief, K.B. Stochastic joint radio and computational resource management for multi-user mobile-edge computing systems. IEEE Trans. Wirel. Commun. 2017, 16, 5994–6009. [Google Scholar] [CrossRef]
- Munoz, O.; Pascual-Iserte, A.; Vidal, J. Optimization of radio and computational resources for energy efficiency in latency-constrained application offloading. IEEE Trans. Veh. Technol 2015, 64, 4738–4755. [Google Scholar] [CrossRef]
- You, C.; Huang, K.; Chae, H.; Kim, B.-H. Energy-efficient resource allocation for mobile-edge computation offloading. IEEE Trans. Wirel. Commun. 2017, 16, 1397–1411. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, J.; Letaief, K.B. Joint subcarrier and cpu time allocation for mobile edge computing. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Wang, Y.; Sheng, M.; Wang, X.; Wang, L.; Li, J. Mobile-edge computing: Partial computation offloading using dynamic voltage scaling. IEEE Trans. Commun. 2016, 64, 4268–4282. [Google Scholar] [CrossRef]
- Guo, S.; Xiao, B.; Yang, Y.; Yang, Y. Energy-efficient dynamic offloading and resource scheduling in mobile cloud computing. In Proceedings of the 35th Annual IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–14 April 2016; pp. 1–9. [Google Scholar]
- Chen, M.-H.; Liang, B.; Dong, M. Joint offloading and resource allocation for computation and communication in mobile cloud with computing access point. In Proceedings of the IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Chen, X.; Jiao, L.; Li, W.; Fu, X. Efficient multi-user computation offloading for mobile-edge cloud computing. IEEE/ACM Trans. Netw. 2016, 24, 2795–2808. [Google Scholar] [CrossRef]
- Chen, X. Decentralized computation offloading game for mobile cloud computing. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 974–983. [Google Scholar] [CrossRef]
- Jošilo, S.; Dán, G. A game theoretic analysis of selfish mobile computation offloading. In Proceedings of the IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Apostolopoulos, P.A.; Tsiropoulou, E.E.; Papavassiliou, S. Game-Theoretic Learning-Based QoS Satisfaction in Autonomous Mobile Edge Computing. In Proceedings of the IEEE Global Information Infrastructure and Networking Symposium (GIIS), Thessaloniki, Greece, 23–25 October 2018; pp. 1–5. [Google Scholar]
- Zhang, K.; Mao, Y.; Leng, S.; Maharjan, S.; Zhang, Y. Optimal delay constrained offloading for vehicular edge computing networks. In Proceedings of the IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Xie, K.; Wang, X.; Xie, G.; Xie, D.; Cao, J.; Ji, Y.; Wen, J. Distributed multi-dimensional pricing for efficient application offloading in mobile cloud computing. IEEE Trans. Serv. Comput. 2016. [Google Scholar] [CrossRef]
- Jararweh, Y.; Ahmad Doulat, A.D.; Mohammad Alsmirat, M.A.A.; Benkhelifa, E. SDMEC: Software defined system for mobile edge computing. In Proceedings of the 2016 IEEE International Conference on Cloud Engineering Workshop (IC2EW), Berlin, Germany, 4–8 April 2016; pp. 88–93. [Google Scholar]
- Wang, J.; Li, D. Adaptive Computing Optimization in Software-Defined Network-Based Industrial Internet of Things with Fog Computing. Sensors 2018, 18, 2509. [Google Scholar] [CrossRef] [PubMed]
- Porambage, P.; Okwuibe, J.; Liyanage, M.; Ylianttila, M.; Taleb, T. Survey on multi-access edge computing for internet of things realization. IEEE Commun. Surv. Tutor. 2018, 20, 2961–2991. [Google Scholar] [CrossRef]
- Baktir, A.C.; Ozgovde, A.; Ersoy, C. How can edge computing benefit from software-defined networking: A survey, use cases, and future directions. IEEE Commun. Surv. Tutor. 2017, 19, 2359–2391. [Google Scholar] [CrossRef]
- Ali, S.; Ghazal, M. Real-time Heart Attack Mobile Detection Service (RHAMDS): An IoT use case for Software Defined Networks. In Proceedings of the 30th IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Windsor, ON, Canada, 30 April–3 May 2017; pp. 1–6. [Google Scholar]
- Huang, A.; Nikaein, N.; Stenbock, T.; Ksentini, A.; Bonnet, C. Low Latency MEC Framework for SDN-based LTE/LTE-A Networks. In Proceedings of the IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Hossain, M.S.; Xu, C.; Li, Y.; Pathan, A.-S.K.; Bilbao, J.; Zeng, W.; El Saddik, A. Impact of Next-Generation Mobile Technologies on IoT-Cloud Convergence. Commun. Mag. 2017, 55, 18–19. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Kousis, G.; Thanou, A.; Lykourentzou, I.; Papavassiliou, S. Quality of Experience in Cyber-Physical Social Systems Based on Reinforcement Learning and Game Theory. Future Internet 2018, 10, 108. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Vamvakas, P.; Papavassiliou, S. Joint customized price and power control for energy-efficient multi-service wireless networks via S-modular theory. IEEE Trans. Green Commun. Netw. 2017, 1, 17–28. [Google Scholar] [CrossRef]

| Server | Cost c | Discount |
|---|---|---|
| server 1 | 0.12 | 0.05 |
| server 2 | 0.14 | 0.04 |
| server 3 | 0.20 | 0.02 |
| server 4 | 0.17 | 0.03 |
| server 5 | 0.13 | 0.05 |
| Learning Rate | Execution Time (s) | Number of Timeslots |
|---|---|---|
| 147.2 s | 11053 | |
| 27.5 s | 2959 | |
| 11.6 s | 1357 | |
| 6.4 s | 773 | |
| 4.2 s | 504 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitsis, G.; Apostolopoulos, P.A.; Tsiropoulou, E.E.; Papavassiliou, S. Intelligent Dynamic Data Offloading in a Competitive Mobile Edge Computing Market. Future Internet 2019, 11, 118. https://doi.org/10.3390/fi11050118
Mitsis G, Apostolopoulos PA, Tsiropoulou EE, Papavassiliou S. Intelligent Dynamic Data Offloading in a Competitive Mobile Edge Computing Market. Future Internet. 2019; 11(5):118. https://doi.org/10.3390/fi11050118
Chicago/Turabian StyleMitsis, Giorgos, Pavlos Athanasios Apostolopoulos, Eirini Eleni Tsiropoulou, and Symeon Papavassiliou. 2019. "Intelligent Dynamic Data Offloading in a Competitive Mobile Edge Computing Market" Future Internet 11, no. 5: 118. https://doi.org/10.3390/fi11050118
APA StyleMitsis, G., Apostolopoulos, P. A., Tsiropoulou, E. E., & Papavassiliou, S. (2019). Intelligent Dynamic Data Offloading in a Competitive Mobile Edge Computing Market. Future Internet, 11(5), 118. https://doi.org/10.3390/fi11050118







