Abstract
Social networks have attracted a lot of attention as novel information or advertisement diffusion media for viral marketing. Influence maximization describes the problem of finding a small subset of seed nodes in a social network that could maximize the spread of influence. A lot of algorithms have been proposed to solve this problem. Recently, in order to achieve more realistic viral marketing scenarios, some constrained versions of influence maximization, which consider time constraints, budget constraints and so on, have been proposed. However, none of them considers the memory effect and the social reinforcement effect, which are ubiquitous properties of social networks. In this paper, we define a new constrained version of the influence maximization problem that captures the social reinforcement and memory effects. We first propose a novel propagation model to capture the dynamics of the memory and social reinforcement effects. Then, we modify two baseline algorithms and design a new algorithm to solve the problem under the model. Experiments show that our algorithm achieves the best performance with relatively low time complexity. We also demonstrate that the new version captures some important properties of viral marketing in social networks, such as such as social reinforcements, and could explain some phenomena that cannot be explained by existing influence maximization problem definitions.
1. Introduction
The study of the spreading process on social networks has attracted a lot of attention recently for its great practical value in word-of-mouth marketing or viral marketing [1,2]. Domingos et al. [3] and Kempe et al. [4] first treated the viral marketing problem as an influence maximization problem, which chooses a limited number of initial nodes to spread information of a product in a social network such that the resulting number of customers that bought the product is maximized. They discarded some important properties of viral marketing in order to simplify the problem. Recently, some properties, such as time, budget and memory networks, have been carefully studied [5,6,7,8,9]. However, none of that research considered the memory and social reinforcement effects, which are two common and significant characteristics of social networks.
Memory effect means that previous contacts in a social network could affect the information spread in real time [10]. Social reinforcement effect means that if more than one neighbor approves the information and transfers it to you, there is a high probability that you will approve it [11]. For example, in viral marketing, if a person receives a product advertisement recommended by his or her neighbors twice, his/her approval probability for the product should be more than twice as large as the probability with a single recommendation. Once he/she has bought a certain kind of product, the possibility of buying the same product again will be greatly increased.
Online human interactions take place within a dynamic hierarchy, where social influence is determined by qualities such as status, eloquence, trustworthiness, authority and persuasiveness. In this paper, we extend the traditional influence maximization problem to a more realistic viral marketing problem considering memory effect and social reinforcement effect. We first propose a new propagation model, Dependent Cascade Model for Viral Marketing (DCM4VM), to capture the dynamics of memory effect and social reinforcement effect. Then, we present new algorithms to solve the problem under DCM4VM and prove their effectiveness through theoretical and experimental analyses. Finally, we try to explain why the actual effect of current celebrity micro-blogging marketing is not as good as expected through experimental simulation.
The rest of this paper is organized as follows. We introduce related work in Section 2. In Section 3, we propose a novel Dependent Cascade Model for Viral Marketing and redefine the influence maximization problem under the model. Section 4 gives two modified algorithms and a new algorithm to solve the influence maximization problem. In Section 5, we discuss the corresponding experiments. We make some conclusions and describe our future work in Section 6.
2. Related Work
Research in the area of viral marketing [12,13,14,15] takes advantage of social network, wherein friends recommend a product to their friends, who in turn recommend it to others, and so forth, creating a cascade of recommendations. In this way, the ad of the product can spread through the network from a small set of initial nodes to a potentially much larger group.
Domingos and Richardson [3] first formulated viral marketing on social network as an influence maximization problem. They modelled the problem using Markov random fields and proposed heuristic solutions. Kempe et al. [4] studies influence maximization as an optimization problem. They showed that the problem is NP-hard under both Independent Cascade (IC) and Linear Threshold (LT) Models, and proposed a greedy algorithm to solve the problem. In an effort to improve the efficiency of greedy algorithms, Leskovec et al. [16] recognized that not all remaining nodes need to be evaluated in each round and propose CELF. Goyal et al. further proposed CELF++ [17], that has been shown to run from 35% to 55% faster than CELF. Both CELF and CELF++ are based on sub modularity. In [18], Chen et al. studied the efficient influence maximization from two complementary directions. One is to propose New Greedy to improve the original greedy algorithm, and the second is to propose Degree Discount heuristics that improves influence spread. Chen et al. devised several heuristic algorithms for influence spread computation [18,19,20]. In Degree Discount [18], the expected number of additional nodes influenced by adding a node v in the seed set is estimated based on v’s one hop neighborhoods. Chen et al. [21] proposed a new framework, called community-based influence maximization (CIM), to tackle the influence maximization problem with an emphasis on the time efficiency issue. In [19,20], two approximation algorithms, PMIA and LDAG are proposed to compute the maximum influence set under IC and LT models, respectively. In LDAG, it has been proven that under the LT model, computing influence spread in a DAG has linear time complexity, and a heuristic on local DAG construction is provided to further reduce the computation time.
Chen et al. [5] and Liu et al. [6] independently proposed the time-critical influence maximization problem, in which the propagation model considers time constrain. They proved the monotonicity and sub modularity of the time constrained influence spread function and propose algorithms to solve the problem. Li et al. [22] argued that, in more real-world cases, marketers usually target certain products at particular groups of customers. So, they proposed the labeled influence maximization problem, which aims to find a set of seed nodes which can trigger the maximum spread of influence on the target customers in a labeled social network. In order to build a more realistic problem of viral marketing, Huy Nguyen and Rong Zheng further proposed the budgeted influence maximization problem (BIM), which involves selecting a set of seed nodes to maximize the total number of nodes influenced in social networks at a total cost no more than the budget [7]. Amit Goyal et al. studied influence maximization from a novel data-based perspective. They introduced a new model, which is called credit distribution, that directly leverages available propagation traces to learn how influence flows in the network and uses this to estimate expected influence spread [23]. Li et al. [24] proposed a novel network model and an influence propagation model taking influence propagation in both online social networks and the physical world into consideration by using mobile crowd sourced data. Chen et al. [25] proposed an extension to the Independent Cascade Model (ICM) that incorporates the emergence and propagation of negative opinions which is commonly acknowledged in the social psychology literature. Jing Guo et al. [26] studied a new interesting problem on social network influence maximization recently. The problem is defined as, given a target user w, finding the top-k most influential nodes for the user (i.e., local optima). Wang et al. [27] design an independent cascade-based model for influence maximization, called IMIC-OC, to calculate positive influence.
To the best of our knowledge, no existing work on influence maximization considers network dynamic properties such as social reinforcements which are common phenomenon in social network and viral marketing. There are many different types of reinforcement, but when it comes to human beings, one of the most common is the naturally occurring social rein forcers that we encounter all around us every day. Social reinforcement refers to reinforces such as smiles, acceptance, praise, acclaim, and attention from other people. In some cases, simply being in the presence of other people can serve as a natural social reinforcement. Researchers have found that social reinforcement can play a vital role in a variety of areas, including health. The influence of people in our social networks can influence the type of health choices and decisions that we make. Although this simplifies the problem, it results in the disagreement between actual and theoretical situations and discounts the practical value of the theoretical research. Laflin et al. [28]. discuss the temporal nature of viral marketing in practice on big data with a set of visual accompaniments and novel methodology.
Some researchers also view social reinforcement as a type of affinity [29], which develops a dynamical information diffusion model referred the affinity of people; however, the research of reinforcement in the reference [29] is still different from the research in our research, because this method in the reference [29] only considers three kinds of nodes, and the method in this paper consider the spread reasons.
This paper proposes a new propagation model to capture the dynamic changes of memory effect and social reinforcement effect, and improves this model. Experimental results show that the improved model can capture some important features of viral marketing in social networks and explain some phenomena that cannot be explained by the existing definition of impact maximization problem. What’s more, the improved model also has lower time complexity.
3. Influence Maximization under DCM4VM
3.1. Traditional Influence Maximization Problem
Influence maximization is the problem of finding a small subset of nodes (seed nodes) in a social network that could maximize the spread of influence [4,18].
Problem 1. Given a social network modeled as an indirect graph G = (V, E, PE) (vertical V representing the individuals in the network, edges E denoting the relationship between individuals, and edge probabilities PE = {Pu,v|u, v ∈ V} illustrating the possibility that a node can influence its neighbor on the other side of the edge, and Pu,v illustrating the probability of both u and v), a specific propagation model called “M” and a small number called “k”, the influence maximization problem is to find a initial set called “S” with k nodes in the graph such that under the propagation model M, the expected number of nodes influenced by S is as large as possible. Assume (S) represents all influenced nodes, this problem can be formally defined as:
3.2. Dependent Cascade Model for Viral Marketing
Generally, the most commonly used propagation model is Independent Cascade Model (ICM) [13,14]. However, there are only two states considered in ICM, namely active and inactive. In addition, the probability that a node changes from inactive to active is independent of the history of the process. This is insufficient for the actual viral marketing problem. In this paper, we propose a new propagation model, namely Dependent Cascade Model for Viral Marketing which is more suitable for the viral marketing problem, which also could be used for viruses spreading and any other living beings spreading.
We stipulate that each node has five states: unknown, known, interested, accepted and exhausted. In viral marketing, unknown means that the node never heard about the product advertisement; “known” means that the node hears about the advertisement; “interested” means that the node is interested in the product but may or may not buy the product; “accepted” means that the node is interested in the product and purchases it; “exhausted” means that the node never purchases the product and also loses interest in the product.
The state transition process is shown in Figure 1. Initially, most nodes are unknown about the product. And a small subset of initial known nodes tries to propagate the product information to their neighbors. Once known about the information, a node v becomes interested in it with probability Pu,v. The interested node will spread the information to its neighbors and become accepted with probability Pv. After spreading the information, the interested node becomes accepted or exhausted and will not spread it any more.
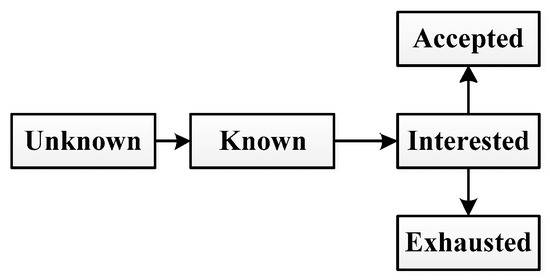
Figure 1.
Dependent Cascade Model for Viral Marketing.
As shown in Figure 1, it doesn’t consider time delay [30], and time delays can be divided into two types, namely, communication delay and processing delay. But In this paper, the propagation problems we study are all concerned with the fact that there is no delay between each node of the network. The research is carried out in the case of average delay, and we will carry out further research in terms of time delay.
We observed that whether a person will buy a product or not relies on two factors: internal factors and external factors. Internal factors reflect a person’s inherent preference for the product. In other words, it is the probability that the person purchases the product without any influence from his/her friends. External factors reflect the effect of outside environment to user purchasing behaviors. For example, social reinforcement effect and memory effect are important external factors. That is, the more friends of a person have bought the product, the more likely the person will buy it.
As shown in Figure 1, at the beginning, the user does not know the product. After the user knows it, he may become interested, and then the user may accept the product.
Formally, for a given node v, the probability Pv(t) that the node v purchases a product at time t is computed as follows [10]:
The components of Function (2) are summarized as follows: is the purchasing probability reflecting the internal factors. m1() and m2() are the numbers of neighbors of node v at state interested and accepted until time t respectively, which reflect the memory effect. r1 > 0 and r2 > 0 are parameters which reflect the social reinforcement effect for interested and accepted states respectively. is the upper bound of the probability indicating maximal purchasing probability, which is used to control the maximal effect of social reinforcement effect and memory effect when increasing m1() and m2(), Pv(t) will gradually approach and the speed is determined by the parameters r1 > 0 and r2 > 0.
3.3. Influence Maximization under DCM4VM
In this section, we will redefine the influence maximization problem under DCM4VM and analysis some properties of the problem.
Problem 2. Given a social network graph G = (V, E, ) (V is the node set, E is the edge set, is the node purchase probability set where denotes node v’s purchase probability, and is the edge influence probability set where represents the influence probability on the edge composed by nodes v and u), At the very beginning, the propagation model DCM4VM with a small number k, on the basis, the influence maximization problem under DCM4VM is to find an initial set S with k nodes in the graph such that the expected sum of accepted nodes is maximized. Assume T is the final time after which the propagation process is completed, is the number of accepted nodes the by the time T, this problem can be formally defined as:
where state (v,t) is the state of node v at time t, N(v) is the outer neighbors of node v.
There may be more than one optimal solution for problem 2. Undoubtedly, problem 2 is NP-hard. NP [31] problems are generally problems where the correctness of the solution can be “easily checked,” where “easily checked” refers to the existence of a polynomial check algorithm. If Turing reduces all problems in NP to a certain problem, the problem is NP-hard.
4. Algorithms
In this section, we try to propose algorithms to solve problem 2. The propagation simulation of problem 2 is quite different from that of traditional influence maximization problem. First, we target at those accepted nodes not all nodes that influenced (interested or accepted). Second, once one round of propagation simulation is completed, we must recalculate . We propose a new propagation simulation method according to DCM4VM. Specially, for each round of propagation simulation, we toss a coin to judge whether the known nodes will turn to interested, then for each node that is interested, we toss a coin again to judge whether this node will turn to state of accepted and finally we recalculate of each nodes according to Function 2 to prepare for the next round of propagation simulation. After R rounds of propagation simulation, we average the total accepted nodes as the expected result . The propagation simulation algorithm for problem 2 is described in Algorithm 1.
4.1. General Greedy Algorithm
The General Greedy [4] can be extended to solve the influence maximization problem under DCM4VM. We consider the expected number of accepted nodes when estimating the influence spread of certain seeds set. Thus, the expected number of influenced nodes in the original algorithm is replaced by . Then the greedy method is the same to select the node which maximizes the marginal gain of influence spread, []. The General Greedy Algorithm is described in Algorithm 2.
| Algorithm 1: Propagation Simulation | |
| Input: network graph, initial seeds Output: accepted seeds number | |
| 1 | , ; |
| 2 | for each nodedo |
| 3 | ; |
| 4 | ; |
| 5 | end |
| 6 | whilenot empty do |
| 7 | ; |
| 8 | ; |
| 9 | //assume all newly interested or accepted nodes spread immediately and simultaneously, is the out neighbors of ; |
| 10 | for each nodedo |
| 11 | for each nodedo |
| 12 | ifthen |
| 13 | continue; |
| 14 | end |
| 15 | ifthen |
| 16 | ; |
| 17 | Ifthen |
| 18 | ; |
| 19 | ; |
| 20 | end |
| 21 | else |
| 22 | ; |
| 23 | end |
| 24 | end |
| 25 | else |
| 26 | ; |
| 27 | end |
| 28 | Ifthen |
| 29 | ; |
| 30 | end |
| 31 | end |
| 32 | end |
| 33 | //whether the newly exposed interested nodes at time t will turn to accepted; |
| 34 | for eachdo |
| 35 | recalculateaccording to (2); |
| 36 | ; |
| 37 | Ifthen |
| 38 | ; |
| 39 | ; |
| 40 | end |
| 41 | end |
| 42 | ; |
| 43 | end |
| 44 | return; |
| Algorithm 2: | |
| Input: network graph, initial seeds size Output: accepted seeds | |
| 1 | Initializeand; |
| 2 | fortodo |
| 3 | for each node vdo |
| 4 | ; |
| 5 | fortodo |
| 6 | ; |
| 7 | |
| 8 | ; |
| 9 | end |
| 10 | ; |
| 11 | end |
| 12 | return; |
4.2. Degree Discount Algorithm
Degree is frequently used for selecting seeds in influence maximization. Chen et al. [18] propose the Degree Discount heuristic to efficiently find the seed nodes. Degree Discount considers only one-step neighbor nodes and selects nodes with high degree values, which tends to have higher expectations of influence, to be seeds.
We modified the Degree Discount heuristic algorithm to solve the viral marketing problem under DCM4VM, described as Algorithm 3. The central idea is to compute and update the expectations of accepted nodes (which is influenced nodes in the original algorithm) in each round of selection considering only one-step neighbor nodes. Once a node is chosen as a seed, we discount the potential (represented as dd in Algorithm 3) of its neighbors to be seeds. Finally, we recalculate each round according to:
| Algorithm 3: | |
| Input: network graph , initial seeds size Output: accepted seeds | |
| 1 | Initialize ; |
| 2 | for eachnodedo |
| 3 | compute its degree ; |
| 4 | ; |
| 5 | Initialize to 0; |
| 6 | end |
| 7 | fortodo |
| 8 | ; |
| 9 | |
| 10 | //recalculate ; |
| 11 | update according to (4); |
| 12 | //discount degree; |
| 13 | for eachnodedo |
| 14 | ; |
| 15 | ; |
| 16 | end |
| 17 | end |
| 18 | return; |
4.3. Exchangeable Greedy Algorithm
Both Greedy Algorithms and Heuristic Algorithms are useful in solving influence maximization problems approximately. Actually, we can further improve the result by combining greedy strategies and heuristic strategies. We use two processes to express that. The first process is to generate potential seeds using heuristic methods and the second process is to exchange some of the seeds iteratively to further approximate the optimum. If the potential seeds set are around the global optimum, we are likely to find the optimal solution finally. The algorithm is described in Algorithm 4.
If m = 1 and S is initialized a set of NULL values of k sizes (line 2), then in the next k rounds from t = 1 to t = k, the Exchangeable Greedy Algorithm picks a NULL out of S and puts a node that maximizes [] to S which is exactly the process done by General Greedy Algorithm. That means Exchangeable Greedy Algorithm, which has better potential performance than General Greedy Algorithm.
However, the time complexity can be very expensive. Some strategies must be used to make the algorithm practical.
We find that most of nodes cannot make any improvement though they all have potentials. Experimental results in [4] showed that selecting nodes with maximum degrees as seeds results in larger influence spread than other heuristics. This is true because most nodes have less out-degrees according to power-law distribution [32] and are less likely to influence many nodes.
| Algorithm 4: | |
| Input: network graph , initial seeds size Output: accepted seeds | |
| 1 | Initialize ; |
| 2 | Initialize with nodes using heuristic algorithms; |
| 3 | whilenot converge anddo |
| 4 | pick one node out of with heuristic strategies or simply by order; |
| 5 | ; |
| 6 | for each node do |
| 7 | ; |
| 8 | for to do |
| 9 | ; |
| 10 | end |
| 11 | ; |
| 12 | end |
| 13 | ; |
| 14 | ; |
| 15 | end |
| 16 | return; |
Heuristic strategies have lower time complexity but are less effective. Greedy strategies are just the opposite. In this paper, we propose to combine heuristic strategies and greedy strategies by two processes, namely Sampling and Verification, to make the algorithm more practical. In each round, we only sample fixed number of candidate nodes (Sampling). Once the candidates are produced, we run greedy algorithm to verify the guess (Verification). Specially, each node is chosen as a candidate with a Potential Probability PP which will be increased or decreased due to its performance.
Initially, the probability PP of each node is set according to its out-degree.
where is the out-degree of node .
Then, is recalculated according to its performance in each round.
where = (S {v}) − (S {u}) is the increased or decreased accepted nodes exchanging u with v. The more potential a node has, the more likely it is to be selected. With enough iteration, every node has the chance to improve the result. The heuristic update strategy of PP is very important. If the strategy is good enough, then it is expected to approximate the optimal solution effectively. This is more like the idea of boosting in machine learning literature which increases the weights of misclassified data and decreases the weights of correctly classified data by last classifier. The Exchangeable Greedy with Sampling and Verification Algorithm is described in Algorithm 5.
| Algorithm 5: | |
| Input: network graph , initial seeds size , number of iterations , number of nodes sampled each time Output: accepted seeds | |
| 1 | Initialize ; |
| 2 | Initialize with nodes using heuristic algorithms; |
| 3 | Initialize according to (5); |
| 4 | whilenot converge anddo |
| 5 | pick one node out of with heuristic strategies or simply by order; |
| 6 | ; |
| 7 | Sampling stage: |
| 8 | sample out of randomly; |
| 9 | Verification stage: |
| 10 | for each node do |
| 11 | ; |
| 12 | Fortodo |
| 13 | ; |
| 14 | end |
| 15 | ; |
| 16 | update according to (6); |
| 17 | end |
| 18 | ; |
| 19 | ; |
| 20 | remove from ; |
| 21 | ; |
| 22 | end |
| 23 | return; |
Time complexities of all algorithms in this paper are summarized in Table 1 for convenience of comparison. N is the number of nodes, E is the number of edges and T is the time complexity of Propagation Simulation. Note that m|n is much less than N usually and the time complexity of EG-SV is independent of the size of the network which means we can apply EG-SV to large networks. Also, we can continue a terminated EG-SV until a good performance is achieved.

Table 1.
Time complexities of algorithms in this paper.
5. Experiment
In order to show the effectiveness of the algorithm proposed in this paper, experiments are carried out to improve the algorithm. We summarize our experiment results for different algorithms and discuss their performance in this section.
5.1. Analysis of DCM4VM
As explained in a comprehensive way, we modified the Degree Discount heuristic algorithm to solve the viral marketing problem under DCM4VM, described as Algorithm 3.
Figure 2 shows the accepted probability as a function of m1 and m2, given different r1 and r2. Larger r1 and r2 indicate stronger social reinforcement. And considering accepted neighbors’ are more influential than interested neighbors’, so r2 should be larger than r1. In this paper, r1 is set to 0.2 and r2 is set to 0.5. and are set to 0.1 and 0.8 respectively, which has been tested many times.
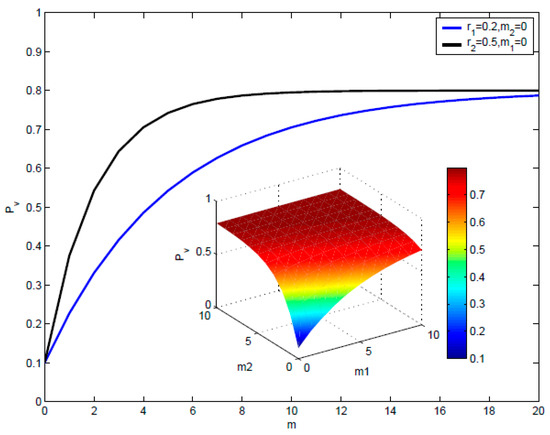
Figure 2.
Accepted probability of Social Reinforcements in DCM4VM.
5.2. Analysis of Algorithms
The networks used in this paper are Arxiv CA-GrQc [4] and NetHEPT [17] which are frequently used in current researches. We use fixed propagation probability P in the experiments. And in order to make the results more discriminative, we set P to 0.05 and 0.1 in CA-GrQc and NetHEPT respectively. For EG-SV, n is set to 100, m is tried from 1 to 5.
The experiment results are shown in Figure 3. GG is too complex to run in NetHEPT. Overall, the performance of EG-SV (m ≥ 2) is almost the same as GG. And for both CA-GrQc and NetHEPT, the results of EG-SV converge reasonably well for m ≥ 2. The results of Degree and DD are worse than those of EG-SV and GG. DD performs much better than Degree in CA-GrQc but sometime performs worse than Degree in NetHEPT. The possible reason may be that we hope the overlaps of all seeds’ propagation coverage areas to be as little as possible in traditional influence maximization problem. However, the propagation coverage overlaps in the new problem may result in more accepted nodes for the affection of social reinforcement effect. So, we encourage propagation coverage overlaps to some extent. As a result, Degree Discount heuristic is not effective anymore and is likely to work even worse than Degree sometimes (see Figure 3d).
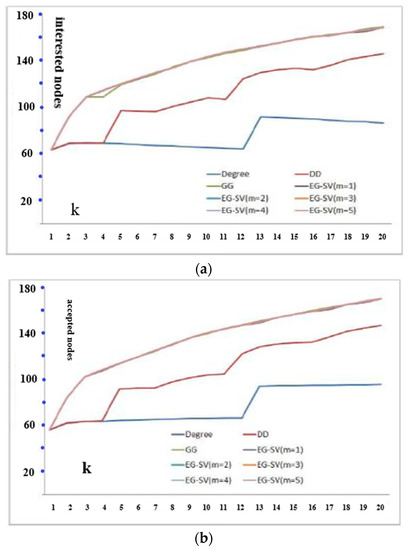
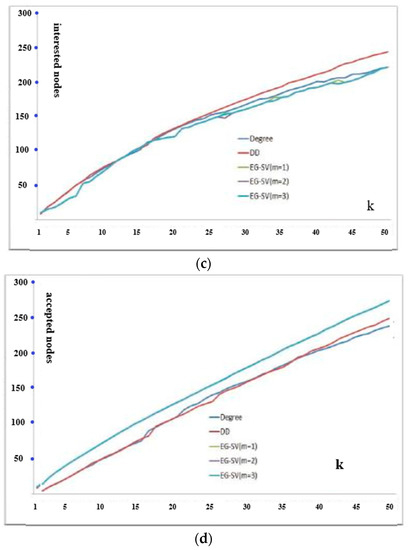
Figure 3.
Interested and Accepted Nodes: (a) Interested Nodes P = 0.05 in CA-GrQc (a,b); (b) Accepted Nodes with P = 0.05 in CA-GrQc (a,b); (c) Interested Nodes with P = 0.1 in NetHEPT (c,d); (d) Accepted Nodes with P = 0.1 in NetHEPT (c,d).
From Figure 3c,d, we can explain a realistic phenomenon in viral marketing that why microblogging marketing through celebrities is not as good as expected usually. Most celebrities have a lot of fans, which means the celebrity nodes in social networks have high out-degrees. Selecting them as the seeds is the same as what Degree heuristic or DD does. Although Degree heuristic or DD can influence a lot of nodes (See Figure 3c, even more than EG-SV), the final accepted nodes of them are much less than that of EG-SV (See Figure 3d). This is because the fans of a celebrity seldom know each other. Most fans only get the information once in the propagation and have less probability to turn to accepted state. In other words, social reinforcement effect can hardly happen during such information propagation process which lowers the number of final accepted nodes.
6. Comparison of Propagation Performance
In order to illustrate the effectiveness of the algorithm proposed in this paper in the propagation process, this part compares the DCM4VM method proposed in this paper with the information spreading model based on relative weight in social network (RWSIR) [33].
6.1. Experimental Data
In this paper, three network topologies of most popular online social network are selected, such as, Twitter [34], sina microblog [35] and Epinions [36], and the relevant data are all from Internet resources [37,38]. We assume that the edges of each network are indirect and powerless, and the relevant topological characteristic parameters of each network are shown in Table 2.

Table 2.
Correlated characteristic parameters of each network.
6.2. Experimental Parameters
In this section, two models, DCM4VM and RWSIR, are simulated in the above three network topological models. A random node with low connectivity is selected as the propagation node, and the rest nodes are healthy nodes. Considering the network sizes, the connection degrees of Epinions network, Twitter network and sina microblog are 5, 10 and 10. It should be noted that, considering the characteristics of the real network, the nodes selection did not select the node with the minimum degree of 1, but the node with a small degree of connection. The basic popularity of information was calculated as , and 100 times for each experiment, then the average value was calculated.
6.3. Evaluation Index
Maximum infection rate (MIR), which is the ratio of the number of infected nodes to the total number of network nodes after the completion of the infection process. Since all infected nodes in the model will eventually become immune nodes, we can consider the proportion of the final immune nodes as the final infection rate. MIR is used to characterize the final influence range of propagation nodes on the entire network.
6.4. Results and Analysis of Experiment
From the experimental results, which are showed in Figure 4, we could see that the value of MIR increases with the increase of λ. Except the MIR of Epinions, Twitter and sina weibo in RWSIR model were between 0.4–0.6, the other MIRs were all close to 1, and the information basically covered the whole network.
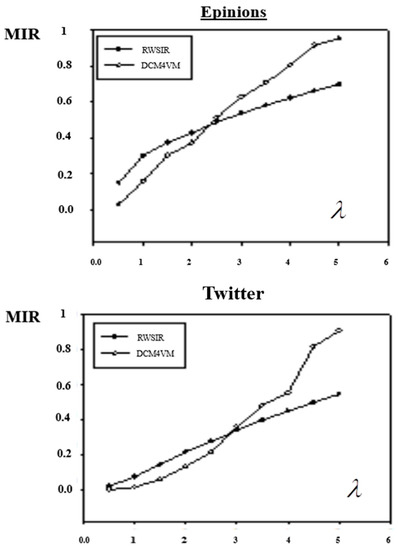
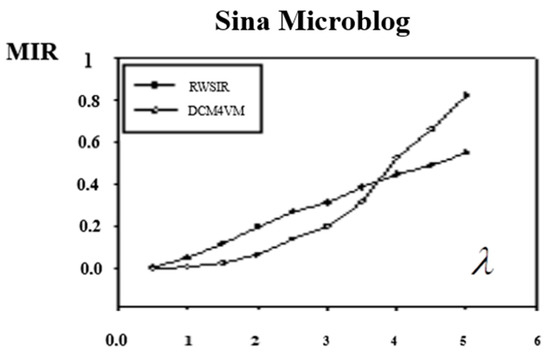
Figure 4.
Comparison in maximum infection rate (MIR).
Compared with the two models, when λ is small, the MIR of RWSIR is lower than DCM4VM, meanwhile, when λ is large, it is the opposite. In other words, with the increase of the importance of the propagation object, the algorithm proposed in this paper could achieve a greater range of influence.
7. Conclusions
This paper proposes a new propagation model to capture the dynamic changes of memory effect and social reinforcement effect, and improves this model. Experimental results show that the improved model can capture some important features of viral marketing in social networks and explain some phenomena that cannot be explained by the existing definition of impact maximization problem. What’s more, the improved model also has lower time complexity. Finally, in order to illustrate the effectiveness of the algorithm proposed in this paper in the propagation process, this paper compares the DCM4VM method proposed in this paper with a method called RWSIR; the result also shows that the method in this paper has a much greater effect.
Although this paper could achieve good results in terms of performance and time complexity, further research and improvements are needed in the following aspects:
- In the degree discount algorithm, a method is adopted to compute and update the expectations of accepted nodes (which is influenced nodes in the original algorithm) in each round of selection considering only one-step neighbor nodes. This calculation method has a certain randomness. In the next step, empirical value and experimental value can be considered to replace the existing method and reduce the complexity of calculation.
- This paper adopts a combination of greedy and heuristic algorithms to improve the problem of impact maximization, and divides the whole process into two parts. In future research, these two parts could be iterated to further improve the effect. This method also has a hidden danger of falling into local optimization. The next step is to consider the most effective method to prevent local entanglement, such as some bionic algorithms.
- The propagation problem studied in this paper does not take into account the time delay. In fact, time delay has a very important impact on this study, which will also be the focus of future research.
Author Contributions
Writing—original draft, F.W.; Writing—review & editing, Z.Z. and P.L.; Data curation, P.W.; Methodology, P.L.; Software, P.W.; Funding acquisition, P.L.; Project administration, Z.Z.; Supervision, P.L.
Funding
This work was supported National Natural Science Foundation (61373148), National Social Science Fund (12BXW040); Science Foundation of Ministry of Education of China(14YJC860042), Shandong Provincial Social Science Planning Project (18CXWJ01, 18BJYJ04, 19BJCJ51).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qiu, X.; Zhao, L.; Wang, J.; Wang, X.; Wang, Q. Effects of time-dependent diffusion behaviors on the rumor spreading in social networks. Phys. Lett. A 2016, 380, 2054–2063. [Google Scholar] [CrossRef]
- Ma, J.; Li, D.; Tian, Z. Rumor spreading in online social networks by considering the bipolar social reinforcement. Phys. A Stat. Mech. Appl. 2016, 447, 108–115. [Google Scholar] [CrossRef]
- Domingos, P.; Richardson, M. Mining the network value of customers. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 26–29 August 2001; pp. 57–66. [Google Scholar]
- Kempe, D.; Kleinberg, J.; Tardos, E. Maximizing the spread of influence through a social network. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 137–146. [Google Scholar]
- Chen, W.; Lu, W.; Zhang, N. Time-critical influence maximization in social networks with time-delayed diffusion process. In Proceedings of the Conference on Artificial Intelligence, Toronto, ON, Canada, 22–26 July 2012; pp. 1–26. [Google Scholar]
- Liu, B.; Cong, G.; Xu, D.; Zeng, Y. Time constrained influence maximization in social networks. In Proceedings of the IEEE 12th International Conference on Data Mining, Brussels, Belgium, 10 December 2012; pp. 439–448. [Google Scholar]
- Nguyen, H.; Zheng, R. On budgeted influence maximization in social networks. IEEE J. Sel. Areas Commun. 2013, 31, 1084–1094. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Z. Information spreading on dynamic social networks. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 896–904. [Google Scholar] [CrossRef]
- Holme, P. Modern temporal network theory: A colloquium. Eur. Phys. J. B 2015, 88, 234. [Google Scholar] [CrossRef]
- Dodds, P.; Watts, D. Universal behavior in a generalized model of contagion. Phys. Rev. Lett. 2014, 92, 218701. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Chen, D.; Zhou, T. The small world yields the most effective information spreading. New J. Phys. 2011, 13, 123005. [Google Scholar] [CrossRef]
- Brown, J.; Reingen, P. Social ties and word-of-mouth referral behavior. J. Consum. Res. 1987, 14, 350–362. [Google Scholar] [CrossRef]
- Goldenberg, J.; Libai, B.; Muller, E. Using complex systems analysis to advance marketing theory development: Modeling heterogeneity effects on new product growth through stochastic cellular automata. Acad. Mark. Sci. Rev. 2001, 9, 1–18. [Google Scholar]
- Goldenberg, J.; Libai, B.; Muller, E. Talk of the network: A complex systems look at the underlying process of word-of-mouth. Mark. Lett. 2001, 12, 211–223. [Google Scholar] [CrossRef]
- Nguyen, H.; Thai, M.; Dinh, T. A billion-scale approximation algorithm for maximizing benefit in viral marketing. IEEE/ACM Trans. Netw. 2017, 25, 1–11. [Google Scholar] [CrossRef]
- Leskovec, J.; Krause, A.; Guestrin, C.; Faloutsos, C.; Van-Briesen, J.; Glance, N. Cost-effective outbreak detection in networks. In Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Jose, CA, USA, 12–15 August 2007; pp. 420–429. [Google Scholar]
- Goyal, A.; Lu, W.; Lakshmanan, L. Celf++: Optimizing the greedy algorithm for influence maximization in social networks. In Proceedings of the 20th International Conference Companion on World Wide Web, Hyderabad, India, 28 March–1 April 2011; pp. 47–48. [Google Scholar]
- Chen, W.; Wang, Y.; Yang, S. Efficient influence maximization in social networks. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 199–208. [Google Scholar]
- Chen, W.; Wang, C.; Wang, Y. Scalable influence maximization for prevalent viral marketing in large-scale social networks. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010; pp. 1029–1038. [Google Scholar]
- Chen, W.; Yuan, Y.; Zhang, L. Scalable influence maximization in social networks under the linear threshold model. In Proceedings of the 10th IEEE International Conference on Data Mining, Sydney, Australia, 13–17 December 2010; pp. 88–97. [Google Scholar]
- Chen, Y.; Zhu, W.; Peng, W.; Lee, W.; Lee, S.Y. Cim: Community-based influence maximization in social networks. ACM Trans. Intell. Syst. Technol. 2014, 5, 25. [Google Scholar] [CrossRef]
- Li, F.; Li, C.; Shan, M. Labeled influence maximization in social networks for target marketing. In Proceedings of the International Conference on Privacy, Security, Risk and Trust, 10th IEEE International Conference on Social Computing, Boston, MA, USA, 9–11 October 2011; pp. 560–563. [Google Scholar]
- Goyal, A.; Bonchi, F.; Lakshmanan, L. A data-based approach to social influence maximization. Proc. VLDB Endow. 2011, 5, 73–84. [Google Scholar] [CrossRef]
- Li, J.; Cai, Z.; Yan, M.; Li, Y. Using crowdsourced data in location-based social networks to explore influence maximization. In Proceedings of the 35th Annual IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–14 April 2016; pp. 1–9. [Google Scholar]
- Chen, W.; Collins, A.; Cummings, R.; Ke, T.; Liu, Z.; Rincon, D.; Sun, X.; Wang, Y.; Wei, W.; Yuan, Y. Influence maximization in social networks when negative opinions may emerge and propagate. In Proceedings of the SDM, Mesa, AZ, USA, 28–30 April 2011; pp. 379–390. [Google Scholar]
- Guo, J.; Zhang, P.; Zhou, C.; Cao, Y.; Guo, L. Personalized influence maximization on social networks. In Proceedings of the 22nd ACM International Conference on Conference on Information & Knowledge Management, San Francisco, CA, USA, 27 October–1 November 2013; pp. 199–208. [Google Scholar]
- Wang, Q.; Jin, Y.; Lin, Z.; Cheng, S.; Yang, T. Influence maximization in social networks under an independent cascade-based model. Phys. A Stat. Mech. Appl. 2016, 444, 20–34. [Google Scholar] [CrossRef]
- Laflin, P.; Mantzaris, A.V.; Ainley, F.; Otley, A.; Grindrod, P.; Higham, D.J. Discovering and validating influence in a dynamic online social network. Soc. Netw. Anal. Min. 2013, 3, 1311–1323. [Google Scholar] [CrossRef]
- Shang, Y. Lie algebraic discussion for affinity based information diffusion in social networks. Open Phys. 2017, 15, 705–711. [Google Scholar] [CrossRef]
- Shang, Y. On the Delayed Scaled Consensus Problems. Appl. Sci. 2017, 7, 713. [Google Scholar] [CrossRef]
- Wang, L. NP-hard [M]. In Encyclopedia of Systems Biology; Dubitzky, W., Wolkenhauer, O., Cho, K.H., Yokota, H., Eds.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Adamic, L.; Huberman, B. Power-law distribution of the world wide web. Science 2000, 287, 2115. [Google Scholar] [CrossRef]
- Wang, J.L.; Liu, F.A.; Zhu, Z.F. An information-spreading model based on relative weight in social network. Acta Phys. Sin. 2015, 64, 050501. [Google Scholar]
- Available online: http://twitter.com/ (accessed on 10 March 2019).
- Available online: http://weibo.com/ (accessed on 10 March 2019).
- Available online: http://www.epinions.com/ (accessed on 10 March 2019).
- Available online: http://www.datatang.com/ (accessed on 10 March 2019).
- Available online: http://www.nlpir.org/ (accessed on 10 March 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).