An Optimal Energy-Saving Strategy for Home Energy Management Systems with Bounded Customer Rationality
Abstract
1. Introduction
- (1)
- In order to define a utility function for all kinds of electric appliances for residents, this paper categorizes general appliances into two types: The time-sensitive type, and the temperature-sensitive type. Based on this clustering, we extend the utility function leveraged in [13,14] into two types, covering more kinds of electric appliances in HEMS.
- (2)
- Considering the bounded rationality of customers in an energy-saving program, prospect theory in behavioral economics is incorporated to extend the utility functions into a novel concept; the energy-saving cost. This depicts the real behavior of customers in energy-saving better than conventional utility functions.
- (3)
- An energy-saving cost-based optimal appliance scheduling model is formulated. In our model, the energy-saving cost is used as a constraint, and HEMS only need to minimize the electric power consumption in acceptable regions. The method is computationally efficient, making it suitable for use with HEMS.
2. Electric Appliance Utility Function and Energy-Saving Cost
2.1. Introduction of Definitions
2.2. Time-Sensitive Utility Function
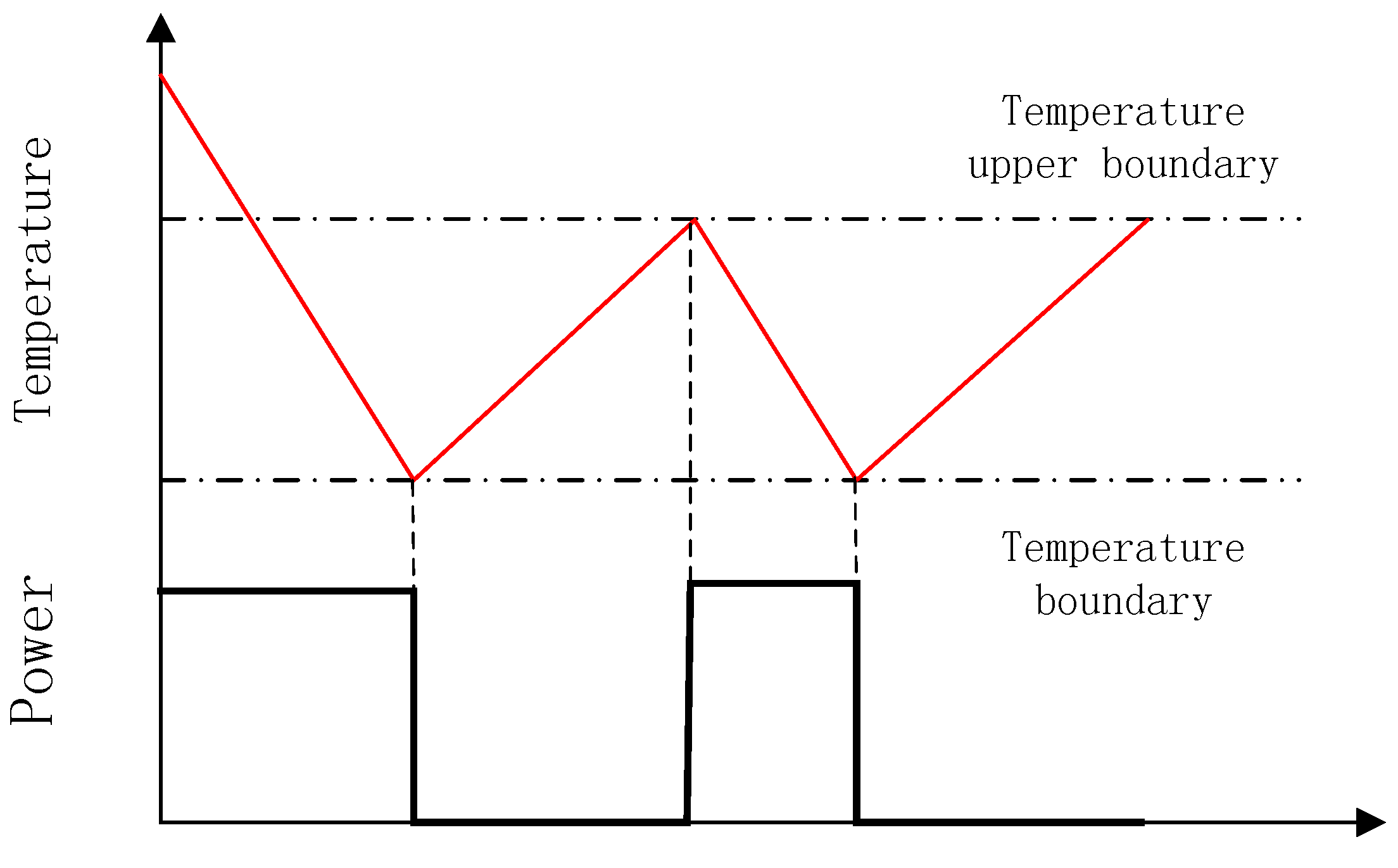
2.3. Temperature Utility Function
2.4. Energy-Saving Costs
3. Energy-Saving Optimization Model
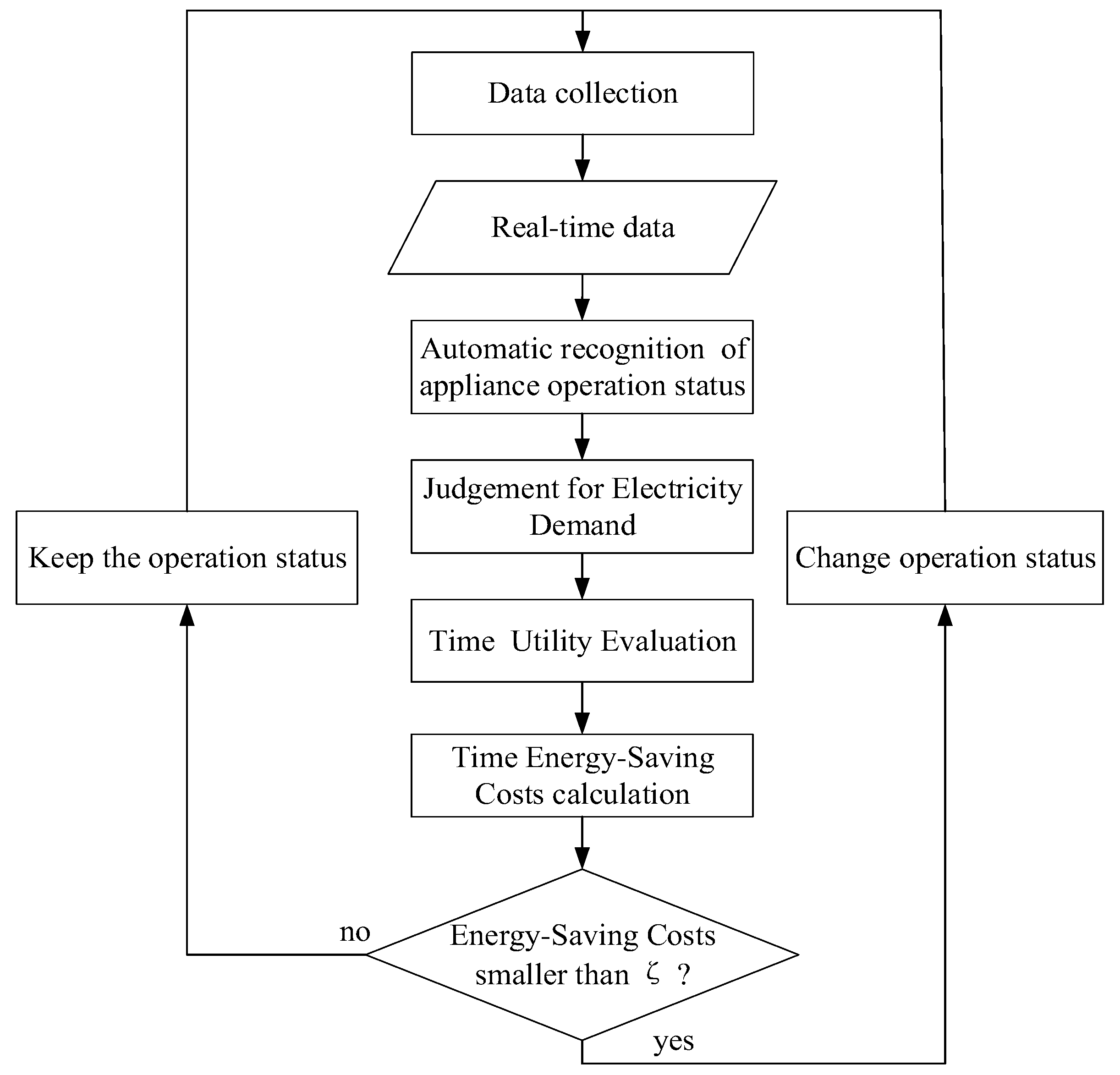
3.1. Automatic Recognition of Appliance Status
3.2. Power Demand Estimation
3.3. Energy-Saving Optimization Algorithm Flow
3.3.1. Time Dimension
- (1)
- Recognize the operating status of the electrical appliance using the automatic recognition method of the appliance operation status with real-time collected operating power data;
- (2)
- Select the power demand mining method which applies to the appliance according to the characteristics of electrical appliances. Then, the current demand for power consumption is discriminated;
- (3)
- Evaluate the real-time time utility according to the electrical appliance operation status and the power demand;
- (4)
- Calculate the energy-saving costs if the electrical operation mode is changed (previously turned on, assumed to be off; or closed initially, and assumed to be on);
- (5)
- Determine the relationship between the energy-saving costs and the energy-saving threshold . If the energy-saving cost value is lower than , the optimization strategy is to change the electrical operation mode; if it is higher than , the optimization strategy is to keep the original operating mode unchanged.
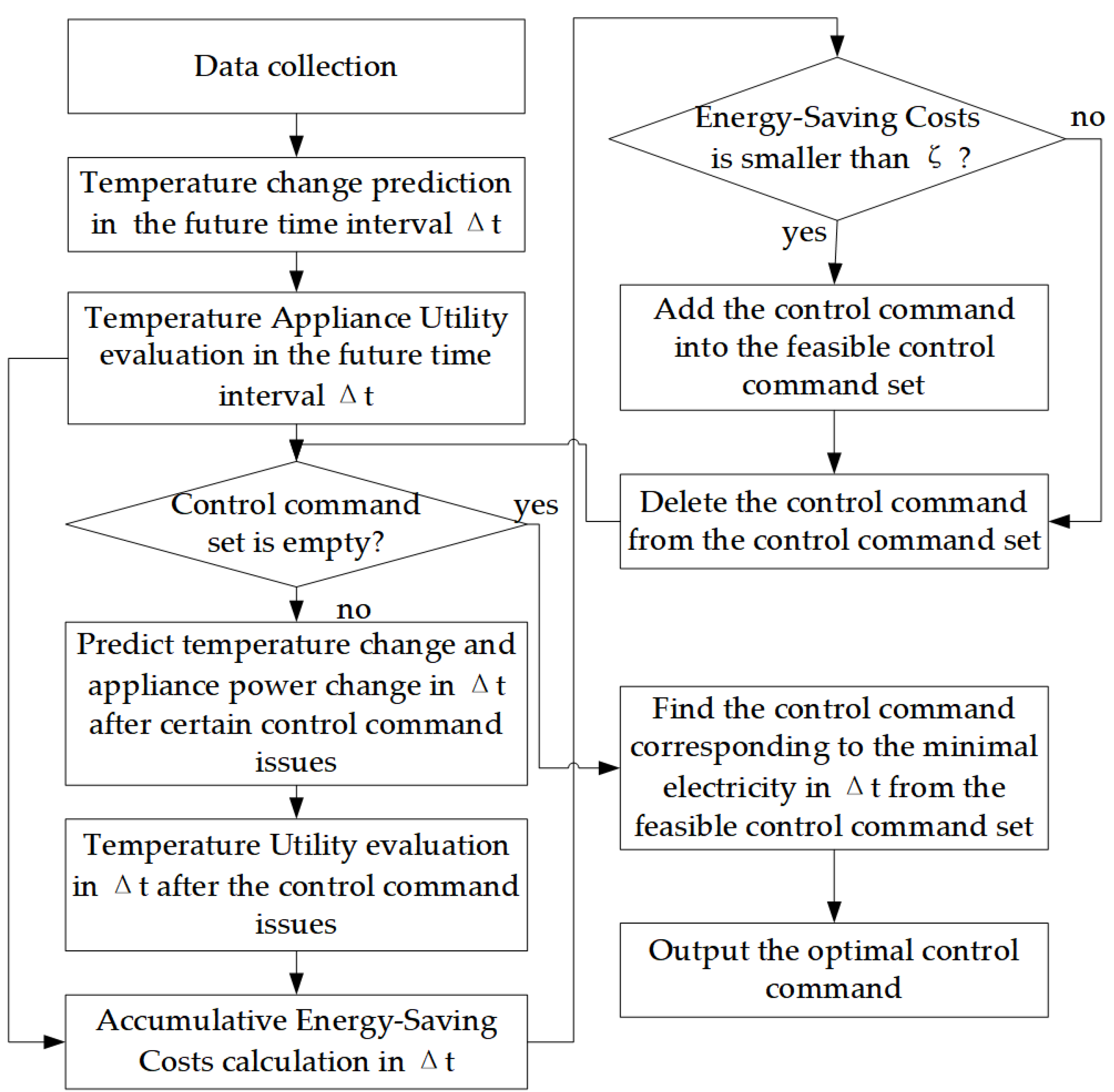
3.3.2. Temperature Dimension
- (1)
- Predict the indoor temperature change under the condition that the operating mode remains unchanged in the future period of ;
- (2)
- Pre-evaluate the temperature utility during the future time period of in combination with the operating status and the indoor temperature prediction curve;
- (3)
- Mark the set of all the currently operational control commands as the control command set, and determine whether the control command set is empty. If it is empty, go to (7); if not, go to (4);
- (4)
- Select one of the operable control commands to predict the operating status, operating power, and indoor temperature change of the future period of after the control command is issued;
- (5)
- Pre-evaluate the temperature utility by combining the new operation status and indoor temperature prediction;
- (6)
- Combine the temperature utility estimation result before and after taking the control command, calculate the energy-saving costs brought by the control command, and judge whether it is less than the setting energy-saving temperature utility cost threshold . If it is less than , the control command is put into the available control command set and would be deleted from the control command set; if it is higher than , delete the control command from the control command set. Then, return to step (4);
- (7)
- Traverse all control commands of the available control command set, perform an integral calculation on the power curve predicted in (4), and find the control command with the smallest total power consumption, which is the optimal energy-saving control strategy.
4. Case Study
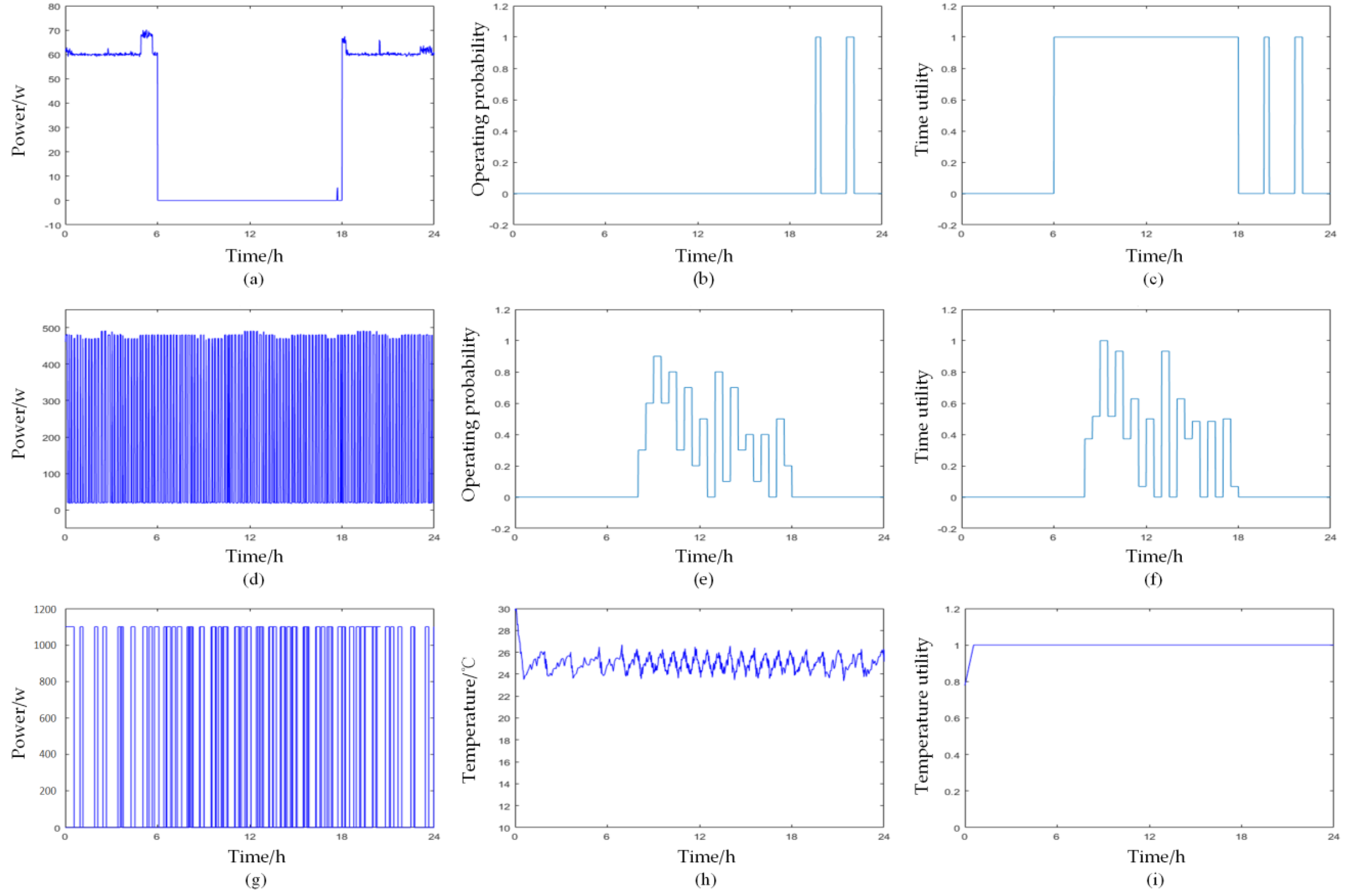
4.1. The Basic Test of the Proposed Algorithm
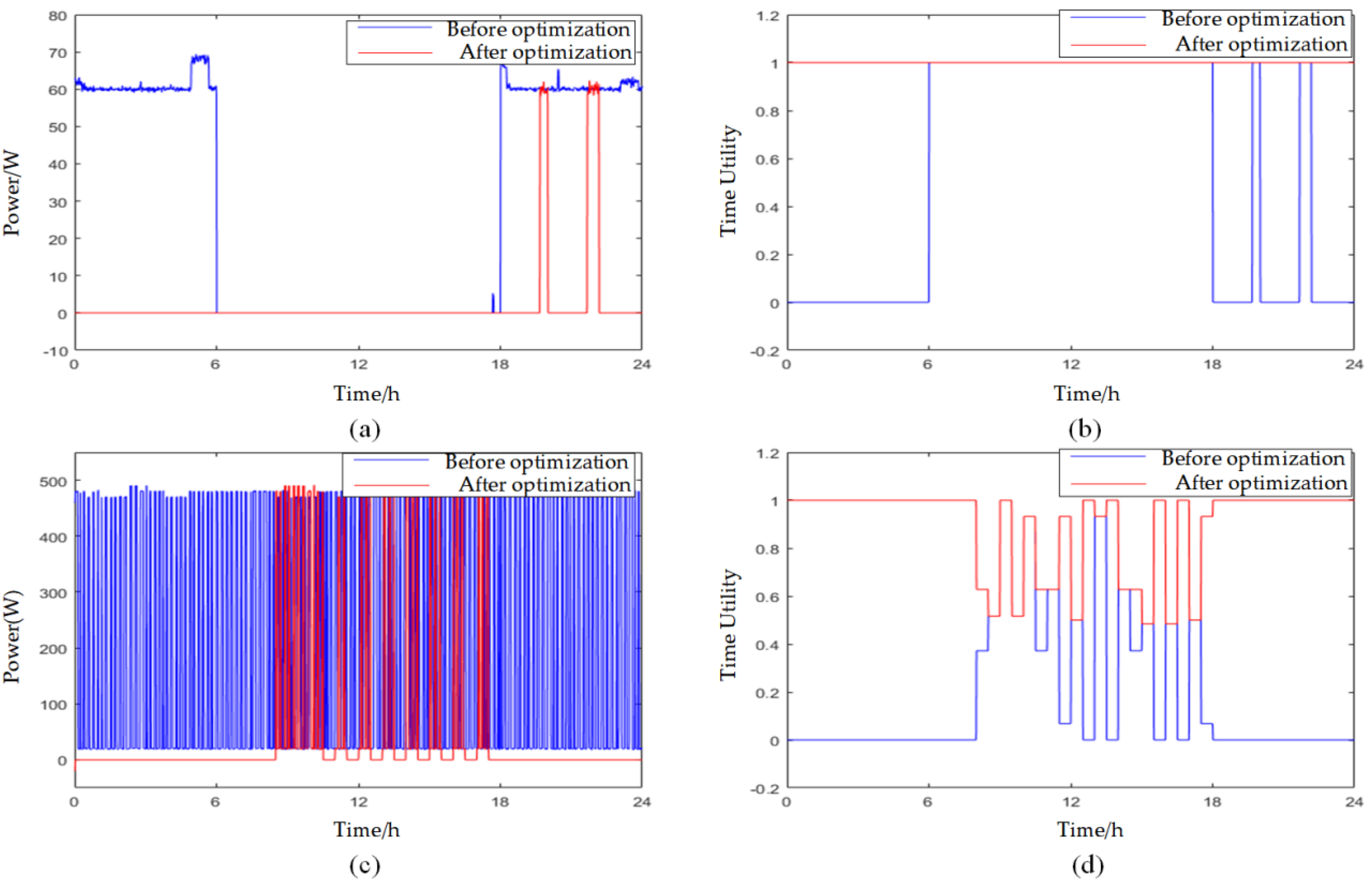
4.1.1. Optimization for Time-Sensitive Appliances
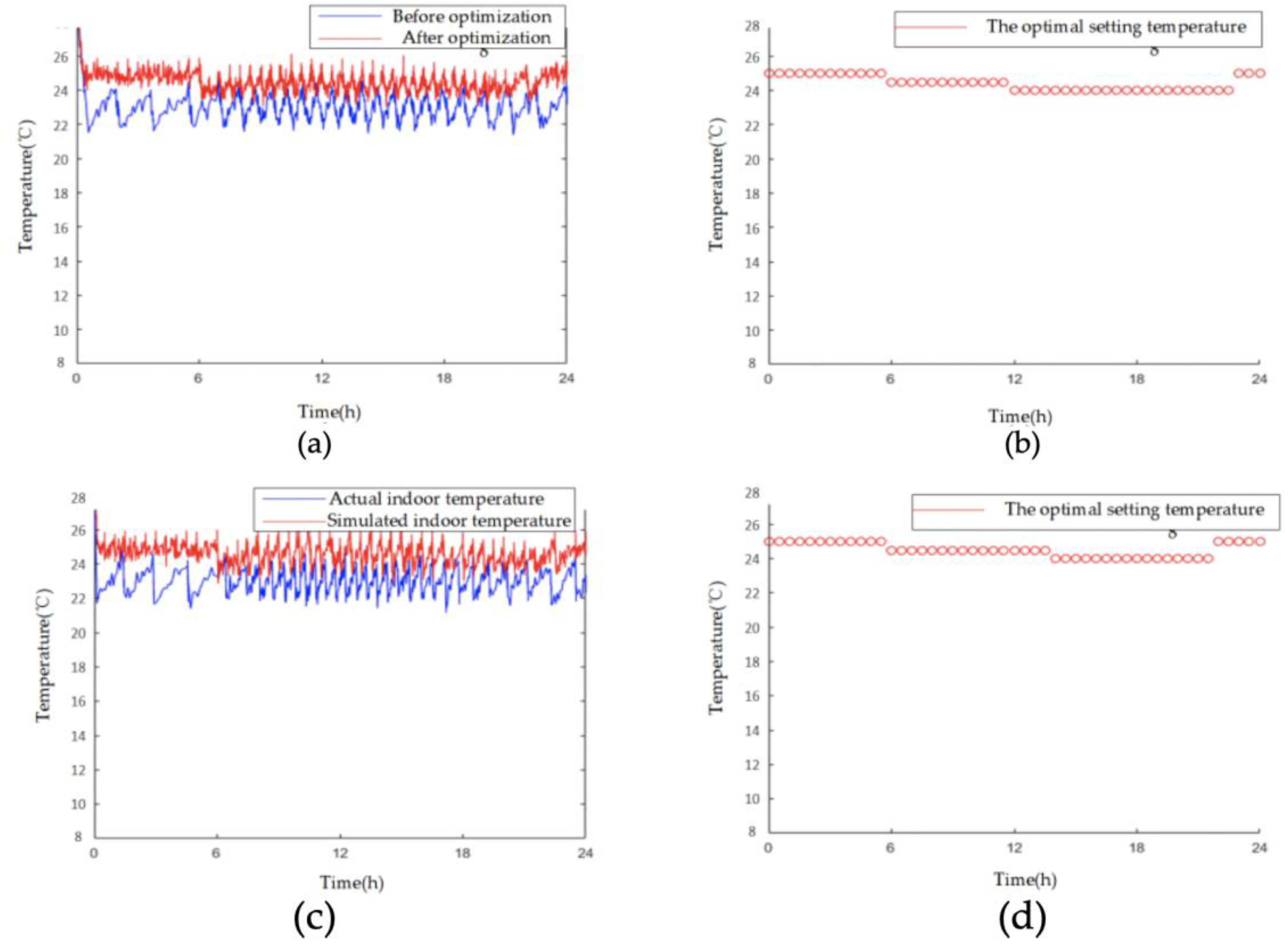
4.1.2. The Optimization Simulation for an Air Conditioner
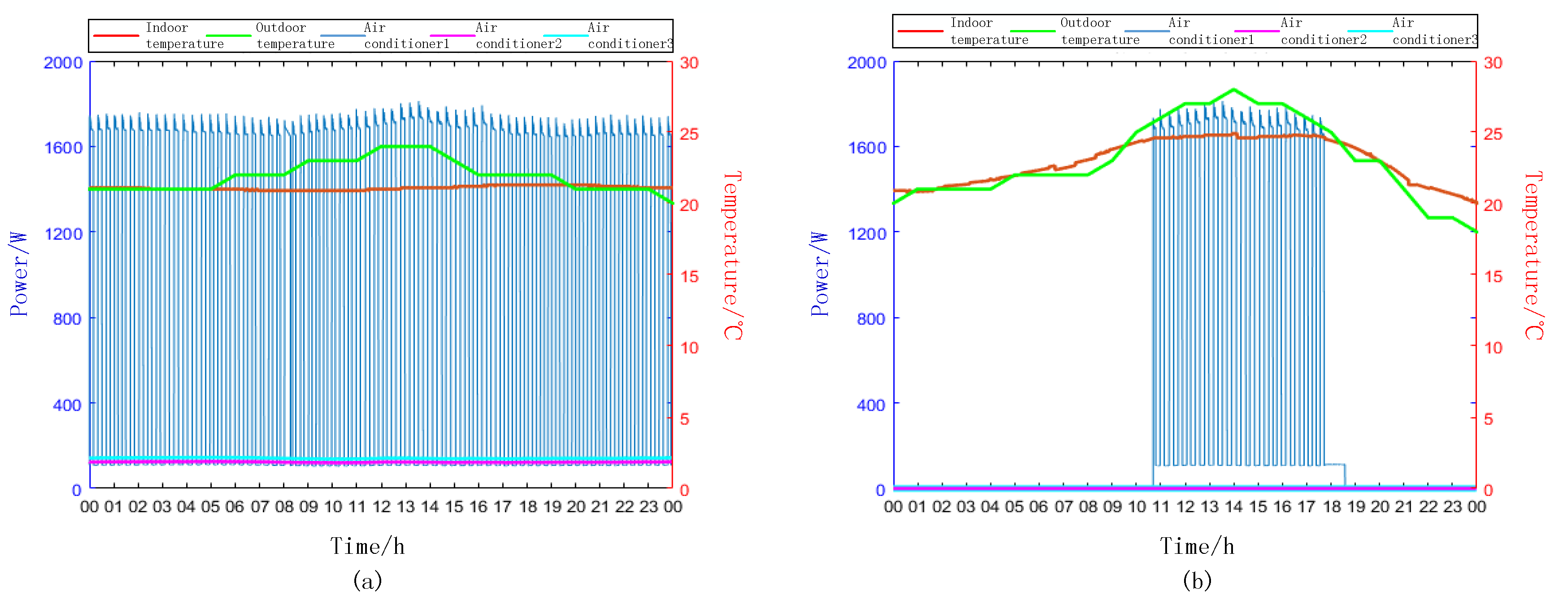
4.2. The Energy Saving Effect Test Based on Field Data
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gottwalt, S.; Gärttner, J.; Schmeck, H.; Weinhardt, C. Modeling and valuation of residential demand flexibility for renewable energy integration. IEEE Trans. Smart Grid 2017, 8, 2565–2574. [Google Scholar] [CrossRef]
- Jia, K.; Wang, Z.; Fan, S.; Zhai, S.; He, G. Data-Centric Approach: A Novel Systematic Approach for Cyber Physical System Heterogeneity in Smart Grid. IEEJ Trans. Electr. Electron. Eng. 2019. [Google Scholar] [CrossRef]
- Pecorella, T.; Pierucci, L.; Nizzi, F. “Network Sentiment” Framework to Improve Security and Privacy for Smart Home. Future Internet 2018, 10, 125. [Google Scholar] [CrossRef]
- He, J.; Xiao, Q.; He, P.; Pathan, M.S. An Adaptive Privacy Protection Method for Smart Home Environments Using Supervised Learning. Future Internet 2017, 9, 7. [Google Scholar] [CrossRef]
- Fan, S.; Jia, K.; Guo, B.; Jiang, L.; Wang, Z.; He, G. Collaborative Optimal Operation Strategy for Decentralized Electric Heating Loads. Autom. Electr. Power Syst. 2017, 41, 20–29. [Google Scholar]
- Alonso, S.; Morán, A.; Prada, M.Á.; Reguera, P.; Fuertes, J.J.; Domínguez, M. A Data-Driven Approach for Enhancing the Efficiency in Chiller Plants: A Hospital Case Study. Energies 2019, 12, 827. [Google Scholar] [CrossRef]
- Gomes, L.; Ramos, C.; Jozi, A.; Serra, B.; Paiva, L.; Vale, Z. IoH: A Platform for the Intelligence of Home with a Context Awareness and Ambient Intelligence Approach. Future Internet 2019, 11, 58. [Google Scholar] [CrossRef]
- Pan, F.; Lin, G.; Lin, J.; Fan, S.; He, G.; Jia, K. Design and Simulation of the Autonomous Decentralized Dispatching System of Generalized Demand Side Resources. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Singapore, 22–25 May 2018. [Google Scholar]
- Jia, K.; Xiao, J.; Fan, S.; He, G. A MQTT/MQTT-SN-Based User Energy Management System for Automated Residential Demand Response: Formal Verification and Cyber-Physical Performance Evaluation. Appl. Sci. 2018, 8, 1035. [Google Scholar] [CrossRef]
- Diaz Lozano Patino, E.; Siegel, J.A. Indoor environmental quality in social housing: A literature review. Build. Environ. 2018, 131, 231–241. [Google Scholar] [CrossRef]
- Caniato, M.; Bettarello, F.; Ferluga, A.; Marsich, L.; Schmid, C.; Fausti, P. Thermal and acoustic performance expectations on timber buildings. Build. Acoust. 2017, 24, 219–237. [Google Scholar] [CrossRef]
- Gupta, R.; Chandiwala, S. Understanding occupants: Feedback techniques for large-scale low-carbon domestic refurbishments. Build. Res. Inf. 2010, 38, 530–548. [Google Scholar] [CrossRef]
- Fan, S.; He, G.; Jia, K.; Wang, Z. A Novel Distributed Large-Scale Demand Response Scheme in High Proportion Renewable Energy Sources Integration Power Systems. Appl. Sci. 2018, 8, 452. [Google Scholar] [CrossRef]
- Fan, S.; He, G.; Guo, B.; Wang, Z. A user energy management system (UEMS)-based microgrid economic dispatch model. In Proceedings of the IEEE Asia-Pacific Power & Energy Engineering Conference, Bangalore, India, 8–10 November 2018. [Google Scholar]
- Mohajeryami, S.; Moghaddam, I.N.; Doostan, M.; Vatani, B.; Schwarz, P. A novel economic model for price-based demand response. Electr. Power Syst. Res. 2016, 135, 1–9. [Google Scholar] [CrossRef]
- Lin, C.-M.; Wu, C.-Y.; Tseng, K.-Y.; Ku, C.-C.; Lin, S.-F. Applying Two-Stage Differential Evolution for Energy Saving in Optimal Chiller Loading. Energies 2019, 12, 622. [Google Scholar] [CrossRef]
- Odkhuu, N.; Lee, K.-B.; A. Ahmed, M.; Kim, Y.-C. Optimal Energy Management of V2B with RES and ESS for Peak Load Minimization. Appl. Sci. 2018, 8, 2125. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Jia, K.; He, G.; Yang, L.; Zhou, N. Preference Analyses of Residential Appliances in Demand Response: A Novel Perspective Based on Behavioral Economics. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Sarajevo, Bosnia and Herzegovina, 21–25 October 2018. [Google Scholar]
- Jia, K.; He, G.; Zhai, S.; Lin, G.; Lu, S.; Pan, F. Utility-Based Real-Time Estimation of Appliance Dispatching Cost for Residential Energy Management. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Singapore, 22–25 May 2018. [Google Scholar]
- Wang, J.; Fang, K.; Dai, J.; Yang, Y.; Zhou, Y. Optimal Scheduling of Industrial Task-Continuous Load Management for Smart Power Utilization. Appl. Sci. 2017, 7, 281. [Google Scholar] [CrossRef]
- Bradac, Z.; Kaczmarczyk, V.; Fiedler, P. Optimal Scheduling of Domestic Appliances via MILP. Energies 2015, 8, 217–232. [Google Scholar] [CrossRef]
- Singh, M.; Jha, R.C. Object-Oriented Usability Indices for Multi-Objective Demand Side Management Using Teaching-Learning Based Optimization. Energies 2019, 12, 370. [Google Scholar] [CrossRef]
- Dunkelberg, H.; Sondermann, M.; Meschede, H.; Hesselbach, J. Assessment of Flexibilisation Potential by Changing Energy Sources Using Monte Carlo Simulation. Energies 2019, 12, 711. [Google Scholar] [CrossRef]
- Lin, G.; Pan, F.; Yang, Y.; Yang, L.; He, G.; Fan, S. The Pattern Recognition of Residential Power Consumption Based on HMM. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Singapore, 22–25 May 2018; pp. 413–418. [Google Scholar]
- Liu, M.; Wu, Y.; Wu, R.; Fan, S.; He, G.; Jia, K. User-Side Self-Approximate Optimization Method and Its Application Based on Power Utility and Electrical Appliance Parameter Characterization. Electr. Power Constr. 2017. [Google Scholar] [CrossRef]
- Kwac, J.; Flora, J.; Rajagopal, R. Household Energy Consumption Segmentation Using Hourly Data. IEEE Trans. Smart Grid 2014, 5, 420–430. [Google Scholar] [CrossRef]
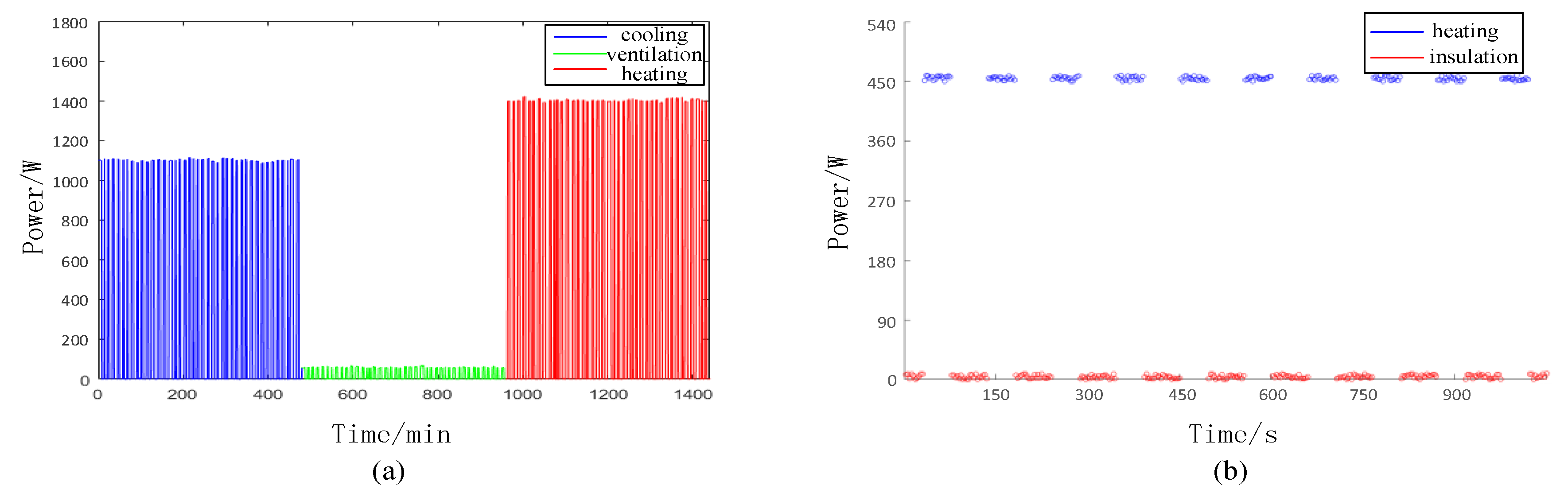
| Appliances | Operating Status | Clustering Center/W |
|---|---|---|
| Light | On | 58.28 |
| Water Dispenser | Insulation | 0.46928 |
| Heating | 426.26 | |
| Air Conditioning | Cooling | 1139.77 |
| Heating | 1407.65 | |
| Ventilation | 56.25 | |
| Standby | 20.56 |
| Appliances | Before Optimization/kWh | After Optimization /kWh | The amount of Energy Saving/kWh | Energy Saving Rate |
|---|---|---|---|---|
| Single air conditioner | 15.48 | 14.75 | 0.73 | 4.7% |
| Air conditioner group (four devices) | 63.29 | 47.66 | 15.63 | 24.7% |
| Type of Area | Appliances | Number |
|---|---|---|
| Hyperbaric chamber/Central control room | Air conditioner | 6 |
| Office | Air conditioner | 3 |
| Office | Water dispenser | 3 |
| Outdoor area | Lighting | 5 |
| Indoor area | Lighting | 5 |
| Appliances | Before Optimization/kWh | After Optimization/kWh | Total Energy Savings/kWh | Energy-Saving Rate | Ratio of Energy-Saving |
|---|---|---|---|---|---|
| Air conditioner in the equipment room | 459.41 | 149.69 | 309.72 | 67.4% | 48.9% |
| Air conditioner in the office | 356.04 | 131.13 | 224.91 | 63.2% | 35.5% |
| Water dispenser | 18.46 | 10.78 | 7.68 | 41.6% | 1.2% |
| Indoor lighting | 10.89 | 7.86 | 3.03 | 27.8% | 0.5% |
| Outdoor lighting | 121.48 | 33.5 | 87.98 | 72.4% | 13.9% |
| Total amount | 966.28 | 332.96 | 633.32 | 65.5% | 100% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, G.; Yang, Y.; Pan, F.; Zhang, S.; Wang, F.; Fan, S. An Optimal Energy-Saving Strategy for Home Energy Management Systems with Bounded Customer Rationality. Future Internet 2019, 11, 88. https://doi.org/10.3390/fi11040088
Lin G, Yang Y, Pan F, Zhang S, Wang F, Fan S. An Optimal Energy-Saving Strategy for Home Energy Management Systems with Bounded Customer Rationality. Future Internet. 2019; 11(4):88. https://doi.org/10.3390/fi11040088
Chicago/Turabian StyleLin, Guoying, Yuyao Yang, Feng Pan, Sijian Zhang, Fen Wang, and Shuai Fan. 2019. "An Optimal Energy-Saving Strategy for Home Energy Management Systems with Bounded Customer Rationality" Future Internet 11, no. 4: 88. https://doi.org/10.3390/fi11040088
APA StyleLin, G., Yang, Y., Pan, F., Zhang, S., Wang, F., & Fan, S. (2019). An Optimal Energy-Saving Strategy for Home Energy Management Systems with Bounded Customer Rationality. Future Internet, 11(4), 88. https://doi.org/10.3390/fi11040088




