Acquiring Ontology Axioms through Mappings to Data Sources ^†

Abstract

Although current languages used in ontology-based data access (OBDA) systems allow for mapping source data to instances of concepts and relations in the ontology, several application domains need more flexible tools for inferring knowledge from data, which are able to dynamically acquire axioms about new concepts and relations directly from the data. In this paper we introduce the notion of mapping-based knowledge base (MKB) to formalize the situation where both the extensional and the intensional level of the ontology are determined by suitable mappings to a set of data sources. This allows for making the intensional level of the ontology as dynamic as the extensional level traditionally is. To do so, we resort to the meta-modeling capabilities of higher-order description logics, in particular the description logic $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$, which allows seeing concepts and relations as individuals, and vice versa. The challenge in this setting is to design efficient algorithms for answering queries posed to MKBs. Besides the definition of MKBs, our main contribution is to prove that answering instance queries posed to MKBs expressed in $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ can be done efficiently.

1. Introduction

Ontology-based data access (OBDA) [1,2] is a paradigm for accessing data using a conceptual representation of the domain of interest expressed as an ontology. An OBDA system relies on a three-level architecture, consisting of the data layer, the ontology, and the mapping between the two. More in detail,

• the data layer is constituted by the existing data sources that are relevant for the organization,
• the ontology is a declarative and explicit representation of the domain of interest for the organization, formulated in a description logic (DL) [3] so as to take advantage of various reasoning capabilities in accessing data,
• the mapping is a set of declarative assertions specifying how the sources in the data layer relate to the ontology.

Several OBDA projects have been carried out in recent years [4,5,6,7], and various OBDA management systems have been designed to support OBDA applications, e.g., [8,9,10]. In current OBDA systems the ontology is expressed as a DL TBox, i.e., a set of assertions on the relevant concepts and roles (i.e., binary relationships between concepts) of the domain of interest, constituting the intensional level of the representation, and the mapping assertions are used to specify how the data at the sources correspond to the instances of the concepts and the relations, which form the extensional level of the representation. Thus, the mapping assertions, together with the source data, determine the so-called virtual ABox, in the sense that the instance assertions are not explicitly given but are specified through the relationships between the data and the elements of the TBox.

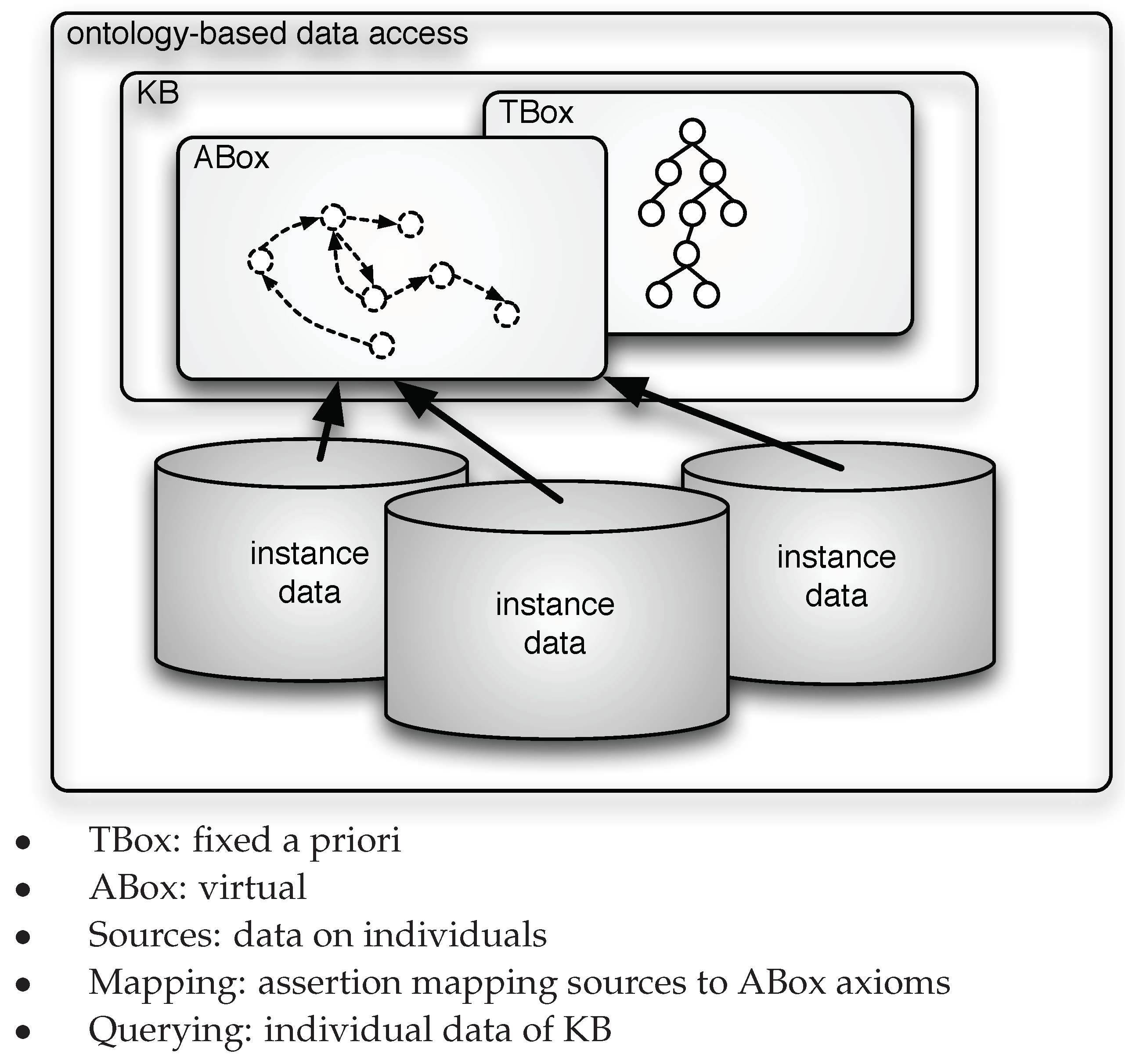
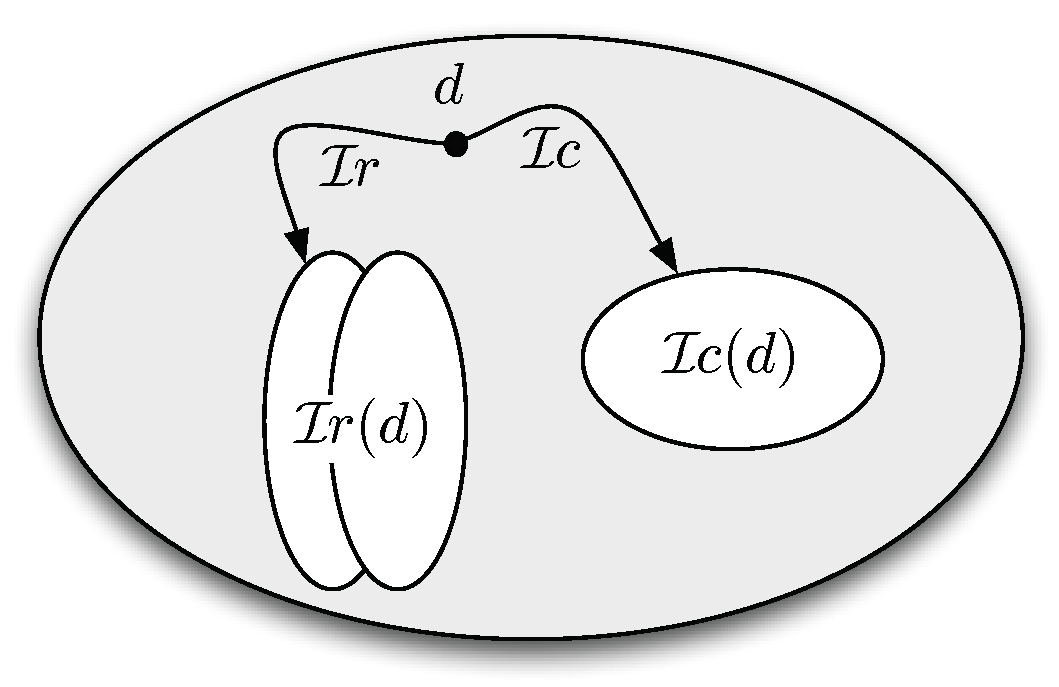
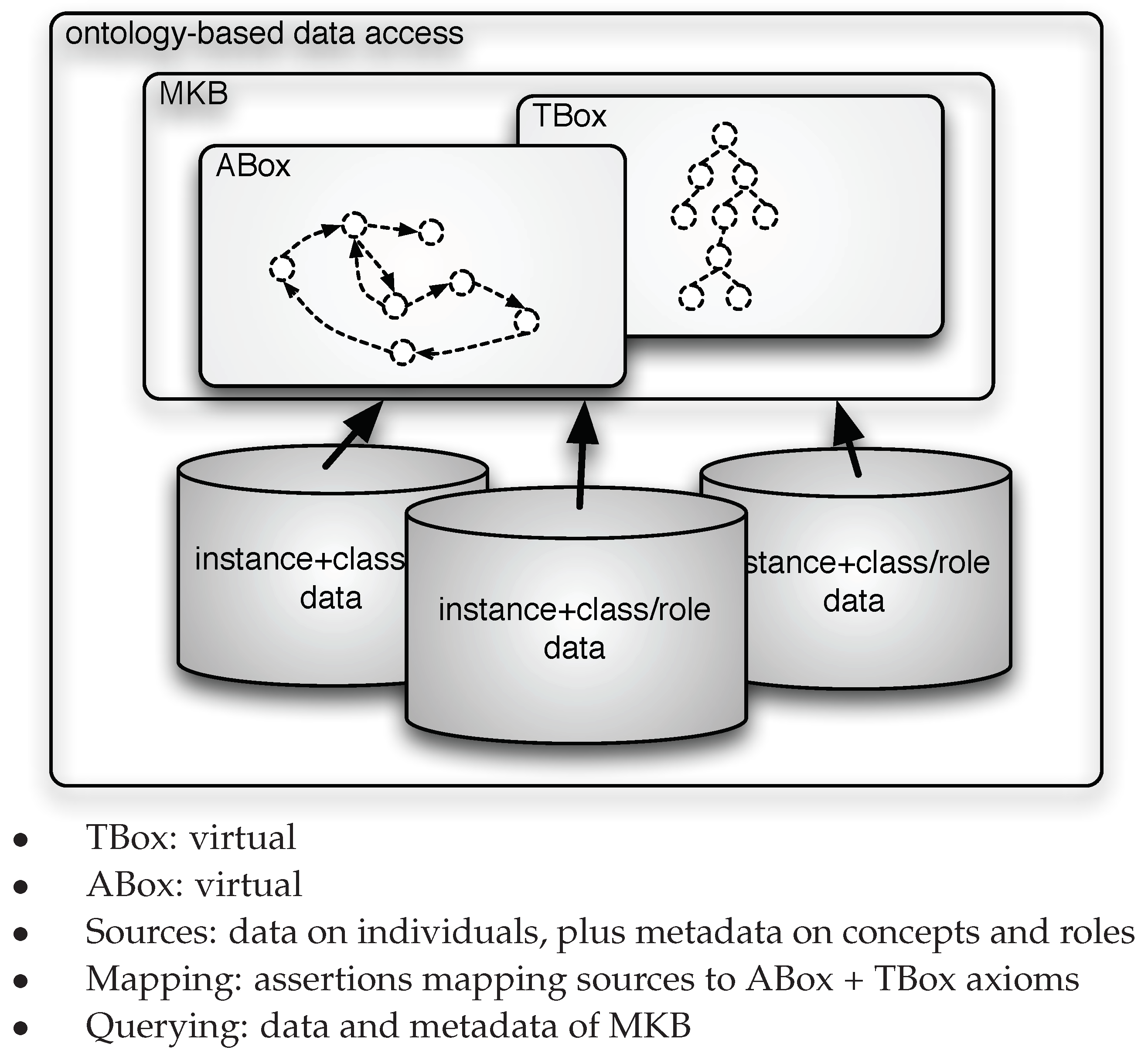
From the above observations it should be clear that current works on OBDA share the idea, originally stemmed in data integration and in data exchange [11,12,13,14], that mappings are used to (virtually) retrieve extensional information of the ontology from the sources, as shown in Figure 1, while the intensional level information, represented by the TBox, remains fixed a priori, once and for all. In this paper, we challenge this preconception and propose to adopt a virtual approach to the specification of the TBox, thus virtualizing both the extensional and the intensional level of the ontology. In other words, we propose a setting where not only the ABox but also the TBox is specified through mappings linking the data to the ontology, as illustrated in Figure 2. Our approach is based on addressing two issues.

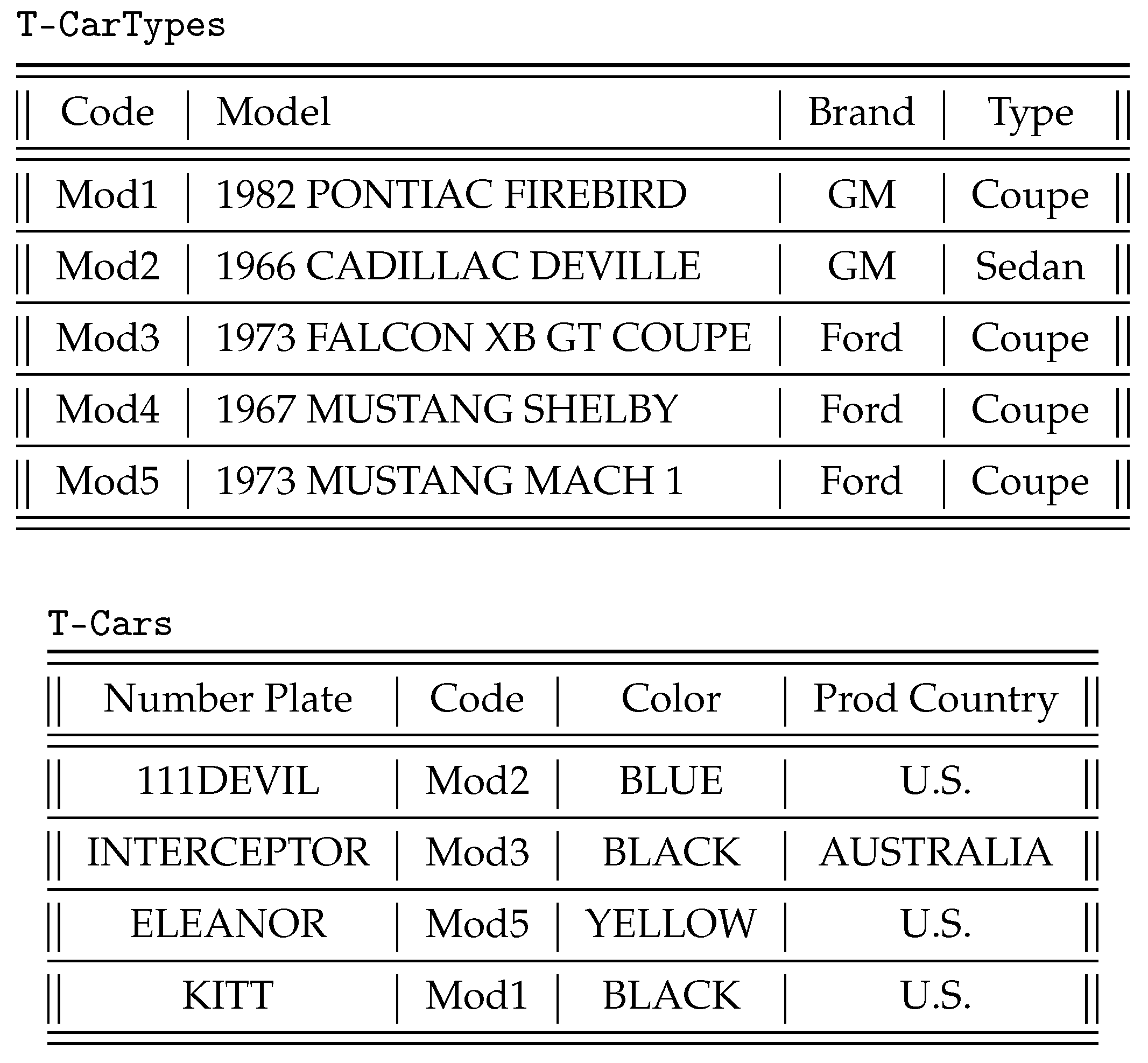
The first issue is related to looking at the content of the data sources to identify concepts and roles that are relevant to the domain of interest but that have not been modeled in the TBox, because they were not known at design time. As an example, the database $\mathcal{D}$ in Figure 3 stores data about different models and different types of cars manufactured by motor companies (table T-CarTypes), as well as various cars of such types (table T-Cars). If we look carefully at the semantics of the data in $\mathcal{D}$, we realize that such database not only stores information about the instances of the concepts in the domain of interest (e.g., the first row of table T-Cars collects data about an instance of the concept Car) but contains also pieces of data denoting new concepts of the domain. In particular, table T-CarTypes contains data denoting concepts such as 1973 FALCON XB GT, 1967 MUSTANG SHELBY, 1973 MUSTANG MACH 1, and so on. Considering the context where these concepts appear, it is not difficult to conclude that they are all mutually disjoint subconcepts of Car. Table T-Cars, on the other hand, provides information about the instances of the various concepts, as well as other properties about them (i.e., Color, ProdCountry). We observe that, in order to acquire the knowledge about the concepts mentioned in the data sources, we need a flexible mechanism that is able to map data at the sources to concepts in the ontology. Without such flexibility, the designer would be forced to manually inspect the data sources and enrich the ontology off-line.

The second issue is related to the need of meta-modeling constructs in the language used to specify the ontology [16,17,18,19]. Meta-modeling allows concepts and relations to be conceived as first-order citizens and to see them as individuals that are instances of other concepts, called meta-concepts. By exploiting meta-modeling we might introduce in the ontology the meta-concept Car-Type, with Coupe, Sedan, etc. as its specializations. Note that the instances of such specialized concepts include the subconcepts of cars listed in the rows stored in table T-CarTypes. With this mechanism, the designer is allowed to specify the means for dynamically acquiring TBox axioms, through simple queries asking for the instances of the meta-concept Car-Type. Indeed, without the possibility of using meta-concepts in the ontology, it would be impossible to deal with the first issue mentioned above, that is exactly based on the idea of using mappings in order to transfer the knowledge fragments residing in the data sources to the TBox of the ontology. Note that for the technical development related to meta-modeling, we base our work on the approach and the results reported in [18].

In this paper, we deal with both the issue of acquiring TBox axioms from data sources and the issue of meta-modeling. In particular, we focus on designing tractable algorithms for query answering in such a setting. Indeed, looking for query answering algorithms that are tractable in data complexity is a distinguishing characteristic of OBDA systems. We follow [20], and we work with the $\mathit{DL-Lite}$ family of DLs, which enjoys the first-order logic (FOL) rewritability properties. In a DL, enjoying such property answering (unions) of conjunctive queries can be done in two steps. The first one, called rewriting, uses the TBox axioms in order to transform the query q into a new FOL query $q^{\prime }$. The second step evaluates $q^{\prime }$ over the ABox seen as a database.

The challenge we face in this paper is to design tractable query answering algorithms even in cases where the mapping assertions map the data at the sources to both the extensional and the intensional level of the ontology and both meta-concepts and meta-relations are used in the queries. In particular, we present the following contributions.

• We formalize the notion of mapping-based knowledge base (MKB), that captures the idea of acquiring the axioms of both the extensional and the intensional level of the ontology through mapping assertions linking the source data to the ontology. This mechanism allows the designer to achieve a level of flexibility that is not possible in current OBDA systems. Our formalization relies on the notion of higher-order DL, as introduced in [18]. Indeed, De Giacomo et al. [18] describe a methodology that, starting from a traditional DL $\mathcal{L}$, allows one to define its higher-order version $Hi(\mathcal{L})$. Here, we apply this idea and make use of the higher-order DL $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$.
• We propose to query mapping-based knowledge bases by means of an extension of unions of conjunctive queries (UCQs), taking advantage of the higher-order features of $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$. In particular we define a suitable class of such queries, the so-called instance higher-order UCQs (IHUCQs), enjoying nice computational properties. The basic characteristic of IHUCQs is to allow higher-order features (i.e., meta-concepts and meta-properties) in the query expression but to disregard subclass and subproperty assertions in the body of the query.
• We study the problem of answering IHUCQs posed to MKBs expressed in $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$. We show that this problem is efficiently solvable by exhibiting an algorithm based on FOL rewriting. The algorithm works in $A{C}^0$ with respect to the extensional level of the data sources, i.e., the portion of the data sources that is not involved in the intensional level of the ontology. More precisely, our algorithm, given an IHUCQ q over an MKB, reformulates q into a FOL query that is evaluated taking into account only the portion of the MKB involving the extensional level of the ontology. As a consequence, query answering can be delegated to a database management system, exactly as in the traditional OBDA approach.

To sum up, the main achievement of this paper is to prove that we can extend the mapping language used in current OBDA systems so as to talk about concepts and roles as objects (requiring higher-order features), thus realizing the idea of virtualizing both the extensional and the intensional information in a way that is natural and even very effective. Indeed, our $A{C}^0$ result can be interpreted as follows: the complexity of answering higher-order queries posed on knowledge bases built using such extended mappings remains the same as in traditional OBDA settings, when measured only with respect to the extensional level of the data sources.

We observe that initial ideas on generating the intensional level of a representation through mappings was explored in the data exchange setting. In particular, Papotti and Torlone [21] propose a setting where both data and meta-data stored in relational tables typical of DBMSs, are exchanged. In the context of RDF, the standard language R2RML (https://www.w3.org/TR/r2rml/) for mapping relational databases to RDF datasets, also allows to map patterns in the relational data to assertions (e.g., subsetting) on RDF predicates. In this sense, this is in the same spirit as our proposal, that however is tailored to ontologies and not only to RDF data. In the context of ontologies, this issue is actually new. Indeed, to the best of our knowledge, the only reference dealing with generating TBoxes through mappings is [15], of which this paper is an extended version. More specifically, with respect to [15], the reader can find in the present paper additional examples and discussions, a detailed description of our technique for query answering, and complete proofs for all our results. Furthermore, we revised the analysis of combined complexity of query answering over $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ MKBs (Theorem 3).

The rest of this paper is structured as follows. In Section 2 we recall the definition of $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$, the DL adopted in our work. In Section 3 we introduce and discuss the notion of mapping-based knowledge base. In Section 4 we illustrate the kinds of queries that we consider in this paper, and in Section 5 we present our algorithm for query answering. Section 6 concludes the paper.

2. Higher-Order ${\mathit{DL-Lite}}_{\mathcal{R}}$

We start by recalling some notions on DLs in general and ${\mathit{DL-Lite}}_{\mathcal{R}}$ in particular. Then, we provide the syntax and the semantics of $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$, i.e., the higher-order version of ${\mathit{DL-Lite}}_{\mathcal{R}}$.

DLs [3] are logics that represent the domain of interest in terms of concepts, denoting sets of objects, and roles, denoting binary relations between (instances of) concepts. Complex concept and role expressions are constructed starting from a set of atomic concepts and roles and by recursively applying suitable constructs.

A DL knowledge base (KB) $\mathcal{K}$ is constituted by two components, $\mathcal{T}$ and $\mathcal{A}$, i.e., $\mathcal{K}=\mathcal{T}\cup \mathcal{A}$, where:

• $\mathcal{T}$, called TBox, is the terminological component of $\mathcal{K}$, which contains statements representing intensional knowledge, and
• $\mathcal{A}$, called ABox, is the assertional component of $\mathcal{K}$, which contains assertions representing extensional knowledge.

${\mathit{DL-Lite}}_{\mathcal{R}}$ is a member of the $\mathit{DL-Lite}$ family of tractable DLs [22,23] and is the logical basis of OWL 2 QL, one of the profiles of OWL, the W3C standard for representing ontologies [24].

${\mathit{DL-Lite}}_{\mathcal{R}}$ expressions are given by the following syntax:

• Concept expressions:

  $$\begin{array}{c}\hfill \begin{array}{ccccc}B& ::=& A& |& \exists Q\\ C& ::=& B& |& \neg B\end{array}\end{array}$$
• Role expressions:

  $$\begin{array}{c}\hfill \begin{array}{ccccc}Q& ::=& P& |& P^{-}\\ R& ::=& Q& |& \neg Q\end{array}\end{array}$$

  where A is an atomic concept (i.e., a unary predicate from the signature of the knowledge base), B is a basic concept (i.e, an atomic concept A or an existential restriction on a role $\exists Q$, which denotes individuals occurring in the first component of the role Q, which is called the domain of Q), C is a general concept (i.e., a basic concept B or its negation $\neg B$), P is an atomic role (i.e., a binary predicate from the signature of the knowledge base), Q is a basic role (i.e., an atomic role P or its inverse $P^{-}$), and R is a general role (i.e., a basic role Q or its negation $\neg Q$). The domain of $P^{-}$ (i.e., $\exists P^{-}$) is also called the range of P.

A TBox in ${\mathit{DL-Lite}}_{\mathcal{R}}$ is a finite set of assertions in form:

$$\begin{array}{cc}\hfill B⊑C& (conceptinclusionassertion)\hfill \\ \hfill Q⊑R& (roleinclusionassertion)\hfill \end{array}$$

When C and R above assume the form $\neg B^{\prime }$ and $\neg Q^{\prime }$, respectively, the above inclusions are called negative inclusions and allow us to specify disjointness between concepts or between roles, respectively. Otherwise, the above inclusions are called positive inclusions and allow us to specify is_a relations between concepts or roles, respectively.

An Abox in ${\mathit{DL-Lite}}_{\mathcal{R}}$ is a finite set of membership assertions (i.e., facts) of the form:

$$\begin{array}{cc}\hfill A(a)& (conceptmembershipassertion)\hfill \\ \hfill P(a,b)& (rolemebershipassertion)\hfill \end{array}$$

where a and b are constants, that is, names for individuals (i.e., predicates of arity 0 from the signature of the knowledge base).

We are now ready to describe the higher-order DL $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$. We start by observing that, as discussed in [18], every traditional DL $\mathcal{L}$ can be characterized by a set $\mathit{OP}(\mathcal{L})$ of operators, used to form concept and role expressions and a set of $\mathit{MP}(\mathcal{L})$ of meta-predicates, used to form assertions. Each operator and each meta-predicate have an associated arity. Given a symbol T, we write $T/n$ to denote that T has arity n. For ${\mathit{DL-Lite}}_{\mathcal{R}}$, we simply have:

• $\mathit{OP}({\mathit{DL-Lite}}_{\mathcal{R}})=\{\mathit{Inv}/1,\mathit{Exists}/1\}$,
• $\mathit{MP}({\mathit{DL-Lite}}_{\mathcal{R}})=\{{\mathit{Inst}}_C/2,{\mathit{Inst}}_R/3,{\mathit{Isa}}_C/2,{\mathit{Isa}}_R/2,{\mathit{Disj}}_C/2,{\mathit{Disj}}_R/2\}$,

provided that $\mathit{Inv}$ and $\mathit{Exists}$ take only a role as argument, ${\mathit{Inst}}_C$ takes an individual as first argument and a concept as second argument, ${\mathit{Inst}}_R$ takes an individual as first and second argument and a role as third argument, ${\mathit{Isa}}_C$ and ${\mathit{Disj}}_C$ take two concepts as arguments, and ${\mathit{Isa}}_R$ and ${\mathit{Disj}}_R$ take two roles as arguments.

Example 1.

Consider the following${\mathit{DL-Lite}}_{\mathcal{R}}$knowledge base:

$$\begin{array}{ccc}Ford\hfill & ⊑& Car\hfill \\ \exists produced\_in\hfill & ⊑& Car\hfill \\ \exists produced\_i{n}^{-}\hfill & ⊑& ProdCountry\hfill \\ \multicolumn{3}{c}{Ford(\mathrm{INTERCEPTOR})}\\ \multicolumn{3}{c}{produced\_in(\mathrm{INTERCEPTOR},\mathrm{AUSTRALIA})}\end{array}$$

In words, the knowledge base says that$Ford$is a concept that specializes the concept$Car$,$produced\_in$is a role typed on$Car$and$ProdCountry$, which is a concept denoting production countries. More precisely, the domain of$produced\_in$can be instantiated only with instances of$Car$, as stated by the second inclusion, whereas the range of$produced\_in$can be instantiated only with instances of$ProdCountry$, as stated by the third inclusion. The above knowledge base can be reformulated in the high-order style syntax for${\mathit{DL-Lite}}_{\mathcal{R}}$as follows:

$$\begin{array}{c}{\mathit{Isa}}_C(Ford,Car)\hfill \\ {\mathit{Isa}}_C(\mathit{Exists}(\mathrm{produced}\_\mathrm{in}),\mathrm{Car})\hfill \\ {\mathit{Isa}}_C(\mathit{Exists}(\mathit{Inv}(\mathrm{produced}\_\mathrm{in})),\mathrm{ProdCountry})\hfill \\ {\mathit{Inst}}_C(\mathrm{INTERCEPTOR},Ford)\hfill \\ {\mathit{Inst}}_R(\mathrm{INTERCEPTOR},\mathrm{AUSTRALIA},produced\_in)\hfill \end{array}$$

We finally note that in both syntaxes given above, the first three assertions constitute the TBox of the KB, whereas the last two assertions constitute the ABox of the KB.

Let us turn our attention to the definition of the syntax of $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$. Hereinafter we assume the existence of two disjoint, countably infinite alphabets: $\mathcal{S}$, the set of predicates, also called names and $\mathcal{V}$, the set of variables. Intuitively, the names in $\mathcal{S}$ are the symbols denoting the atomic elements of a $Hi({\mathit{DL-Lite}}_{\mathcal{R}})$ knowledge base. The building blocks of such a knowledge base are assertions, which in turn are based on terms and atoms.

We inductively define the set of terms, denoted by ${\tau }_{{\mathit{DL-Lite}}_{\mathcal{R}}}(\mathcal{S},\mathcal{V})$, over the alphabets $\mathcal{S}$ and $\mathcal{V}$ for $Hi({\mathit{DL-Lite}}_{\mathcal{R}})$ as follows:

• if $e\in \mathcal{S}\cup \mathcal{V}$ then $e\in {\tau }_{{\mathit{DL-Lite}}_{\mathcal{R}}}(\mathcal{S},\mathcal{V})$;
• if $e\in {\tau }_{{\mathit{DL-Lite}}_{\mathcal{R}}}(\mathcal{S},\mathcal{V})$, and e is not of the form $\mathit{Inv}(e^{\prime })$ (where $e^{\prime }$ is any term), then $\mathit{Inv}(e)\in {\tau }_{{\mathit{DL-Lite}}_{\mathcal{R}}}(\mathcal{S},\mathcal{V})$ (Differently from [18], we avoid the construction of terms of the form $\mathit{Inv}(\mathit{Inv}(e))$ which, as roles, are equivalent to e. Under this assumption, we do not have safe-range issues when dealing with queries, thus, differently form [18], we consider here non-Boolean queries.);
• if $e\in {\tau }_{{\mathit{DL-Lite}}_{\mathcal{R}}}(\mathcal{S},\mathcal{V})$ then $\mathit{Exists}(e)\in {\tau }_{{\mathit{DL-Lite}}_{\mathcal{R}}}(\mathcal{S},\mathcal{V})$.

Intuitively, a term denotes either an atomic element, the inverse of an atomic element, or the projection of an atomic element on either the first or the second component.

Example 2.

If the names$\mathit{car},\mathit{produced}\_\mathit{in}$belong to the alphabet$\mathcal{S}$, then the following are$\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$terms:$\mathit{Car}$,$\mathit{Inv}(\mathit{produced}\_\mathit{in})$,$\mathit{Exists}(\mathit{Inv}(\mathit{produced}\_\mathit{in}))$, which, intuitively, denote the concept representing the set of cars, the role$\mathit{produced}\_\mathit{in}$, and the concept representing those individuals (e.g., countries) where something is$\mathit{produced}$.

Ground terms, i.e., terms without variables, are called expressions, and the set of expressions is denoted by ${\tau }_{{\mathit{DL-Lite}}_{\mathcal{R}}}(\mathcal{S})$. The terms in the example above are all expressions.

A $Hi({\mathit{DL-Lite}}_{\mathcal{R}})$-atom, or simply atom, over the alphabets $\mathcal{S}$ and $\mathcal{V}$ for $Hi({\mathit{DL-Lite}}_{\mathcal{R}})$ is a statement of the form $p_1(e_1,e_2)$ or $p_2(e_1,e_2,e_3)$ where $p_1/2$, $p_2/3$ belong to $\mathit{MP}({\mathit{DL-Lite}}_{\mathcal{R}})$, and $e_1,e_2,e_3\in {\tau }_{{\mathit{DL-Lite}}_{\mathcal{R}}}(\mathcal{S},\mathcal{V})$. Note that $Hi({\mathit{DL-Lite}}_{\mathcal{R}})$-atoms (and even terms) are not required to respect the proviso we have introduced before to limit the usage of predicates from $OP({\mathit{DL-Lite}}_{\mathcal{R}})$ and $MP({\mathit{DL-Lite}}_{\mathcal{R}})$ so that through them it is possible to express (only) ${\mathit{DL-Lite}}_{\mathcal{R}}$ knowledge bases. For instance, a ${\mathit{Inst}}_C(C,D)$ and ${\mathit{Isa}}_C(C,E)$ are both legal $Hi({\mathit{DL-Lite}}_{\mathcal{R}})$-atoms, that is, differently from ${\mathit{DL-Lite}}_{\mathcal{R}}$ we can instantiate a concept with another concept. If X is a subset of $\mathcal{V}$, a is an atom, and all variables appearing in a belong to X, then a is called an X-atom.

Ground $Hi({\mathit{DL-Lite}}_{\mathcal{R}})$-atoms, i.e., $Hi({\mathit{DL-Lite}}_{\mathcal{R}})$-atoms without variables, are called $Hi({\mathit{DL-Lite}}_{\mathcal{R}})$-assertions, or simply assertions. Thus, an assertion is simply an application of a meta-predicate to a set of expressions, which intuitively means that an assertion is an axiom that predicates over a set of individuals, concepts, or roles.

A $Hi({\mathit{DL-Lite}}_{\mathcal{R}})$KB over $\mathcal{S}$ is a finite set of $Hi({\mathit{DL-Lite}}_{\mathcal{R}})$-assertions over $\mathcal{S}$. To agree with the usual terminology of DLs, we use the term TBox to denote a set of ${\mathit{Isa}}_C$, ${\mathit{Isa}}_R$, ${\mathit{Disj}}_C$ and ${\mathit{Disj}}_R$ assertions, also called intensional assertions, and the term ABox to denote a set of ${\mathit{Inst}}_C$ and ${\mathit{Inst}}_R$ assertions, also called extensional assertions. Obviously, a ${\mathit{DL-Lite}}_{\mathcal{R}}$ KB is also (a special case of) an $Hi({\mathit{DL-Lite}}_{\mathcal{R}})$ KB.

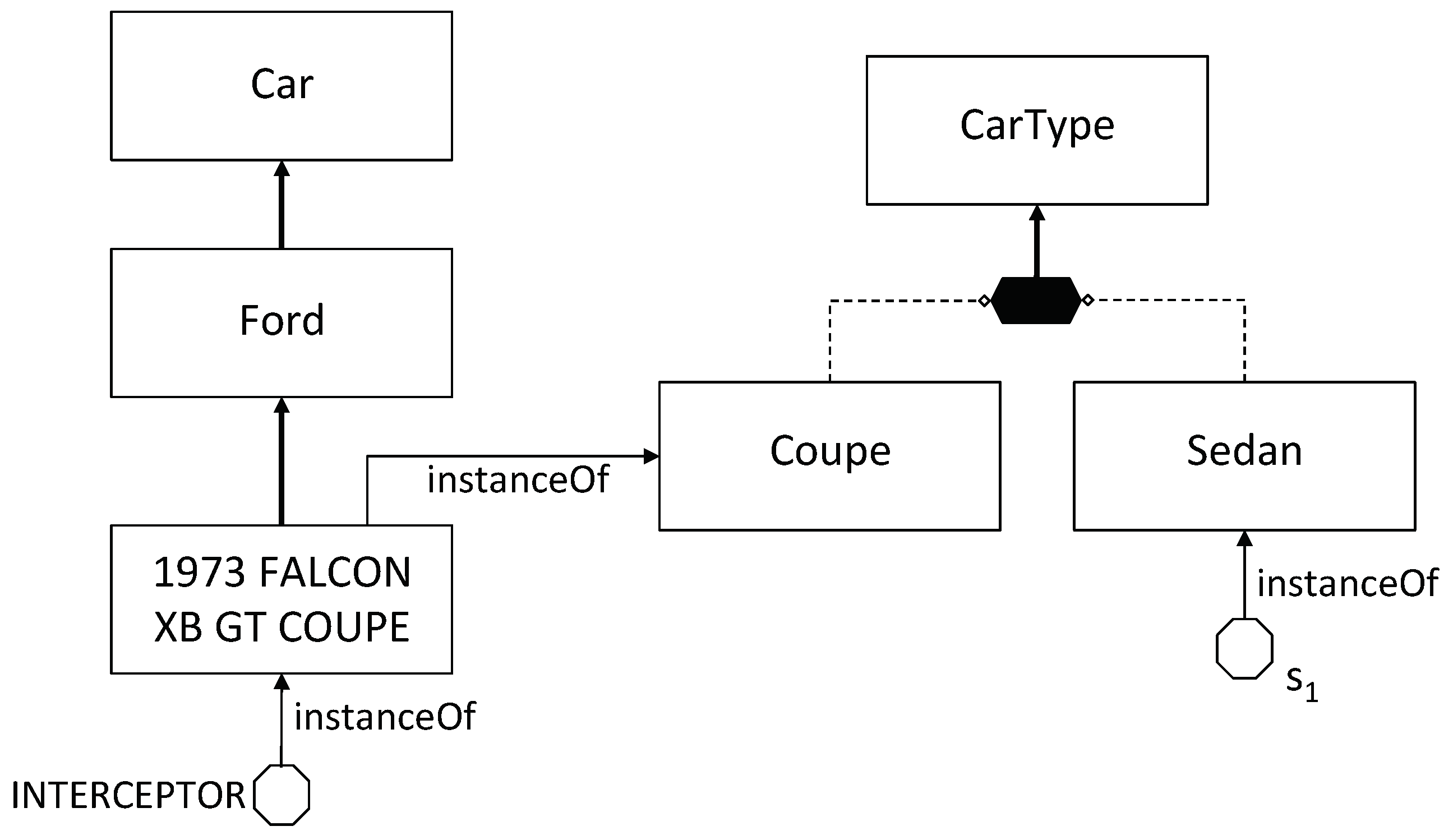
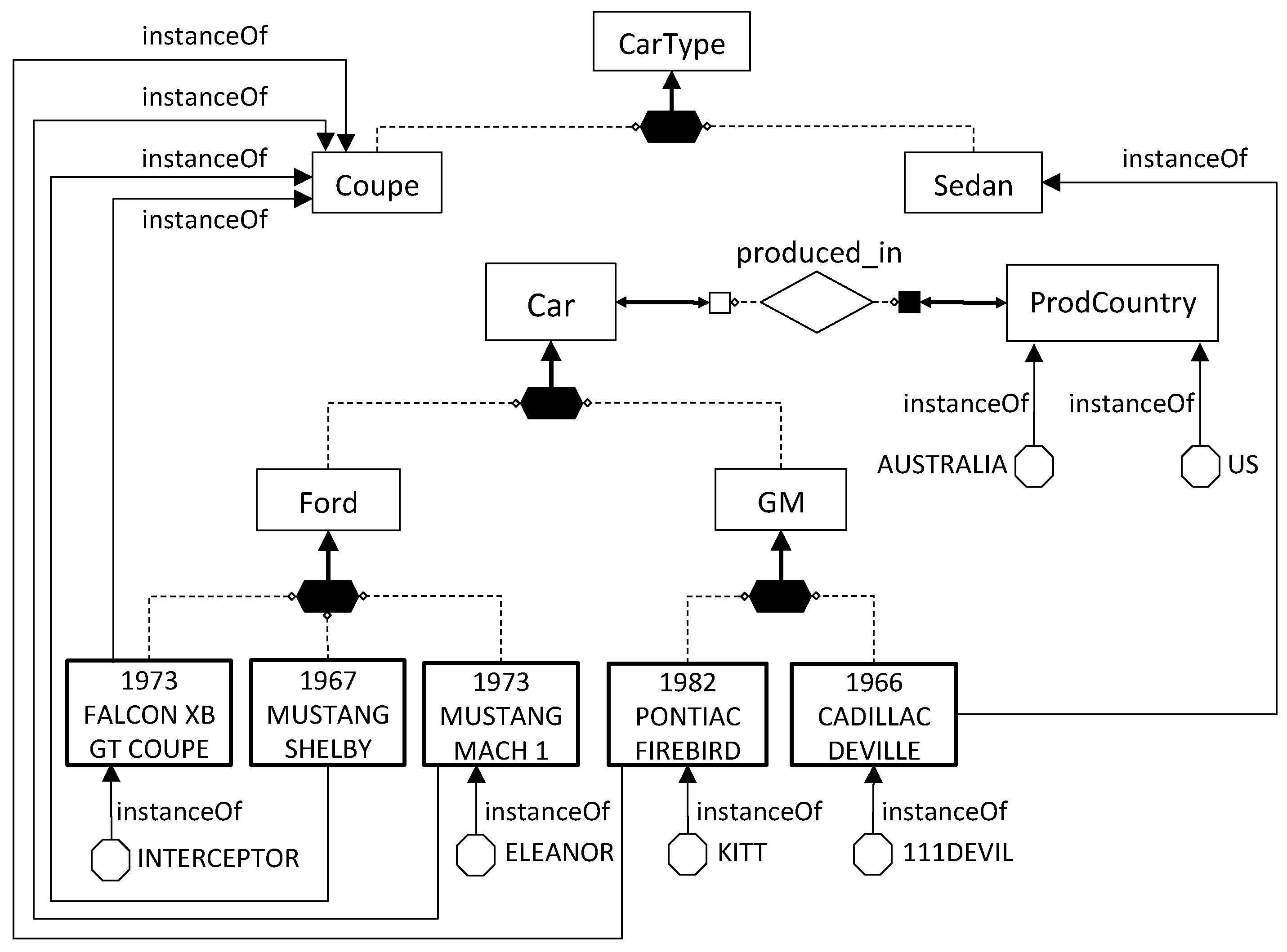
Example 3.

In Figure 4 we provide a graphical representation of a$\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$KB modeling (a portion of) the domain of cars that we use throughout the paper in our examples. The ontology is drawn in Graphol, a diagrammatic language that allows OWL ontologies to be graphically specified [25,26]. In Graphol, as in ER diagrams, concepts and roles are denoted by rectangles and diamonds, respectively, and solid directed arrows represent inclusions. The full hexagon denotes at the same time the union of the concepts connected to it through a dashed line and the disjunction of such concepts. Finally, each octagon represents an individual, and each arrow labeled instance Of from and element A to an element B specifies that A is an instance of B. In words, the ontology is saying that$\mathit{Coupe}$and$\mathit{Sedan}$are specific types of Cars (i.e., they are sub-concepts of$\mathit{CarType}$), and that they are disjoint. In addition,$1973\_\mathrm{FALCON}\_\mathrm{XB}\_\mathrm{GT}\_\mathrm{COUPE}$is an instance of Coupe (in this respect it can also be seen as an individual) and at the same time it is a concept that specializes$\mathit{Ford}$(i.e., it is a subconcept of$\mathit{Ford}$) and has$\mathrm{INTERCEPTOR}$as an instance. Finally,$\mathit{Ford}$is a subconcept of$\mathit{Car}$, and${\mathit{s}}_1$is an instance of$\mathit{Sedan}$.

Below we provide the above ontology through formulas, using the higher order notation given in this section:

$$\begin{array}{c}{\mathit{Inst}}_C(\mathrm{INTERCEPTOR},1973\_\mathrm{FALCON}\_\mathrm{XB}\_\mathrm{GT}\_\mathrm{COUPE})\hfill \\ {\mathit{Inst}}_C(1973\_\mathrm{FALCON}\_\mathrm{XB}\_\mathrm{GT}\_\mathrm{COUPE},Coupe)\hfill \\ {\mathit{Inst}}_C(s_1,Sedan)\hfill \\ {\mathit{Isa}}_C(Coupe,CarType)\hfill \\ {\mathit{Isa}}_C(Sedan,CarType)\hfill \\ {\mathit{Isa}}_C(Ford,Car)\hfill \\ {\mathit{Isa}}_C(1973\_\mathrm{FALCON}\_\mathrm{XB}\_\mathrm{GT}\_\mathrm{COUPE},Ford)\hfill \\ {\mathit{Disj}}_C(Coupe,Sedan)\hfill \end{array}$$

Notice how the second assertion exploits the meta-modeling capabilities of$\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$, i.e., it treats the concept1973_FALCON_XB_GT_COUPEas an individual instance of the concept Coupe, rather than as a concept (which is instead the way the penultimate assertion refers to it).

The semantics of $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ is based on the notion of interpretation structure. An interpretation structure is a triple $\Sigma =\langle \Delta ,{\mathcal{I}}_c,{\mathcal{I}}_r\rangle$ where (see Figure 5):

• $\Delta$ is a non-empty, possibly countably infinite, set;
• ${\mathcal{I}}_c$ is a function that maps each $d\in \Delta$ into a subset of $\Delta$; and
• ${\mathcal{I}}_r$ is a function that maps each $d\in \Delta$ into a subset of $\Delta \times \Delta$.

In other words, $\Sigma$ treats every element of $\Delta$ simultaneously as:

• an individual;
• a unary relation, i.e., a concept, through ${\mathcal{I}}_c$; and
• a binary relation, i.e., a role, through ${\mathcal{I}}_r$.

An interpretation for $\mathcal{S}$ (simply called an interpretation, when $\mathcal{S}$ is clear from the context) over the interpretation structure $\Sigma$ is a pair $\mathcal{I}=\langle \Sigma ,{\mathcal{I}}_o\rangle$, where

• $\Sigma =\langle \Delta ,{\mathcal{I}}_c,{\mathcal{I}}_r\rangle$ is an interpretation structure, and
• ${\mathcal{I}}_o$ is a function that maps:

  -

  each element of $\mathcal{S}$ to a single object in $\Delta$; and

  -

  each element $op\in \mathit{OP}({\mathit{DL-Lite}}_{\mathcal{R}})$ to a function $o{p}^{{\mathcal{I}}_o}:\Delta \to \Delta$ that satisfies the conditions characterizing the operator $op$. In particular, the conditions for the operators in $\mathit{OP}({\mathit{DL-Lite}}_{\mathcal{R}})$ are as follows:

  *

  for each $d_1,d_2\in \Delta$ such that $d_2$=${\mathit{Inv}}^{{\mathcal{I}}_o}(d_1)$, we have that $d_2^{{\mathcal{I}}_r}$=${(d_1^{{\mathcal{I}}_r})}^{-1}$, where ${(d_1^{{\mathcal{I}}_r})}^{-1}$ is the inverse of the relation $d_1^{{\mathcal{I}}_r}$, and

  *

  for each $d_1,d_2\in \Delta$ such that $d_2=\mathit{Exists}(d_1)$ we have that $d_2^{{\mathcal{I}}_c}=\{o\mid \mathrm{there}\mathrm{exists}{o}^{\prime }\mathrm{such}\mathrm{that}\langle o,o^{\prime }\rangle \in d_1^{{\mathcal{I}}_r}\}$.

We now turn our attention to the interpretation of terms in $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$. To interpret non-ground terms, we need assignments over interpretations, where an assignment $\mu$ over $\langle \Sigma ,{\mathcal{I}}_o\rangle$ is a function $\mu :\mathcal{V}\to \Delta$. Given an interpretation $\mathcal{I}=\langle \Sigma ,{\mathcal{I}}_o\rangle$ and an assignment $\mu$ over $\mathcal{I}$, the interpretation of terms is specified by the function ${(·)}^{{\mathcal{I}}_o,\mu }:{\tau }_{{\mathit{DL-Lite}}_{\mathcal{R}}}(\mathcal{S},\mathcal{V})\to \Delta$ defined as follows:

• if $e\in \mathcal{S}$ then $e^{{\mathcal{I}}_o,\mu }=e^{{\mathcal{I}}_o}$;
• if $e\in \mathcal{V}$ then $e^{{\mathcal{I}}_o,\mu }=\mu (e)$;
• $op{(e)}^{{\mathcal{I}}_o,\mu }=o{p}^{{\mathcal{I}}_o}(e^{{\mathcal{I}}_o,\mu })$.

Finally, we define the semantics of atoms, by defining the notion of satisfaction of an atom with respect to an interpretation $\mathcal{I}$ and an assignment $\mu$ over $\mathcal{I}$ as follows:

• $\mathcal{I},\mu \vDash {\mathit{Inst}}_C(e_1,e_2)$ if $e_1^{{\mathcal{I}}_o,\mu }\in {(e_2^{{\mathcal{I}}_o,\mu })}^{{\mathcal{I}}_c}$;
• $\mathcal{I},\mu$⊧${\mathit{Inst}}_R(e_1,e_2,e_3)$ if $\langle e_1^{{\mathcal{I}}_o,\mu },e_2^{{\mathcal{I}}_o,\mu }\rangle$∈${(e_3^{{\mathcal{I}}_o,\mu })}^{{\mathcal{I}}_r}$;
• $\mathcal{I},\mu \vDash {\mathit{Isa}}_C(e_1,e_2)$ if ${(e_1^{{\mathcal{I}}_o,\mu })}^{{\mathcal{I}}_c}\subseteq {(e_2^{{\mathcal{I}}_o,\mu })}^{{\mathcal{I}}_c}$;
• $\mathcal{I},\mu \vDash {\mathit{Isa}}_R(e_1,e_2)$ if ${(e_1^{{\mathcal{I}}_o,\mu })}^{{\mathcal{I}}_r}\subseteq {(e_2^{{\mathcal{I}}_o,\mu })}^{{\mathcal{I}}_r}$;
• $\mathcal{I},\mu \vDash {\mathit{Disj}}_C(e_1,e_2)$ if ${(e_1^{{\mathcal{I}}_o,\mu })}^{{\mathcal{I}}_c}\cap {(e_2^{{\mathcal{I}}_o,\mu })}^{{\mathcal{I}}_c}=Ø$;
• $\mathcal{I},\mu \vDash {\mathit{Disj}}_R(e_1,e_2)$ if ${(e_1^{{\mathcal{I}}_o,\mu })}^{{\mathcal{I}}_r}\cap {(e_2^{{\mathcal{I}}_o,\mu })}^{{\mathcal{I}}_r}=Ø$.

A $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ KB $\mathcal{H}$ is satisfied by $\mathcal{I}$ if all the assertions in $\mathcal{H}$ are satisfied by $\mathcal{I}$ (We do not need to mention assignments here, since all assertions in $\mathcal{H}$ are ground.). As usual, the interpretations $\mathcal{I}$ satisfying $\mathcal{H}$ are called the models of $\mathcal{H}$. A $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ KB $\mathcal{H}$ is satisfiable if it has at least one model.

3. Mapping-Based Knowledge Bases

In a traditional OBDA system, the axioms concerning the intensional level of the representation are stated once and for all at design time. This is a reasonable assumption in many cases, for example when the ontology is built from scratch for a specific application. However, there are application domains where, with the goal of achieving a higher level of flexibility, it is convenient to build on-the-fly the KB directly from a set of data sources, through suitable mappings that insist both on extensional information (as usual in OBDA) and intensional information. The result is that all the axioms (not only the ones relative to the extensional level, like in current OBDA systems) of the knowledge base are defined by mappings to such data sources. This is exactly the idea behind the notion of mapping-based knowledge base (MKB), that we define in detail in this section.

In what follows, we assume that the data sources are structured as a relational database. We observe that this does not hamper the generality of our work, since existing data federation tools support the designer in wrapping a set of heterogeneous data sources so as to present them as a single relational database. In addition, we assume that the relational data sources store directly the symbols in $\mathcal{S}$ and in particular the names of elements used in the MKB. In other words, here we ignore the problem of the impedance mismatch between sources that store “data values” and the MKB that contains ontology elements [20]. Note, however, that all the results presented in this paper can be extended to the case where the impedance mismatch is dealt with as in [20].

Definition 1.

A$\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ mapping-based knowledge base (MKB) is a pair $\mathcal{K}=\langle \mathit{DB},\mathcal{M}\rangle$ such that:

• $\mathit{DB}$is a relational database;
• $\mathcal{M}$is a mapping, i.e., a set of mapping assertions, each one of the form $\Phi (\overrightarrow{x})⇝\psi$, where Φ is an arbitrary FOL query over $\mathit{DB}$ of arity $n\ge 0$ with free variables $\overrightarrow{x}=\langle x_1,\dots ,x_n\rangle$, and ψ is an X-atom in ${\mathit{DL-Lite}}_{\mathcal{R}}$, with $X=\{x_1,\dots ,x_n\}$.

Note that when the arity n of $\Phi$ is 0, then $\Phi$ is a boolean query and $\psi$ is a ground atom. In particular, when the $\Phi$ is the query $\mathit{true}$, then the mapping assertion $\Phi (\overrightarrow{x})⇝\psi$ corresponds to the $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ assertion constituted by the ground atom $\psi$. In this way, we can easily specify through $\mathcal{M}$ also $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ assertions that are “static”, i.e., that do not depend on the current source database instance, and thus we do not need to include a different component in the formalization of an MKB for such static assertions.

We now turn to the semantics of a $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ MKB $\mathcal{K}=\langle \mathit{DB},\mathcal{M}\rangle$. We start by defining when an interpretation satisfies an assertion in $\mathcal{M}$ with respect to the source data $\mathit{DB}$. To this end, we make use of the notion of ground instance of an atom and the notion of answer to a query over $\mathit{DB}$. Let $\psi$ be an X-atom with $X=\{x_1,\dots ,x_n\}$, and let $\overrightarrow{v}$ be a tuple of arity n with values from $\mathit{DB}$. Then the ground instance $\psi [\overrightarrow{x}/\overrightarrow{v}]$ of $\psi$ is the formula obtained by substituting every occurrence of $x_i$ with $v_i$ (for $i\in \{1,\dots ,n\}$) in $\psi$. If $\mathit{DB}$ is a relational database, and $\Phi$ is a query over $\mathit{DB}$, we write $\mathit{ans}(\Phi ,\mathit{DB})$ to denote the set of answers to $\Phi$ over $\mathit{DB}$. With this notion at hand, we are ready to present the following definition.

Definition 2.

An interpretation$\mathcal{I}$ satisfies a mapping assertion $\Phi (\overrightarrow{x})⇝\psi$ with respect to a database $\mathit{DB}$, if for every tuple of values $\overrightarrow{v}\in \mathit{ans}(\Phi ,\mathit{DB})$, the ground atom $\psi [\overrightarrow{x}/\overrightarrow{v}]$ is satisfied by $\mathcal{I}$. The interpretation $\mathcal{I}$ is called a model of $\mathcal{K}=\langle \mathit{DB},\mathcal{M}\rangle$ if it satisfies every assertion in $\mathcal{M}$ with respect to $\mathit{DB}$.

We now present an example of MKB, with the goal of illustrating how such a notion can capture real world situations by introducing a notable flexibility in modeling the domain of interest.

Example 4.

Consider the$\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ MKB $\mathcal{K}=\langle \mathcal{D},\mathcal{M}\rangle$, where $\mathcal{D}$ is the database shown in the introduction (cf. Figure 3) and $\mathcal{M}$ is the following set of mapping assertions:

• M1:$\{m,b|$T-CarTypes$(a,m,b,c)\}⇝{\mathit{Isa}}_C(m,b)$
• M2:$\left\{b\right|$T-CarTypes$(a,m,b,c)\}⇝{\mathit{Isa}}_C(b,Car)$
• M3:$\left\{t\right|$T-CarTypes$(a,m,b,t)\}⇝{\mathit{Isa}}_C(t,\mathrm{CarType})$
• M4:$\{t1,t2|$T-CarTypes$(a,b,c,t1)\wedge$T-CarTypes$(d,e,f,t2)$$\wedge t1\ne t2\}⇝{\mathit{Disj}}_C(t1,t2)\}$
• M5:$\{m1,m2|$T-CarTypes$(c1,m1,a,b)\wedge$T-CarTypes$(c2,m2,d,e)$$\wedge m1\ne m2\}⇝{\mathit{Disj}}_C(m1,m2)$
• M6:$\mathit{true}⇝{\mathit{Isa}}_C(\mathrm{Car},\mathit{Exists}(\mathrm{produced}\_\mathrm{in}))$
• M7:$\mathit{true}⇝{\mathit{Isa}}_C(\mathrm{ProdCountry},\mathit{Exists}(\mathit{Inv}(\mathrm{produced}\_\mathrm{in})))$
• M8:$\mathit{true}⇝{\mathit{Isa}}_C(\mathit{Exists}(\mathrm{produced}\_\mathrm{in}),\mathrm{Car})$
• M9:$\mathit{true}⇝{\mathit{Isa}}_C(\mathit{Exists}(\mathit{Inv}(\mathrm{produced}\_in)),\mathrm{ProdCountry})$
• M10:$\{x,p|$T-CarTypes$(x,a,b,p)\}⇝{\mathit{Inst}}_R(x,p,\mathrm{produced}\_\mathrm{in})$
• M11:$\left\{p\right|$T-CarTypes$(a,b,c,p)\}⇝{\mathit{Inst}}_C(p,\mathrm{ProdCountry})$
• M12:$\{m,t|$T-CarTypes$(a,m,b,t)\}⇝{\mathit{Inst}}_C(m,t)$
• M13:$\{x,y|$T-CarTypes$(x,c1,a,b)\wedge$T-CarTypes$(c1,y,d,e)\}$$⇝{\mathit{Inst}}_C(x,y)$

M1 asserts that for every tuple t of theT-CarTypestable, the value appearing in the second column of t denotes a subconcept of the concept denoted by the value in the third column of the same tuple. Thus, for example, considering the fifth tuple$t_5$ofT-CarTypes, M1 states that 1973 MUSTANG MACH 1 is a subconcept of the concept Ford. M2 asserts that every value appearing in the third column ofT-CarTypesis a subconcept ofCar. For example, by referring to$t_5$again, such tuple states that Ford is a subconcept ofCar. Analogously, M3 asserts that every value appearing in the fourth column ofT-CarTypesis a subconcept ofCarType. For example,$t_5$states that Coupe is a subconcept ofCarType. M4 (resp., M5) asserts that the values appearing in the fifth column (resp., second column) ofT-CarTypesdenote concepts that are pairwise disjoint. M6–M9 assert properties about the relation produced_in, between the concepts Car and ProdCountry . M10 populates the relation produced_in, and M11 does the same for the concept ProdCountry . Mapping M12 exploits the meta-modeling capabilities of $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ and relates the different car models to their specific type. For example, looking at tuple $t_5$ again, we can infer by M12 that 1973 FALCON XB GT COUPE is an instance of the concept Coupe. Note that M1 asserted that 1973 FALCON XB GT COUPE is a concept, and therefore, we are taking advantage of the possibility provided by $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ of defining a concept to be an instance of another concept (a metaconcept). Finally, M13 allows us to correctly assign the instances stored in the T-Cars table to the concepts corresponding to the different car models. For example, through this mapping we can infer that the “Mad Max“ police car INTERCEPTOR is an instance of 1973 FALCON XB GT COUPE (see the second tuple of T-Cars ), the famous car ELEANOR of movie “Gone in 60 s“ is an instance of the concept 1973 MUSTANG MACH 1 (third tuple), and the “Supercar“ KITT is an instance of 1982 PONTIAC FIREBIRD (fourth tuple).

We hope that the above example clarifies the potential of MKBs in acquiring ontology axioms in a flexible way. In particular, let us observe how the domain ontology is dynamically built through the mapping, even though no information about the different types of cars and the different models produced by the motor companies was available at design time. Indeed, the mappings in $\mathcal{M}$ retrieve at run-time both intensional and extensional knowledge from the current database instance. Suppose, for example, that a motor company, say GM, decides to produce cars of new model, say 1967 CADILLAC ELDORADO. Given the structure of the database and its intended usage, the natural thing to do for the organization is to add suitable tuples (e.g., $\langle \mathtt{Mod}\mathtt{6},\mathtt{1967}\mathtt{CADILLACELDORADO},\mathtt{GM},\mathtt{Coupe}\rangle$) in the T-CarTypes table. In our approach, the new information is automatically detected at run-time by the mappings in $\mathcal{M}$ and correctly introduced in the ontology. So, instead of manually changing the ontology and “re-compiling it” at design time, the new concept is dynamically captured at run-time.

In Figure 6, using the Graphol language, we provide the graphical representation of the ontology dynamically constructed from the database $\mathcal{D}$ used in the example (In addition to the Graphol constructs already used in Figure 4, in Figure 6 we also use a diamond to denote a role (namely $\mathit{produced}\_\mathit{in}$), and a blank and a full box connected to such role through a dashed line in order to denote its domain and range, respectively. Moreover, the solid double arrowed line denotes a mutual inclusion between concepts (i.e, an equivalence). By using it, we say, for instance, that $\mathit{Car}$ is equivalent to the domain of $\mathit{produced}\_\mathit{in}$, that is, every car is produced somewhere and only cars are produced (somewhere). It is analogous for the range of $\mathit{produced}\_\mathit{in}$ (cf. mapping assertion M6–M9).).

We also want to add that, although the Example 4 does not show it, our framework allows variables to be used inside operators, in the right-hand side of mapping assertions. This is useful, in particular, to extract knowledge from the database catalog. For example, if FK is the database table storing information about foreign keys between binary tables, and such binary tables correspond to roles in the ontology, the mapping assertion

$$FK(x,2,y,1)⇝{\mathit{Isa}}_C(\mathit{Exists}(\mathit{Inv}(x)),y)$$

allows us to transfer the foreign key property at the level of the ontology, by correctly representing every foreign key as an inclusion between the corresponding roles.

4. Queries

In this section we describe the class of queries that we consider in this paper. We start by introducing “query atoms”. Intuitively, a query atom is an atom constituted by a meta-predicate applied to a set of arguments, where each argument is either an expression or a variable. The precise definition relies on the notion of q-terms: a q-term is any element of the set ${\tau }_{{\mathit{DL-Lite}}_{\mathcal{R}}}(\mathcal{S})\cup \mathcal{V}$. Thus a q-term is either an expression in ${\mathit{DL-Lite}}_{\mathcal{R}}$ or a variable. In other words, we do not allow for non-ground terms in queries, except for variables themselves. We are now ready to define the notion of query atom. A query atom is an atom constituted by the application of a meta-predicate in $\mathit{MP}({\mathit{DL-Lite}}_{\mathcal{R}})$ to a set of q-terms. A query atom is called ground if no variable occurs in it and is called an instance-query atom if its meta-predicate is ${\mathit{Inst}}_C$ or ${\mathit{Inst}}_R$. The definition of the syntax of the class of queries that we are interested in is as follows.

Definition 3.

A higher-order conjunctive query (HCQ) is an expression of the form

$$q(x_1,\dots ,x_n)\leftarrow a_1,\dots ,a_m$$

, where q, called the query predicate, is a symbol not in $\mathcal{S}\cup \mathcal{V}$, n is the arity of the query, every $a_i$ is a (possibly non-ground) query atom, and all variables $x_1,\dots ,x_n$ belong to $\mathcal{V}$ and occur in some $a_j$. The variables $x_1,\dots ,x_n$ are called the free variables (or distinguished variables) of the query, while the other variables occurring in $a_1,\dots ,a_m$ are called existential variables. A higher-order union of conjunctive queries (HUCQ) is a set of HCQs of the same arity with the same query predicate.

Notice that an HCQ corresponds to an HUCQ formed by a single query. A HCQ is called Boolean if it has no free variables. It is analogous for an HUCQ.

An HCQ (HUCQ) constituted by instance-query atoms only is called an instance HCQ or IHCQ (IHUCQ).

We now turn our attention to the semantics of queries. Let $\mathcal{I}$ be an interpretation and $\mu$ an assignment over $\mathcal{I}$. A Boolean HCQ q of the form $q\leftarrow a_1,\dots ,a_n$ is satisfied in $\mathcal{I},\mu$ if every query atom $a_i$ is satisfied in $\mathcal{I},\mu$.

Given a Boolean HCQ q and a $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ KB (or MKB) $\mathcal{K}$, we say that q is logically implied by $\mathcal{K}$ (denoted by $\mathcal{K}\vDash q$) if for each model $\mathcal{I}$ of $\mathcal{K}$ there exists an assignment $\mu$ such that q is satisfied by $\mathcal{I},\mu$.

Given a non-Boolean HCQ q of the form $q(e_1,\dots ,e_n)\leftarrow a_1,\dots ,a_m$, a grounding substitution of q is a substitution $\theta$ such that $e_1\theta ,\dots ,e_n\theta$ are ground terms. We call $e_1\theta ,\dots ,e_n\theta$ a grounding tuple.

Definition 4.

Given a$\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$KB$\mathcal{K}$and a non-Boolean HCQ q of the form$q(e_1,\dots ,e_n)\leftarrow a_1,\dots ,a_m$, The set of certain answers to q in $\mathcal{K}$, denoted by $\mathit{cert}(q,\mathcal{K})$, is the set of grounding tuples $e_1\theta ,\dots ,e_n\theta$ that make the Boolean query $q_{\theta }\leftarrow a_1\theta ,\dots ,a_m\theta$ logically implied by $\mathcal{K}$.

These notions extend immediately to HUCQs.

Example 5.

We illustrate some examples of HCQs that can be posed to the MKB$\mathcal{K}$of Example 4.

(i) 

Compute the instances ofFordthat were produced in Australia and are of typeCoupe; note that an instance x ofFordof certain type T is an instance of a car model y such that y is an instance of T (this in fact holds for all instances ofCar, not only for instances ofFord). It follows that the correct query expression is as follows:

$$q(x)\leftarrow {\mathit{Inst}}_C(x,Ford),{\mathit{Inst}}_C(x,y),{\mathit{Inst}}_C(y,Coupe),{\mathit{Inst}}_R(x,\mathrm{AUSTRALIA},\mathrm{produced}\_\mathrm{in}).$$

(ii) 

Compute the pairs of cars, one of type Coupe, and one of type Sedan that were produced in the same country:

$$\begin{array}{c}q(x,y)\leftarrow {\mathit{Inst}}_R(x,z,\mathrm{produced}\_\mathrm{in}),{\mathit{Inst}}_R(y,z,\mathrm{produced}\_\mathrm{in}),\hfill \\ \phantom{q(x,y)\leftarrow }{\mathit{Inst}}_C(x,v),{\mathit{Inst}}_C(y,w),{\mathit{Inst}}_C(v,Coupe),{\mathit{Inst}}_C(w,Sedan).\hfill \end{array}$$

(iii) 

Compute all the concepts in the ontology to which a given object (e.g., Eleanor) belongs to:

$$q(x)\leftarrow {\mathit{Inst}}_C(\mathrm{ELEANOR},x).$$

(iv) 

Compute all the concepts in the ontology whose instances are the concepts to which Eleanor or Kitt belong to:

$$q(y)\leftarrow {\mathit{Inst}}_C(\mathrm{ELEANOR},x),{\mathit{Inst}}_C(x,y)\cup {\mathit{Inst}}_C(\mathrm{KITT},x),{\mathit{Inst}}_C(x,y).$$

We observe that all queries in the above example are actually IHCUQs. This is the class of queries that we deal with in the next section.

5. Query Answering

In this section we study how to answer IHUCQs over $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ MKBs. In the following we consider only consistent MKBs, i.e., MKBs that have at least one model. This is indeed not a limitation, considering that consistency of a MKB can be checked through query answering, by means of methods similar to those used for checking consistency of $\mathit{DL-Lite}$ KBs [23].

Before delving into the details of our technique, we introduce some useful definitions. In what follows, we refer to a MKB $\mathcal{K}=\langle \mathit{DB},\mathcal{M}\rangle$.

• We denote by ${\mathcal{M}}_{\mathit{A}}$ the set of assertions contained in $\mathcal{M}$ having either ${\mathit{Inst}}_C$ or ${\mathit{Inst}}_R$ as predicate in their right-hand side.
• We denote by ${\mathcal{M}}_{\mathit{T}}$ the set $\mathcal{M}\backslash {\mathcal{M}}_{\mathit{A}}$, that is, the set of assertions contained in $\mathcal{M}$ having any of ${\mathit{Isa}}_C$, ${\mathit{Isa}}_R$, ${\mathit{Disj}}_C$, ${\mathit{Disj}}_R$ as predicate in their right-hand side.
• $\mathcal{M}$ is called an instance-mapping if ${\mathit{Inst}}_C$ and ${\mathit{Inst}}_R$ are the only predicates that appear in the right-hand side of the mapping assertions in $\mathcal{M}$.
• We say that e occurs as a concept argument in the atoms ${\mathit{Inst}}_C$($e,e^{\prime }$), ${\mathit{Isa}}_C$($e,e^{\prime }$), ${\mathit{Isa}}_C$($e^{\prime },e$), ${\mathit{Disj}}_C$($e,e^{\prime }$), and ${\mathit{Disj}}_C$($e^{\prime },e$).
• We say that e occurs as a role argument in the atoms ${\mathit{Inst}}_R$($e^{\prime },e^{\prime \prime },e$), ${\mathit{Isa}}_R$($e,e^{\prime }$), ${\mathit{Isa}}_R$($e^{\prime },e$), ${\mathit{Disj}}_R$($e,e^{\prime }$), and ${\mathit{Disj}}_R$($e^{\prime },e$).
• A $DL$ atom is an atom of the form $N(e)$ or $N(e_1,e_2)$, where N is a name and $e,e_1,e_2$ are either variables or names.
• An extended CQ (ECQ) is an expression of the form $q(x_1,\dots ,x_n)\leftarrow a_1,\dots ,a_m$ such that $x_1,\dots ,x_n$ belong to $\mathcal{V}$, $a_1,\dots ,a_m$ is a conjunction of atoms, each atom $a_j$ (with $1\le j\le m$) is either a $DL$ atom or an instance-query atom (i.e., an atom whose meta-predicate is ${\mathit{Inst}}_C$ or ${\mathit{Inst}}_R$), and each $x_i$ (with $1\le j\le n$) occurs in at least one $a_j$. An extended UCQ (EUCQ) is a union of ECQs.
• Given a TBox $\mathcal{T}$ (specified in high-order style syntax, cf. Section 2), we define $\mathit{Concepts}(\mathcal{T})=\{e,\mathit{Exists}(e^{\prime }),\mathit{Exists}(\mathit{Inv}(e^{\prime }))\mid e$ occurs as a concept argument in $\mathcal{T} \mathrm{and} e^{\prime }$ occurs as a role argument in $\mathcal{T}\}$, and $\mathit{Roles}(\mathcal{T})=$$\{e,\mathit{Inv}(e)\mid e$ occurs as a role argument in $\mathcal{T}\}$.
• Given a mapping $\mathcal{M}$ and a database $\mathit{DB}$, $\mathit{Retrieve}(\mathcal{M},\mathit{DB})$ denotes the $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ KB $\mathcal{H}$ defined as follows:

  $$\mathcal{H}=\{\psi (\overrightarrow{t})\mid \Phi (\overrightarrow{x})⇝\psi \in \mathcal{M}\mathrm{and}\mathit{DB}\vDash (\overrightarrow{t})\}$$

  where $\overrightarrow{t}$ is a tuple of constants and $\overrightarrow{x}$ is a tuple of variables having the same arity.
• Given an instance-mapping $\mathcal{M}$ and an ABox $\mathcal{A}$, we say that $\mathcal{A}$ is retrievable through $\mathcal{M}$ if there exists a database $\mathit{DB}$ such that $\mathcal{A}=\mathit{Retrieve}(\mathcal{M},\mathit{DB})$.

The query answering technique we are about to present is based on the following four main steps.

• In the first step, all intensional assertions are gathered by accessing the sources and using the mapping, in particular the ${\mathcal{M}}_{\mathit{T}}$ portion. This way, a ${\mathit{DL-Lite}}_{\mathcal{R}}$ TBox $\mathcal{T}$ is available for the subsequent steps.
• In the second step, the input query is rewritten on the basis of $\mathcal{T}$, using the algorithm $\mathit{PerfectRef}$ presented in [23]. In fact this is not just a trivial call to $\mathit{PerfectRef}$, since we need to transform the input IHUCQ, which cannot be given directly in input to $\mathit{PerfectRef}$, into a EUCQ. Similarly, we also need to translate the rewriting produced by $\mathit{PerfectRef}$ in a form that is compatible with the syntax used in the mapping (which is required by the following steps of our algorithm).
• In the third step, the query obtained by the second step is unfolded using the mapping, in particular the ${\mathcal{M}}_{\mathit{A}}$ portion, so as to obtain a query expressed over the alphabet of the source schema.
• In the fourth step, the query obtained by the third step is evaluated over the source data, so as to obtain the final result.

In Section 5.1 we deal with the second step of our technique. In particular, we study the problem of computing a perfect rewriting of an IHUCQ over a ${\mathit{DL-Lite}}_{\mathcal{R}}$ TBox. We recall that given a query q, a perfect rewriting of q with respect to a TBox $\mathcal{T}$ is a query $q^{\prime }$ such that, for every ABox $\mathcal{A}$, $\mathit{cert}(q,\mathcal{T}\cup \mathcal{A})=\mathit{cert}(q^{\prime },\mathcal{A})$ [23]. That is, to obtain the certain answers to q in $\mathcal{T}\cup \mathcal{A}$, it is sufficient to evaluate $q^{\prime }$ over $\mathcal{A}$ seen as a database (such an evaluation indeed returns the certain answers to q in $\mathcal{A}$). As said, in our rewriting algorithm we first retrieve a TBox through the mapping (step 1). We thus adapt the above notion to the context of MKBs as follows. Given an MKB $\mathcal{K}=\langle DB,\mathcal{M}\rangle$, let $\mathcal{T}=\mathit{Retrieve}({\mathcal{M}}_{\mathit{T}},DB)$, a perfect rewriting to q with respect to $\mathcal{T}$ and the instance-mapping ${\mathcal{M}}_A$ is a query $q^{\prime }$ such that, for every ABox $\mathcal{A}$ retrievable through ${\mathcal{M}}_A$, $\mathit{cert}(q,{\mathcal{M}}_T\cup \mathcal{A})=\mathit{cert}(q^{\prime },\mathcal{A})$.

After the detailed description of the second step above, in the subsequent Section 5.2, we present the complete query answering algorithm for MKBs based on our perfect rewriting technique.

5.1. Query Rewriting

The basic idea of our technique is to reduce the computation of the perfect rewriting of an IHUCQ over a ${\mathit{DL-Lite}}_{\mathcal{R}}$ TBox to the computation of the perfect rewriting of an UCQ over a ${\mathit{DL-Lite}}_{\mathcal{R}}$ TBox, which can be then done by using the algorithm $\mathit{PerfectRef}$ described in [23].

To this aim, we first transform the IHUCQ into a standard UCQ, actually an EUCQ. This is realized through a first partial grounding of the query, using the function $\mathit{PMG}$ and then through the functions $\mathit{Normalize}$ and $\tau$. In particular, the function $\mathit{PMG}$ eliminates the meta-variables, i.e., the variables occurring as a concept or as a role argument, from the query, $\mathit{Normalize}$ substitutes ${\mathit{Inst}}_C$ atoms whose second argument is of the form $\mathit{Exists}(e)$ into ${\mathit{Inst}}_R$ atoms (i.e., the instance of the domain or the range of a role expression e is reformulated as an instance of e), and $\tau$ transforms ${\mathit{Inst}}_C$ and ${\mathit{Inst}}_R$ atoms in DL atoms.

Afterwards, the query resulting from the perfect rewriting of the EUCQ is transformed back into an IHUCQ, by the functions $\mathit{Denormalize}$ and ${\tau }^{-}$. This is because the third step of the query answering algorithm assumes the query to be an IHUCQ.

We now describe in more detail the functions $\mathit{PMG}$, $\mathit{Normalize}$, $\mathit{Denormalize}$, $\tau$ and ${\tau }^{-}$.

If $q,q^{\prime }$ are two IHCQs, and $\mathcal{T}$ is a TBox, then $q^{\prime }$ is a partial metagrounding of q with respect to $\mathcal{T}$ if $q^{\prime }=\sigma (q)$, where $\sigma$ is a partial substitution of the meta-variables of q with the expressions occurring in $\mathcal{T}$ such that, for each meta-variable x of q, either $\sigma (x)=x$ or:

-

if x occurs in a concept position in q, then $\sigma (x)\in \mathit{Concepts}(\mathcal{T})$;

-

if x occurs in a role position in q, then $\sigma (x)\in \mathit{Roles}(\mathcal{T})$.

Given an IHCQ q and a TBox $\mathcal{T}$, the function $\mathit{PMG}$ applied to q and $\mathcal{T}$ computes the set of all partial metagroundings of q with respect to $\mathcal{T}$, i.e., it computes the IHUCQ $Q=\{q^{\prime }\mid q^{\prime } \mathrm{is} \mathrm{a} \mathrm{partial} \mathrm{metagrounding} \mathrm{of} q \mathrm{w}.\mathrm{r}.\mathrm{t}.\mathcal{T}\}$. When applied to an IHUCQ Q and a TBox $\mathcal{T}$, the function $\mathit{PMG}$ computes the IHUCQ ${\bigcup }_{q\in Q}\mathit{PMG}(q,\mathcal{T})$.

Example 6.

Consider the MKB$\mathcal{K}=\langle \mathcal{D},\mathcal{M}\rangle$given in Example 4, the TBox$\mathcal{T}$dynamically constructed from$\mathcal{D}$through$\mathcal{M}$, and represented inFigure 6, and the query (i) given in Example 5. Then,$\mathit{Concepts}(\mathcal{T})=\{Car,Coupe,Ford,\cdots ,\mathtt{1973} \mathit{FALCON} \mathit{XB} \mathit{GT} \mathit{COUPE},\cdots ,Exists(produced\_in),\cdots \}$,$\mathit{Roles}(\mathcal{T})=\{produced\_in,\mathit{Inv}(produced\_in)\}$, and$\mathit{PMG}(q,\mathcal{T})$, contains, among other queries, the query:

$$q(x)\leftarrow {\mathit{Inst}}_C(x,Ford),{\mathit{Inst}}_C(x,\mathit{FALCON}),{\mathit{Inst}}_C(\mathit{FALCON},Coupe),{\mathit{Inst}}_R(x,\mathrm{AUSTRALIA},\mathrm{produced}\_\mathrm{in})$$

(1)

where we abbreviated1973 FALCON XB GT COUPEintoFALCON(to obtain all other queries in$\mathit{PMG}(q,\mathcal{T})$substituteFALCONwith all elements of$\mathit{Concepts}(\mathcal{T})$).

Notice that the notion of partial metagrounding $\mathit{PMG}$ is crucial for our rewriting method. Indeed, even if in $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ the set of expressions that can be constructed from a finite set of names occurring in the TBox is infinite, we can in fact limit to ground the meta-variables in the query on a finite set of expressions only, as stated by the following lemma.

Lemma 1.

If Q is an IHUCQ, and$\mathcal{T}$is a TBox, then for every ABox$\mathcal{A}$,$\mathit{cert}(Q,\mathcal{T}\cup \mathcal{A})=\mathit{cert}(\mathit{PMG}(Q,\mathcal{T}),\mathcal{T}\cup \mathcal{A})$.

Proof. 

Assume $\mathit{cert}(Q,\mathcal{T}\cup \mathcal{A})\ne \mathit{cert}(\mathit{PMG}(Q,\mathcal{T}),\mathcal{T}\cup \mathcal{A})$. It is easy to prove that $\mathit{cert}(Q,\mathcal{T}\cup \mathcal{A})\supset \mathit{cert}(\mathit{PMG}(Q,\mathcal{T}),\mathcal{T}\cup \mathcal{A})$. Thus, there exists a tuple t such that $t\in \mathit{cert}(Q,\mathcal{T}\cup \mathcal{A})-\mathit{cert}(\mathit{PMG}(Q,\mathcal{T}),\mathcal{T}\cup \mathcal{A})$. This implies that there exists a model $\mathcal{I}$ for $\mathcal{T}\cup \mathcal{A}$ such that $\mathcal{I}\vDash Q(t)$ and $\mathcal{I}\neg \vDash \mathit{PMG}(Q,\mathcal{T})(t)$. Let $\Delta$ be the domain of $\mathcal{I}$. We define below an interpretation ${\mathcal{I}}^{\downarrow }$ over the same domain $\Delta$. For every $d\in \Delta$:

• $d^{{\mathcal{I}}_0^{\downarrow }}=d^{{\mathcal{I}}_0}$;
• $d^{{\mathcal{I}}_c^{\downarrow }}=d^{{\mathcal{I}}_c}$ if there exists $e\in \mathit{Concepts}(\mathcal{T})$ such that $e^{{\mathcal{I}}_0}=d$, otherwise $d^{{\mathcal{I}}_c^{\downarrow }}=Ø$;
• $d^{{\mathcal{I}}_r^{\downarrow }}=d^{{\mathcal{I}}_r}$ if there exists $e\in \mathit{Roles}(\mathcal{T})$ such that $e^{{\mathcal{I}}_0}=d$, otherwise $d^{{\mathcal{I}}_r^{\downarrow }}=Ø$.

It is easy to see that ${\mathcal{I}}^{\downarrow }$ is a model for the KB $\mathcal{T}\cup \mathcal{A}$. However, it is also straightforward to verify that ${\mathcal{I}}^{\downarrow }\vDash Q(t)$ if and only if ${\mathcal{I}}^{\downarrow }\vDash \mathit{PMG}(Q,T)(t)$, and since by hypothesis $\mathcal{I}\neg \vDash \mathit{PMG}(Q,T)(t)$, then ${\mathcal{I}}^{\downarrow }\neg \vDash \mathit{PMG}(Q,T)(t)$ as well. As a consequence, ${\mathcal{I}}^{\downarrow }\neg \vDash Q(t)$, which contradicts the hypothesis that $t\in \mathit{cert}(Q,\mathcal{T}\cup \mathcal{A})$, thus proving the thesis. □

We now turn our attention to the functions $\mathit{Normalize}$ and $\mathit{Denormalize}$.

Let $\alpha$ be an instance atom, $\mathit{Normalize}(\alpha )$ returns a new atom defined as follows:

• if $\alpha ={\mathit{Inst}}_C(e_1,e_2)$ and $e_2$ has the form $\mathit{Exists}(e^{\prime })$ where $e^{\prime }$ is an expression which is not of the form $\mathit{Inv}(e^{\prime \prime })$, then $\mathit{Normalize}(\alpha )={\mathit{Inst}}_R(e_1,\_,e^{\prime })$, where _ denotes an existentially quantified variables;
• if $\alpha ={\mathit{Inst}}_C(e_1,e_2)$ and $e_2$ has the form $\mathit{Exists}(\mathit{Inv}(e^{\prime }))$ where $e^{\prime }$ is any expression, then $\mathit{Normalize}(\alpha )={\mathit{Inst}}_R(\_,e_1,e^{\prime })$.

The above definition naturally extends to queries. More precisely, let $q\leftarrow {\alpha }_1,\dots ,{\alpha }_n$ be an IHCQ, $\mathit{Normalize}(q)$ computes the IHCQ $q\leftarrow \mathit{Normalize}({\alpha }_1),\dots ,\mathit{Normalize}({\alpha }_n)$. Finally, if Q is an IHUCQ, then $\mathit{Normalize}(Q)$ returns the query ${\bigcup }_{q\in Q}\mathit{Normalize}(q)$. As an example, consider the query

$$\begin{array}{ccc}q(x)\hfill & \leftarrow & {\mathit{Inst}}_C(x,Ford),{\mathit{Inst}}_C(x,Exists(produced\_in)),{\mathit{Inst}}_R(x,\mathrm{AUSTRALIA},produced\_in).\hfill \end{array}$$

$\mathit{Normalize}(q)$ returns the query

$$\begin{array}{ccc}q(x)\hfill & \leftarrow & {\mathit{Inst}}_C(x,Ford),{\mathit{Inst}}_R(x,\_,produced\_in),{\mathit{Inst}}_R(x,\mathrm{AUSTRALIA},produced\_in).\hfill \end{array}$$

Then, let q be an IHCQ and $\mathcal{M}$ be an instance-mapping, $\mathit{Denormalize}(q,\mathcal{M})$ is the IHUCQ Q defined inductively as follows:

• $q\in Q$;
• if $q^{\prime }\in Q$ and $q^{\prime }$ contains an atom $\alpha$ of the form ${\mathit{Inst}}_R(e_1,\_,e_2)$, and either $\mathit{Exists}(e_2)$ occurs in $\mathcal{M}$ or $\mathit{Exists}(x)$ (where x is a variable) occurs in $\mathcal{M}$, then the query obtained from $q^{\prime }$ by replacing $\alpha$ with the atom ${\mathit{Inst}}_C(e_1,\mathit{Exists}(e_2))$ belongs to Q;
• if $q^{\prime }\in Q$ and $q^{\prime }$ contains an atom $\alpha$ of the form ${\mathit{Inst}}_R(\_,e_1,e_2)$, and either $\mathit{Exists}(\mathit{Inv}(e_2))$ occurs in $\mathcal{M}$ or $\mathit{Exists}(\mathit{Inv}(x))$ (where x is a variable) occurs in $\mathcal{M}$, then the query obtained from $q^{\prime }$ by replacing $\alpha$ with the atom ${\mathit{Inst}}_C(e_1,\mathit{Exists}(\mathit{Inv}(e_2)))$ belongs to Q;
• if $q^{\prime }\in Q$ and $q^{\prime }$ contains an atom $\alpha$ of the form ${\mathit{Inst}}_R(e_1,e_2,e_3)$ and either $\mathit{Inv}(e_3)$ occurs in $\mathcal{M}$ or $\mathit{Inv}(x)$ (where x is a variable) occurs in $\mathcal{M}$, then the query obtained from $q^{\prime }$ by replacing $\alpha$ with the atom ${\mathit{Inst}}_R(e_2,e_1,\mathit{Inv}(e_3))$ belongs to Q.

Finally, let Q be an IHUCQ and let $\mathcal{M}$ be a mapping, we define $\mathit{Denormalize}(Q,\mathcal{M})$ as ${\bigcup }_{q\in Q}\mathit{Denormalize}(q,\mathcal{M})$.

We formally introduce below the functions $\tau$ and ${\tau }^{-}$, which transform IHUCQs into EUCQs and vice versa. Let q be an IHCQ and let $\mathcal{T}$ be a TBox, $\tau (q,\mathcal{T})$ is the ECQ obtained from q as follows:

• each atom of q of the form ${\mathit{Inst}}_C(e_1,e_2)$, such that $e_2\in \mathit{Concepts}(\mathcal{T})$, is replaced with the atom $e_2(e_1)$;
• each atom of q of the form ${\mathit{Inst}}_R(e_1,e_2,e_3)$, such that $e_3\in \mathit{Roles}(\mathcal{T})$, is replaced with the atom $e_3(e_1,e_2)$.

Example 7.

Let us now apply the function τ to the query (1) (which is already normalized), and obtain the query

$$q(x)\leftarrow Ford(x),\mathit{FALCON}(x),Coupe(\mathit{FALCON}),produced\_in(x,\mathrm{AUSTRALIA}).$$

(2)

Then, given an IHUCQ Q, we define $\tau (Q,\mathcal{T})=\{\tau (q,\mathcal{T})\mid q\in Q\}$.

Let q be an ECQ and $\mathcal{T}$ be a TBox, then ${\tau }^{-}(q,\mathcal{T})$ is the IHCQ obtained from q as follows:

• each atom of q of the form $e_2(e_1)$ is replaced with the atom ${\mathit{Inst}}_C(e_1,e_2)$;
• each atom of q of the form $e_3(e_1,e_2)$ is replaced with the atom ${\mathit{Inst}}_R(e_1,e_2,e_3)$.

Then, given an IHUCQ Q, we define ${\tau }^{-}(Q,\mathcal{T})=\{{\tau }^{-}(q,\mathcal{T})\mid q\in Q\}$. An example of application of ${\tau }^{-}(Q,\mathcal{T})$ can be obtained by simply reversing the transformation shown in Example 7.

We can now formally define our algorithm for query rewriting. The algorithm takes as input an IHUCQ, a TBox and an instance-mapping, and returns a new IHUCQ. Given an IHUCQ Q and a TBox $\mathcal{T}$, we denote by $\mathit{PerfectRef}(Q,\mathcal{T})$ the EUCQ returned by the query rewriting algorithm for ${\mathit{DL-Lite}}_{\mathcal{R}}$ presented in [23] (Actually, we consider a slight generalization of that algorithm, allowing for the presence of a ternary relation (${\mathit{Inst}}_R$) in the query.).

ALGORITHM $\mathit{RewriteIHUCQ}(Q,\mathcal{T},\mathcal{M})$

INPUT: IHUCQ Q, ${\mathit{DL-Lite}}_{\mathcal{R}}$ TBox $\mathcal{T}$, instance-mapping $\mathcal{M}$

OUTPUT: IHUCQ $Q^{\prime }$

begin

 $Q_0=\mathit{PMG}(Q,\mathcal{T})$;

 $Q_1=\mathit{Normalize}(Q_0)$;

 $Q_2=\tau (Q_1,\mathcal{T})$;

 $Q_3=\mathit{PerfectRef}(Q_2,\mathcal{T})$;

 $Q_4={\tau }^{-}(Q_3,\mathcal{T})$;

 $Q^{\prime }=\mathit{Denormalize}(Q_4,\mathcal{M})$;

 return $Q^{\prime }$;

end

Example 8.

To provide an example of a complete execution of the algorithm$\mathit{RewriteIHUCQ}(Q,\mathcal{T},\mathcal{M})$, let us now continue the rewriting described in Example 6 and in Example 7. Let us focus on the$\mathit{PerfectRef}$function, and apply it to the query (2) (which is contained in the set$Q_2$of CQs).$\mathit{PerfectRef}$transforms the atoms of the query using TBox inclusions as rewriting rules, from right to left. For example, according to the inclusionFALCON ⊑ Ford, it rewrites the atom $Ford(x)$ in query (2) into the atom FALCON (x) (intuitively, the $\mathit{PerfectRef}$ encodes in the rewriting the knowledge expressed by the ontology saying that to obtain instances of $Ford$ one has to look also for instances of FALCON). In this way $\mathit{PerfectRef}$ produces the following query and adds it to the set $Q_3$ (notice that the atom FALCON(x) was already present in the query, thus the effect of the rewriting in this case is simply dropping the first atom of the query):

$$q(x)\leftarrow \mathit{FALCON}(x),Coupe(\mathit{FALCON}),produced\_in(x,\mathrm{AUSTRALIA}).$$

(3)

A similar reformulation is performed for all atoms whose predicate occurs in the right-hand side of a positive inclusion (provided that its arguments are not bound, as described in [23]). Among the queries returned by $\mathit{PerfectRef}$ we consider in the following only query (3), which, as we will see later, will allow us to obtain the answer to the original query (the other queries returned by $\mathit{RewriteIHUCQ}(Q,\mathcal{T},\mathcal{M})$ do not really contribute to the final answer in our example). Finally, $\mathit{RewriteIHUCQ}(Q,\mathcal{T},\mathcal{M})$ applies ${\tau }^{-}$ and $\mathit{Denormalize}$ (which in this case is immaterial) to query (3), thus returning the query

$$q(x)\leftarrow {\mathit{Inst}}_C(x,\mathit{FALCON}),{\mathit{Inst}}_C(\mathit{FALCON},Coupe),{\mathit{Inst}}_R(x,\mathrm{AUSTRALIA},\mathrm{produced}\_\mathrm{in}).$$

(4)

The IHUCQ returned by $\mathit{RewriteIHUCQ}(Q,\mathcal{T},\mathcal{M})$ constitutes a perfect rewriting of the query Q with respect to the TBox $\mathcal{T}$ and the mapping $\mathcal{M}$, as formally stated by the following theorem.

Theorem 1.

Let$\mathcal{T}$be a TBox, let$\mathcal{M}$be an instance-mapping and let Q be an IHUCQ. Then, for every ABox$\mathcal{A}$that is a retrievable through$\mathcal{M}$,$\mathit{cert}(Q,\mathcal{T}\cup \mathcal{A})=\mathit{cert}(\mathit{RewriteIHUCQ}(Q,\mathcal{T},\mathcal{M}),\mathcal{A})$.

Proof. 

The proof follows from Definition 4, from Lemma 1, from the correctness of the algorithm $\mathit{PerfectRef}$ [23], and from the fact that the functions $\mathit{Normalize}$, $\tau$, ${\tau }^{-}$ and $\mathit{Denormalize}$ just perform equivalent transformations of the query. □

5.2. Query Answering

We now provide an algorithm for query answering over MKBs, which makes use of the query rewriting technique presented in the previous subsection. As already said, our idea is to first compute a ${\mathit{DL-Lite}}_{\mathcal{R}}$ TBox by evaluating the mapping assertions involving the predicates ${\mathit{Isa}}_C$, ${\mathit{Isa}}_R$, ${\mathit{Disj}}_C$, ${\mathit{Disj}}_R$ over the database of the MKB; then, such a TBox is used to compute the perfect rewriting of the input IHUCQ.

To complete query answering, we have to also consider the mapping of the predicates ${\mathit{Inst}}_C$ and ${\mathit{Inst}}_R$ and reformulate the query thus obtained by replacing the above predicates with the FOL queries occurring in the corresponding mapping assertions (step 3 of our technique). In this way we obtain an FOL query expressed over the database. This second rewriting step, usually called unfolding, can be performed by the algorithm $\mathsf{UnfoldDB}$ presented in [20] (Here, we assume that the algorithm $\mathsf{UnfoldDB}$ takes as input an EUCQ and an instance-mapping. This corresponds to actually considering a straightforward extension of the algorithm presented in [20] in order to deal with the presence of the ternary predicate ${\mathit{Inst}}_R$.). In the following, given a mapping $\mathcal{M}$ and a database $\mathit{DB}$, we denote by ${\mathit{DB}}_{{\mathcal{M}}_{\mathit{T}}}$ the database constituted by every relation R of $\mathit{DB}$ such that R occurs in ${\mathcal{M}}_{\mathit{T}}$. Furthermore, we define ${\mathit{DB}}_{{\mathcal{M}}_{\mathit{A}}}$ as the database ${\mathit{DB-DB}}_{{\mathcal{M}}_{\mathit{T}}}$ (i.e., ${\mathit{DB}}_{{\mathcal{M}}_{\mathit{A}}}$ is the portion of $\mathit{DB}$ which is not involved by the mapping ${\mathcal{M}}_{\mathit{T}}$). We are now ready to present our query answering algorithm.

ALGORITHM $\mathit{Answer}(Q,\mathcal{K})$

INPUT: IHUCQ Q, $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ MKB $\mathcal{K}=\langle \mathit{DB},\mathcal{M}\rangle$

OUTPUT: $\mathit{cert}(Q,K)$

begin

 $\mathcal{T}=\mathit{Retrieve}({\mathcal{M}}_{\mathit{T}},{\mathit{DB}}_{{\mathcal{M}}_{\mathit{T}}})$;

 $Q^{\prime }=\mathit{RewriteIHUCQ}(Q,\mathcal{T},{\mathcal{M}}_{\mathit{A}})$;

 $Q^{″}=\mathsf{UnfoldDB}(Q^{\prime },{\mathcal{M}}_{\mathit{A}})$;

 return$\mathit{IntEval}(Q^{″},{\mathit{DB}}_{{\mathcal{M}}_{\mathit{A}}})$

end

The algorithm starts by retrieving (function $\mathit{Retrieve}({\mathcal{M}}_{\mathit{T}},{\mathit{DB}}_{{\mathcal{M}}_{\mathit{T}}})$) the TBox $\mathcal{T}$ from ${\mathit{DB}}_{{\mathcal{M}}_{\mathit{T}}}$ through the mapping ${\mathcal{M}}_{\mathit{T}}$. Then, it computes (function $\mathit{RewriteIHUCQ}(Q,\mathcal{T},{\mathcal{M}}_{\mathit{A}})$) the perfect rewriting of the query with respect to the retrieved TBox and next computes (function $\mathsf{UnfoldDB}(Q^{\prime },{\mathcal{M}}_{\mathit{A}})$) the unfolding of such a query with respect to the mapping ${\mathcal{M}}_{\mathit{A}}$. Finally, it evaluates (function $\mathit{IntEval}(Q^{″},{\mathit{DB}}_{{\mathcal{M}}_{\mathit{A}}})$ the query over the database and returns the result of the evaluation.

Example 9.

Let us consider again the MKD system and the query of Example 6. We notice that${\mathcal{M}}_{\mathit{T}}$and${\mathcal{M}}_{\mathit{A}}$consists of the mapping assertions M1-M9 and M10-M-13 given in Example 4, respectively, and${\mathit{DB}}_{{\mathcal{M}}_{\mathit{T}}}={\mathit{DB}}_{{\mathcal{M}}_{\mathit{A}}}$coincides with the database$\mathcal{D}$described in Figure 3. Thus, the TBox$\mathcal{T}$returned by$\mathit{Retrieve}({\mathcal{M}}_{\mathit{T}},{\mathit{DB}}_{{\mathcal{M}}_{\mathit{T}}})$coincides with the TBox described in Figure 6 (not considering InstanceOf arrows).$Q^{\prime }$is as discussed in Example 8. As said, amog all queries in$Q^{\prime }$we consider only query (4). By unfolding it through$\mathsf{UnfoldDB}(Q^{\prime },{\mathcal{M}}_{\mathit{A}})$, we obtain (among other queries) the FOL query

$$\begin{array}{ccc}\{x\hfill & |& \mathit{T-Cars}(x,c1,a,b)\wedge \mathit{T-CarTypes}(c1,FALCON,d,e)\wedge \mathit{T-CarTypes}(a^{\prime },FALCON,b^{\prime },coupe)\wedge \hfill \\ & & \mathit{T-Cars}(x,a^{″},b^{″},\mathrm{AUSTRALIA})\}\hfill \end{array}$$

More in detail, we have unfolded the atom${\mathit{Inst}}_C(x,FALCON)$using mapping M13, atom${\mathit{Inst}}_C(FALCON,coupe)$using mapping M12, and the atom${\mathit{Inst}}_R(x,\mathrm{AUSTRALIA},produced\_in)$using mapping M10. Notice also that other queries are produced by the function$\mathsf{UnfoldDB}$applied to the query (4) and the${\mathcal{M}}_{\mathit{A}}$(e.g., by unfolding${\mathit{Inst}}_C(FALCON,coupe)$through M12). However, the one we showed is sufficient to obtain the answers to the original query. It is indeed easy to see that by evaluating the above query over${\mathit{DB}}_{{\mathcal{M}}_{\mathit{A}}}$(see Figure 3), we obtain the answerINTERCEPTOR, and this is the only answer to the query (i) given in Example 5 evaluated over the MKD system$\mathcal{K}$.

To prove correctness of the above algorithm, we first state the following property, whose proof immediately follows from the definition of $\mathit{Retrieve}(\mathcal{M},\mathit{DB})$ and the definition of model of a $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ MKB.

Lemma 2.

Let$\mathcal{K}=\langle \mathit{DB},\mathcal{M}\rangle$be a$\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$MKB and let$\mathcal{H}=\mathit{Retrieve}(\mathcal{M},\mathit{DB})$. The set of models of$\mathcal{K}$and$\mathcal{H}$coincide.

We also need the following additional property.

Lemma 3.

Let$\mathcal{M}$be an instance-mapping, and let Q be an IHUCQ. Then, for every database$\mathit{DB}$,

$$\mathit{cert}(Q,\langle \mathcal{M},\mathit{DB}\rangle )=\mathit{IntEval}(\mathsf{UnfoldDB}(Q,\mathcal{M}),\mathit{DB}).$$

Proof. 

The proof follows from Definition 4 and by a natural, slight extension (which we leave to the reader) of the proof of correctness of the algorithm $\mathsf{UnfoldDB}$ shown in [20]. □

We are now ready to show the correctness of the algorithm $\mathit{Answer}$.

Theorem 2.

Let$\mathcal{K}$=$\langle \mathit{DB},\mathcal{M}\rangle$be a$\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$MKB, let Q be an IHUCQ, and let U be the set of tuples returned by$\mathit{Answer}(Q,\mathcal{K})$. Then,$\mathit{cert}(Q,\mathcal{K})=U$.

Proof. 

The proof immediately follows from Theorem 1 and Lemmas 2 and 3. □

Finally, from the algorithm $\mathit{Answer}$ we are able to derive the following complexity results for query answering over $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ MKBs.

Theorem 3.

Let$\mathcal{K}$=$\langle \mathit{DB},\mathcal{M}\rangle$be a$\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$MKB, let Q be an IHUCQ and let$\overrightarrow{t}$be a tuple of expressions. Deciding whether$\mathcal{K}\vDash Q(\overrightarrow{t})$is in$A{C}^0$with respect to the size of${\mathit{DB}}_{{\mathcal{M}}_{\mathit{A}}}$, is in PSPACE with respect to the size of$\mathcal{K}$, and is NP-complete with respect to the size of$Q(\overrightarrow{t})$.

Proof. 

To decide whether $\mathcal{K}\vDash Q(\overrightarrow{t})$ we can execute $\mathit{Answer}(Q(\overrightarrow{t}),\mathcal{K})$. Then, membership in $A{C}^0$ with respect to the size of ${\mathit{DB}}_{{\mathcal{M}}_{\mathit{A}}}$ follows from the fact that the only step of the algorithm $\mathit{Answer}$ that depends on ${\mathit{DB}}_{{\mathcal{M}}_{\mathit{A}}}$ is $\mathit{IntEval}(Q^{″},{\mathit{DB}}_{{\mathcal{M}}_{\mathit{A}}})$, where $Q^{″}$ is a FOL query and the fact that evaluating an FOL query over a database is in $A{C}^0$ in data complexity. Membership in PSPACE with respect to the size of $\mathcal{K}$ follows from the fact that evaluating a FOL query is in PSPACE in combined complexity (whereas the other steps of the algorithm $\mathit{Answer}$ are in PTIME with respect to the size of the $\mathcal{K}$). Finally, NP-completeness with respect to the size of $Q(\overrightarrow{t})$ follows from Lemma 2, from the fact that computing $\mathit{Retrieve}(\mathcal{M},DB)$ can obviously be done in constant time with respect to the size of $Q(\overrightarrow{t})$ and from the fact that evaluating an IHUCQ over a $\mathit{Hi}({\mathit{DL-Lite}}_{\mathcal{R}})$ KB is NP-complete in query complexity. □

6. Conclusions

In this paper we have investigated the issue of generating both the TBox and the ABox of a DL ontology on the fly from data stored in data sources through asserted mappings. The two main ingredients for obtaining such a degree of flexibility are $(i)$ enriching the mapping language so as to extract from the data sources the knowledge about possible concepts and roles that are relevant to the domain of interest and $(ii)$ relying on higher-order description logics which blur the distinction between concepts/roles at the intensional level and individuals at the extensional level.

The approach presented here can be useful in a number of scenarios. Although in this paper we have discussed a single example, we point out that such example can actually be seen as a prototypical instance of so-called product databases, where one needs to model information about types and models of products (akin to the table T-CarTypes in Figure 3), as well as specific data about single products (like table T-Car in Figure 3). In the applications with product databases, for example in the context of e-commerce, when new products become available, they are typically acquired by accessing catalogues, where the above mentioned information about types and models of products is reported. In our framework, such catalogues are simply modelled as data sources with suitable mappings to the ontology (similarly to the mappings from the table T-CarTypes in Example 4), and such mappings are used to dynamically extend the ontology with new classes and relationships between them present in the catalogue.

We believe that the approach described in this paper can be a starting point for several investigations going beyond what we have presented here. For example, we may allow for the coexistence of multiple TBoxes within the same data sources and allow the user to select which TBox to load when querying the system, possibly depending on the query, much in the spirit of [27]. In addition, the user can in principle even compose on the fly the TBox to use when answering a query. Obviously notions such as authorization views and consistency acquire an intriguing flavor in this setting. As for the former notion, the mechanisms described in this paper can be used to hide intensional knowledge for privacy purposes, thus extending the approaches aiming at filtering only extensional knowledge. As for consistency, an interesting idea is to allow for contradicting TBox axioms coming to the data sources to coexist as long as they are not used together when performing query answering. Other promising directions to pursue include handling possible inconsistencies in MKBs, in the spirit of [28], considering more sophisticated form of mappings, such as the ones in the context of peer-to-peer data integration [29], conceiving the assertions coming from the mapping as updates on the current knowledge base (in the spirit of [30]), and exploiting the ideas presented here as a basis for the problem of acquiring knowledge graphs (see [31]) from existing data sources.