Wideband Spectrum Sensing Based on Reconfigurable Filter Bank in Cognitive Radio
Abstract
:1. Introduction
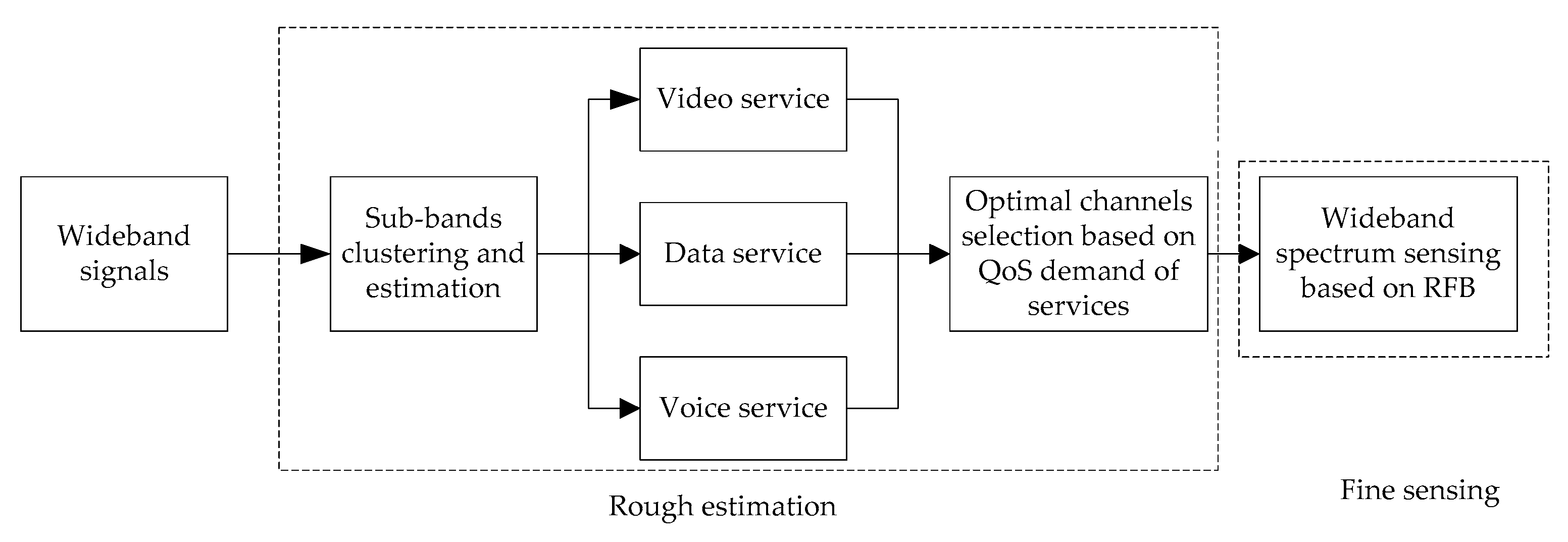
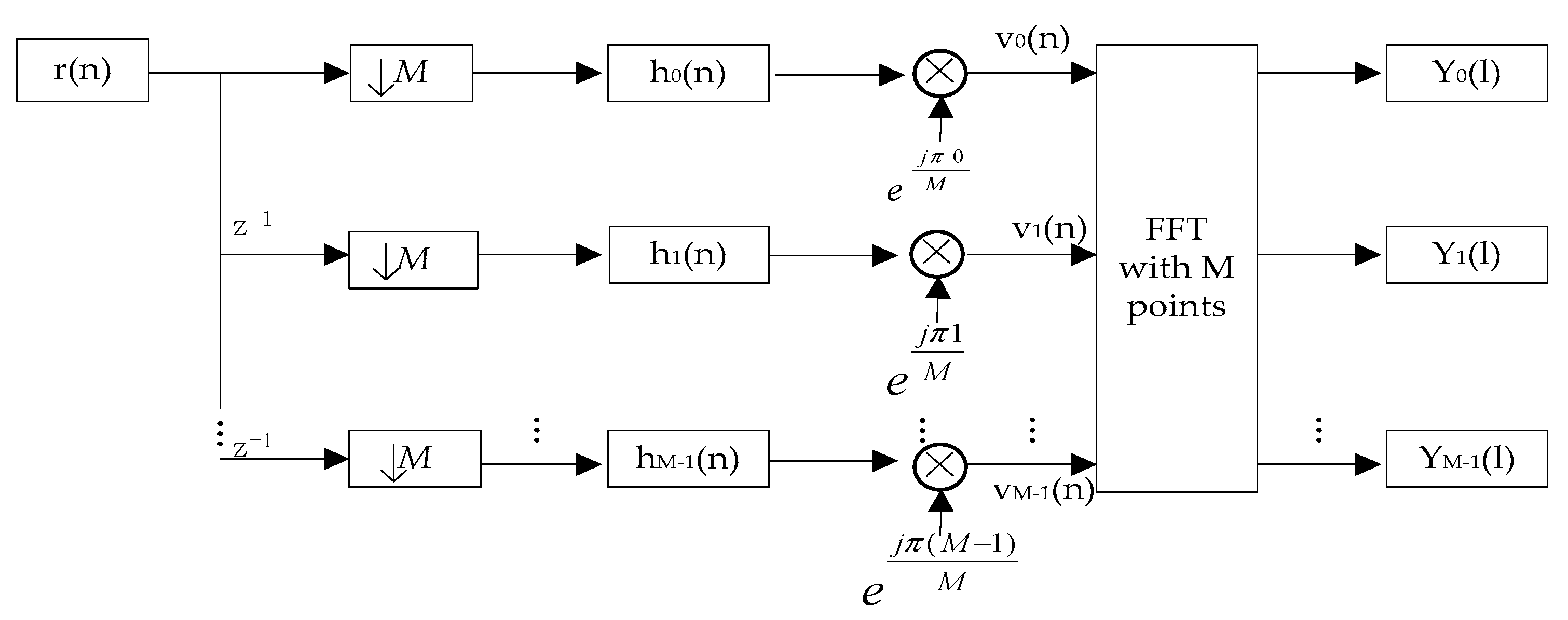
2. System Model
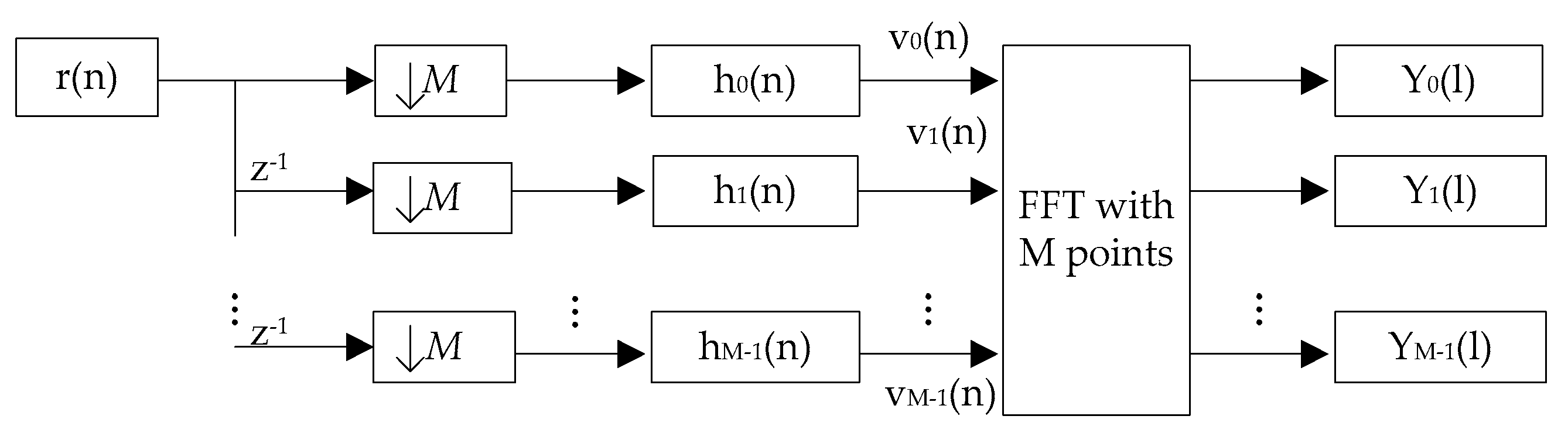
3. Design of Reconfigurable P-DFTFB
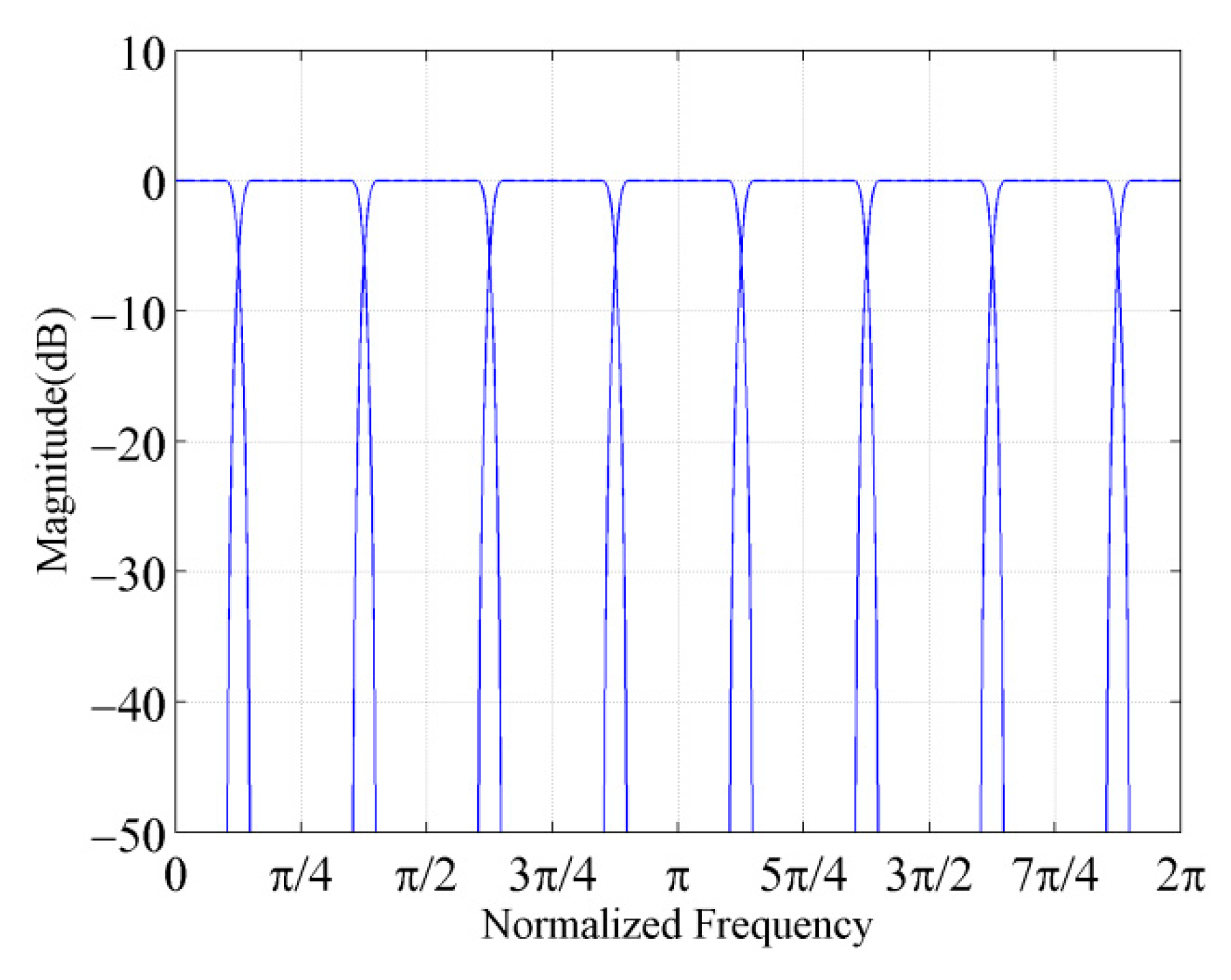
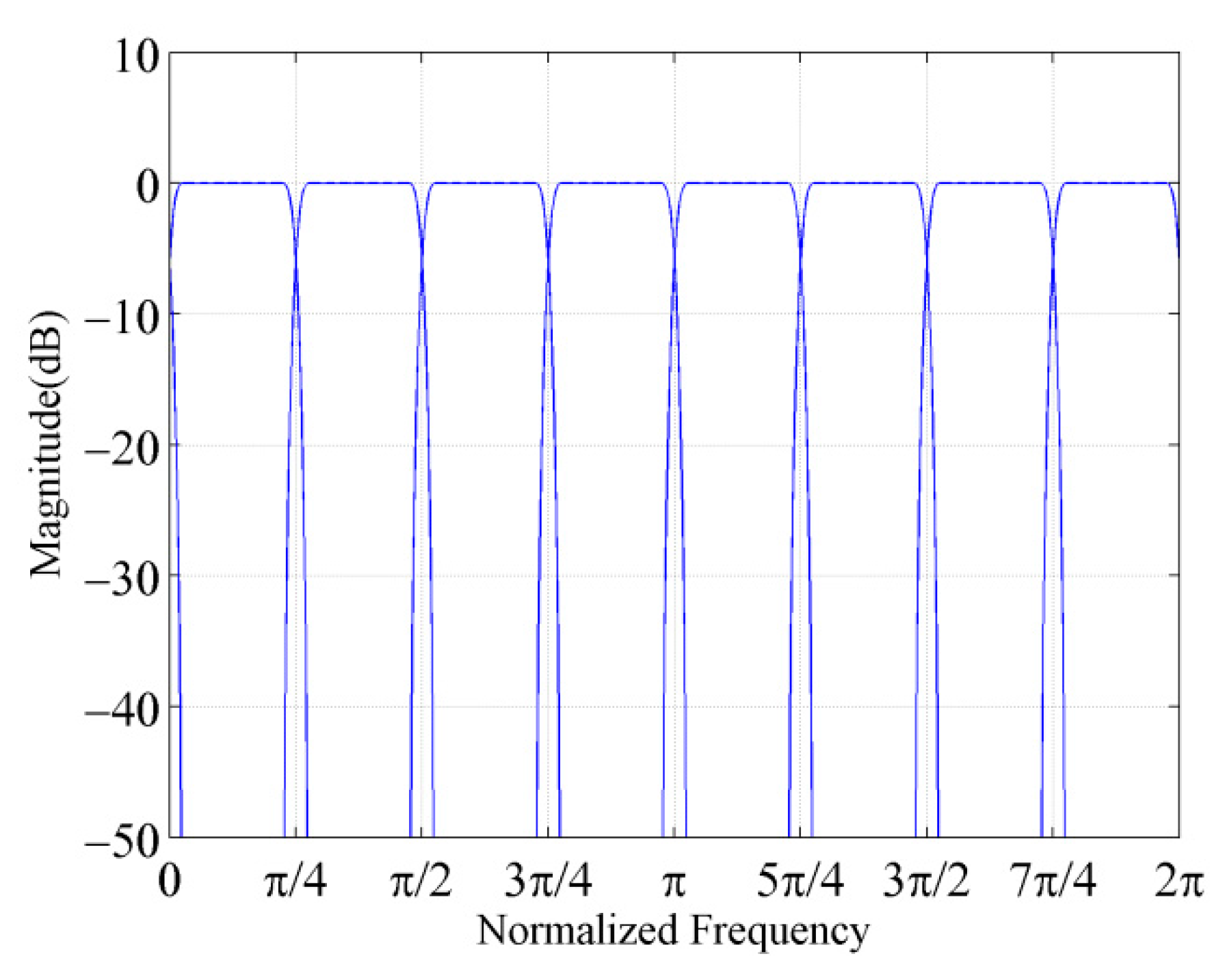
3.1. Design of Analysis P-DFTFB
3.2. Design of Improved Analysis P-DFTFB
3.3. Reconfiguration
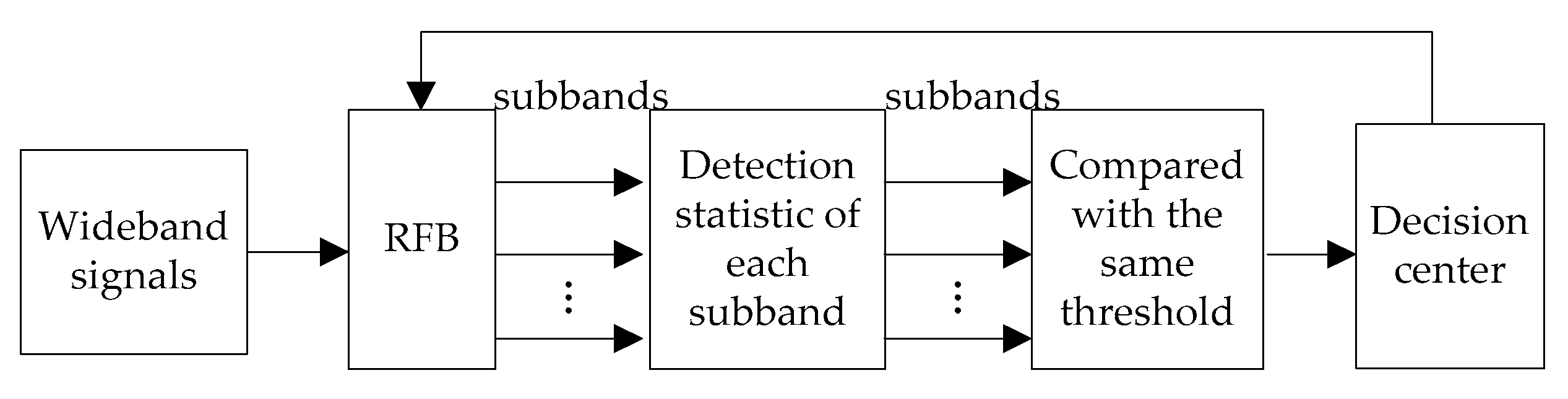
4. Wideband Spectrum-Sensing Based on RFB
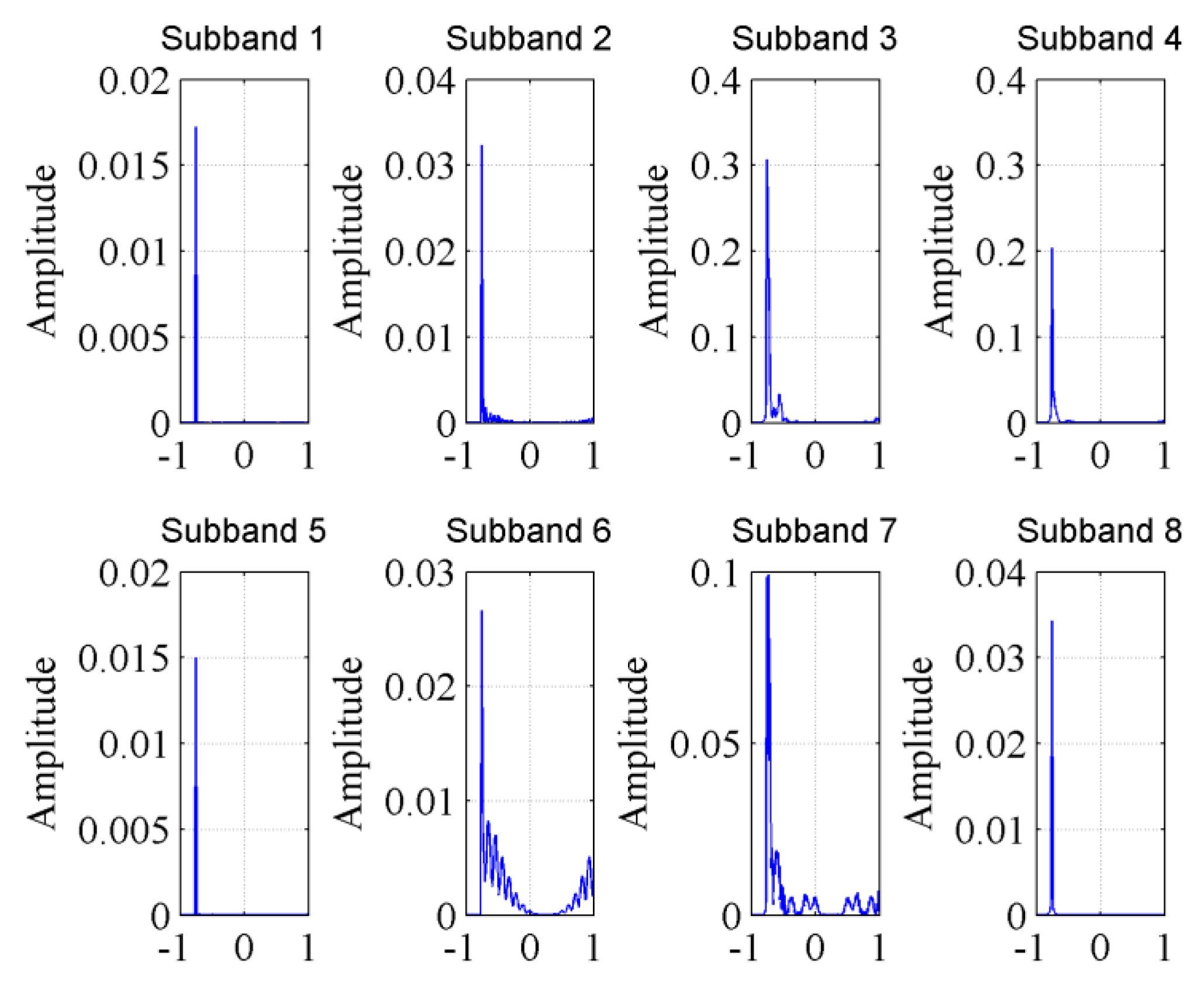
4.1. Energy Detection for Sub-Bands
4.2. Selection of RFB Sub-Bands Number
| Algorithm 1 Selection of |
| 1: Initialization: . 2: If , if end else end 3: If , if end else end 4: Otherwise, the would be unchanged at the next sensing time. |
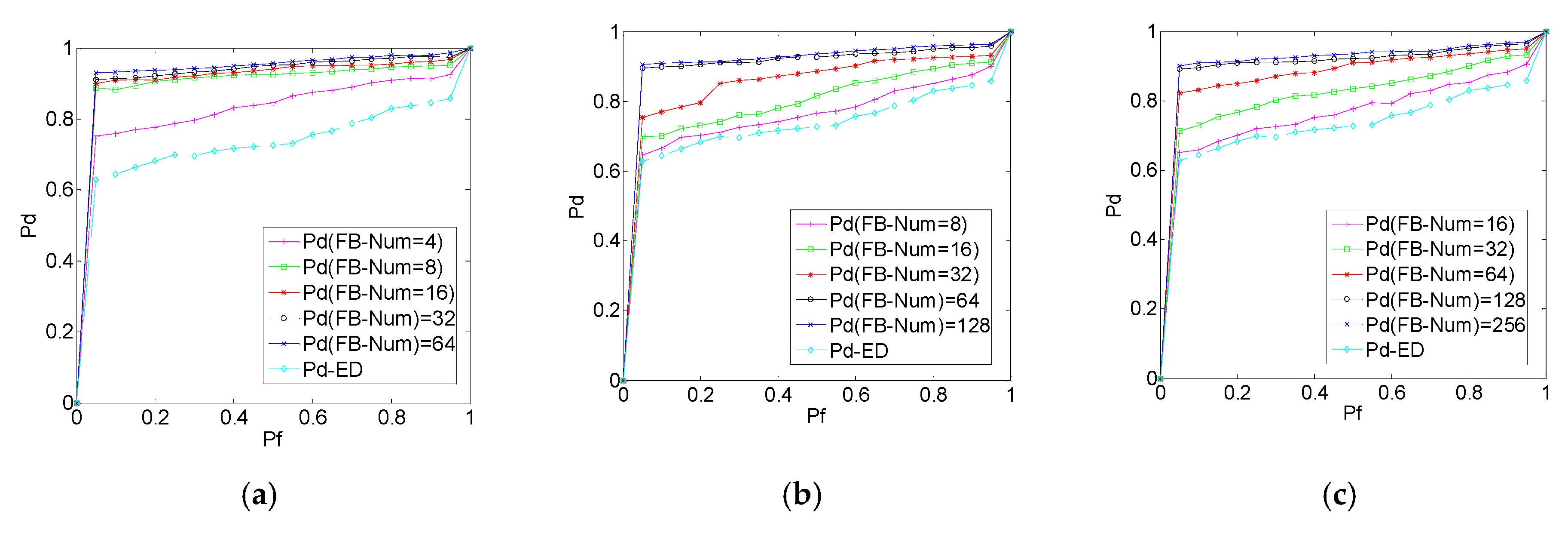
5. Simulation Results and Analysis
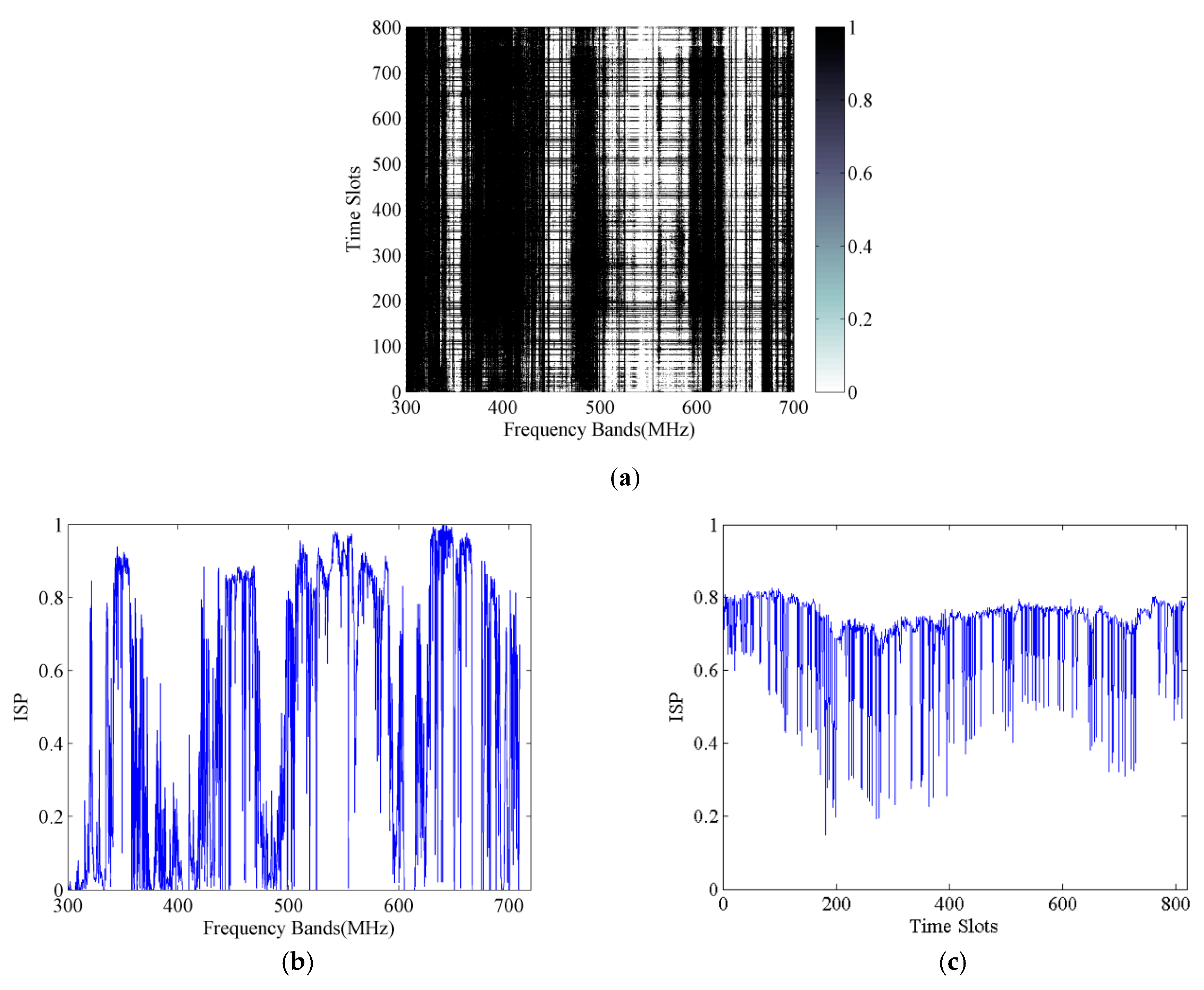
5.1. Data Preprocessing
5.2. Wideband Spectrum Sensing Based on RFB
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, Y.F.; Oh, H.S. A Survey of Measurement-based Spectrum Occupancy Modeling for Cognitive Radios. IEEE Commun. Surv. Tutor. 2016, 18, 848–859. [Google Scholar] [CrossRef]
- Ma, Y.; Gao, Y.; Cavallaro, A.; Parini, C.G.; Zhang, W.; Liang, Y.C. Sparsity Independent Sub-Nyquist Rate Wideband Spectrum Sensing on Real-Time TV White Space. IEEE Trans. Veh. Technol. 2017, 66, 8784–8794. [Google Scholar] [CrossRef]
- Mohsen, G.; Ali, S. Adaptive data-driven wideband compressive spectrum sensing for cognitive radio networks. J. Commun. Inf. Netw. 2018, 3, 84–92. [Google Scholar]
- Dibal, P.Y.; Onwuka, E.N.; Agajo, J.; Alenoghena, C.O. Application of wavelet transform in spectrum sensing for cognitive radio: A survey. Phys. Commun. 2018, 28, 45–57. [Google Scholar] [CrossRef]
- Saeedzarandi, M.; Azmi, P. Cooperative multiband joint detection in cognitive radio networks using artificial immune system. Ann. Telecommun. 2013, 68, 239–246. [Google Scholar] [CrossRef]
- Smitha, K.G.; Vinod, A.P. A Multi-Resolution Fast Filter Bank for Spectrum Sensing in Military Radio Receivers. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2012, 20, 1323–1327. [Google Scholar] [CrossRef]
- Zhang, H.J.; Ruyet, D.L.; Roviras, D.; Sun, H. Polyphase filter bank based multi-band spectrum sensing in cognitive radio systems. Int. J. Commun. Syst. 2016, 29, 1844–1862. [Google Scholar] [CrossRef]
- Zheng, S.L.; Yang, X.N. Wideband spectrum sensing based on group testing utilizing polyphase filter banks. In Proceedings of the 2014 19th International Conference on Digital Signal Processing, Hong Kong, China, 20–23 August 2014; pp. 592–596. [Google Scholar]
- Samuel, C.P.; Kankar, D.S. A Low-Complexity Multistage Polyphase Filter Bank for Wireless Microphone Detection in CR. Circuits Syst. Signal Process. 2017, 36, 1671–1685. [Google Scholar] [CrossRef]
- Smitha, K.G.; Vinod, A.P.; Nair, P.R. Low power DFT filter bank based two-stage spectrum sensing. In Proceedings of the International Conference on Innovations in Information Technology (IIT), Abu Dhabi, UAE, 18–20 March 2012; pp. 173–177. [Google Scholar]
- Narendar, M.; Vinod, A.P.; Madhukumar, A.S.; Krishna, A.K. A tree-structured DFT filter bank based spectrum sensor for estimation of radio channel edge frequencies in military wideband receivers. In Proceedings of the 10th International Conference on Information Science, Signal Processing and their Applications (ISSPA 2010), Kuala Lumpur, Malaysia, 10–13 May 2010; pp. 534–537. [Google Scholar]
- Kim, C.; Shin, Y.; Im, S.; Lee, W. SDR-based digital channelizer/de-channelizer for multiple CDMA signals. In Proceedings of the Vehicular Technology Conference Fall 2000, Boston, MA, USA, 24–28 September 2000; pp. 2862–2869. [Google Scholar]
- Yin, S.X.; Chen, D.W.; Zhang, Q.; Liu, M.Y.; Li, S.F. Mining Spectrum Usage Data: A Large-Scale Spectrum Measurement Study. IEEE Trans. Mob. Comput. 2012, 11, 1033–1046. [Google Scholar]
- Gao, M.F.; Yan, X.; Zhang, Y.C.; Liu, C.Y.; Zhang, Y.F.; Feng, Z.Y. Fast Spectrum Sensing: A Combination of Channel Correlation and Markov Model. In Proceedings of the 2014 IEEE Military Communications Conference, Baltimore, MD, USA, 6–8 October 2014; pp. 405–410. [Google Scholar]
- Huang, S.; Feng, Z.Y.; Yao, Y.Y.; Zhang, Y.F.; Zhang, P. Multi-centers cooperative estimation based fast spectrum sensing. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar]
- Hao, J.G.; Pei, W.J.; Xia, Y.L.; Wang, K. Design of low complexity reconfigurable variable bandwidth filter bank. J. Electron. Meas. Instrum. 2015, 29, 1057–1063. [Google Scholar]
- Darak, S.J.; Vinod, A.P.; Lai, E.M.K. A low complexity reconfigurable non-uniform filter bank for channelization in multi-standard wireless communication receivers. J. Signal Process. Syst. 2012, 68, 95–111. [Google Scholar] [CrossRef]
- Ambede, A.; Smitha, K.G.; Vinod, A.P. A Low-Complexity Uniform and Non-uniform Digital Filter Bank Based on an Improved Coefficient Decimation Method for Multi-standard Communication Channelizers. Circuits Syst. Signal Process. 2013, 32, 2543–2557. [Google Scholar] [CrossRef]
- Lee, D.; Kim, D.S.; Lim, C.M. Performance analysis of frequency hopping satellite communication system reducing the transient response of Polyphase DFT filter. In Proceedings of the 20th Asia-Pacific Conference on Communication (APCC 2014), Pattaya, Thailand, 1–3 October 2014; pp. 199–202. [Google Scholar]
- Darak, S.J.; Palicot, J.; Zhang, H.G.; Prasad, V.A.; Moy, C. Reconfigurable Filter Bank With Complete Control Over Subband Bandwidths for Multistandard Wireless Communication Receivers. IEEE Trans. Very Large Scale Integr. Syst. 2015, 23, 1772–1782. [Google Scholar] [CrossRef]
- Jiang, T.; Grace, D.; Liu, Y. Two-stage reinforcement-learning-based cognitive radio with exploration control. IET Commun. 2011, 5, 644–651. [Google Scholar] [CrossRef]
- Wellens, M.; Mahonen, P. Lessons learned from an extensive spectrum occupancy measurement campaign and a stochastic duty cycle model. In Proceedings of the 2009 5th International Conference on Testbeds and Research Infrastructures for the Development of Networks & Communities and Workshops, Washington, DC, USA, 6–8 April 2009; pp. 1–9. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wu, B.; Yao, Y.; Qin, M. Wideband Spectrum Sensing Based on Reconfigurable Filter Bank in Cognitive Radio. Future Internet 2019, 11, 244. https://doi.org/10.3390/fi11110244
Wang H, Wu B, Yao Y, Qin M. Wideband Spectrum Sensing Based on Reconfigurable Filter Bank in Cognitive Radio. Future Internet. 2019; 11(11):244. https://doi.org/10.3390/fi11110244
Chicago/Turabian StyleWang, Huan, Bin Wu, Yuancheng Yao, and Mingwei Qin. 2019. "Wideband Spectrum Sensing Based on Reconfigurable Filter Bank in Cognitive Radio" Future Internet 11, no. 11: 244. https://doi.org/10.3390/fi11110244
APA StyleWang, H., Wu, B., Yao, Y., & Qin, M. (2019). Wideband Spectrum Sensing Based on Reconfigurable Filter Bank in Cognitive Radio. Future Internet, 11(11), 244. https://doi.org/10.3390/fi11110244




