Body-to-Body Cooperation in Internet of Medical Things: Toward Energy Efficiency Improvement
Abstract
:1. Introduction
Related Work
- A new IoMT system is proposed that describes the journey of the data from the human body to the health cloud over four tiers.
- We propose a new protocol that allows neighbouring WBSNs to cooperate with each other through different communication technologies and devices within the IoMT system. The proposed protocol is called the ‘inter-WBSN cooperation in IoMT system’, which is abbreviated as ‘IWC-IoMT’.
- A mathematical model of the proposed protocol is formulated and derived for two important metrics: outage probability and energy efficiency. The mathematical model describes the transmission of the data between WBSNs and beyond their communication range.
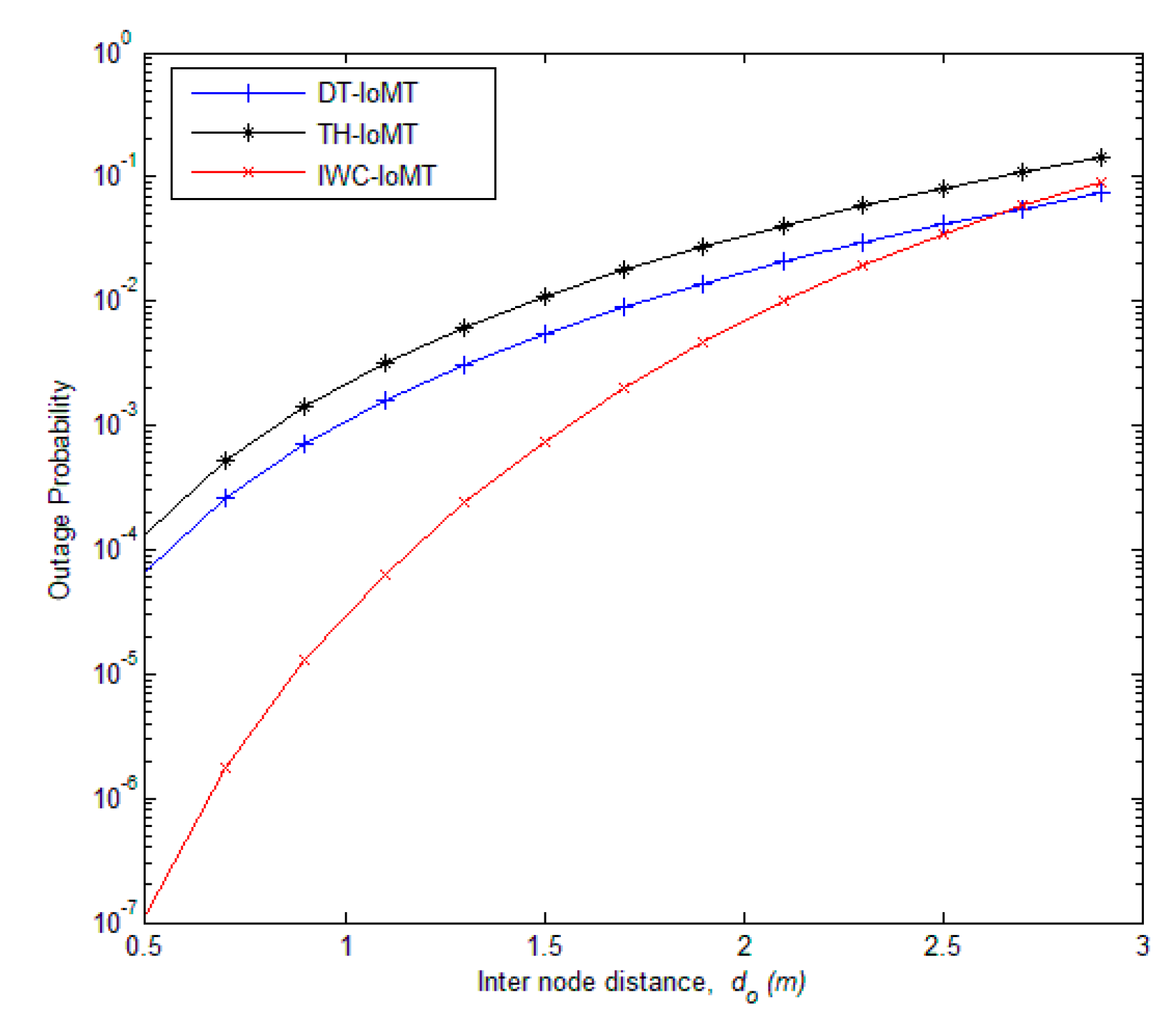
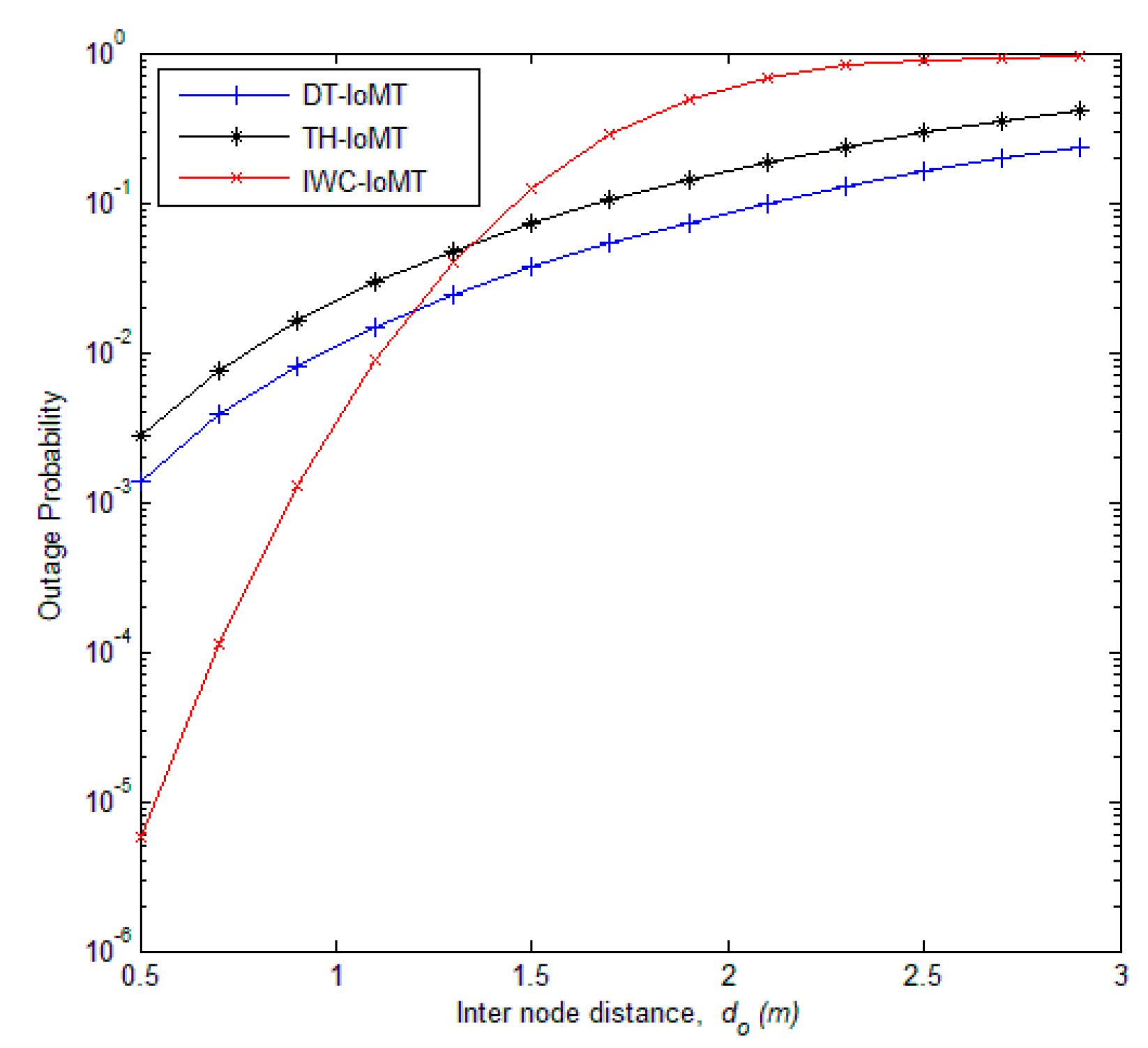
- We reveal that the proposed IWC-IoMT protocol can achieve better performance in terms of the outage probability and energy efficiency of the IoMT system.
2. WBSN Networks Architecture
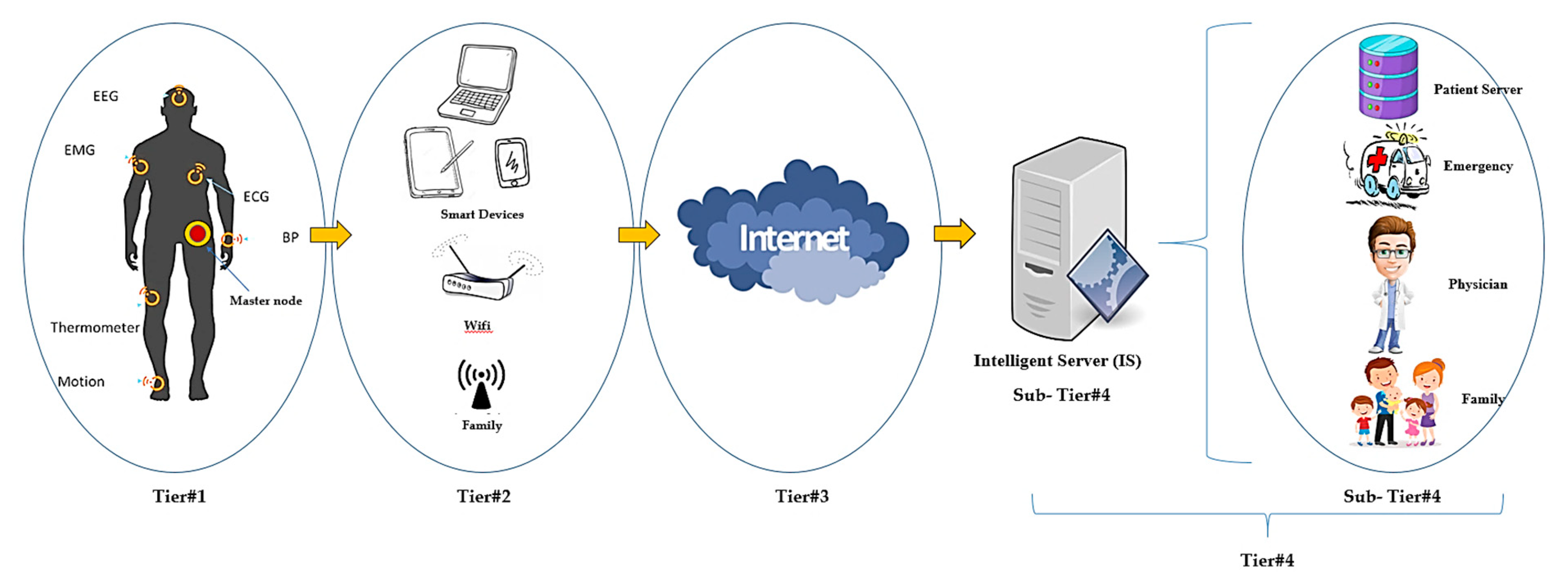
2.1. WBSN in IoMT-based Health Network
- The WBSN tier (tier 1): In this tier, sensors might be attached directly to the human body or sewed into fabric, or embedded inside the human body. Such sensors can be EEG, ECG, or EMG, etc. The data recorded via sensors are transmitted to the coordinator node via wireless 802.15.6 standard, after that the CN transfer what were transmitted by the sensors to the next tier over one of the wireless technology or cables.
- Smart\wireless technology interface tier (tier 2): In this tier, smart devices are utilized, (i.e., smart phone, laptop or tablet). In this tier, data are inspected and analysed, then the data transferred to tier 3 over one of the smart devices or one of the chosen wireless communication technologies (i.e., Bluetooth, Wi-Fi or cellular base-station). Tier 2 represents the bridge tier that is join the WBSN to the infrastructure internet, and some time located within WBSN area.
- Infrastructure internet tier (tier 3): This level bridge the gap between the tier 2 and tier 4 via exiting backbone communication technology.
- Care-Services tier (tier 4): In this tier, the data is received and forwarded to the intelligent server (IS), the intelligent server is stored the data, analysed and forwarded to the suitable service, such as emergency response, a physician, or family.
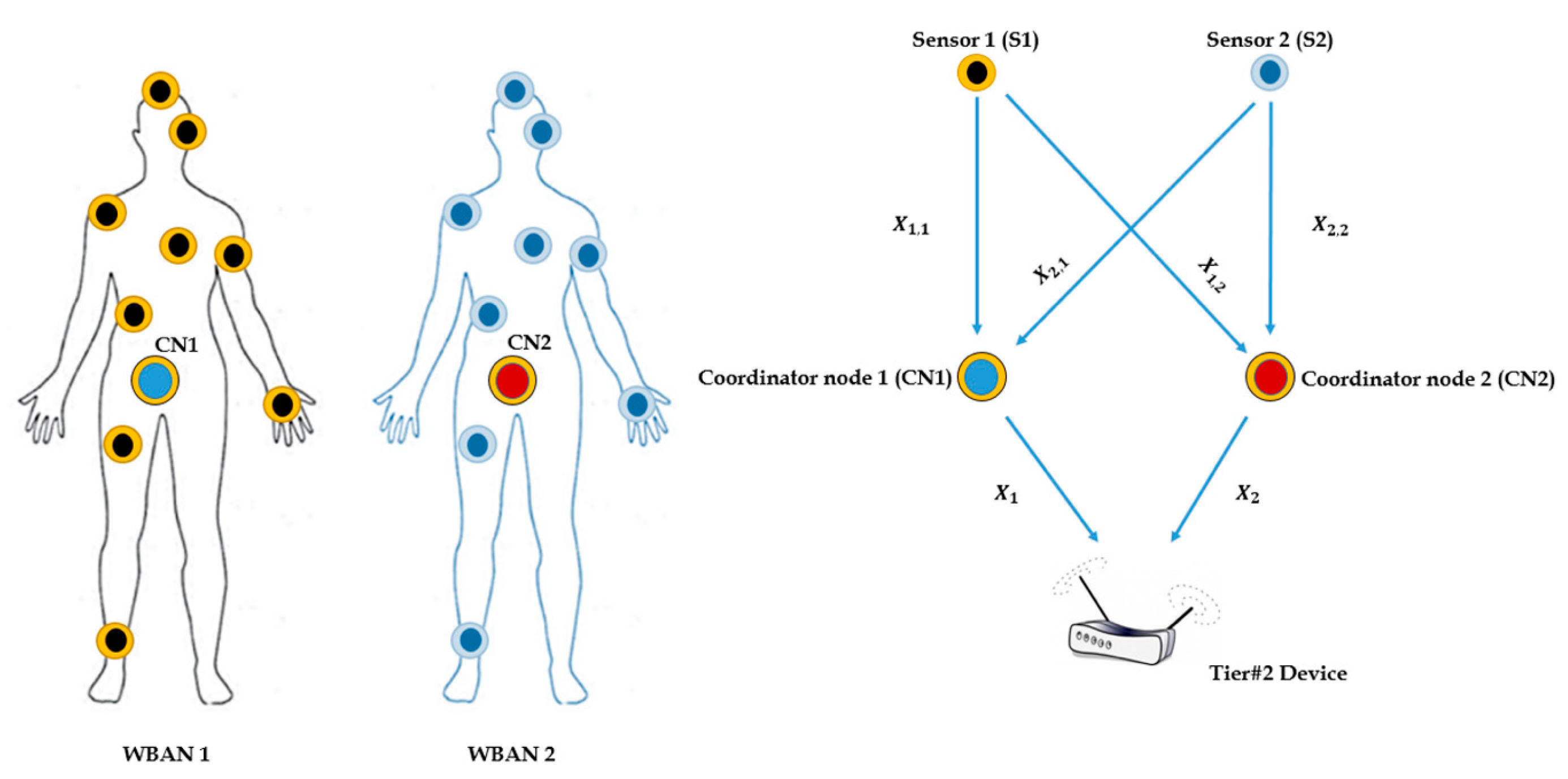
2.2. Proposed Inter-WBSN Cooperation Network Architecture
- Each sensor gathers the data then forwards it to the second tier (T2) over two phases, as depicted in Figure 2.
- In the first phase, sensor 1 of the WBAN1 broadcasts the gathered data to CN1 and CN2. In the second phase, CN1 and CN2 transmit what is received from sensor 1 to the tier 2 device (T2).
- The devices in T2 combine the received signals via maximal ratio combing (MRC) [23].
3. Link and Outage Probability Analysis
- is the transmission power;
- is the noise power;
- is a complex Gaussian random variable with unit variance;
- is given as ;
- is the distance between two nodes;
- is the total gain of the transmit and receive antennae;
- is the wavelength;
- is the noise figure at the receiver; and
- is the link margin.
Outage Probability Analysis of IWC-IoMT
4. Energy Efficiency of the IWC-IoMT
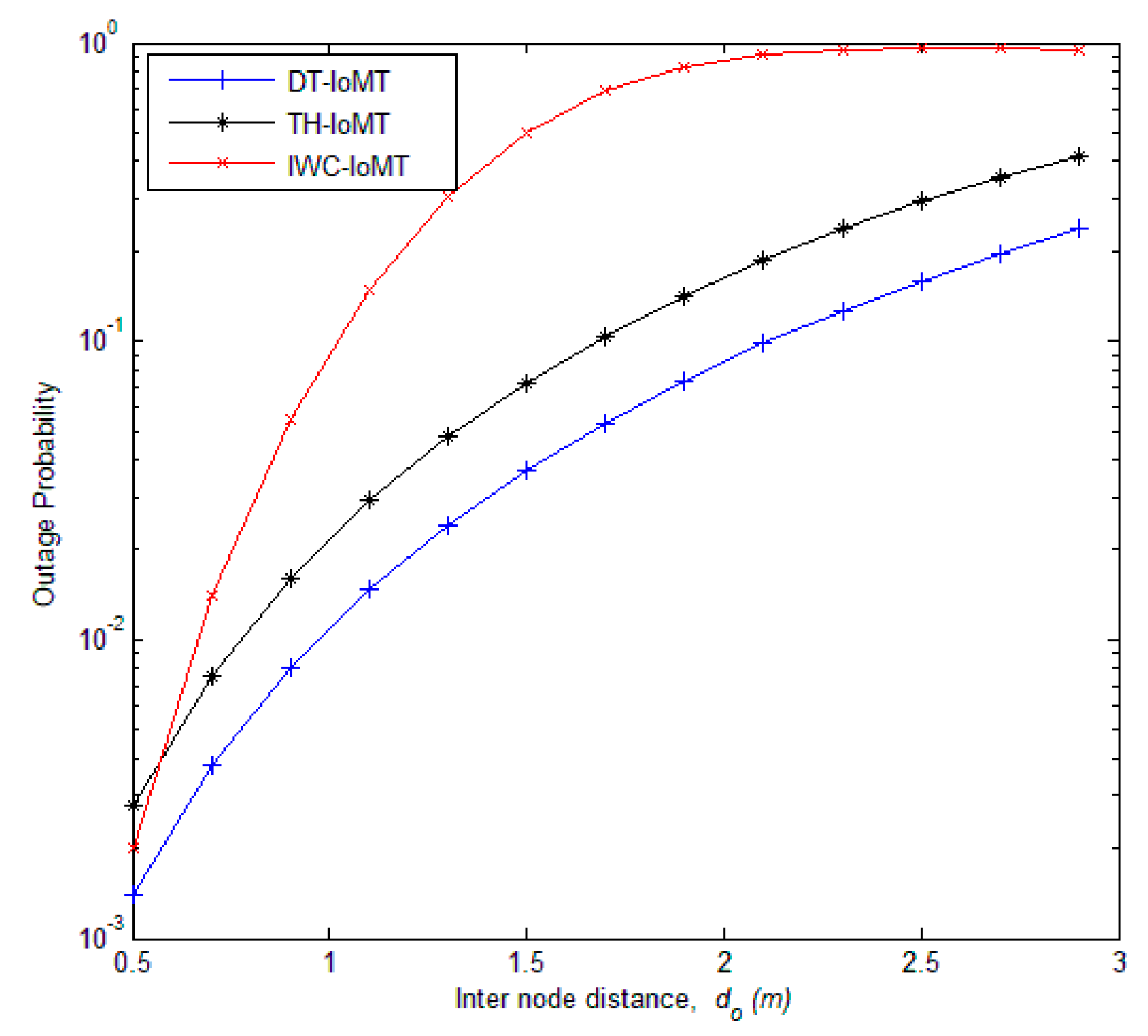
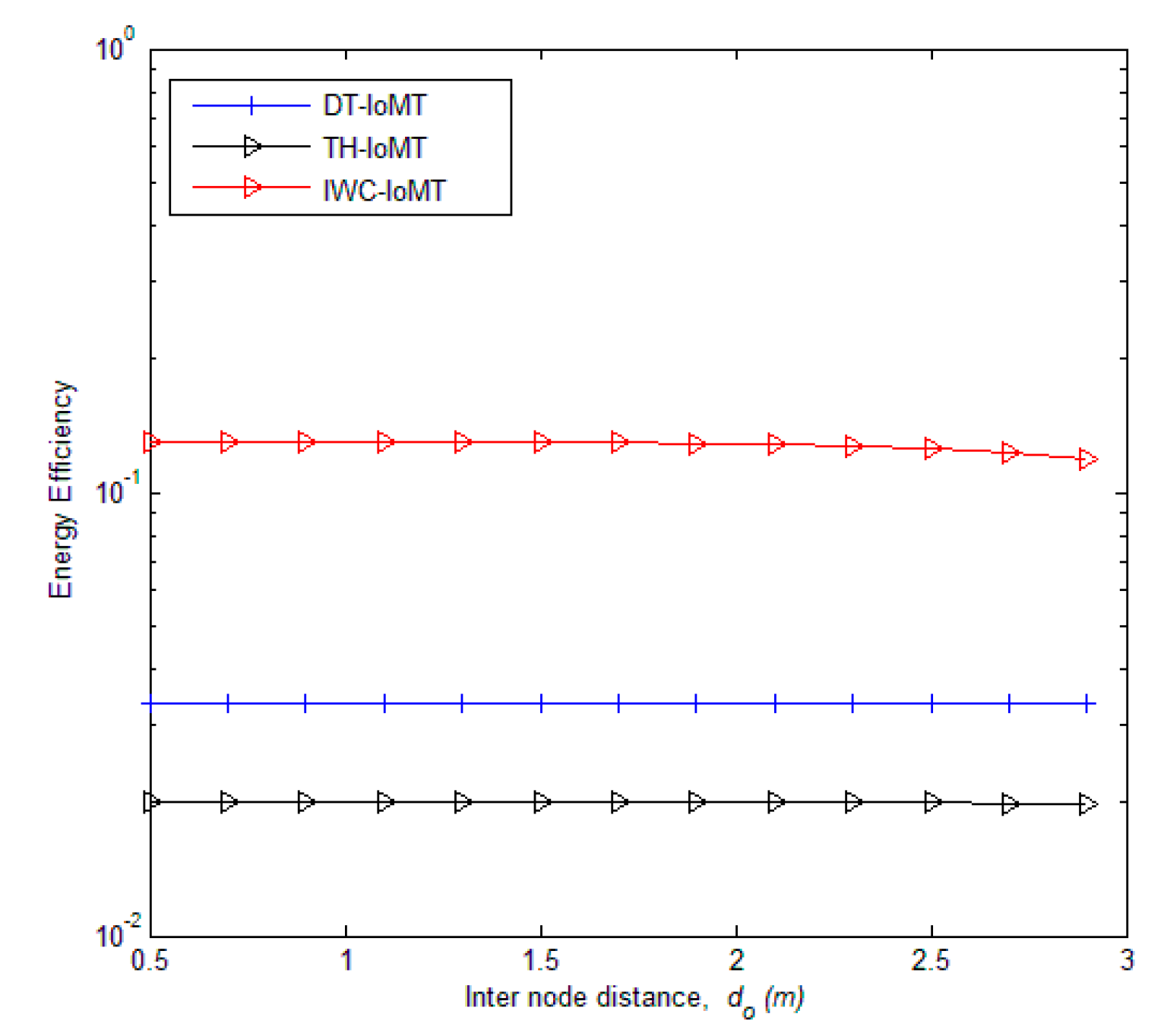
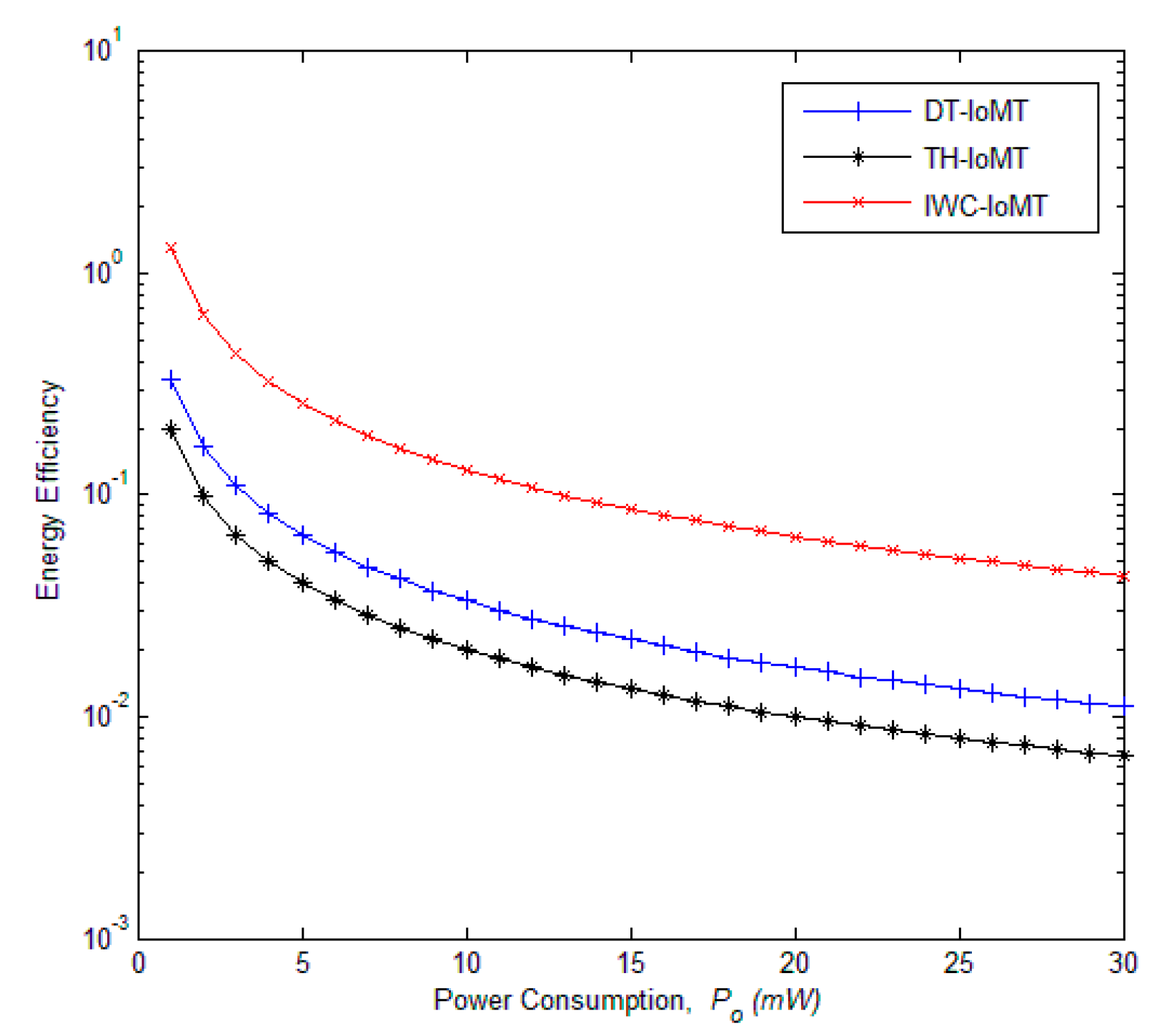
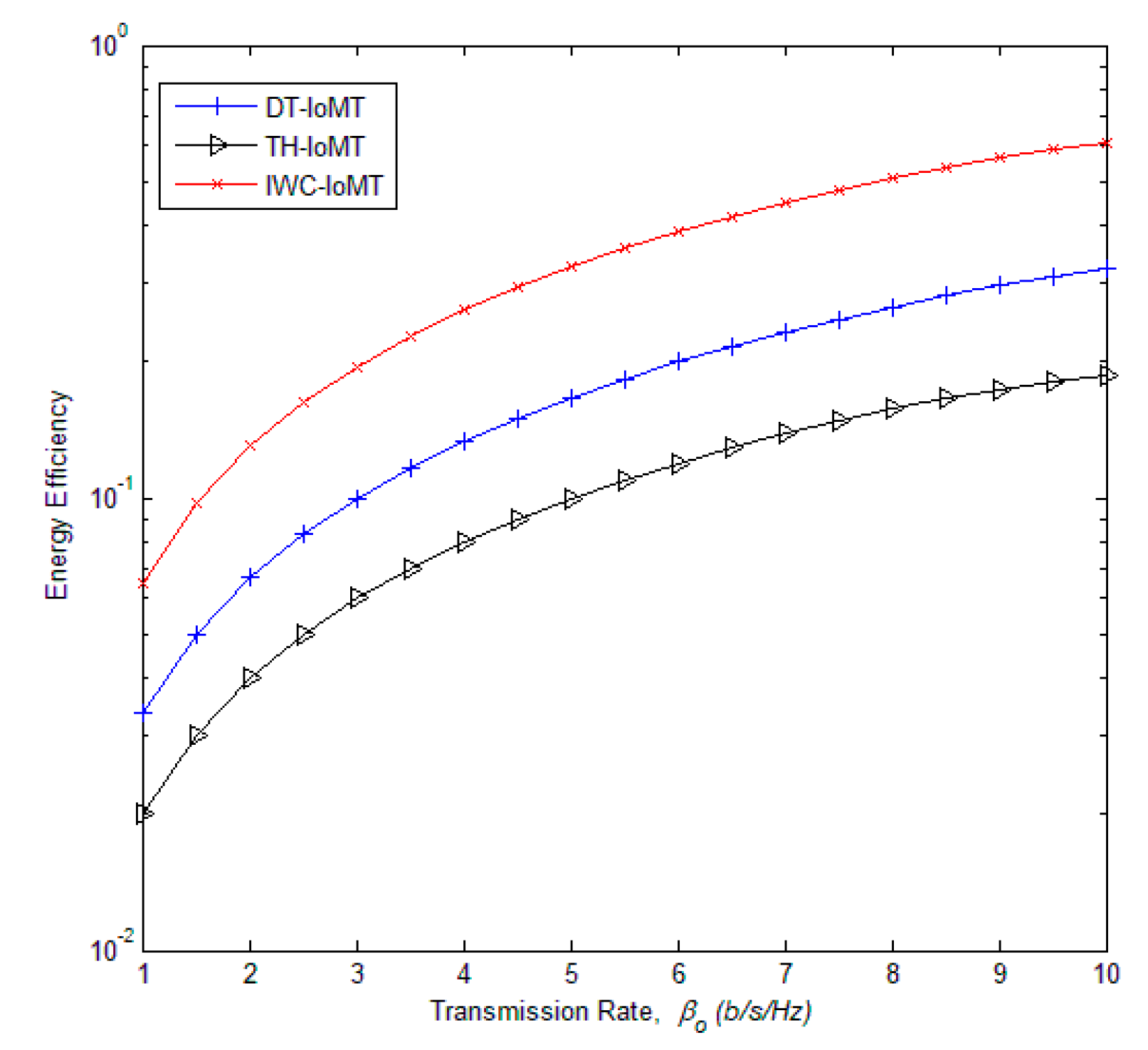
5. Simulation and Discussion
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Yang, G.; Xie, L.; Mäntysalo, M.; Zhou, X.; Pang, Z.; Da Xu, L.; Kao-Walter, S.; Chen, Q.; Zheng, L.R. A health-IoT platform based on the integration of intelligent packaging, unobtrusive bio-sensor, and intelligent medicine box. IEEE Trans. Ind. Inform. 2014, 10, 2180–2191. [Google Scholar] [CrossRef]
- Hassanalieragh, M.; Page, A.; Soyata, T.; Sharma, G.; Aktas, M.; Mateos, G.; Kantarci, B.; Andreescu, S. Health monitoring and management using Internet-of-Things (IoT) sensing with cloud-based processing: Opportunities and challenges. In Proceedings of the 2015 IEEE International Conference on Services Computing 2015, New York, NY, USA, 27 Jun–2 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 285–292. [Google Scholar]
- Bui, N.; Zorzi, M. Health care applications: A solution based on the internet of things. In Proceedings of the 4th International Symposium on Applied Sciences in Biomedical and Communication Technologies, Barcelona, Spain, 26–29 October 2011; ACM: New York, NY, USA, 2011; p. 131. [Google Scholar]
- Santos, J.; Rodrigues, J.J.; Silva, B.M.; Casal, J.; Saleem, K.; Denisov, V. An IoT-based mobile gateway for intelligent personal assistants on mobile health environments. J. Netw. Comput. Appl. 2016, 71, 194–204. [Google Scholar] [CrossRef]
- Kumar, P.; Lee, H.J. Security issues in healthcare applications using wireless medical sensor networks: A survey. Sensors 2012, 12, 55–91. [Google Scholar] [CrossRef] [PubMed]
- Al-Mishmish, H.; Alkhayyat, A.; Rahim, H.; Hammood, D.; Ahmad, R.; Abbasi, Q. Critical data-based incremental cooperative communication for wireless body area network. Sensors 2018, 18, 3661. [Google Scholar] [CrossRef] [PubMed]
- Abdulmohsin Hammood, D.; Rahim, H.A.; Alkhayyat, A.; Ahmed, R.B.; Abbasi, Q.H. Reliable emergency data transmission using transmission mode selection in wireless body area network. Cogent Eng. 2018, 5, 1562859. [Google Scholar] [CrossRef]
- Yeh, K.H. A secure IoT-based healthcare system with body sensor networks. IEEE Access 2016, 4, 10288–10299. [Google Scholar] [CrossRef]
- Ghamari, M.; Janko, B.; Sherratt, R.S.; Harwin, W.; Piechockic, R.; Soltanpur, C. A survey on wireless body area networks for ehealthcare systems in residential environments. Sensors 2016, 16, 831. [Google Scholar] [CrossRef]
- Liao, Y.; Leeson, M.; Higgins, M.; Bai, C. Analysis of in-to-out wireless body area network systems: Towards QoS-aware health internet of things applications. Electronics 2016, 5, 38. [Google Scholar] [CrossRef]
- Madhumathi, R.M.; Jagadeesan, A.; Kaushik, S. Healthcare Monitoring System Using Body Sensor Network. In Proceedings of the International Conference on Engineering Innovations and Solutions (ICEIS-2016), Rome, Italy, 25–28 April 2016; pp. 171–176. [Google Scholar]
- Moosavi, S.R.; Gia, T.N.; Nigussie, E.; Rahmani, A.M.; Virtanen, S.; Tenhunen, H.; Isoaho, J. End-to-end security scheme for mobility enabled healthcare Internet of Things. Future Gener. Comput. Syst. 2016, 64, 108–124. [Google Scholar] [CrossRef]
- Yuehong, Y.I.; Zeng, Y.; Chen, X.; Fan, Y. The internet of things in healthcare: An overview. J. Ind. Inform. Integr. 2016, 1, 3–13. [Google Scholar]
- Wu, T.; Wu, F.; Redouté, J.M.; Yuce, M.R. An autonomous wireless body area network implementation towards IoT connected healthcare applications. IEEE Access 2017, 5, 11413–11422. [Google Scholar] [CrossRef]
- Catarinucci, L.; De Donno, D.; Mainetti, L.; Palano, L.; Patrono, L.; Stefanizzi, M.L.; Tarricone, L. An IoT-aware architecture for smart healthcare systems. IEEE Internet Things J. 2015, 2, 515–526. [Google Scholar] [CrossRef]
- Chen, X.; Ma, M.; Liu, A. Dynamic power management and adaptive packet size selection for IoT in e-Healthcare. Comput. Electr. Eng. 2018, 65, 357–375. [Google Scholar] [CrossRef]
- Jabbar, S.; Ullah, F.; Khalid, S.; Khan, M.; Han, K. Semantic interoperability in heterogeneous IoT infrastructure for healthcare. Wireless Commun. Mobile Comput. 2017, 2017. [Google Scholar] [CrossRef]
- Darwish, A.; Hassanien, A.E.; Elhoseny, M.; Sangaiah, A.K.; Muhammad, K. The impact of the hybrid platform of internet of things and cloud computing on healthcare systems: Opportunities, challenges, and open problems. J. Ambient Intell. Humaniz. Comput. 2019, 10, 4151–4166. [Google Scholar] [CrossRef]
- Luo, E.; Bhuiyan, M.Z.; Wang, G.; Rahman, M.A.; Wu, J.; Atiquzzaman, M. Privacyprotector: Privacy-protected patient data collection in IoT-based healthcare systems. IEEE Commun. Mag. 2018, 56, 163–168. [Google Scholar] [CrossRef]
- Ali, F.; Islam, S.R.; Kwak, D.; Khan, P.; Ullah, N.; Yoo, S.J.; Kwak, K.S. Type-2 fuzzy ontology–aided recommendation systems for IoT–based healthcare. Comput. Commun. 2018, 119, 138–155. [Google Scholar] [CrossRef]
- Thabit, A.A.; Mahmoud, M.S.; Alkhayyat, A.; Abbasi, Q.H. Energy harvesting Internet of Things health-based paradigm: Towards outage probability reduction through inter–wireless body area network cooperation. Int. J. Distrib. Sens. Netw. 2019, 15, 10. [Google Scholar] [CrossRef]
- Alkhayyat, A.; Thabit, A.A.; Al-Mayali, F.A.; Abbasi, Q.H. WBSN in IoT Health-Based Application: Toward Delay and Energy Consumption Minimization. J. Sens. 2019, 2019. [Google Scholar] [CrossRef]
- Hammood, D.A.; Rahim, H.A.; Badlishah Ahmad, R.; Alkhayyat, A.; Salleh, M.E.M.; Abdulmalek, M.; Jusoh, M.; Abbasi, Q.H. Enhancement of the Duty Cycle Cooperative Medium Access Control for Wireless Body Area Networks. IEEE Access 2019, 7, 3348–3359. [Google Scholar] [CrossRef]
- Laneman, J.N.; Tse, D.N.C.; Wornell, G.W. Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Trans. Inform. Theory 2004, 50, 3062–3080. [Google Scholar] [CrossRef]
- Promwongsa, N.; Sanguankotchakorn, T. Packet size optimization for energy-efficient 2-hop in multipath fading for WBAN. In Proceedings of the 2016 22nd Asia-Pacific Conference on Communications (APCC), Yogyakarta, Indonesia, 25–27 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 445–450. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulmohsin Hammood, D.; Rahim, H.A.; Alkhayyat, A.; Ahmad, R.B. Body-to-Body Cooperation in Internet of Medical Things: Toward Energy Efficiency Improvement. Future Internet 2019, 11, 239. https://doi.org/10.3390/fi11110239
Abdulmohsin Hammood D, Rahim HA, Alkhayyat A, Ahmad RB. Body-to-Body Cooperation in Internet of Medical Things: Toward Energy Efficiency Improvement. Future Internet. 2019; 11(11):239. https://doi.org/10.3390/fi11110239
Chicago/Turabian StyleAbdulmohsin Hammood, Dalal, Hasliza A. Rahim, Ahmed Alkhayyat, and R. Badlishah Ahmad. 2019. "Body-to-Body Cooperation in Internet of Medical Things: Toward Energy Efficiency Improvement" Future Internet 11, no. 11: 239. https://doi.org/10.3390/fi11110239




