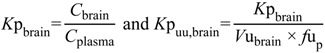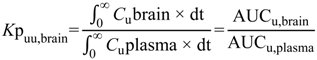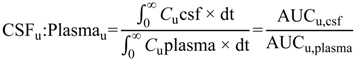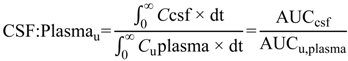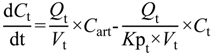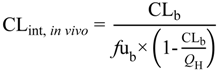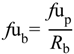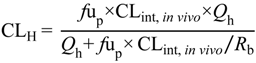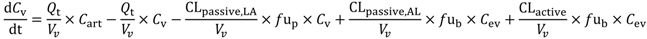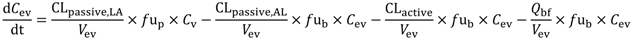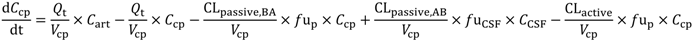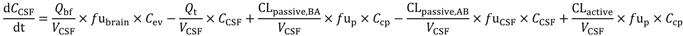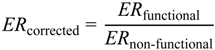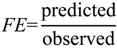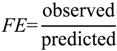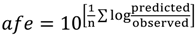1. Introduction
Quantification of central nervous system (CNS) drug levels in brain interstitial fluid (ISF) and cerebrospinal fluid (CSF) is often achieved by complex
in vivo experimental procedures, such as microdialysis. This technique has the inherent advantage of directly measuring the concentration of unbound drug in the accessible brain biophase under non-steady state and steady-state conditions [
1,
2], reflecting both drug influx and efflux processes acting within the CNS. To be able to quantify the brain pharmacokinetics of a compound of interest, microdialysis offers the advantage of multiple time-point sampling within the same animal, although the procedure leads to local tissue damage around the site of probe insertion [
3,
4] and is an experimental procedure often limited to lower-species, although neuroimaging techniques, such as positron emission tomography, have been utilised in both lower- and higher-species to quantify temporal drug concentrations in brain [
5]. Microdialysis and PET (positron emission tomography) are often considered the “gold-standard” for assessing (regional) brain disposition of drugs, but can be limiting due to their technical and experimental complexity, which may hinder widespread use in pre-clinical studies.
The ability to determine the relationship between systemic exposure and CNS drug disposition is an important focus for pharmaceutical industry and drug development programs. Typically, pre-clinical measurement of drug partitioning between the CNS (brain tissue and CSF components) and plasma to yield total brain-to-plasma concentration ratio,
Kp
brain is conducted in rodents and
Kp
brain is then converted to the unbound concentration ratio (
Kp
uu,brain) by multiplication with plasma unbound drug fraction (
fu
p) (Equation (1)
C, total concentration;
Cu, unbound concentration;
Vu, unbound brain volume of distribution) [
6]. The steady-state unbound brain-to-plasma ratio (
Kp
uu,brain) (Equation (2)) or steady-state cerebrospinal fluid-to-plasma concentration ratios (CSF
u:Plasma
u and CSF:Plasma
u) (Equations (3) and (4) respectively) are routinely used to represent CNS disposition of pharmacologically active drugs within the CNS.
Kpuu,brain and CSFu:Plasmau values less than 1 typically indicate restricted entry into the brain or CSF-compartments, predominantly a result of efflux or uptake transport proteins respectively, whereas values greater than 1 indicate unrestricted entry into the brain or CSF, facilitated by active transport. Values close to unity indicate predominantly passive transport of drug.
A major factor in successful delivery of drugs to the CNS is circumvention of physiological barriers. The ATP-binding Cassette (ABC) efflux transporters P-glycoprotein [
7], breast cancer resistance protein (BCRP) and several multidrug resistance-associated proteins (MRPs) are expressed at the BBB (blood–brain barrier) [
7,
8,
9,
10].
Mdr1 knockout studies in mice reveal that P-glycoprotein significantly influences CNS disposition of both non-CNS targeted and CNS targeted therapeutics including amitriptyline, nortriptyline [
11], olanzipine [
12], buspirone, chlorpromazine, fluvoxamine, risperidone, zolpidem [
13] and fexofenadine [
14]. Similar reports of altered brain penetration of imatinib [
15], oseltamivir [
16] and genistein [
17] have been reported in breast cancer resistance protein knockout mice. In addition to BBB-associated ABC transporters influencing CNS drug disposition, expression of highly restrictive tight junction complexes at the BBB (the transcellular electrical resistance is reported to be between 1000 and 1800 Ω cm
2 [
18,
19,
20]) results in only limited passive diffusion of hydrophilic, low molecular weight (<400 Da) compounds [
21] across the BBB into the CNS.
The blood-cerebrospinal fluid barrier (BCSFB) also can regulate entry of compounds into the CNS [
22] and is an important consideration when describing CNS drug disposition. The BCSFB is located next to the choroidal epithelium, a continuous single layer of polarized epithelial-like cells, possessing tight junctions [
23], which line the surface of the choroid plexuses. There are important physiological differences between the BBB and BCSFB.
In vitro measurements suggest the transcellular electrical resistance of the BCSFB is approximately 10- to 15-fold less than that of the BBB, at 80–100 Ω cm
2 [
18,
19,
20]. Unlike the BBB, the choroidal epithelium possesses extensive microvilli and studies suggest the total surface area of the choroid plexuses may be 10-fold greater than previous estimates, placing the surface area within a similar order of magnitude to that of the BBB [
24,
25,
26,
27,
28], and resulting in
in vivo BCSFB clearance measurements, per gram of brain, which may be similar to or greater than that at the BBB [
29]. However, both P-glycoprotein [
30,
31] and BCRP [
31] have been reported to be expressed at the apical plasma membrane of the choroidal epithelium, and have the potential to transport drugs from the choroidal epithelium into the ventricular CSF. It is therefore important that the differential transport directionalities at the BBB and BCSFB sites are taken into consideration when attempting to predict drug disposition within the CNS.
Efflux transporter proteins at the BBB will therefore limit penetration of compounds into the brain and impact on CNS disposition, whereas efflux transports at the BCSFB will act to potentially enhance the accumulation of compounds in the CSF. Consequently, for highly effluxed drugs there is often a discrepancy between the effects of efflux at the BBB (influencing
Kp
uu,brain) and the BCSFB (influencing CSF
u:Plasma
u) [
32,
33,
34].
Clearly, the measurement of brain unbound concentrations would provide a better indicator for assessing CNS disposition, but microdialysis is not an option routinely employed, pre-clinically. However, determination of the extent of non-specific brain tissue binding (
fu
brain), using brain slice and brain homogenate methods, is utilised to drive forward an understanding of overall brain drug penetration. Thus, an understanding of the role of drug transporter proteins at both the BBB and BCSFB coupled with knowledge of brain tissue binding is crucial in order to more effectively predict CNS drug disposition (
Kp
uu,brain and CSF
u:Plasma
u) and facilitate early pharmacokinetic predictions and selection of compounds for further development [
13,
35].
A key paradigm in CNS drug development is the prediction of brain accumulation of candidate compounds [
36,
37]. The application of physiologically-based pharmacokinetic modeling provides an approach to mechanistically incorporate routinely determined
in vitro data, such as drug permeability and protein binding, into a pharmacokinetic model capable of estimating CNS drug disposition. There is, however, a significant lack of predictive models capable of quantifying CNS drug disposition. In non-physiological models, the CNS is described by either a 1-compartment model (representing brain) or a 2-compartment model (representing brain interstitial fluid and brain intravascular fluid (IVF)) with such models often being used in conjunction with brain microdialysis data to describe CNS drug disposition [
2,
3]. Semi-physiological models have also been proposed that attempt to mechanistically describe drug disposition within the brain [
38,
39,
40,
41,
42] but are nonetheless hindered by the requirement for some
a priori clinically-derived input data.
Recently Ball
et al. [
43] described the development of a whole-body physiologically based pharmacokinetic (PBPK) model for the prediction of unbound drug concentration-time profiles in the rat brain, utilising a mechanistic approach to described drug transfer across the blood–brain barrier. Despite this, there is a lack of fully mechanistic CNS PBPK models employed to describe CNS pharmacokinetics, which limits the application of such models to the prediction of CNS drug disposition.
A key challenge in predicting CNS drug disposition is the extrapolation of cell line-derived permeability data obtained
in vitro to an
in vivo permeability metric.
In vitro permeability data derived from immortalised non-cerebral and cerebral cell lines [
44,
45,
46,
47,
48,
49] has been used previously to assess BBB penetration [
50,
51,
52] despite clear phenotypic differences (e.g., efflux transporter expression profile, enzyme activity) between many of the cell lines used, e.g., Caco-2 (human colorectal adenocarcinoma cell line) and MDCK (Madin-Darby canine kidney cells), and blood–brain barrier endothelial cells.
Recently, positive correlations between drug permeability assessed in the L-mdr1a cell line (the LLC-PK1 porcine kidney cell line transfected with murine P-glycoprotein) and the extent of CNS drug disposition (
Kp
brain) have been reported [
53,
54,
55]. Of fundamental importance to this correlation is P-glycoprotein protein abundance in transfected cell lines compared to brain microvascular endothelial cells within the BBB. Recent progress in the quantification of absolute expression levels of P-glycoprotein in brain capillaries has estimated total
mdr1a protein abundance in mouse brain capillaries to be 14.1 fmol/μg protein [
56] and rat brain capillaries to be 19.1 fmol/μg protein [
57] which is very similar to the
in vitro protein abundance in L-mdr1a cells, 15.2 fmol/μg protein [
54,
55], but higher in comparison to that measured in human brain capillaries (6.06 fmol/μg protein) [
54]. Such findings suggest data derived from L-mdr1a cells could be incorporated into predictive physiologically-based pharmacokinetic models and may prove useful in assessing CNS drug disposition for P-glycoprotein substrates.
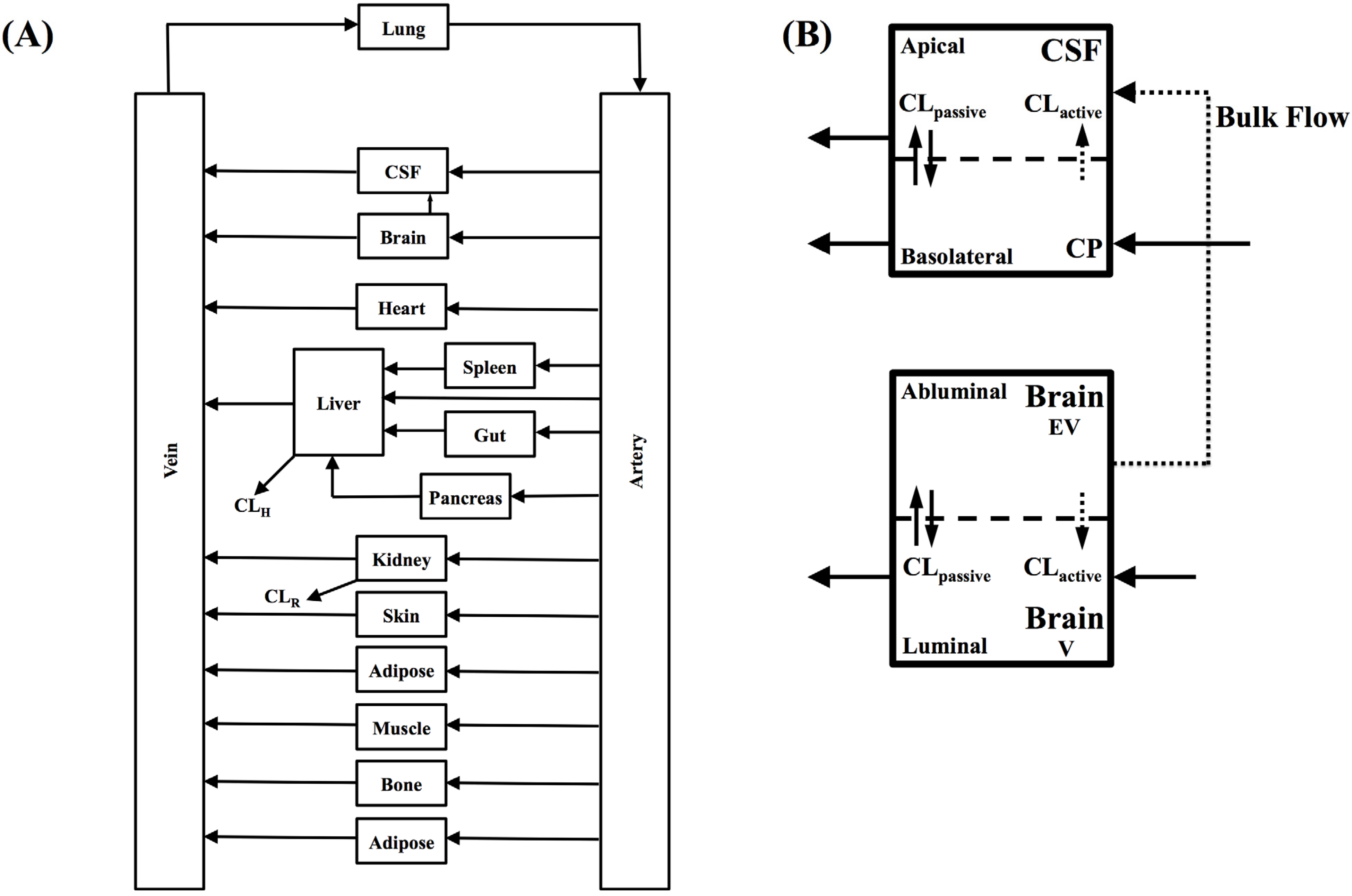
In the present study we describe a predictive, physiologically-based pharmacokinetic model of the rat CNS which incorporates discrete brain and CSF components and is able to predict brain-to-plasma and CSF-to-plasma ratios using
in vitro permeability parameters and drug protein/tissue binding data. In addition, we also developed a mouse whole-body PBPK model which, when populated with mouse physiological parameters and L-mdr1a cell-derived data, allowed prediction of mouse
Kp
uu,brain and CSF:Plasma
u (see
Supplementary Information).
3. Results and Discussion
The availability of
in vivo permeability measurements for candidate compounds undergoing pre-clinical assessment often remains a limiting factor for efficient and effective use of pharmacokinetic models attempting to model CNS drug disposition. Consequently,
in vitro permeability data for passively and actively transported compounds are often used to extrapolate to
in vivo permeability. Polli
et al. [
92] demonstrated a linear relationship between brain penetration (Kin) in rat
in situ brain perfusion studies and apparent permeability in MDCK type-1 cells with a correlation coefficient of 0.86. A similar trend was reported between brain uptake index (BUI) and permeability across bovine brain endothelial cell cultures, with a correlation coefficient of 0.89 [
50]. In more recent studies Uchida
et al. [
54] and Kodaira
et al. [
53] have demonstrated the utility of murine-mdr1a-expressing LLC-PK1 cells (L-mdr1a) to reconstruct
Kp
uu,brain and CSF
u:Plasma
u for a handful of P-glycoprotein substrates.
Our primary goal was to build upon existing approaches aimed at mechanistically predicting CNS drug disposition and examine the potential application of drug permeability data derived from L-mdr1a cells to predict Kpuu,brain in mice and both Kpuu,brain and CSFu:Plasmau in rats. Development of a PBPK model capable of predicting CNS drug disposition by extrapolation of in vitro-derived data may prove a valuable resource for rapid pre-clinical screening of candidate compounds during development.
3.1. Validation of the PBPK Model
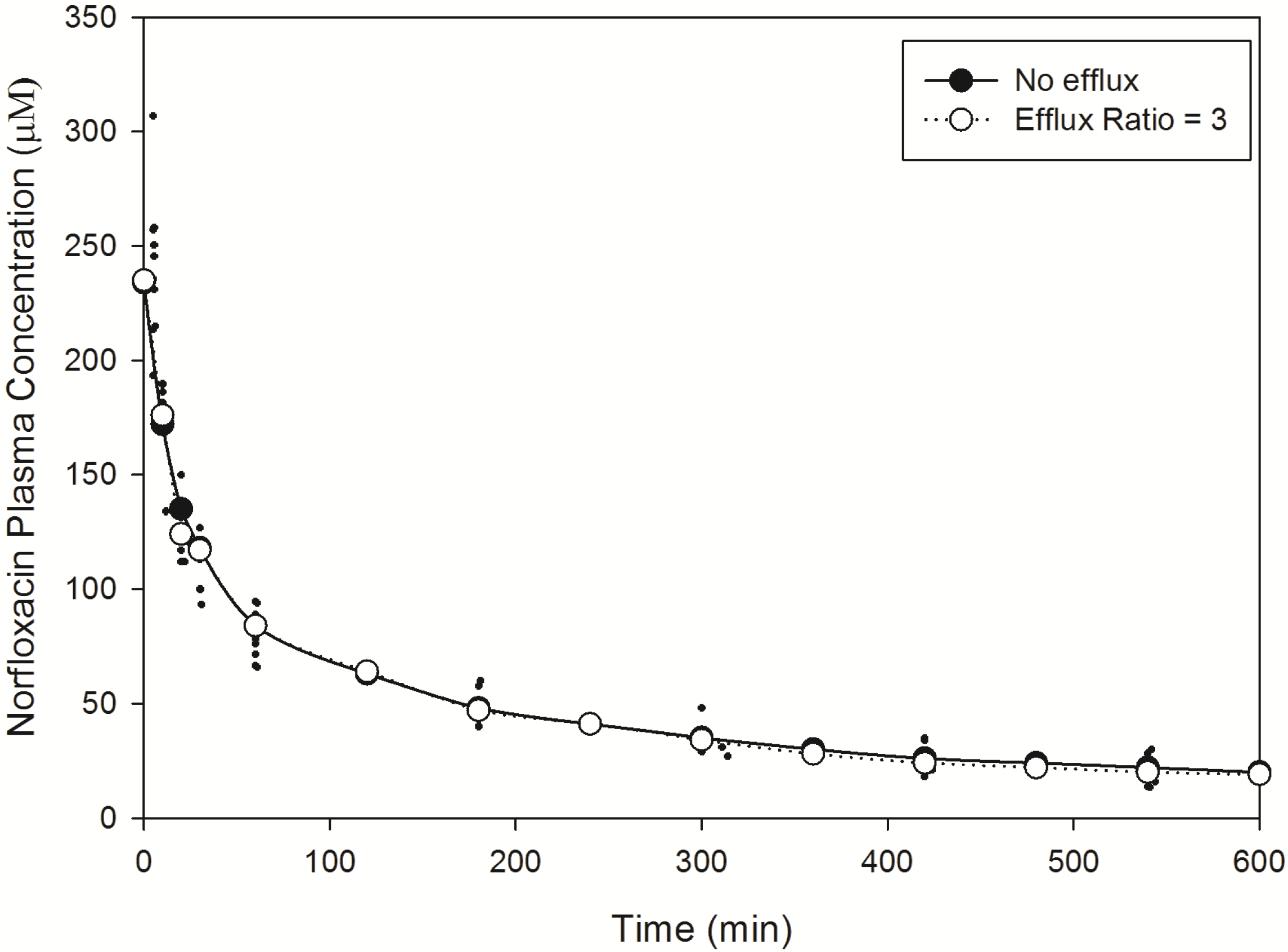
To validate the PBPK model structure and the ability to predict both plasma and brain ISF temporal concentrations, we selected norfloxacin as a model compound and utilised published rat norfloxacin plasma data and brain pharmacokinetic data obtained by microdialysis [
88].
Norfloxacin plasma (
Figure 2) and brain (
Figure 3) temporal concentration profiles were both predicted to be within the ranges observed
in vivo. Simulation of brain ISF norfloxacin concentration-time profile using literature derived CL
passive (value obtained from fitting to
in vivo data) [
76,
77] in the absence of a P-glycoprotein/BCRP-type active efflux component yielded predictions in which the absorption and elimination phases were outside the range observed
in vivo (
Figure 3). Subsequent simulations using a CL
passive 2-fold higher than the initial fitted value (
Table 2) and P-glycoprotein/BCRP-type active efflux processes (efflux ratio of 3) resulted in absorption and elimination phases within the range reported in 10 rats by Chenel
et al. [
88] (
Figure 3).
Importantly, incorporation of an active efflux component (P-glycoprotein/BCRP type) within our simulations corrected the over-prediction in brain ISF drug concentrations and demonstrated the importance of an efflux clearance mechanism in governing norfloxacin CNS drug disposition. These findings are consistent with those of Chenel
et al. [
88] who demonstrated the influence of efflux clearance mechanisms on norfloxacin brain pharmacokinetics. The inclusion of a P-glycoprotein/BCRP type active efflux component within our norfloxacin simulations is supported by a recent report demonstrating norfloxacin to be a BCRP substrate [
93].
Figure 2.
Model predicted norfloxacin plasma concentrations in rats. Small closed circles represent literature reported plasma concentrations determined in rats following an IV-bolus dose [
88]. Large closed circles represent model predicted norfloxacin plasma concentrations in rats in the absence of efflux. Large open circles represent model predicted norfloxacin plasma concentrations in rats in the presence of efflux (efflux ratio = 3).
Figure 2.
Model predicted norfloxacin plasma concentrations in rats. Small closed circles represent literature reported plasma concentrations determined in rats following an IV-bolus dose [
88]. Large closed circles represent model predicted norfloxacin plasma concentrations in rats in the absence of efflux. Large open circles represent model predicted norfloxacin plasma concentrations in rats in the presence of efflux (efflux ratio = 3).
Figure 3.
Model predicted norfloxacin brain concentrations in rats. Crosses represent literature reported brain concentration determined in rats following an IV-bolus dose [
88]. Closed circles represent model predicted norfloxacin brain concentrations in rats in the absence of efflux. Open circles represent model predicted norfloxacin brain concentrations in rats in the presence of efflux (efflux ratio = 3).
Figure 3.
Model predicted norfloxacin brain concentrations in rats. Crosses represent literature reported brain concentration determined in rats following an IV-bolus dose [
88]. Closed circles represent model predicted norfloxacin brain concentrations in rats in the absence of efflux. Open circles represent model predicted norfloxacin brain concentrations in rats in the presence of efflux (efflux ratio = 3).
Norfloxacin
Kp
brain was predicted to be 0.141, within 2-fold of the observed
Kp
brain of 0.091, whilst norfloxacin CSF:plasma was predicted to be 0.089, within 2.1-fold of the observed CSF:plasma of 0.043 (
Table 2). Predicted plasma half-life was extremely close to observed half-life whilst brain ISF half-life was within 1.5-fold of the observed value (
Table 2).
Table 2.
Prediction of norfloxacin plasma, brain and CSF pharmacokinetics.
Table 2.
Prediction of norfloxacin plasma, brain and CSF pharmacokinetics.
| Parameter | Value | Unit |
|---|
| Predicted Kpbrain | 0.141 | |
| Mean observed Kpbrain | 0.093 a | |
| Predicted CSF:Plasma | 0.089 | |
| Observed CSF:Plasma | 0.043 b | |
| Predicted t1/2,plasma (ER = 3) | 183 | (min−1) |
| Observed t 1/2,plasma c | 202 ± 45 | (min−1) |
| Predicted t1/2,ISF (ER = 3) | 231 | (min−1) |
| Observed t1/2,ISF d | 255 ± 97 | (min−1) |
| Predicted AUCplasma | 340 | (µM min−1) |
| Predicted AUCISF (ER = 0) | 329 | (µM min−1) |
| Predicted AUCISF (ER = 3) | 47.9 | (µM min−1) |
| Predicted AUCCSF (ER = 3) | 30.4 | (µM min−1) |
| Predicted ISF Cmax (ER = 0) | 52.4 | (µM) |
| Predicted ISF Cmax (ER = 3) | 16.3 | (µM) |
3.2. Prediction of Central Nervous System (CNS) Disposition Using L-mdr1a in Vitro Permeability Data
Recent studies report positive correlations between drug permeability assessed in the LLC-PK1 porcine kidney cell line transfected with murine
mdr1 (to produce the L-mdr1a cell line) and
in vivo brain distribution of P-glycoprotein substrates in rats and mice [
53].
Furthermore, due to the similarity in the abundance of P-glycoprotein in L-mdr1a cells (15.2 fmol/μg protein) compared to the abundance in brain capillaries (Mouse: 14.1 fmol/μg protein [
56]; rat: 19.1 fmol/μg protein [
57]), we examined the use of L-mdr1a-derived
in vitro permeability data in predicting CNS drug disposition.
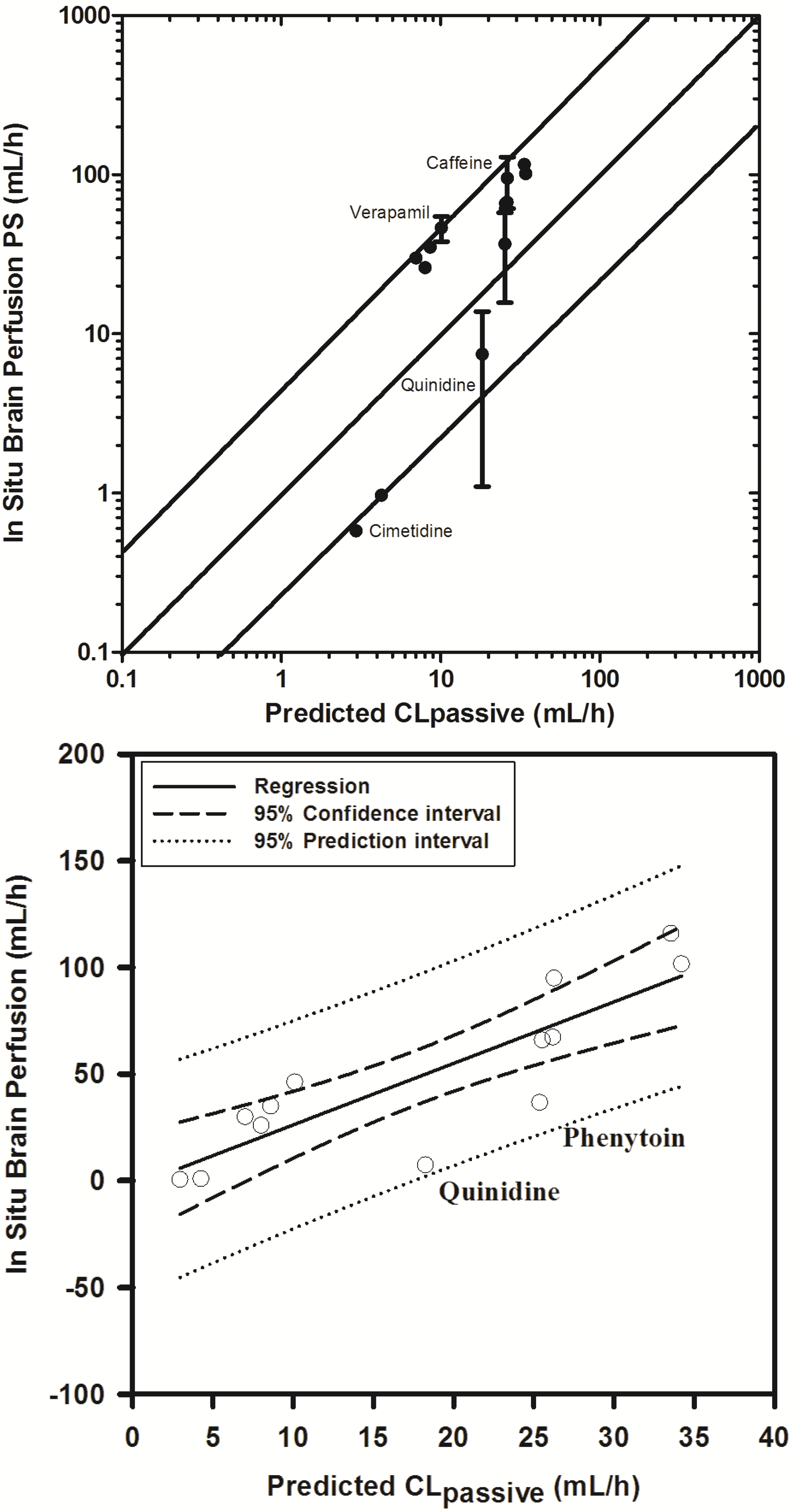
In an attempt to examine the validity of the scaling approach to determine permeability clearance at the BBB, based on extrapolating in vitro permeability data, we obtained literature reported in situ brain permeability-surface area products (PS) for 16 compounds spanning over a 100-fold range of PS.
With the exception of three compounds (midazolam, diazepam and sertraline), 11 of 13 compounds fell within 3-fold and 2 within 4-fold of the reported PS values (see
Supplementary Information Section 4). Similar trends have been previously reported by Uchida
et al. (2011) in LLC-PK1 cells [
55], Polli
et al. (2000) [
92] and Summerfield
et al. (2007) [
96] in cultured kidney epithelial cells, and support the extrapolation approach.
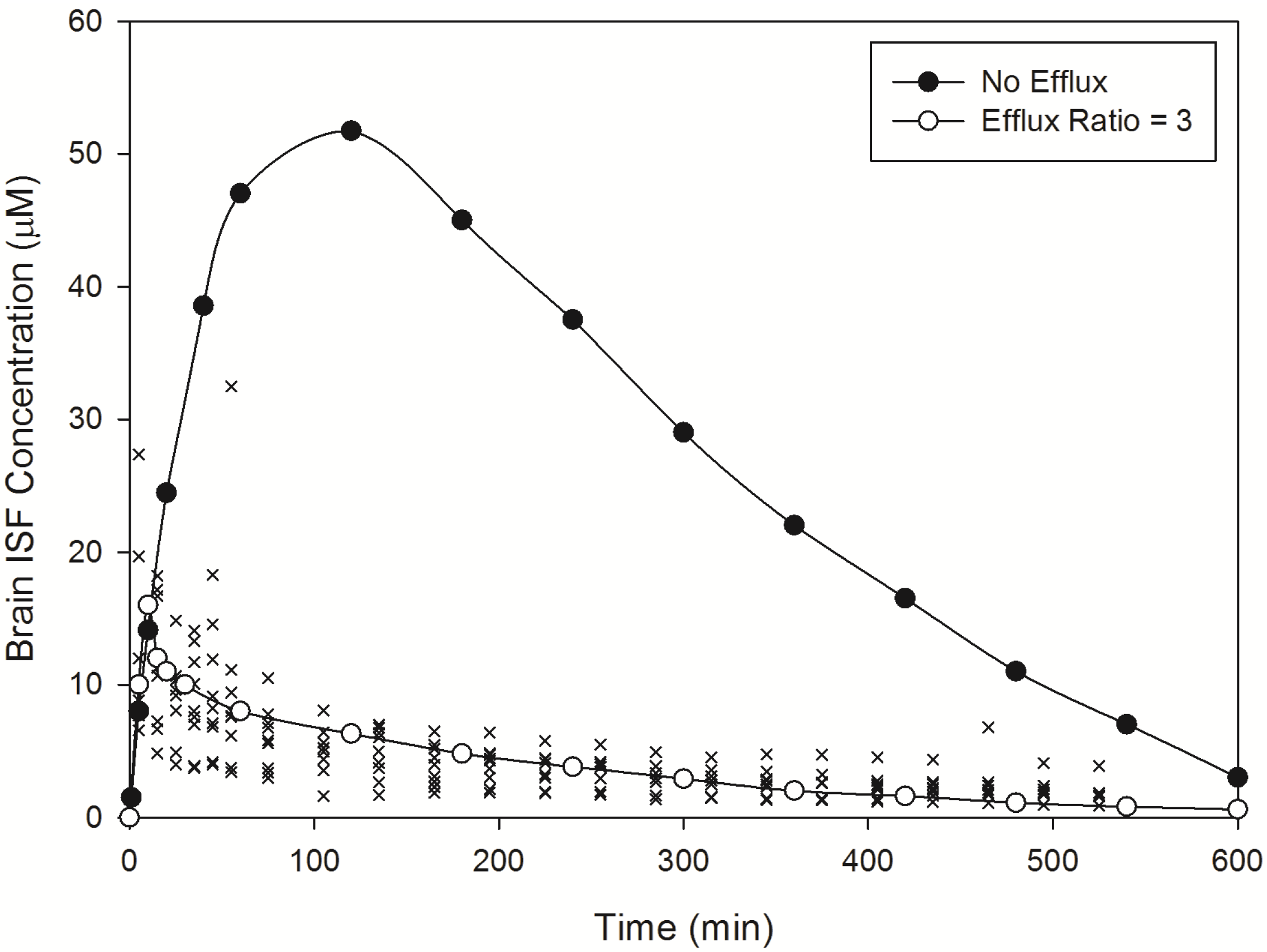
3.2.1. Prediction of Kpuu,brain for 11 Actively Transported Compounds in Mice
Using L-mdr1a-derived permeability data reported by Uchida
et al. [
55], the predicted
Kp
uu,brain for over 90% of P-glycoprotein substrates was within 4-fold of observed
Kp
uu,brain. The predicted
Kp
uu,brain for all compounds was within 5-fold of observed
Kp
uu,brain (
Figure 4A,B), with an overall
afe and
rmse of 0.7 and 0.23 respectively (
Table 3).
Figure 4.
Comparison of predicted and reported Kpuu,brain in mice. (A) Solid bold mid-line represents the line of unity and solid outer-lines represent 4-fold prediction error; and (B) residuals plot.
Figure 4.
Comparison of predicted and reported Kpuu,brain in mice. (A) Solid bold mid-line represents the line of unity and solid outer-lines represent 4-fold prediction error; and (B) residuals plot.
Table 3.
Statistics for the model predictions.
Table 3.
Statistics for the model predictions.
| Species | Tissue | n | afe | rmse | % within 3-fold | % within 4-fold | % within 5-fold | % > 5-fold |
|---|
| Mouse | Brain | 11 | 0.7 | 0.23 | 63.6 | 90.9 | 100 | 0 |
| Rat | Brain | 27 | 1.19 | 0.43 | 63 | 81.5 | 88.9 | 11.1 |
| CSF | 27 | 0.8 | 0.32 | 77.8 | 81.5 | 96.3 | 3.7 |
Uchida
et al. [
55] successfully demonstrated that
Kp
brain (and
Kp
uu,brain) could effectively be reconstructed though the integration of
in vitro mdr1a transport activity and mdr1a protein expression levels in the brain capillaries and in mdr1a-transfected cell monolayers. Our model yielded reasonable predictions for passively transported and actively transported P-glycoprotein substrates and demonstrated the successful extrapolation of
in vitro permeability data to yield an
in vivo transfer clearance across the brain capillaries.
The basis of these predictions is quantitative calculation of the temporal drug concentrations in plasma and brain compartments. Whilst Uchida
et al. [
55] initially reconstructed
Kp
uu,brain, for the first time we have shown that, using a well-designed PBPK modeling approach, plasma and brain ISF temporal concentrations, and
Kp
uu,brain can be adequately predicted in mice for a range of P-glycoprotein substrates, using a simple set of physiochemical and pre-clinically determined parameters.
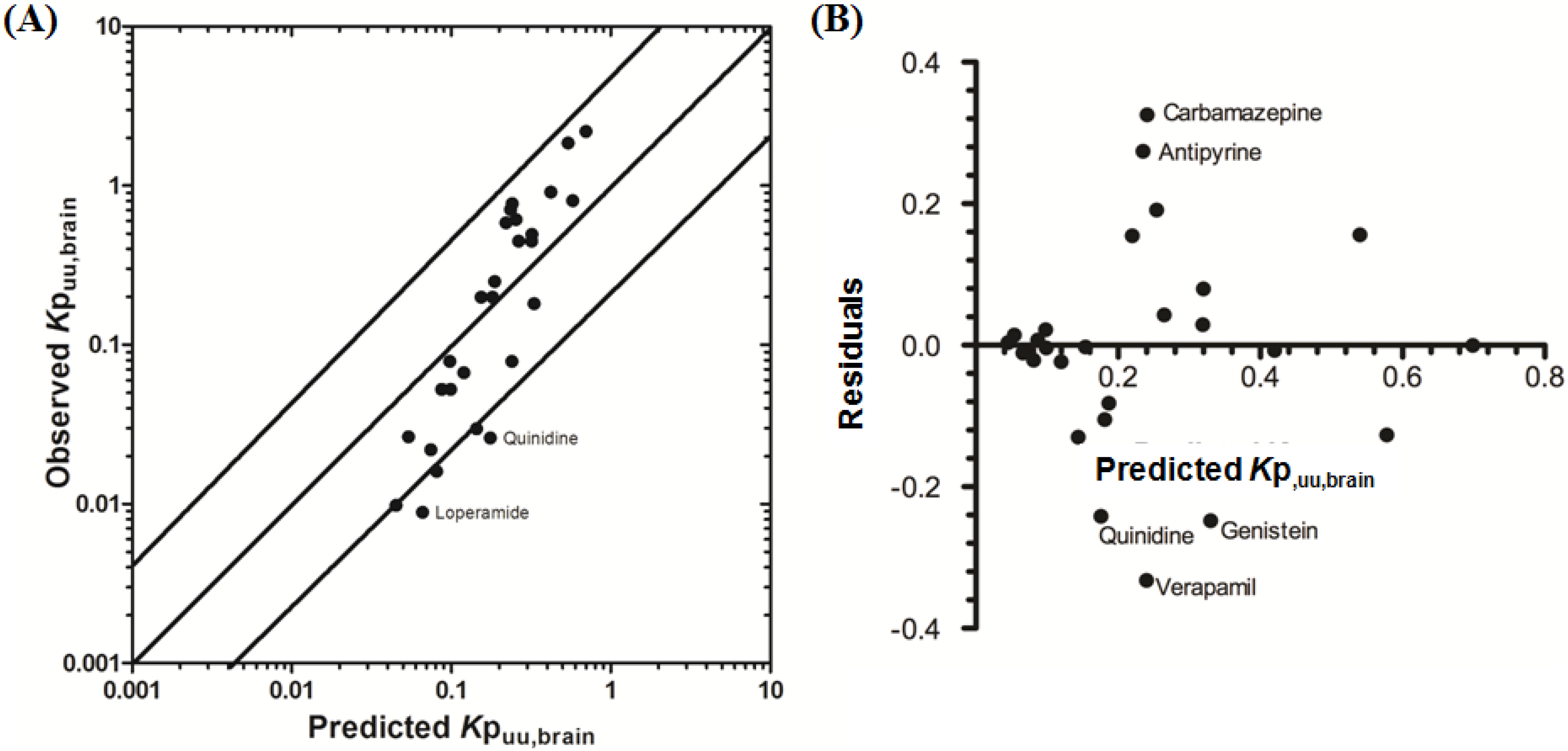
3.2.2. Prediction of Rat Kpuu,brain and CSFu:Plasmau
In an attempt to assess the utility of L-mdr1a-derived permeability data to predict cross-species CNS distribution, we utilised L-mdr1a permeability data from 25 compounds to predict
in vivo CNS distribution (
Kp
uu,brain and CSF
u:Plasma
u) in rat. Our reported model was capable of predicting rat brain disposition (
Kp
uu,brain) for 81.5% of compounds simulated to within 4-fold of the reported
Kp
uu,brain (
Table 3 and
Figure 5). The predicted
Kp
uu,brain of quinidine was within 6.8-fold of observed
Kp
uu,brain, whilst that of loperamide within 7.4-fold. The overall
afe and
rmse were 1.19 and 0.43 respectively (
Table 3).
Predicted
Kp
uu,brain, for compounds with observed
Kp
uu,brain less than 0.01 and greater than 1 deviated further from the line of unity (
Figure 5A and local regression (LOESS) plot in
Supplementary Information Section 5) but were nevertheless predicted within 4-fold of the reported
Kp
uu,brain.
For flavopirodol and perfloxacin, the use of either MDCKII or LLC-PK1-derived cell permeability data did not significantly alter model predictions.
Kp
brain for P-glycoprotein substrates ranges from 1 to 50 [
97]. The
Kp
uu,brain of quindine and loperamide, typical P-glycoprotein substrates, were 7.4-fold over-predicted in our model. Recent reports have identified a 39.4-fold [
55] to 44-fold [
53] increase in
Kp
brain when comparing wild-type to knock-out mice for quinidine and 23.3-fold [
55] for loperamide. For these highly effluxed compounds, the use of
in vitro permeability data may not truly reflect the extent of
in vivo efflux and therefore the use of knock-out-to-wild-type
Kp
brain (or
Kp
uu,brain) could also be used as a surrogate metric for efflux. Such an approach improved model predictions of both loperamide (
Kp
uu,brain = 0.025) and quinidine (
Kp
uu,brain = 0.071) to within a 3-fold prediction window (see
Supplementary Information Section 6).
Figure 5.
Comparison of predicted and reported Kpuu,brain in rat. (A) Solid bold mid-line represents the line of unity and solid outer-lines represent 4-fold prediction error; and (B) residuals plot.
Figure 5.
Comparison of predicted and reported Kpuu,brain in rat. (A) Solid bold mid-line represents the line of unity and solid outer-lines represent 4-fold prediction error; and (B) residuals plot.
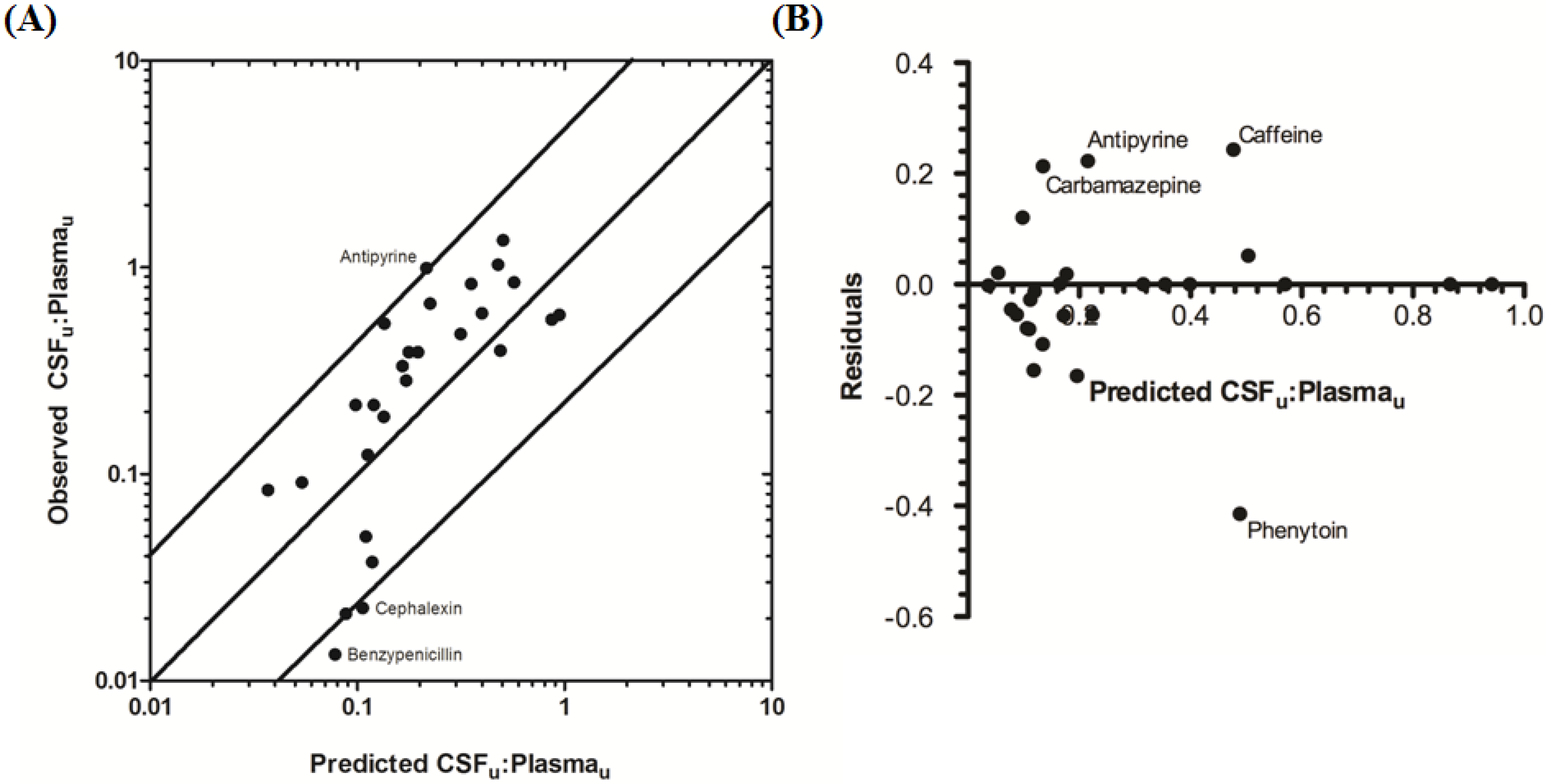
The rat CNS whole-body PBPK model was successful in predicting CSF
u:Plasma
u for 81.5% of compounds to within 4-fold of observed CSF
u:Plasma
u (
Table 3 and
Figure 6A,B), with CSF
u:Plasma
u of benzylpenicillin 5.8-fold over predicted. The overall
afe and
rmse were 0.8 and 0.32 respectively (
Table 3).
Figure 6.
Comparison of predicted and reported CSFu:Plasmau in rat. (A) Solid bold mid-line represents the line of unity and solid outer-lines represent 4-fold prediction error; and (B) residuals plot.
Figure 6.
Comparison of predicted and reported CSFu:Plasmau in rat. (A) Solid bold mid-line represents the line of unity and solid outer-lines represent 4-fold prediction error; and (B) residuals plot.
3.3. Model Sensitivity Analysis
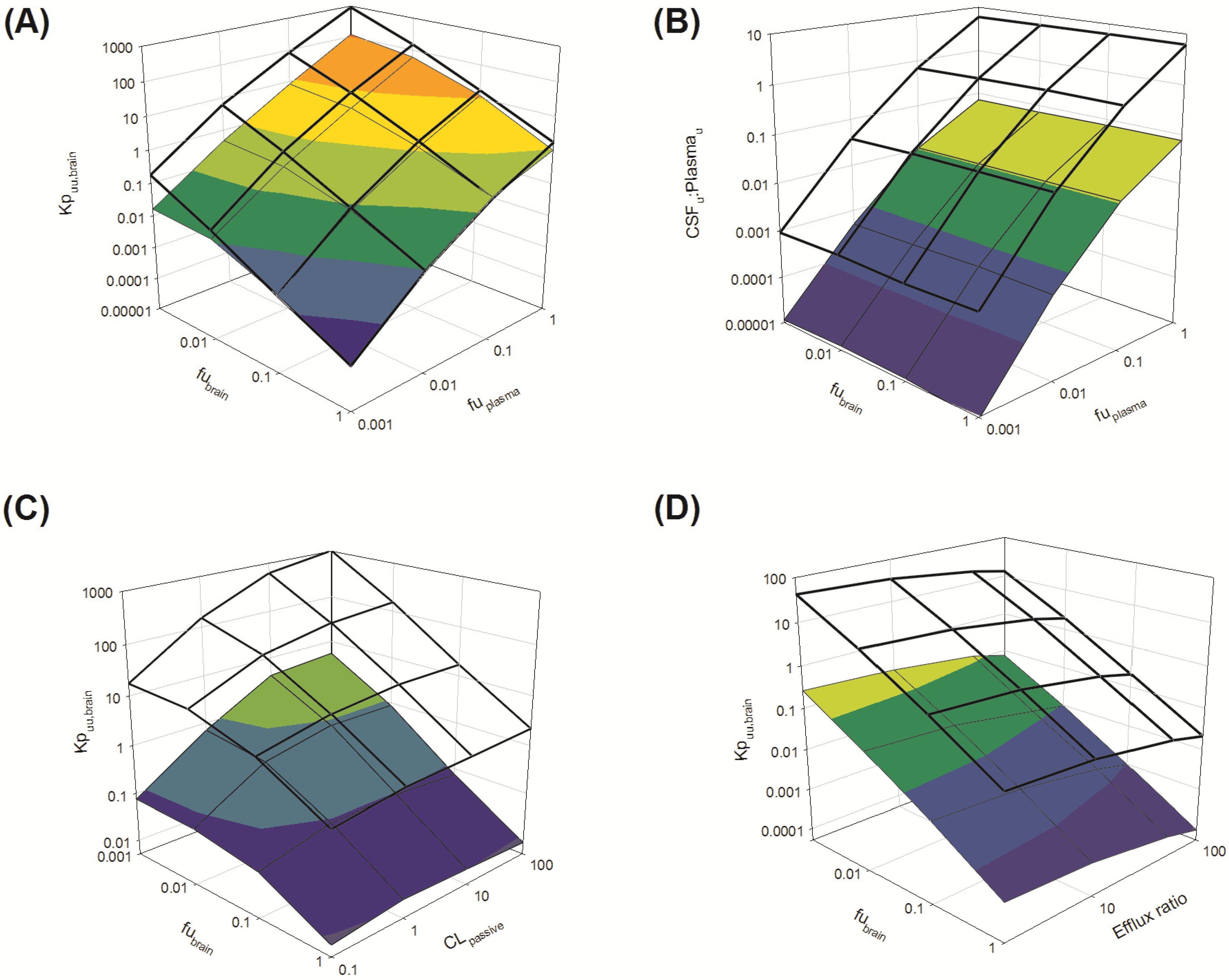
Several parameters, particularly passive clearance, active efflux, fubrain and fuplasma, have the potential to significantly impact CNS drug distribution by influencing drug clearance across the BBB and BCSFB. To further explore the relationship between drug clearance across the BBB and BCSFB and the extent of protein/tissue binding, risperidone was selected as a model candidate compound and the impact of variation in passive clearance, active efflux, fubrain and fuplasma on Kpuu,brain and CSFu:Plasmau was assessed.
3.3.1. Passive Clearance
3.3.1.1. Impact of Variation in fuplasma and fubrain on Kpuu,brain and CSFu:Plasmau
Irrespective of whether the passive clearance (CL
passive) (
i.e., passive permeability) of risperidone at the BBB and BCSFB was low (CL
passive 0.34 mL/h) or high (64 mL/h), increasing
fu
plasma (from 0.001 to 1) resulted in a substantial increase in
Kp
uu,brain across the range of
fu
brain (0.001 to 1) simulated (
Figure 7A: transparent mesh indicates high permeability condition; coloured profile indicates low permeability condition).
Under conditions of both low and high CL
passive, an increase in
fu
brain (from 0.001 to 1) was associated with a decrease in brain partitioning (
Kp
uu,brain) of risperidone. This decrease was observed across the range of
fu
plasma (0.001 to 1) simulated (
Figure 7A: transparent mesh indicates high permeability condition; coloured profile indicates low permeability condition).
Overall, Kpuu,brain at high CLpassive was greater than Kpuu,brain at low CLpassive when fubrain < 0.1.
Brain penetration is therefore influenced by the extent of plasma protein binding (
fu
plasma) and the extent of drug binding within the brain (
fu
brain). Whilst these observations are relatively intuitive, the importance of both
fu
plasma (and hence unbound drug concentration in plasma) and drug permeability across CNS barriers in influencing CNS drug disposition is clearly demonstrated for drugs that exhibit high non-specific binding to brain tissue (
fu
brain). For drugs that are highly bound to brain,
fu
plasma drives entry of drug into the brain. Such drugs are retained within the bulk of the brain (bound-unbound cycling) creating a sink effect, and increasing BBB CL
passive would enhance this sink effect further increasing
Kp
uu,brain [
98,
99,
100].
The disposition of drug into the CSF was demonstrated to be sensitive to
fu
plasma, with increased CSF
u:Plasma
u associated with increasing
fu
plasma. This finding was apparent for both low and high CL
passive conditions (
Figure 7B: transparent mesh indicates high permeability; coloured profile indicates low CL
passive conditions). However, simulations were insensitive to any change in
fu
brain (0.001–1) (
Figure 7B). These simulations demonstrated no apparent relationship between the extent of
fu
brain and CSF
u:Plasma
u, suggesting
fu
brain alone does not significantly influence the unbound concentration of drug within the CSF. These findings support the notion that the extent of free drug in plasma is an important factor influencing drug penetration across the BCSFB into the CSF.
Figure 7.
Sensitively analysis of the whole-body physiologically based pharmacokinetic (PBPK) model. The impact of variations in fubrain, fuplasma, CLpassive and efflux ratio on Kpuu,brain and CSFu:Plasmau.
Figure 7.
Sensitively analysis of the whole-body physiologically based pharmacokinetic (PBPK) model. The impact of variations in fubrain, fuplasma, CLpassive and efflux ratio on Kpuu,brain and CSFu:Plasmau.
3.3.1.2. Impact of Variation in fubrain and CLpassive on Kpuu,brain
Irrespective of the extent of plasma protein binding (
fu
plasma 0.01 (low) or 1 (high)),
Kp
uu,brain was insensitive to changes in CL
passive at higher
fu
brain (
fu
brain > 0.1) (
Figure 7C: transparent mesh indicates high
fu
plasma; coloured profile indicates low high
fu
plasma). The sensitivity of
Kp
uu,brain to changes in CL
passive increased as
fu
brain decreased (<0.1) (
Figure 7C).
As already established, fuplasma determines the unbound plasma drug concentration available to penetrate the BBB and BCSBF, where higher fuplasma results in an increase in the unbound drug concentration available to cross the BBB and BCSFB. Equally, drug binding in brain provides a driving force for retention of drug within the brain mass, which is evident by the increasing Kpuu,brain as fubrain decreases (irrespective of changes in CLpassive). However the important role fubrain plays in determining Kpuu,brain for highly brain-bound drugs (fubrain < 0.1) is particularly evident for lower permeability compounds (CLpassive < 1); Kpuu,brain appeared not to change significantly when fubrain was between 0.001 and 0.1. However Kpuu,brain was reduced when fubrain was between 0.1 and 1 (these findings were observed with both high fuplasma and low high fuplasma conditions).
3.3.2. Active Clearance
3.3.2.1. Impact of Variation in fubrain and Active Efflux on Kpuu,brain
Irrespective of the extent of plasma protein binding (
fu
plasma: 0.01 (low) or 1 (high)),
Kp
uu,brain was influenced by variations in both
fu
brain over the range studied (
fu
brain 0.001–1) and efflux ratio (2–100) (
Figure 7D: transparent mesh indicates high
fu
plasma; coloured profile indicates low
fu
plasma).
Kp
uu,brain increased as
fu
brain decreased from 1 to 0.001, with extensive brain accumulation (
Kp
uu,brain greater than 1) when
fu
plasma was high (
fu
plasma = 1) (
Figure 7D).
The increase in
Kp
uu,brain as
fu
brain decreases can be rationalised by considering that
Kp
uu,brain is largely driven by a combination of membrane permeability (passive and active) and drug free fraction in plasma and brain. Where permeability is low (<0.5 mL/h) the impact of variation in
fu
brain on
Kp
uu,brain is limited (
Figure 7C). When passive permeability increases (CL
passive > 0.5 mL/h), and with increasing active efflux at the BBB (
Figure 7D), the extent of dug passive permeability may augment
Kp
uu,brain and counter the impact a reduction in
fu
brain would have on
Kp
uu,brain.
3.3.2.2. Impact of Variation in CLpassive and Efflux Ratio on Kpuu,brain
The extent of non-specific binding of drug in brain (
fu
brain) had a significant effect on the sensitivity of
Kp
uu,brain to CL
passive and to active efflux (
Figure 8). When drug was highly bound in brain (
Figure 8A:
fu
brain = 0.01 and
fu
plasma = 1), increasing the extent of drug efflux (efflux ratio 2–50) resulted in a progressive decrease in
Kp
uu,brain, which was more apparent at higher CL
passive (>10 mL/h).
Interestingly, at lower CL
passive (<1 mL/h), increasing the extent of active efflux had minimal effects on
Kp
uu,brain compared to higher CL
passive (>1 mL/h). This effect was diminished when
fu
brain was high (
Figure 8B:
fu
brain = 1 and
fu
plasma = 1), since
Kp
uu,brain was not sensitive to changes in CL
passive over a range of efflux ratios (2–50).
Figure 8.
Sensitively analysis of the whole-body PBPK model. The impact of variations in fubrain (A) low fubrain and (B) high fubrain, CLpassive and efflux ratio on Kpuu,brain (see text for details).
Figure 8.
Sensitively analysis of the whole-body PBPK model. The impact of variations in fubrain (A) low fubrain and (B) high fubrain, CLpassive and efflux ratio on Kpuu,brain (see text for details).
Fu
brain governs the unbound drug concentration in brain and, in conjunction with the clearance of drug across the BBB, helps to regulate the rate and extent of CNS drug accumulation. With extensive non-specific drug binding in brain tissue (
Figure 8A),
Kp
uu,brain was higher than when
fu
brain is not a limiting factor (
Figure 8B). In the absence of an efflux effect the sensitivity of
Kp
uu,brain to
fu
brain, particularly at low CL
passive (
Figure 8A), may reflect enhancement of the sink effect as drug is readily able to cross the BBB and accumulate within the brain mass with a diminished abluminal-to-luminal clearance. As active efflux increases, this effect is diminished as efflux provides an additional driving force to rebalance the partition of drug between intravascular spaces and brain biophase.
4. Conclusions
With development of therapeutic drugs targeted to the CNS lagging behind development of drugs for other therapeutic areas there is an urgent requirement to better predict CNS drug disposition. The application of brain microdialysis and PET imaging techniques will provide a true quantitative understanding of the temporal (regional) brain concentrations, but the techniques and equipment needed for their applications in understanding CNS drug disposition is often a limiting factor to their widespread use.
To address this issue, we have developed a mechanistic, whole-body physiologically-based pharmacokinetic model incorporating both brain biophase (brain ISF) and cerebrospinal fluid compartments, which provided reasonable estimates of brain-to-plasma and CSF-to-plasma ratios using routinely determined experimental parameters (e.g., in vitro permeability, efflux ratio, fuplasma or fublood and fubrain). This model not only allows the simultaneous prediction of brain-to-plasma and CSF-to-plasma ratios and examination of the impact of drug permeability and blood flow on CNS drug disposition, but allows a quantitative prediction of unbound drug concentration within the CNS.
Despite the lack of availability of
in vitro permeability data from representative
in vitro choroid plexus cell models (such as the immortalised Z310 rat cell line [
101]), the model adequately predicted CSF-to-plasma ratios for over 90% of the compounds simulated. The lack of predictive models currently capable of quantifying both brain biophase and CSF drug disposition significantly hinders the assessment of drug disposition within the CNS. Current methods utilising CSF drug kinetics as surrogates for brain drug kinetics remain controversial [
95,
102], with many studies disagreeing with the use of CSF as a surrogate for brain [
103,
104,
105]. The physiological differences between the BCSFB and the BBB, advocate the viewpoint that CSF and BCSFB are distinct entities when compared to the BBB. In particular, since CSF drug concentrations do not accurately reflect brain drug concentrations for many actively transported compounds, it is essential that the brain and CSF be considered as separate entities within mechanistic models.
Clearly, in the context of the interactions of drug substrates with transporter proteins, the benefit of the proposed PBPK model would be to effectively incorporate the impact of temporal concentrations on transporter activity and the impact this would have on CNS pharmacokinetics.
The proposed model is capable of predicting temporal CNS drug concentrations, however due to the lack of routinely available transporter-specific Michaelis–Menten terms for drug substrates, the proposed approach of examining overall CNS disposition (
Kp
uu,brain and CSF
u:Plasma
u) is a valid one. In addition, the complexity of modeling the kinetics of drug-transporter protein interaction, at a cellular level, is now recognised and could potentially be examined further within the proposed model if BBB and BCSFB cellular compartments were expanded towards a semi-systems biology based model [
106]. It is prudent to note however, that such approaches would benefit from the use of microdialysis or PET imaging in combination with more elaborate semi-systems biology models, to aid in the development and validation of models.
The present study reports, for the first time, a PBPK CNS model that predicts Kpuu,brain and CSF:Plasma (bound and unbound) for compounds possessing diverse pharmacokinetic characteristics. Additionally, this study illustrates the potential use of in vitro L-mdr1a-derived permeability data to predict rat CNS drug disposition within an acceptable tolerance.