Tissue Distribution and Pharmacokinetic Characteristics of Aztreonam Based on Multi-Species PBPK Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals and Reagents
2.2. Experimental Animals and Sample Collection
2.2.1. Rat Experiment
2.2.2. Data of Mice, Dogs, Monkeys, and Humans
2.3. Analytical Method Development
2.3.1. LC-MS/MS Analysis
2.3.2. Sample Preparation
2.3.3. Method Validation
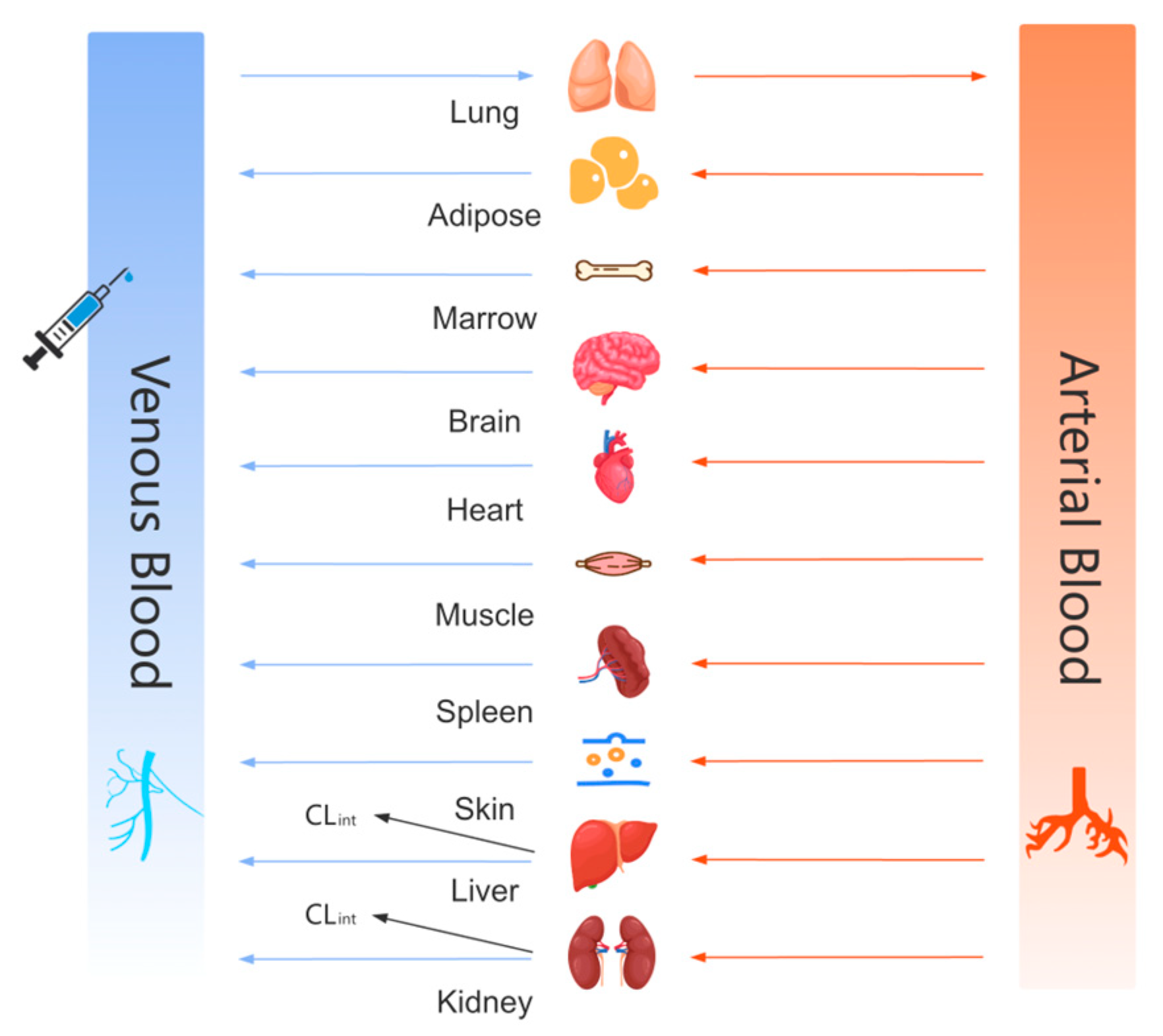
2.4. PBPK Model Building
2.4.1. Modeling Strategy and Parameter Prediction
- Rat, Mouse, and Human Models
- Dog and Monkey Models
- Metabolic Assumptions
2.4.2. Model Optimization and Cross-Species Validation
2.4.3. Model Evaluation Criteria
- Goodness-of-Fit Assessment
- Model Validation
2.4.4. Parameter Sensitivity Analysis
3. Results
3.1. Method Validation Results
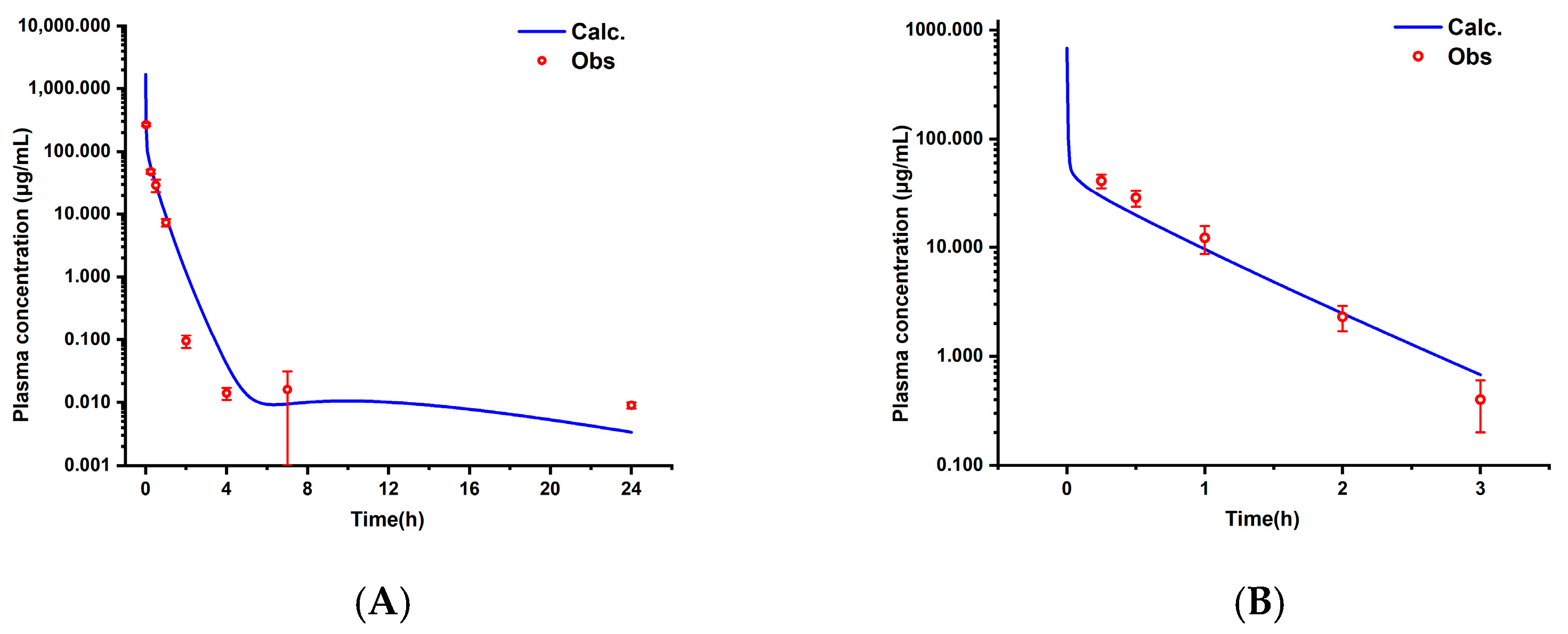
3.2. Pharmacokinetic Characteristics and Model Validation in Rats
3.2.1. Pharmacokinetic Results in Rats
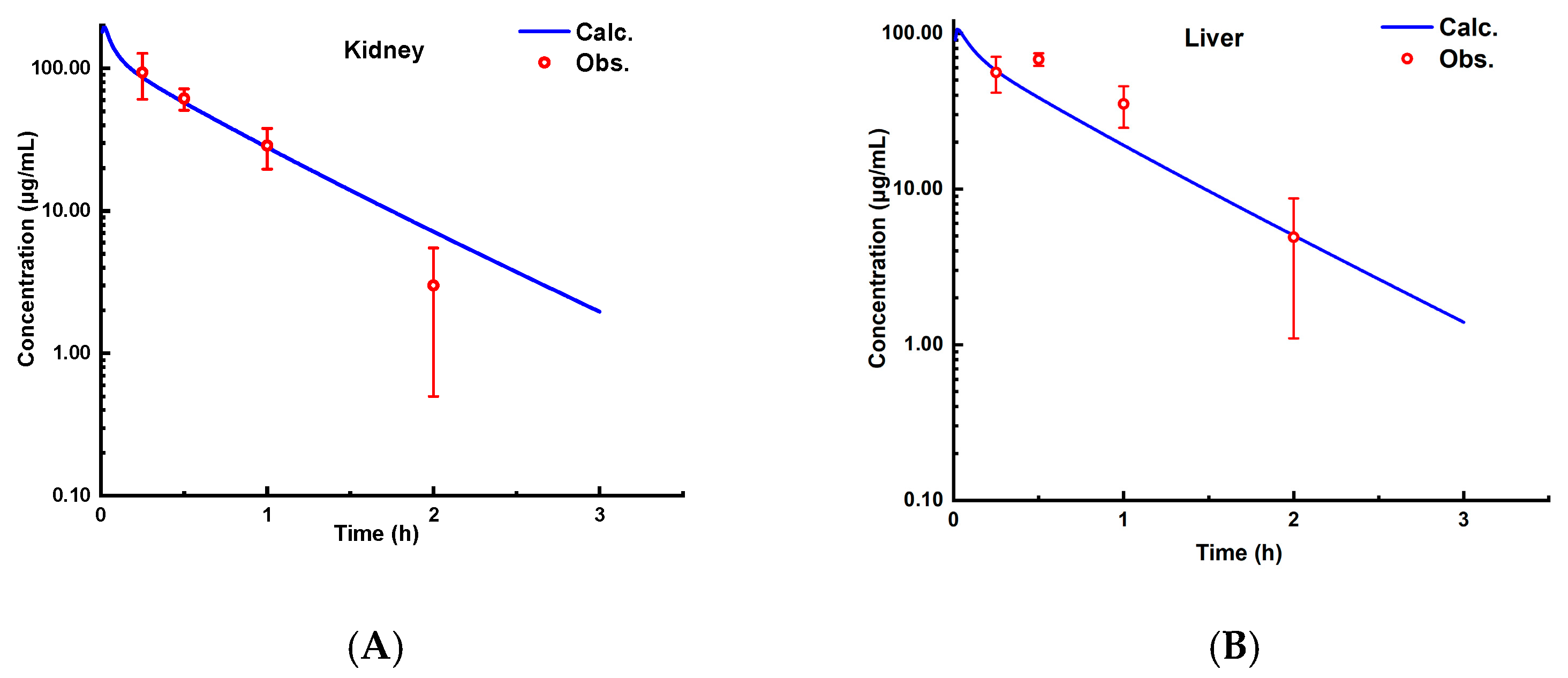
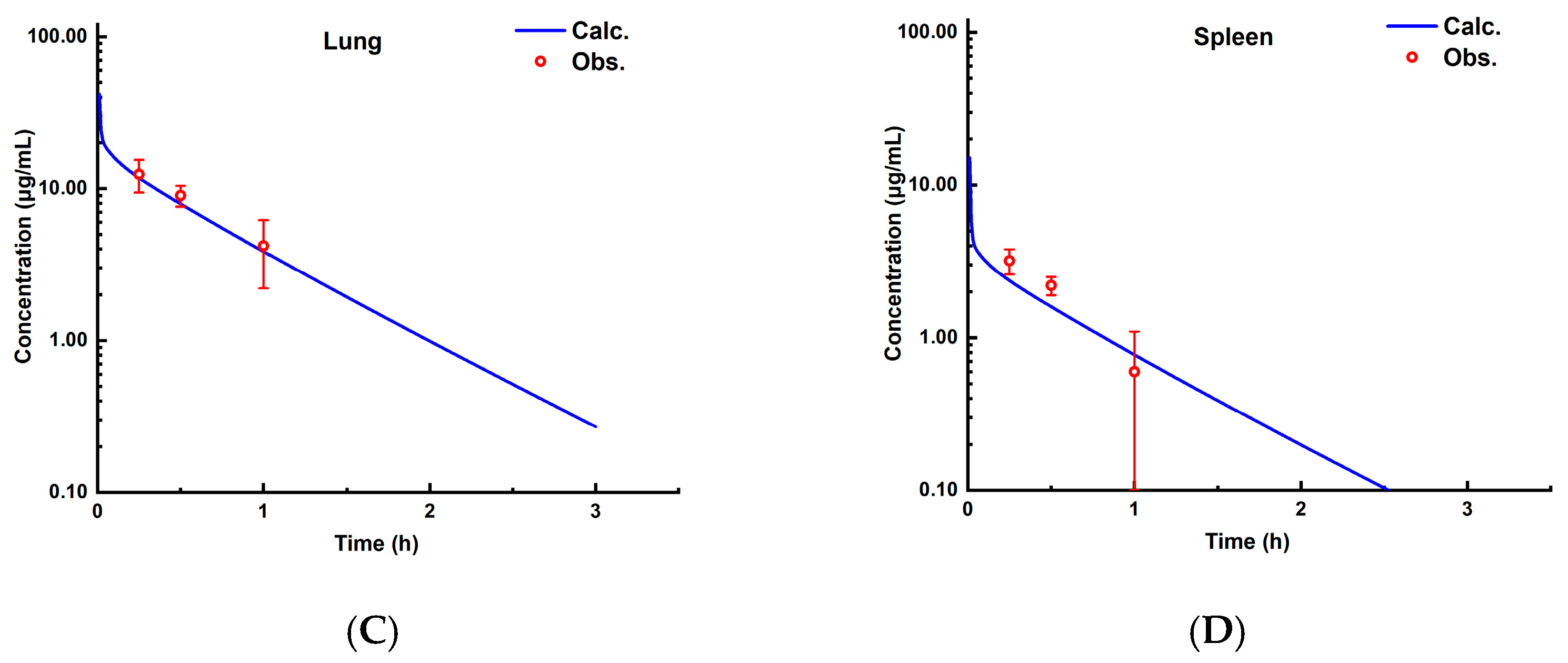
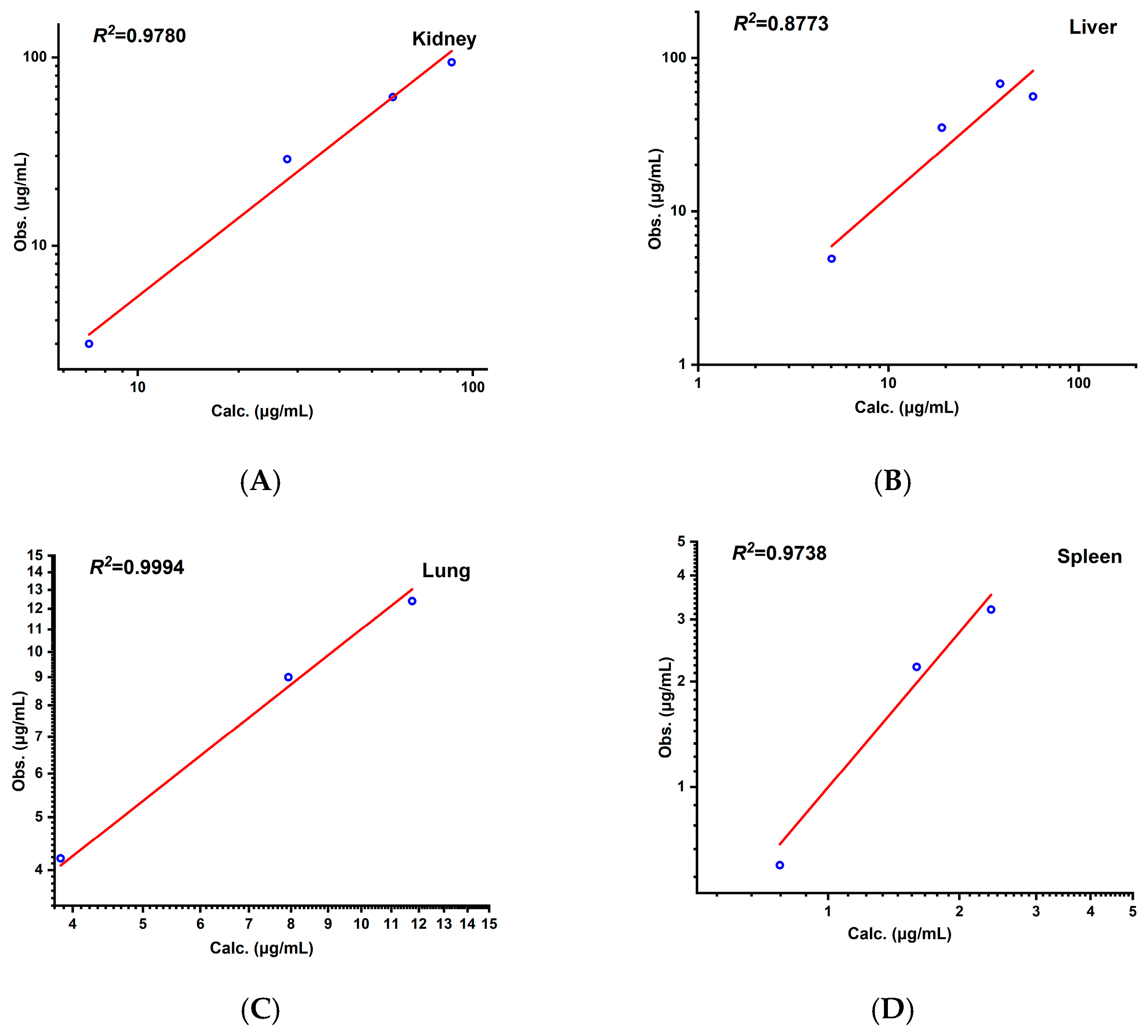
3.2.2. PBPK Model in Rats
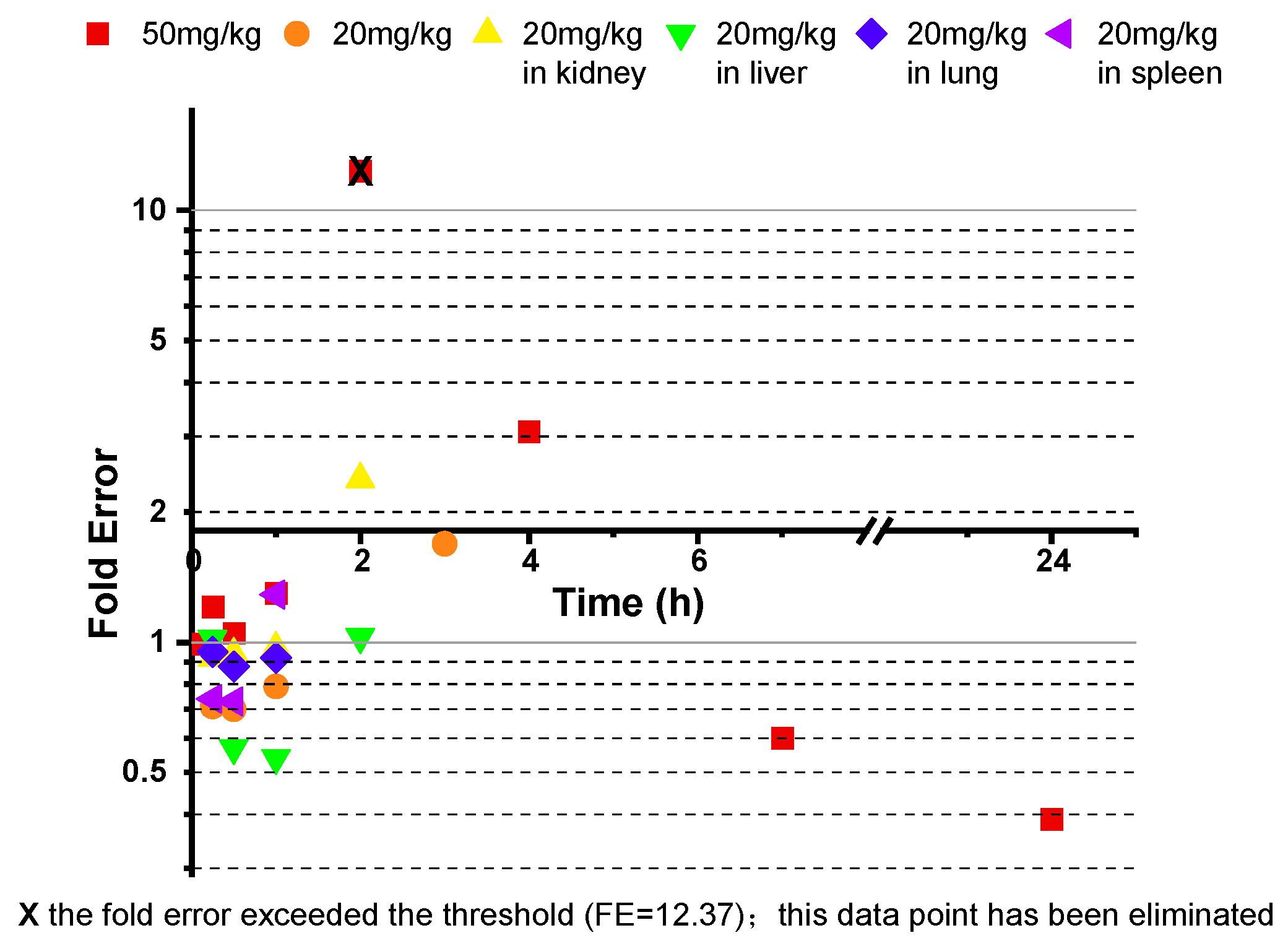
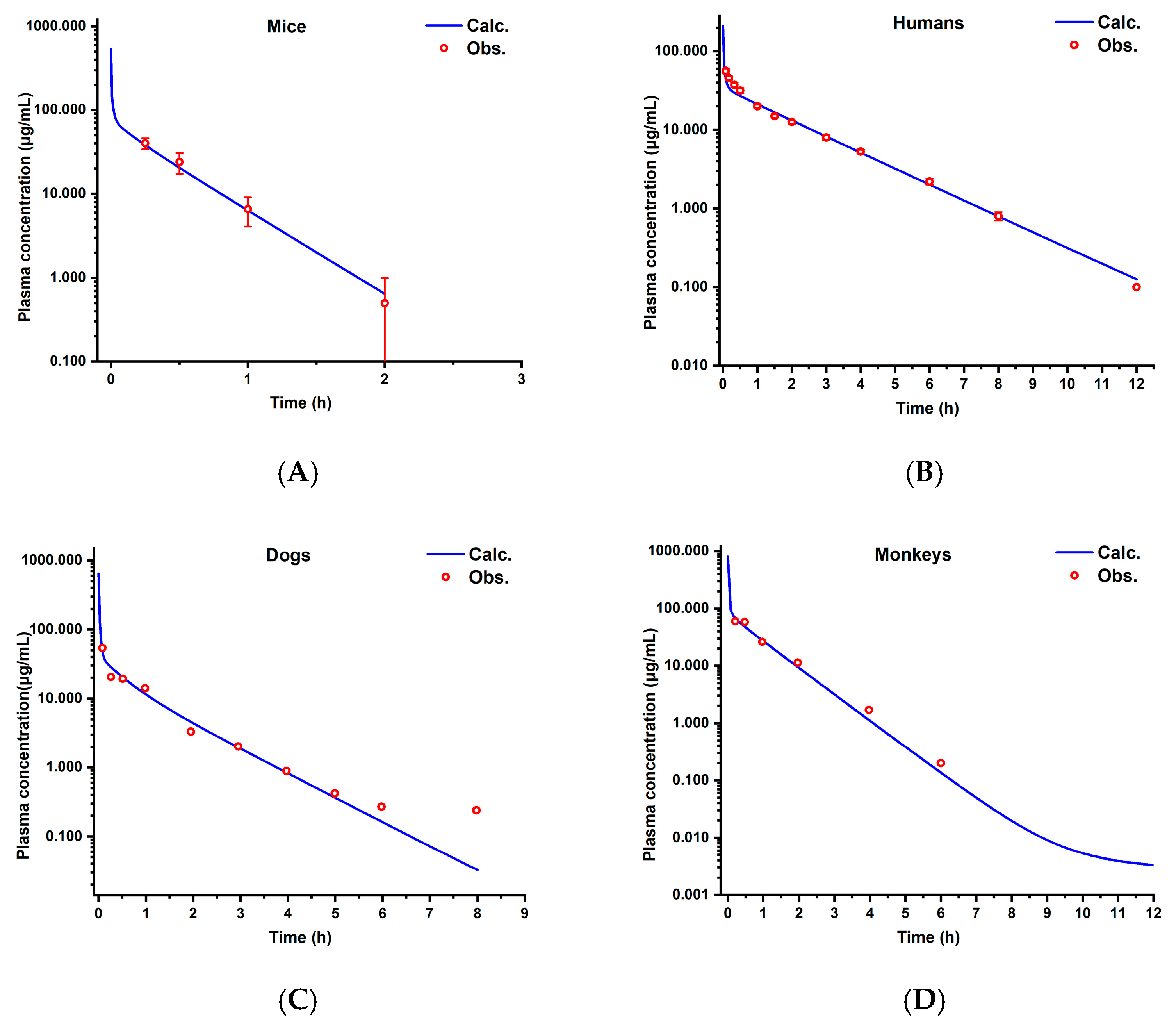
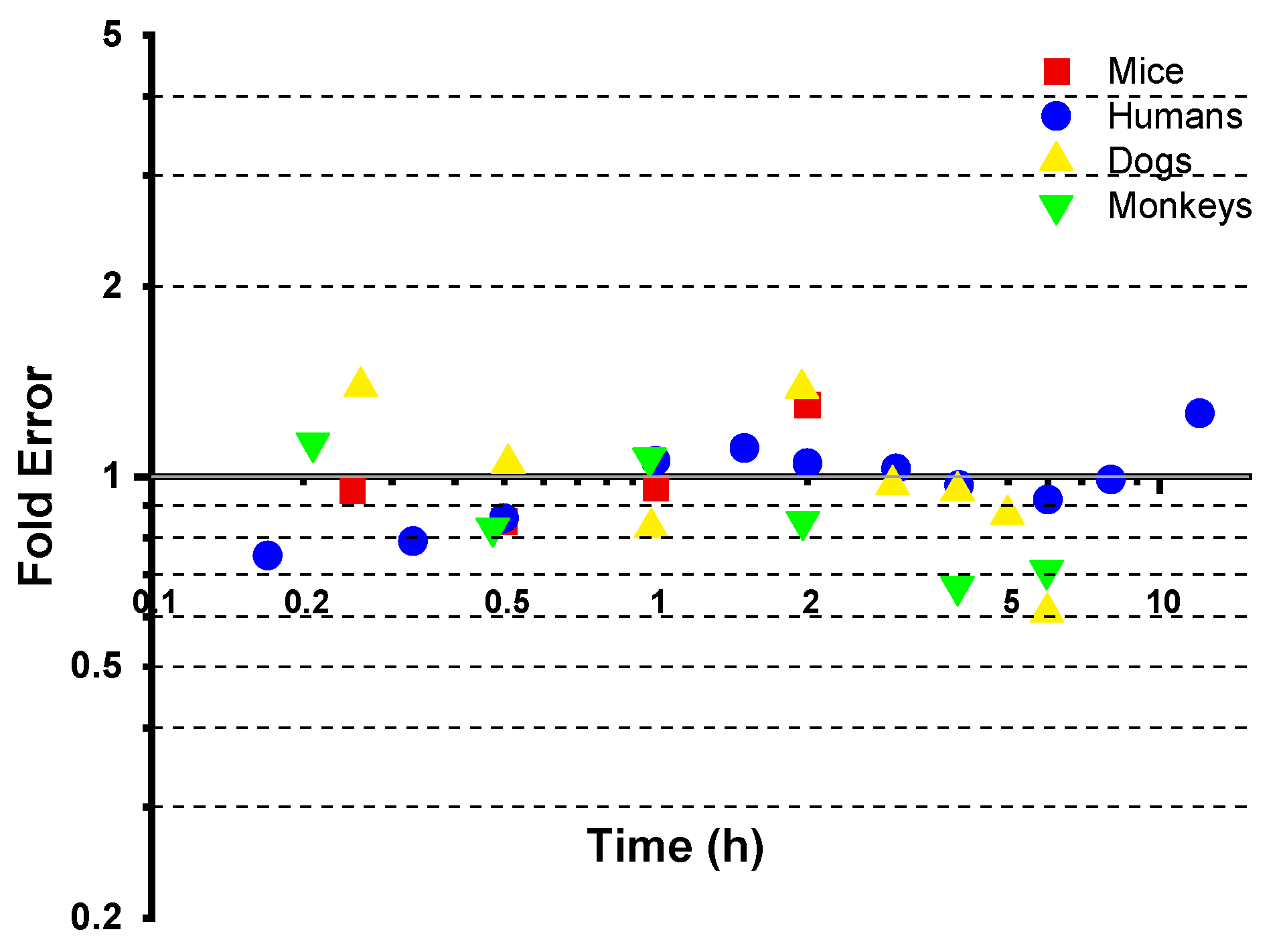
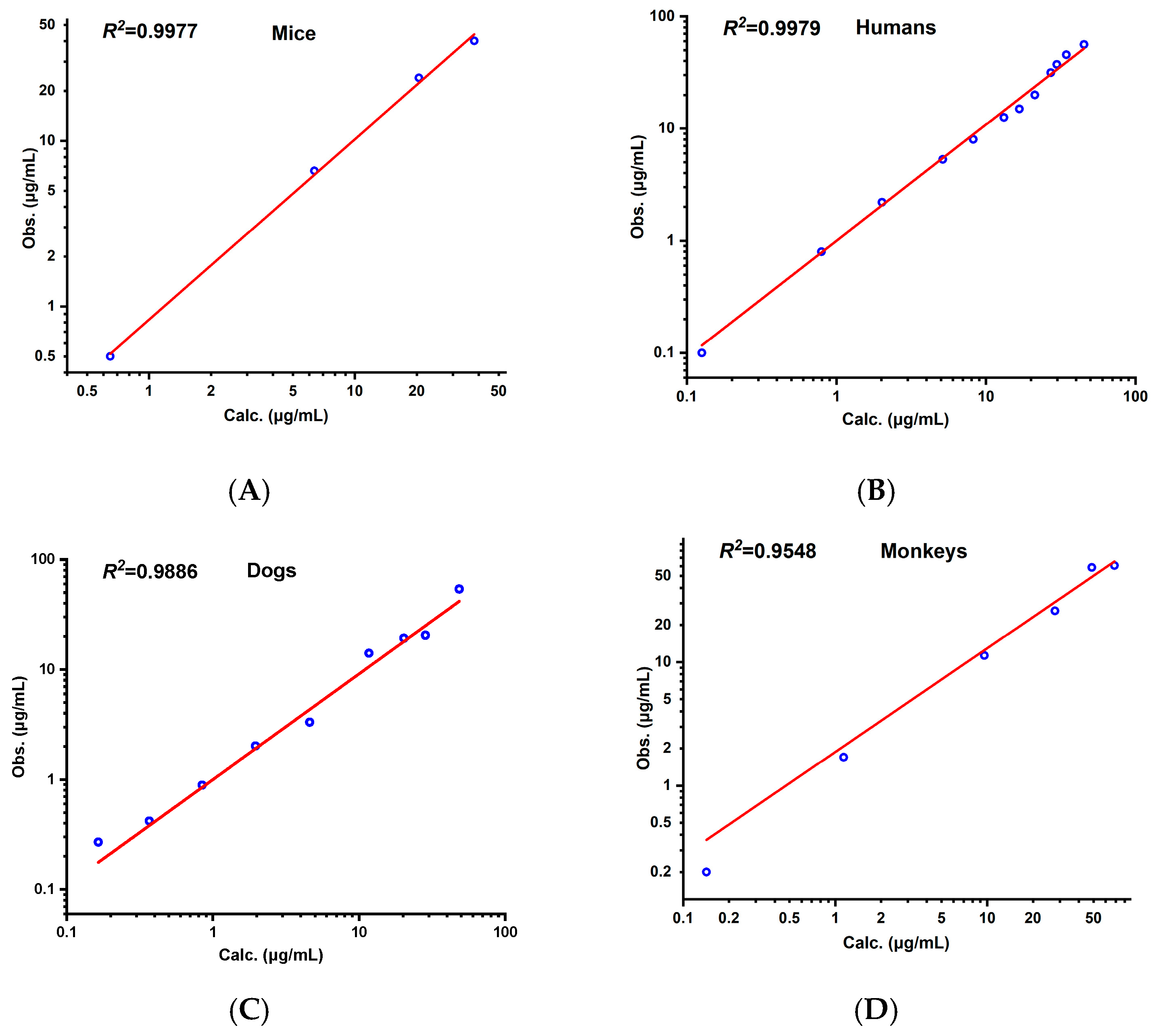
3.3. Cross-Species Extrapolation Verification
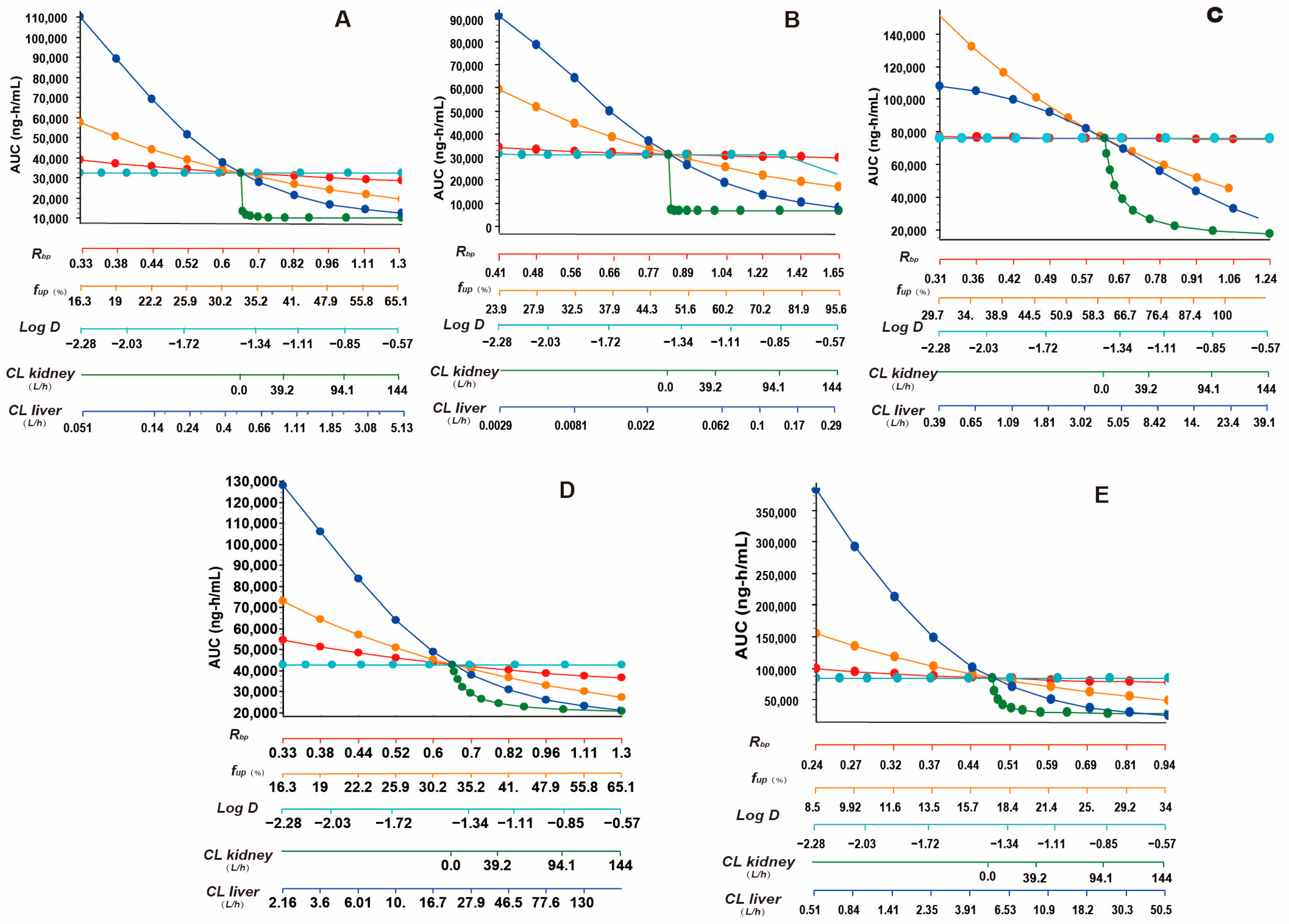
3.4. Results of Parameter Sensitivity Analysis
4. Discussion
4.1. Model Validation and Cross-Species Applicability
4.2. Insights from Parameter Sensitivity Analysis
4.3. Dose-Dependent Pharmacokinetics and Species-Specific Linearity
4.4. Interspecies Variability and Model Limitations
4.5. The Limitations of This Study
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sepkowitz, K.A. Finland, Weinstein, and the Birth of Antibiotic Regret. N. Engl. J. Med. 2012, 367, 102–103. [Google Scholar] [CrossRef]
- McManus, M.C. Mechanisms of Bacterial Resistance to Antimicrobial Agents. Am. J. Health Syst. Pharm. 1997, 54, 1420–1433. [Google Scholar] [CrossRef] [PubMed]
- Baran, A.; Kwiatkowska, A.; Potocki, L. Antibiotics and Bacterial Resistance—A Short Story of an Endless Arms Race. Int. J. Mol. Sci. 2023, 24, 5777. [Google Scholar] [CrossRef]
- Zakhour, J.; El Ayoubi, L.W.; Kanj, S.S. Metallo-Beta-Lactamases: Mechanisms, Treatment Challenges, and Future Prospects. Expert Rev. Anti Infect. Ther. 2024, 22, 189–201. [Google Scholar] [CrossRef] [PubMed]
- Gauba, A.; Rahman, K.M. Evaluation of Antibiotic Resistance Mechanisms in Gram-Negative Bacteria. Antibiotics 2023, 12, 1590. [Google Scholar] [CrossRef] [PubMed]
- Brogden, R.N.; Heel, R.C. Aztreonam. A Review of Its Antibacterial Activity, Pharmacokinetic Properties and Therapeutic Use. Drugs 1986, 31, 96–130. [Google Scholar] [CrossRef] [PubMed]
- Neu, H.C. Aztreonam: The First Monobactam. Med. Clin. N. Am. 1988, 72, 555–566. [Google Scholar] [CrossRef]
- Ramsey, C.; MacGowan, A.P. A Review of the Pharmacokinetics and Pharmacodynamics of Aztreonam. J. Antimicrob. Chemother. 2016, 71, 2704–2712. [Google Scholar] [CrossRef]
- Hidalgo-Tenorio, C.; Bou, G.; Oliver, A.; Rodríguez-Aguirregabiria, M.; Salavert, M.; Martínez-Martínez, L. The Challenge of Treating Infections Caused by Metallo-β-Lactamase-Producing Gram-Negative Bacteria: A Narrative Review. Drugs 2024, 84, 1519–1539. [Google Scholar] [CrossRef]
- Mauri, C.; Maraolo, A.E.; Di Bella, S.; Luzzaro, F.; Principe, L. The Revival of Aztreonam in Combination with Avibactam against Metallo-β-Lactamase-Producing Gram-Negatives: A Systematic Review of In Vitro Studies and Clinical Cases. Antibiotics 2021, 10, 1012. [Google Scholar] [CrossRef]
- Sangiorgio, G.; Calvo, M.; Stefani, S. Aztreonam and Avibactam Combination Therapy for Metallo-β-Lactamase-Producing Gram-Negative Bacteria: A Comprehensive Review. Clin. Microbiol. Infect. 2024, 31, 971–978. [Google Scholar] [CrossRef] [PubMed]
- Kita, Y.; Fugono, T.; Imada, A. Comparative Pharmacokinetics of Carumonam and Aztreonam in Mice, Rats, Rabbits, Dogs, and Cynomolgus Monkeys. Antimicrob. Agents Chemother. 1986, 29, 127–134. [Google Scholar] [CrossRef] [PubMed]
- Kripalani, K.J.; Singhvi, S.M.; Weinstein, S.H.; Everett, D.W.; Bathala, M.S.; Dean, A.V.; Ita, C.E.; Lawrence, L.; Meeker, F.S.; Shaw, J.M. Disposition of [14C]Aztreonam in Rats, Dogs, and Monkeys. Antimicrob. Agents Chemother. 1984, 26, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Swabb, E.A.; Singhvi, S.M.; Leitz, M.A.; Frantz, M.; Sugerman, A. Metabolism and Pharmacokinetics of Aztreonam in Healthy Subjects. Antimicrob. Agents Chemother. 1983, 24, 394–400. [Google Scholar] [CrossRef]
- Adams, K.; Li, X.; Rohan, L.; Bies, R. PBPK Models of the Female Reproductive Tract: Current and Future Analysis. Expert Opin. Drug Metab. Toxicol. 2025, 21, 429–444. [Google Scholar] [CrossRef]
- Tan, Y.-M.; Chan, M.; Chukwudebe, A.; Domoradzki, J.; Fisher, J.; Hack, C.E.; Hinderliter, P.; Hirasawa, K.; Leonard, J.; Lumen, A.; et al. PBPK Model Reporting Template for Chemical Risk Assessment Applications. Regul. Toxicol. Pharmacol. 2020, 115, 104691. [Google Scholar] [CrossRef]
- Xia, B.; Heimbach, T.; Lin, T.; He, H.; Wang, Y.; Tan, E. Novel Physiologically Based Pharmacokinetic Modeling of Patupilone for Human Pharmacokinetic Predictions. Cancer Chemother. Pharmacol. 2012, 69, 1567–1582. [Google Scholar] [CrossRef]
- Tang, H.; Mayersohn, M. A Novel Model for Prediction of Human Drug Clearance by Allometric Scaling. Drug Metab. Dispos. 2005, 33, 1297–1303. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A General Model for the Origin of Allometric Scaling Laws in Biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef]
- Davies, B.; Morris, T. Physiological Parameters in Laboratory Animals and Humans. Pharm. Res. 1993, 10, 1093–1095. [Google Scholar] [CrossRef]
- Liu, X.; Du, R.; Zhang, T.; Li, Y.; Li, L.; Yang, Z.; Zhang, Y.; Wang, Q. Predicting Pharmacokinetics of Active Constituents in Spatholobi Caulis by Using Physiologically Based Pharmacokinetic Models. Pharmaceuticals 2024, 17, 1621. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; He, Q.; Zhang, S.; Li, M.; Tang, Z.; Zhu, X.; Jiao, Z.; Cai, W.; Xiang, X. Application of Physiologically Based Pharmacokinetic Modeling in Preclinical Studies: A Feasible Strategy to Practice the Principles of 3Rs. Front. Pharmacol. 2022, 13, 895556. [Google Scholar] [CrossRef]
- Jogiraju, V.K.; Avvari, S.; Gollen, R.; Taft, D.R. Application of Physiologically Based Pharmacokinetic Modeling to Predict Drug Disposition in Pregnant Populations. Biopharm. Drug Dispos. 2017, 38, 426–438. [Google Scholar] [CrossRef] [PubMed]
- Tan, Z.; Zhang, Y.; Wang, C.; Sun, L. Physiologically Based Pharmacokinetic Modeling of Cefadroxil in Mouse, Rat, and Human to Predict Concentration-Time Profile at Infected Tissue. Front. Pharmacol. 2021, 12, 692741. [Google Scholar] [CrossRef]
- De Sutter, P.-J.; De Cock, P.; Johnson, T.N.; Musther, H.; Gasthuys, E.; Vermeulen, A. Predictive Performance of Physiologically Based Pharmacokinetic Modelling of Beta-Lactam Antibiotic Concentrations in Adipose, Bone, and Muscle Tissues. Drug Metab. Dispos. 2023, 51, 499–508. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.-M.; Rowland, M. The Role of Physiologically Based Pharmacokinetic Modeling in Regulatory Review. Clin. Pharmacol. Ther. 2012, 91, 542–549. [Google Scholar] [CrossRef]
- Jones, H.M.; Chen, Y.; Gibson, C.; Heimbach, T.; Parrott, N.; Peters, S.A.; Snoeys, J.; Upreti, V.V.; Zheng, M.; Hall, S.D. Physiologically Based Pharmacokinetic Modeling in Drug Discovery and Development: A Pharmaceutical Industry Perspective. Clin. Pharmacol. Ther. 2015, 97, 247–262. [Google Scholar] [CrossRef]
- Madsen, P.O.; Dhruv, R.; Friedhoff, L.T. Aztreonam Concentrations in Human Prostatic Tissue. Antimicrob. Agents Chemother. 1984, 26, 20–21. [Google Scholar] [CrossRef]
- Beam, T.R.; Galask, R.P.; Friedhoff, L.T.; Platt, T.B.; Leitz, M.A. Aztreonam Concentrations in Human Tissues Obtained during Thoracic and Gynecologic Surgery. Antimicrob. Agents Chemother. 1986, 30, 505–507. [Google Scholar] [CrossRef]
- Zobell, J.T.; Young, D.C.; Waters, C.D.; Stockmann, C.; Ampofo, K.; Sherwin, C.M.T.; Spigarelli, M.G. Optimization of Anti-Pseudomonal Antibiotics for Cystic Fibrosis Pulmonary Exacerbations: I. Aztreonam and Carbapenems. Pediatr. Pulmonol. 2012, 47, 1147–1158. [Google Scholar] [CrossRef]
- Bader, M.S.; Loeb, M.; Leto, D.; Brooks, A.A. Treatment of Urinary Tract Infections in the Era of Antimicrobial Resistance and New Antimicrobial Agents. Postgrad. Med. 2020, 132, 234–250. [Google Scholar] [CrossRef] [PubMed]
- Kuepfer, L.; Niederalt, C.; Wendl, T.; Schlender, J.-F.; Willmann, S.; Lippert, J.; Block, M.; Eissing, T.; Teutonico, D. Applied Concepts in PBPK Modeling: How to Build a PBPK/PD Model. CPT Pharmacomet. Syst. Pharmacol. 2016, 5, 516–531. [Google Scholar] [CrossRef] [PubMed]
- Martinez, M.N. Interspecies Differences in Physiology and Pharmacology: Extrapolating Preclinical Data to Human Populations. Preclinical Drug Development, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 35–70. [Google Scholar] [CrossRef]

| Reference | Subject | Dosing Regimen |
|---|---|---|
| Kita et al., 1986, [12] | SD rats weighing 210 to 250 g, male (n = 6) | Intramuscularly to rats (10 mg/mL, 0.2 mL/100 g) |
| ICR mice weighing 20 to 25 g, 7-week-old male Jcl (n = 6) | A single dose of 20 mg of the aztreonam per kg of body weight was administered subcutaneously to mice (2 mg/mL, 0.1 mL/10 g) | |
| Swabb et al., 1983, [14] | Healthy male subjects, a mean age of 28 years (range 21 to 30), mean height of 177 cm (range 168 to 187), and mean wight of 73.3 kg (range 69.2 to 90.1) (n = 4) | 500 mg doses of aztreonam administered as single 2 min intravenous infusions |
| Kripalani et al., 1984, [13] | Young adult male purebred beagles (9 to 11 kg) (n = 4) | Single 25 mg/kg doses of aztreonam i.v. |
| Kita et al., 1986, [12] | Female cynomolgus monkeys weighing 2.8 to 3.7 kg (n = 3) | 20 mg/mL per kg |
| Compound Parameter | Aztreonam |
|---|---|
| Predicted Value | |
| Molecular weight | 435.43 |
| Oil–water partition coefficient (log P) | −1.141 |
| Water solubility (mg/mL) (pH 7.4) | 1.187 |
| Plasma free fraction (fup) (%) | 59.4 (human) 32.568 (rat) 47.787 (mouse) |
| Dissociation constant (pKa) | 4.09; −0.56; −5.27 |
| Blood–plasma concentration ratio (Rbp) | 0.997 (human) 0.65 (rat) 0.827 (mouse) |
| Tissue | Rats (0.25 kg) | Mice (0.025 kg) | Humans (70 kg) | Dogs (10 kg) | Monkeys (4 kg) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Volume (mL) | Blood Flow (mL/s) | Volume (mL) | Blood Flow (mL/s) | Volume (mL) | Blood Flow (mL/s) | Volume (mL) | Blood Flow (mL/s) | Volume (mL) | Blood Flow (mL/s) | |
| Lung | 2.1 | 0.7990 | 0.1583 | 0.1135 | 914.4144 | 85.7230 | 86.6667 | 18.4029 | 34 | 8.6929 |
| Arterial Supply | 5.6 | 0.7990 | 0.57 | 0.1135 | 189.8027 | 85.7230 | 300 | 18.4029 | 107 | 8.6929 |
| Venous Return | 11.3 | 0.7990 | 1.13 | 0.1135 | 3619.6054 | 85.7230 | 600 | 18.4029 | 213 | 8.6929 |
| Adipose | 10 | 0.0067 | 1.9105 | 0.0013 | 23,762.7391 | 8.3374 | 1637.5546 | 0.5830 | 437 | 0.2670 |
| Muscle | 122 | 0.1251 | 9.2219 | 0.0152 | 17,027.0270 | 8.9701 | 4385.2065 | 4.1659 | 2000 | 1.5 |
| Liver | 10.3 | 0.1967 | 1.6636 | 0.0335 | 13,440.0901 | 21.6172 | 303.2710 | 5.1501 | 93.46 | 2.4225 |
| ACAT Gut | 0 | 0.1250 | 0 | 0.0250 | 0 | 12.0432 | 0 | 3.5965 | 0 | 1.6667 |
| Spleen | 0.6 | 0.01 | 0.1008 | 0.0015 | 142.1316 | 2.4960 | 24.6679 | 0.4167 | 2.85 | 0.0476 |
| Heart | 1.2 | 0.0650 | 0.1092 | 0.0047 | 265.2499 | 3.4004 | 76.6990 | 0.9 | 13.6 | 0.7572 |
| Brain | 1.2371 | 0.0217 | 0.4165 | 0.0076 | 1411.5727 | 12.6419 | 76.2910 | 0.8643 | 89 | 1.2291 |
| Kidney | 3.7 | 0.1533 | 0.3893 | 0.0213 | 231.8303 | 14.9815 | 50 | 3.6 | 12.4 | 1.1978 |
| Skin | 40.0 | 0.0957 | 3.5158 | 0.0101 | 1608.1081 | 3.3887 | 774.2045 | 2.3017 | 400 | 0.9 |
| Reproductive | 2.5 | 0.0083 | 0.1480 | 0.0005 | 26.3200 | 0.0971 | 16.4 | 0.0574 | 22 | 0.077 |
| Red marrow | 1.8641 | 0.0304 | 0.8320 | 0.0136 | 965.3183 | 5.0855 | 135 | 0.3933 | 36 | 0.18 |
| Yellow marrow | 4.1480 | 0.0068 | 0.5245 | 0.0009 | 2683.2505 | 1.4136 | 64.6 | 0.0188 | 102 | 0.051 |
| Rest of body | 24.421 | 0.0884 | 1.3735 | 0.0050 | 10,989.8249 | 5.7896 | 736.7420 | 0.3684 | 222.6144 | 0.1113 |
| Parameters | Rats 50 mg/kg | Rats 20 mg/kg | ||||||
|---|---|---|---|---|---|---|---|---|
| Observed | Predicted | RPE (%) | ARE (%) | Observed | Predicted | RPE (%) | ARE (%) | |
| AUC0–t (μg·h/mL) | 53.61 | 55.40 | 3.4 | 3.4 | 37.69 | 31.83 | −15.5 | 15.5 |
| AUC0–∞ (μg·h/mL) | 53.62 | 55.43 | 3.3 | 3.3 | 37.93 | 32.36 | −14.7 | 14.7 |
| CL (L/H) | 0.21 | 0.216 | 2.4 | 2.4 | 0.122 | 0.145 | 18.9 | 18.9 |
| Vss (L) | 0.06 | 0.068 | 6.3 | 6.3 | 0.074 | 0.09 | 21.6 | 21.6 |
| Tissue | Predicted Kp Values by Observed Kp Values in Lukacova (Rodgers-Single) Method Using GastroPlus™ | Observed Kp Values in Rats | Predicted Kp Values by Observed Kp Values in Humans |
|---|---|---|---|
| Lung | 0.40 | 0.38 | 0.32 |
| Adipose | 0.09 | / | 0.07 |
| Muscle | 0.29 | / | 0.24 |
| Liver | 2.5 | 2.3 | 2.03 |
| Spleen | 0.08 | 0.08 | 0.06 |
| Heart | 0.36 | / | 0.29 |
| Brain | 0.30 | / | 0.24 |
| Kidney | 3.0 | 2.6 | 2.43 |
| Skin | 0.28 | / | 0.23 |
| Reproductive organ | 0.44 | / | 0.36 |
| Red marrow | 0.25 | / | 0.20 |
| Yellow marrow | 0.09 | / | 0.07 |
| Rest of body | 0.34 | / | 0.28 |
| Parameters | Mice 20 mg/kg | Humans 500 mg | ||||||
|---|---|---|---|---|---|---|---|---|
| Observed | Predicted | RPE (%) | ARE (%) | Observed | Predicted | RPE (%) | ARE (%) | |
| AUC0–t (μg·h/mL) | 30.05 | 31.26 | 4.0 | 4.0 | 79.78 | 75.76 | −5.0 | 5.0 |
| AUC0–∞ (μg·h/mL) | 30.24 | 31.54 | 4.3 | 4.3 | 79.97 | 76.04 | −4.9 | 4.9 |
| CL (L/H) | 0.017 | 0.016 | −3.2 | 3.2 | 6.16 | 6.56 | 6.4 | 6.4 |
| Vss (L) | 0.007 | 0.005 | −27.5 | 27.5 | 13.190 | 13.140 | −0.4 | 0.4 |
| Parameters | Dogs 25 mg/kg | Monkeys 20 mg/kg | ||||||
|---|---|---|---|---|---|---|---|---|
| Observed | Predicted | RPE (%) | ARE (%) | Observed | Predicted | RPE (%) | ARE (%) | |
| AUC0–t (μg·h/mL) | 37.10 | 42.96 | 15.8 | 15.8 | 77.68 | 84.831 | 9.2 | 9.2 |
| AUC0-∞ (μg·h/mL) | 37.47 | 43.00 | 14.8 | 14.8 | 77.88 | 84.821 | 8.9 | 8.9 |
| CL (L/H) | 6.338 | 5.570 | −12.1 | 12.1 | 0.845 | 0.775 | −8.3 | 8.3 |
| Vss (L) | 6.480 | 4.660 | −28.1 | 28.1 | 0.835 | 0.639 | −23.5 | 23.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, X.; Sun, X.; Zhang, J.; Yu, M.; Wen, N.; Geng, X.; Liu, Y. Tissue Distribution and Pharmacokinetic Characteristics of Aztreonam Based on Multi-Species PBPK Model. Pharmaceutics 2025, 17, 748. https://doi.org/10.3390/pharmaceutics17060748
Ye X, Sun X, Zhang J, Yu M, Wen N, Geng X, Liu Y. Tissue Distribution and Pharmacokinetic Characteristics of Aztreonam Based on Multi-Species PBPK Model. Pharmaceutics. 2025; 17(6):748. https://doi.org/10.3390/pharmaceutics17060748
Chicago/Turabian StyleYe, Xiao, Xiaolong Sun, Jianing Zhang, Min Yu, Nie Wen, Xingchao Geng, and Ying Liu. 2025. "Tissue Distribution and Pharmacokinetic Characteristics of Aztreonam Based on Multi-Species PBPK Model" Pharmaceutics 17, no. 6: 748. https://doi.org/10.3390/pharmaceutics17060748
APA StyleYe, X., Sun, X., Zhang, J., Yu, M., Wen, N., Geng, X., & Liu, Y. (2025). Tissue Distribution and Pharmacokinetic Characteristics of Aztreonam Based on Multi-Species PBPK Model. Pharmaceutics, 17(6), 748. https://doi.org/10.3390/pharmaceutics17060748





