3D Porous Collagen Matrices—A Reservoir for In Vitro Simultaneous Release of Tannic Acid and Chlorhexidine
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of Collagen Hydrogels and Matrices
2.3. Matrices Characterization
2.3.1. FT-IR Measurements
2.3.2. Morphology Investigations
2.3.3. UV–VIS Absorption Spectroscopy and Steady-State Fluorescence Measurements
2.3.4. Buffer Uptake into the Collagen-Based Matrices
2.3.5. Resistance to Collagenase Digestion
2.3.6. In Vitro Release of TA and CHDG
3. Results and Discussion
3.1. FT-IR Spectroscopy Analysis of Freeze-Dried Collagen-Based Matrices
3.2. SEM Investigations of Matrices Morphologies
3.3. Isotropic Swelling of Collagen-Based Matrices in an Aqueous PBS-HTAB Environment
- -
- Electrostatic interactions between the chlorhexidine dications (CH++) and the collagen entities negatively charged in the swelling solvent (for more details, see the next section), with a substantial enhancement in the general crosslinking of the collagen network, and
- -
- So-called Yoshida forces or Yoshida H-bonding [84], as quite strong attractive interactions established between proton-donating groups/molecules and π-electron bases represented by entities with delocalized π-electron clouds, especially aromatics.
3.4. Degree of Crosslinking Estimation for Collagen-Based Matrices Revealed by Equilibrium Swelling Measurements in an Aqueous Environment
- -
- Calculation of the total ionic strength corresponding to the solution of PBS (10 mM phosphate buffer, 154 mM NaCl) at pH 7.40 and 37 °C;
- -
- Writing the equation of the Donnan equilibrium by considering an amount of NaCl equivalent to the total ionic strength produced by PBS at the operational parameters.
3.5. Collagenase Digestion
3.6. TA and CHDG Release in a PBS–HTAB Medium
- -
- Construction of a data matrix containing on the upper line and left column the concentration values of TA and CH, covering the possible compositions compatible with the real experimental conditions (Table S2). Every single site of the bidimensional matrix represents a specific, discrete composition expressed as the concentration ratio of TA/CHDG in the releasing solution. Any composition obtained so, taken individually, should follow the Beer–Lambert law by diluting it correspondingly using the same releasing solvent (Figure S9);
- -
- From the UV–VIS spectrum of a certain composition (extracted from the release medium at a desired time), the ratio of absorbances belonging to the two components (A325 nm/A260 nm), corrected by the corresponding extinction coefficients (found to be constant for a broad variety of TA–CHDG compositions), was compared to the values from the data matrix (Table S4). The closest value found in the table defines the relative composition most likely to be in the real system (extracted from the release medium);
- -
- A series of 5–6 solutions of known concentrations (keeping the same ratio of TA/CHDG) were used to generate a calibration curve (a straight line, according to the Beer–Lambert law) on which the specific values of A325nm and A260nm allowed for finding the TA and CHDG concentrations in the real sample.
4. Conclusions
- -
- Was monitored spectrophotometrically (UV–VIS) according to an original algorithm designed and successfully applied;
- -
- Was kinetically studied and, to the best of our knowledge, an adapted kinetic approach developed in this study led, for the first time, to general results of anomalous diffusion able to be rationally split into the two contribution parts related to the pure Fickian and non-Fickian Case II regime of diffusion/release, respectively;
- -
- Was strongly influenced, and eventually able to be controlled, by both the density of non-covalent crosslinkages of the collagen network produced by TA and CHDG and the dynamic capacity of HTAB micelles contained in the release environment to solubilize TA and CHDG.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sezer, A.D.; Cevher, E. Biopolymers as Wound Healing Materials: Challenges and New Strategies. In Biomaterials Applications for Nanomedicine; Pignatello, R., Ed.; InTech: Rang-Du-Fliers, France, 2011; pp. 383–414. [Google Scholar]
- Seaman, S. Dressing Selection in Chronic Wound Management. J. Am. Podiatr. Med. Assoc. 2002, 92, 24–33. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.H.; Singla, A.; Lee, Y. Biomedical applications of collagen. Int. J. Pharm. 2001, 221, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Friess, W. Collagen—Biomaterial for drug delivery. Eur. J. Pharm. Biopharm. 1998, 45, 113–136. [Google Scholar] [CrossRef]
- Yannas, I.V. Biologically Active Analogues of the Extracellular Matrix: Artificial Skin and Nerves. Angew. Chem. Int. Ed. 1990, 29, 20–35. [Google Scholar] [CrossRef]
- Pachence, J.M.; Berg, R.A.; Silver, F.H. Collagen: Its place in the medical device industry. Med. Device Diagn. Ind. 1987, 9, 49–55. [Google Scholar]
- Hayward, P.G.; Morrison, W.A. Current concepts in wound dressings. Aust. Prescr. 1996, 19, 11–13. [Google Scholar] [CrossRef]
- Sripriya, R.; Kumar, M.S.; Sehgal, P.K. Improved collagen bilayer dressing for the controlled release of drugs. J. Biomed. Mater. Res. 2004, 70B, 389–396. [Google Scholar] [CrossRef]
- Stemberger, A.; Grimm, H.; Bader, F.; Rahn, H.D.; Ascherl, R. Local treatment of bone and soft tissue infections with the collagen-gentamicin sponge. Eur. J. Surg. Suppl. 1997, 578, 17–26. [Google Scholar]
- Rutten, H.J.T.; Nijhuis, P.H.A. Prevention of wound infection in elective colorectal surgery by local application of gentamicin-containing collagen sponge. Eur. J. Surg. Suppl. 1997, 163, 31–35. [Google Scholar]
- Chokotho, L.; Van Hasselt, E. The use of tannins in the local treatment of burn wounds—A pilot study. Malawi Med. J. 2005, 17, 19–20. [Google Scholar] [CrossRef]
- de Maquinarias, V.; Monografias, M. The use of tannic acid in the local treatment of burn wounds: Intriguing old and new perspectives. Wounds 2001, 13, 144–158. [Google Scholar]
- Davidson, E.C. Tannic acid in the treatment of burns. Surg. Gynecol. Obstet. 1925, 41, 202–221. [Google Scholar]
- Haslam, E. Plant Polyphenols: Vegetable Tannins Revisited; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Meek, K.M.; Weiss, J.B. Differential fixation of poly(L-arginine) and poly(L-lysine) by tannic acid and its application to the fixation of collagen in electron microscopy. Biochim. Biophys. Acta 1979, 587, 112–120. [Google Scholar] [CrossRef] [PubMed]
- Futaesaku, Y.; Mizuhira, V.; Nakamura, H. The new fixation method using tannic acid for electron microscope and some observation of biological specimens. Proc. Int. Congr. Histochem. Cytochem. Kyoto 1972, 4, 155. [Google Scholar]
- Madhan, B.; Dhathathreyan, A.; Subramanian, V.; Ramasami, T. Investigations on geometrical features in induced ordering of collagen by small molecules. J. Chem. Sci. 2003, 115, 751–766. [Google Scholar] [CrossRef]
- Velmurugan, P.; Singam, E.R.A.; Jonnalagadda, R.R.; Subramanian, V. Investigation on interaction of tannic acid with type I collagen and its effect on thermal, enzymatic, and conformational stability for tissue engineering applications. Biopolymers 2014, 101, 471–483. [Google Scholar] [CrossRef]
- Tang, H.R.; Covington, A.D.; Hancock, R.A. Structure-activity relationships in the hydrophobic interactions of polyphenols with cellulose and collagen. Biopolymers 2003, 70, 403–413. [Google Scholar] [CrossRef]
- Oh, H.I.; Hoff, J.E.; Armstrong, G.S.; Haff, L.A. Hydrophobic interaction in tannin-protein complexes. J. Agric. Food Chem. 1980, 28, 394–398. [Google Scholar] [CrossRef]
- Charulatha, V.; Rajaram, A. Influence of different crosslinking treatments on the physical properties of collagen membranes. Biomaterials 2003, 24, 759–767. [Google Scholar] [CrossRef]
- Demeter, M.; Meltzer, V.; Calina, I.; Scarisoreanu, A.; Micutz, M.; Albu Kaya, M.G. Highly elastic superabsorbent collagen/PVP/PAA/PEO hydrogels crosslinked via e-beam radiation. Rad. Phys. Chem. 2020, 174, 108898. [Google Scholar] [CrossRef]
- Demeter, M.; Călina, I.; Scărișoreanu, A.; Micutz, M.; Kaya, M.A. Correlations on the Structure and Properties of Collagen Hydrogels Produced by E-Beam Crosslinking. Materials 2022, 15, 7663. [Google Scholar] [CrossRef] [PubMed]
- Demeter, M.; Călina, I.; Scărișoreanu, A.; Micutz, M. E-Beam Cross-Linking of Complex Hydrogels Formulation: The Influence of Poly(Ethylene Oxide) Concentration on the Hydrogel Properties. Gels 2021, 8, 27. [Google Scholar] [CrossRef] [PubMed]
- Micutz, M.; Lungu, R.M.; Circu, V.; Ilis, M.; Staicu, T. Hydrogels Obtained via γ-Irradiation Based on Poly(Acrylic Acid) and Its Copolymers with 2-Hydroxyethyl Methacrylate. Appl. Sci. 2020, 10, 4960. [Google Scholar] [CrossRef]
- Călina, I.; Demeter, M.; Scărișoreanu, A.; Micutz, M. Development of Novel Superabsorbent Hybrid Hydrogels by E-Beam Crosslinking. Gels 2021, 7, 189. [Google Scholar] [CrossRef]
- Chen, C.; Yang, H.; Yang, X.; Ma, Q. Tannic acid: A crosslinker leading to versatile functional polymeric networks: A review. RSC Adv. 2022, 12, 7689–7711. [Google Scholar] [CrossRef]
- Baldwin, A.; Uy, L.; Booth, B.W. Characterization of collagen type I/tannic acid beads as a cell scaffold. J. Bioact. Compat. Polym. 2021, 36, 124–138. [Google Scholar] [CrossRef]
- Michalska-Sionkowska, M.; Warzynska, O.; Kaczmarek-Szczepanska, B.; Łukowicz, K.; Osyczka, A.M.; Walczak, M. Characterization of collagen/beta glucan hydrogels crosslinked with tannic acid. Polymers 2021, 13, 3412. [Google Scholar] [CrossRef]
- Baldwin, A.; Uy, L.; Frank-Kamenetskii, A.; Strizzi, L.; Booth, B.W. The in vivo biocompatibility of novel tannic acid-collagen type I injectable bead scaffold material for breast reconstruction post-lumpectomy. J. Biomater. Appl. 2020, 34, 1315–1329. [Google Scholar] [CrossRef]
- Reed, E.B.; Ard, S.; La, J.; Park, C.Y.; Culligan, L.; Fredberg, J.J.; Smolyaninova, L.V.; Orlov, S.N.; Chen, B.; Guzy, R.; et al. Anti-fibrotic effects of tannic acid through regulation of a sustained TGF-beta receptor signaling. Respir. Res. 2019, 20, 168. [Google Scholar] [CrossRef]
- Cass, C.A.P.; Burg, K.J.L. Tannic acid cross-linked collagen scaffolds and their anti-cancer potential in a tissue engineered breast implant. J. Biomater. Sci. Polym. Ed. 2012, 23, 281–298. [Google Scholar] [CrossRef]
- Wang, R.; Yu, R.; Wang, J.; Xiang, J.; Chen, C.; Liu, G.; Liao, X. Hierarchical collagen fibers complexed with tannic acid and Fe3+ as a heterogeneous catalyst for enhancing sulfate radical-based advanced oxidation process. Environ. Sci. Pollut. Res. 2022, 29, 58675–58684. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Liao, W.; Zhang, J.; Chen, W. Thermal behavior of collagen crosslinked with tannic acid under microwave heating. J. Therm. Anal. Calorim. 2019, 135, 2329–2335. [Google Scholar] [CrossRef]
- Ngobili, T.A.; Shah, H.; Park, J.P.; Kwist, K.W.; Inskeep, B.; Burg, K.J.L.; Booth, B.W. Remodeling of tannic acid crosslinked collagen type I induces apoptosis in ER+ breast cancer cells. Anticancer Res. 2015, 35, 1285–1290. [Google Scholar]
- Pilloni, A.; Ceccarelli, S.; Bosco, D.; Gerini, G.; Marchese, C.; Marini, L.; Rojas, M.A. Effect of chlorhexidine digluconate in early wound healing of human gingival tissues. A histological, immunohistochemical and biomolecular analysis. Antibiotics 2021, 10, 1192. [Google Scholar] [CrossRef]
- Gränicher, K.A.; Karygianni, L.; Attin, T.; Thurnheer, T. Low concentrations of chlorhexidine inhibit the formation and structural integrity of enzyme-treated multispecies oral biofilms. Front. Microbiol. 2021, 12, 741863. [Google Scholar] [CrossRef]
- Pratt, R.; Pellowe, C.; Wilson, J.; Loveday, H.; Harper, P.; Jones, S.; McDougall, C.; Wilcox, M. epic2: National Evidence-Based Guidelines for Preventing Healthcare-Associated Infections in NHS Hospitals in England. J. Hosp. Infect. 2007, 65, S1–S59. [Google Scholar] [CrossRef]
- Filoche, S.; Soma, K.; Sissons, C.H. Antimicrobial effects of essential oils in combination with chlorhexidine digluconate. Oral Microbiol. Immunol. 2005, 20, 221–225. [Google Scholar] [CrossRef]
- O’Grady, N.P.; Alexander, M.; Dellinger, E.P.; Gerberding, J.L.; Heard, S.O.; Maki, D.G.; Masur, H.; McCormick, R.D.; Mermel, L.A.; Pearson, M.L.; et al. Guidelines for the prevention of intravascular catheter-related infections. Centers for disease control and prevention. MMWR Recomm. Rep. 2002, 51, 1–29. [Google Scholar]
- McDonnell, G.; Russell, A.D. Antiseptics and disinfectants: Activity, action, and resistance. Clin. Microbiol. Rev. 1999, 12, 147–179. [Google Scholar] [CrossRef]
- Jones, C.G. Chlorhexidine: Is it still the gold standard? Periodontology 1997, 15, 55–62. [Google Scholar] [CrossRef]
- Wakshlak, R.B.-K.; Pedahzur, R.; Menagen, B.; Avnir, D. An antibacterial copper composite more bioactive than metallic silver. J. Mater. Chem. B 2016, 4, 4322–4329. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, S.; Soussan, L.S.; Bechelany, M.B.; Teyssier, C.T.; Cavaillès, V.C.; Pochat-Bohatier, C.; Miele, P.; Kalkura, N.; Janot, J.-M.; Balme, S. Novel biocompatible electrospun gelatin fibers mat with antibiotic drug delivery properties. J. Mater. Chem. B 2016, 4, 1134–1141. [Google Scholar] [CrossRef]
- Al-Obaidy, S.S.M.; Greenway, G.M.; Paunov, V.N. Enhanced antimicrobial action of chlorhexidine loaded in shellac nanoparticles with cationic surface functionality. Pharmaceutics 2021, 13, 1389. [Google Scholar] [CrossRef]
- Al-Awady, M.J.; Weldrick, P.J.; Hardman, M.J.; Greenway, G.M.; Paunov, V.N. Amplified antimicrobial action of chlorhexidine encapsulated in PDAC-functionalized acrylate copolymer nanogel carriers. Mater. Chem. Front. 2018, 2, 2032–2044. [Google Scholar] [CrossRef]
- Cai, X.; Han, B.; Liu, Y.; Tian, F.; Liang, F.; Wang, X. Chlorhexidine-loaded amorphous calcium phosphate nanoparticles for inhibiting degradation and inducing mineralization of type I collagen. ACS Appl. Mater. Interfaces 2017, 9, 12949–12958. [Google Scholar] [CrossRef] [PubMed]
- Rudolf, J.-L.; Moser, C.; Sculean, A.; Eick, S. In-vitro antibiofilm activity of chlorhexidine digluconate on polylactide-based and collagen-based membranes. Oral Health 2019, 19, 291. [Google Scholar] [CrossRef]
- Coquet, L.; Obry, A.; Borghol, N.; Hardouin, J.; Mora, L.; Othmane, A.; Jouenne, T. Impact of chlorhexidine digluconate and temperature on curli production in Escherichia coli—Consequence on its adhesion ability. AIMS Microbiol. 2017, 3, 915–937. [Google Scholar] [CrossRef]
- Nomura, R.; Inaba, H.; Matayoshi, S.; Yoshida, S.; Matsumi, Y.; Matsumoto-Nakano, M.; Nakano, K. Inhibitory effect of a mouth rinse formulated with chlorhexidine gluconate, ethanol, and green tea extract against major oral bacterial species. J. Oral Sci. 2020, 62, 206–211. [Google Scholar] [CrossRef]
- Wakshlak, R.B.-K.; Pedahzur, R.; Avnir, D. Antibacterial Activity of Chlorhexidine-Killed Bacteria: The Zombie Cell Effect. ACS Omega 2019, 4, 20868–20872. [Google Scholar] [CrossRef]
- Karpanen, T.J.; Worthington, T.; Hendry, E.R.; Conway, B.R.; Lambert, P.A. Antimicrobial efficacy of chlorhexidine digluconate alone and in combination with eucalyptus oil, tea tree oil and thymol against planktonic and biofilm cultures of Staphylococcus epidermidis. J. Antimicrob. Chemother. 2008, 62, 1031–1036. [Google Scholar] [CrossRef]
- Suresh, B.; Sriram, S.; Dhanaraj, S.; Elango, K.; Chinnaswamy, K. Anticandidal activity of Santolina chamaecyparissus volatile oil. J. Ethnopharmacol. 1997, 55, 151–159. [Google Scholar] [CrossRef]
- Boruziniat, A.; Babazadeh, M.; Gifani, M.; Nasirzadeh, M. Effect of tannic acid application on durability of bond of etch and rinse adhesive resins. J. Dent. Mater. Tech. 2017, 6, 125–130. [Google Scholar]
- Netmeds. Chlorhexidine 0.2% + Tannic Acid 3% + Zinc Chloride 1%. Available online: https://www.netmeds.com/generics/chlorhexidine-0-2-tannic-acid-3-zinc-chloride-1- (accessed on 19 November 2022).
- Şulea, D.; Ghica, M.V.; Micutz, M.; Albu, M.G.; Brăzdaru, L.; Staicu, T.; Leca, M.; Popa, L. Characterization and in vitro release of chlorhexidine digluconate comprised in type I collagen hydrogels. Rev. Roum. Chim. 2010, 55, 543–551. [Google Scholar]
- Şulea, D.; Micutz, M.; Albu, M.G.; Staicu, T.; Leca, M. Collagen-thuja tincture biomaterials for wound treatment. 2. Hydrogels and porous matrices. Rev. Roum. Chim. 2011, 56, 129–136. [Google Scholar]
- Micutz, M.; Staicu, T.; Leca, M.; Ghica, C. Adsorption complexes of collagenous polypeptide-ionic surfactant in aqueous medium. 1. The formation of micellar structure of ionic surfactant adsorbed onto collagenous polypeptide chain. Rev. Roum. Chim. 2009, 54, 1077–1095. [Google Scholar]
- Meng, Z.; Zheng, X.; Tang, K.; Liu, J.; Ma, Z.; Zhao, Q. Dissolution and regeneration of collagen fibers using ionic liquid. Int. J. Biol. Macromol. 2012, 51, 440–448. [Google Scholar] [CrossRef]
- Rabotyagova, O.S.; Cebe, P.; Kaplan, D.L. Collagen structural hierarchy and susceptibility to degradation by ultraviolet radiation. Mater. Sci. Eng. C Mater. Biol. Appl. 2008, 28, 1420–1429. [Google Scholar] [CrossRef]
- Tronci, G.; Doyle, A.; Russell, S.J.; Wood, D.J. Structure-property-function relationships in triple-helical collagen hydrogels. MRS Proc. 2012, 1498, 145–150. [Google Scholar] [CrossRef]
- Ribeiro, A.R.; Barbaglio, A.; Oliveira, M.J.; Santos, R.; Coelho, A.V.; Ribeiro, C.C.; Wilkie, I.C.; Carnevali, M.D.C.; Barbosa, M.A. Correlations Between the Biochemistry and Mechanical States of a Sea-Urchin Ligament: A Mutable Collagenous Structure. Biointerphases 2012, 7, 38. [Google Scholar] [CrossRef]
- Nagai, T.; Suzuki, N.; Tanoue, Y.; Kai, N.; Nagashima, T. Characterization of acid-soluble collagen from skins of surf smelt (Hypomesus pretiosus japonicus Brevoort). Food Nutr. Sci. 2010, 1, 59–66. [Google Scholar] [CrossRef]
- Palpandi, C.; Ramasamy, P.; Rajinikanth, T.; Vairamani, S.; Shanmugam, A. Extraction of collagen from mangrove Archeaogastropod Nerita (Dostia) crepidularia Lamarck, 1822. Am.-Euras. J. Sci. Res. 2010, 5, 23–30. [Google Scholar]
- Belbachir, K.; Noreen, R.; Gouspillou, G.; Petibois, C. Collagen types analysis and differentiation by FTIR spectroscopy. Anal. Bioanal. Chem. 2009, 395, 829–837. [Google Scholar] [CrossRef] [PubMed]
- Doyle, B.B.; Bendit, E.G.; Blout, E.R. Infrared spectroscopy of collagen and collagen-like polypeptides. Biopolymers 1975, 14, 937–957. [Google Scholar] [CrossRef] [PubMed]
- Kaminska, A.; Sionkowska, A. Effect of UV radiation on the infrared spectra of collagen. Polym. Degrad. Stabil. 1996, 51, 19–26. [Google Scholar] [CrossRef]
- Kong, J.; Yu, S. Fourier transform infrared spectroscopic analysis of protein secondary structures. Acta Biochim. Biophys. Sin. Shanghai 2007, 39, 549–559. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.-H.; Mirkin, N.G.; Krimm, S. A quantitative anharmonic analysis of the amide A band in α-helical poly(L-Alanine). Biopolymers 1999, 49, 195–207. [Google Scholar] [CrossRef]
- Serdyuk, I.N.; Zaccai, N.R.; Zaccai, J. Methods in Molecular Biophysics. Structure, Dynamics, Function; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Surewicz, W.K.; Mantsch, H.H. New insight into protein secondary structure from resolution-enhanced infrared spectra. Biochim. Biophys. Acta BBA Protein Struct. Mol. Enzym. 1988, 952, 115–130. [Google Scholar] [CrossRef]
- Guilbert, M.; Said, G.; Happillon, T.; Untereiner, V.; Garnotel, R.; Jeannesson, P.; Sockalingum, G.D. Probing non-enzymatic glycation of type I collagen: A novel approach using Raman and infrared biophotonic methods. Biochim. Biophys. Acta BBA Protein Struct. Mol. Enzym. 2013, 1830, 3525–3531. [Google Scholar] [CrossRef]
- Derrick, M. Evaluation of the state of degradation of Dead Sea Scroll samples using FT-IR spectroscopy. Book Pap. Group Annu. 1991, 10, 49–65. [Google Scholar]
- Wary, R.; Sivaraj, S.; Karthikeyan, G.; Pathak, R.K.; Suraj, S.L.M.; Dasararaju, G.; Kannayiram, G. Chitosan gallic acid microsphere incorporated collagen matrix for chronic wounds: Biophysical and biochemical characterization. Int. J. Pharm. Pharm. Sci. 2014, 6, 94–100. [Google Scholar]
- Goissis, G.; Piccirili, L.; Goes, J.C.; Plepis, A.; Das-Gupta, D.K. Anionic Collagen: Polymer Composites with Improved Dielectric and Rheological Properties. Artif. Organs 1998, 22, 203–209. [Google Scholar] [CrossRef]
- Plepis, A.M.D.G.; Goissis, G.; Das-Gupta, D.K. Dielectric and pyroelectric characterization of anionic and native collagen. Polym. Eng. Sci. 1996, 36, 2932–2938. [Google Scholar] [CrossRef]
- Smith, B. Infrared Spectral Interpretation. A Systematic Approach; CRC Press, LLC: Boca Raton, FL, USA, 1999. [Google Scholar]
- Petibois, C.; Gouspillou, G.; Wehbe, K.; Delage, J.-P.; Déléris, G. Analysis of type I and IV collagens by FT-IR spectroscopy and imaging for a molecular investigation of skeletal muscle connective tissue. Anal. Bioanal. Chem. 2006, 386, 1961–1966. [Google Scholar] [CrossRef] [PubMed]
- Gunasekaran, S.; Natarajan, R.K.; Renganayaki, V.; Natarajan, S. Vibrational spectra and thermodynamic analysis of metformin. Indian J. Pure Appl. Phys. 2006, 44, 495–500. [Google Scholar]
- Doillon, C.J.; Silver, F.H. Collagen-based wound dressing: Effects of hyaluronic acid and fibronectin on wound healing. Biomaterials 1986, 7, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Pieper, J.S.; Oosterhof, A.; Dijkstra, P.J.; Veerkamp, J.H.; van Kuppevelt, T.H. Preparation and characterization of porous crosslinked collagenous matrices containing bioavailable chondroitin sulphate. Biomaterials 1999, 20, 847–858. [Google Scholar] [CrossRef]
- Doillon, C.J.; Whyne, C.F.; Berg, R.A.; Olson, R.M.; Silver, F.H. Fibroblast-collagen sponge interactions and the spatial deposition of newly synthesized collagen fibers in vitro and in vivo. Scan. Electron Microsc. 1984, 3, 1313–1320. [Google Scholar]
- Pal, K.; Banthia, A.K.; Majumdar, D.K. Polymeric hydrogels: Characterization and biomedical applications. Des. Monomers Polym. 2009, 12, 197–220. [Google Scholar] [CrossRef]
- Yoshida, Z.; Oda, R. Intermolecular hydrogen bond involving a π-base as the proton acceptor. I. Detection by the refractive index method. J. Phys. Chem. 1964, 68, 2895–2898. [Google Scholar] [CrossRef]
- Blackburn, R.S.; Burkinshaw, S.M. Treatment of cellulose with cationic, nucleophilic polymers to enable reactive dyeing at neutral pH without electrolyte addition. J. Appl. Polym. Sci. 2003, 89, 1026–1031. [Google Scholar] [CrossRef]
- Blackburn, R.S.; Harvey, A.; Kettle, L.L.; Manian, A.P.; Payne, J.D.; Russell, S.J. Sorption of Chlorhexidine on Cellulose: Mechanism of Binding and Molecular Recognition. J. Phys. Chem. B 2007, 111, 8775–8784. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J. Principles of Polymer Chemistry, 8th ed.; Cornell University Press: Ithaca, NY, USA; London, UK, 1971; pp. 590–593. [Google Scholar]
- Bray, J.K.; Merrill, E.W. Poly(vinyl alcohol) hydrogels. Formation by electron beam irradiation of aqueous solutions and subsequent crystallization. J. App. Polym. Sci. 1973, 17, 3779–3794. [Google Scholar] [CrossRef]
- Ofner, C.M.; Bubnis, W.A. Chemical and swelling evaluations of amino group crosslinking in gelatin and modified gelatin matrices. Pharm. Res. 1996, 13, 1821–1827. [Google Scholar] [CrossRef] [PubMed]
- Bohidar, H.B.; Jena, S.S. Kinetics of sol–gel transition in thermoreversible gelation of gelatin. J. Chem. Phys. 1993, 98, 8970–8977. [Google Scholar] [CrossRef]
- Tanioka, A.; Tazawa, T.; Miyasaka, K.; Ishikawa, K. Effects of water on the mechanical properties of gelatin films. Biopolymers 1974, 13, 753–764. [Google Scholar] [CrossRef] [PubMed]
- Tanford, C. Physical Chemistry of Macromolecules; John Wiley & Sons, Inc.: New York, NY, USA, 1961; pp. 225–227. [Google Scholar]
- Nelson, D.L.; Cox, M.M. Lehninger Principles of Biochemistry, 4th ed.; W.H. Freeman: New York, NY, USA, 2004; p. 78. [Google Scholar]
- Stoll, V.S.; Blanchard, J.S. Buffers: Principles and practice. In Methods in Enzymology. Guide to Protein Purification, 2nd ed.; Abelson, J.N., Simon, M.I., Eds.; Elsevier Inc.: Amsterdam, The Netherlands, 2009; Volume 463, pp. 43–56. [Google Scholar]
- Davies, C.W. The extent of dissociation of salt in water. Part VIII. An equation for the mean ionic activity coefficient of an electrolyte in water, and a revision of the dissociation constants of some sulphates. J. Chem. Soc. 1938, 2093–2098. [Google Scholar] [CrossRef]
- Davies, C.W. Ion Association; Butterworths: London, UK, 1962; pp. 37–53. [Google Scholar]
- Ritsema, C.J. Estimation of activity coefficients of individual ions in solutions with ionic strengths up to 0.3 mol dm−3. J. Soil. Sci. 1993, 44, 307–315. [Google Scholar] [CrossRef]
- Fietzek, P.P.; Kuhn, K. The Primary Structure of Collagen. In International Review of Connective Tissue Research; Hall, D.A., Jackson, D.S., Eds.; Academic Press: New York, NY, USA, 1976; pp. 1–60. [Google Scholar]
- Mokrousova, O.R.; Volfkovich, Y.M. Hide and Skin of Mammals. In Structural Properties of Porous Materials and Powders Used in Different Fields of Science and Technology; Volfkovich, Y.M., Filoppov, A.N., Bagotsky, V.S., Eds.; Springer: London, UK, 2014; pp. 251–264. [Google Scholar]
- Muiznieks, L.D.; Keeley, F.W. Molecular assembly and mechanical properties of the extracellular matrix: A fibrous protein perspective. Biochim. Biophys. Acta BBA Mol. Basis Dis. 2013, 1832, 866–875. [Google Scholar] [CrossRef]
- Shoulders, M.D.; Raines, R.T. Collagen structure and stability. Annu. Rev. Biochem. 2009, 78, 929–958. [Google Scholar] [CrossRef]
- Ventre, M.; Padovani, M.; Cavington, A.D.; Netti, P.A. Composition, Structure and Physical Properties of Fetal Calf Skin. In Proceedings of the IULTCS Eurocongress 2006, Istanbul, Turkey, 24–26 May 2006; pp. 1–21. [Google Scholar]
- Brosse, J.; Sabatier, B. Use of Superabsorbent Polymers for Treating Raw Skins, Corresponding Compositions and Methods and Resulting Treated Skins. U.S. Patent US6964745B1, 15 November 2005. [Google Scholar]
- Manicourt, D.-H.; Devogelaer, J.-P.; Thonar, E.J.-M.A. Products of Cartilage Metabolism. In Dynamics of Bone and Cartilage Metabolism, 2nd ed.; Seibels, M.J., Robins, S.P., Bilezikian, J.P., Eds.; Academic Press: San Diego, CA, USA, 2006; pp. 421–449. [Google Scholar]
- Kuhn, K. The Classical Collagens: Type I., II, and III. In Structure and Function of Collagen Types; Mayne, R., Burgeson, R.E., Eds.; Academic Press: Orlando, FL, USA, 1987; pp. 1–42. [Google Scholar]
- Cawston, T.E.; Murphy, G. [52] Mammalian collagenases. Methods Enzymol. 1981, 80, 711–722. [Google Scholar]
- Welgus, H.G.; Jeffrey, J.J.; Stricklin, G.P.; Roswit, W.T.; Eisen, A.Z. Characteristics of the action of human skin fibroblast collagenase on fibrillar collagen. J. Biol. Chem. 1980, 255, 6806–6813. [Google Scholar] [CrossRef] [PubMed]
- Grassi, M.; Grassi, G.; Lapasin, R.; Colombo, I. Understanding Drug Release and Absorption Mechanisms. A Physical and Mathematical Approach; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2007. [Google Scholar]
- Boateng, J.S.; Matthews, K.H.; Stevens, H.N.; Eccleston, G.M. Wound Healing Dressings and Drug Delivery Systems: A Review. J. Pharm. Sci. 2008, 97, 2892–2923. [Google Scholar] [CrossRef] [PubMed]
- Wu, N.; Wang, L.-S.; Tan, D.C.-W.; Moochhala, S.M.; Yang, Y.-Y. Mathematical modeling and in vitro study of controlled drug release via a highly swellable and dissoluble polymer matrix: Polyethylene oxide with high molecular weights. J. Control. Release 2005, 102, 569–581. [Google Scholar] [CrossRef]
- Brazel, C.S.; Peppas, N.A. Modeling of drug release from swellable polymers. Eur. J. Pharm. Biopharm. 2000, 49, 47–58. [Google Scholar] [CrossRef]
- Peppas, N.A.; Bures, P.; Leobandung, W.; Ichikawa, H. Hydrogels in pharmaceutical formulations. Eur. J. Pharm. Biopharm. 2000, 50, 27–46. [Google Scholar] [CrossRef]
- Grassi, M.; Lapasn, R.; Pricl, S. Modeling of Drug Release from a Swellable Matrix. Chem. Eng. Commun. 1998, 169, 79–109. [Google Scholar] [CrossRef]
- Morawetz, H. Nature of the hypercoiled form of poly(methacrylic acid) in water at low pH. Macromolecules 1996, 29, 2689–2690. [Google Scholar] [CrossRef]
- Kalyanasundaram, K.; Thomas, J.K. Environmental effects on vibronic band intensities in pyrene monomer fluorescence and their application in studies of micellar systems. J. Am. Chem. Soc. 1977, 99, 2039–2044. [Google Scholar] [CrossRef]
- Winnik, F.M.; Regismond, S.T.A. Fluorescence methods in the study of polymer-surfactant systems. In Polymer-Surfactant Systems; Kwak, J.K.T., Ed.; Marcel Dekker, Inc.: New York, NY, USA, 1998; pp. 267–316. [Google Scholar]
- Zana, R.; Lévy, H.; Kwetkat, K. Mixed micellization of dimeric (gemini) surfactants and conventional surfactants. I. Mixtures of an anionic dimeric surfactant and of the nonionic surfactants C12E5and C12E8. J. Colloid Interface Sci. 1998, 197, 370–376. [Google Scholar] [CrossRef]
- Regev, O.; Zana, R. Aggregation behavior of Tyloxapol, a nonionic surfactant oligomer, in aqueous solution. J. Colloid Interface Sci. 1999, 210, 8–17. [Google Scholar] [CrossRef]
- Micutz, M.; Staicu, T.; Leca, M. Fluorescence and electron microscopy studies on collagen type I-ionic surfactants systems with gel consistency. Rev. Roum. Chim. 2005, 50, 547–553. [Google Scholar]
- Holmberg, K.; Jonsson, B.; Kronberg, B.; Lindman, B. Surfactants and Polymers in Aqueous Solution, 2nd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2004. [Google Scholar]
- Rosen, M.J. Surfactants and Interfacial Phenomena, 3rd ed.; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2004. [Google Scholar]
- Adane, L.; Bharatam, P.V. Tautomeric preferences and electron delocalization in biurets, thiobiurets, and dithiobiurets: An ab initio study. Int. J. Quantum Chem. 2008, 108, 1277–1286. [Google Scholar] [CrossRef]
- Bharatam, P.V.; Patel, D.S.; Iqbal, P. Pharmacophiric features of biguanide derivatives: An electronic and structural analysis. J. Med. Chem. 2005, 48, 7615–7622. [Google Scholar] [CrossRef] [PubMed]
- Ernst, S.R.; Cagle, F.W., Jr. Biguanide. Acta Cryst. 1977, B33, 235–237. [Google Scholar] [CrossRef]
- Maksić, Z.B.; Kovačević, B. Absolute Proton Affinity of Some Polyguanides. J. Org. Chem. 2000, 65, 3303–3309. [Google Scholar] [CrossRef]
- Ernst, S.R. Biguanide hydrochloride. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1977, 33, 237–240. [Google Scholar] [CrossRef]
- Mason, P.E.; Dempsey, C.E.; Vrbka, L.; Heyda, J.; Brady, J.W.; Jungwirth, P. Specificity of ion-protein interactions: Complementary and competitive effects of tetrapropylammonium, guanidinium, sulfate, and chloride ions. J. Phys. Chem. B 2009, 113, 3227–3234. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wu, X. Flurescence enhancement of Fisetin by silver nanoparticles with cetyltrimethyl ammonium bromide micelles. RSC. Adv. 2015, 5, 7433–7439. [Google Scholar] [CrossRef]
- Kuperkar, K.C.; Mata, J.P.; Bahadur, P. Effect of 1-alkanols/salt on the cationic surfactant micellar aqueous solution—A dynamic light scattering study. Colloids Surf. A Physicochem. Eng. Aspects 2011, 380, 60–65. [Google Scholar] [CrossRef]
- Dorshow, R.; Briggs, J.; Bunton, C.A.; Nicoli, D.F. Dynamic light scattering from cetyltrimethylammonium bromide micelles. Intermicellar interactions at low ionic strengths. J. Phys. Chem. 1982, 86, 2388–2395. [Google Scholar] [CrossRef]
- Van Oosten, B.; Marquardt, D.; Komljenović, I.; Bradshaw, J.P.; Sternin, E.; Harroun, T.A. Small molecule interaction with lipid bilayers: A molecular dynamics study of chlorhexidine. J. Mol. Graph. Model. 2014, 48, 96–104. [Google Scholar] [CrossRef] [PubMed]
- Komljenović, I.; Marquardt, D.; Harroun, T.; Sternin, E. Location of chlorhexidine in DMPC model membranes: A neutron diffraction study. Chem. Phys. Lipids 2010, 163, 480–487. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Flanagan, D. Theory of Diffusion and Pharmaceutical applications. In Developing Solid Oral Dosage Forms. Pharmaceutical Theories and Practice; Qiu, Y., Chen, Y., Zhang, G.G.Z., Liu, L., Porter, W.R., Eds.; Academic Press: New York, NY, USA, 2009; pp. 147–162. [Google Scholar]
- Peppas, N.A.; Brannon-Peppas, L. Water diffusion and sorption in amorphous macromolecular systems and foods. J. Food Eng. 1994, 22, 189–210. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Enscore, D.; Hopfenberg, H.; Stannett, V. Effect of particle size on the mechanism controlling n-hexane sorption in glassy polystyrene microspheres. Polymer 1977, 18, 793–800. [Google Scholar] [CrossRef]
- Ritger, P.L.; Peppas, N.A. A simple equation for description of solute release I. Fickian and non-fickian release from non-swellable devices in the form of slabs, spheres, cylinders or discs. J. Control. Release 1987, 5, 23–36. [Google Scholar] [CrossRef]
- Korsmayer, R.W.; Peppas, N.A. Solute and penetrant diffusion in swellable polymers. III. Drug release from glassy poly(HEMA-co-NVP) copolymers. J. Control. Release 1984, 1, 89–98. [Google Scholar] [CrossRef]
- Siepmann, J.; Peppas, N.A. Modeling of drug release from delivery systems based on hydroxypropyl methylcellulose (HPMC). Adv. Drug Deliv. Rev. 2012, 64, 163–174. [Google Scholar] [CrossRef]
- Brazdaru, L.; Micutz, M.; Staicu, T.; Albu, M.G.; Sulea, D.; Leca, M. Structural and rheological properties of collagen hydrogels containing tannic acid and chlorhexidine digluconate intended for topical applications. Comptes Rendus Chim. 2015, 18, 160–169. [Google Scholar] [CrossRef]
- Ghigo, G.; Berto, S.; Minella, M.; Vione, D.; Alladio, E.; Nurchi, V.M.; Lachowicz, J.; Daniele, P.G. New insights into the protogenic and spectroscopic properties of commercial tannic acid. The role of gallic acid impurities. N. J. Chem. 2018, 42, 7703–7712. [Google Scholar] [CrossRef]
- Simoes, M.C.; Hughes, K.J.; Ingham, D.B.; Ma, L.; Pourkashanian, M. Estimation of the thermochemical radii and ionic volumes of complex ions. Inorg. Chem. 2017, 56, 7566–7573. [Google Scholar] [CrossRef]
- Kunz, W. Specific ion effects in colloidal and biological systems. Curr. Opin. Colloid Interface Sci. 2010, 15, 34–39. [Google Scholar] [CrossRef]
- Collins, K. Ions from the Hofmeister series and osmolytes: Effects on proteins in solution and in the crystallization process. Methods 2004, 34, 300–311. [Google Scholar] [CrossRef] [PubMed]
- Micutz, M.; Circu, V.; Ilis, M.; Staicu, T. Novel Gemini Surfactant for Binding Eu(III)-Polyoxometalate into Hydrogels and Polymer Latexes. Gels 2022, 8, 786. [Google Scholar] [CrossRef] [PubMed]
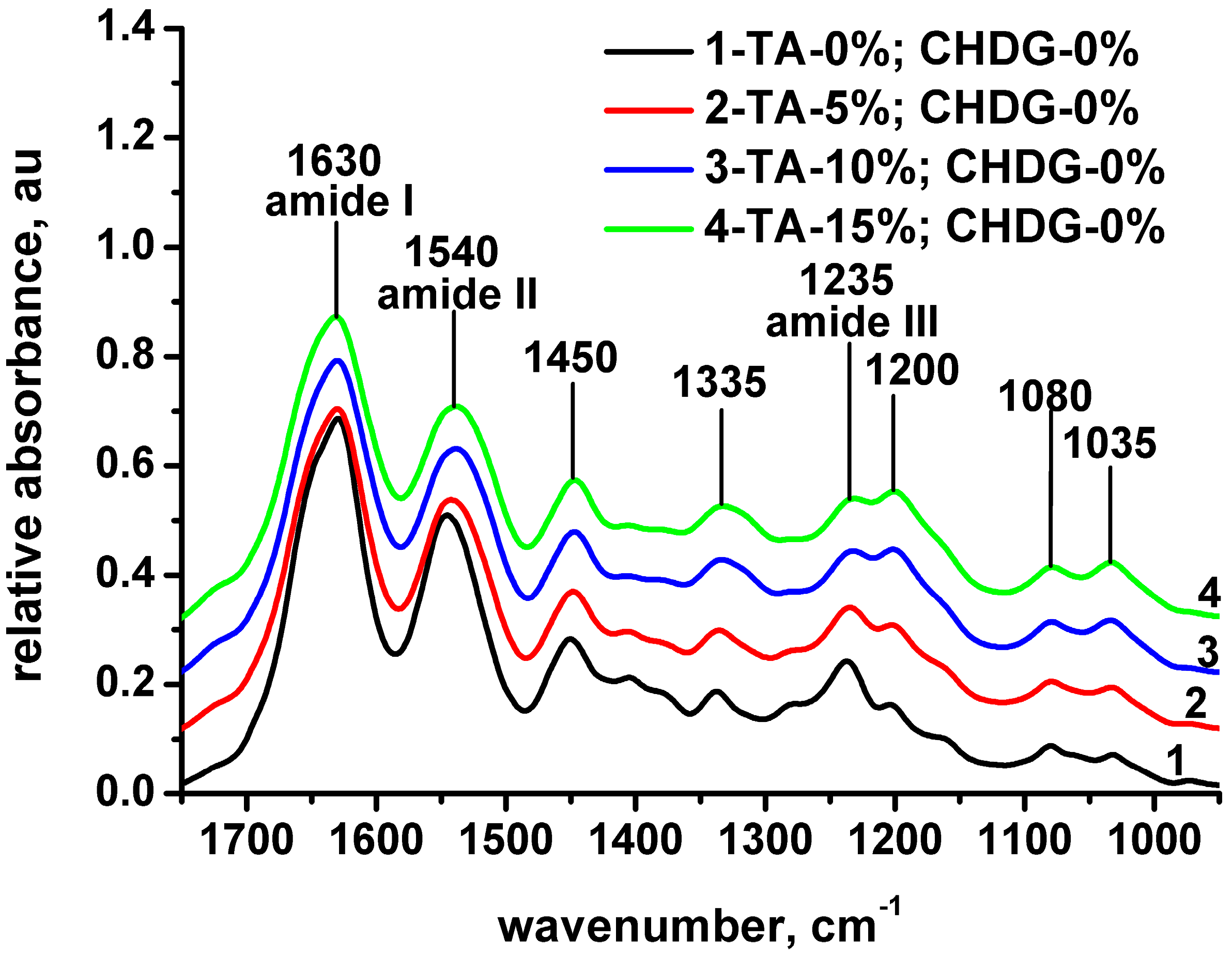


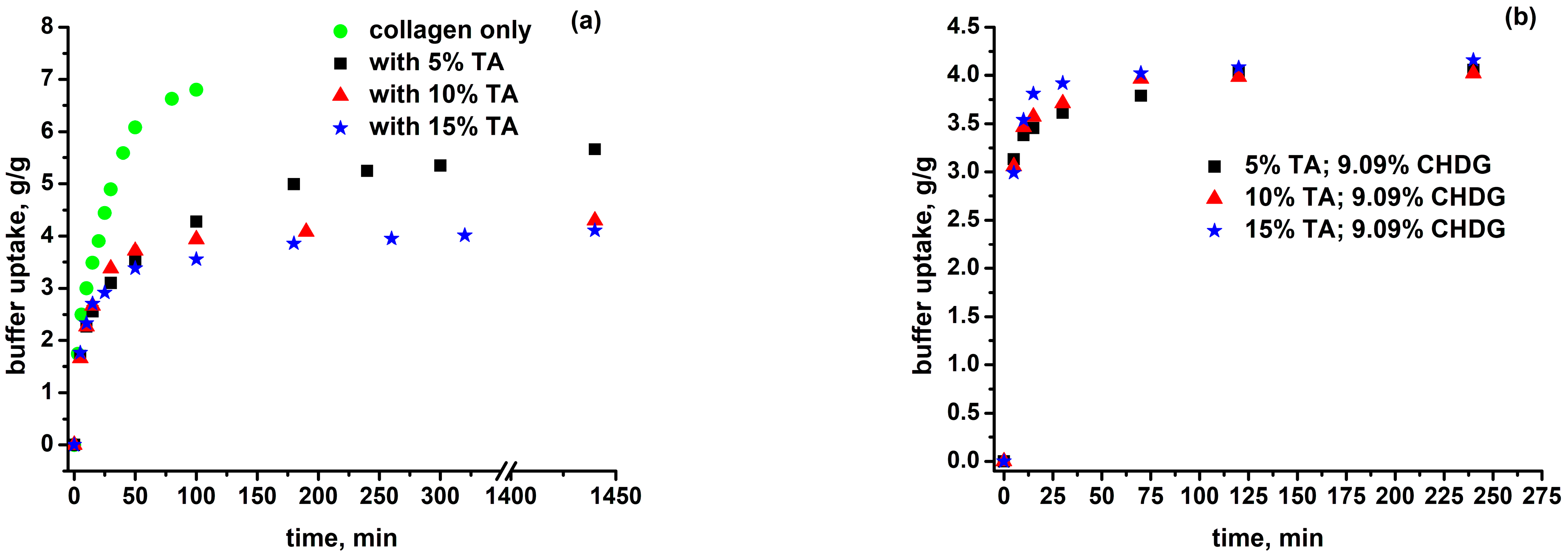


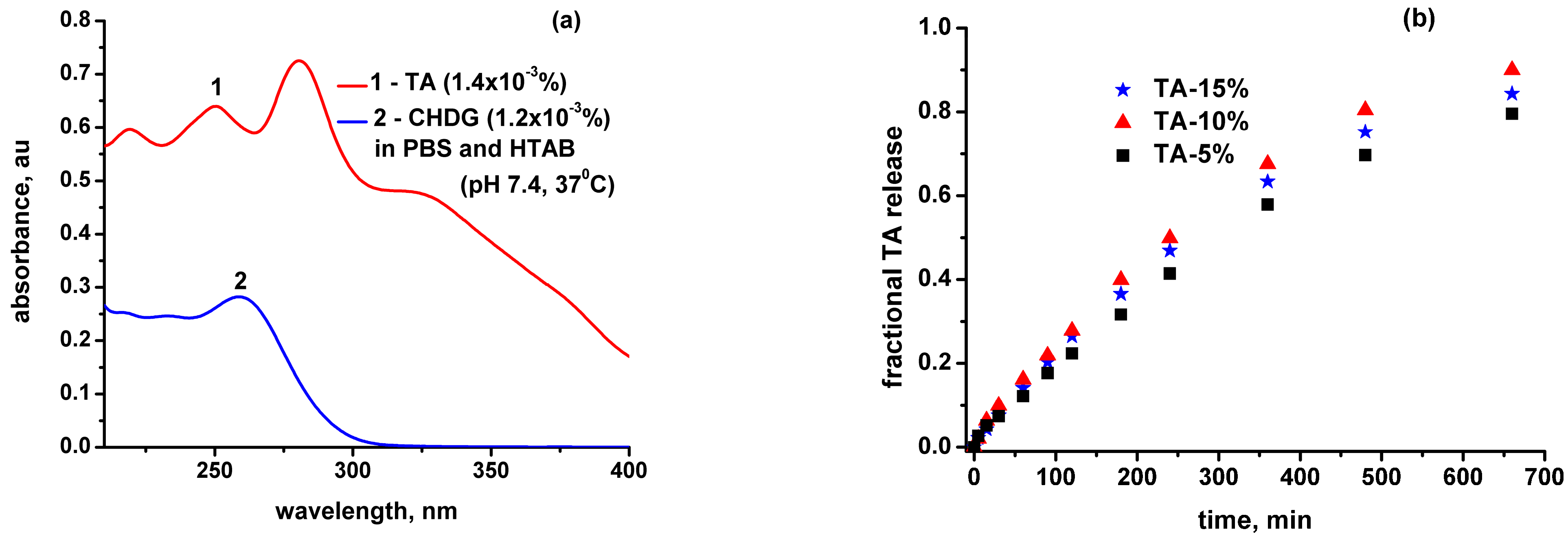
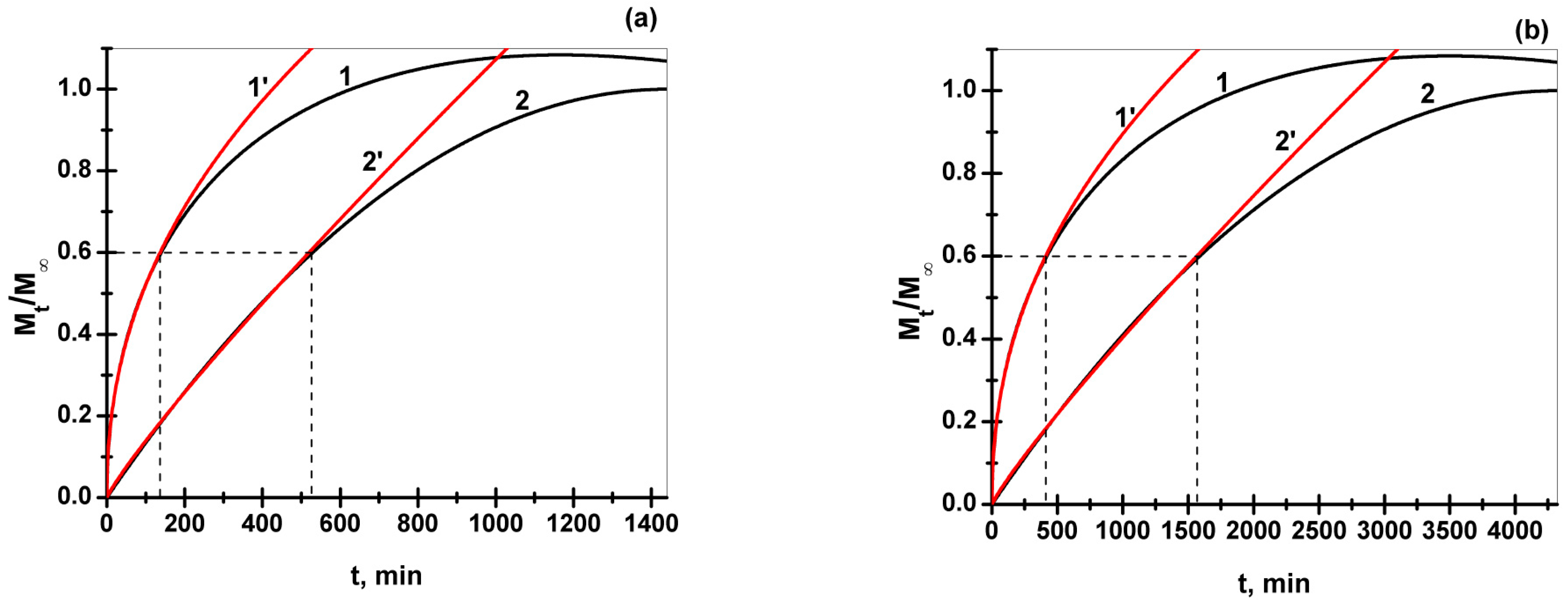
| Designation | Collagen | Collagen TA–5% | Collagen TA–10% | Collagen TA–15% | Collagen TA–5% CHDG–9.09% | Collagen TA–10% CHDG–9.09% | Collagen TA–15% CHDG–9.09% | Assignment |
|---|---|---|---|---|---|---|---|---|
| - | 3455 | 3485 | 3495 | 3500 | 3485 | 3490 | 3500 | (hydrogen bond) hydrogen bonded water |
| Amide A | 3301 | 3292 | 3297 | 3291 | 3306 | 3304 | 3297 | NH stretching/C=N (guanidine) symmetrical stretching |
| Amide B | 3077 | 3078 | 3081 | 3079 | 3081 | 3081 | 3087 | NH stretching |
| - | 2933 | 2937 | 2929 | 2940 | 2933 | 2933 | 2938 | CH2 asymmetrical stretching |
| - | 2873 | 2876 | 2876 | 2881 | 2876 | 2876 | 2876 | CH2 symmetrical stretching CH3 asymmetrical stretching |
| Amide I | 1630 | 1630 | 1630 | 1631 | 1631 | 1632 | 1631 | C=O stretching |
| Amide II | 1545 | 1542 | 1539 | 1539 | 1539 | 1539 | 1536 | CN stretching, NH bending |
| - | 1450 | 1447 | 1447 | 1447 | 1449 | 1448 | 1447 | CH2 bending |
| - | 1339 | 1336 | 1333 | 1333 | 1337 | 1336 | 1335 | in plain OH (phenol) bending |
| Amide III | 1236 | 1234 | 1232 | 1232 | 1237 | 1235 | 1234 | CN stretching, NH bending, CH2 wagging, CN stretching (guanidine) |
| - | 1204 | 1203 | 1201 | 1200 | 1204 | 1202 | 1202 | C-O stretching (C-OH in phenol) |
| - | 1080 | 1080 | 1080 | 1079 | 1081 | 1080 | 1080 | C-O stretching (carbohydrate moiety)/C-O-C asymmetrical stretching |
| - | 1033 | 1033 | 1033 | 1033 | 1033 | 1033 | 1033 | C-O stretching (carbohydrate moiety)/C-O-C symmetrical stretching |
| νamideI-νamideII | 85 | 88 | 91 | 92 | 92 | 93 | 95 | |
| Aamide III/A1450 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 |
| System | ρmatrix, g/cm3 | , g/g | , v/v | ν2eq | cp × 108, mol/cm3 | Δc × 107, mol/cm3 | DC × 105, mol/cm3 |
|---|---|---|---|---|---|---|---|
| Collagen | 1.195 | 6.80 | 7.34/7.34 | 0.136 | 953 | 2.5 | 58 |
| Collagen–TA (5%) | 1.245 | 5.66 | 6.31/6.46 | 0.155 | 1087 | 3.3 | 86 |
| Collagen–TA (10%) | 1.290 | 4.30 | 4.89/5.11 | 0.196 | 1374 | 5.2 | 184 |
| Collagen–TA (15%) | 1.316 | 4.11 | 4.74/5.06 | 0.198 | 1388 | 5.3 | 191 |
| Collagen–TA (5%)-CHDG (9.09%) | 1.248 | 4.06 | 4.49/4.92 | 0.203 | 1423 | 5.6 | 208 |
| Collagen–TA (10%)-CHDG (9.09%) | 1.285 | 4.02 | 4.55/5.09 | 0.196 | 1374 | 5.2 | 184 |
| Collagen–TA (15%)-CHDG (9.09%) | 1.319 | 4.16 | 4.81/5.50 | 0.182 | 1276 | 4.5 | 144 |
| System | ρmatrix, g/cm3 | , g/g | , v/v | ν2eq | cp × 108, mol/cm3 | Δc × 107, mol/cm3 | DC × 105, mol/cm3 |
|---|---|---|---|---|---|---|---|
| Collagen | 1.195 | 6.80 | 7.34 | 0.136 | 953 | 2.5 | 58 |
| Collagen–TA (5%) | 1.245 | 5.66 | 6.09 | 0.164 | 1150 | 3.7 | 103 |
| Collagen–TA (10%) | 1.290 | 4.30 | 4.61 | 0.217 | 1521 | 6.4 | 261 |
| Collagen–TA (15%) | 1.316 | 4.11 | 4.40 | 0.227 | 1591 | 7.0 | 306 |
| Collagen–TA (5%)-CHDG (9.09%) | 1.248 | 4.06 | 4.35 | 0.230 | 1612 | 7.2 | 321 |
| Collagen–TA (10%)-CHDG (9.09%) | 1.285 | 4.02 | 4.30 | 0.233 | 1633 | 7.4 | 336 |
| Collagen–TA (15%)-CHDG (9.09%) | 1.319 | 4.16 | 4.45 | 0.225 | 1577 | 6.9 | 297 |
| Solute | Case I | Case II | ||||
|---|---|---|---|---|---|---|
| k × 102, min−n | n | R2 | k × 103, min−n | n | R2 | |
| TA | 6.569 ± 0.087 | 0.4497 ± 0.0030 | 0.99765 | 2.34 ± 0.02 | 0.88703 ± 0.00167 | 0.99938 |
| CHDG | 4.009 ± 0.066 | 0.4497 ± 0.0030 | 0.99765 | 0.88 ± 0.01 | 0.88703 ± 0.00167 | 0.99938 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brăzdaru, L.; Staicu, T.; Albu Kaya, M.G.; Chelaru, C.; Ghica, C.; Cîrcu, V.; Leca, M.; Ghica, M.V.; Micutz, M. 3D Porous Collagen Matrices—A Reservoir for In Vitro Simultaneous Release of Tannic Acid and Chlorhexidine. Pharmaceutics 2023, 15, 76. https://doi.org/10.3390/pharmaceutics15010076
Brăzdaru L, Staicu T, Albu Kaya MG, Chelaru C, Ghica C, Cîrcu V, Leca M, Ghica MV, Micutz M. 3D Porous Collagen Matrices—A Reservoir for In Vitro Simultaneous Release of Tannic Acid and Chlorhexidine. Pharmaceutics. 2023; 15(1):76. https://doi.org/10.3390/pharmaceutics15010076
Chicago/Turabian StyleBrăzdaru, Lavinia, Teodora Staicu, Mădălina Georgiana Albu Kaya, Ciprian Chelaru, Corneliu Ghica, Viorel Cîrcu, Minodora Leca, Mihaela Violeta Ghica, and Marin Micutz. 2023. "3D Porous Collagen Matrices—A Reservoir for In Vitro Simultaneous Release of Tannic Acid and Chlorhexidine" Pharmaceutics 15, no. 1: 76. https://doi.org/10.3390/pharmaceutics15010076
APA StyleBrăzdaru, L., Staicu, T., Albu Kaya, M. G., Chelaru, C., Ghica, C., Cîrcu, V., Leca, M., Ghica, M. V., & Micutz, M. (2023). 3D Porous Collagen Matrices—A Reservoir for In Vitro Simultaneous Release of Tannic Acid and Chlorhexidine. Pharmaceutics, 15(1), 76. https://doi.org/10.3390/pharmaceutics15010076










