A Guide to In Silico Drug Design
Abstract
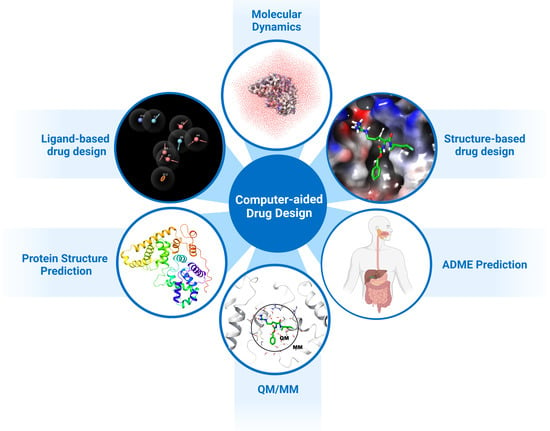
1. Introduction
2. Structure-Based Drug Design
2.1. Protein Structure Prediction
2.1.1. Homology Modelling
2.1.2. Ab Initio Protein Structure Prediction
2.1.3. Protein Model Validation
2.2. Docking-Based Virtual Screening
2.2.1. Binding Site Detection
2.2.2. Ligand Flexibility
2.2.3. Protein Flexibility
2.2.4. Scoring Functions
| Program | Ligand Flexibility | Receptor Flexibility | Scoring Functions | Examples of Application |
|---|---|---|---|---|
| Glide (HTVS, SP and XP) [94,95,189] | Exhaustive ligand conformation search | Soft docking | Empirical | Discovery of novel fibroblast growth factor receptor 1 kinase inhibitors [190] and CDK5 inhibitors [191] |
| GOLD [93] | Genetic algorithm | Soft docking Ensemble docking Side-chain flexibility | Goldscore (empirical) Chemscore (empirical) ChemPLP (empirical) ASP (knowledge based) | Design of non-peptide MDM2 inhibitors [192] |
| Autodock 4 [193] | Genetic Algorithm Simulated Annealing Local Search Lamarckian Genetic Algorithm | Side-chain flexibility | Semi-empirical free energy force field | Discovery of reversible NEDD8 activating enzyme inhibitor [194] |
| DOCK 6 [195] | Incremental construction algorithm | Rigid | Force field | Design and development of potent and selective dual BRD4/PLK1 Inhibitors [196] |
| Internal Coordinates Mechanics (ICM) [197] | Stochastic search (MC) | Side-chain flexibility (rotamer libraries) | Force field | Discovery of novel retinoic acid receptor agonist [198] and enoyl-acyl carrier protein reductase inhibitors in Plasmodium falciparum [199] |
| Surflex [200,201] | Incremental construction algorithm | Ensemble docking | Empirical | Discovery of novel inhibitors of Leishmania donovani γ-glutamylcysteine synthetase [202] |
| MOE [99,203,204,205] | Systematic (exhaustive) Stochastic High throughput Conformational Import (incremental construction + stochastic) [99] | Rigid | ASE (empirical) Affinity dG (empirical) Alpha HB (empirical) GBVI/WSA (force field) | Identification of novel monoamine oxidase B inhibitors [206] and Chk1 inhibitors [207] |
| FlexX [208,209] | Incremental construction algorithm | Rigid | Empirical | Identification of PKB inhibitors [210] and phosphodiesterase 4 inhibitors [211] |
| FRED [212,213] | Systematic (exhaustive) search, precomputed using Omega (using torsion and ring libraries) [138] | Rigid | Chemgauss 3 (empirical) Chemgauss 4 (empirical) | Discovery of selective butyrylcholinesterase inhibitors [214] |
3. Ligand-Based Drug Design
3.1. Similarity Search
3.2. Quantitative Structure-Activity Relationship (QSAR)
3.3. Pharmacophores
3.3.1. Pharmacophore Validation
3.3.2. Pharmacophore Screening
3.4. Scaffold Hopping
4. De Novo and Fragment-Based Drug Design
5. Hierarchical Virtual Screening (HLVS)
6. Molecular Mechanical/Generalised Born Surface Area (MM-GBSA)
7. Molecular Dynamics
8. QM/MM and DFT Approaches
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- (FDA), U.S.F.D.A. The Drug Development Process. Available online: https://www.fda.gov/patients/learn-about-drug-and-device-approvals/drug-development-process (accessed on 2 February 2022).
- Wouters, O.J.; McKee, M.; Luyten, J. Estimated research and development investment needed to bring a new medicine to market, 2009–2018. Jama 2020, 323, 844–853. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.H.; Siah, K.W.; Lo, A.W. Estimation of clinical trial success rates and related parameters. Biostatistics 2019, 20, 273–286. [Google Scholar] [CrossRef] [PubMed]
- DiMasi, J.A.; Grabowski, H.G.; Hansen, R.W. Innovation in the pharmaceutical industry: New estimates of R&D costs. J. Health Econ. 2016, 47, 20–33. [Google Scholar] [PubMed]
- DiMasi, J.A.; Hansen, R.W.; Grabowski, H.G. The price of innovation: New estimates of drug development costs. J. Health Econ. 2003, 22, 151–185. [Google Scholar] [CrossRef] [PubMed]
- Paul, S.M.; Mytelka, D.S.; Dunwiddie, C.T.; Persinger, C.C.; Munos, B.H.; Lindborg, S.R.; Schacht, A.L. How to improve R&D productivity: The pharmaceutical industry’s grand challenge. Nat. Rev. Drug Discov. 2010, 9, 203–214. [Google Scholar] [PubMed]
- Yang, Y.; Adelstein, S.J.; Kassis, A.I. Target discovery from data mining approaches. Drug Discov. Today 2009, 14, 147–154. [Google Scholar] [CrossRef]
- Moffat, J.G.; Rudolph, J.; Bailey, D. Phenotypic screening in cancer drug discovery—Past, present and future. Nat. Rev. Drug Discov. 2014, 13, 588–602. [Google Scholar] [CrossRef]
- Hart, C.P. Finding the target after screening the phenotype. Drug Discov. Today 2005, 10, 513–519. [Google Scholar] [CrossRef]
- Xia, X. Bioinformatics and drug discovery. Curr. Top. Med. Chem. 2017, 17, 1709–1726. [Google Scholar] [CrossRef]
- Morgan, P.; Brown, D.G.; Lennard, S.; Anderton, M.J.; Barrett, J.C.; Eriksson, U.; Fidock, M.; Hamren, B.; Johnson, A.; March, R.E. Impact of a five-dimensional framework on R&D productivity at AstraZeneca. Nat. Rev. Drug Discov. 2018, 17, 167–181. [Google Scholar]
- Morgan, P.; Van Der Graaf, P.H.; Arrowsmith, J.; Feltner, D.E.; Drummond, K.S.; Wegner, C.D.; Street, S.D.A. Can the flow of medicines be improved? Fundamental pharmacokinetic and pharmacological principles toward improving Phase II survival. Drug Discov. Today 2012, 17, 419–424. [Google Scholar] [CrossRef] [PubMed]
- Maple, H.J.; Garlish, R.A.; Rigau-Roca, L.; Porter, J.; Whitcombe, I.; Prosser, C.E.; Kennedy, J.; Henry, A.J.; Taylor, R.J.; Crump, M.P. Automated protein–ligand interaction screening by mass spectrometry. J. Med. Chem. 2012, 55, 837–851. [Google Scholar] [CrossRef] [PubMed]
- Dalvit, C. NMR methods in fragment screening: Theory and a comparison with other biophysical techniques. Drug Discov. Today 2009, 14, 1051–1057. [Google Scholar] [CrossRef] [PubMed]
- O’Reilly, M.; Cleasby, A.; Davies, T.G.; Hall, R.J.; Ludlow, R.F.; Murray, C.W.; Tisi, D.; Jhoti, H. Crystallographic screening using ultra-low-molecular-weight ligands to guide drug design. Drug Discov. Today 2019, 24, 1081–1086. [Google Scholar] [CrossRef]
- Shuker, S.B.; Hajduk, P.J.; Meadows, R.P.; Fesik, S.W. Discovering high-affinity ligands for proteins: SAR by NMR. Science 1996, 274, 1531–1534. [Google Scholar] [CrossRef]
- Madsen, D.; Azevedo, C.; Micco, I.; Petersen, L.K.; Hansen, N.J.V. Chapter Four—An overview of DNA-encoded libraries: A versatile tool for drug discovery. In Progress in Medicinal Chemistry; Witty, D.R., Cox, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; Volume 59, pp. 181–249. [Google Scholar]
- Macarron, R.; Banks, M.N.; Bojanic, D.; Burns, D.J.; Cirovic, D.A.; Garyantes, T.; Green, D.V.S.; Hertzberg, R.P.; Janzen, W.P.; Paslay, J.W.; et al. Impact of high-throughput screening in biomedical research. Nat. Rev. Drug Discov. 2011, 10, 188–195. [Google Scholar] [CrossRef]
- Shoichet, B.K. Virtual screening of chemical libraries. Nature 2004, 432, 862–865. [Google Scholar] [CrossRef]
- Kola, I.; Landis, J. Can the pharmaceutical industry reduce attrition rates? Nat. Rev. Drug Discov. 2004, 3, 711–716. [Google Scholar] [CrossRef]
- Bajorath, J. Integration of virtual and high-throughput screening. Nat. Rev. Drug Discov. 2002, 1, 882–894. [Google Scholar] [CrossRef]
- Karplus, M.; Petsko, G.A. Molecular dynamics simulations in biology. Nature 1990, 347, 631–639. [Google Scholar] [CrossRef]
- Shoichet, B.K.; McGovern, S.L.; Wei, B.; Irwin, J.J. Lead discovery using molecular docking. Curr. Opin. Chem. Biol. 2002, 6, 439–446. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Shoichet, B.K. Molecular docking and ligand specificity in fragment-based inhibitor discovery. Nat. Chem. Biol. 2009, 5, 358–364. [Google Scholar] [CrossRef] [PubMed]
- Schneider, G.; Fechner, U. Computer-based de novo design of drug-like molecules. Nat. Rev. Drug Discov. 2005, 4, 649–663. [Google Scholar] [CrossRef] [PubMed]
- EMBL-EBI UniProtKB/TrEMBL Protein Database Release 2022_02 Statistics. Available online: https://www.ebi.ac.uk/uniprot/TrEMBLstats (accessed on 27 July 2022).
- Bank, R.P.D. PDB Statistics: Overall Growth of Released Structures Per Year. Available online: https://www.rcsb.org/stats/growth/growth-released-structures (accessed on 27 July 2022).
- Consortium, U. UniProt: A hub for protein information. Nucleic Acids Res. 2015, 43, D204–D212. [Google Scholar] [CrossRef] [PubMed]
- Altschul, S.F.; Madden, T.L.; Schäffer, A.A.; Zhang, J.; Zhang, Z.; Miller, W.; Lipman, D.J. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 1997, 25, 3389–3402. [Google Scholar] [CrossRef]
- Bernstein, F.C.; Koetzle, T.F.; Williams, G.J.; Meyer Jr, E.F.; Brice, M.D.; Rodgers, J.R.; Kennard, O.; Shimanouchi, T.; Tasumi, M. The Protein Data Bank: A computer-based archival file for macromolecular structures. Eur. J. Biochem. 1977, 80, 319–324. [Google Scholar] [CrossRef]
- Sánchez, R.; Šali, A. Comparative protein structure modeling as an optimization problem. J. Mol. Struct. THEOCHEM 1997, 398–399, 489–496. [Google Scholar] [CrossRef]
- Madeira, F.; Park, Y.M.; Lee, J.; Buso, N.; Gur, T.; Madhusoodanan, N.; Basutkar, P.; Tivey, A.R.; Potter, S.C.; Finn, R.D. The EMBL-EBI search and sequence analysis tools APIs in 2019. Nucleic Acids Res. 2019, 47, W636–W641. [Google Scholar] [CrossRef]
- Needleman, S.B.; Wunsch, C.D. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 1970, 48, 443–453. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef]
- Smith, T.F.; Waterman, M.S. Identification of common molecular subsequences. J. Mol. Biol. 1981, 147, 195–197. [Google Scholar] [CrossRef] [PubMed]
- Thompson, J.D.; Gibson, T.J.; Higgins, D.G. Multiple sequence alignment using ClustalW and ClustalX. Curr. Protoc. Bioinform. 2003, 1, 2–3. [Google Scholar] [CrossRef]
- Notredame, C.; Higgins, D.G.; Heringa, J. T-Coffee: A novel method for fast and accurate multiple sequence alignment. J. Mol. Biol. 2000, 302, 205–217. [Google Scholar] [CrossRef]
- Edgar, R.C. MUSCLE: Multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004, 32, 1792–1797. [Google Scholar] [CrossRef]
- Pei, J.; Kim, B.H.; Grishin, N.V. PROMALS3D: A tool for multiple protein sequence and structure alignments. Nucleic Acids Res. 2008, 36, 2295–2300. [Google Scholar] [CrossRef] [PubMed]
- Garibsingh, R.-A.A.; Otte, N.J.; Ndaru, E.; Colas, C.; Grewer, C.; Holst, J.; Schlessinger, A. Homology Modeling Informs Ligand Discovery for the Glutamine Transporter ASCT2. Front. Chem. 2018, 6, 279. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Deane, C.M. FREAD revisited: Accurate loop structure prediction using a database search algorithm. Proteins Struct. Funct. Bioinform. 2010, 78, 1431–1440. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Simon, R.; MacKerell Jr, A.D. Conformational preference of serogroup B Salmonella O polysaccharide in presence and absence of the monoclonal antibody Se155–4. J. Phys. Chem. B 2017, 121, 3412–3423. [Google Scholar] [CrossRef]
- Stein, A.; Kortemme, T. Improvements to robotics-inspired conformational sampling in rosetta. PLoS ONE 2013, 8, e63090. [Google Scholar] [CrossRef]
- Guaitoli, G.; Raimondi, F.; Gilsbach, B.K.; Gómez-Llorente, Y.; Deyaert, E.; Renzi, F.; Li, X.; Schaffner, A.; Jagtap, P.K.A.; Boldt, K. Structural model of the dimeric Parkinson’s protein LRRK2 reveals a compact architecture involving distant interdomain contacts. Proc. Natl. Acad. Sci. USA 2016, 113, E4357–E4366. [Google Scholar] [CrossRef]
- Wang, Q.; Canutescu, A.A.; Dunbrack Jr, R.L. SCWRL and MolIDE: Computer programs for side-chain conformation prediction and homology modeling. Nat. Protoc. 2008, 3, 1832. [Google Scholar] [CrossRef] [PubMed]
- Moro, S.; Deflorian, F.; Bacilieri, M.; Spalluto, G. Ligand-based homology modeling as attractive tool to inspect GPCR structural plasticity. Curr. Pharm. Des. 2006, 12, 2175–2185. [Google Scholar] [CrossRef] [PubMed]
- Gacasan, S.B.; Baker, D.L.; Parrill, A.L. G protein-coupled receptors: The evolution of structural insight. AIMS Biophys. 2017, 4, 491. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, D.; Ranganathan, A.; Carlsson, J. Strategies for improved modeling of GPCR-drug complexes: Blind predictions of serotonin receptors bound to ergotamine. J. Chem. Inf. Model. 2014, 54, 2004–2021. [Google Scholar] [CrossRef] [PubMed]
- Kołaczkowski, M.; Bucki, A.; Feder, M.; Pawłowski, M. Ligand-optimized homology models of D1 and D2 dopamine receptors: Application for virtual screening. J. Chem. Inf. Model. 2013, 53, 638–648. [Google Scholar] [CrossRef]
- Cichero, E.; Menozzi, G.; Guariento, S.; Fossa, P. Ligand-based homology modelling of the human CB2 receptor SR144528 antagonist binding site: A computational approach to explore the 1, 5-diaryl pyrazole scaffold. MedChemComm 2015, 6, 1978–1986. [Google Scholar] [CrossRef]
- Evers, A.; Klebe, G. Successful virtual screening for a submicromolar antagonist of the neurokinin-1 receptor based on a ligand-supported homology model. J. Med. Chem. 2004, 47, 5381–5392. [Google Scholar] [CrossRef]
- Freyd, T.; Warszycki, D.; Mordalski, S.; Bojarski, A.J.; Sylte, I.; Gabrielsen, M. Ligand-guided homology modelling of the GABAB2 subunit of the GABAB receptor. PLoS ONE 2017, 12, e0173889. [Google Scholar] [CrossRef]
- Schaller, D.; Hagenow, S.; Stark, H.; Wolber, G. Ligand-guided homology modeling drives identification of novel histamine H3 receptor ligands. PLoS ONE 2019, 14, e0218820. [Google Scholar] [CrossRef]
- Hameduh, T.; Haddad, Y.; Adam, V.; Heger, Z. Homology modeling in the time of collective and artificial intelligence. Comput. Struct. Biotechnol. J. 2020, 18, 3494–3506. [Google Scholar] [CrossRef]
- Bonneau, R.; Strauss, C.E.; Rohl, C.A.; Chivian, D.; Bradley, P.; Malmström, L.; Robertson, T.; Baker, D. De novo prediction of three-dimensional structures for major protein families. J. Mol. Biol. 2002, 322, 65–78. [Google Scholar] [CrossRef] [PubMed]
- Goodsell, D.S.; Olson, A.J. Structural Symmetry and Protein Function. Annu. Rev. Biophys. Biomol. Struct. 2000, 29, 105–153. [Google Scholar] [CrossRef] [PubMed]
- Anfinsen, C.B. Principles that govern the folding of protein chains. Science 1973, 181, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Klepeis, J.L.; Floudas, C.A. ASTRO-FOLD: A Combinatorial and Global Optimization Framework for Ab Initio Prediction of Three-Dimensional Structures of Proteins from the Amino Acid Sequence. Biophys. J. 2003, 85, 2119–2146. [Google Scholar] [CrossRef] [PubMed]
- Subramani, A.; Wei, Y.; Floudas, C.A. ASTRO-FOLD 2.0: An Enhanced Framework for Protein Structure Prediction. AIChE J 2012, 58, 1619–1637. [Google Scholar] [CrossRef] [PubMed]
- Ołdziej, S.; Czaplewski, C.; Liwo, A.; Chinchio, M.; Nanias, M.; Vila, J.; Khalili, M.; Arnautova, Y.; Jagielska, A.; Makowski, M.O. Physics-based protein-structure prediction using a hierarchical protocol based on the UNRES force field: Assessment in two blind tests. Proc. Natl. Acad. Sci. USA 2005, 102, 7547–7552. [Google Scholar] [CrossRef]
- Bowie, J.U.; Eisenberg, D. An evolutionary approach to folding small alpha-helical proteins that uses sequence information and an empirical guiding fitness function. Proc. Natl. Acad. Sci. USA 1994, 91, 4436–4440. [Google Scholar] [CrossRef]
- Hart, T.N.; Read, R.J. A multiple-start Monte Carlo docking method. Proteins Struct. Funct. Bioinform. 1992, 13, 206–222. [Google Scholar] [CrossRef]
- Shim, J.; MacKerell Jr, A.D. Computational ligand-based rational design: Role of conformational sampling and force fields in model development. Medchemcomm 2011, 2, 356–370. [Google Scholar] [CrossRef]
- Alford, R.F.; Leaver-Fay, A.; Jeliazkov, J.R.; O′Meara, M.J.; DiMaio, F.P.; Park, H.; Shapovalov, M.V.; Renfrew, P.D.; Mulligan, V.K.; Kappel, K.; et al. The Rosetta All-Atom Energy Function for Macromolecular Modeling and Design. J. Chem. Theory Comput. 2017, 13, 3031–3048. [Google Scholar] [CrossRef]
- Roy, A.; Kucukural, A.; Zhang, Y. I-TASSER: A unified platform for automated protein structure and function prediction. Nat. Protoc. 2010, 5, 725–738. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zhang, J.; Roy, A.; Zhang, Y. Automated protein structure modeling in CASP9 by I-TASSER pipeline combined with QUARK-based ab initio folding and FG-MD-based structure refinement. Proteins Struct. Funct. Bioinform. 2011, 79, 147–160. [Google Scholar] [CrossRef] [PubMed]
- Mistry, J.; Chuguransky, S.; Williams, L.; Qureshi, M.; Salazar Gustavo, A.; Sonnhammer, E.L.L.; Tosatto, S.C.E.; Paladin, L.; Raj, S.; Richardson, L.J.; et al. Pfam: The protein families database in 2021. Nucleic Acids Res. 2021, 49, D412–D419. [Google Scholar] [CrossRef] [PubMed]
- Marks, D.S.; Colwell, L.J.; Sheridan, R.; Hopf, T.A.; Pagnani, A.; Zecchina, R.; Sander, C. Protein 3D structure computed from evolutionary sequence variation. PLoS ONE 2011, 6, e28766. [Google Scholar] [CrossRef] [PubMed]
- Tetchner, S.; Kosciolek, T.; Jones, D.T. Opportunities and limitations in applying coevolution-derived contacts to protein structure prediction. Bio-Algorithms Med. Syst. 2014, 10, 243–254. [Google Scholar] [CrossRef]
- Xu, J. Distance-based protein folding powered by deep learning. Proc. Natl. Acad. Sci. USA 2019, 116, 16856–16865. [Google Scholar] [CrossRef]
- Uziela, K.; Menéndez Hurtado, D.; Shu, N.; Wallner, B.; Elofsson, A. ProQ3D: Improved model quality assessments using deep learning. Bioinformatics 2017, 33, 1578–1580. [Google Scholar] [CrossRef]
- Zheng, W.; Li, Y.; Zhang, C.; Zhou, X.; Pearce, R.; Bell, E.W.; Huang, X.; Zhang, Y. Protein structure prediction using deep learning distance and hydrogen-bonding restraints in CASP14. Proteins Struct. Funct. Bioinform. 2021, 89, 1734–1751. [Google Scholar] [CrossRef]
- Du, Z.; Su, H.; Wang, W.; Ye, L.; Wei, H.; Peng, Z.; Anishchenko, I.; Baker, D.; Yang, J. The trRosetta server for fast and accurate protein structure prediction. Nat. Protoc. 2021, 16, 5634–5651. [Google Scholar] [CrossRef]
- Baek, M.; DiMaio, F.; Anishchenko, I.; Dauparas, J.; Ovchinnikov, S.; Lee, G.R.; Wang, J.; Cong, Q.; Kinch, L.N.; Schaeffer, R.D. Accurate prediction of protein structures and interactions using a three-track neural network. Science 2021, 373, 871–876. [Google Scholar] [CrossRef]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.; Bridgland, A. Protein structure prediction using multiple deep neural networks in the 13th Critical Assessment of Protein Structure Prediction (CASP13). Proteins Struct. Funct. Bioinform. 2019, 87, 1141–1148. [Google Scholar] [CrossRef] [PubMed]
- Zemla, A. LGA: A method for finding 3D similarities in protein structures. Nucleic Acids Res. 2003, 31, 3370–3374. [Google Scholar] [CrossRef]
- Antoniak, A.; Biskupek, I.; Bojarski, K.K.; Czaplewski, C.; Giełdoń, A.; Kogut, M.; Kogut, M.M.; Krupa, P.; Lipska, A.G.; Liwo, A. Modeling protein structures with the coarse-grained UNRES force field in the CASP14 experiment. J. Mol. Graph. Model. 2021, 108, 108008. [Google Scholar] [CrossRef] [PubMed]
- Varadi, M.; Anyango, S.; Deshpande, M.; Nair, S.; Natassia, C.; Yordanova, G.; Yuan, D.; Stroe, O.; Wood, G.; Laydon, A. AlphaFold Protein Structure Database: Massively expanding the structural coverage of protein-sequence space with high-accuracy models. Nucleic Acids Res. 2022, 50, D439–D444. [Google Scholar] [CrossRef] [PubMed]
- Hooft, R.W.; Vriend, G.; Sander, C.; Abola, E.E. Errors in protein structures. Nature 1996, 381, 272. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, G.T.; Sasisekharan, V. Conformation of polypeptides and proteins. In Advances in Protein Chemistry; Elsevier: Amsterdam, The Netherlands, 1968; Volume 23, pp. 283–437. [Google Scholar]
- Eisenberg, D.; Lüthy, R.; Bowie, J.U. [20] VERIFY3D: Assessment of protein models with three-dimensional profiles. In Methods in Enzymology; Elsevier: Amsterdam, The Netherlands, 1997; Volume 277, pp. 396–404. [Google Scholar]
- Chen, V.B.; Arendall, W.B.; Headd, J.J.; Keedy, D.A.; Immormino, R.M.; Kapral, G.J.; Murray, L.W.; Richardson, J.S.; Richardson, D.C. MolProbity: All-atom structure validation for macromolecular crystallography. Acta Crystallogr. Sect. D Biol. Crystallogr. 2010, 66, 12–21. [Google Scholar] [CrossRef]
- Williams, C.J.; Headd, J.J.; Moriarty, N.W.; Prisant, M.G.; Videau, L.L.; Deis, L.N.; Verma, V.; Keedy, D.A.; Hintze, B.J.; Chen, V.B. MolProbity: More and better reference data for improved all-atom structure validation. Protein Sci. 2018, 27, 293–315. [Google Scholar] [CrossRef]
- Weichenberger, C.X.; Sippl, M.J. NQ-Flipper: Recognition and correction of erroneous asparagine and glutamine side-chain rotamers in protein structures. Nucleic Acids Res. 2007, 35 (Suppl. S2), W403–W406. [Google Scholar] [CrossRef]
- Rochira, W.; Agirre, J. Iris: Interactive all-in-one graphical validation of 3D protein model iterations. Protein Sci. 2021, 30, 93–107. [Google Scholar] [CrossRef]
- Bienert, S.; Waterhouse, A.; De Beer, T.A.; Tauriello, G.; Studer, G.; Bordoli, L.; Schwede, T. The SWISS-MODEL Repository—New features and functionality. Nucleic Acids Res. 2017, 45, D313–D319. [Google Scholar] [CrossRef]
- Bond, P.S.; Wilson, K.S.; Cowtan, K.D. Predicting protein model correctness in Coot using machine learning. Acta Crystallogr. Sect. D Struct. Biol. 2020, 76, 713–723. [Google Scholar] [CrossRef] [PubMed]
- Emsley, P.; Lohkamp, B.; Scott, W.G.; Cowtan, K. Features and development of Coot. Acta Crystallogr. Sect. D Biol. Crystallogr. 2010, 66, 486–501. [Google Scholar] [CrossRef] [PubMed]
- Emsley, P.; Cowtan, K. Coot: Model-building tools for molecular graphics. Acta Crystallogr. Sect. D Biol. Crystallogr. 2004, 60, 2126–2132. [Google Scholar] [CrossRef]
- O’Reilly, F.J.; Rappsilber, J. Cross-linking mass spectrometry: Methods and applications in structural, molecular and systems biology. Nat. Struct. Mol. Biol. 2018, 25, 1000–1008. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.L.; Lindert, S.; Zhu, W.; Wang, K.; McCammon, J.A.; Oldfield, E. Taxodione and arenarone inhibit farnesyl diphosphate synthase by binding to the isopentenyl diphosphate site. Proc. Natl. Acad. Sci. USA 2014, 111, E2530-9. [Google Scholar] [CrossRef]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef] [PubMed]
- Verdonk, M.L.; Cole, J.C.; Hartshorn, M.J.; Murray, C.W.; Taylor, R.D. Improved protein–ligand docking using GOLD. Proteins Struct. Funct. Bioinform. 2003, 52, 609–623. [Google Scholar] [CrossRef] [PubMed]
- Friesner, R.A.; Banks, J.L.; Murphy, R.B.; Halgren, T.A.; Klicic, J.J.; Mainz, D.T.; Repasky, M.P.; Knoll, E.H.; Shelley, M.; Perry, J.K. Glide: A new approach for rapid, accurate docking and scoring. 1. Method and assessment of docking accuracy. J. Med. Chem. 2004, 47, 1739–1749. [Google Scholar] [CrossRef]
- Halgren, T.A.; Murphy, R.B.; Friesner, R.A.; Beard, H.S.; Frye, L.L.; Pollard, W.T.; Banks, J.L. Glide: A new approach for rapid, accurate docking and scoring. 2. Enrichment factors in database screening. J. Med. Chem. 2004, 47, 1750–1759. [Google Scholar] [CrossRef]
- Grosdidier, A.; Zoete, V.; Michielin, O. SwissDock, a protein-small molecule docking web service based on EADock DSS. Nucleic Acids Res. 2011, 39 (Suppl. S2), W270–W277. [Google Scholar] [CrossRef]
- Santos, K.B.; Guedes, I.A.; Karl, A.L.; Dardenne, L.E. Highly flexible ligand docking: Benchmarking of the DockThor program on the LEADS-PEP protein–peptide data set. J. Chem. Inf. Model. 2020, 60, 667–683. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Grimm, M.; Dai, W.-t.; Hou, M.-c.; Xiao, Z.-X.; Cao, Y. CB-Dock: A web server for cavity detection-guided protein–ligand blind docking. Acta Pharmacol. Sin. 2020, 41, 138–144. [Google Scholar] [CrossRef] [PubMed]
- Chemical Computing Group Inc. Molecular Operating Environment (MOE); Chemical Computing Group Inc.: Montreal, QC, Canada, 2022. [Google Scholar]
- Sastry, G.M.; Adzhigirey, M.; Day, T.; Annabhimoju, R.; Sherman, W. Protein and ligand preparation: Parameters, protocols, and influence on virtual screening enrichments. J. Comput. Aided Mol. Des. 2013, 27, 221–234. [Google Scholar] [CrossRef] [PubMed]
- Lengauer, T.; Rarey, M. Computational methods for biomolecular docking. Curr. Opin. Struct. Biol. 1996, 6, 402–406. [Google Scholar] [CrossRef]
- Fischer, E. Einfluss der Configuration auf die Wirkung der Enzyme. Ber. Der Dtsch. Chem. Ges. 1894, 27, 2985–2993. [Google Scholar] [CrossRef]
- López, G.; Valencia, A.; Tress, M.L. firestar—Prediction of functionally important residues using structural templates and alignment reliability. Nucleic Acids Res. 2007, 35 (Suppl. S2), W573–W577. [Google Scholar] [CrossRef][Green Version]
- Wass, M.N.; Kelley, L.A.; Sternberg, M.J. 3DLigandSite: Predicting ligand-binding sites using similar structures. Nucleic Acids Res. 2010, 38 (Suppl. S2), W469–W473. [Google Scholar] [CrossRef]
- Toti, D.; Viet Hung, L.; Tortosa, V.; Brandi, V.; Polticelli, F. LIBRA-WA: A web application for ligand binding site detection and protein function recognition. Bioinformatics 2018, 34, 878–880. [Google Scholar] [CrossRef]
- Viet Hung, L.; Caprari, S.; Bizai, M.; Toti, D.; Polticelli, F. Libra: Ligand binding site recognition application. Bioinformatics 2015, 31, 4020–4022. [Google Scholar] [CrossRef]
- Laskowski, R.A. SURFNET: A program for visualizing molecular surfaces, cavities, and intermolecular interactions. J. Mol. Graph. 1995, 13, 323–330. [Google Scholar] [CrossRef]
- Halgren, T. New method for fast and accurate binding-site identification and analysis. Chem. Biol. Drug Des. 2007, 69, 146–148. [Google Scholar] [CrossRef] [PubMed]
- Halgren, T.A. Identifying and characterizing binding sites and assessing druggability. J. Chem. Inf. Model. 2009, 49, 377–389. [Google Scholar] [CrossRef] [PubMed]
- Brenke, R.; Kozakov, D.; Chuang, G.-Y.; Beglov, D.; Hall, D.; Landon, M.R.; Mattos, C.; Vajda, S. Fragment-based identification of druggable ‘hot spots’ of proteins using Fourier domain correlation techniques. Bioinformatics 2009, 25, 621–627. [Google Scholar] [CrossRef]
- Laurie, A.T.; Jackson, R.M. Q-SiteFinder: An energy-based method for the prediction of protein–ligand binding sites. Bioinformatics 2005, 21, 1908–1916. [Google Scholar] [CrossRef]
- Capra, J.A.; Laskowski, R.A.; Thornton, J.M.; Singh, M.; Funkhouser, T.A. Predicting protein ligand binding sites by combining evolutionary sequence conservation and 3D structure. PLoS Comput. Biol. 2009, 5, e1000585. [Google Scholar] [CrossRef]
- Lu, C.; Liu, Z.; Zhang, E.; He, F.; Ma, Z.; Wang, H. MPLs-Pred: Predicting membrane protein-ligand binding sites using hybrid sequence-based features and ligand-specific models. Int. J. Mol. Sci. 2019, 20, 3120. [Google Scholar] [CrossRef]
- Jiménez, J.; Doerr, S.; Martínez-Rosell, G.; Rose, A.S.; De Fabritiis, G. DeepSite: Protein-binding site predictor using 3D-convolutional neural networks. Bioinformatics 2017, 33, 3036–3042. [Google Scholar] [CrossRef] [PubMed]
- Stepniewska-Dziubinska, M.M.; Zielenkiewicz, P.; Siedlecki, P. Improving detection of protein-ligand binding sites with 3D segmentation. Sci. Rep. 2020, 10, 5035. [Google Scholar] [CrossRef]
- Cui, Y.; Dong, Q.; Hong, D.; Wang, X. Predicting protein-ligand binding residues with deep convolutional neural networks. BMC Bioinform. 2019, 20, 93. [Google Scholar] [CrossRef]
- Vajda, S.; Beglov, D.; Wakefield, A.E.; Egbert, M.; Whitty, A. Cryptic binding sites on proteins: Definition, detection, and druggability. Curr. Opin. Chem. Biol. 2018, 44, 1–8. [Google Scholar] [CrossRef]
- Cimermancic, P.; Weinkam, P.; Rettenmaier, T.J.; Bichmann, L.; Keedy, D.A.; Woldeyes, R.A.; Schneidman-Duhovny, D.; Demerdash, O.N.; Mitchell, J.C.; Wells, J.A. CryptoSite: Expanding the druggable proteome by characterization and prediction of cryptic binding sites. J. Mol. Biol. 2016, 428, 709–719. [Google Scholar] [CrossRef] [PubMed]
- Cheng, A.C.; Coleman, R.G.; Smyth, K.T.; Cao, Q.; Soulard, P.; Caffrey, D.R.; Salzberg, A.C.; Huang, E.S. Structure-based maximal affinity model predicts small-molecule druggability. Nat. Biotechnol. 2007, 25, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Finan, C.; Gaulton, A.; Kruger, F.A.; Lumbers, R.T.; Shah, T.; Engmann, J.; Galver, L.; Kelley, R.; Karlsson, A.; Santos, R. The druggable genome and support for target identification and validation in drug development. Sci. Transl. Med. 2017, 9, eaag1166. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.; Wang, Q.; Wu, F.; Huang, Z. In Silico Methods for Identification of Potential Active Sites of Therapeutic Targets. Molecules 2022, 27, 7103. [Google Scholar] [CrossRef] [PubMed]
- Schmidtke, P.; Barril, X. Understanding and predicting druggability. A high-throughput method for detection of drug binding sites. J. Med. Chem. 2010, 53, 5858–5867. [Google Scholar] [CrossRef] [PubMed]
- Sheridan, R.P.; Maiorov, V.N.; Holloway, M.K.; Cornell, W.D.; Gao, Y.-D. Drug-like density: A method of quantifying the “bindability” of a protein target based on a very large set of pockets and drug-like ligands from the Protein Data Bank. J. Chem. Inf. Model. 2010, 50, 2029–2040. [Google Scholar] [CrossRef]
- Krasowski, A.; Muthas, D.; Sarkar, A.; Schmitt, S.; Brenk, R. DrugPred: A structure-based approach to predict protein druggability developed using an extensive nonredundant data set. J. Chem. Inf. Model. 2011, 51, 2829–2842. [Google Scholar] [CrossRef]
- Volkamer, A.; Kuhn, D.; Rippmann, F.; Rarey, M. DoGSiteScorer: A web server for automatic binding site prediction, analysis and druggability assessment. Bioinformatics 2012, 28, 2074–2075. [Google Scholar] [CrossRef]
- Ngan, C.H.; Bohnuud, T.; Mottarella, S.E.; Beglov, D.; Villar, E.A.; Hall, D.R.; Kozakov, D.; Vajda, S. FTMAP: Extended protein mapping with user-selected probe molecules. Nucleic Acids Res. 2012, 40, W271–W275. [Google Scholar] [CrossRef]
- Borrel, A.; Regad, L.; Xhaard, H.; Petitjean, M.; Camproux, A.-C. PockDrug: A model for predicting pocket druggability that overcomes pocket estimation uncertainties. J. Chem. Inf. Model. 2015, 55, 882–895. [Google Scholar] [CrossRef]
- Volkamer, A.; Griewel, A.; Grombacher, T.; Rarey, M. Analyzing the topology of active sites: On the prediction of pockets and subpockets. J. Chem. Inf. Model. 2010, 50, 2041–2052. [Google Scholar] [CrossRef] [PubMed]
- Volkamer, A.; Kuhn, D.; Grombacher, T.; Rippmann, F.; Rarey, M. Combining global and local measures for structure-based druggability predictions. J. Chem. Inf. Model. 2012, 52, 360–372. [Google Scholar] [CrossRef] [PubMed]
- Michel, M.; Homan, E.J.; Wiita, E.; Pedersen, K.; Almlöf, I.; Gustavsson, A.-L.; Lundbäck, T.; Helleday, T.; Warpman Berglund, U. In silico druggability assessment of the NUDIX hydrolase protein family as a workflow for target prioritization. Front. Chem. 2020, 8, 443. [Google Scholar] [CrossRef] [PubMed]
- Doñate-Macian, P.; Duarte, Y.; Rubio-Moscardo, F.; Pérez-Vilaró, G.; Canan, J.; Díez, J.; González-Nilo, F.; Valverde, M.A. Structural determinants of TRPV4 inhibition and identification of new antagonists with antiviral activity. Br. J. Pharmacol. 2022, 179, 3576–3591. [Google Scholar] [CrossRef] [PubMed]
- Irwin, J.J.; Tang, K.G.; Young, J.; Dandarchuluun, C.; Wong, B.R.; Khurelbaatar, M.; Moroz, Y.S.; Mayfield, J.; Sayle, R.A. ZINC20—A free ultralarge-scale chemical database for ligand discovery. J. Chem. Inf. Model. 2020, 60, 6065–6073. [Google Scholar] [CrossRef]
- Wishart, D.S.; Feunang, Y.D.; Guo, A.C.; Lo, E.J.; Marcu, A.; Grant, J.R.; Sajed, T.; Johnson, D.; Li, C.; Sayeeda, Z. DrugBank 5.0: A major update to the DrugBank database for 2018. Nucleic Acids Res. 2018, 46, D1074–D1082. [Google Scholar] [CrossRef]
- Kim, S.; Chen, J.; Cheng, T.; Gindulyte, A.; He, J.; He, S.; Li, Q.; Shoemaker, B.A.; Thiessen, P.A.; Yu, B. PubChem in 2021: New data content and improved web interfaces. Nucleic Acids Res. 2021, 49, D1388–D1395. [Google Scholar] [CrossRef]
- Beusen, D.D.; Shands, E.B.; Karasek, S.; Marshall, G.R.; Dammkoehler, R.A. Systematic search in conformational analysis. J. Mol. Struct. THEOCHEM 1996, 370, 157–171. [Google Scholar] [CrossRef]
- Smellie, A.; Stanton, R.; Henne, R.; Teig, S. Conformational analysis by intersection: CONAN. J. Comput. Chem. 2003, 24, 10–20. [Google Scholar] [CrossRef]
- Hawkins, P.C.D. Conformation Generation: The State of the Art. J. Chem. Inf. Model. 2017, 57, 1747–1756. [Google Scholar] [CrossRef]
- Hawkins, P.C.; Skillman, A.G.; Warren, G.L.; Ellingson, B.A.; Stahl, M.T. Conformer generation with OMEGA: Algorithm and validation using high quality structures from the Protein Databank and Cambridge Structural Database. J. Chem. Inf. Model. 2010, 50, 572–584. [Google Scholar] [CrossRef]
- Watts, K.S.; Dalal, P.; Murphy, R.B.; Sherman, W.; Friesner, R.A.; Shelley, J.C. ConfGen: A Conformational Search Method for Efficient Generation of Bioactive Conformers. J. Chem. Inf. Model. 2010, 50, 534–546. [Google Scholar] [CrossRef] [PubMed]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Spellmeyer, D.C.; Wong, A.K.; Bower, M.J.; Blaney, J.M. Conformational analysis using distance geometry methods. J. Mol. Graph. Model. 1997, 15, 18–36. [Google Scholar] [CrossRef]
- Vainio, M.J.; Johnson, M.S. Generating conformer ensembles using a multiobjective genetic algorithm. J. Chem. Inf. Model. 2007, 47, 2462–2474. [Google Scholar] [CrossRef] [PubMed]
- Jones, G.; Willett, P.; Glen, R.C.; Leach, A.R.; Taylor, R. Development and validation of a genetic algorithm for flexible docking. J. Mol. Biol. 1997, 267, 727–748. [Google Scholar] [CrossRef]
- Sisquellas, M.; Cecchini, M. PrepFlow: A Toolkit for Chemical Library Preparation and Management for Virtual Screening. Mol. Inform. 2021, 40, 2100139. [Google Scholar] [CrossRef]
- Gally, J.-M.; Bourg, S.; Fogha, J.; Do, Q.-T.; Aci-Sèche, S.; Bonnet, P. VSPrep: A KNIME workflow for the preparation of molecular databases for virtual screening. Curr. Med. Chem. 2020, 27, 6480–6494. [Google Scholar] [CrossRef]
- Ropp, P.J.; Spiegel, J.O.; Walker, J.L.; Green, H.; Morales, G.A.; Milliken, K.A.; Ringe, J.J.; Durrant, J.D. Gypsum-DL: An open-source program for preparing small-molecule libraries for structure-based virtual screening. J. Cheminformatics 2019, 11, 34. [Google Scholar] [CrossRef]
- Miteva, M.A.; Guyon, F.; Tufféry, P. Frog2: Efficient 3D conformation ensemble generator for small compounds. Nucleic Acids Res. 2010, 38 (Suppl. S2), W622–W627. [Google Scholar] [CrossRef]
- Sommer, K.; Friedrich, N.-O.; Bietz, S.; Hilbig, M.; Inhester, T.; Rarey, M. UNICON: A Powerful and Easy-to-Use Compound Library Converter; ACS Publications: Washington, DC, USA, 2016. [Google Scholar]
- Cozzini, P.; Kellogg, G.E.; Spyrakis, F.; Abraham, D.J.; Costantino, G.; Emerson, A.; Fanelli, F.; Gohlke, H.; Kuhn, L.A.; Morris, G.M. Target flexibility: An emerging consideration in drug discovery and design. J. Med. Chem. 2008, 51, 6237–6255. [Google Scholar] [CrossRef] [PubMed]
- Palma, P.N.; Krippahl, L.; Wampler, J.E.; Moura, J.J. BiGGER: A new (soft) docking algorithm for predicting protein interactions. Proteins Struct. Funct. Bioinform. 2000, 39, 372–384. [Google Scholar] [CrossRef]
- Jiang, F.; Kim, S.-H. “Soft docking”: Matching of molecular surface cubes. J. Mol. Biol. 1991, 219, 79–102. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, C.; Boelens, R.; Bonvin, A.M. HADDOCK: A protein− protein docking approach based on biochemical or biophysical information. J. Am. Chem. Soc. 2003, 125, 1731–1737. [Google Scholar] [CrossRef]
- Apostolakis, J.; Plückthun, A.; Caflisch, A. Docking small ligands in flexible binding sites. J. Comput. Chem. 1998, 19, 21–37. [Google Scholar] [CrossRef]
- Knegtel, R.M.; Kuntz, I.D.; Oshiro, C. Molecular docking to ensembles of protein structures. J. Mol. Biol. 1997, 266, 424–440. [Google Scholar] [CrossRef]
- Motta, S.; Bonati, L. Modeling Binding with Large Conformational Changes: Key Points in Ensemble-Docking Approaches. J. Chem. Inf. Model. 2017, 57, 1563–1578. [Google Scholar] [CrossRef]
- Leach, A.R. Ligand docking to proteins with discrete side-chain flexibility. J. Mol. Biol. 1994, 235, 345–356. [Google Scholar] [CrossRef]
- Huang, S.-Y.; Zou, X. Advances and challenges in protein-ligand docking. Int J Mol Sci 2010, 11, 3016–3034. [Google Scholar] [CrossRef]
- Davis, I.W.; Baker, D. RosettaLigand docking with full ligand and receptor flexibility. J. Mol. Biol. 2009, 385, 381–392. [Google Scholar] [CrossRef]
- Miao, Y.; McCammon, J.A. G-protein coupled receptors: Advances in simulation and drug discovery. Curr. Opin. Struct. Biol. 2016, 41, 83–89. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.Y.; Zou, X. Ensemble docking of multiple protein structures: Considering protein structural variations in molecular docking. Proteins Struct. Funct. Bioinform. 2007, 66, 399–421. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, M.P.; Friesner, R.A.; Xiang, Z.; Honig, B. On the role of the crystal environment in determining protein side-chain conformations. J. Mol. Biol. 2002, 320, 597–608. [Google Scholar] [CrossRef]
- Jacobson, M.P.; Pincus, D.L.; Rapp, C.S.; Day, T.J.; Honig, B.; Shaw, D.E.; Friesner, R.A. A hierarchical approach to all-atom protein loop prediction. Proteins Struct. Funct. Bioinform. 2004, 55, 351–367. [Google Scholar] [CrossRef]
- Sherman, W.; Day, T.; Jacobson, M.P.; Friesner, R.A.; Farid, R. Novel procedure for modeling ligand/receptor induced fit effects. J. Med. Chem. 2006, 49, 534–553. [Google Scholar] [CrossRef]
- Maurer, M.; Oostenbrink, C. Water in protein hydration and ligand recognition. J. Mol. Recognit. 2019, 32, e2810. [Google Scholar] [CrossRef] [PubMed]
- Davis, A.M.; St-Gallay, S.A.; Kleywegt, G.J. Limitations and lessons in the use of X-ray structural information in drug design. Drug Discov. Today 2008, 13, 831. [Google Scholar] [CrossRef]
- Renaud, J.-P.; Chari, A.; Ciferri, C.; Liu, W.-t.; Rémigy, H.-W.; Stark, H.; Wiesmann, C. Cryo-EM in drug discovery: Achievements, limitations and prospects. Nat. Rev. Drug Discov. 2018, 17, 471–492. [Google Scholar] [CrossRef]
- Roux, B.; Simonson, T. Implicit solvent models. Biophys. Chem. 1999, 78, 1–20. [Google Scholar] [CrossRef]
- Kleinjung, J.; Fraternali, F. Design and application of implicit solvent models in biomolecular simulations. Curr. Opin. Struct. Biol. 2014, 25, 126–134. [Google Scholar] [CrossRef]
- Raymer, M.L.; Sanschagrin, P.C.; Punch, W.F.; Venkataraman, S.; Goodman, E.D.; Kuhn, L.A. Predicting conserved water-mediated and polar ligand interactions in proteins using a K-nearest-neighbors genetic algorithm. J. Mol. Biol. 1997, 265, 445–464. [Google Scholar] [CrossRef] [PubMed]
- García-Sosa, A.T.; Mancera, R.L.; Dean, P.M. WaterScore: A novel method for distinguishing between bound and displaceable water molecules in the crystal structure of the binding site of protein-ligand complexes. J. Mol. Model. 2003, 9, 172–182. [Google Scholar] [CrossRef] [PubMed]
- Wade, R.C.; Clark, K.J.; Goodford, P.J. Further development of hydrogen bond functions for use in determining energetically favorable binding sites on molecules of known structure. 1. Ligand probe groups with the ability to form two hydrogen bonds. J. Med. Chem. 1993, 36, 140–147. [Google Scholar] [CrossRef] [PubMed]
- Wade, R.C.; Goodford, P.J. Further development of hydrogen bond functions for use in determining energetically favorable binding sites on molecules of known structure. 2. Ligand probe groups with the ability to form more than two hydrogen bonds. J. Med. Chem. 1993, 36, 148–156. [Google Scholar] [CrossRef] [PubMed]
- Kovalenko, A.; Hirata, F. Self-consistent description of a metal–water interface by the Kohn–Sham density functional theory and the three-dimensional reference interaction site model. J. Chem. Phys. 1999, 110, 10095–10112. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Three-dimensional density profiles of water in contact with a solute of arbitrary shape: A RISM approach. Chem. Phys. Lett. 1998, 290, 237–244. [Google Scholar] [CrossRef]
- SZMAP, version 1.6.4.1; OpenEye Scientific Software: Santa Fe, NM, USA, 2013.
- Wang, L.; Berne, B.; Friesner, R. Ligand binding to protein-binding pockets with wet and dry regions. Proc. Natl. Acad. Sci. USA 2011, 108, 1326–1330. [Google Scholar] [CrossRef]
- Nguyen, C.N.; Kurtzman Young, T.; Gilson, M.K. Grid inhomogeneous solvation theory: Hydration structure and thermodynamics of the miniature receptor cucurbit [7] uril. J. Chem. Phys. 2012, 137, 044101. [Google Scholar] [CrossRef]
- Michel, J.; Tirado-Rives, J.; Jorgensen, W.L. Prediction of the water content in protein binding sites. J. Phys. Chem. B 2009, 113, 13337–13346. [Google Scholar] [CrossRef]
- Meng, E.C.; Shoichet, B.K.; Kuntz, I.D. Automated docking with grid-based energy evaluation. J. Comput. Chem. 1992, 13, 505–524. [Google Scholar] [CrossRef]
- Huang, N.; Kalyanaraman, C.; Bernacki, K.; Jacobson, M.P. Molecular mechanics methods for predicting protein–ligand binding. Phys. Chem. Chem. Phys. 2006, 8, 5166–5177. [Google Scholar] [CrossRef] [PubMed]
- Weiner, S.J.; Kollman, P.A.; Case, D.A.; Singh, U.C.; Ghio, C.; Alagona, G.; Profeta, S.; Weiner, P. A new force field for molecular mechanical simulation of nucleic acids and proteins. J. Am. Chem. Soc. 1984, 106, 765–784. [Google Scholar] [CrossRef]
- Weiner, S.J.; Kollman, P.A.; Nguyen, D.T.; Case, D.A. An all atom force field for simulations of proteins and nucleic acids. J. Comput. Chem. 1986, 7, 230–252. [Google Scholar] [CrossRef] [PubMed]
- Böhm, H.J. The development of a simple empirical scoring function to estimate the binding constant for a protein-ligand complex of known three-dimensional structure. J. Comput. -Aided Mol. Des. 1994, 8, 243–256. [Google Scholar] [CrossRef]
- Eldridge, M.D.; Murray, C.W.; Auton, T.R.; Paolini, G.V.; Mee, R.P. Empirical scoring functions: I. The development of a fast empirical scoring function to estimate the binding affinity of ligands in receptor complexes. J. Comput. Aided Mol. Des. 1997, 11, 425–445. [Google Scholar] [CrossRef]
- Sippl, M.J. Calculation of conformational ensembles from potentials of mena force: An approach to the knowledge-based prediction of local structures in globular proteins. J. Mol. Biol. 1990, 213, 859–883. [Google Scholar] [CrossRef]
- Allen, F.H. The Cambridge Structural Database: A quarter of a million crystal structures and rising. Acta Crystallogr. Sect. B Struct. Sci. 2002, 58, 380–388. [Google Scholar] [CrossRef]
- Thomas, P.D.; Dill, K.A. An iterative method for extracting energy-like quantities from protein structures. Proc. Natl. Acad. Sci. USA 1996, 93, 11628–11633. [Google Scholar] [CrossRef]
- Thomas, P.D.; Dill, K.A. Statistical potentials extracted from protein structures: How accurate are they? J. Mol. Biol. 1996, 257, 457–469. [Google Scholar] [CrossRef]
- Friesner, R.A.; Murphy, R.B.; Repasky, M.P.; Frye, L.L.; Greenwood, J.R.; Halgren, T.A.; Sanschagrin, P.C.; Mainz, D.T. Extra Precision Glide: Docking and Scoring Incorporating a Model of Hydrophobic Enclosure for Protein−Ligand Complexes. J. Med. Chem. 2006, 49, 6177–6196. [Google Scholar] [CrossRef]
- Ravindranathan, K.P.; Mandiyan, V.; Ekkati, A.R.; Bae, J.H.; Schlessinger, J.; Jorgensen, W.L. Discovery of Novel Fibroblast Growth Factor Receptor 1 Kinase Inhibitors by Structure-Based Virtual Screening. J. Med. Chem. 2010, 53, 1662–1672. [Google Scholar] [CrossRef] [PubMed]
- Khair, N.Z.; Lenjisa, J.L.; Tadesse, S.; Kumarasiri, M.; Basnet, S.K.C.; Mekonnen, L.B.; Li, M.; Diab, S.; Sykes, M.J.; Albrecht, H.; et al. Discovery of CDK5 Inhibitors through Structure-Guided Approach. Acs Med. Chem. Lett. 2019, 10, 786–791. [Google Scholar] [CrossRef] [PubMed]
- Ding, K.; Lu, Y.; Nikolovska-Coleska, Z.; Qiu, S.; Ding, Y.; Gao, W.; Stuckey, J.; Krajewski, K.; Roller, P.P.; Tomita, Y.; et al. Structure-Based Design of Potent Non-Peptide MDM2 Inhibitors. J. Am. Chem. Soc. 2005, 127, 10130–10131. [Google Scholar] [CrossRef] [PubMed]
- Morris, G.M.; Huey, R.; Lindstrom, W.; Sanner, M.F.; Belew, R.K.; Goodsell, D.S.; Olson, A.J. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009, 30, 2785–2791. [Google Scholar] [CrossRef] [PubMed]
- Lu, P.; Liu, X.; Yuan, X.; He, M.; Wang, Y.; Zhang, Q.; Ouyang, P. Discovery of a novel NEDD8 Activating Enzyme Inhibitor with Piperidin-4-amine Scaffold by Structure-Based Virtual Screening. ACS Chem. Biol. 2016, 11, 1901–1907. [Google Scholar] [CrossRef]
- Allen, W.J.; Balius, T.E.; Mukherjee, S.; Brozell, S.R.; Moustakas, D.T.; Lang, P.T.; Case, D.A.; Kuntz, I.D.; Rizzo, R.C. DOCK 6: Impact of new features and current docking performance. J. Comput. Chem. 2015, 36, 1132–1156. [Google Scholar] [CrossRef]
- Liu, S.; Yosief, H.O.; Dai, L.; Huang, H.; Dhawan, G.; Zhang, X.; Muthengi, A.M.; Roberts, J.; Buckley, D.L.; Perry, J.A.; et al. Structure-Guided Design and Development of Potent and Selective Dual Bromodomain 4 (BRD4)/Polo-like Kinase 1 (PLK1) Inhibitors. J. Med. Chem. 2018, 61, 7785–7795. [Google Scholar] [CrossRef]
- Neves, M.A.; Totrov, M.; Abagyan, R. Docking and scoring with ICM: The benchmarking results and strategies for improvement. J. Comput.-Aided Mol. Des. 2012, 26, 675–686. [Google Scholar] [CrossRef]
- Schapira, M.; Raaka, B.M.; Samuels, H.H.; Abagyan, R. In silico discovery of novel retinoic acid receptor agonist structures. Bmc Struct. Biol. 2001, 1, 1–7. [Google Scholar] [CrossRef]
- Nicola, G.; Smith, C.A.; Lucumi, E.; Kuo, M.R.; Karagyozov, L.; Fidock, D.A.; Sacchettini, J.C.; Abagyan, R. Discovery of novel inhibitors targeting enoyl–acyl carrier protein reductase in Plasmodium falciparum by structure-based virtual screening. Biochem. Biophys. Res. Commun. 2007, 358, 686–691. [Google Scholar] [CrossRef][Green Version]
- Cleves, A.E.; Jain, A.N. ForceGen 3D structure and conformer generation: From small lead-like molecules to macrocyclic drugs. J. Comput. -Aided Mol. Des. 2017, 31, 419–439. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.N. Surflex: Fully automatic flexible molecular docking using a molecular similarity-based search engine. J. Med. Chem. 2003, 46, 499–511. [Google Scholar] [CrossRef] [PubMed]
- Agnihotri, P.; Mishra, A.K.; Mishra, S.; Sirohi, V.K.; Sahasrabuddhe, A.A.; Pratap, J.V. Identification of Novel Inhibitors of Leishmania donovani γ-Glutamylcysteine Synthetase Using Structure-Based Virtual Screening, Docking, Molecular Dynamics Simulation, and in Vitro Studies. J. Chem. Inf. Model. 2017, 57, 815–825. [Google Scholar] [CrossRef] [PubMed]
- Corbeil, C.R.; Williams, C.I.; Labute, P. Variability in docking success rates due to dataset preparation. J. Comput. Aided Mol. Des. 2012, 26, 775–786. [Google Scholar] [CrossRef]
- Ye, W.L.; Shen, C.; Xiong, G.L.; Ding, J.J.; Lu, A.-P.; Hou, T.J.; Cao, D.S. Improving docking-based virtual screening ability by integrating multiple energy auxiliary terms from molecular docking scoring. J. Chem. Inf. Model. 2020, 60, 4216–4230. [Google Scholar] [CrossRef] [PubMed]
- Chen, I.J.; Foloppe, N. Conformational sampling of druglike molecules with MOE and catalyst: Implications for pharmacophore modeling and virtual screening. J. Chem. Inf. Model. 2008, 48, 1773–1791. [Google Scholar] [CrossRef]
- Geldenhuys, W.J.; Darvesh, A.S.; Funk, M.O.; Van der Schyf, C.J.; Carroll, R.T. Identification of novel monoamine oxidase B inhibitors by structure-based virtual screening. Bioorganic Med. Chem. Lett. 2010, 20, 5295–5298. [Google Scholar] [CrossRef] [PubMed]
- Foloppe, N.; Fisher, L.M.; Howes, R.; Potter, A.; Robertson, A.G.S.; Surgenor, A.E. Identification of chemically diverse Chk1 inhibitors by receptor-based virtual screening. Bioorganic Med. Chem. 2006, 14, 4792–4802. [Google Scholar] [CrossRef] [PubMed]
- Rarey, M.; Kramer, B.; Lengauer, T.; Klebe, G. A Fast Flexible Docking Method using an Incremental Construction Algorithm. J. Mol. Biol. 1996, 261, 470–489. [Google Scholar] [CrossRef]
- Kramer, B.; Rarey, M.; Lengauer, T. Evaluation of the FLEXX incremental construction algorithm for protein–ligand docking. Proteins Struct. Funct. Bioinform. 1999, 37, 228–241. [Google Scholar] [CrossRef]
- Forino, M.; Jung, D.; Easton, J.B.; Houghton, P.J.; Pellecchia, M. Virtual docking approaches to protein kinase B inhibition. J. Med. Chem. 2005, 48, 2278–2281. [Google Scholar] [CrossRef] [PubMed]
- Krier, M.; de Araújo-Júnior, J.X.; Schmitt, M.; Duranton, J.; Justiano-Basaran, H.; Lugnier, C.; Bourguignon, J.-J.; Rognan, D. Design of small-sized libraries by combinatorial assembly of linkers and functional groups to a given scaffold: Application to the structure-based optimization of a phosphodiesterase 4 inhibitor. J. Med. Chem. 2005, 48, 3816–3822. [Google Scholar] [CrossRef]
- McGann, M. FRED and HYBRID docking performance on standardized datasets. J. Comput. -Aided Mol. Des. 2012, 26, 897–906. [Google Scholar] [CrossRef] [PubMed]
- McGann, M. FRED pose prediction and virtual screening accuracy. J. Chem. Inf. Model. 2011, 51, 578–596. [Google Scholar] [CrossRef]
- Brus, B.; Košak, U.; Turk, S.; Pišlar, A.; Coquelle, N.; Kos, J.; Stojan, J.; Colletier, J.-P.; Gobec, S. Discovery, Biological Evaluation, and Crystal Structure of a Novel Nanomolar Selective Butyrylcholinesterase Inhibitor. J. Med. Chem. 2014, 57, 8167–8179. [Google Scholar] [CrossRef] [PubMed]
- Vázquez, J.; López, M.; Gibert, E.; Herrero, E.; Luque, F.J. Merging ligand-based and structure-based methods in drug discovery: An overview of combined virtual screening approaches. Molecules 2020, 25, 4723. [Google Scholar] [CrossRef] [PubMed]
- Gao, K.; Nguyen, D.D.; Sresht, V.; Mathiowetz, A.M.; Tu, M.; Wei, G.-W. Are 2D fingerprints still valuable for drug discovery? Phys. Chem. Chem. Phys. 2020, 22, 8373–8390. [Google Scholar] [CrossRef]
- Durrant, J.D.; Cao, R.; Gorfe, A.A.; Zhu, W.; Li, J.; Sankovsky, A.; Oldfield, E.; McCammon, J.A. Non-bisphosphonate inhibitors of isoprenoid biosynthesis identified via computer-aided drug design. Chem. Biol. Drug Des. 2011, 78, 323–332. [Google Scholar] [CrossRef]
- Sheridan, R.P.; Miller, M.D.; Underwood, D.J.; Kearsley, S.K. Chemical Similarity Using Geometric Atom Pair Descriptors. J. Chem. Inf. Comput. Sci. 1996, 36, 128–136. [Google Scholar] [CrossRef]
- Daylight Chemical Information Systems, I. Fingerprints—Screening and Similarity. Available online: https://www.daylight.com/dayhtml/doc/theory/theory.finger.html (accessed on 25 February 2022).
- Bender, A.; Mussa, H.Y.; Glen, R.C.; Reiling, S. Similarity Searching of Chemical Databases Using Atom Environment Descriptors (MOLPRINT 2D): Evaluation of Performance. J. Chem. Inf. Comput. Sci. 2004, 44, 1708–1718. [Google Scholar] [CrossRef]
- Rogers, D.; Hahn, M. Extended-connectivity fingerprints. J. Chem. Inf. Model. 2010, 50, 742–754. [Google Scholar] [CrossRef] [PubMed]
- Glem, R.C.; Bender, A.; Arnby, C.H.; Carlsson, L.; Boyer, S.; Smith, J. Circular fingerprints: Flexible molecular descriptors with applications from physical chemistry to ADME. Idrugs 2006, 9, 199–204. [Google Scholar] [PubMed]
- Seo, M.; Shin, H.K.; Myung, Y.; Hwang, S.; No, K.T. Development of Natural Compound Molecular Fingerprint (NC-MFP) with the Dictionary of Natural Products (DNP) for natural product-based drug development. J. Cheminformatics 2020, 12, 6. [Google Scholar] [CrossRef] [PubMed]
- Rogers, D.J.; Tanimoto, T.T. A computer program for classifying plants. Science 1960, 132, 1115–1118. [Google Scholar] [CrossRef]
- Sheridan, R.P. Chemical similarity searches: When is complexity justified? Expert Opin. Drug Discov. 2007, 2, 423–430. [Google Scholar] [CrossRef]
- Bajusz, D.; Rácz, A.; Héberger, K. Why is Tanimoto index an appropriate choice for fingerprint-based similarity calculations? J. Cheminformatics 2015, 7, 20. [Google Scholar] [CrossRef]
- Thomas, I.R.; Bruno, I.J.; Cole, J.C.; Macrae, C.F.; Pidcock, E.; Wood, P.A. WebCSD: The online portal to the Cambridge Structural Database. J. Appl. Crystallogr. 2010, 43, 362–366. [Google Scholar] [CrossRef]
- Wang, T.; Yang, Z.; Zhang, Y.; Yan, W.; Wang, F.; He, L.; Zhou, Y.; Chen, L. Discovery of novel CDK8 inhibitors using multiple crystal structures in docking-based virtual screening. Eur. J. Med. Chem. 2017, 129, 275–286. [Google Scholar] [CrossRef]
- Biovia, D.S. Discovery Studio; Dassault Systèmes: San Diego, CA, USA, 2021. [Google Scholar]
- Hansch, C.; Fujita, T. p-σ-π Analysis. A Method for the Correlation of Biological Activity and Chemical Structure. J. Am. Chem. Soc. 1964, 86, 1616–1626. [Google Scholar] [CrossRef]
- Overton, C.E. Studien über die Narkose: Zugleich ein Beitrag zur Allgemeinen Pharmakologie; G. Fischer: Schaffhausen, Switzerland, 1901. [Google Scholar]
- Free, S.M.; Wilson, J.W. A mathematical contribution to structure-activity studies. J. Med. Chem. 1964, 7, 395–399. [Google Scholar] [CrossRef]
- Cramer, R.D.; Patterson, D.E.; Bunce, J.D. Comparative molecular field analysis (CoMFA). 1. Effect of shape on binding of steroids to carrier proteins. J. Am. Chem. Soc. 1988, 110, 5959–5967. [Google Scholar] [CrossRef] [PubMed]
- Klebe, G.; Abraham, U.; Mietzner, T. Molecular similarity indices in a comparative analysis (CoMSIA) of drug molecules to correlate and predict their biological activity. J. Med. Chem. 1994, 37, 4130–4146. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, M.; von Mering, C.; Campillos, M.; Jensen, L.J.; Bork, P. STITCH: Interaction networks of chemicals and proteins. Nucleic Acids Res. 2008, 36, D684–D688. [Google Scholar] [CrossRef] [PubMed]
- Alam, S.; Khan, F. 3D-QSAR studies on Maslinic acid analogs for Anticancer activity against Breast Cancer cell line MCF-7. Sci. Rep. 2017, 7, 6019. [Google Scholar] [CrossRef]
- Ehrlich, P. Über den jetzigen Stand der Chemotherapie. Ber. Der Dtsch. Chem. Ges. 1909, 42, 17–47. [Google Scholar] [CrossRef]
- Güner, O.F. History and evolution of the pharmacophore concept in computer-aided drug design. Curr. Top. Med. Chem. 2002, 2, 1321–1332. [Google Scholar] [CrossRef]
- Schueler, F.W. Chemobiodynamics and drug design. Acad. Med. 1961, 36, 285–286. [Google Scholar]
- Beckett, A.; Harper, N.; Clitherow, J. The importance of stereoisomerism in muscarinic activity. J. Pharm. Pharmacol. 1963, 15, 362–371. [Google Scholar] [CrossRef]
- Kier, L.B. Molecular orbital calculation of preferred conformations of acetylcholine, muscarine, and muscarone. Mol. Pharmacol. 1967, 3, 487–494. [Google Scholar]
- Wermuth, C.G.; Ganellin, C.; Lindberg, P.; Mitscher, L. Glossary of terms used in medicinal chemistry (IUPAC Recommendations 1998). Pure Appl. Chemistry. Chim. Pure Et Appl. 1998, 70, 1129–1143. [Google Scholar] [CrossRef]
- Seidel, T.; Bryant, S.D.; Ibis, G.; Poli, G.; Langer, T. 3D Pharmacophore Modeling Techniques in Computer-Aided Molecular Design Using LigandScout. In Tutorials in Chemoinformatics; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Arthur, G.; Oliver, W.; Klaus, B.; Thomas, S.; Gökhan, I.; Sharon, B.; Isabelle, T.; Pierre, D.; Thierry, L. Hierarchical Graph Representation of Pharmacophore Models. Front. Mol. Biosci. 2020, 7, 599059. [Google Scholar] [CrossRef] [PubMed]
- Wilcken, R.; Zimmermann, M.O.; Lange, A.; Joerger, A.C.; Boeckler, F.M. Principles and applications of halogen bonding in medicinal chemistry and chemical biology. J. Med. Chem. 2013, 56, 1363–1388. [Google Scholar] [CrossRef] [PubMed]
- Schaller, D.; Šribar, D.; Noonan, T.; Deng, L.; Nguyen, T.N.; Pach, S.; Machalz, D.; Bermudez, M.; Wolber, G. Next generation 3D pharmacophore modeling. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2020, 10, e1468. [Google Scholar] [CrossRef]
- Greene, J.; Kahn, S.; Savoj, H.; Sprague, P.; Teig, S. Chemical function queries for 3D database search. J. Chem. Inf. Comput. Sci. 1994, 34, 1297–1308. [Google Scholar] [CrossRef]
- Wolber, G.; Seidel, T.; Bendix, F.; Langer, T. Molecule-pharmacophore superpositioning and pattern matching in computational drug design. Drug Discov. Today 2008, 13, 23–29. [Google Scholar] [CrossRef]
- Barnum, D.; Greene, J.; Smellie, A.; Sprague, P. Identification of common functional configurations among molecules. J. Chem. Inf. Comput. Sci. 1996, 36, 563–571. [Google Scholar] [CrossRef]
- Dixon, S.L.; Smondyrev, A.M.; Rao, S.N. PHASE: A Novel Approach to Pharmacophore Modeling and 3D Database Searching. Chem. Biol. Drug Des. 2006, 67, 370–372. [Google Scholar] [CrossRef]
- Dixon, S.L.; Smondyrev, A.M.; Knoll, E.H.; Rao, S.N.; Shaw, D.E.; Friesner, R.A. PHASE: A new engine for pharmacophore perception, 3D QSAR model development, and 3D database screening: 1. Methodology and preliminary results. J. Comput. Aided Mol. Des. 2006, 20, 647–671. [Google Scholar] [CrossRef]
- Richmond, N.J.; Abrams, C.A.; Wolohan, P.R.; Abrahamian, E.; Willett, P.; Clark, R.D. GALAHAD: 1. Pharmacophore identification by hypermolecular alignment of ligands in 3D. J. Comput. Aided Mol. Des. 2006, 20, 567–587. [Google Scholar] [CrossRef]
- Dror, O.; Shulman-Peleg, A.; Nussinov, R.; Wolfson, H.J. Predicting molecular interactions in silico: I. an updated guide to pharmacophore identification and its applications to drug design. Front. Med. Chem. 2006, 551, 551–584. [Google Scholar]
- Rampogu, S.; Son, M.; Baek, A.; Park, C.; Rana, R.M.; Zeb, A.; Parameswaran, S.; Lee, K.W. Targeting natural compounds against HER2 kinase domain as potential anticancer drugs applying pharmacophore based molecular modelling approaches. Comput. Biol. Chem. 2018, 74, 327–338. [Google Scholar] [CrossRef] [PubMed]
- Kaserer, T.; Beck, K.R.; Akram, M.; Odermatt, A.; Schuster, D. Pharmacophore Models and Pharmacophore-Based Virtual Screening: Concepts and Applications Exemplified on Hydroxysteroid Dehydrogenases. Molecules 2015, 20, 22799–22832. [Google Scholar] [CrossRef] [PubMed]
- Salam, N.K.; Nuti, R.; Sherman, W. Novel method for generating structure-based pharmacophores using energetic analysis. J. Chem. Inf. Model. 2009, 49, 2356–2368. [Google Scholar] [CrossRef] [PubMed]
- Böhm, H.J. The computer program LUDI: A new method for the de novo design of enzyme inhibitors. J. Comput. Aided Mol. Des. 1992, 6, 61–78. [Google Scholar] [CrossRef] [PubMed]
- Goodford, P.J. A computational procedure for determining energetically favorable binding sites on biologically important macromolecules. J. Med. Chem. 1985, 28, 849–857. [Google Scholar] [CrossRef] [PubMed]
- Saxena, S.; Abdullah, M.; Sriram, D.; Guruprasad, L. Discovery of novel inhibitors of Mycobacterium tuberculosis MurG: Homology modelling, structure based pharmacophore, molecular docking, and molecular dynamics simulations. J. Biomol. Struct. Dyn. 2018, 36, 3184–3198. [Google Scholar] [CrossRef] [PubMed]
- Mysinger, M.M.; Carchia, M.; Irwin, J.J.; Shoichet, B.K. Directory of useful decoys, enhanced (DUD-E): Better ligands and decoys for better benchmarking. J. Med. Chem. 2012, 55, 6582–6594. [Google Scholar] [CrossRef]
- Rohrer, S.G.; Baumann, K. Maximum unbiased validation (MUV) data sets for virtual screening based on PubChem bioactivity data. J. Chem. Inf. Model. 2009, 49, 169–184. [Google Scholar] [CrossRef]
- Bauer, M.R.; Ibrahim, T.M.; Vogel, S.M.; Boeckler, F.M. Evaluation and optimization of virtual screening workflows with DEKOIS 2.0–a public library of challenging docking benchmark sets. J. Chem. Inf. Model. 2013, 53, 1447–1462. [Google Scholar] [CrossRef]
- Kirchmair, J.; Ristic, S.; Eder, K.; Markt, P.; Wolber, G.; Laggner, C.; Langer, T. Fast and efficient in silico 3D screening: Toward maximum computational efficiency of pharmacophore-based and shape-based approaches. J. Chem. Inf. Model. 2007, 47, 2182–2196. [Google Scholar] [CrossRef]
- Jacobsson, M.; Lidén, P.; Stjernschantz, E.; Boström, H.; Norinder, U. Improving structure-based virtual screening by multivariate analysis of scoring data. J. Med. Chem. 2003, 46, 5781–5789. [Google Scholar] [CrossRef]
- Güner, O.F.; Henry, D.R. Metric for analyzing hit lists and pharmacophores. In Pharmacophore Perception, Development, And Use in Drug Design; International University: Line La Jolla, CA, USA, 2000; pp. 191–211. [Google Scholar]
- Kumar, R.; Bavi, R.; Jo, M.G.; Arulalapperumal, V.; Baek, A.; Rampogu, S.; Kim, M.O.; Lee, K.W. New compounds identified through in silico approaches reduce the α-synuclein expression by inhibiting prolyl oligopeptidase in vitro. Sci. Rep. 2017, 7, 10827. [Google Scholar] [CrossRef]
- Triballeau, N.; Acher, F.; Brabet, I.; Pin, J.P.; Bertrand, H.O. Virtual screening workflow development guided by the “receiver operating characteristic” curve approach. Application to high-throughput docking on metabotropic glutamate receptor subtype 4. J. Med. Chem. 2005, 48, 2534–2547. [Google Scholar] [CrossRef]
- Hurst, T. Flexible 3D searching: The directed tweak technique. J. Chem. Inf. Comput. Sci. 1994, 34, 190–196. [Google Scholar] [CrossRef]
- Wolber, G.; Langer, T. LigandScout: 3-D pharmacophores derived from protein-bound ligands and their use as virtual screening filters. J. Chem. Inf. Model. 2005, 45, 160–169. [Google Scholar] [CrossRef]
- Feng, J.; Sanil, A.; Young, S.S. PharmID: Pharmacophore identification using Gibbs sampling. J. Chem. Inf. Model. 2006, 46, 1352–1359. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, M.; Wang, J.; Ding, Z.; Sun, B. Construction of antifungal dual-target (SE, CYP51) pharmacophore models and the discovery of novel antifungal inhibitors. RSC Adv. 2019, 9, 26302–26314. [Google Scholar] [CrossRef]
- Butina, D.; Segall, M.D.; Frankcombe, K. Predicting ADME properties in silico: Methods and models. Drug Discov. Today 2002, 7, S83–S88. [Google Scholar] [CrossRef]
- Baell, J.B.; Holloway, G.A. New substructure filters for removal of pan assay interference compounds (PAINS) from screening libraries and for their exclusion in bioassays. J. Med. Chem. 2010, 53, 2719–2740. [Google Scholar] [CrossRef]
- Schneider, G.; Neidhart, W.; Giller, T.; Schmid, G. “Scaffold-hopping” by topological pharmacophore search: A contribution to virtual screening. Angew. Chem. Int. Ed. 1999, 38, 2894–2896. [Google Scholar] [CrossRef]
- Sun, H.; Tawa, G.; Wallqvist, A. Classification of scaffold-hopping approaches. Drug Discov. Today 2012, 17, 310–324. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Stumpfe, D.; Bajorath, J. Recent advances in scaffold hopping: Miniperspective. J. Med. Chem. 2017, 60, 1238–1246. [Google Scholar] [CrossRef] [PubMed]
- Blaquiere, N.; Castanedo, G.M.; Burch, J.D.; Berezhkovskiy, L.M.; Brightbill, H.; Brown, S.; Chan, C.; Chiang, P.C.; Crawford, J.J.; Dong, T.; et al. Scaffold-Hopping Approach To Discover Potent, Selective, and Efficacious Inhibitors of NF-κB Inducing Kinase. J. Med. Chem. 2018, 61, 6801–6813. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Fang, K.; Cheng, J.; Li, Y.; Huang, Y.; Chen, S.; Dong, G.; Wu, S.; Sheng, C. Scaffold Hopping of Natural Product Evodiamine: Discovery of a Novel Antitumor Scaffold with Excellent Potency against Colon Cancer. J. Med. Chem. 2019, 63, 696–713. [Google Scholar] [CrossRef]
- Vinkers, H.M.; de Jonge, M.R.; Daeyaert, F.F.; Heeres, J.; Koymans, L.M.; van Lenthe, J.H.; Lewi, P.J.; Timmerman, H.; Van Aken, K.; Janssen, P.A. Synopsis: Synthesize and optimize system in silico. J. Med. Chem. 2003, 46, 2765–2773. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Ruiz-Caro, J.; Tirado-Rives, J.; Basavapathruni, A.; Anderson, K.S.; Hamilton, A.D. Computer-aided design of non-nucleoside inhibitors of HIV-1 reverse transcriptase. Bioorganic Med. Chem. Lett. 2006, 16, 663–667. [Google Scholar] [CrossRef]
- Wang, R.; Gao, Y.; Lai, L. LigBuilder: A multi-purpose program for structure-based drug design. Mol. Model. Annu. 2000, 6, 498–516. [Google Scholar] [CrossRef]
- Hao, G.-F.; Jiang, W.; Ye, Y.-N.; Wu, F.-X.; Zhu, X.-L.; Guo, F.-B.; Yang, G.-F. ACFIS: A web server for fragment-based drug discovery. Nucleic Acids Res. 2016, 44, W550–W556. [Google Scholar] [CrossRef]
- Marchand, J.-R.; Caflisch, A. In silico fragment-based drug design with SEED. Eur. J. Med. Chem. 2018, 156, 907–917. [Google Scholar] [CrossRef]
- Clark, D.E.; Frenkel, D.; Levy, S.A.; Li, J.; Murray, C.W.; Robson, B.; Waszkowycz, B.; Westhead, D.R. PRO_LIGAND: An approach to de novo molecular design. 1. Application to the design of organic molecules. J. Comput. Aided Mol. Des. 1995, 9, 13–32. [Google Scholar] [CrossRef]
- Nishibata, Y.; Itai, A. Automatic creation of drug candidate structures based on receptor structure. Starting point for artificial lead generation. Tetrahedron 1991, 47, 8985–8990. [Google Scholar] [CrossRef]
- Bohacek, R.S.; McMartin, C. Multiple highly diverse structures complementary to enzyme binding sites: Results of extensive application of a de novo design method incorporating combinatorial growth. J. Am. Chem. Soc. 1994, 116, 5560–5571. [Google Scholar] [CrossRef]
- Lewis, R.A.; Roe, D.C.; Huang, C.; Ferrin, T.E.; Langridge, R.; Kuntz, I.D. Automated site-directed drug design using molecular lattices. J. Mol. Graph. 1992, 10, 66–78. [Google Scholar] [CrossRef] [PubMed]
- Ni, S.; Yuan, Y.; Huang, J.; Mao, X.; Lv, M.; Zhu, J.; Shen, X.; Pei, J.; Lai, L.; Jiang, H.; et al. Discovering Potent Small Molecule Inhibitors of Cyclophilin A Using de Novo Drug Design Approach. J. Med. Chem. 2009, 52, 5295–5298. [Google Scholar] [CrossRef] [PubMed]
- McInnes, C. Virtual screening strategies in drug discovery. Curr. Opin. Chem. Biol. 2007, 11, 494–502. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Zhang, K.Y.J. Hierarchical virtual screening approaches in small molecule drug discovery. Methods 2015, 71, 26–37. [Google Scholar] [CrossRef]
- Di Pizio, A.; Laghezza, A.; Tortorella, P.; Agamennone, M. Probing the S1’ Site for the Identification of Non-Zinc-Binding MMP-2 Inhibitors. Chemmedchem 2013, 8, 1475–1482. [Google Scholar] [CrossRef]
- Wang, Q.; Park, J.; Devkota, A.K.; Cho, E.J.; Dalby, K.N.; Ren, P. Identification and Validation of Novel PERK Inhibitors. J. Chem. Inf. Model. 2014, 54, 1467–1475. [Google Scholar] [CrossRef]
- Kollman, P.A.; Massova, I.; Reyes, C.; Kuhn, B.; Huo, S.; Chong, L.; Lee, M.; Lee, T.; Duan, Y.; Wang, W. Calculating structures and free energies of complex molecules: Combining molecular mechanics and continuum models. Acc. Chem. Res. 2000, 33, 889–897. [Google Scholar] [CrossRef]
- Srinivasan, J.; Cheatham, T.E.; Cieplak, P.; Kollman, P.A.; Case, D.A. Continuum Solvent Studies of the Stability of DNA, RNA, and Phosphoramidate−DNA Helices. J. Am. Chem. Soc. 1998, 120, 9401–9409. [Google Scholar] [CrossRef]
- Wang, E.; Sun, H.; Wang, J.; Wang, Z.; Liu, H.; Zhang, J.Z.; Hou, T. End-point binding free energy calculation with MM/PBSA and MM/GBSA: Strategies and applications in drug design. Chem. Rev. 2019, 119, 9478–9508. [Google Scholar] [CrossRef] [PubMed]
- Gilson, M.K.; Honig, B. Calculation of the total electrostatic energy of a macromolecular system: Solvation energies, binding energies, and conformational analysis. Proteins Struct. Funct. Bioinform. 1988, 4, 7–18. [Google Scholar] [CrossRef] [PubMed]
- Karplus, M.; McCammon, J.A. Molecular dynamics simulations of biomolecules. Nat. Struct. Biol. 2002, 9, 646–652. [Google Scholar] [CrossRef] [PubMed]
- Piana, S.; Klepeis, J.L.; Shaw, D.E. Assessing the accuracy of physical models used in protein-folding simulations: Quantitative evidence from long molecular dynamics simulations. Curr. Opin. Struct. Biol. 2014, 24, 98–105. [Google Scholar] [CrossRef] [PubMed]
- Latorraca, N.R.; Fastman, N.M.; Venkatakrishnan, A.; Frommer, W.B.; Dror, R.O.; Feng, L. Mechanism of substrate translocation in an alternating access transporter. Cell 2017, 169, 96–107.e12. [Google Scholar] [CrossRef]
- Wacker, D.; Wang, S.; McCorvy, J.D.; Betz, R.M.; Venkatakrishnan, A.; Levit, A.; Lansu, K.; Schools, Z.L.; Che, T.; Nichols, D.E. Crystal structure of an LSD-bound human serotonin receptor. Cell 2017, 168, 377–389.e12. [Google Scholar] [CrossRef]
- Clark, A.J.; Tiwary, P.; Borrelli, K.; Feng, S.; Miller, E.B.; Abel, R.; Friesner, R.A.; Berne, B.J. Prediction of protein–ligand binding poses via a combination of induced fit docking and metadynamics simulations. J. Chem. Theory Comput. 2016, 12, 2990–2998. [Google Scholar] [CrossRef]
- Chen, Q.; Cheng, X.; Wei, D.; Xu, Q. Molecular dynamics simulation studies of the wild type and E92Q/N155H mutant of Elvitegravir-resistance HIV-1 integrase. Interdiscip. Sci. Comput. Life Sci. 2015, 7, 36–42. [Google Scholar]
- Fields, J.B.; Németh-Cahalan, K.L.; Freites, J.A.; Vorontsova, I.; Hall, J.E.; Tobias, D.J. Calmodulin gates aquaporin 0 permeability through a positively charged cytoplasmic loop. J. Biol. Chem. 2017, 292, 185–195. [Google Scholar] [CrossRef]
- Liu, Y.; Ke, M.; Gong, H. Protonation of Glu135 facilitates the outward-to-inward structural transition of fucose transporter. Biophys. J. 2015, 109, 542–551. [Google Scholar] [CrossRef]
- Dror, R.O.; Arlow, D.H.; Maragakis, P.; Mildorf, T.J.; Pan, A.C.; Xu, H.; Borhani, D.W.; Shaw, D.E. Activation mechanism of the β 2-adrenergic receptor. Proc. Natl. Acad. Sci. USA 2011, 108, 18684–18689. [Google Scholar] [CrossRef] [PubMed]
- McCammon, J.A.; Gelin, B.R.; Karplus, M. Dynamics of folded proteins. Nature 1977, 267, 585–590. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ‘t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Phillips, J.C.; Hardy, D.J.; Maia, J.D.; Stone, J.E.; Ribeiro, J.V.; Bernardi, R.C.; Buch, R.; Fiorin, G.; Hénin, J.; Jiang, W. Scalable molecular dynamics on CPU and GPU architectures with NAMD. J. Chem. Phys. 2020, 153, 044130. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks III, C.L.; Mackerell Jr, A.D.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef]
- Bowers, K.J.; Chow, D.E.; Xu, H.; Dror, R.O.; Eastwood, M.P.; Gregersen, B.A.; Klepeis, J.L.; Kolossvary, I.; Moraes, M.A.; Sacerdoti, F.D. Scalable Algorithms for Molecular Dynamics Simulations on Commodity Clusters. In Proceedings of the 2006 ACM/IEEE Conference on Supercomputing, Tampa, FL, USA, 11–17 November 2006; IEEE: Piscataway, NJ, USA, 2006; p. 43. [Google Scholar]
- Liu, X.; Shi, D.; Zhou, S.; Liu, H.; Liu, H.; Yao, X. Molecular dynamics simulations and novel drug discovery. Expert Opin. Drug Discov. 2018, 13, 23–37. [Google Scholar] [CrossRef]
- Burg, J.S.; Ingram, J.R.; Venkatakrishnan, A.; Jude, K.M.; Dukkipati, A.; Feinberg, E.N.; Angelini, A.; Waghray, D.; Dror, R.O.; Ploegh, H.L. Structural basis for chemokine recognition and activation of a viral G protein–coupled receptor. Science 2015, 347, 1113–1117. [Google Scholar] [CrossRef]
- Yang, L.-J.; Zou, J.; Xie, H.-Z.; Li, L.-L.; Wei, Y.-Q.; Yang, S.-Y. Steered molecular dynamics simulations reveal the likelier dissociation pathway of imatinib from its targeting kinases c-Kit and Abl. PLoS ONE 2009, 4, e8470. [Google Scholar] [CrossRef]
- Paul, F.; Thomas, T.; Roux, B. Diversity of long-lived intermediates along the binding pathway of imatinib to Abl kinase revealed by MD simulations. J. Chem. Theory Comput. 2020, 16, 7852–7865. [Google Scholar] [CrossRef] [PubMed]
- Śledź, P.; Caflisch, A. Protein structure-based drug design: From docking to molecular dynamics. Curr. Opin. Struct. Biol. 2018, 48, 93–102. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Ye, W.; Yu, Q.; Jiang, C.; Zhang, J.; Luo, R.; Chen, H.-F. Conformational selection and induced fit in specific antibody and antigen recognition: SPE7 as a case study. J. Phys. Chem. B 2013, 117, 4912–4923. [Google Scholar] [CrossRef] [PubMed]
- Wada, M.; Kanamori, E.; Nakamura, H.; Fukunishi, Y. Selection of in silico drug screening results for G-protein-coupled receptors by using universal active probes. J. Chem. Inf. Model. 2011, 51, 2398–2407. [Google Scholar] [CrossRef]
- Li, D.; Jiang, K.; Teng, D.; Wu, Z.; Li, W.; Tang, Y.; Wang, R.; Liu, G. Discovery of New Estrogen-Related Receptor α Agonists via a Combination Strategy Based on Shape Screening and Ensemble Docking. J. Chem. Inf. Model. 2022, 62, 486–497. [Google Scholar] [CrossRef]
- Mohammadi, S.; Narimani, Z.; Ashouri, M.; Firouzi, R.; Karimi-Jafari, M.H. Ensemble learning from ensemble docking: Revisiting the optimum ensemble size problem. Sci. Rep. 2022, 12, 410. [Google Scholar] [CrossRef]
- Ricci-Lopez, J.; Aguila, S.A.; Gilson, M.K.; Brizuela, C.A. Improving structure-based virtual screening with ensemble docking and machine learning. J. Chem. Inf. Model. 2021, 61, 5362–5376. [Google Scholar] [CrossRef]
- Minuesa, G.; Albanese, S.K.; Xie, W.; Kazansky, Y.; Worroll, D.; Chow, A.; Schurer, A.; Park, S.-M.; Rotsides, C.Z.; Taggart, J.; et al. Small-molecule targeting of MUSASHI RNA-binding activity in acute myeloid leukemia. Nat. Commun. 2019, 10, 2691. [Google Scholar] [CrossRef]
- Wu, M.-Y.; Esteban, G.; Brogi, S.; Shionoya, M.; Wang, L.; Campiani, G.; Unzeta, M.; Inokuchi, T.; Butini, S.; Marco-Contelles, J. Donepezil-like multifunctional agents: Design, synthesis, molecular modeling and biological evaluation. Eur. J. Med. Chem. 2016, 121, 864–879. [Google Scholar] [CrossRef]
- Miller, E.B.; Murphy, R.B.; Sindhikara, D.; Borrelli, K.W.; Grisewood, M.J.; Ranalli, F.; Dixon, S.L.; Jerome, S.; Boyles, N.A.; Day, T. Reliable and Accurate Solution to the Induced Fit Docking Problem for Protein–Ligand Binding. J. Chem. Theory Comput. 2021, 17, 2630–2639. [Google Scholar] [CrossRef]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed]
- Stirling, A.; Iannuzzi, M.; Laio, A.; Parrinello, M. Azulene-to-Naphthalene Rearrangement: The Car–Parrinello Metadynamics Method Explores Various Reaction Mechanisms. ChemPhysChem 2004, 5, 1558–1568. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Perrey, D.A.; Decker, A.M.; Langston, T.L.; Mavanji, V.; Harris, D.L.; Kotz, C.M.; Zhang, Y. Discovery of arylsulfonamides as dual orexin receptor agonists. J. Med. Chem. 2021, 64, 8806–8825. [Google Scholar] [CrossRef] [PubMed]
- Izrailev, S.; Stepaniants, S.; Isralewitz, B.; Kosztin, D.; Lu, H.; Molnar, F.; Wriggers, W.; Schulten, K. Steered molecular dynamics. In Computational Molecular Dynamics: Challenges, Methods, Ideas; Springer: Berlin/Heidelberg, Germany, 1999; pp. 39–65. [Google Scholar]
- Hamelberg, D.; Mongan, J.; McCammon, J.A. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120, 11919–11929. [Google Scholar] [CrossRef]
- Sugita, Y.; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar] [CrossRef]
- Rudd, R.E.; Broughton, J.Q. Coarse-grained molecular dynamics and the atomic limit of finite elements. Phys. Rev. B 1998, 58, R5893. [Google Scholar] [CrossRef]
- Hollingsworth, S.A.; Dror, R.O. Molecular dynamics simulation for all. Neuron 2018, 99, 1129–1143. [Google Scholar] [CrossRef]
- Wang, R.; Zheng, Q. Multiple molecular dynamics simulations of the inhibitor GRL-02031 complex with wild type and mutant HIV-1 protease reveal the binding and drug-resistance mechanism. Langmuir 2020, 36, 13817–13832. [Google Scholar] [CrossRef]
- Wang, R.-G.; Zhang, H.-X.; Zheng, Q.-C. Revealing the binding and drug resistance mechanism of amprenavir, indinavir, ritonavir, and nelfinavir complexed with HIV-1 protease due to double mutations G48T/L89M by molecular dynamics simulations and free energy analyses. Phys. Chem. Chem. Phys. 2020, 22, 4464–4480. [Google Scholar] [CrossRef]
- Xue, W.; Jin, X.; Ning, L.; Wang, M.; Liu, H.; Yao, X. Exploring the molecular mechanism of cross-resistance to HIV-1 integrase strand transfer inhibitors by molecular dynamics simulation and residue interaction network analysis. J. Chem. Inf. Model. 2013, 53, 210–222. [Google Scholar] [CrossRef]
- Liu, S.; Huynh, T.; Stauft, C.B.; Wang, T.T.; Luan, B. Structure–Function Analysis of Resistance to Bamlanivimab by SARS-CoV-2 Variants Kappa, Delta, and Lambda. J. Chem. Inf. Model. 2021, 61, 5133–5140. [Google Scholar] [CrossRef] [PubMed]
- Platania, C.B.M.; Bucolo, C. Molecular dynamics simulation techniques as tools in drug discovery and pharmacology: A focus on allosteric drugs. In Allostery; Springer: Berlin/Heidelberg, Germany, 2021; pp. 245–254. [Google Scholar]
- Morando, M.A.; Saladino, G.; D’Amelio, N.; Pucheta-Martinez, E.; Lovera, S.; Lelli, M.; López-Méndez, B.; Marenchino, M.; Campos-Olivas, R.; Gervasio, F.L. Conformational Selection and Induced Fit Mechanisms in the Binding of an Anticancer Drug to the c-Src Kinase. Sci. Rep. 2016, 6, 24439. [Google Scholar] [CrossRef]
- Beglov, D.; Hall, D.R.; Wakefield, A.E.; Luo, L.; Allen, K.N.; Kozakov, D.; Whitty, A.; Vajda, S. Exploring the structural origins of cryptic sites on proteins. Proc. Natl. Acad. Sci. USA 2018, 115, E3416–E3425. [Google Scholar] [CrossRef] [PubMed]
- Herbert, C.; Schieborr, U.; Saxena, K.; Juraszek, J.; De Smet, F.; Alcouffe, C.; Bianciotto, M.; Saladino, G.; Sibrac, D.; Kudlinzki, D. Molecular mechanism of SSR128129E, an extracellularly acting, small-molecule, allosteric inhibitor of FGF receptor signaling. Cancer Cell 2013, 23, 489–501. [Google Scholar] [CrossRef] [PubMed]
- Bono, F.; De Smet, F.; Herbert, C.; De Bock, K.; Georgiadou, M.; Fons, P.; Tjwa, M.; Alcouffe, C.; Ny, A.; Bianciotto, M. Inhibition of tumor angiogenesis and growth by a small-molecule multi-FGF receptor blocker with allosteric properties. Cancer Cell 2013, 23, 477–488. [Google Scholar] [CrossRef]
- Guvench, O.; MacKerell Jr, A.D. Computational fragment-based binding site identification by ligand competitive saturation. PLoS Comput. Biol. 2009, 5, e1000435. [Google Scholar] [CrossRef]
- Bakan, A.; Nevins, N.; Lakdawala, A.S.; Bahar, I. Druggability assessment of allosteric proteins by dynamics simulations in the presence of probe molecules. J. Chem. Theory Comput. 2012, 8, 2435–2447. [Google Scholar] [CrossRef]
- Zuzic, L.; Samsudin, F.; Shivgan, A.T.; Raghuvamsi, P.V.; Marzinek, J.K.; Boags, A.; Pedebos, C.; Tulsian, N.K.; Warwicker, J.; MacAry, P. Uncovering cryptic pockets in the SARS-CoV-2 spike glycoprotein. Structure 2022, 30, 1062–1074.e4. [Google Scholar] [CrossRef]
- Dyson, H.J.; Wright, P.E. Intrinsically unstructured proteins and their functions. Nat. Rev. Mol. Cell Biol. 2005, 6, 197–208. [Google Scholar] [CrossRef]
- Wang, W. Recent advances in atomic molecular dynamics simulation of intrinsically disordered proteins. Phys. Chem. Chem. Phys. 2021, 23, 777–784. [Google Scholar] [CrossRef]
- Man, V.H.; He, X.; Derreumaux, P.; Ji, B.; Xie, X.-Q.; Nguyen, P.H.; Wang, J. Effects of all-atom molecular mechanics force fields on amyloid peptide assembly: The case of aβ16–22 dimer. J. Chem. Theory Comput. 2019, 15, 1440–1452. [Google Scholar] [CrossRef] [PubMed]
- Man, V.H.; He, X.; Gao, J.; Wang, J. Effects of all-atom molecular mechanics force fields on amyloid peptide assembly: The case of PHF6 peptide of tau protein. J. Chem. Theory Comput. 2021, 17, 6458–6471. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zhong, H.; Liu, X.; Zhou, S.; Tan, S.; Liu, H.; Yao, X. Disclosing the Mechanism of Spontaneous Aggregation and Template-Induced Misfolding of the Key Hexapeptide (PHF6) of Tau Protein Based on Molecular Dynamics Simulation. ACS Chem. Neurosci. 2019, 10, 4810–4823. [Google Scholar] [CrossRef]
- Cournia, Z.; Allen, B.K.; Beuming, T.; Pearlman, D.A.; Radak, B.K.; Sherman, W. Rigorous Free Energy Simulations in Virtual Screening. J. Chem. Inf. Model. 2020, 60, 4153–4169. [Google Scholar] [CrossRef]
- Menchon, G.; Maveyraud, L.; Czaplicki, G. Molecular dynamics as a tool for virtual ligand screening. In Computational Drug Discovery and Design; Springer: Berlin/Heidelberg, Germany, 2018; pp. 145–178. [Google Scholar]
- Sabe, V.T.; Ntombela, T.; Jhamba, L.A.; Maguire, G.E.; Govender, T.; Naicker, T.; Kruger, H.G. Current trends in computer aided drug design and a highlight of drugs discovered via computational techniques: A review. Eur. J. Med. Chem. 2021, 224, 113705. [Google Scholar] [CrossRef]
- Chodera, J.D.; Mobley, D.L.; Shirts, M.R.; Dixon, R.W.; Branson, K.; Pande, V.S. Alchemical free energy methods for drug discovery: Progress and challenges. Curr. Opin. Struct. Biol. 2011, 21, 150–160. [Google Scholar] [CrossRef]
- Mezei, M. The finite difference thermodynamic integration, tested on calculating the hydration free energy difference between acetone and dimethylamine in water. J. Chem. Phys. 1987, 86, 7084–7088. [Google Scholar] [CrossRef]
- Zwanzig, R.W. High-temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Kirkwood, J.G. Statistical mechanics of fluid mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar] [CrossRef]
- Åqvist, J.; Luzhkov, V.B.; Brandsdal, B.O. Ligand binding affinities from MD simulations. Acc. Chem. Res. 2002, 35, 358–365. [Google Scholar] [CrossRef]
- Hansson, T.; Marelius, J.; Åqvist, J. Ligand binding affinity prediction by linear interaction energy methods. J. Comput. Aided Mol. Des. 1998, 12, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Massova, I.; Kollman, P.A. Combined molecular mechanical and continuum solvent approach (MM-PBSA/GBSA) to predict ligand binding. Perspect. Drug Discov. Des. 2000, 18, 113–135. [Google Scholar] [CrossRef]
- He, X.; Liu, S.; Lee, T.-S.; Ji, B.; Man, V.H.; York, D.M.; Wang, J. Fast, accurate, and reliable protocols for routine calculations of protein–ligand binding affinities in drug design projects using AMBER GPU-TI with ff14SB/GAFF. ACS Omega 2020, 5, 4611–4619. [Google Scholar] [CrossRef] [PubMed]
- Cournia, Z.; Allen, B.; Sherman, W. Relative binding free energy calculations in drug discovery: Recent advances and practical considerations. J. Chem. Inf. Model. 2017, 57, 2911–2937. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wu, Y.; Deng, Y.; Kim, B.; Pierce, L.; Krilov, G.; Lupyan, D.; Robinson, S.; Dahlgren, M.K.; Greenwood, J. Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. J. Am. Chem. Soc. 2015, 137, 2695–2703. [Google Scholar] [CrossRef]
- Homeyer, N.; Gohlke, H. FEW: A workflow tool for free energy calculations of ligand binding. J. Comput. Chem. 2013, 34, 965–973. [Google Scholar] [CrossRef]
- Lee, T.-S.; Allen, B.K.; Giese, T.J.; Guo, Z.; Li, P.; Lin, C.; McGee Jr, T.D.; Pearlman, D.A.; Radak, B.K.; Tao, Y. Alchemical binding free energy calculations in AMBER20: Advances and best practices for drug discovery. J. Chem. Inf. Model. 2020, 60, 5595–5623. [Google Scholar] [CrossRef]
- Raman, E.P.; Paul, T.J.; Hayes, R.L.; Brooks III, C.L. Automated, accurate, and scalable relative protein–ligand binding free-energy calculations using lambda dynamics. J. Chem. Theory Comput. 2020, 16, 7895–7914. [Google Scholar] [CrossRef]
- Carvalho Martins, L.; Cino, E.A.; Ferreira, R.S. PyAutoFEP: An automated free energy perturbation workflow for GROMACS integrating enhanced sampling methods. J. Chem. Theory Comput. 2021, 17, 4262–4273. [Google Scholar] [CrossRef]
- Marelius, J.; Kolmodin, K.; Feierberg, I.; Åqvist, J. Q: A molecular dynamics program for free energy calculations and empirical valence bond simulations in biomolecular systems. J. Mol. Graph. Model. 1998, 16, 213–225. [Google Scholar] [CrossRef]
- Tang, H.; Jensen, K.; Houang, E.; McRobb, F.M.; Bhat, S.; Svensson, M.; Bochevarov, A.; Day, T.; Dahlgren, M.K.; Bell, J.A. Discovery of a Novel Class of d-Amino Acid Oxidase Inhibitors Using the Schrödinger Computational Platform. J. Med. Chem. 2022, 65, 6775–6802. [Google Scholar] [CrossRef]
- Zou, J.; Li, Z.; Liu, S.; Peng, C.; Fang, D.; Wan, X.; Lin, Z.; Lee, T.-S.; Raleigh, D.P.; Yang, M. Scaffold Hopping Transformations Using Auxiliary Restraints for Calculating Accurate Relative Binding Free Energies. J. Chem. Theory Comput. 2021, 17, 3710–3726. [Google Scholar] [CrossRef] [PubMed]
- Pearlman, D.A.; Kollman, P.A. A new method for carrying out free energy perturbation calculations: Dynamically modified windows. J. Chem. Phys. 1989, 90, 2460–2470. [Google Scholar] [CrossRef]
- Lee, T.-S.; Hu, Y.; Sherborne, B.; Guo, Z.; York, D.M. Toward fast and accurate binding affinity prediction with pmemdGTI: An efficient implementation of GPU-accelerated thermodynamic integration. J. Chem. Theory Comput. 2017, 13, 3077–3084. [Google Scholar] [CrossRef] [PubMed]
- Loeffler, H.H.; Michel, J.; Woods, C. FESetup: Automating setup for alchemical free energy simulations. J. Chem. Inf. Model. 2015, 55, 2485–2490. [Google Scholar]
- Zavitsanou, S.; Tsengenes, A.; Papadourakis, M.; Amendola, G.; Chatzigoulas, A.; Dellis, D.; Cosconati, S.; Cournia, Z. FEPrepare: A Web-Based Tool for Automating the Setup of Relative Binding Free Energy Calculations. J. Chem. Inf. Model. 2021, 61, 4131–4138. [Google Scholar] [CrossRef]
- Jespers, W.; Esguerra, M.; Åqvist, J.; Gutiérrez-de-Terán, H. QligFEP: An automated workflow for small molecule free energy calculations in Q. J. Cheminformatics 2019, 11, 26. [Google Scholar] [CrossRef]
- Jespers, W.; Isaksen, G.V.; Andberg, T.A.; Vasile, S.; van Veen, A.; Åqvist, J.; Brandsdal, B.O.; Gutiérrez-de-Terán, H. QresFEP: An automated protocol for free energy calculations of protein mutations in Q. J. Chem. Theory Comput. 2019, 15, 5461–5473. [Google Scholar] [CrossRef]
- Dodda, L.S.; Cabeza de Vaca, I.; Tirado-Rives, J.; Jorgensen, W.L. LigParGen web server: An automatic OPLS-AA parameter generator for organic ligands. Nucleic Acids Res. 2017, 45, W331–W336. [Google Scholar] [CrossRef]
- Kim, S.; Oshima, H.; Zhang, H.; Kern, N.R.; Re, S.; Lee, J.; Roux, B.; Sugita, Y.; Jiang, W.; Im, W. CHARMM-GUI free energy calculator for absolute and relative ligand solvation and binding free energy simulations. J. Chem. Theory Comput. 2020, 16, 7207–7218. [Google Scholar] [CrossRef]
- Kuhn, M.; Firth-Clark, S.; Tosco, P.; Mey, A.S.; Mackey, M.; Michel, J. Assessment of binding affinity via alchemical free-energy calculations. J. Chem. Inf. Model. 2020, 60, 3120–3130. [Google Scholar] [CrossRef]
- Edinger, S.R.; Cortis, C.; Shenkin, P.S.; Friesner, R.A. Solvation free energies of peptides: Comparison of approximate continuum solvation models with accurate solution of the Poisson− Boltzmann equation. J. Phys. Chem. B 1997, 101, 1190–1197. [Google Scholar] [CrossRef]
- Bashford, D.; Case, D.A. Generalized born models of macromolecular solvation effects. Annu. Rev. Phys. Chem. 2000, 51, 129–152. [Google Scholar] [CrossRef] [PubMed]
- Cramer, C.J.; Truhlar, D.G. Implicit solvation models: Equilibria, structure, spectra, and dynamics. Chem. Rev. 1999, 99, 2161–2200. [Google Scholar] [CrossRef] [PubMed]
- Sanner, M.F.; Olson, A.J.; Spehner, J.C. Reduced surface: An efficient way to compute molecular surfaces. Biopolymers 1996, 38, 305–320. [Google Scholar] [CrossRef]
- Gilson, M.K.; Sharp, K.A.; Honig, B.H. Calculating the electrostatic potential of molecules in solution: Method and error assessment. J. Comput. Chem. 1988, 9, 327–335. [Google Scholar] [CrossRef]
- Warwicker, J.; Watson, H. Calculation of the electric potential in the active site cleft due to α-helix dipoles. J. Mol. Biol. 1982, 157, 671–679. [Google Scholar] [CrossRef]
- Feig, M.; Onufriev, A.; Lee, M.S.; Im, W.; Case, D.A.; Brooks III, C.L. Performance comparison of generalized born and Poisson methods in the calculation of electrostatic solvation energies for protein structures. J. Comput. Chem. 2004, 25, 265–284. [Google Scholar] [CrossRef]
- Onufriev, A.; Case, D.A.; Bashford, D. Effective Born radii in the generalized Born approximation: The importance of being perfect. J. Comput. Chem. 2002, 23, 1297–1304. [Google Scholar] [CrossRef]
- Onufriev, A.; Bashford, D.; Case, D.A. Modification of the generalized Born model suitable for macromolecules. J. Phys. Chem. B 2000, 104, 3712–3720. [Google Scholar] [CrossRef]
- Still, W.C.; Tempczyk, A.; Hawley, R.C.; Hendrickson, T. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 1990, 112, 6127–6129. [Google Scholar] [CrossRef]
- Poli, G.; Granchi, C.; Rizzolio, F.; Tuccinardi, T. Application of MM-PBSA methods in virtual screening. Molecules 2020, 25, 1971. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.-Y.; Chen, X.; Dong, J.; Yang, J.-F.; Xiao, H.; Ye, Y.; Li, L.-H.; Zhan, C.-G.; Yang, W.-C.; Yang, G.-F. Rational redesign of enzyme via the combination of quantum mechanics/molecular mechanics, molecular dynamics, and structural biology study. J. Am. Chem. Soc. 2021, 143, 15674–15687. [Google Scholar] [CrossRef] [PubMed]
- Sobeh, M.M.; Kitao, A. Dissociation pathways of the p53 DNA binding domain from DNA and critical roles of key residues elucidated by dPaCS-MD/MSM. J. Chem. Inf. Model. 2022, 62, 1294–1307. [Google Scholar] [CrossRef] [PubMed]
- Zoete, V.; Michielin, O. Comparison between computational alanine scanning and per-residue binding free energy decomposition for protein–protein association using MM-GBSA: Application to the TCR-p-MHC complex. Proteins Struct. Funct. Bioinform. 2007, 67, 1026–1047. [Google Scholar] [CrossRef] [PubMed]
- Zoete, V.; Irving, M.; Michielin, O. MM–GBSA binding free energy decomposition and T cell receptor engineering. J. Mol. Recognit. Interdiscip. J. 2010, 23, 142–152. [Google Scholar] [CrossRef]
- Hornig, M.; Klamt, A. COSMO f rag: A Novel Tool for High-Throughput ADME Property Prediction and Similarity Screening Based on Quantum Chemistry. J. Chem. Inf. Model. 2005, 45, 1169–1177. [Google Scholar] [CrossRef]
- Masso, M. A Multibody Atomic Statistical Potential for Predicting Enzyme-Inhibitor Binding Energy. Biophys. J. 2013, 104, 405a. [Google Scholar] [CrossRef]
- Fernandes, H.S.; Sousa, S.F.; Cerqueira, N.M. New insights into the catalytic mechanism of the SARS-CoV-2 main protease: An ONIOM QM/MM approach. Mol. Divers. 2022, 26, 1373–1381. [Google Scholar] [CrossRef]
- Yildiz, I.; Yildiz, B.S. Computational Analysis of the Inhibition Mechanism of NOTUM by the ONIOM Method. ACS Omega 2022, 7, 13333–13342. [Google Scholar] [CrossRef]
- Vuppala, S.; Kim, J.; Joo, B.-S.; Choi, J.-M.; Jang, J. A Combination of Pharmacophore-Based Virtual Screening, Structure-Based Lead Optimization, and DFT Study for the Identification of S. epidermidis TcaR Inhibitors. Pharmaceuticals 2022, 15, 635. [Google Scholar] [CrossRef]
- Elkaeed, E.B.; Yousef, R.G.; Elkady, H.; Gobaara, I.M.M.; Alsfouk, B.A.; Husein, D.Z.; Ibrahim, I.M.; Metwaly, A.M.; Eissa, I.H. Design, Synthesis, Docking, DFT, MD Simulation Studies of a New Nicotinamide-Based Derivative: In Vitro Anticancer and VEGFR-2 Inhibitory Effects. Molecules 2022, 27, 4606. [Google Scholar] [CrossRef] [PubMed]
- Chung, L.W.; Sameera, W.M.C.; Ramozzi, R.; Page, A.J.; Hatanaka, M.; Petrova, G.P.; Harris, T.V.; Li, X.; Ke, Z.; Liu, F.; et al. The ONIOM Method and Its Applications. Chem. Rev. 2015, 115, 5678–5796. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Bursch, M.; Mewes, J.-M.; Hansen, A.; Grimme, S. Best Practice DFT Protocols for Basic Molecular Computational Chemistry. Angew. Chem. 2022, 134, e202205735. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Tirado-Rives, J.; Jorgensen, W.L. Performance of B3LYP Density Functional Methods for a Large Set of Organic Molecules. J. Chem. Theory Comput. 2008, 4, 297–306. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Hill, J.G. Gaussian basis sets for molecular applications. Int. J. Quantum Chem. 2013, 113, 21–34. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self—Consistent molecular orbital methods. XII. Further extensions of Gaussian—Type basis sets for use in molecular orbital studies of organic molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
- Gill, P.M.; Johnson, B.G.; Pople, J.A.; Frisch, M.J. The performance of the Becke—Lee—Yang—Parr (B—LYP) density functional theory with various basis sets. Chem. Phys. Lett. 1992, 197, 499–505. [Google Scholar] [CrossRef]
- Rassolov, V.A.; Ratner, M.A.; Pople, J.A.; Redfern, P.C.; Curtiss, L.A. 6-31G* basis set for third-row atoms. J. Comput. Chem. 2001, 22, 976–984. [Google Scholar] [CrossRef]
- Kříž, K.; Řezáč, J. Benchmarking of Semiempirical Quantum-Mechanical Methods on Systems Relevant to Computer-Aided Drug Design. J. Chem. Inf. Model. 2020, 60, 1453–1460. [Google Scholar] [CrossRef]
- Honig, B.; Karplus, M. Implications of torsional potential of retinal isomers for visual excitation. Nature 1971, 229, 558–560. [Google Scholar] [CrossRef] [PubMed]
- Karplus, M. Development of multiscale models for complex chemical systems: From H+H2 to biomolecules (Nobel lecture). Angew. Chem. Int. Ed. 2014, 53, 9992–10005. [Google Scholar] [CrossRef] [PubMed]
- Vreven, T.; Byun, K.S.; Komáromi, I.; Dapprich, S.; Montgomery Jr, J.A.; Morokuma, K.; Frisch, M.J. Combining quantum mechanics methods with molecular mechanics methods in ONIOM. J. Chem. Theory Comput. 2006, 2, 815–826. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Frisch, M.E.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Petersson, G.; Nakatsuji, H. Gaussian 16; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Lin, Z.; Johnson, M.E. Proposed cation-π mediated binding by factor Xa: A novel enzymatic mechanism for molecular recognition. FEBS Lett. 1995, 370, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Gleeson, M.P.; Gleeson, D. QM/MM calculations in drug discovery: A useful method for studying binding phenomena? J. Chem. Inf. Model. 2009, 49, 670–677. [Google Scholar] [CrossRef]
- Puthanveedu, V.; Muraleedharan, K. Phytochemicals as Potential Inhibitors for COVID-19 Revealed by Molecular Docking, Molecular Dynamic Simulation and DFT Studies. Struct. Chem. 2022, 33, 1423–1443. [Google Scholar] [CrossRef] [PubMed]
- Bím, D.; Navrátil, M.; Gutten, O.; Konvalinka, J.; Kutil, Z.; Culka, M.; Navrátil, V.; Alexandrova, A.N.; Bařinka, C.; Rulíšek, L.R. Predicting Effects of Site-Directed Mutagenesis on Enzyme Kinetics by QM/MM and QM Calculations: A Case of Glutamate Carboxypeptidase II. J. Phys. Chem. B 2022, 126, 132–143. [Google Scholar] [CrossRef]
- Dushanan, R.; Weerasinghe, S.; Dissanayake, D.P.; Senthilinithy, R. Implication of Ab Initio, QM/MM, and molecular dynamics calculations on the prediction of the therapeutic potential of some selected HDAC inhibitors. Mol. Simul. 2022, 48, 1464–1475. [Google Scholar] [CrossRef]
- Srivastava, R.; Gupta, S.K.; Naaz, F.; Gupta, P.S.S.; Yadav, M.; Singh, V.K.; Singh, A.; Rana, M.K.; Gupta, S.K.; Schols, D. Alkylated benzimidazoles: Design, synthesis, docking, DFT analysis, ADMET property, molecular dynamics and activity against HIV and YFV. Comput. Biol. Chem. 2020, 89, 107400. [Google Scholar] [CrossRef]
- Bag, A. Dft based computational methodology of ic50 prediction. Curr. Comput. Aided Drug Des. 2021, 17, 244–253. [Google Scholar] [CrossRef]
- Parlak, C.; Alver, Ö.; Bağlayan, Ö.; Ramasami, P. Theoretical insights of the drug-drug interaction between favipiravir and ibuprofen: A DFT, QTAIM and drug-likeness investigation. J. Biomol. Struct. Dyn. 2022, 40, 1–8. [Google Scholar] [CrossRef]
- Prieto, D.C.; De Araujo, R.V.; de Souza Lima, S.; Assad, F.Z.; Grayson, S.M.; Braga, A.A.; Lourenço, F.R.; Giarolla, J. Succinylated isoniazid potential prodrug: Design of Experiments (DoE) for synthesis optimization and computational study of the reaction mechanism by DFT calculations. J. Mol. Struct. 2022, 1254, 132323. [Google Scholar] [CrossRef]
- Becke, A. The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Gohlke, H.; Klebe, G. Approaches to the description and prediction of the binding affinity of small-molecule ligands to macromolecular receptors. Angew. Chem. Int. Ed. 2002, 41, 2644–2676. [Google Scholar] [CrossRef]
- Alinejad, A.; Raissi, H.; Hashemzadeh, H. Understanding co-loading of doxorubicin and camptothecin on graphene and folic acid-conjugated graphene for targeting drug delivery: Classical MD simulation and DFT calculation. J. Biomol. Struct. Dyn. 2020, 38, 2737–2745. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Safaei, B.; Jen, T.-C. Theorical investigation of adsorption mechanism of doxorubicin anticancer drug on the pristine and functionalized single-walled carbon nanotube surface as a drug delivery vehicle: A DFT study. J. Mol. Liq. 2021, 322, 114890. [Google Scholar] [CrossRef]
- Zeng, Q.; Jones, M.R.; Brooks, B.R. Absolute and relative pKa predictions via a DFT approach applied to the SAMPL6 blind challenge. J. Comput. Aided Mol. Des. 2018, 32, 1179–1189. [Google Scholar] [CrossRef]
- Geerlings, P.; De Proft, F.; Langenaeker, W. Conceptual density functional theory. Chem. Rev. 2003, 103, 1793–1874. [Google Scholar] [CrossRef]
- Lawler, R.; Liu, Y.-H.; Majaya, N.; Allam, O.; Ju, H.; Kim, J.Y.; Jang, S.S. DFT-Machine Learning Approach for Accurate Prediction of p K a. J. Phys. Chem. A 2021, 125, 8712–8722. [Google Scholar] [CrossRef]
- Flores-Holguín, N.; Frau, J.; Glossman-Mitnik, D. In silico pharmacokinetics, ADMET study and conceptual DFT analysis of two plant cyclopeptides isolated from rosaceae as a computational Peptidology approach. Front. Chem. 2021, 9, 570. [Google Scholar] [CrossRef]
- Gulbis, J.; Mackay, M.; Holan, G.; Marcuccio, S. Structure of a dideoxynucleoside active against the HIV (AIDS) virus. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1993, 49, 1095–1097. [Google Scholar] [CrossRef]
- Garrec, J.; Sautet, P.; Fleurat-Lessard, P. Understanding the HIV-1 protease reactivity with DFT: What do we gain from recent functionals? J. Phys. Chem. B 2011, 115, 8545–8558. [Google Scholar] [CrossRef]
- Ibeji, C.U. Molecular dynamics and DFT study on the structure and dynamics of N-terminal domain HIV-1 capsid inhibitors. Mol. Simul. 2020, 46, 62–70. [Google Scholar] [CrossRef]
- Liang, Z.; Li, L.; Wang, Y.; Chen, L.; Kong, X.; Hong, Y.; Lan, L.; Zheng, M.; Guang-Yang, C.; Liu, H. Molecular basis of NDM-1, a new antibiotic resistance determinant. PLoS ONE 2011, 6, e23606. [Google Scholar] [CrossRef]
- Duan, H.; Liu, X.; Zhuo, W.; Meng, J.; Gu, J.; Sun, X.; Zuo, K.; Luo, Q.; Luo, Y.; Tang, D. 3D-QSAR and molecular recognition of Klebsiella pneumoniae NDM-1 inhibitors. Mol. Simul. 2019, 45, 694–705. [Google Scholar] [CrossRef]
- Caburet, J.; Boucherle, B.; Bourdillon, S.; Simoncelli, G.; Verdirosa, F.; Docquier, J.-D.; Moreau, Y.; Krimm, I.; Crouzy, S.; Peuchmaur, M. A fragment-based drug discovery strategy applied to the identification of NDM-1 β-lactamase inhibitors. Eur. J. Med. Chem. 2022, 240, 114599. [Google Scholar] [CrossRef]
- Vasudevan, A.; Kesavan, D.K.; Wu, L.; Su, Z.; Wang, S.; Ramasamy, M.K.; Hopper, W.; Xu, H. In Silico and In Vitro Screening of Natural Compounds as Broad-Spectrum β-Lactamase Inhibitors against Acinetobacter baumannii New Delhi Metallo-β-lactamase-1 (NDM-1). BioMed. Res. Int. 2022, 2022, 4230788. [Google Scholar] [CrossRef]
- Khandelwal, A.; Lukacova, V.; Comez, D.; Kroll, D.M.; Raha, S.; Balaz, S. A combination of docking, QM/MM methods, and MD simulation for binding affinity estimation of metalloprotein ligands. J. Med. Chem. 2005, 48, 5437–5447. [Google Scholar] [CrossRef]
- Guedes, I.A.; Costa, L.S.; Dos Santos, K.B.; Karl, A.L.; Rocha, G.K.; Teixeira, I.M.; Galheigo, M.M.; Medeiros, V.; Krempser, E.; Custódio, F.L. Drug design and repurposing with DockThor-VS web server focusing on SARS-CoV-2 therapeutic targets and their non-synonym variants. Sci. Rep. 2021, 11, 5543. [Google Scholar] [CrossRef]
- Hodos, R.A.; Kidd, B.A.; Shameer, K.; Readhead, B.P.; Dudley, J.T. In silico methods for drug repurposing and pharmacology. Wiley Interdiscip. Rev. Syst. Biol. Med. 2016, 8, 186–210. [Google Scholar] [CrossRef]
- Xu, X.; Huang, M.; Zou, X. Docking-based inverse virtual screening: Methods, applications, and challenges. Biophys. Rep. 2018, 4, 1–16. [Google Scholar] [CrossRef]
- McNutt, A.T.; Francoeur, P.; Aggarwal, R.; Masuda, T.; Meli, R.; Ragoza, M.; Sunseri, J.; Koes, D.R. GNINA 1.0: Molecular docking with deep learning. J. Cheminformatics 2021, 13, 43. [Google Scholar] [CrossRef]
- Gentile, F.; Agrawal, V.; Hsing, M.; Ton, A.-T.; Ban, F.; Norinder, U.; Gleave, M.E.; Cherkasov, A. Deep docking: A deep learning platform for augmentation of structure based drug discovery. ACS Cent. Sci. 2020, 6, 939–949. [Google Scholar] [CrossRef]
- Walters, W.P.; Barzilay, R. Applications of deep learning in molecule generation and molecular property prediction. Acc. Chem. Res. 2020, 54, 263–270. [Google Scholar] [CrossRef]
- Soleimany, A.P.; Amini, A.; Goldman, S.; Rus, D.; Bhatia, S.N.; Coley, C.W. Evidential deep learning for guided molecular property prediction and discovery. ACS Cent. Sci. 2021, 7, 1356–1367. [Google Scholar] [CrossRef]
- Dong, J.; Zhao, M.; Liu, Y.; Su, Y.; Zeng, X. Deep learning in retrosynthesis planning: Datasets, models and tools. Brief. Bioinform. 2022, 23, bbab391. [Google Scholar] [CrossRef]
- Thakkar, A.; Chadimová, V.; Bjerrum, E.J.; Engkvist, O.; Reymond, J.-L. Retrosynthetic accessibility score (RAscore)–rapid machine learned synthesizability classification from AI driven retrosynthetic planning. Chem. Sci. 2021, 12, 3339–3349. [Google Scholar] [CrossRef]
- Segler, M.H.S.; Preuss, M.; Waller, M.P. Planning chemical syntheses with deep neural networks and symbolic AI. Nature 2018, 555, 604–610. [Google Scholar] [CrossRef]
- Krishnan, S.R.; Bung, N.; Bulusu, G.; Roy, A. Accelerating de novo drug design against novel proteins using deep learning. J. Chem. Inf. Model. 2021, 61, 621–630. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Wang, Z.; Sun, H.; Wang, J.; Shen, C.; Weng, G.; Chai, X.; Li, H.; Cao, D.; Hou, T. Deep learning approaches for de novo drug design: An overview. Curr. Opin. Struct. Biol. 2022, 72, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Fujita, T.; Winkler, D.A. Understanding the roles of the “two QSARs”. J. Chem. Inf. Model. 2016, 56, 269–274. [Google Scholar] [CrossRef] [PubMed]


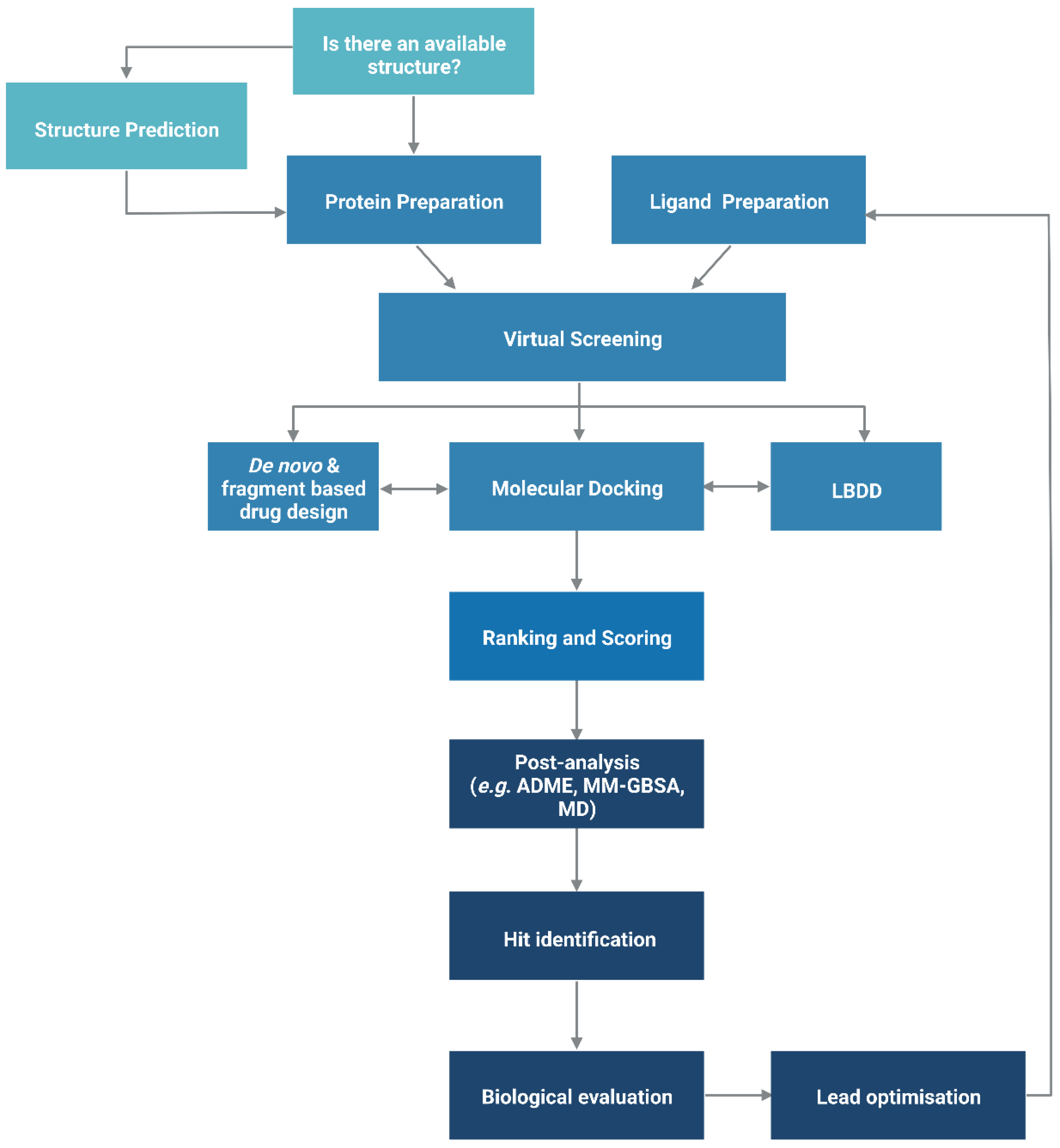
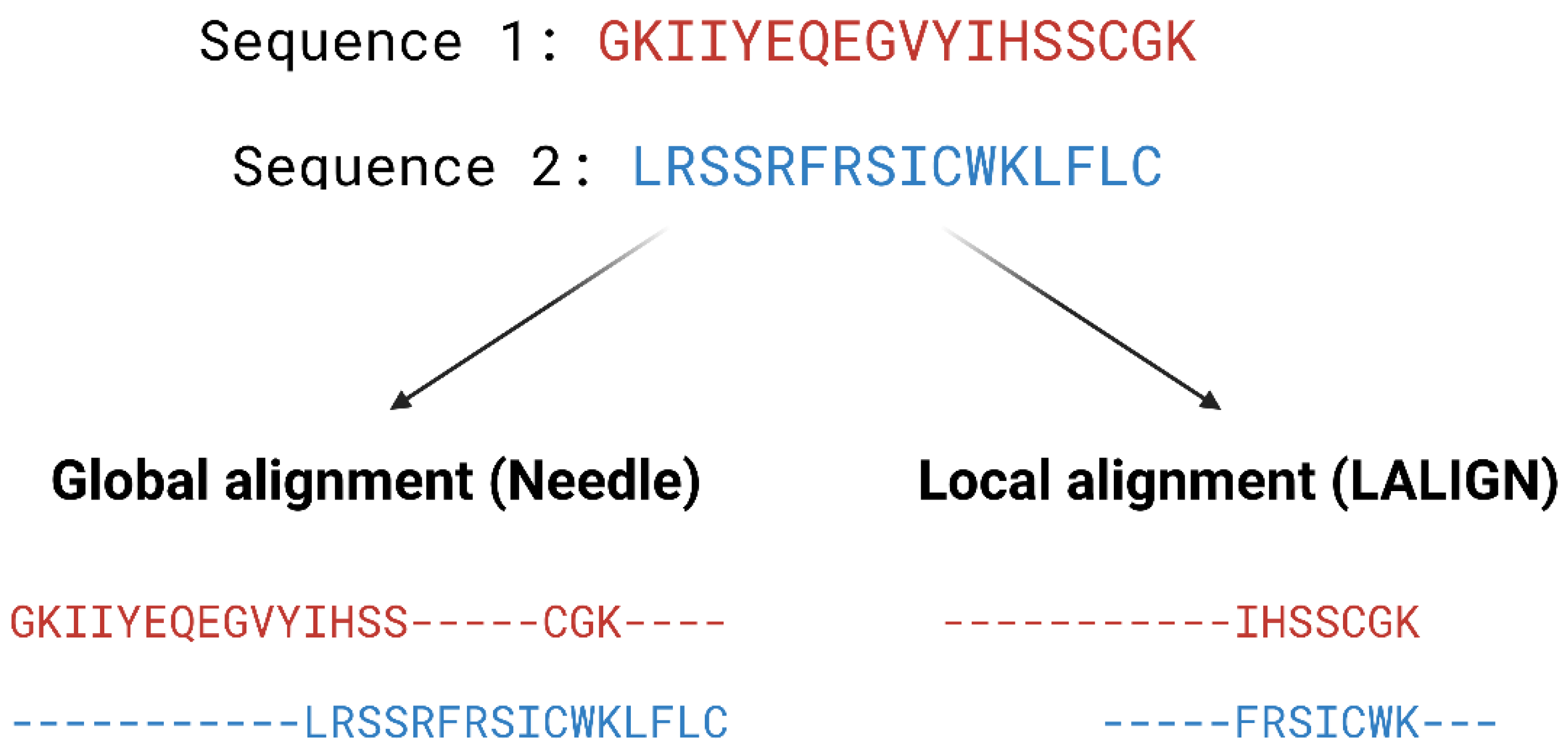
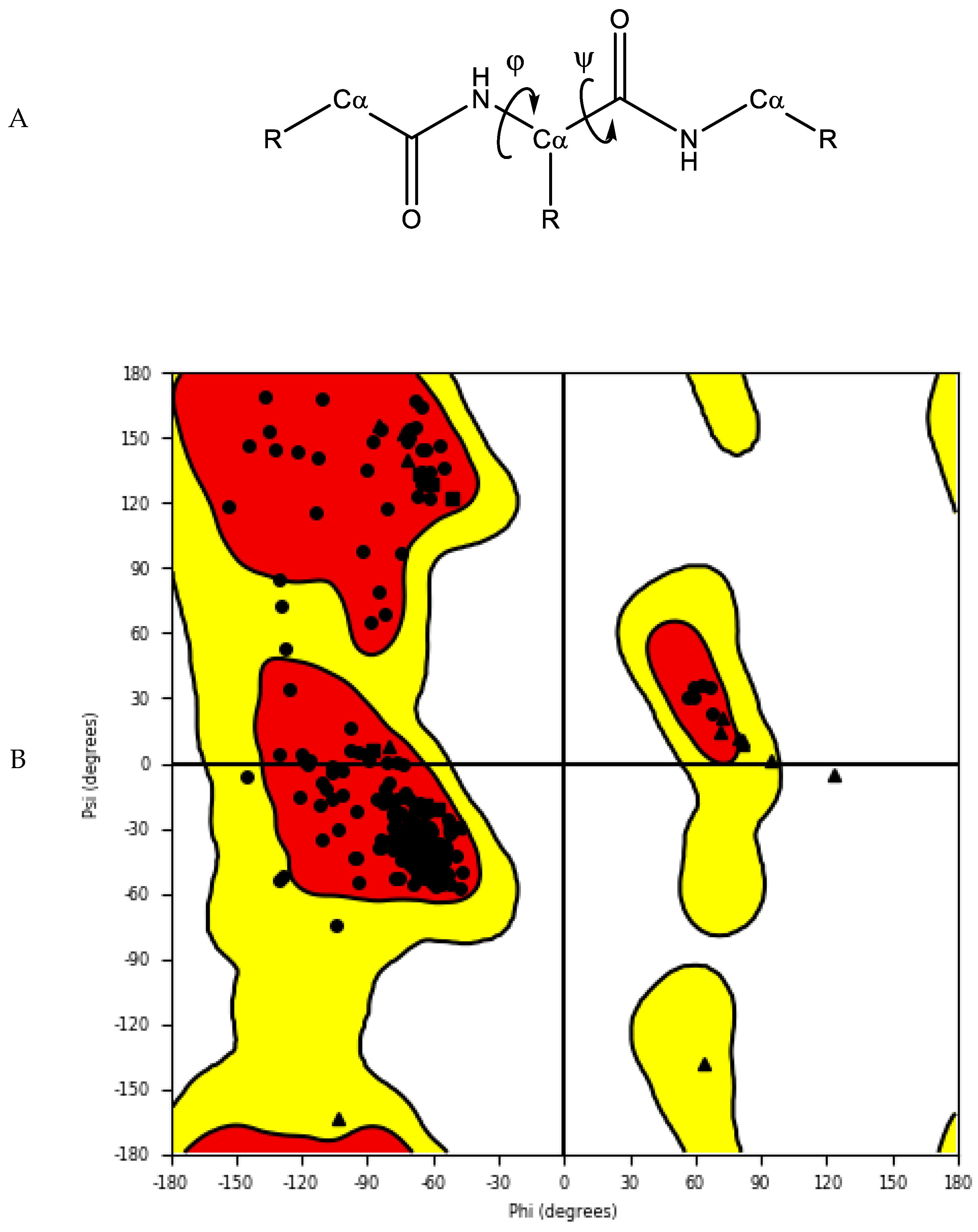



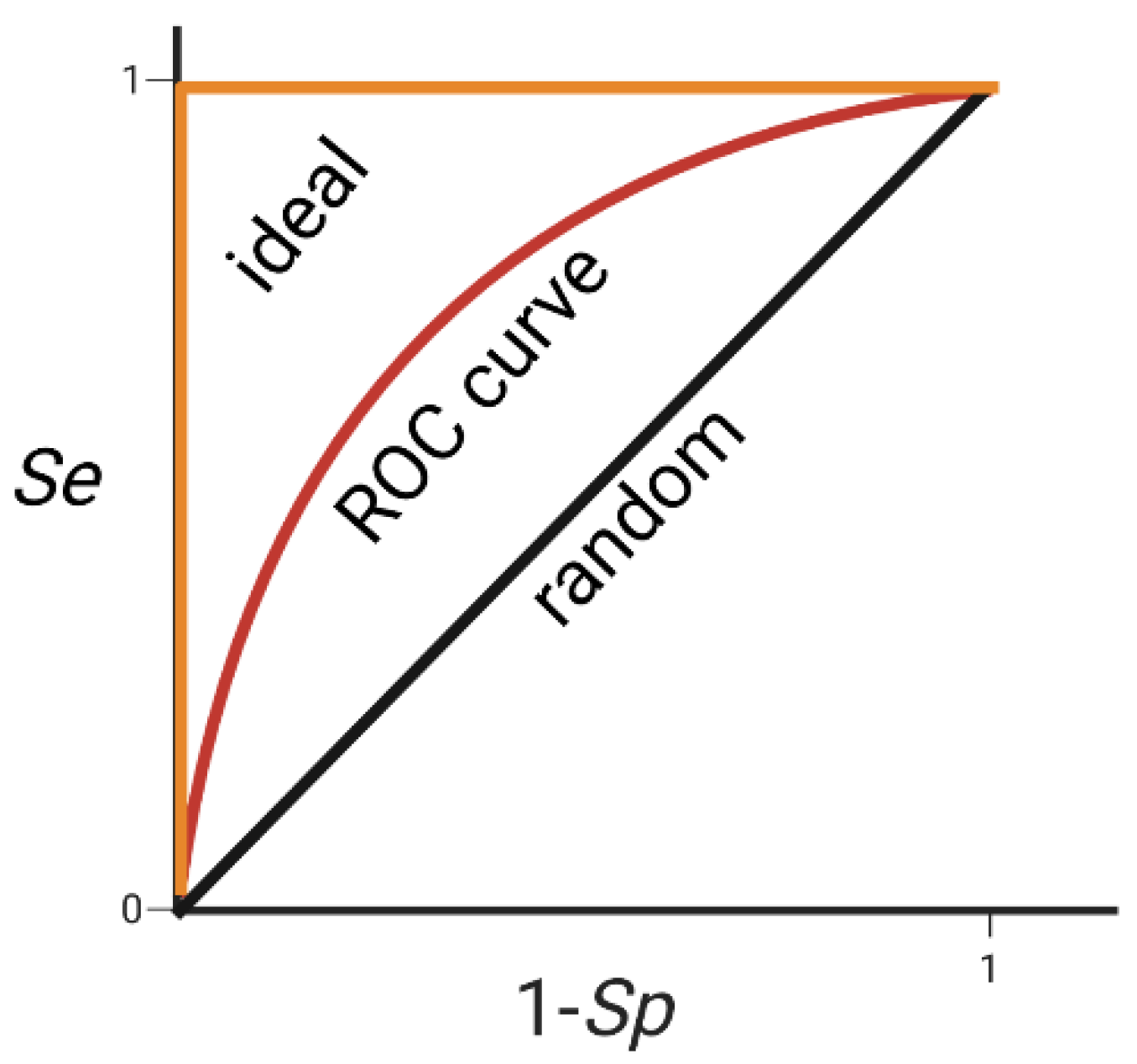
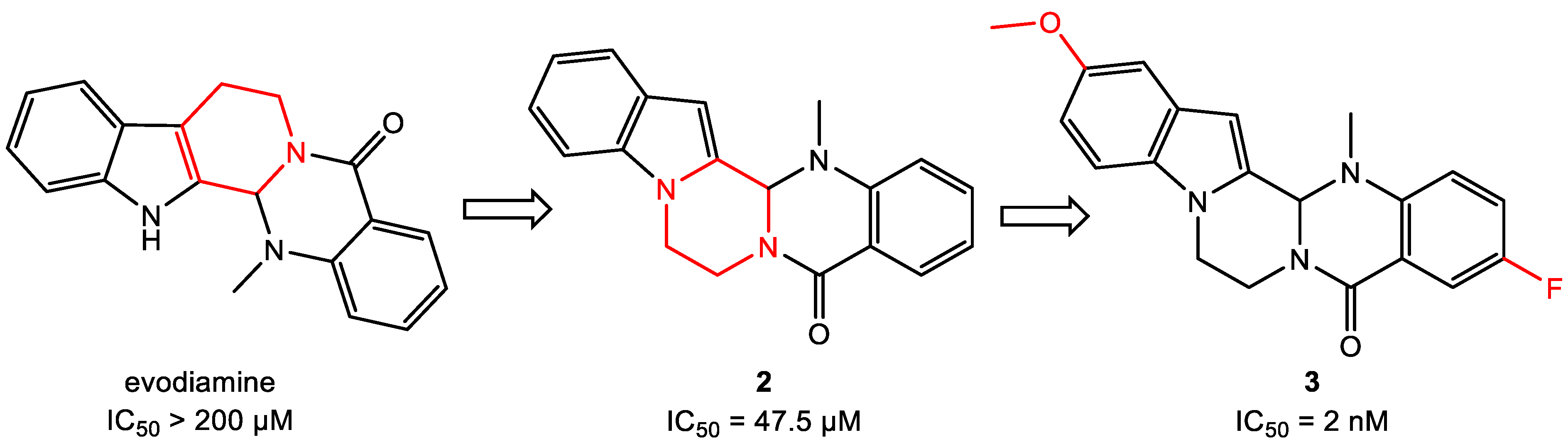
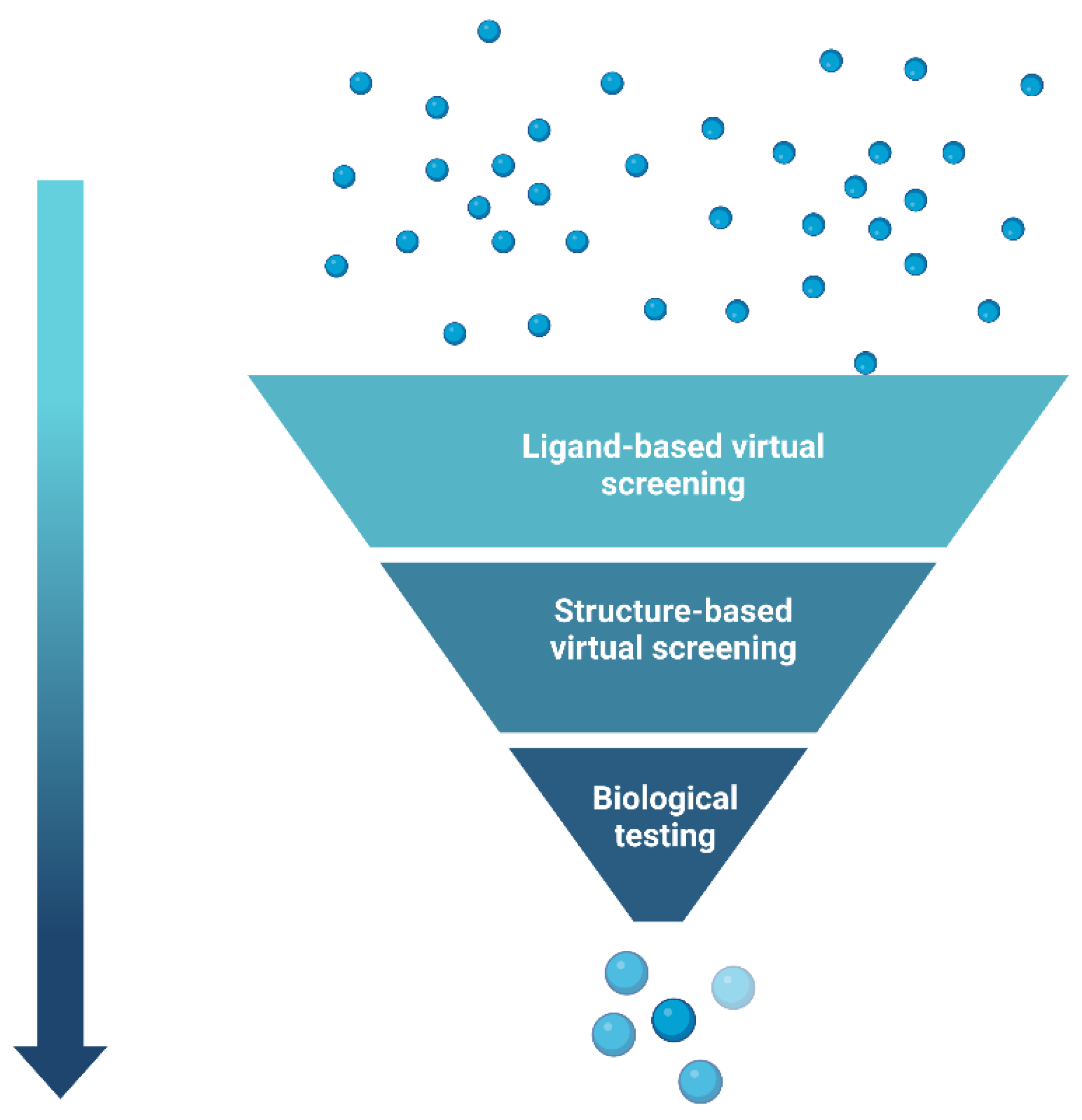

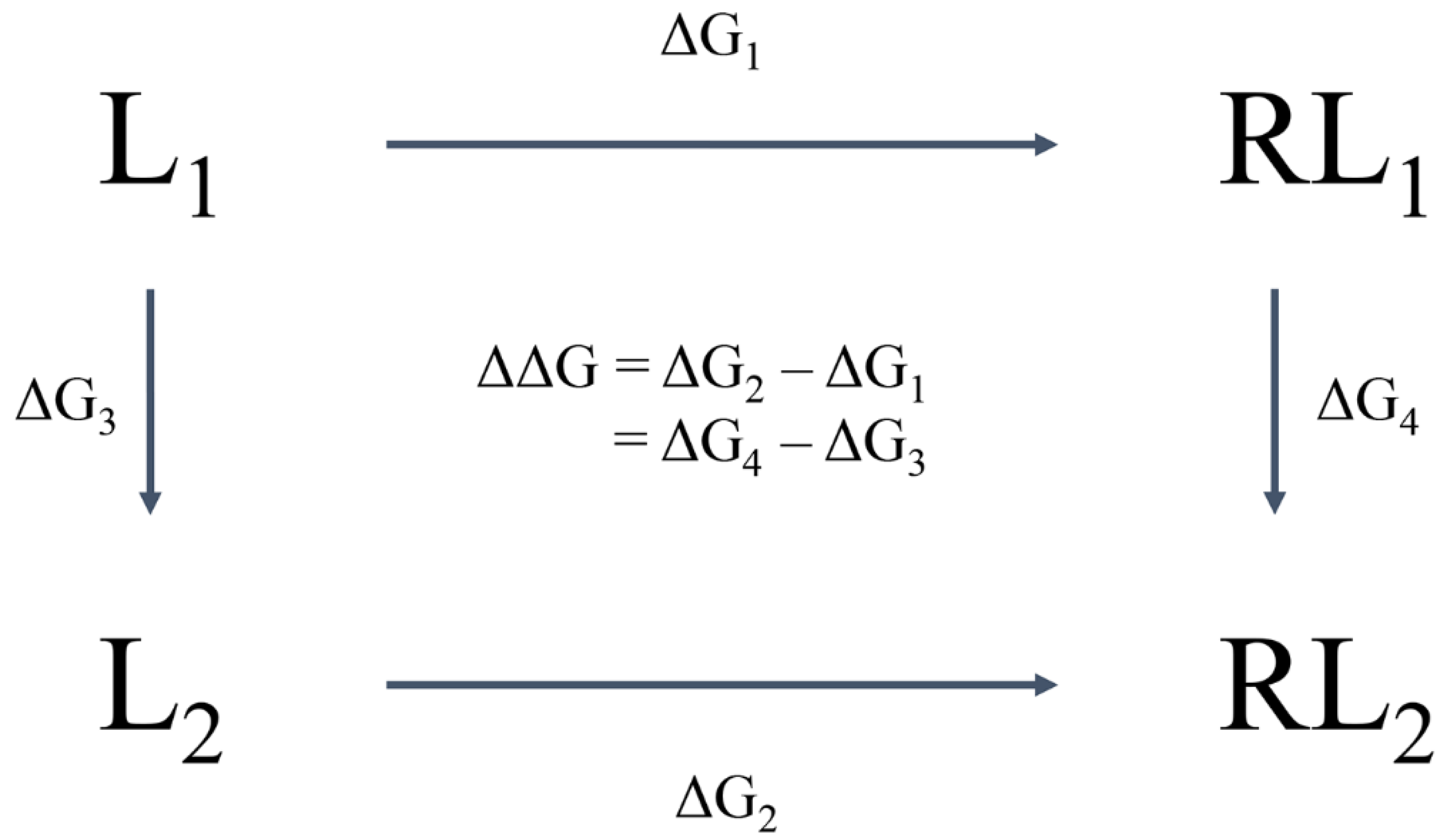
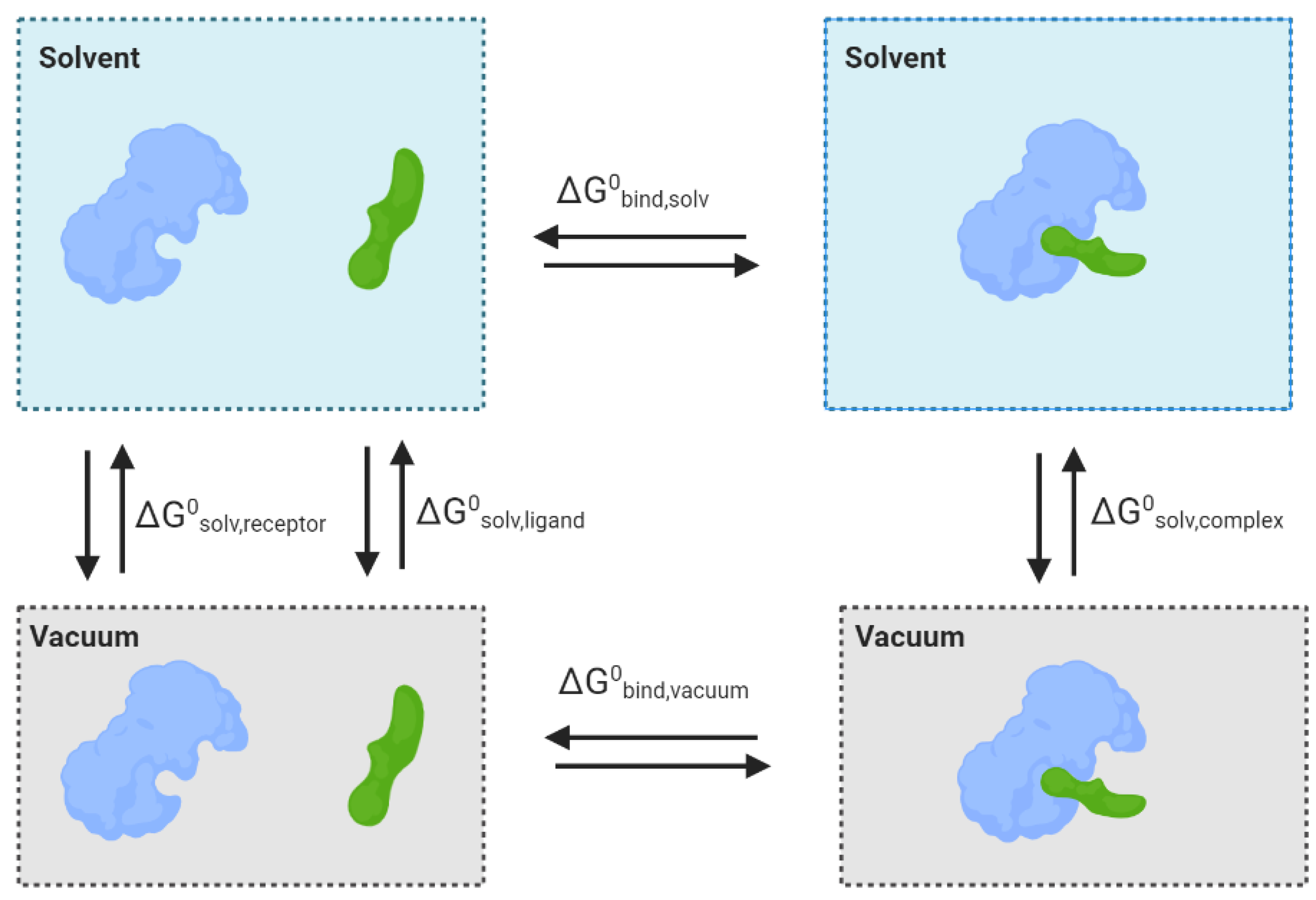
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.; Hawkins, B.A.; Du, J.J.; Groundwater, P.W.; Hibbs, D.E.; Lai, F. A Guide to In Silico Drug Design. Pharmaceutics 2023, 15, 49. https://doi.org/10.3390/pharmaceutics15010049
Chang Y, Hawkins BA, Du JJ, Groundwater PW, Hibbs DE, Lai F. A Guide to In Silico Drug Design. Pharmaceutics. 2023; 15(1):49. https://doi.org/10.3390/pharmaceutics15010049
Chicago/Turabian StyleChang, Yiqun, Bryson A. Hawkins, Jonathan J. Du, Paul W. Groundwater, David E. Hibbs, and Felcia Lai. 2023. "A Guide to In Silico Drug Design" Pharmaceutics 15, no. 1: 49. https://doi.org/10.3390/pharmaceutics15010049
APA StyleChang, Y., Hawkins, B. A., Du, J. J., Groundwater, P. W., Hibbs, D. E., & Lai, F. (2023). A Guide to In Silico Drug Design. Pharmaceutics, 15(1), 49. https://doi.org/10.3390/pharmaceutics15010049