Formation Thermodynamics of Carbamazepine with Benzamide, Para-Hydroxybenzamide and Isonicotinamide Cocrystals: Experimental and Theoretical Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of Multi-Component Crystals
2.2.1. Slurry Experiment
2.2.2. Solution Crystallization
2.3. Solid State Characterizations of CBZ Multi-Component Crystals
2.4. Single Crystal X-ray Diffraction (SCXRD)
2.5. Differential Scanning Calorimetry (DSC)
2.6. Competitive Grinding of Three Component Samples
2.7. Solubility Determination of the Individual Components and Cocrystals
2.8. High-Performance Liquid Chromatography (HPLC)
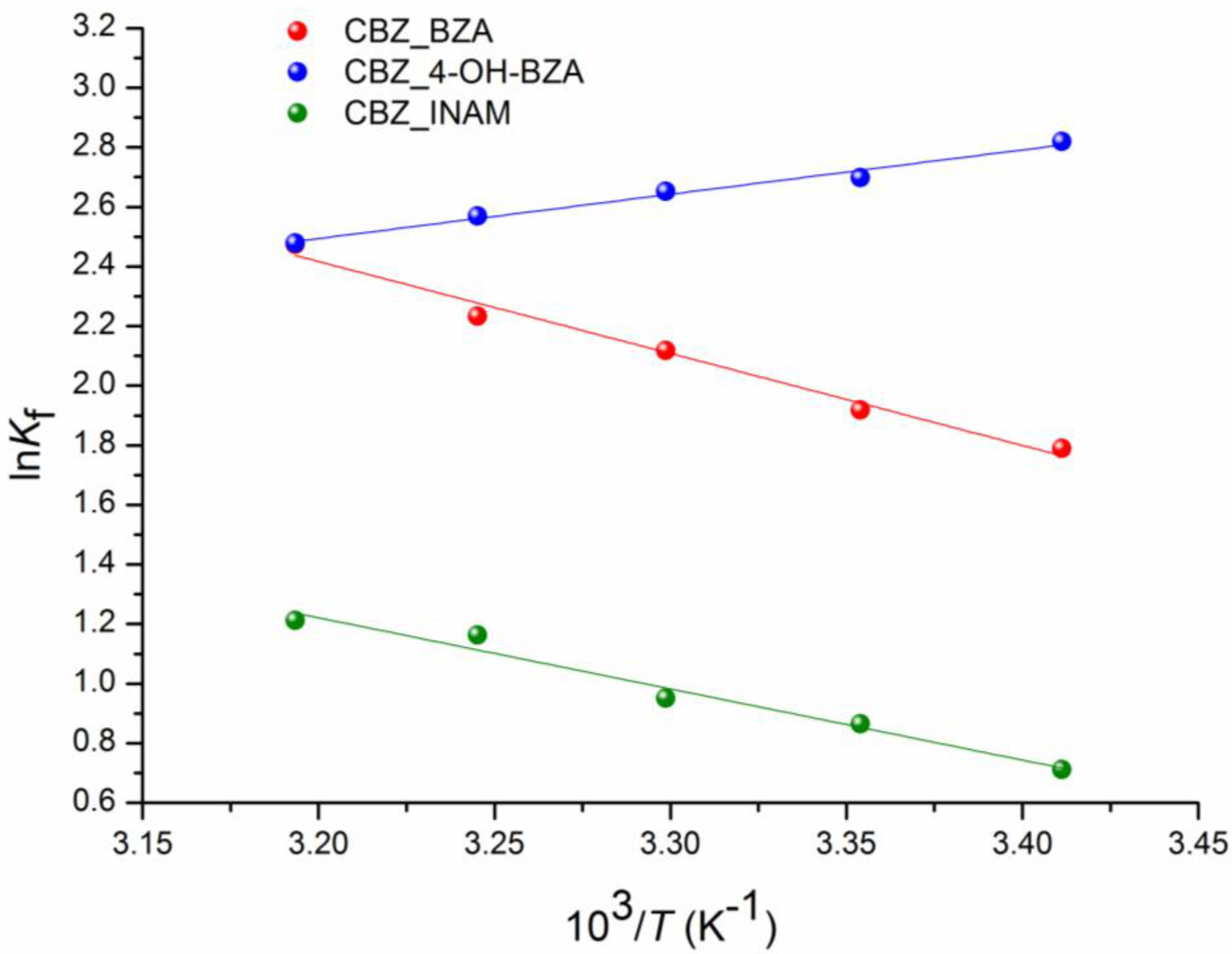
2.9. Thermodynamic Parameters Calculation
2.10. H-Bond Propensity Analysis
3. Results and Discussion
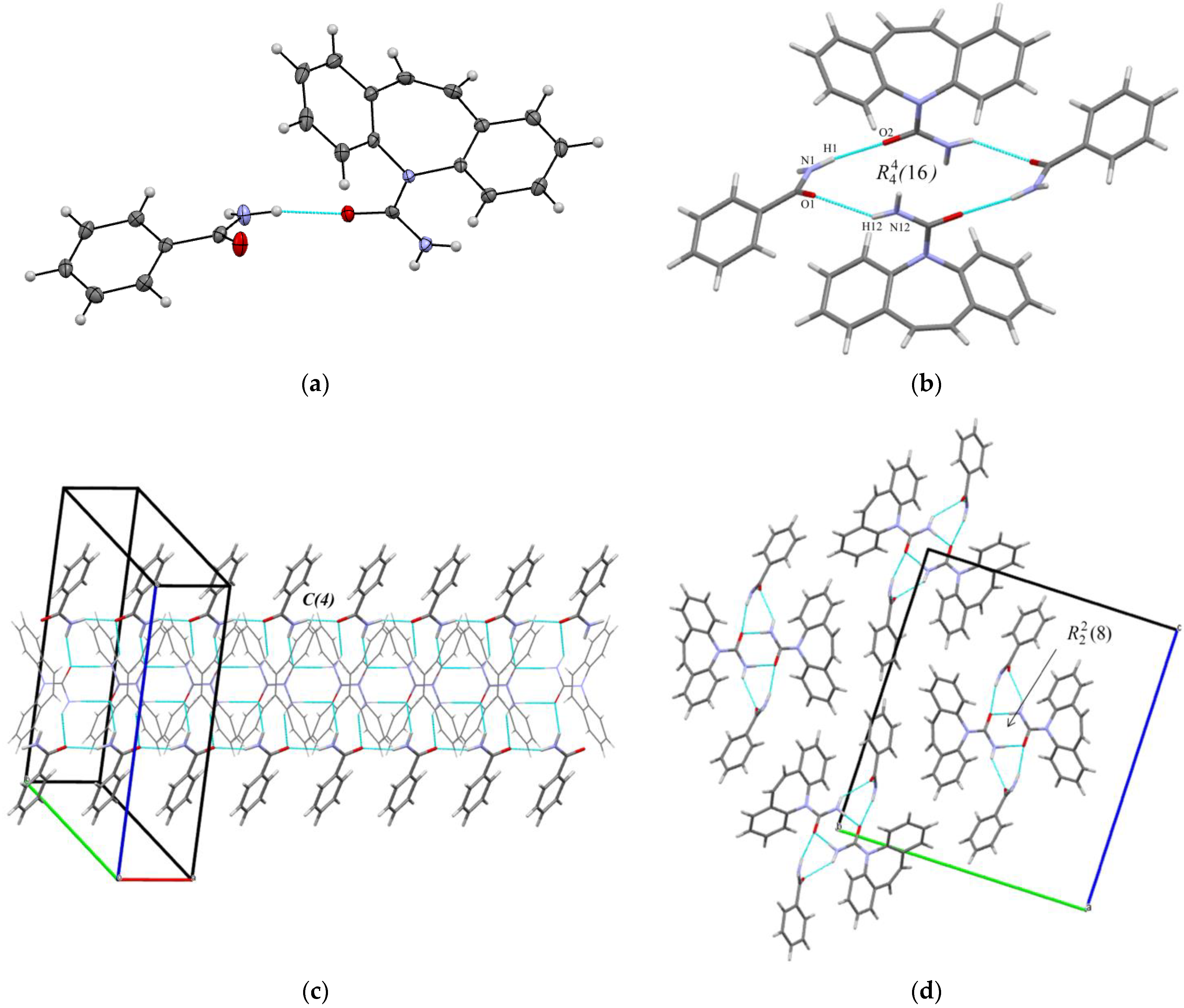
3.1. Crystal Structure Analysis
3.2. Solubility Experiments
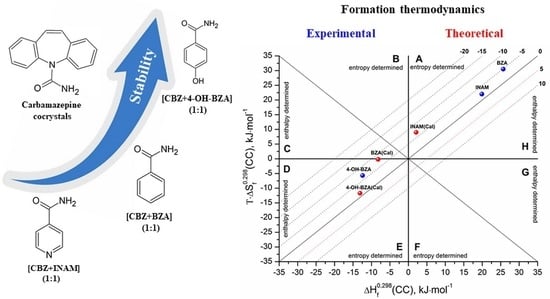
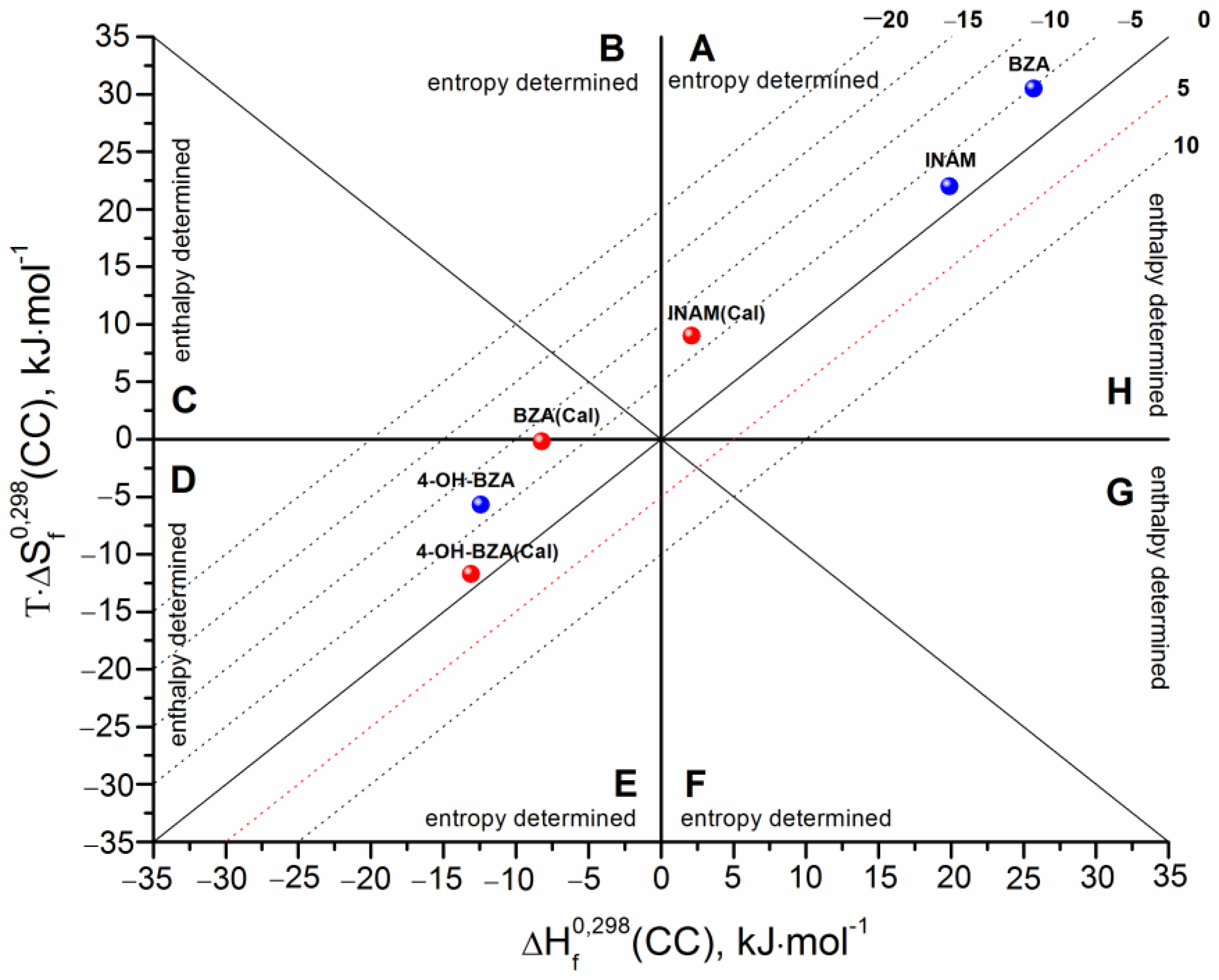
3.3. Cocrystals Formation Thermodynamics
3.4. H-Bond Propensity Analysis
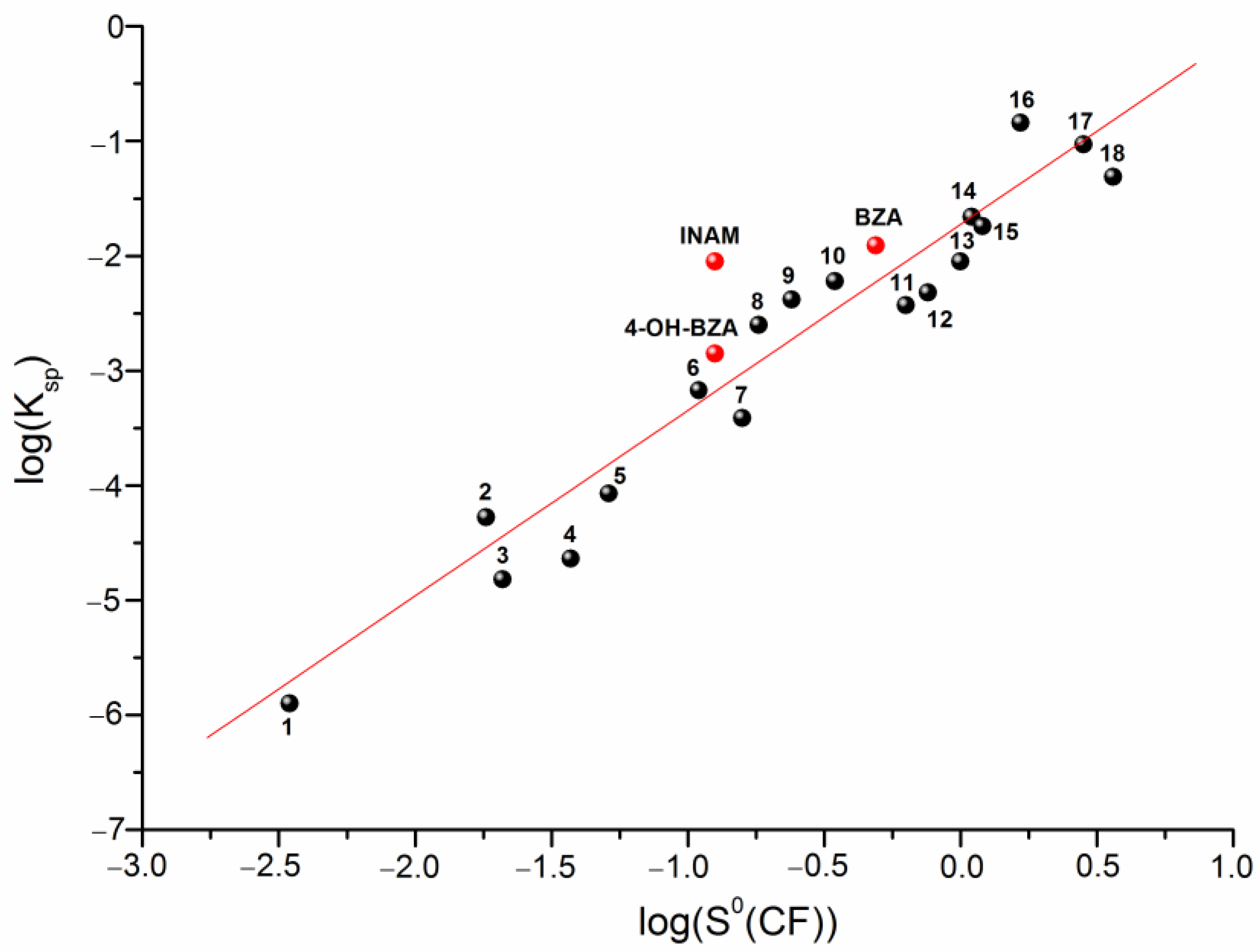
3.5. Competitive Reactions Method
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gadade, D.D.; Sanjay, S.S. Pharmaceutical cocrystals: Regulatory and strategic aspects, design and development. Adv. Pharm. Bull. 2016, 6, 479–494. [Google Scholar] [CrossRef] [PubMed]
- Good, D.J.; Rodríguez-Hornedo, N. Solubility advantage of pharmaceutical cocrystals. Cryst. Growth Des. 2009, 9, 2252–2264. [Google Scholar] [CrossRef]
- Almarsson, ö.; Zaworotko, M.J. Crystal engineering of the composition of pharmaceutical phases. Do pharmaceutical co-crystals represent a new path to improved medicines? Chem. Commun. 2004, 17, 1889–1896. [Google Scholar] [CrossRef] [PubMed]
- Ngilirabanga, J.B.; Samsodien, H. Pharmaceutical co-crystal: An alternative strategy for enhanced physicochemical properties and drug synergy. Nano Select. 2021, 2, 512–526. [Google Scholar] [CrossRef]
- Perlovich, G.L. Thermodynamic characteristics of cocrystal formation and melting points for rational design of pharmaceutical two-component systems. CrystEngComm 2015, 17, 7019–7028. [Google Scholar] [CrossRef]
- Schartman, R.R. On the thermodynamics of cocrystal formation. Int. J. Pharm. 2009, 365, 77–80. [Google Scholar] [CrossRef]
- Contardo-Jara, V.; Lorenz, C.; Pflugmacher, S.; Nützmann, G.; Kloas, W.; Wiegand, C. Exposure to human pharmaceuticals carbamazepine, ibuprofen and bezafibrate causes molecular effects in dreissena polymorpha. Aquat. Toxicol. 2011, 105, 428–437. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, J.; Mao, L.; Li, J.; Yuan, Z.; Bond, P.L.; Guo, J. Antiepileptic drug carbamazepine promotes horizontal transfer of plasmid-borne multi-antibiotic resistance genes within and across bacterial genera. ISME J. 2019, 13, 509–522. [Google Scholar] [CrossRef]
- Porter, W.W.; Elie, S.C.; Matzger, A.J. Polymorphism in carbamazepine cocrystals. Cryst. Growth Des. 2008, 8, 14–16. [Google Scholar] [CrossRef]
- Fu, Q.; Han, Y.; Xie, Y.; Gong, N.; Guo, F. Carbamazepine cocrystals with several aromatic carboxylic acids in different stoichiometries: Structures and solid state characterization. J. Mol. Struct. 2018, 1168, 145–152. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, Y.; Qiao, N.; Chen, Y.; Gao, L. Preparation and Characterization of Carbamazepine Cocrystal in Polymer Solution. Pharmaceutics 2017, 9, 54. [Google Scholar] [CrossRef] [PubMed]
- Drozd, K.V.; Manin, A.N.; Churakov, A.V.; Perlovich, G.L. A novel drug-drug cocrystal of carbamazepine with para-aminosalicylic acid: Screening, crystal structure and comparative study of carbamazepine cocrystals formation thermodynamics. CrystEngComm 2017, 19, 4273–4286. [Google Scholar] [CrossRef]
- Oliveira, M.A.; Peterson, M.L.; Davey, R.J. Relative enthalpy of formation for co-crystals of small organic molecules. Cryst. Growth Des. 2011, 11, 449–457. [Google Scholar] [CrossRef]
- Shayanfar, A.; Velaga, S.; Jouyban, A. Solubility of carbamazepine, nicotinamide and carbamazepine–nicotinamide cocrystal in ethanol–water mixtures. Fluid Phase Equilibria 2014, 363, 97–105. [Google Scholar] [CrossRef]
- Sheldrick, G. SADABS, Program for Scaling and Correction of Area Detector Data; University of Göttingen: Gottingen, Germany, 1997. [Google Scholar]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Kuminek, G.; Cavanagh, K.L.; Rodríguez-Hornedo, N. Measurement and mathematical relationships of cocrystal thermodynamic properties. In Pharmaceutical Crystals: Science and Engineering; Li, T.L., Mattei, A., Eds.; John Wiley & Sons Inc.: New York, NY, USA, 2018; pp. 234–271. [Google Scholar]
- Galek, P.T.A.; Allen, F.H.; Fábián, L.; Feeder, N. Knowledge-based H-bond prediction to aid experimental polymorph screening. CrystEngComm 2009, 11, 2634–2639. [Google Scholar] [CrossRef]
- Delori, A.; Galek, P.T.A.; Pidcock, E.; Patni, M.; Jones, W. Knowledge-based hydrogen bond prediction and the synthesis of salts and cocrystals of the anti-malarial drug pyrimethamine with various drug and GRAS molecules. CrystEngComm 2013, 15, 2916–2928. [Google Scholar] [CrossRef]
- Galek, P.T.A.; Fábián, L.; Allen, F.H. Universal prediction of intramolecular hydrogen bonds in organic crystals. Acta Cryst. 2010, 66, 237–252. [Google Scholar] [CrossRef]
- Macrae, C.F.; Bruno, I.J.; Chisholm, J.A.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Rodriguez-Monge, L.; Taylor, R.; van de Streek, J.; Wood, P.A. Mercury CSD 2.0—new features for the visualization and investigation of crystal structures. J. Appl. Cryst. 2008, 41, 466–470. [Google Scholar] [CrossRef]
- Wood, P.A.; Feeder, N.; Furlow, M.; Galek, P.T.A.; Groom, C.R.; Pidcock, E. Knowledge-based approaches to co-crystal design. CrystEngComm 2014, 16, 5839–5848. [Google Scholar] [CrossRef]
- Galek, P.T.A.; Chisholm, J.A.; Pidcock, E.; Wood, P.A. Hydrogen-bond coordination in organic crystal structures: Statistics, predictions and applications. Acta Cryst. 2014, 70, 91–105. [Google Scholar] [CrossRef] [PubMed]
- Majumder, M.; Buckton, G.; Rawlinson-Malone, C.F.; Williams, A.C.; Spillman, M.J.; Pidcocke, E.; Shankland, K. Application of hydrogen-bond propensity calculations to an indomethacin–nicotinamide (1:1) co-crystal. CrystEngComm 2013, 15, 4041–4044. [Google Scholar] [CrossRef]
- Sathisaran, I.; Dalvi, S.V. Cocrystallization of carbamazepine with amides: Cocrystal and eutectic phases with improved dissolution. J. Mol. Struct. 2019, 1193, 398–415. [Google Scholar] [CrossRef]
- Ter Horst, J.H.; Cains, P.W. Co-crystal polymorphs from a solvent-mediated transformation. Cryst. Growth Des. 2008, 8, 2537–2542. [Google Scholar] [CrossRef]
- Ter Horst, J.H.; Deij, M.A.; Cain, P.W. Discovering new co-crystals. Cryst. Growth Des. 2009, 9, 1531–1537. [Google Scholar] [CrossRef]
- Grzesiak, A.L.; Lang, M.; Kim, K.; Matzger, A.J. Comparison of the four anhydrous Polymorphs of carbamazepine and the crystal structure of form I. J. Pharm. Sci. 2003, 92, 2260–2271. [Google Scholar] [CrossRef]
- Avdeef, A. Cocrystal solubility product prediction using an in combo model and simulations to improve design of experiments. Pharm. Res. 2018, 35, 40. [Google Scholar] [CrossRef]
- Surov, A.O.; Manin, A.N.; Voronin, A.P.; Boycov, D.E.; Magdysyuk, O.V.; Perlovich, G.L. New pharmaceutical cocrystal forms of flurbiprofen: Structural, physicochemical, and thermodynamic characterization. Cryst. Growth Des. 2019, 19, 5751–5761. [Google Scholar] [CrossRef]
- Perlovich, G.L. Prediction of solubility of two-component molecular crystals. CrystEngComm 2022, 24, 2217–2220. [Google Scholar] [CrossRef]
- Perlovich, G.L.; Raevsky, O.A. Sublimation of molecular crystals: Prediction of sublimation functions on the basis of HYBOT physicochemical descriptors and structural clusterization. Cryst. Growth Des. 2010, 10, 2707–2712. [Google Scholar] [CrossRef]
- Perlovich, G.L.; Kurkov, S.V.; Kinchin, A.N.; Bauer-Brandl, A. Thermodynamics of solutions III: Comparison of the solvation of (+)-naproxen with other NSAIDs. Eur. J. Pharm. Biopharm. 2004, 57, 411–420. [Google Scholar] [CrossRef] [PubMed]
- Habgood, M.; Deij, M.A.; Mazurek, J.; Price, S.L.; ter Horst, J.H. Carbamazepine co-crystallization with pyridine carboxamides: Rationalization by complementary phase diagrams and crystal energy landscapes. Cryst. Growth Des. 2010, 10, 903–912. [Google Scholar] [CrossRef]
- Sarkar, N.; Aakerӧy, C.B. Evaluating hydrogen-bond propensity, hydrogen-bond coordination and hydrogen-bond energy as tools for predicting the outcome of attempted co-crystallisations. Supramol. Chem. 2020, 32, 81–90. [Google Scholar] [CrossRef]
- Sarkar, N.; Gonnella, N.C.; Krawiec, M.; Xin, D.; Aakeröy, C.B. Evaluating the predictive abilities of protocols based on hydrogen-bond propensity, molecular complementarity, and hydrogen-bond energy for cocrystal screening. Cryst. Growth Des. 2020, 20, 7320–7327. [Google Scholar] [CrossRef]
- Fischer, F.; Lubjuhn, D.; Greiser, S.; Rademann, K.; Emmerling, F. Supply and demand in the ball mill: Competitive cocrystal reactions. Cryst. Growth Des. 2016, 16, 5843–5851. [Google Scholar] [CrossRef]
- Fischer, F.; Joester, M.; Rademann, K.; Emmerling, F. Survival of the fittest: Competitive co-crystal reactions in the ball mill. Chem. Eur. J. 2015, 21, 14969–14974. [Google Scholar] [CrossRef]
- Shayanfar, A.; Asadpour-Zeynali, K.; Jouyban, A. Solubility and dissolution rate of a carbamazepine–cinnamic acid cocrystal. J. Mol. Liq. 2013, 178, 171–176. [Google Scholar] [CrossRef]
- Huang, D.; Chan, H.C.S.; Wu, Y.; Li, L.; Zhang, L.; Lv, Y.; Yang, X.; Zhou, Z. Phase solubility investigation and theoretical calculations on drug-drug cocrystals of carbamazepine with Emodin, Paeonol. J. Mol. Liq. 2021, 329, 115604. [Google Scholar] [CrossRef]

| Chemical Formula | C15H12N2O·C7H7NO |
|---|---|
| Formula weight | 357.40 |
| Crystal system | Monoclinic |
| Space group | P21/n |
| Crystal size | 0.18 × 0.03 × 0.02 |
| Temperature, K | 100(2) |
| a, Å | 5.0522(2) |
| b, Å | 17.6934(8) |
| c, Å | 19.9582(7) |
| β, º | 90.3848(16) |
| Volume, Å3 | 1784.04(12) |
| Calc. density, g·cm−3 | 1.331 |
| Z | 4 |
| Total reflections | 15,579 |
| Independent reflections | 3901 |
| Rint | 0.0417 |
| R1 (all data) | 0.0662 |
| wR2 (all data) | 0.1043 |
| R1[I > 2σ(I)] | 0.0491 |
| wR2[I > 2σ(I)] | 0.0980 |
| GOF | 1.069 |
| CCDC no. | 2196018 |
| Cocrystal | 5 | ||||||
|---|---|---|---|---|---|---|---|
| 1 [CBZ + BZA] (1:1) | −4.8 ± 0.3 | 25.7 ± 1.9 | 30.5 ± 2.9 | −8.0 | −8.2 | −0.2 | 6.2 |
| 2 [CBZ + 4-OH-BZA] (1:1) | −6.7 ± 0.5 | −12.4 ± 0.9 | −5.7 ± 0.5 | −1.5 | −13.1 | −11.7 | −19.0 |
| 3 [CBZ + INAM] (1:1) | −2.1 ± 0.1 | 19.9 ± 1.9 | 22.0 ± 2.5 | −7.0 | 2.1 | 9.0 | 6.1 |
| 4 [CBZ + Saccharin] (1:1) | −4.6 ± 0.1 | −5.9 ± 0.9 | −1.3 ± 0.3 | 0.4 | 3.5 | 3.1 | −2.5 |
| [CBZ + BZA] (1:1) | [CBZ + 4-OH-BZA] (1:1) | [CBZ + INAM] (1:1) | |
|---|---|---|---|
| MC score (HBP) | 0.08 | 0.07 | −0.05 |
| (intHBP) | −0.03 | 0.08 | −0.09 |
| εHBP | 0.19 | 1.06 | −0.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manin, A.N.; Boycov, D.E.; Simonova, O.R.; Volkova, T.V.; Churakov, A.V.; Perlovich, G.L. Formation Thermodynamics of Carbamazepine with Benzamide, Para-Hydroxybenzamide and Isonicotinamide Cocrystals: Experimental and Theoretical Study. Pharmaceutics 2022, 14, 1881. https://doi.org/10.3390/pharmaceutics14091881
Manin AN, Boycov DE, Simonova OR, Volkova TV, Churakov AV, Perlovich GL. Formation Thermodynamics of Carbamazepine with Benzamide, Para-Hydroxybenzamide and Isonicotinamide Cocrystals: Experimental and Theoretical Study. Pharmaceutics. 2022; 14(9):1881. https://doi.org/10.3390/pharmaceutics14091881
Chicago/Turabian StyleManin, Alex N., Denis E. Boycov, Olga R. Simonova, Tatyana V. Volkova, Andrei V. Churakov, and German L. Perlovich. 2022. "Formation Thermodynamics of Carbamazepine with Benzamide, Para-Hydroxybenzamide and Isonicotinamide Cocrystals: Experimental and Theoretical Study" Pharmaceutics 14, no. 9: 1881. https://doi.org/10.3390/pharmaceutics14091881
APA StyleManin, A. N., Boycov, D. E., Simonova, O. R., Volkova, T. V., Churakov, A. V., & Perlovich, G. L. (2022). Formation Thermodynamics of Carbamazepine with Benzamide, Para-Hydroxybenzamide and Isonicotinamide Cocrystals: Experimental and Theoretical Study. Pharmaceutics, 14(9), 1881. https://doi.org/10.3390/pharmaceutics14091881