Machine Learning and Pharmacometrics for Prediction of Pharmacokinetic Data: Differences, Similarities and Challenges Illustrated with Rifampicin
Abstract
:1. Introduction
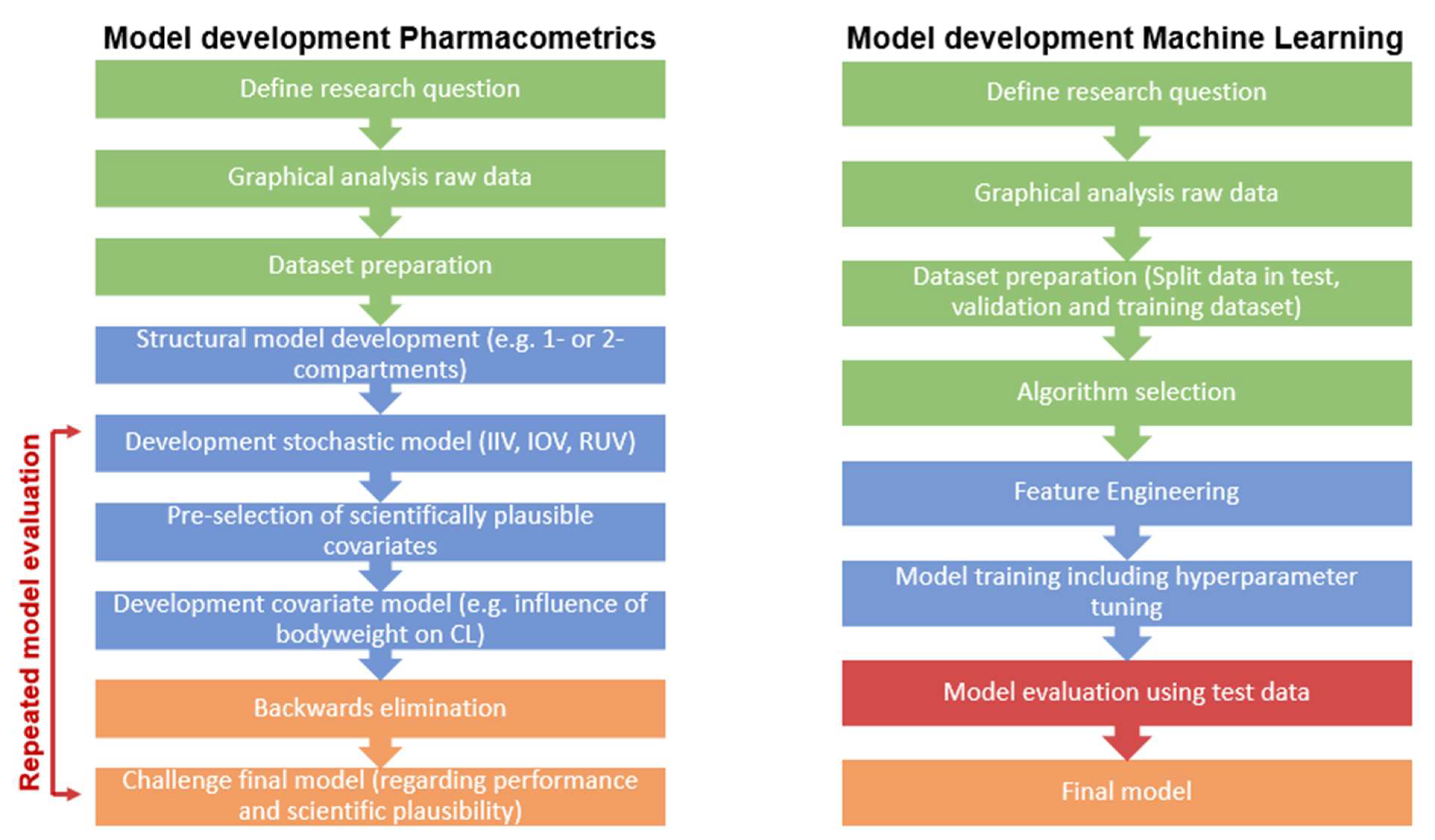
1.1. Pharmacometrics and Machine Learning
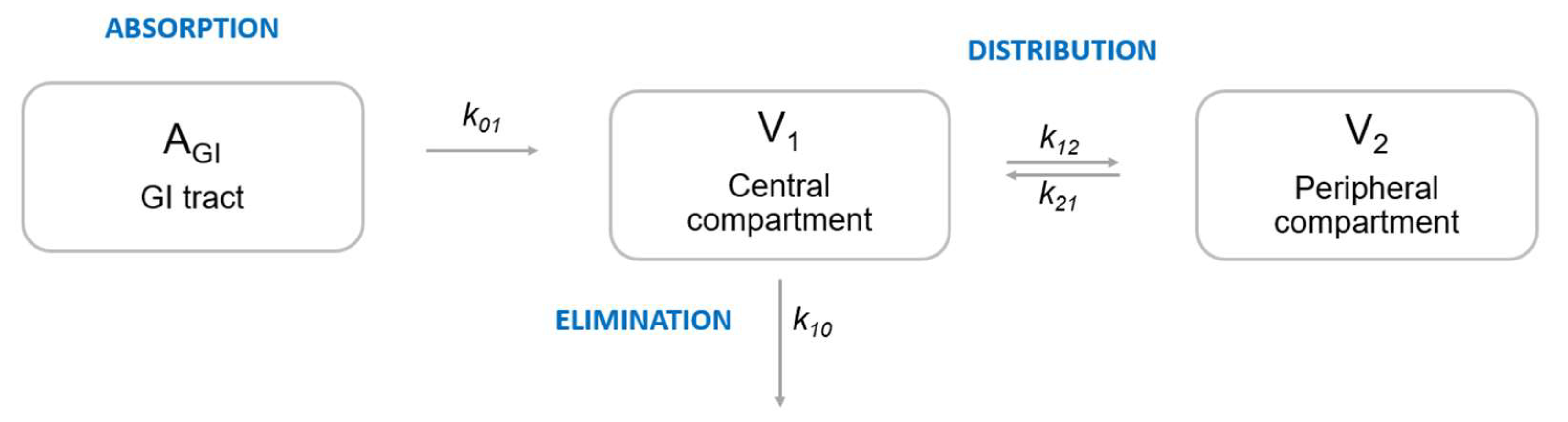
1.1.1. Pharmacometrics
1.1.2. Machine Learning
1.1.3. Terminology
| Term | Description | |
|---|---|---|
| PM | ML | |
| Covariates | Features | Both terms describe predictors. Features are all input variables used to train a model. Covariates are predictors explaining variability between patients in addition to the variables already included in the structural pharmacometrics model. |
| Objective function value (OFV) | Loss | The OFV is one of the main metrics for model evaluation in pharmacometrics model building. It is proportional to −2*log likelihood that the model parameter values occur from the data [37,38]. In ML, the loss is used as a goodness of fit. It represents the distance between predictions and observations which can be computed in different ways, such as L1, L2 or MAPE. |
| Build/Fit a model | Train a model | Both terms define the process of developing a model by determining model parameters that describe the input data in order to reach a predefined objective. |
| Validation dataset | Validation dataset | In PM, the term validation dataset is often used for external validation. In ML, the term is commonly used for the data that are held back for internal validation to evaluate model performance during training. |
| Overparameterization | Overfitting | In PM, a model can be overparameterized, meaning too many parameters are estimated in relation to the amount of information, leading to minimization issues. Overfitting in ML describes a phenomenon where the model has been trained to fit the training data too well. The model is forced to predict in a very narrow direction, which may result in poor predictive ability. |
| Model parameters | Model parameters | Even though both communities use the same term, model parameters in PM are different from parameters in ML. Model parameters in PM describe biological or pharmacological processes, such as drug clearance, drug distribution volume or rate of absorption. These parameters are directly interpretable. In ML, on the other hand, model parameters are mathematical parameters learnt during the model training process and are part of the final model describing the data. They do not provide biological interpretation in the first instance at least. |
| Model averaging | Ensemble model | An ensemble model combines multiple ML algorithms, which in most cases leads to better predictive performance compared to single algorithms [60]. There is a similar method used in PM called model averaging [61], where several models are combined using weights determined by their individual fit to the data. |
| Shrinkage | Shrinkage | The term “shrinkage” has a different meaning in the PM and ML communities. In PM, shrinkage describes overparameterization, where 0 indicates very informative data and no overfit, and 1 uninformative data and overfitting. In ML, shrinkage methods in different ML models reduce the possibility of overfitting or underfitting by providing a trade-off between bias and variance. |
| Bootstrapping | Bootstrapping | Describes a random resampling method with replacement. In PM, it is used during model development and evaluation for estimation of the model performance. In ML, bootstrapping is part of some algorithms, such as XGBoost or Random Forest, and is also used to estimate the model’s predictive performance. |
| Cross-validation | Cross-validation | In PM, cross-validation is used occasionally, for example, in covariate selection procedures in order to assess the true alpha error. In ML, cross-validation is commonly applied to prevent overfitting and to obtain robust predictions. Cross-validation describes the process of splitting the data into a training dataset and a test dataset. The training dataset is used for model development and the test dataset for external model evaluation. In n-fold cross-validation, the data are split into n non-overlapping subsets, where n − 1 subsets are used for training and the left-out subset for evaluation. This procedure is repeated until all subsets have been used for model evaluation. Model performance is then computed across all test sets [45]. |
| - | Holdout/test dataset | Describes the test/unseen dataset used for external validation. It is of great importance that the holdout/test data is not used for model training or hyperparameter tuning in order not to overestimate the model’s predictive performance [45]. |
| - | Oversampling/Upsampling | Oversampling is an approach used to deal with highly imbalanced data. Data in areas with sparse data are resampled or synthesized using different methods, for example, Synthetic Minority Oversampling Technique (SMOTE) [62]. |
| Empirical Bayes Estimates (EBEs) | Bayesian optimization | EBEs in PM are the model parameter estimates for an individual, estimated based on the final model parameters as well as observed data using Bayesian estimation [63]. In artificial intelligence (AI), Bayesian optimization is used to tune artificial neural networks (ANNs), particularly in deep learning. |
| Typical value | Typical value | The typical value in PM is the most likely parameter estimate for the whole population given a set of covariates. It could, e.g., be the drug clearance estimate that best summarizes the clearance of the whole population. In ML, the typical value in unsupervised learning, for example, is the center of a cluster (e.g., k-means). |
| Inter-individual variability (IIV) | - | Variability between individuals in a population. Describes the difference between typical and individual PK parameters. Often assumed to be log-normally distributed. |
| Inter-occasion variability (IOV) | - | Variability within an individual on different occasions (e.g., sampling or dosing occasions). Often assumed to be log-normally distributed. |
| Residual error variability (RUV) | - | Remaining random unexplained variability. Describes the difference between individual prediction and observed value. |
| Population prediction | - | The population prediction is the most likely representation of the population given a set of covariates. |
| Individual prediction | - | Predictions for an individual using the population estimates in combination with the observed data for this individual, computed in a Bayesian posthoc step. |
2. Materials and Methods
2.1. Data
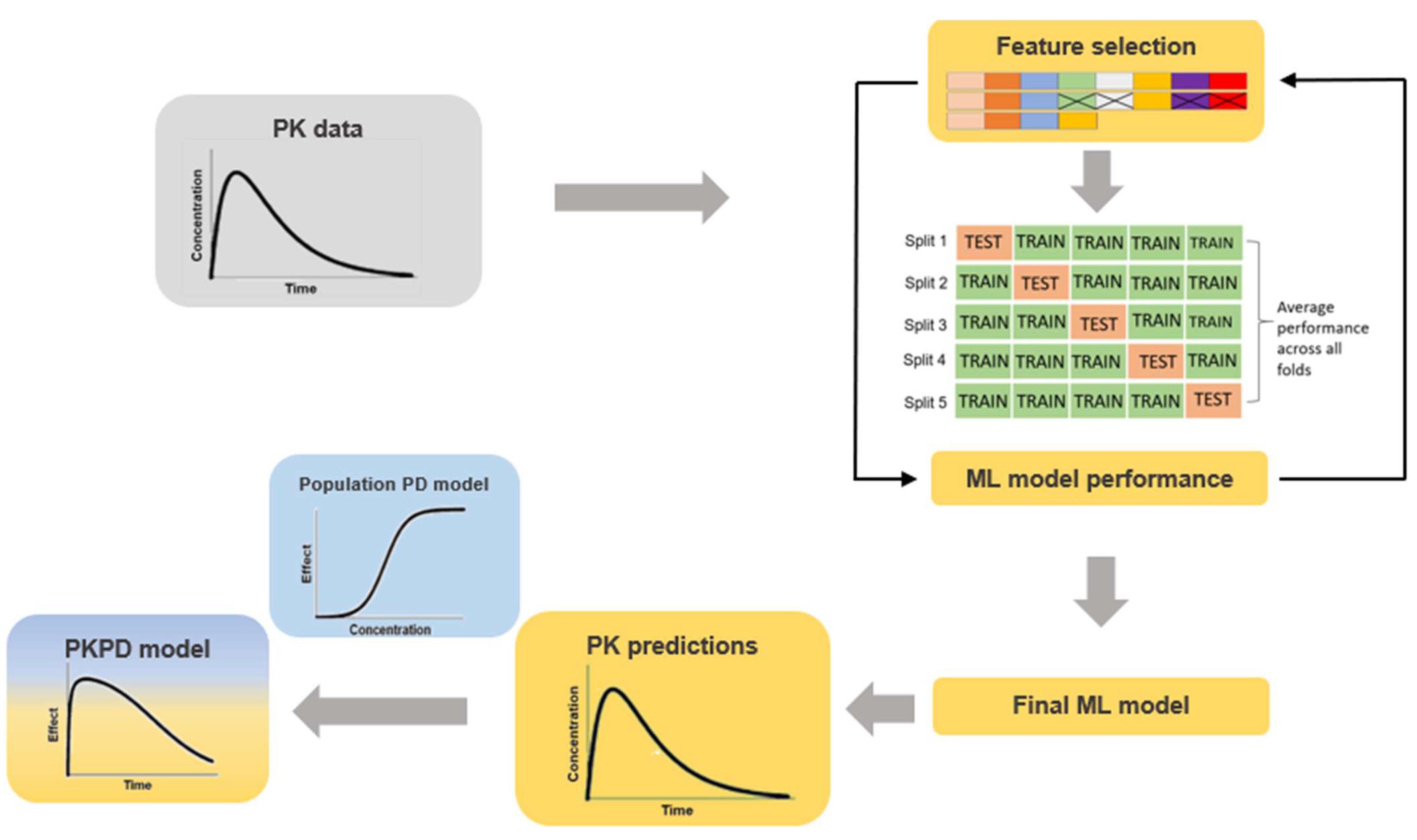
2.2. ML Model Training
2.3. Feature Ranking
2.4. PK Predictions
2.5. Model Evaluation
2.6. Software
3. Results
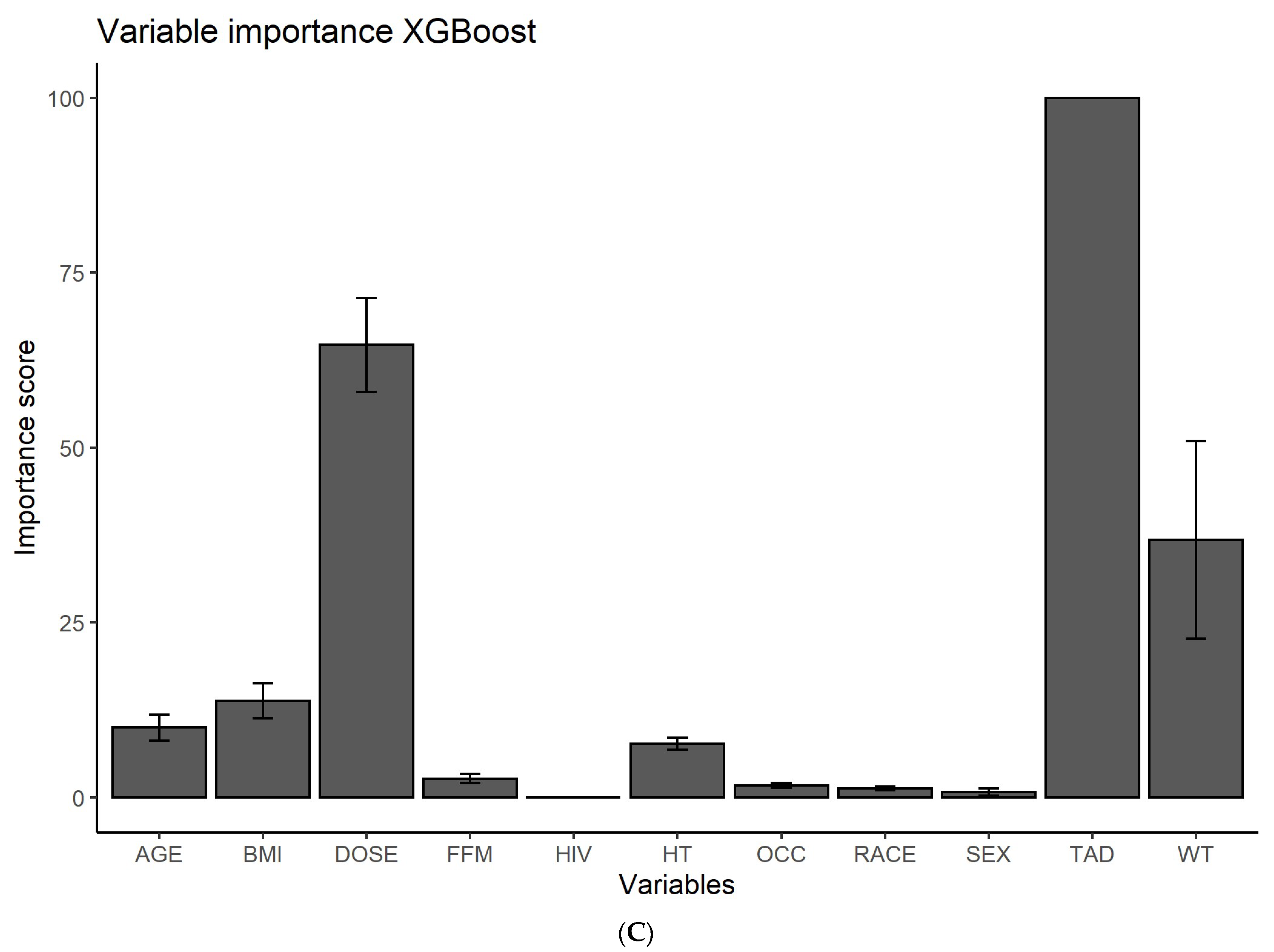
3.1. Feature Ranking
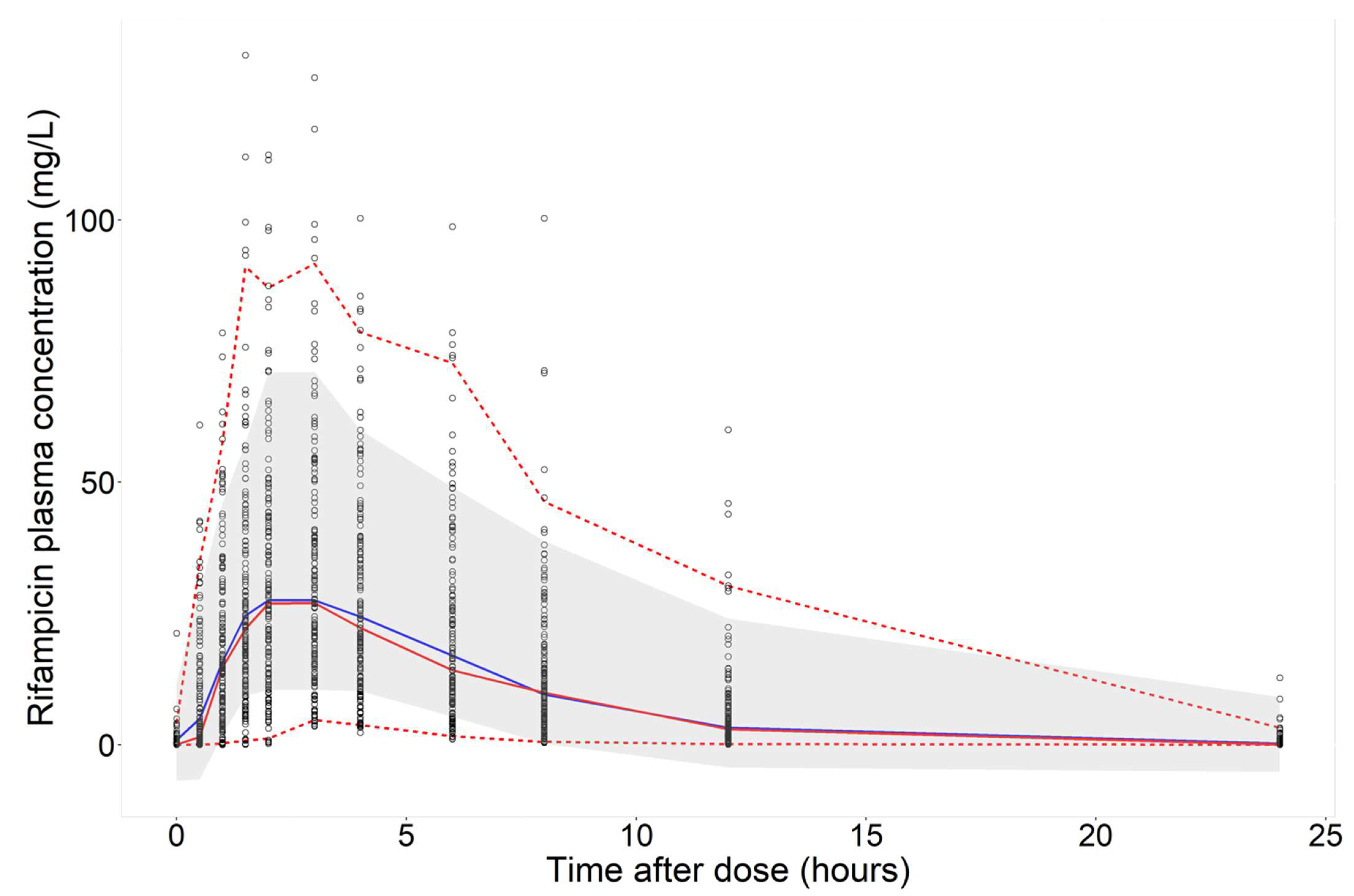
3.2. Predictions of Rifampicin Plasma Concentration over Time
3.3. Predictions of Rifampicin AUC0–24h
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Upton, R.N.; Mould, D.R. Basic Concepts in Population Modeling, Simulation, and Model-Based Drug Development: Part 3—Introduction to Pharmacodynamic Modeling Methods. CPT Pharmacomet. Syst. Pharmacol. 2014, 3, e88. [Google Scholar] [CrossRef] [PubMed]
- Meibohm, B.; Derendorf, H. Basic concepts of pharmacokinetic/pharmacodynamic (PK/PD) modelling. Int. J. Clin. Pharmacol. Ther. 1997, 35, 401–413. [Google Scholar] [PubMed]
- Réda, C.; Kaufmann, E.; Delahaye-Duriez, A. Machine learning applications in drug development. Comput. Struct. Biotechnol. J. 2020, 18, 241–252. [Google Scholar] [CrossRef] [PubMed]
- McComb, M.; Bies, R.; Ramanathan, M. Machine learning in pharmacometrics: Opportunities and challenges. Br. J. Clin. Pharmacol. 2021, 88, 1482–1499. [Google Scholar] [CrossRef] [PubMed]
- Poynton, M.R.; Choi, B.; Kim, Y.; Park, I.; Noh, G.; Hong, S.; Boo, Y.; Kang, S. Machine Learning Methods Applied to Pharmacokinetic Modelling of Remifentanil in Healthy Volunteers: A Multi-Method Comparison. J. Int. Med. Res. 2009, 37, 1680–1691. [Google Scholar] [CrossRef]
- Woillard, J.-B.; Labriffe, M.; Prémaud, A.; Marquet, P. Estimation of drug exposure by machine learning based on simulations from published pharmacokinetic models: The example of tacrolimus. Pharmacol. Res. 2021, 167, 105578. [Google Scholar] [CrossRef]
- Woillard, J.; Labriffe, M.; Debord, J.; Marquet, P. Tacrolimus Exposure Prediction Using Machine Learning. Clin. Pharmacol. Ther. 2020, 110, 361–369. [Google Scholar] [CrossRef]
- Koch, G.; Pfister, M.; Daunhawer, I.; Wilbaux, M.; Wellmann, S.; Vogt, J.E. Pharmacometrics and Machine Learning Partner to Advance Clinical Data Analysis. Clin. Pharmacol. Ther. 2020, 107, 926–933. [Google Scholar] [CrossRef] [Green Version]
- Bies, R.R.; Muldoon, M.F.; Pollock, B.G.; Manuck, S.; Smith, G.; Sale, M.E. A Genetic Algorithm-Based, Hybrid Machine Learning Approach to Model Selection. J. Pharmacokinet. Pharmacodyn. 2006, 33, 195–221. [Google Scholar] [CrossRef]
- Sherer, E.A.; Sale, M.E.; Pollock, B.G.; Belani, C.; Egorin, M.J.; Ivy, P.S.; Lieberman, J.A.; Manuck, S.B.; Marder, S.R.; Muldoon, M.F.; et al. Application of a single-objective, hybrid genetic algorithm approach to pharmacokinetic model building. J. Pharmacokinet. Pharmacodyn. 2012, 39, 393–414. [Google Scholar] [CrossRef] [Green Version]
- Janssen, A.; Leebeek, F.; Cnossen, M.; Mathôt, R. The Neural Mixed Effects Algorithm: Leveraging Machine Learning for Pharmacokinetic Modelling. Available online: https://www.page-meeting.org/print_abstract.asp?abstract_id=9826 (accessed on 21 March 2022).
- Lu, J.; Bender, B.; Jin, J.Y.; Guan, Y. Deep learning prediction of patient response time course from early data via neural-pharmacokinetic/pharmacodynamic modelling. Nat. Mach. Intell. 2021, 3, 696–704. [Google Scholar] [CrossRef]
- World Health Organization. Guidelines for Treatment of Drug-Susceptible Tuberculosis and Patient Care; World Health Organization: Geneva, Switzerland, 2017. [Google Scholar]
- Smythe, W.; Khandelwal, A.; Merle, C.; Rustomjee, R.; Gninafon, M.; Lo, M.B.; Sow, O.B.; Olliaro, P.L.; Lienhardt, C.; Horton, J.; et al. A Semimechanistic Pharmacokinetic-Enzyme Turnover Model for Rifampin Autoinduction in Adult Tuberculosis Patients. Antimicrob. Agents Chemother. 2012, 56, 2091–2098. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Svensson, R.J.; Aarnoutse, R.E.; Diacon, A.H.; Dawson, R.; Gillespie, S.; Boeree, M.J.; Simonsson, U.S.H. A Population Pharmacokinetic Model Incorporating Saturable Pharmacokinetics and Autoinduction for High Rifampicin Doses. Clin. Pharmacol. Ther. 2017, 103, 674–683. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chirehwa, M.T.; Rustomjee, R.; Mthiyane, T.; Onyebujoh, P.; Smith, P.; McIlleron, H.; Denti, P. Model-Based Evaluation of Higher Doses of Rifampin Using a Semimechanistic Model Incorporating Autoinduction and Saturation of Hepatic Extraction. Antimicrob. Agents Chemother. 2016, 60, 487–494. [Google Scholar] [CrossRef] [Green Version]
- Keutzer, L.; Simonsson, U.S.H. Individualized Dosing with High Inter-Occasion Variability Is Correctly Handled With Model-Informed Precision Dosing—Using Rifampicin as an Example. Front. Pharmacol. 2020, 11, 794. [Google Scholar] [CrossRef]
- Barrett, J.S.; Fossler, M.J.; Cadieu, K.D.; Gastonguay, M.R. Pharmacometrics: A Multidisciplinary Field to Facilitate Critical Thinking in Drug Development and Translational Research Settings. J. Clin. Pharmacol. 2008, 48, 632–649. [Google Scholar] [CrossRef]
- Trivedi, A.; Lee, R.; Meibohm, B. Applications of pharmacometrics in the clinical development and pharmacotherapy of anti-infectives. Expert Rev. Clin. Pharmacol. 2013, 6, 159–170. [Google Scholar] [CrossRef]
- Meibohm, B.; Derendorf, H. Pharmacokinetic/Pharmacodynamic Studies in Drug Product Development. J. Pharm. Sci. 2002, 91, 18–31. [Google Scholar] [CrossRef]
- Romero, K.; Corrigan, B.; Tornoe, C.W.; Gobburu, J.V.; Danhof, M.; Gillespie, W.R.; Gastonguay, M.R.; Meibohm, B.; Derendorf, H. Pharmacometrics as a discipline is entering the “industrialization” phase: Standards, automation, knowledge sharing, and training are critical for future success. J. Clin. Pharmacol. 2010, 50, 9S. [Google Scholar] [CrossRef]
- Marshall, S.; Madabushi, R.; Manolis, E.; Krudys, K.; Staab, A.; Dykstra, K.; Visser, S.A. Model-Informed Drug Discovery and Development: Current Industry Good Practice and Regulatory Expectations and Future Perspectives. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 87–96. [Google Scholar] [CrossRef]
- Van Wijk, R.C.; Ayoun Alsoud, R.; Lennernäs, H.; Simonsson, U.S.H. Model-Informed Drug Discovery and Development Strategy for the Rapid Development of Anti-Tuberculosis Drug Combinations. Appl. Sci. 2020, 10, 2376. [Google Scholar] [CrossRef] [Green Version]
- Stone, J.A.; Banfield, C.; Pfister, M.; Tannenbaum, S.; Allerheiligen, S.; Wetherington, J.D.; Krishna, R.; Grasela, D.M. Model-Based Drug Development Survey Finds Pharmacometrics Impacting Decision Making in the Pharmaceutical Industry. J. Clin. Pharmacol. 2010, 50, 20S–30S. [Google Scholar] [CrossRef]
- Pfister, M.; D’Argenio, D.Z. The Emerging Scientific Discipline of Pharmacometrics. J. Clin. Pharmacol. 2010, 50, 6S. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhu, H.; Madabushi, R.; Liu, Q.; Huang, S.; Zineh, I. Model-Informed Drug Development: Current US Regulatory Practice and Future Considerations. Clin. Pharmacol. Ther. 2019, 105, 899–911. [Google Scholar] [CrossRef]
- Lindstrom, M.J.; Bates, D. Nonlinear Mixed Effects Models for Repeated Measures Data. Biometrics 1990, 46, 673–687. [Google Scholar] [CrossRef] [PubMed]
- Sheiner, L.B.; Rosenberg, B.; Melmon, K.L. Modelling of individual pharmacokinetics for computer-aided drug dosage. Comput. Biomed. Res. 1972, 5, 441–459. [Google Scholar] [CrossRef]
- Bauer, R.J. NONMEM Tutorial Part II: Estimation Methods and Advanced Examples. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 538–556. [Google Scholar] [CrossRef] [Green Version]
- Bauer, R.J. NONMEM Tutorial Part I: Description of Commands and Options, With Simple Examples of Population Analysis. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 525–537. [Google Scholar] [CrossRef] [Green Version]
- Gieschke, R.; Steimer, J.-L. Pharmacometrics: Modelling and simulation tools to improve decision making in clinical drug development. Eur. J. Drug Metab. Pharmacokinet. 2000, 25, 49–58. [Google Scholar] [CrossRef]
- Rajman, I. PK/PD modelling and simulations: Utility in drug development. Drug Discov. Today 2008, 13, 341–346. [Google Scholar] [CrossRef]
- Chien, J.Y.; Friedrich, S.; Heathman, M.A.; De Alwis, D.P.; Sinha, V. Pharmacokinetics/pharmacodynamics and the stages of drug development: Role of modeling and simulation. AAPS J. 2005, 7, E544–E559. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Svensson, R.J.; Svensson, E.M.; Aarnoutse, R.E.; Diacon, A.H.; Dawson, R.; Gillespie, S.; Moodley, M.; Boeree, M.J.; Simonsson, U.S.H. Greater Early Bactericidal Activity at Higher Rifampicin Doses Revealed by Modeling and Clinical Trial Simulations. J. Infect. Dis. 2018, 218, 991–999. [Google Scholar] [CrossRef] [PubMed]
- Maloney, A.; Karlsson, M.O.; Simonsson, U.S.H. Optimal Adaptive Design in Clinical Drug Development: A Simulation Example. J. Clin. Pharmacol. 2007, 47, 1231–1243. [Google Scholar] [CrossRef] [PubMed]
- Bonate, P.L. Clinical Trial Simulation in Drug Development. Pharm. Res. 2000, 17, 252–256. [Google Scholar] [CrossRef]
- Beal, S.; Sheiner, L.; Boeckmann, A.; Bauer, R. Nonmem 7.4 Users Guides [Internet]; ICON plc: Gaithersburg, MD, USA, 1989; Available online: https://nonmem.iconplc.com/nonmem743/guides (accessed on 21 March 2022).
- Beal, S.L.; Sheiner, L.B. Estimating population kinetics. Crit. Rev. Biomed. Eng. 1982, 8, 195–222. [Google Scholar]
- Karlsson, M.O.; Holford, N.H. A Tutorial on Visual Predictive Checks. Available online: www.page-meeting.org/?abstract=1434 (accessed on 21 March 2022).
- Holford, N.H. The Visual Predictive Check—Superiority to Standard Diagnostic (Rorschach) Plots. Available online: www.page-meeting.org/?abstract=738 (accessed on 21 March 2022).
- Post, T.M.; Freijer, J.I.; Ploeger, B.A.; Danhof, M. Extensions to the Visual Predictive Check to facilitate model performance evaluation. J. Pharmacokinet. Pharmacodyn. 2008, 35, 185–202. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.H.T.; Mouksassi, M.-S.; Holford, N.; Al-Huniti, N.; Freedman, I.; Hooker, A.C.; John, J.; Karlsson, M.O.; Mould, D.R.; Pérez Ruixo, J.J.; et al. Model Evaluation of Continuous Data Pharmacometric Models: Metrics and Graphics. CPT Pharmacomet. Amp. Syst. Pharmacol. 2017, 6, 87–109. [Google Scholar] [CrossRef]
- Keizer, R.J.; Karlsson, M.O.; Hooker, A. Modeling and Simulation Workbench for NONMEM: Tutorial on Pirana, PsN, and Xpose. CPT Pharmacomet. Syst. Pharmacol. 2013, 2, e50. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Talevi, A.; Morales, J.F.; Hather, G.; Podichetty, J.T.; Kim, S.; Bloomingdale, P.C.; Kim, S.; Burton, J.; Brown, J.D.; Winterstein, A.G.; et al. Machine Learning in Drug Discovery and Development Part 1: A Primer. CPT Pharmacomet. Syst. Pharmacol. 2020, 9, 129–142. [Google Scholar] [CrossRef]
- Nasteski, V. An overview of the supervised machine learning methods. Horizons B 2017, 4, 51–62. [Google Scholar] [CrossRef]
- Lee, S.; El Naqa, I. Machine Learning Methodology. In Machine Learning in Radiation Oncology: Theory and Applications; El Naqa, I., Li, R., Murphy, M.J., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 21–39. [Google Scholar] [CrossRef]
- Van Engelen, J.E.; Hoos, H.H. A survey on semi-supervised learning. Mach. Learn. 2020, 109, 373–440. [Google Scholar] [CrossRef] [Green Version]
- Vamathevan, J.; Clark, D.; Czodrowski, P.; Dunham, I.; Ferran, E.; Lee, G.; Li, B.; Madabhushi, A.; Shah, P.; Spitzer, M.; et al. Applications of machine learning in drug discovery and development. Nat. Rev. Drug Discov. 2019, 18, 463–477. [Google Scholar] [CrossRef]
- Koromina, M.; Pandi, M.-T.; Patrinos, G.P. Rethinking Drug Repositioning and Development with Artificial Intelligence, Machine Learning, and Omics. Omics J. Integr. Biol. 2019, 23, 539–548. [Google Scholar] [CrossRef] [PubMed]
- Ekins, S.; Puhl, A.C.; Zorn, K.M.; Lane, T.R.; Russo, D.P.; Klein, J.J.; Hickey, A.J.; Clark, A.M. Exploiting machine learning for end-to-end drug discovery and development. Nat. Mater. 2019, 18, 435–441. [Google Scholar] [CrossRef] [PubMed]
- Artificial Intelligence: A Modern Approach, Global Edition-Stuart Russell, Peter Norvig-Pocket (9781292153964)|Adlibris Bokhandel [Internet]. Available online: https://www.adlibris.com/se/bok/artificial-intelligence-a-modern-approach-global-edition-9781292153964?gclid=Cj0KCQjwsLWDBhCmARIsAPSL3_18T0hHwvmO8ajpXmAiu3d9il07p7BqlK_oSHqol6BHokjL-OXZ1TkaAurjEALw_wcB (accessed on 7 April 2021).
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996; Available online: https://www.cambridge.org/core/books/pattern-recognition-and-neural-networks/4E038249C9BAA06C8F4EE6F044D09C5C (accessed on 7 April 2021).
- Baştanlar, Y.; Özuysal, M. Introduction to Machine Learning. In miRNomics: MicroRNA Biology and Computational Analysis; Yousef, M., Allmer, J., Eds.; Humana Press: Totowa, NJ, USA, 2014; pp. 105–128. [Google Scholar] [CrossRef] [Green Version]
- Hutmacher, M.M.; Kowalski, K.G. Covariate selection in pharmacometric analyses: A review of methods. Br. J. Clin. Pharmacol. 2015, 79, 132–147. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Chen, P.-H.; Krause, J.; Peng, L. How to Read Articles That Use Machine Learning: Users’ Guides to the Medical Literature. JAMA 2019, 322, 1806–1816. [Google Scholar] [CrossRef]
- Alajmi, M.S.; Almeshal, A.M. Predicting the Tool Wear of a Drilling Process Using Novel Machine Learning XGBoost-SDA. Materials 2020, 13, 4952. [Google Scholar] [CrossRef]
- Hyperparameter Optimization in Machine Learning [Internet]. DataCamp Community. 2018. Available online: https://www.datacamp.com/community/tutorials/parameter-optimization-machine-learning-models (accessed on 7 April 2021).
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Polikar, R. Ensemble Learning. In Ensemble Machine Learning: Methods and Applications; Zhang, C., Ma, Y., Eds.; Springer: Boston, MA, USA, 2012; pp. 1–34. [Google Scholar] [CrossRef]
- Hjort, N.L.; Claeskens, G. Frequentist Model Average Estimators. J. Am. Stat. Assoc. 2003, 98, 879–899. [Google Scholar] [CrossRef] [Green Version]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Sheiner, L.B.; Beal, S.L. Bayesian Individualization of Pharmacokinetics: Simple Implementation and Comparison with Non-Bayesian Methods. J. Pharm. Sci. 1982, 71, 1344–1348. [Google Scholar] [CrossRef] [PubMed]
- Van Beek, S.W.; Ter Heine, R.; Keizer, R.J.; Magis-Escurra, C.; Aarnoutse, R.E.; Svensson, E.M. Personalized Tuberculosis Treatment Through Model-Informed Dosing of Rifampicin. Clin. Pharmacokinet. 2019, 58, 815–826. [Google Scholar] [CrossRef] [Green Version]
- Boeree, M.J.; Diacon, A.H.; Dawson, R.; Narunsky, K.; du Bois, J.; Venter, A.; Phillips, P.P.J.; Gillespie, S.H.; McHugh, T.D.; Hoelscher, M.; et al. A Dose-Ranging Trial to Optimize the Dose of Rifampin in the Treatment of Tuberculosis. Am. J. Respir. Crit. Care Med. 2015, 191, 1058–1065. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sturkenboom, M.G.G.; Mulder, L.W.; De Jager, A.; Van Altena, R.; Aarnoutse, R.E.; De Lange, W.C.M.; Proost, J.H.; Kosterink, J.G.W.; Van Der Werf, T.S.; Jan-Willem, C. Pharmacokinetic Modeling and Optimal Sampling Strategies for Therapeutic Drug Monitoring of Rifampin in Patients with Tuberculosis. Antimicrob. Agents Chemother. 2015, 59, 4907–4913. [Google Scholar] [CrossRef] [Green Version]
- Wilkins, J. Package ‘Pmxtools’ [Internet]. 2020. Available online: https://github.com/kestrel99/pmxTools (accessed on 21 March 2022).
- Polley, E. SuperLearner: Super Learner Prediction [Internet]. 2019. Available online: https://CRAN.R-project.org/package=SuperLearner (accessed on 21 March 2022).
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013; Available online: https://www.R-project.org/ (accessed on 21 March 2022).
- Bedding, A.; Scott, G.; Brayshaw, N.; Leong, L.; Herrero-Martinez, E.; Looby, M.; Lloyd, P. Clinical Trial Simulations—An Essential Tool in Drug Development. Available online: https://www.abpi.org.uk/publications/clinical-trial-simulations-an-essential-tool-in-drug-development/ (accessed on 21 March 2022).

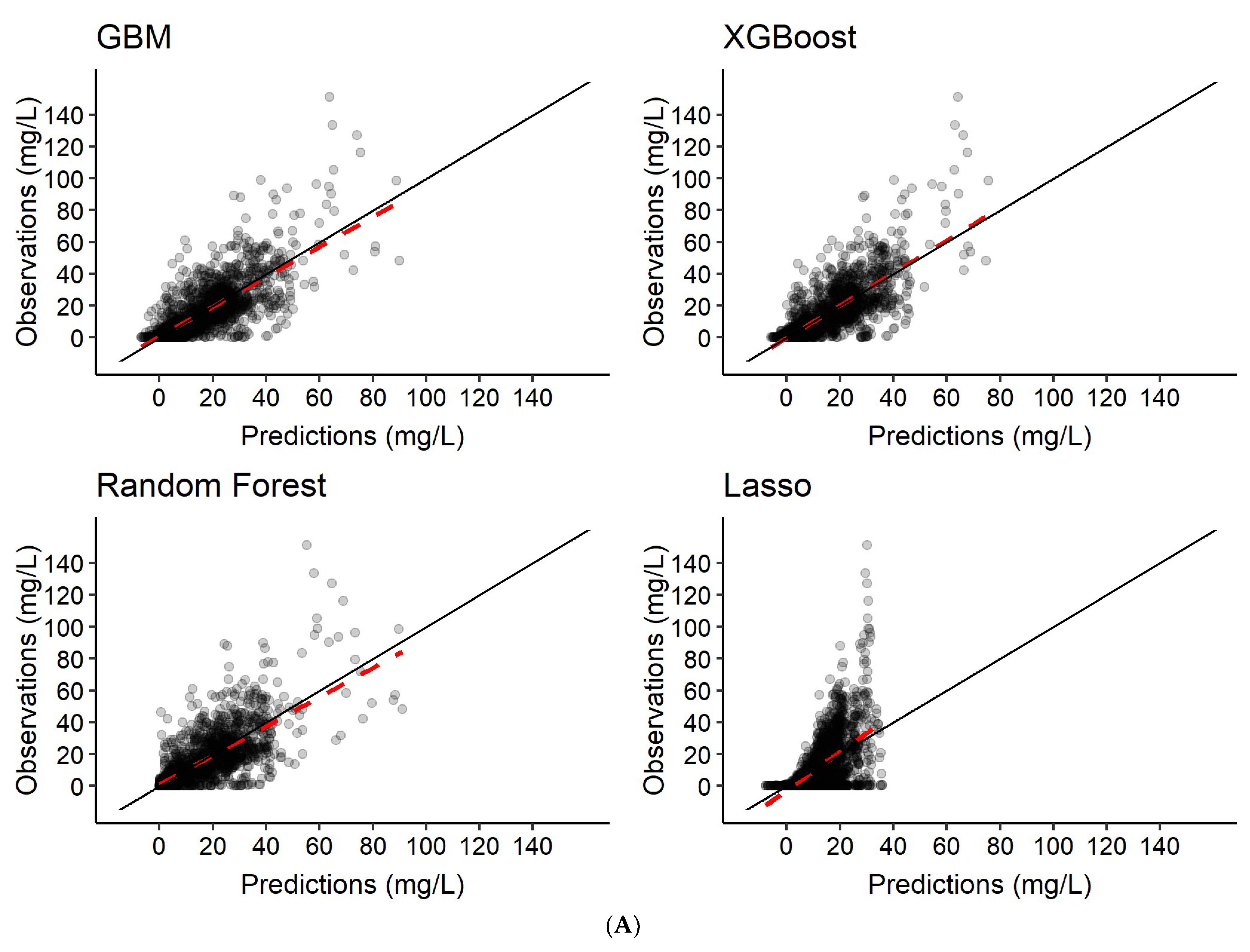
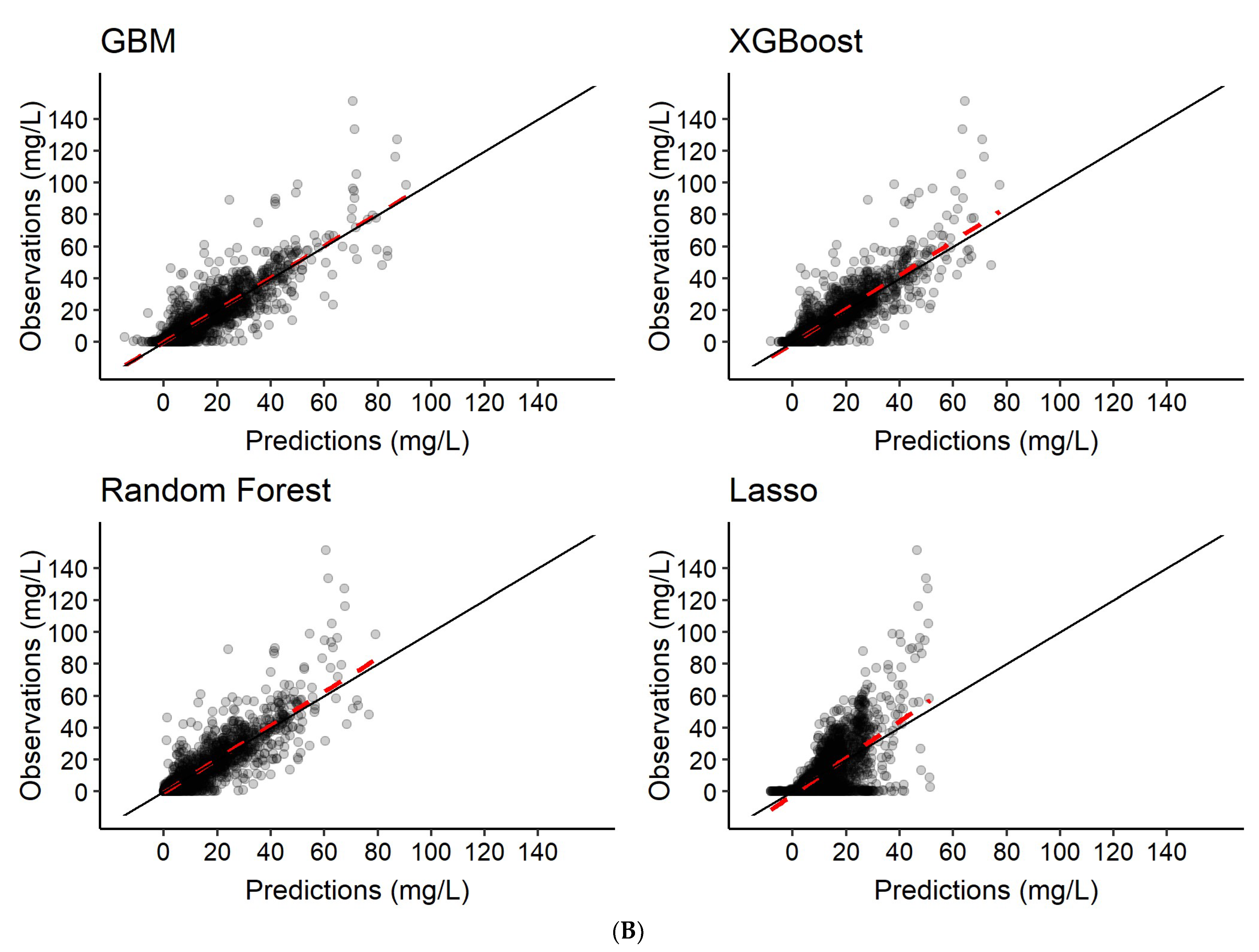
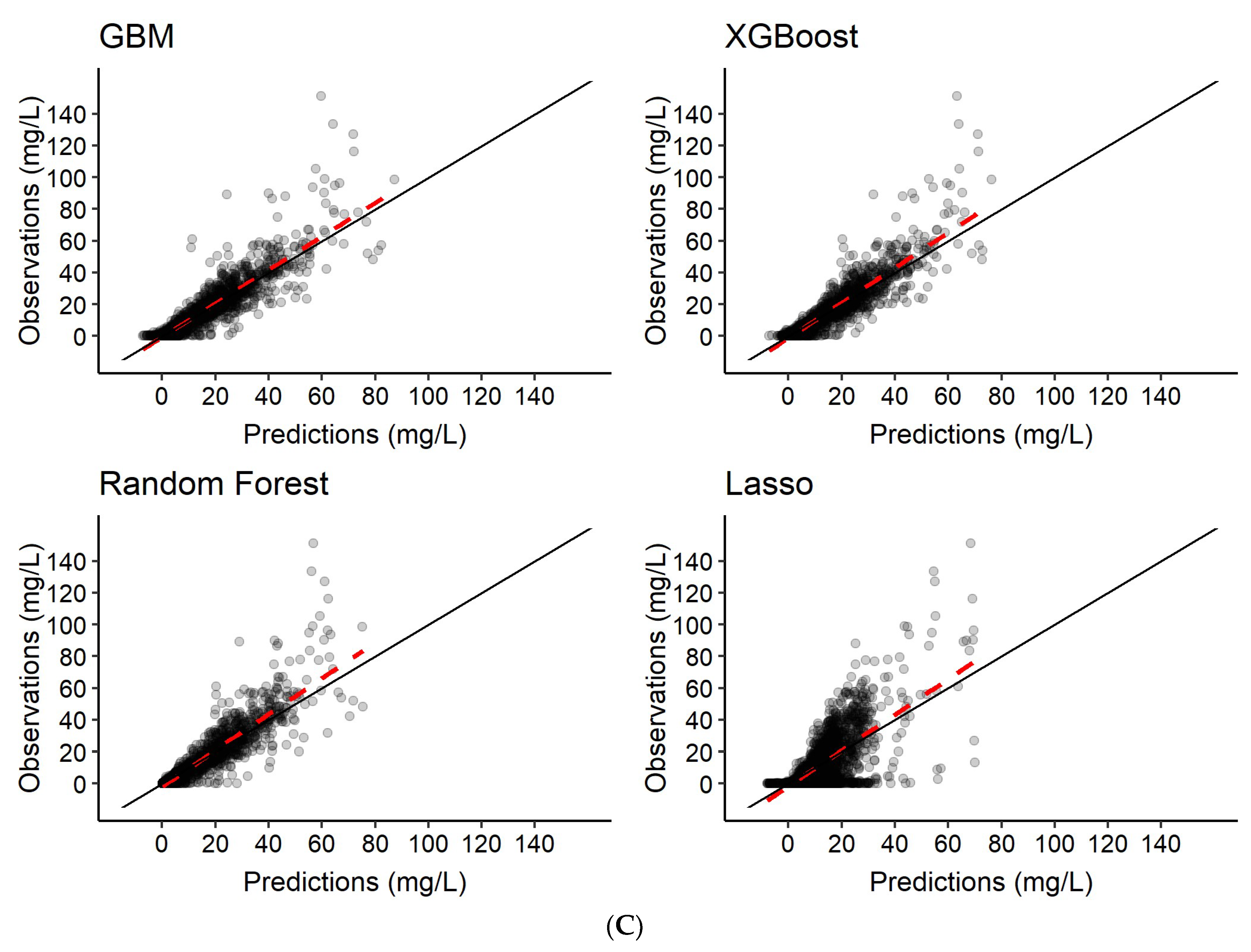

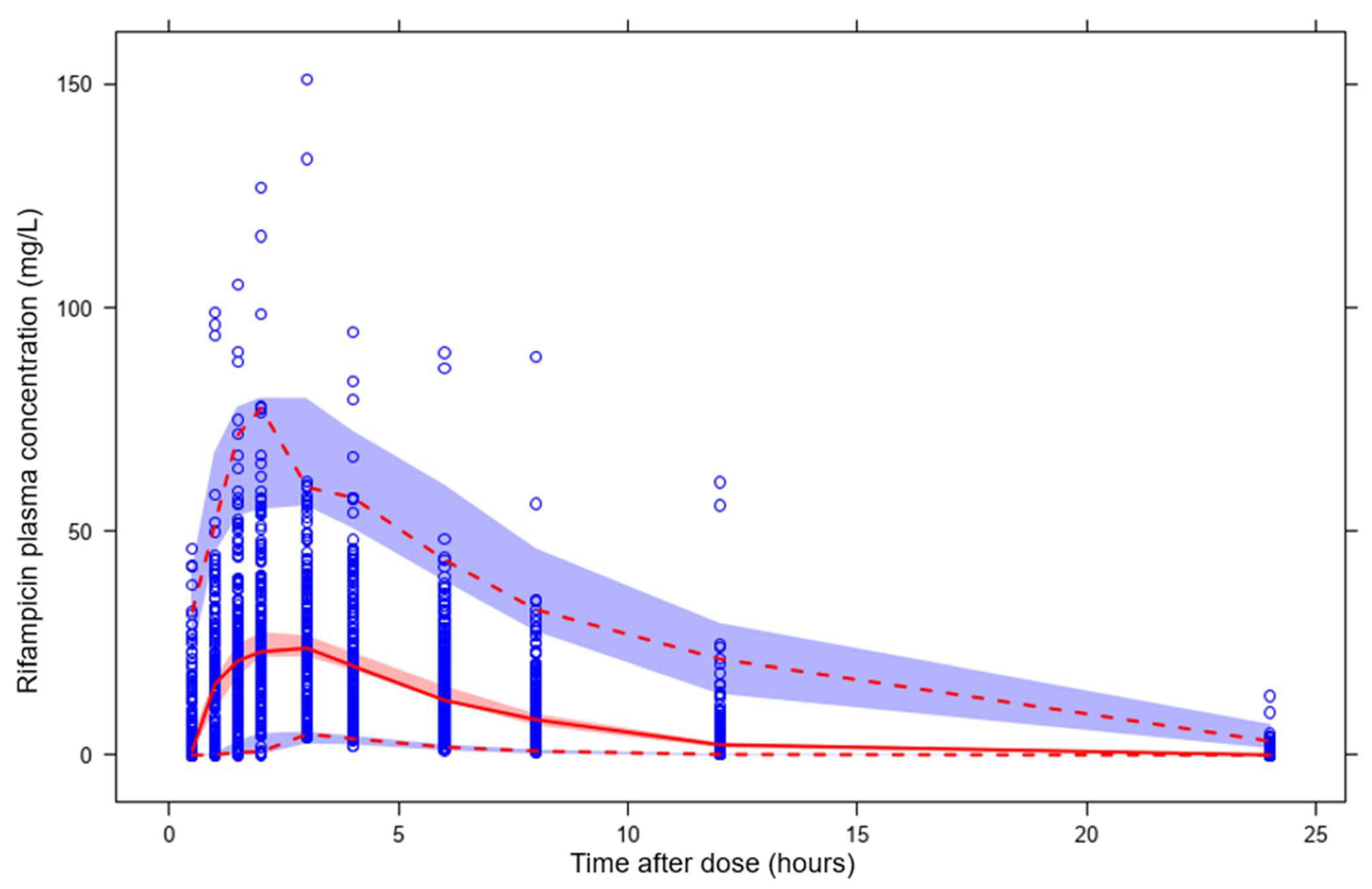
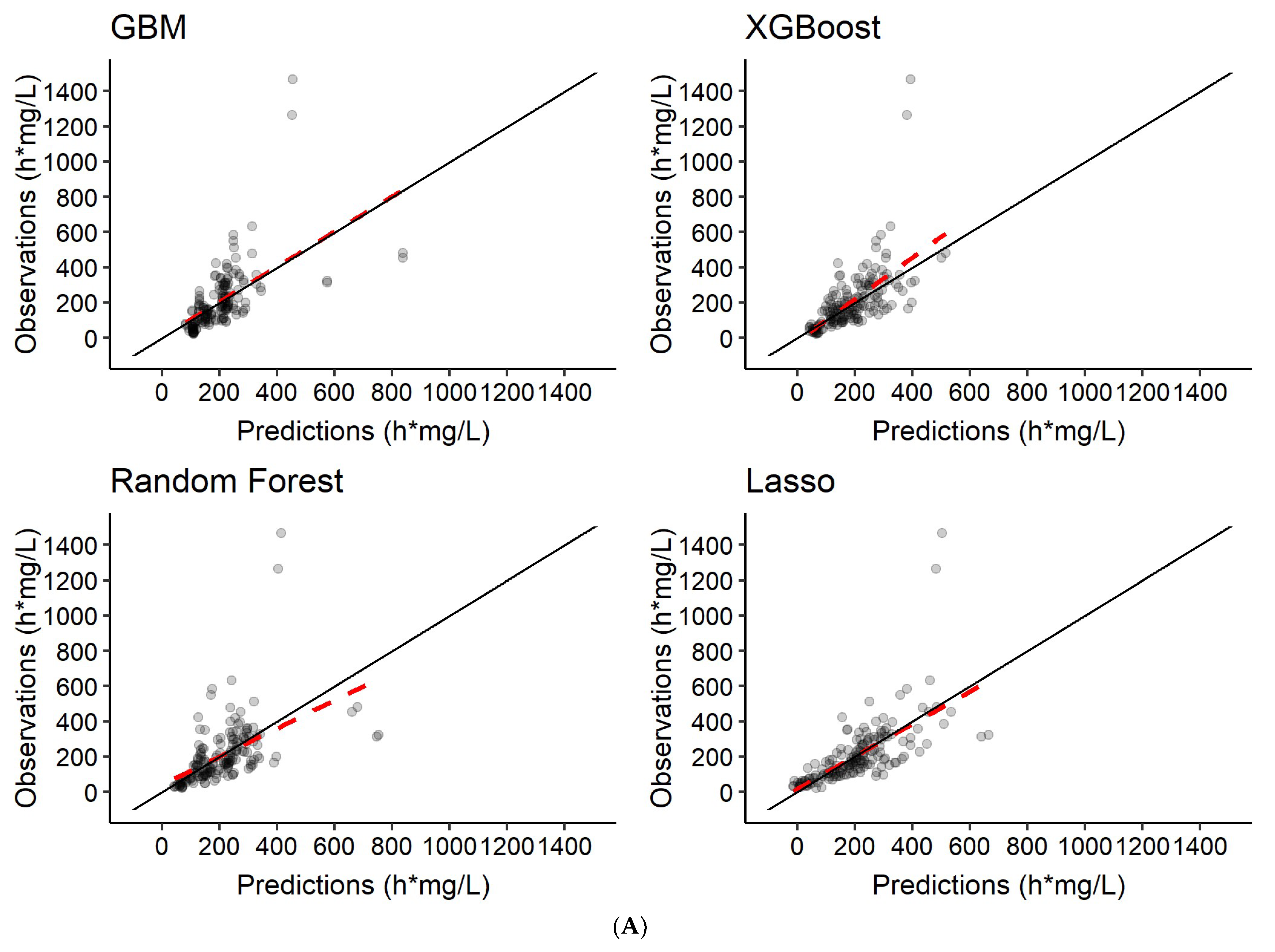
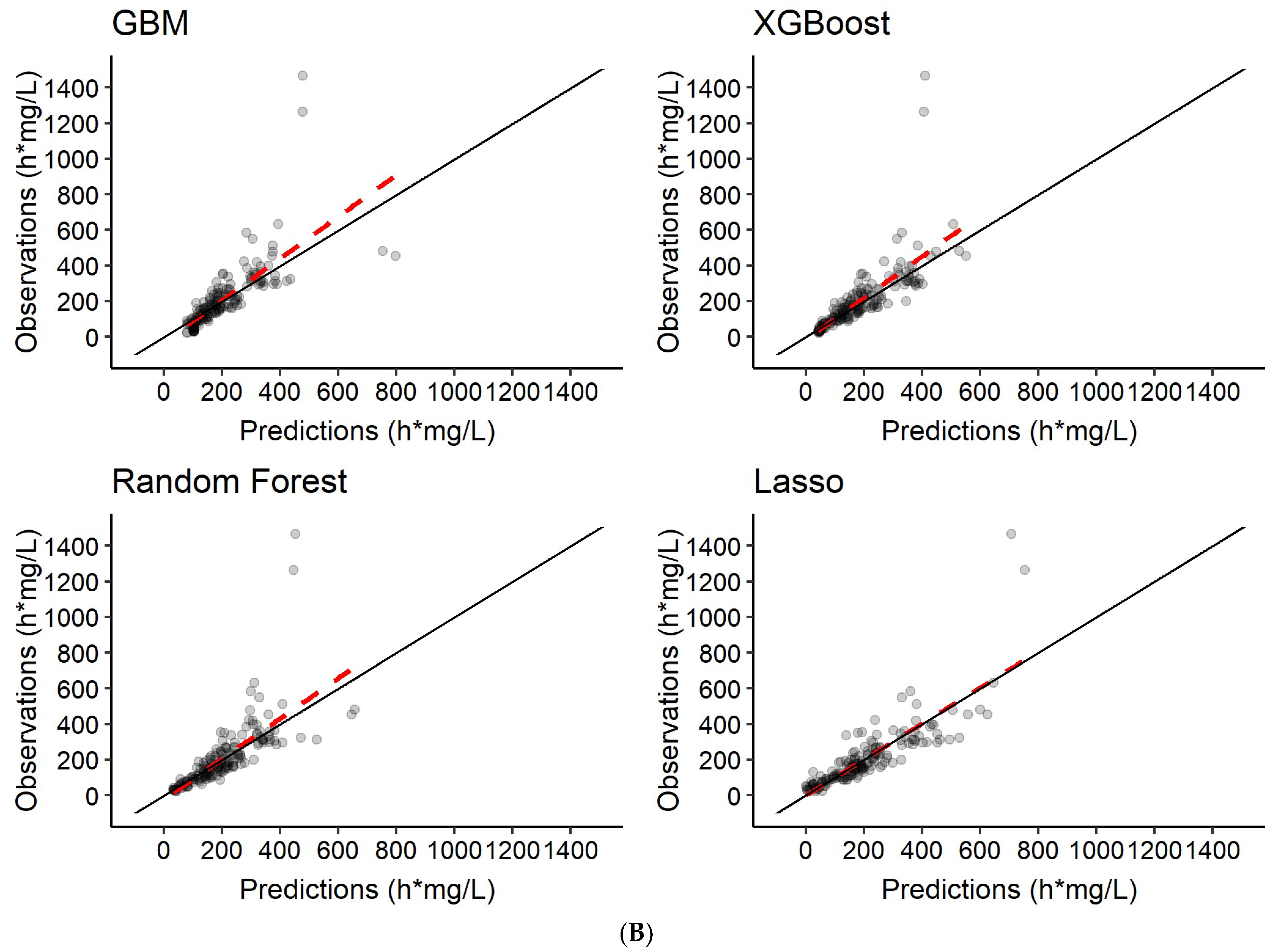
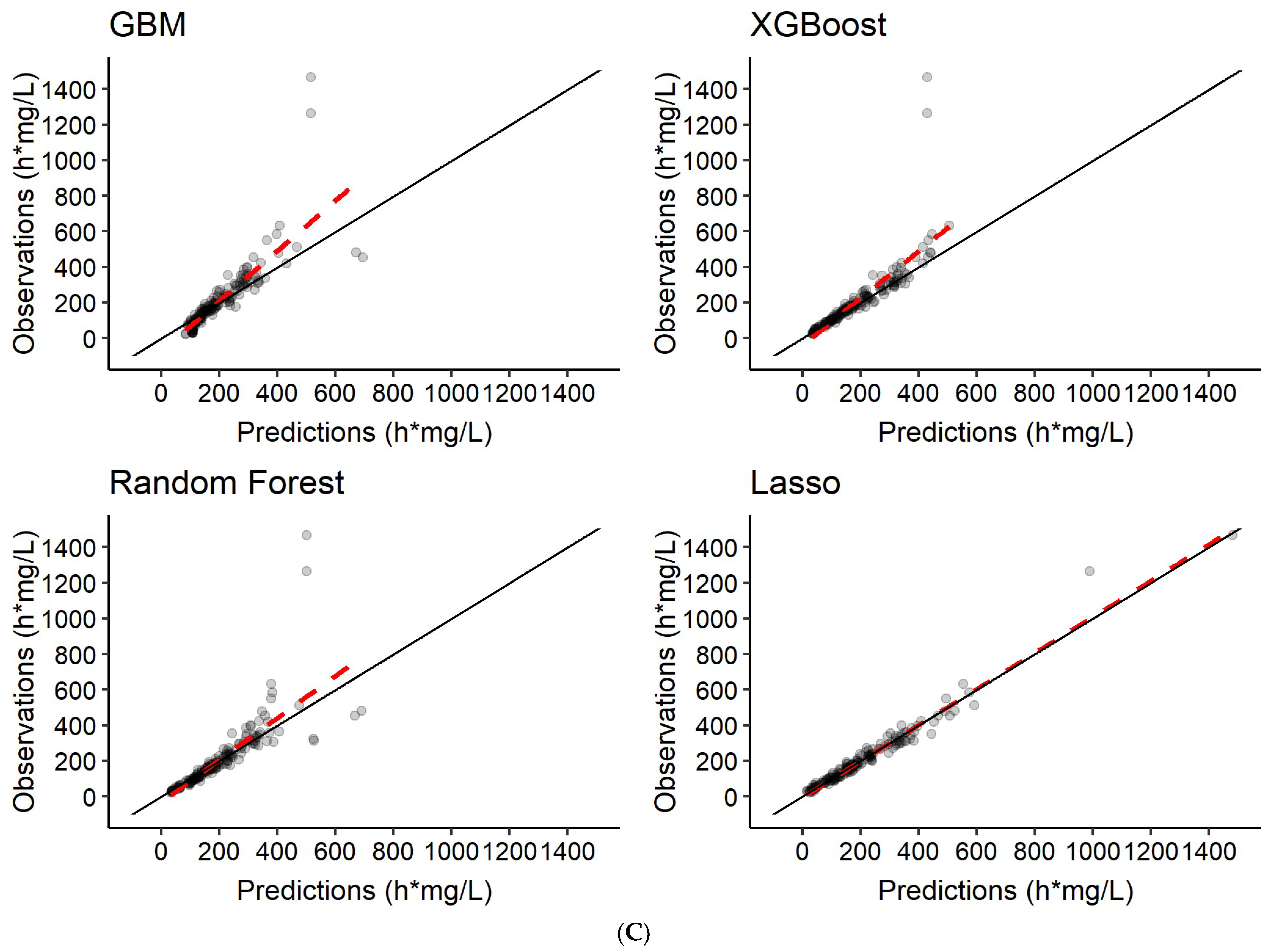
| Scenario | Model | Predictions |
|---|---|---|
| 1 | Features only | Rifampicin concentration-time series c |
| 2 | Features + 2 observed rifampicin concentrations a | Rifampicin concentration-time series c |
| 3 | Features + 6 observed rifampicin concentrations b | Rifampicin concentration-time series c |
| 4 | Features only | AUC0–24h |
| 5 | Features + 2 observed rifampicin concentrations a | AUC0–24h |
| 6 | Features + 6 observed rifampicin concentrations b | AUC0–24h |
| GBM | XGBoost | Random Forest | LASSO | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 1 | Scenario 2 | Scenario 3 | |
| R2 | 0.57 | 0.76 | 0.83 | 0.60 | 0.76 | 0.84 | 0.54 | 0.75 | 0.82 | 0.25 | 0.36 | 0.39 |
| Pearson correlation | 0.77 | 0.87 | 0.90 | 0.78 | 0.87 | 0.91 | 0.75 | 0.86 | 0.90 | 0.52 | 0.62 | 0.65 |
| RMSE (mg/L) | 10.9 (8.9–13.3) | 8.3 (6.8–8.6) | 7.1 (5.1–7.3) | 10.6 (8.9–13.5) | 8.3 (6.7–12.4) | 6.9 (5.1–11.1) | 11.3 (9.8–14.1) | 8.5 (6.9–12.7) | 7.2 (5.3–11.8) | 14.5 (13.4–19.1) | 13.3 (11.5–16.6) | 12.9 (11.3–15.3) |
| MAE (mg/L) | 7.1 (6.0–7.1) | 5.2 (4.3–6.8) | 4.1 (3.3–5.7) | 7.0 (6.0–8.0) | 5.1 (4.2–6.7) | 4.0 (3.2–5.4) | 7.0 (6.4–8.0) | 4.9 (4.2–6.4) | 3.8 (2.8–5.3) | 10.2 (9.9–12.2) | 9.6 (8.4–11.1) | 9.3 (8.1–10.5) |
| Run time (s) | 6.8 | 8.2 | 11.1 | 1.4 | 1.2 | 4.7 | 309.9 | 362.6 | 508.7 | 1.1 | 1.3 | 1.1 |
| GBM | XGBoost | Random Forest | LASSO | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario 4 | Scenario 5 | Scenario 6 | Scenario 4 | Scenario 5 | Scenario 6 | Scenario 4 | Scenario 5 | Scenario 6 | Scenario 4 | Scenario 5 | Scenario 6 | |
| R2 | 0.27 | 0.61 | 0.73 | 0.44 | 0.71 | 0.84 | 0.22 | 0.62 | 0.78 | 0.41 | 0.69 | 0.97 |
| Pearson correlation | 0.59 | 0.73 | 0.83 | 0.63 | 0.75 | 0.83 | 0.55 | 0.73 | 0.83 | 0.67 | 0.84 | 0.98 |
| RMSE (h·mg/L) | 131.7 (86.9–246.6) | 103.0 (49.8–233.1) | 88.2 (41.7–218.2) | 121.0 (57.7–262.8) | 92.6 (38.9–250.1) | 69.6 (21.0–238.3) | 137.1 (76.8–252.8) | 103.5 (48.5–238.7) | 79.9 (30.2–208.5) | 117.9 (76.0–238.5) | 86.8 (48.3–175.5) | 29.1 (20.7–57.3) |
| MAE (h·mg/L) | 85.5 (74.4–121.1) | 61.3 (43.2–105.8) | 47.6 (21.0–238.3) | 76.7 (47.1–122.3) | 52.6 (30.5–110.5) | 30.4 (13.3–82.8) | 84.6 (63.1–118.3) | 59.4 (39.6–102.6) | 38.3 (22.5–74.8) | 74.2 (56.5–119.7) | 54.5 (38.4–87.2) | 18.8 (15.2–29.2) |
| Run time (s) | 1.3 | 1.6 | 1.8 | 0.7 | 4.7 | 4.1 | 20.5 | 21.9 | 22.8 | 1.1 | 1.0 | 1.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keutzer, L.; You, H.; Farnoud, A.; Nyberg, J.; Wicha, S.G.; Maher-Edwards, G.; Vlasakakis, G.; Moghaddam, G.K.; Svensson, E.M.; Menden, M.P.; et al. Machine Learning and Pharmacometrics for Prediction of Pharmacokinetic Data: Differences, Similarities and Challenges Illustrated with Rifampicin. Pharmaceutics 2022, 14, 1530. https://doi.org/10.3390/pharmaceutics14081530
Keutzer L, You H, Farnoud A, Nyberg J, Wicha SG, Maher-Edwards G, Vlasakakis G, Moghaddam GK, Svensson EM, Menden MP, et al. Machine Learning and Pharmacometrics for Prediction of Pharmacokinetic Data: Differences, Similarities and Challenges Illustrated with Rifampicin. Pharmaceutics. 2022; 14(8):1530. https://doi.org/10.3390/pharmaceutics14081530
Chicago/Turabian StyleKeutzer, Lina, Huifang You, Ali Farnoud, Joakim Nyberg, Sebastian G. Wicha, Gareth Maher-Edwards, Georgios Vlasakakis, Gita Khalili Moghaddam, Elin M. Svensson, Michael P. Menden, and et al. 2022. "Machine Learning and Pharmacometrics for Prediction of Pharmacokinetic Data: Differences, Similarities and Challenges Illustrated with Rifampicin" Pharmaceutics 14, no. 8: 1530. https://doi.org/10.3390/pharmaceutics14081530
APA StyleKeutzer, L., You, H., Farnoud, A., Nyberg, J., Wicha, S. G., Maher-Edwards, G., Vlasakakis, G., Moghaddam, G. K., Svensson, E. M., Menden, M. P., Simonsson, U. S. H., & on behalf of the UNITE4TB Consortium. (2022). Machine Learning and Pharmacometrics for Prediction of Pharmacokinetic Data: Differences, Similarities and Challenges Illustrated with Rifampicin. Pharmaceutics, 14(8), 1530. https://doi.org/10.3390/pharmaceutics14081530







