Novel Polymorph of Favipiravir—An Antiviral Medication
Abstract
1. Introduction
2. Materials and Methods
2.1. Powder XRD Studies
2.2. DFT Calculations
3. Results
3.1. Crystallization and Characterization
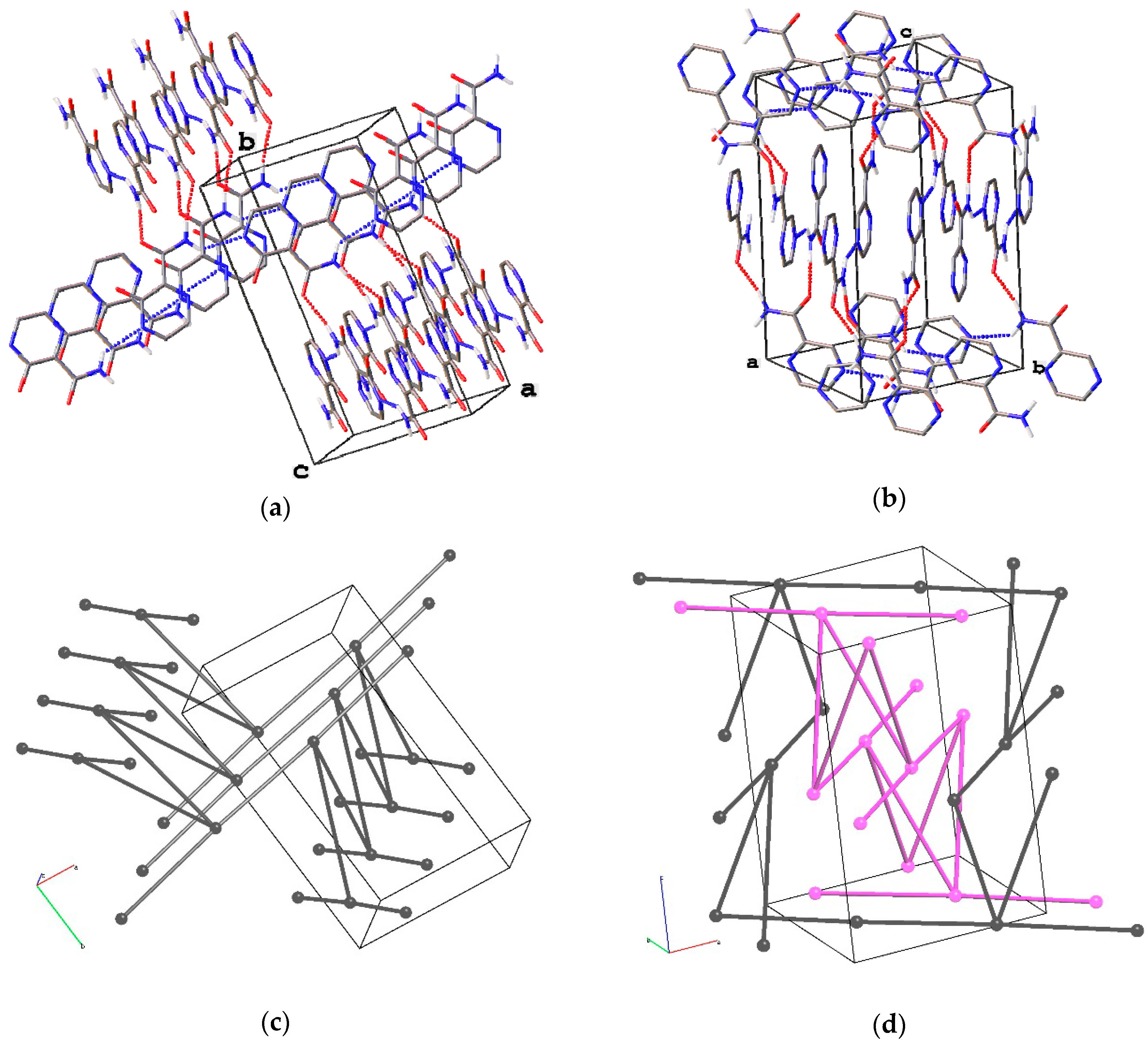
3.2. Crystal Structure of the Tetragonal Polymorph
3.3. DFT Calculations and Charge Density Studies
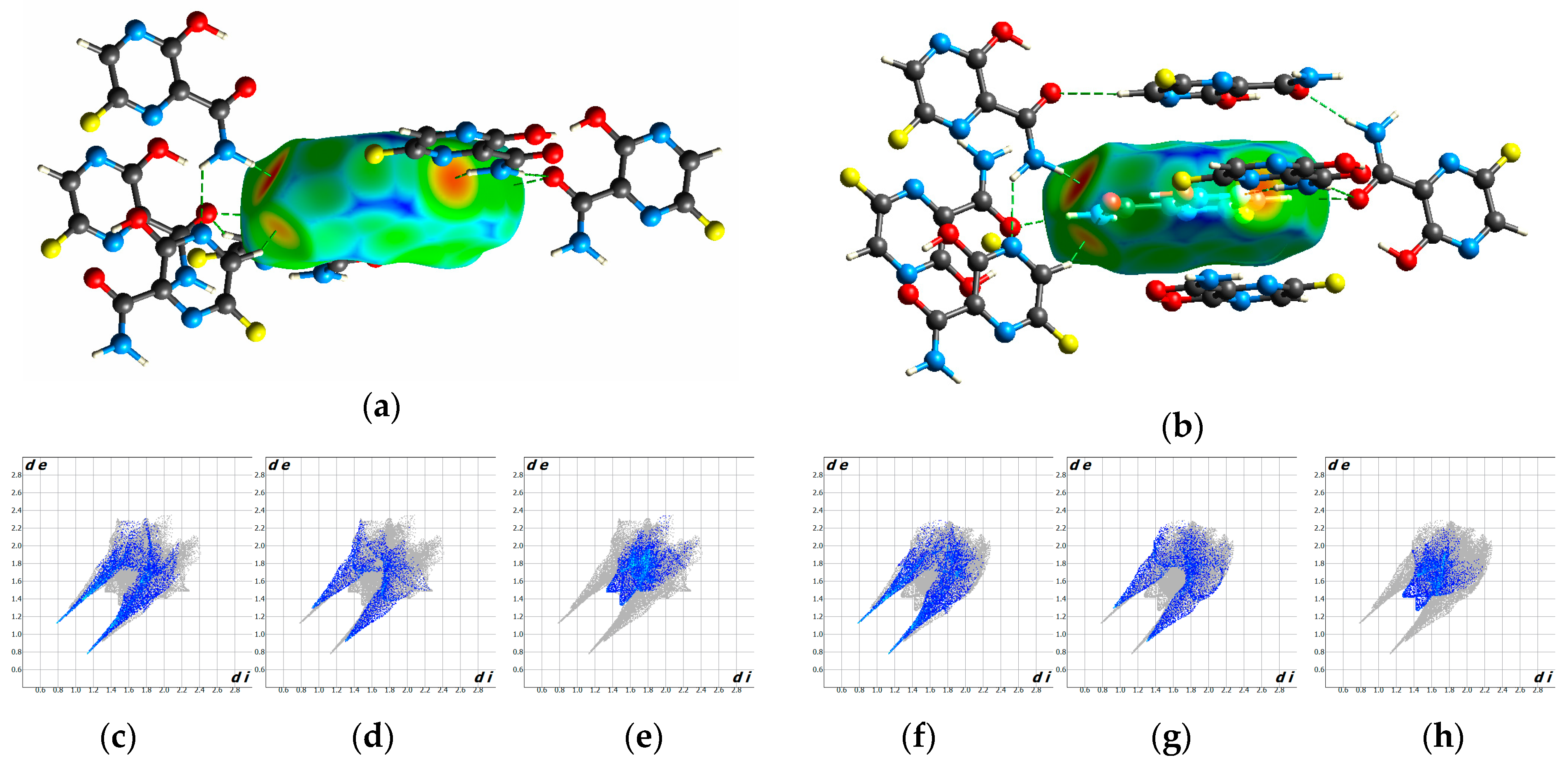
3.4. Hirshfeld Analysis of Two Polymorphs
3.5. Analysis of H-Bonding Network
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Upadhyay, P.; Khomane, K.S.; Kumar, L.; Bansal, A.K. Relationship between Crystal Structure and Mechanical Properties of Ranitidine Hydrochloride Polymorphs. Crystengcomm 2013, 15, 3959–3964. [Google Scholar] [CrossRef]
- Szafraniec-Szczęsny, J.; Antosik-Rogóż, A.; Knapik-Kowalczuk, J.; Kurek, M.; Szefer, E.; Gawlak, K.; Chmiel, K.; Peralta, S.; Niwiński, K.; Pielichowski, K.; et al. Compression-Induced Phase Transitions of Bicalutamide. Pharmaceutics 2020, 12, 438. [Google Scholar] [CrossRef] [PubMed]
- Bauer, J.; Spanton, S.; Henry, R.; Quick, J.; Dziki, W.; Porter, W.; Morris, J. Ritonavir: An Extraordinary Example of Conformational Polymorphism. Pharm. Res. 2001, 18, 859–866. [Google Scholar] [CrossRef] [PubMed]
- Pudipeddi, M.; Serajuddin, A.T.M. Trends in Solubility of Polymorphs. J. Pharm. Sci. 2005, 94, 929–939. [Google Scholar] [CrossRef] [PubMed]
- Elder, D.P.; Patterson, J.E.; Holm, R. The Solid-State Continuum: A Perspective on the Interrelationships between Different Solid-State Forms in Drug Substance and Drug Product: The Solid-State Continuum. J. Pharm. Pharmacol. 2015, 67, 757–772. [Google Scholar] [CrossRef] [PubMed]
- Bučar, D.-K.; Lancaster, R.W.; Bernstein, J. Disappearing Polymorphs Revisited. Angew. Chem. Int. Ed. 2015, 54, 6972–6993. [Google Scholar] [CrossRef]
- Karpinski, P.H. Polymorphism of Active Pharmaceutical Ingredients. Chem. Eng. Technol. 2006, 29, 233–237. [Google Scholar] [CrossRef]
- Bernstein, J. Polymorphism in Molecular Crystals; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Bai, C.-Q.; Mu, J.-S.; Kargbo, D.; Song, Y.-B.; Niu, W.-K.; Nie, W.-M.; Kanu, A.; Liu, W.-W.; Wang, Y.-P.; Dafae, F.; et al. Clinical and Virological Characteristics of Ebola Virus Disease Patients Treated With Favipiravir (T-705)—Sierra Leone, 2014. Clin. Infect. Dis. 2016, 63, 1288–1294. [Google Scholar] [CrossRef]
- Rosenke, K.; Feldmann, H.; Westover, J.B.; Hanley, P.W.; Martellaro, C.; Feldmann, F.; Saturday, G.; Lovaglio, J.; Scott, D.P.; Furuta, Y.; et al. Use of Favipiravir to Treat Lassa Virus Infection in Macaques. Emerg. Infect. Dis. J. 2018, 24, 1696–1698. [Google Scholar] [CrossRef]
- Scavone, C.; Brusco, S.; Bertini, M.; Sportiello, L.; Rafaniello, C.; Zoccoli, A.; Berrino, L.; Racagni, G.; Rossi, F.; Capuano, A. Current Pharmacological Treatments for COVID-19: What’s Next? Br. J. Pharmacol. 2020, 177, 4813–4824. [Google Scholar] [CrossRef]
- Sreekanth Reddy, O.; Lai, W.-F. Tackling COVID-19 Using Remdesivir and Favipiravir as Therapeutic Options. Chembiochem 2020. [Google Scholar] [CrossRef] [PubMed]
- Coelho, A.A. Indexing of Powder Diffraction Patterns by Iterative Use of Singular Value Decomposition. J. Appl. Crystallogr. 2003, 36, 86–95. [Google Scholar] [CrossRef]
- Coelho, A.A. TOPAS and TOPAS-Academic: An Optimization Program Integrating Computer Algebra and Crystallographic Objects Written in C++. J. Appl. Crystallogr. 2018, 51, 210–218. [Google Scholar] [CrossRef]
- Favre-Nicolin, V.; Černý, R. FOX, ‘free Objects for Crystallography’: A Modular Approach to Ab Initio Structure Determination from Powder Diffraction. J. Appl. Crystallogr. 2002, 35, 734–743. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal Amorphous-Semiconductor Transition in Germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Moellmann, J.; Grimme, S. Importance of London Dispersion Effects for the Packing of Molecular Crystals: A Case Study for Intramolecular Stacking in a Bis-Thiophene Derivative. Phys. Chem. Chem. Phys. 2010, 12, 8500. [Google Scholar] [CrossRef]
- Gonze, X.; Beuken, J.-M.; Caracas, R.; Detraux, F.; Fuchs, M.; Rignanese, G.-M.; Sindic, L.; Verstraete, M.; Zerah, G.; Jollet, F.; et al. First-Principles Computation of Material Properties: The ABINIT Software Project. Comput. Mater. Sci. 2002, 25, 478–492. [Google Scholar] [CrossRef]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen Bond Strengths Revealed by Topological Analyses of Experimentally Observed Electron Densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Furuta, Y.; Komeno, T.; Nakamura, T. Favipiravir (T-705), a Broad Spectrum Inhibitor of Viral RNA Polymerase. Proc. Jpn. Acad. Ser. B 2017, 93, 449–463. [Google Scholar] [CrossRef] [PubMed]
- Shi, F.; Li, Z.; Kong, L.; Xie, Y.; Zhang, T.; Xu, W. Synthesis and Crystal Structure of 6-Fluoro-3-Hydroxypyrazine-2-Carboxamide. Drug Discov. Ther. 2014, 8, 117–120. [Google Scholar] [CrossRef] [PubMed]
- Childs, S.L.; Wood, P.A.; Rodríguez-Hornedo, N.; Reddy, L.S.; Hardcastle, K.I. Analysis of 50 Crystal Structures Containing Carbamazepine Using the Materials Module of Mercury CSD. Cryst. Growth Des. 2009, 9, 1869–1888. [Google Scholar] [CrossRef]
- Vologzhanina, A.V. Intermolecular Interactions in Functional Crystalline Materials: From Data to Knowledge. Crystals 2019, 9, 478. [Google Scholar] [CrossRef]
- Etter, M.C. Encoding and Decoding Hydrogen-Bond Patterns of Organic Compounds. Acc. Chem. Res. 1990, 23, 120–126. [Google Scholar] [CrossRef]
- Etter, M. Hydrogen-Bonds as Design Elements in Organic-Chemistry. J. Phys. Chem. 1991, 95, 4601–4610. [Google Scholar] [CrossRef]
- Galek, P.T.A.; Fábián, L.; Motherwell, W.D.S.; Allen, F.H.; Feeder, N. Knowledge-Based Model of Hydrogen-Bonding Propensity in Organic Crystals. Acta Crystallogr. Sect. B 2007, 63, 768–782. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 171–179. [Google Scholar] [CrossRef]
- Delori, A.; Galek, P.T.A.; Pidcock, E.; Jones, W. Quantifying Homo- and Heteromolecular Hydrogen Bonds as a Guide for Adduct Formation. Chem. Eur. J. 2012, 18, 6835–6846. [Google Scholar] [CrossRef]
- Delori, A.; Galek, P.T.A.; Pidcock, E.; Patni, M.; Jones, W. Knowledge-Based Hydrogen Bond Prediction and the Synthesis of Salts and Cocrystals of the Anti-Malarial Drug Pyrimethamine with Various Drug and GRAS Molecules. CrystEngComm 2013, 15, 2916–2928. [Google Scholar] [CrossRef]
- Eddleston, M.D.; Arhangelskis, M.; Fábián, L.; Tizzard, G.J.; Coles, S.J.; Jones, W. Investigation of an Amide-Pseudo Amide Hydrogen Bonding Motif within a Series of Theophylline:Amide Cocrystals. Cryst. Growth Des. 2016, 16, 51–58. [Google Scholar] [CrossRef]
- Galek, P.T.A.; Allen, F.H.; Fábián, L.; Feeder, N. Knowledge-Based H-Bond Prediction to Aid Experimental Polymorph Screening. CrystEngComm 2009, 11, 2634–2639. [Google Scholar] [CrossRef]
- Abramov, Y.A. Current Computational Approaches to Support Pharmaceutical Solid Form Selection. Org. Process Res. Dev. 2013, 17, 472–485. [Google Scholar] [CrossRef]
- Feeder, N.; Pidcock, E.; Reilly, A.M.; Sadiq, G.; Doherty, C.L.; Back, K.R.; Meenan, P.; Docherty, R. The Integration of Solid-Form Informatics into Solid-Form Selection. J. Pharm. Pharmacol. 2015, 67, 857–868. [Google Scholar] [CrossRef] [PubMed]
- Korlyukov, A.A.; Malinska, M.; Vologzhanina, A.V.; Goizman, M.S.; Trzybinski, D.; Wozniak, K. Charge Density View on Bicalutamide Molecular Interactions in the Monoclinic Polymorph and Androgen Receptor Binding Pocket. IUCrJ 2020, 7, 71–82. [Google Scholar] [CrossRef]
- Vologzhanina, A.V.; Ushakov, I.E.; Korlyukov, A.A. Intermolecular Interactions in Crystal Structures of Imatinib-Containing Compounds. Int. J. Mol. Sci. 2020, 21, 8970. [Google Scholar] [CrossRef]
- Macrae, C.F.; Sovago, I.; Cottrell, S.J.; Galek, P.T.A.; McCabe, P.; Pidcock, E.; Platings, M.; Shields, G.P.; Stevens, J.S.; Towler, M.; et al. Mercury 4.0: From Visualization to Analysis, Design and Prediction. J. Appl. Crystallogr. 2020, 53, 226–235. [Google Scholar] [CrossRef]
- Nyman, J.; Day, G.M. Static and Lattice Vibrational Energy Differences between Polymorphs. CrystEngComm 2015, 17, 5154–5165. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules. A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Gavezzotti, A. Are Crystal Structures Predictable? Acc. Chem. Res. 1994, 27, 309–314. [Google Scholar] [CrossRef]
- Gavezzotti, A.; Filippini, G. Geometry of the Intermolecular X-H.Cntdot..Cntdot..Cntdot.Y (X, Y = N, O) Hydrogen Bond and the Calibration of Empirical Hydrogen-Bond Potentials. J. Phys. Chem. 1994, 98, 4831–4837. [Google Scholar] [CrossRef]
- Mackenzie, C.F.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer Model Energies and Energy Frameworks: Extension to Metal Coordination Compounds, Organic Salts, Solvates and Open-Shell Systems. IUCrJ 2017, 4, 575–587. [Google Scholar] [CrossRef] [PubMed]
- Levina, E.O.; Chernyshov, I.Y.; Voronin, A.P.; Alekseiko, L.N.; Stash, A.I.; Vener, M.V. Solving the Enigma of Weak Fluorine Contacts in the Solid State: A Periodic DFT Study of Fluorinated Organic Crystals. RSC Adv. 2019, 9, 12520–12537. [Google Scholar] [CrossRef]
- Spackman, M.A. How Reliable Are Intermolecular Interaction Energies Estimated from Topological Analysis of Experimental Electron Densities? Cryst. Growth Des. 2015, 15, 5624–5628. [Google Scholar] [CrossRef]
- Wolff, S.K.; Grimwood, J.J.; McKinnon, J.J.; Turner, M.J.; Jayatilaka, D.; Spackman, M.A. Crystal Explorer 3.1; The University of Western Australia: Perth, Australia, 2017. [Google Scholar]
- Sundareswaran, S.; Karuppannan, S. Hirshfeld Surface Analysis of Stable and Metastable Polymorphs of Vanillin. Cryst. Res. Technol. 2020, 55, 2000083. [Google Scholar] [CrossRef]
- Cecilia Davila-Miliani, M.; Dugarte-Dugarte, A.; Toro, R.A.; Contreras, J.E.; Camargo, H.A.; Antonio Henao, J.; Miguel Delgado, J.; Diaz de Delgado, G. Polymorphism in the Anti-Inflammatory Drug Flunixin and Its Relationship with Clonixin. Cryst. Growth Des. 2020, 20, 4657–4666. [Google Scholar] [CrossRef]
- Gao, L.; Hao, Y.; Zhang, X.; Huang, X.; Wang, T.; Hao, H. Polymorph Induced Diversity of Photomechanical Motions of Molecular Crystals. Crystengcomm 2020, 22, 3279–3286. [Google Scholar] [CrossRef]
- Jelsch, C.; Ejsmont, K.; Huder, L. The Enrichment Ratio of Atomic Contacts in Crystals, an Indicator Derived from the Hirshfeld Surface Analysis. IUCrJ 2014, 1, 119–128. [Google Scholar] [CrossRef]
- O’Keeffe, M.; Peskov, M.A.; Ramsden, S.J.; Yaghi, O.M. The Reticular Chemistry Structure Resource (RCSR) Database of, and Symbols for, Crystal Nets. Acc. Chem. Res. 2008, 41, 1782–1789. [Google Scholar] [CrossRef]
- TopCryst. Available online: Topcryst.com (accessed on 26 December 2020).
- Mukherjee, A.; Grobelny, P.; Thakur, T.S.; Desiraju, G.R. Polymorphs, Pseudopolymorphs, and Co-Crystals of Orcinol: Exploring the Structural Landscape with High Throughput Crystallography. Cryst. Growth Des. 2011, 11, 2637–2653. [Google Scholar] [CrossRef]
- Crystal Structure of ((carboxymethyl)(Methyl)Ammonio)Acetate. Available online: https://www.ccdc.cam.ac.uk/structures/search?id=doi:10.5517/cct3qcz&sid=DataCite (accessed on 26 December 2020).
- Baburin, I.A.; Blatov, V.A.; Carlucci, L.; Ciani, G.; Proserpio, D.M. Interpenetrated Three-Dimensional Networks of Hydrogen-Bonded Organic Species: A Systematic Analysis of the Cambridge Structural Database. Cryst. Growth Des. 2008, 8, 519–539. [Google Scholar] [CrossRef]
- Blatov, V.A.; Golov, A.A.; Yang, C.; Zeng, Q.; Kabanov, A.A. Network Topological Model of Reconstructive Solid-State Transformations. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Dmitrienko, A.O.; Buzin, M.I.; Setifi, Z.; Setifi, F.; Alexandrov, E.V.; Voronova, E.D.; Vologzhanina, A.V. Solid-State 1D → 3D Transformation of Polynitrile-Based Coordination Polymers by Dehydration Reaction. Dalton Trans. 2020, 49, 7084–7092. [Google Scholar] [CrossRef] [PubMed]
- Blatov, V.A.; Shevchenko, A.P.; Proserpio, D.M. Applied Topological Analysis of Crystal Structures with the Program Package ToposPro. Cryst. Growth Des. 2014, 14, 3576–3586. [Google Scholar] [CrossRef]
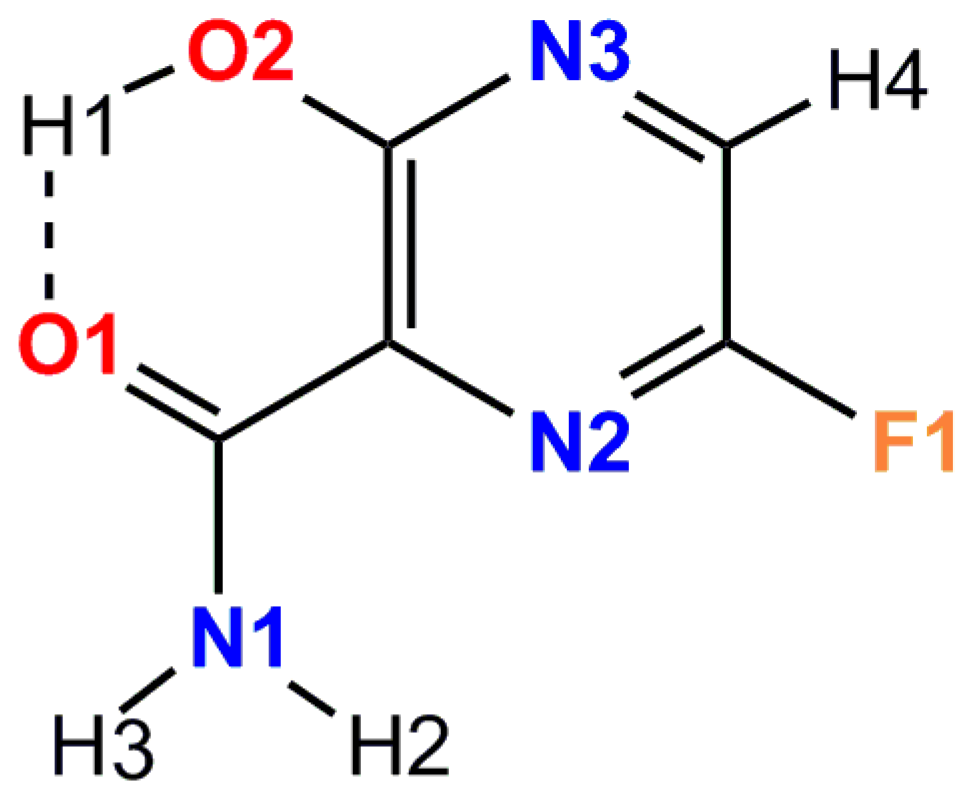
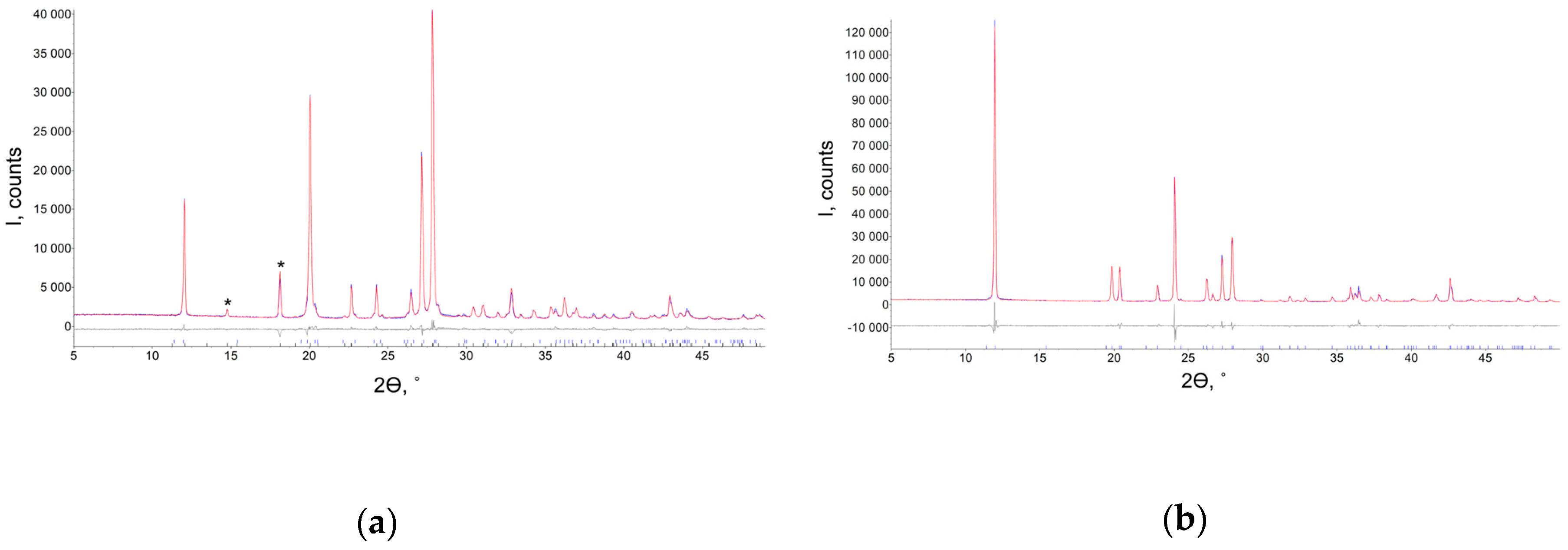

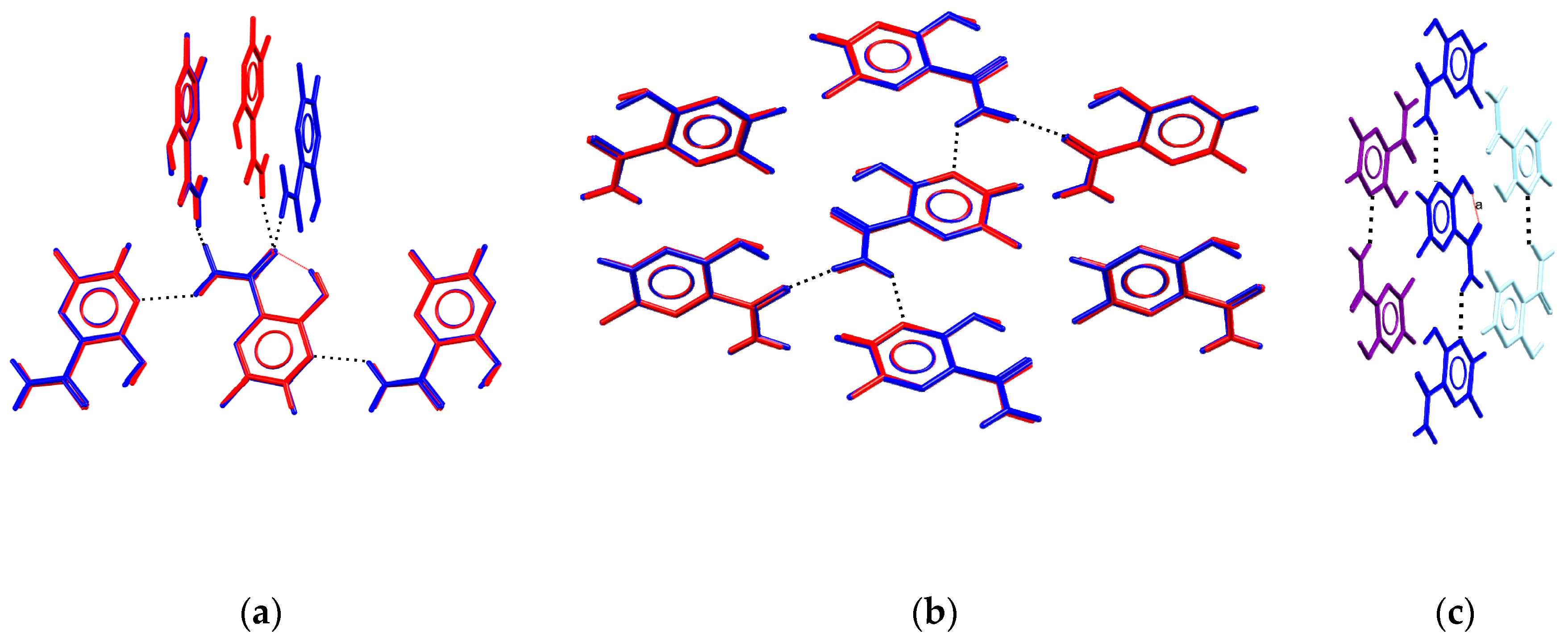
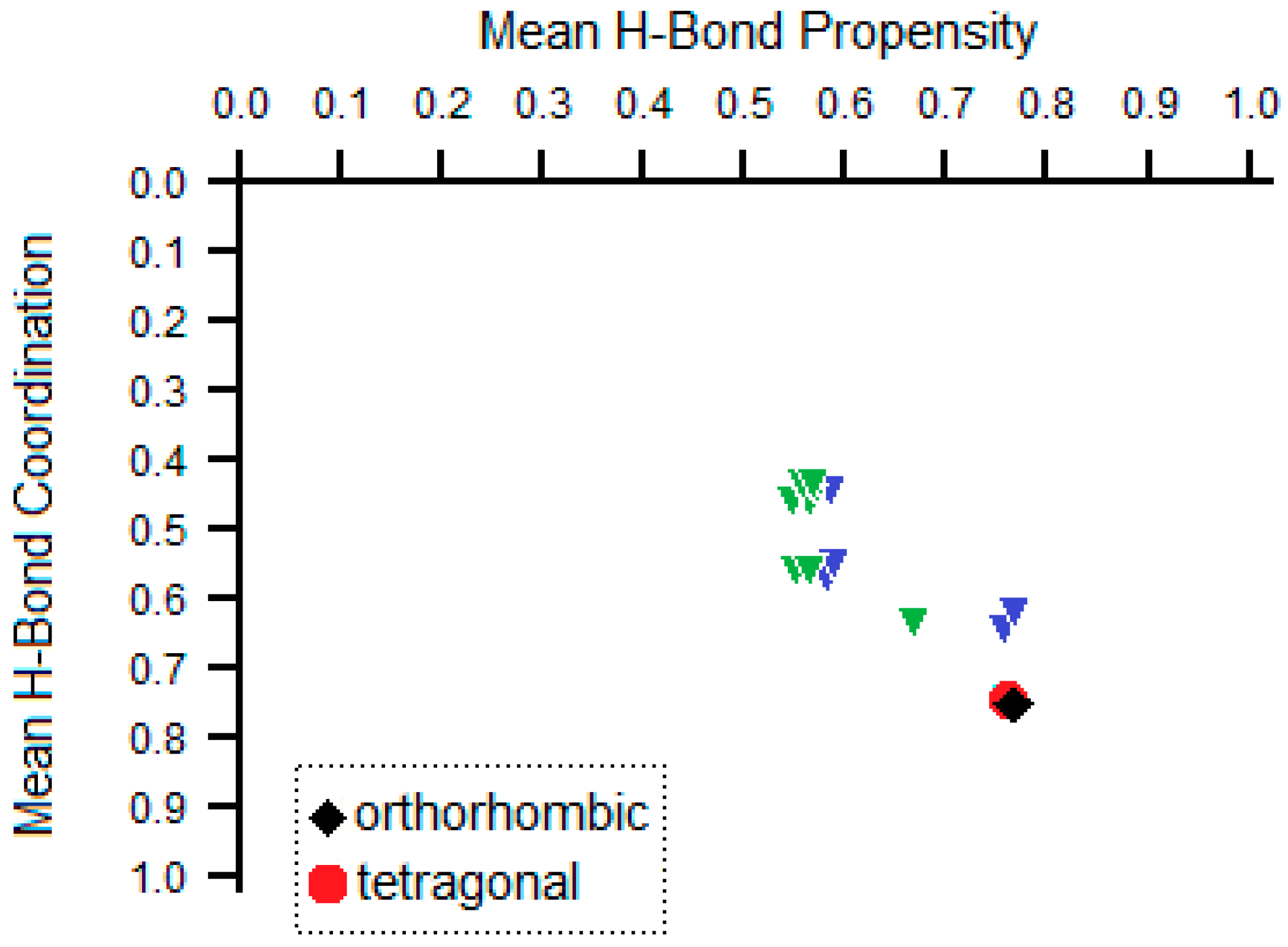
| Unit Cell Parameters | Tetragonal * | Orthorhombic ** |
|---|---|---|
| a, Å | 9.2805(7) | 9.1133(6) |
| b, Å | 9.2805(7) | 14.7708(10) |
| c, Å | 14.6491(13) | 4.6893(3) |
| V, Å3 | 1261.7(2) | 631.23(7) |
| ρ, g/cm3 | 1.6557(3) | 1.6531(2) |
| Rwp, % | 5.190 | 8.339 |
| Rbragg, % | 3.394 | 4.537 |
| Donor | Acceptor | Propensity | Observed in Orthorhombic Polymorphs | Observed in Tetragonal Polymorphs |
|---|---|---|---|---|
| Intermolecular | ||||
| NH (amide) | N3 (pyrazine) | 0.78 | Yes | Yes |
| NH (amide) | O1 (amide) | 0.77 | Yes | Yes |
| NH (amide) | N2 (pyrazine) | 0.75 | ||
| OH | N3(pyrazine) | 0.50 | ||
| OH | O1 (amide) | 0.48 | ||
| OH | N2 (pyrazine) | 0.46 | ||
| NH (amide) | OH | 0.42 | ||
| OH | OH | 0.17 | ||
| Intramolecular | ||||
| NH (amide) | OH | 0.88 | ||
| OH | O1 (amide) | 0.84 | Yes | Yes |
| NH (amide) | N2 (pyrazine) | 0.62 | ||
| D-H...A a | d(D-H), Å | d(H...A), Å | d(D...A), Å | <(DHA), ° | ρ(r) b, a.u. | ∇2ρ(r) b, a.u. | Eint b, kJ/mol |
|---|---|---|---|---|---|---|---|
| Orthorhombic Polymorph | |||||||
| O2-H1...O1 | 1.017 | 1.602 | 2.545 | 152 | 0.064 | 0.142 | −93.9 |
| N1-H3...O1#1 | 1.030 | 1.817 | 2.836 | 169 | 0.035 | 0.084 | −37.8 |
| N1-H2...N3#2 | 1.024 | 2.144 | 2.981 | 138 | 0.021 | 0.062 | −18.9 |
| C4-H4...O1#3 | 1.092 | 2.386 | 3.391 | 152 | 0.010 | 0.040 | −8.1 |
| C4-H4...F1#4 | 1.092 | 2.861 | 3.447 | 114 | 0.001 | 0.008 | −1.0 |
| Tetragonal Polymorph | |||||||
| O2-H1...O1 | 1.017 | 1.599 | 2.543 | 152 | 0.064 | 0.144 | −93.9 |
| N1-H3...O1#5 | 1.029 | 1.820 | 2.839 | 170 | 0.035 | 0.083 | −37.2 |
| N1-H2...N3#6 | 1.023 | 2.202 | 3.018 | 135 | 0.019 | 0.058 | −16.2 |
| C4-H4...O1#7 | 1.091 | 2.406 | 3.381 | 148 | 0.010 | 0.039 | −7.8 |
| C4-H4...F1#8 | 1.091 | 2.795 | 3.346 | 111 | 0.004 | 0.019 | −2.8 |
| Interaction | RXY, % | CXY, a % | EXY | ||
|---|---|---|---|---|---|
| Orthorhombic | Tetragonal | Orthorhombic | Tetragonal | ||
| O...H | 7.1 | 18.2 | 19.0 | 2.6 | 2.7 |
| N...H | 10.7 | 11.2 | 12.9 | 1.1 | 1.2 |
| F...H | 3.6 | 14.9 | 11.2 | 4.2 | 3.2 |
| C..H | 17.8 | 9.5 | 8.1 | 0.5 | 0.5 |
| C...C | 11.1 | 0.0 | 1.7 | 0.0 | 0.2 |
| H...H | 7.1 | 12.7 | 13.6 | 1.8 | 1.9 |
| O...O | 1.8 | 0.0 | 0.3 | 0.0 | 0.2 |
| O...N | 5.3 | 4.6 | 4.3 | 0.9 | 0.8 |
| O...C | 8.9 | 7.0 | 7.4 | 0.8 | 0.8 |
| N...C | 13.3 | 8.1 | 6.0 | 0.6 | 0.5 |
| N...N | 4.0 | 3.8 | 4.1 | 1.0 | 1.0 |
| F...F | 0.4 | 3.7 | 5.3 | 8.3 | 11.9 |
| F...O | 1.8 | 4.5 | 2.9 | 2.5 | 1.6 |
| F...N | 2.7 | 0.2 | 1.3 | 0.1 | 0.5 |
| F...C | 4.4 | 1.4 | 1.9 | 0.3 | 0.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goloveshkin, A.S.; Korlyukov, A.A.; Vologzhanina, A.V. Novel Polymorph of Favipiravir—An Antiviral Medication. Pharmaceutics 2021, 13, 139. https://doi.org/10.3390/pharmaceutics13020139
Goloveshkin AS, Korlyukov AA, Vologzhanina AV. Novel Polymorph of Favipiravir—An Antiviral Medication. Pharmaceutics. 2021; 13(2):139. https://doi.org/10.3390/pharmaceutics13020139
Chicago/Turabian StyleGoloveshkin, Alexander S., Alexander A. Korlyukov, and Anna V. Vologzhanina. 2021. "Novel Polymorph of Favipiravir—An Antiviral Medication" Pharmaceutics 13, no. 2: 139. https://doi.org/10.3390/pharmaceutics13020139
APA StyleGoloveshkin, A. S., Korlyukov, A. A., & Vologzhanina, A. V. (2021). Novel Polymorph of Favipiravir—An Antiviral Medication. Pharmaceutics, 13(2), 139. https://doi.org/10.3390/pharmaceutics13020139






