HCV Spread Kinetics Reveal Varying Contributions of Transmission Modes to Infection Dynamics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Methods
2.1.1. Cells and Virus
2.1.2. Reagents
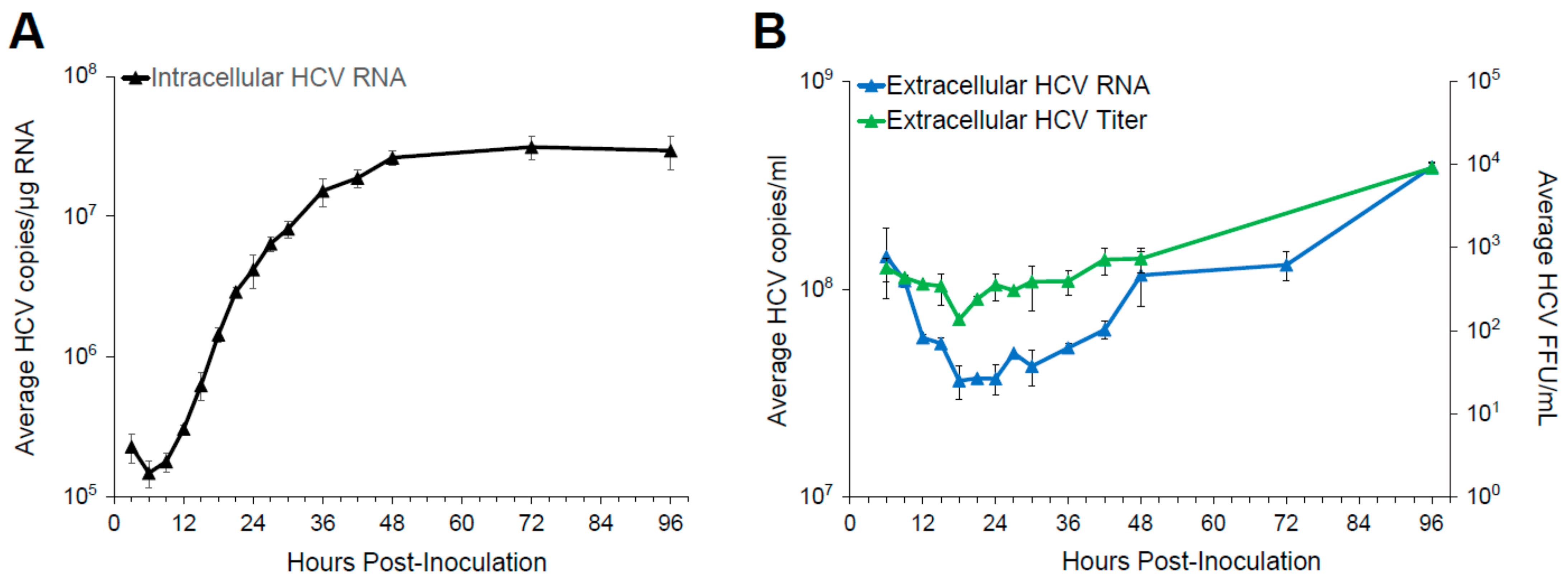
2.1.3. High MOI HCV Life Cycle Kinetics
2.1.4. RNA Isolation and Quantification
2.1.5. HCV Titer Assay
2.1.6. HCV Immunohistochemical Staining
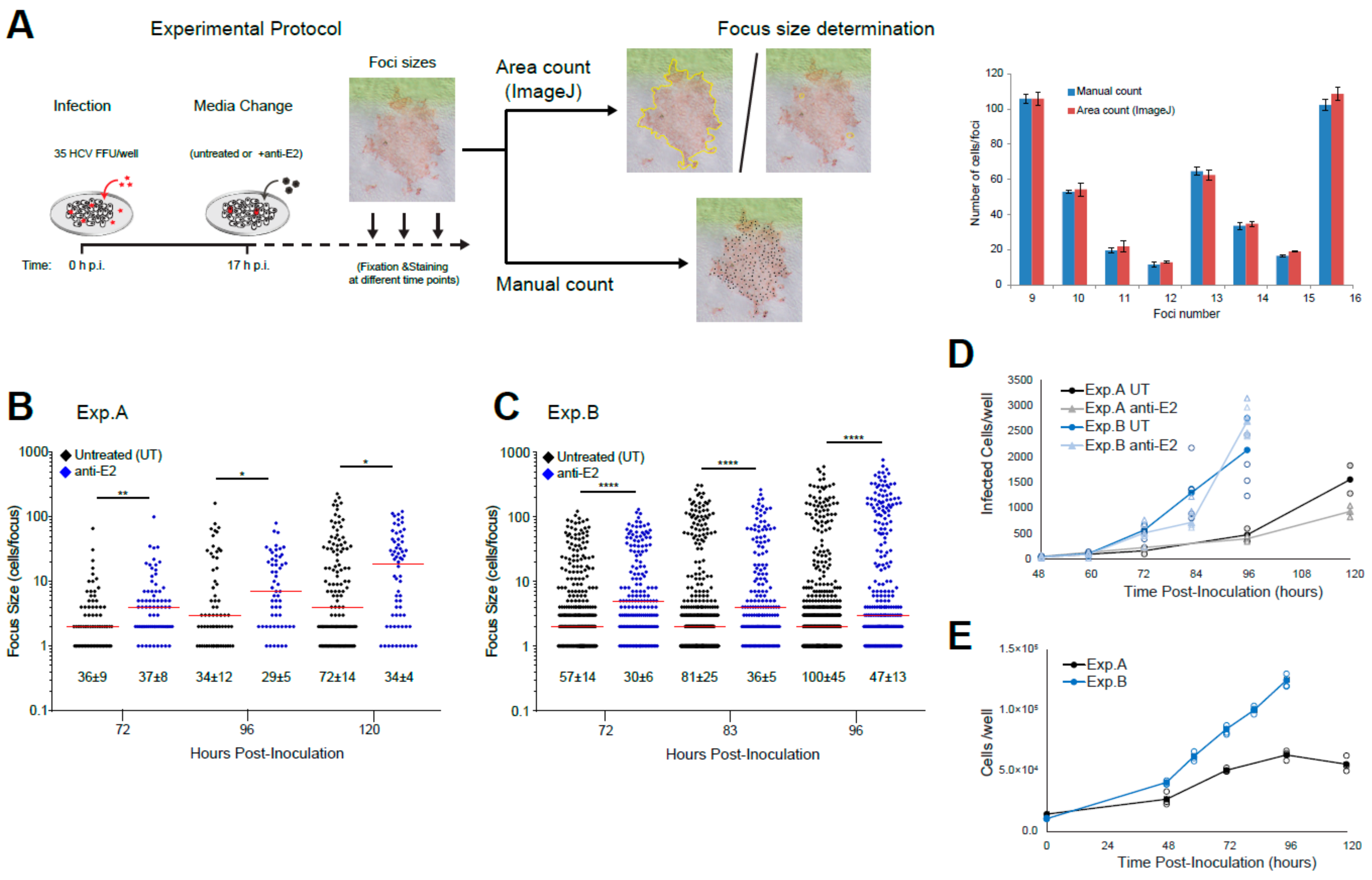
2.1.7. Spread Assay
2.1.8. Quantifying Foci Size
2.2. Mathematical Modeling
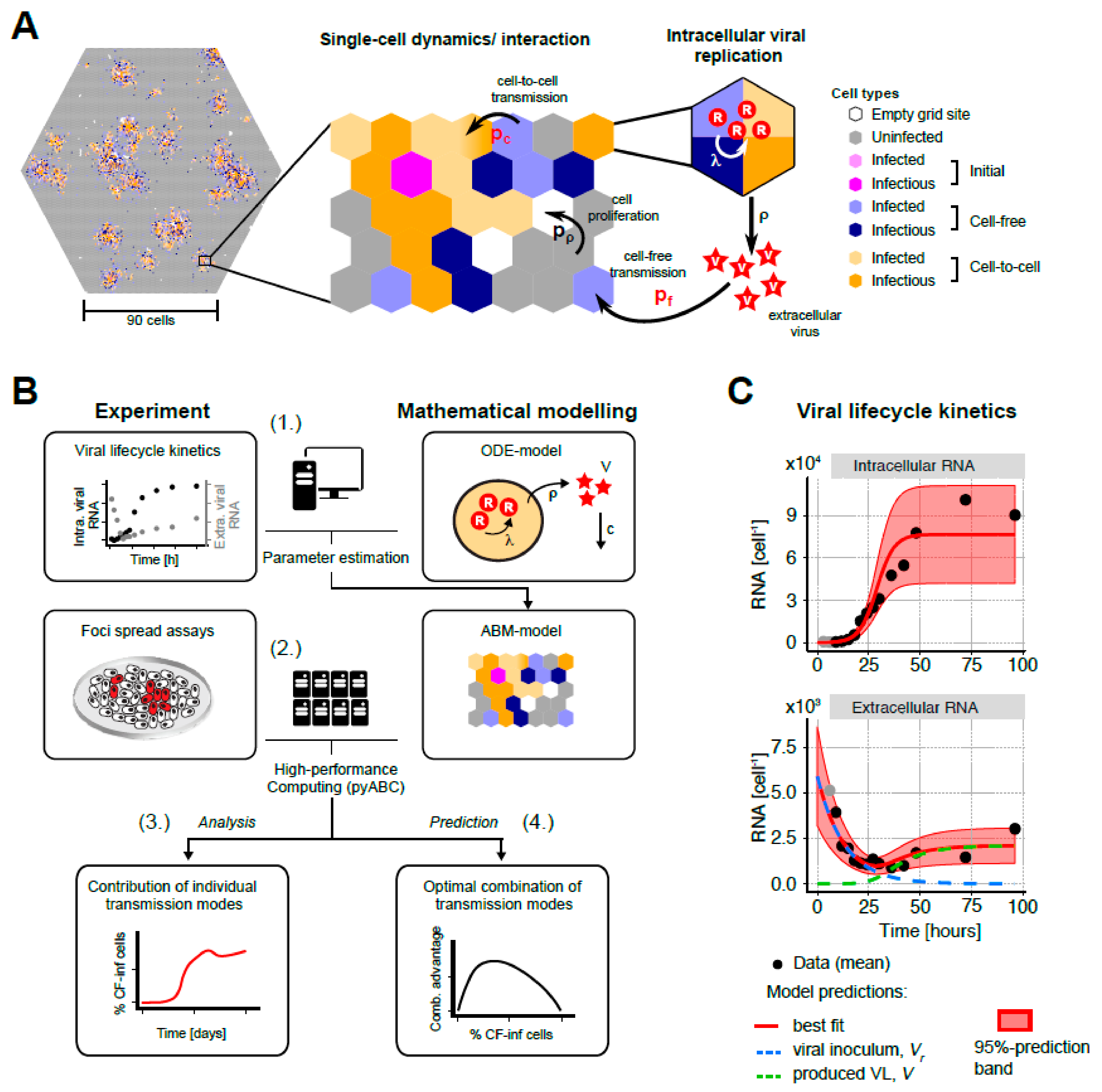
2.2.1. Modeling Viral Life Cycle Kinetics
2.2.2. A Multi-Scale Model to Describe HCV Infection Dynamics
2.2.3. Parameter Inference
2.2.4. Parameter Fitting by pyABC
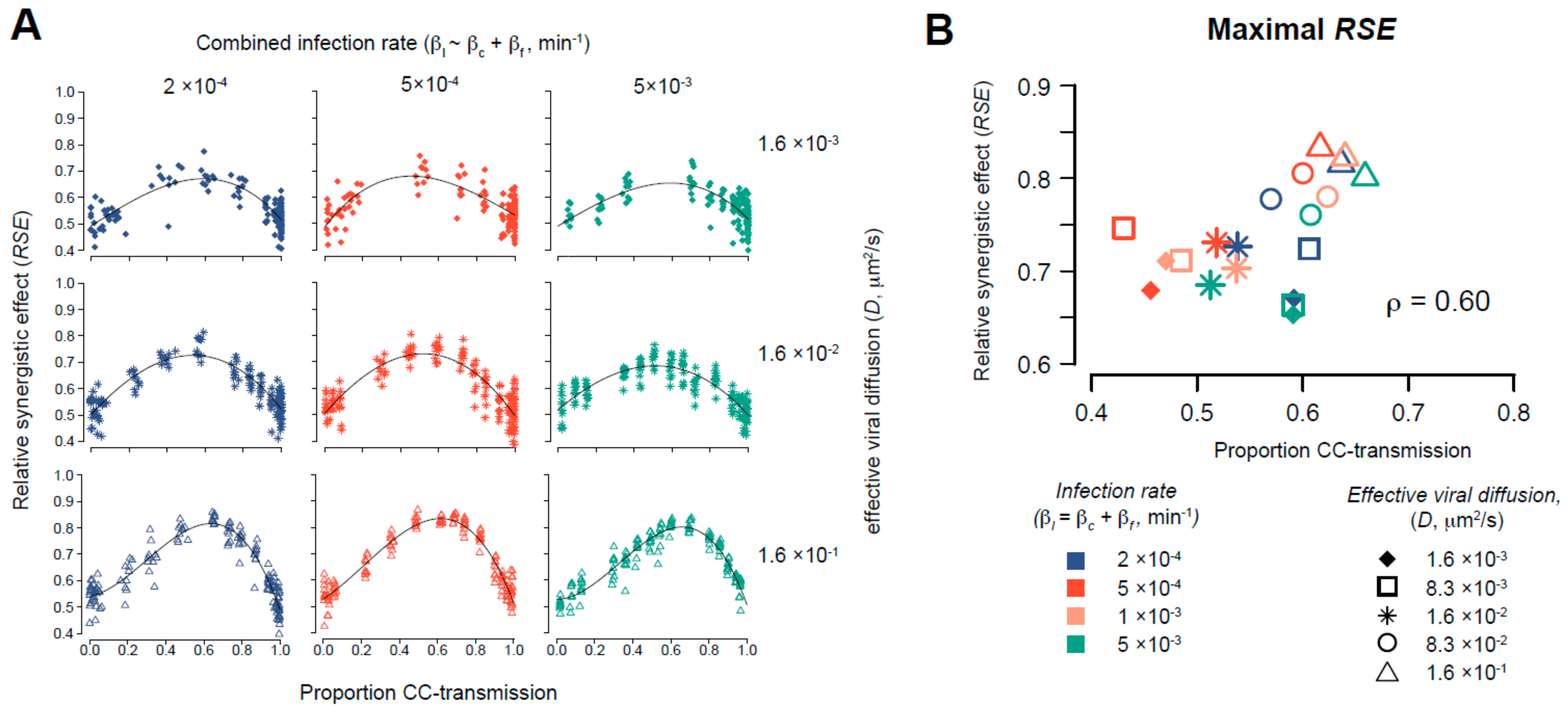
2.3. Evaluating the Synergistic Effect of Simultaneous Occurrence of Cell-Free and Cell-to-Cell Transmission
2.4. Statistical Analysis
3. Results
3.1. Single Round Infection Kinetics Defines the Timing of Viral Life Cycle
3.2. Experimentally Monitoring Viral Spread
3.3. A Multi-Scale Mathematical Model to Analyze HCV Spread Kinetics
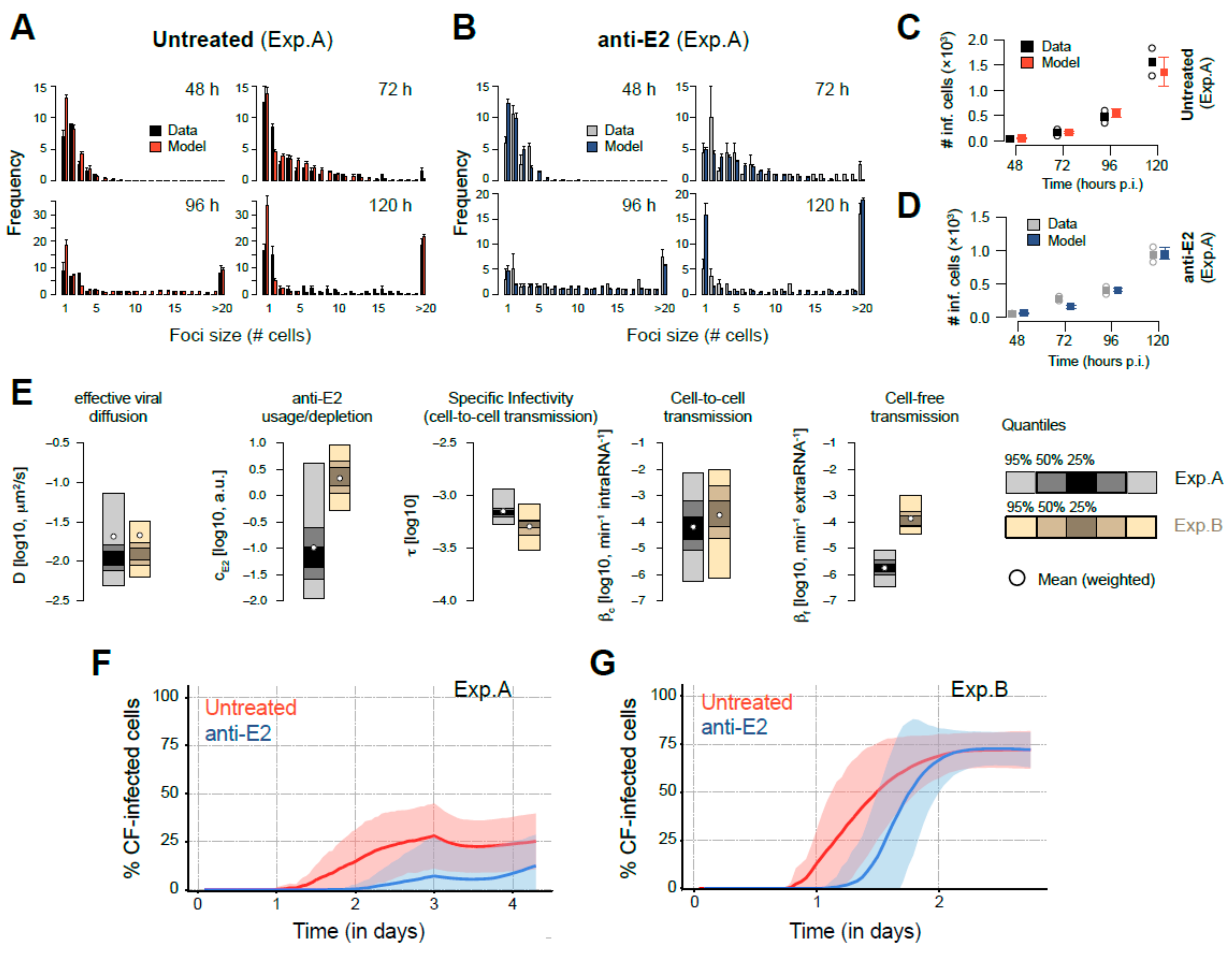
3.4. Mathematical Analysis Allows Determination of Transmission Kinetics and Reveals Varying Contributions of Viral Transmission Modes to HCV Spread
3.5. Simultaneous Occurrence of Cell-Free and Cell-to-Cell Transmission Enhances Viral Spread
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhong, P.; Agosto, L.M.; Munro, J.B.; Mothes, W. Cell-to-cell transmission of viruses. Curr. Opin. Virol. 2013, 3, 44–50. [Google Scholar] [CrossRef] [Green Version]
- Sattentau, Q. Avoiding the void: Cell-to-cell spread of human viruses. Nat. Rev. Microbiol. 2008, 6, 815–826. [Google Scholar] [CrossRef]
- Sewald, X.; Motamedi, N.; Mothes, W. Viruses exploit the tissue physiology of the host to spread in vivo. Curr. Opin. Cell Biol. 2016, 41, 81–90. [Google Scholar] [CrossRef] [Green Version]
- Timpe, J.M.; Stamataki, Z.; Jennings, A.; Hu, K.; Farquhar, M.J.; Harris, H.J.; Schwarz, A.; Desombere, I.; Roels, G.L.; Balfe, P.; et al. Hepatitis C virus cell-cell transmission in hepatoma cells in the presence of neutralizing antibodies. Hepatology 2008, 47, 17–24. [Google Scholar] [CrossRef]
- Brimacombe, C.L.; Grove, J.; Meredith, L.W.; Hu, K.; Syder, A.J.; Flores, M.V.; Timpe, J.M.; Krieger, S.E.; Baumert, T.F.; Tellinghuisen, T.L.; et al. Neutralizing antibody-resistant hepatitis C virus cell-to-cell transmission. J. Virol. 2011, 85, 596–605. [Google Scholar] [CrossRef] [Green Version]
- Abela, I.A.; Berlinger, L.; Schanz, M.; Reynell, L.; Gunthard, H.F.; Rusert, P.; Trkola, A. Cell-cell transmission enables HIV-1 to evade inhibition by potent CD4bs directed antibodies. PLoS Pathog. 2012, 8, e1002634. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.; Hubner, W.; Spinelli, M.A.; Chen, B.K. Predominant mode of human immunodeficiency virus transfer between T cells is mediated by sustained Env-dependent neutralization-resistant virological synapses. J. Virol. 2007, 81, 12582–12595. [Google Scholar] [CrossRef] [Green Version]
- Sigal, A.; Kim, J.T.; Balazs, A.B.; Dekel, E.; Mayo, A.; Milo, R.; Baltimore, D. Cell-to-cell spread of HIV permits ongoing replication despite antiretroviral therapy. Nature 2011, 477, 95–98. [Google Scholar] [CrossRef] [PubMed]
- Barretto, N.; Sainz, B.; Hussain, S., Jr.; Uprichard, S.L. Determining the involvement and therapeutic implications of host cellular factors in hepatitis C virus cell-to-cell spread. J. Virol. 2014, 88, 5050–5061. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barretto, N.; Uprichard, S.L. Hepatitis C virus Cell-to-cell Spread Assay. Bio-Protoc. 2014, 4, e1365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martin, D.N.; Uprichard, S.L. Identification of transferrin receptor 1 as a hepatitis C virus entry factor. Proc. Natl. Acad. Sci. USA 2013, 110, 10777–10782. [Google Scholar] [CrossRef] [Green Version]
- Graw, F.; Perelson, A.S. Modeling Viral Spread. Annu. Rev. Virol. 2016, 3, 555–572. [Google Scholar] [CrossRef] [Green Version]
- Dahari, H.; Ribeiro, R.M.; Rice, C.M.; Perelson, A.S. Mathematical modeling of subgenomic hepatitis C virus replication in Huh-7 cells. J. Virol. 2007, 81, 750–760. [Google Scholar] [CrossRef] [Green Version]
- Graw, F.; Martin, D.N.; Perelson, A.S.; Uprichard, S.L.; Dahari, H. Quantification of Hepatitis C Virus Cell-to-Cell Spread Using a Stochastic Modeling Approach. J. Virol. 2015, 89, 6551–6561. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guedj, J.; Dahari, H.; Rong, L.; Sansone, N.D.; Nettles, R.E.; Cotler, S.J.; Layden, T.J.; Uprichard, S.L.; Perelson, A.S. Modeling shows that the NS5A inhibitor daclatasvir has two modes of action and yields a shorter estimate of the hepatitis C virus half-life. Proc. Natl. Acad. Sci. USA 2013, 110, 3991–3996. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neumann, A.U.; Lam, N.P.; Dahari, H.; Gretch, D.R.; Wiley, T.E.; Layden, T.J.; Perelson, A.S. Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-alpha therapy. Science 1998, 282, 103–107. [Google Scholar] [CrossRef] [PubMed]
- Kumberger, P.; Durso-Cain, K.; Uprichard, S.L.; Dahari, H.; Graw, F. Accounting for Space-Quantification of Cell-To-Cell Transmission Kinetics Using Virus Dynamics Models. Viruses 2018, 10, 200. [Google Scholar] [CrossRef] [Green Version]
- Zhong, J.; Gastaminza, P.; Cheng, G.; Kapadia, S.; Kato, T.; Burton, D.R.; Wieland, S.F.; Uprichard, S.L.; Wakita, T.; Chisari, F.V. Robust hepatitis C virus infection in vitro. Proc. Natl. Acad. Sci. USA 2005, 102, 9294–9299. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wakita, T.; Pietschmann, T.; Kato, T.; Date, T.; Miyamoto, M.; Zhao, Z.; Murthy, K.; Habermann, A.; Kräusslich, H.-G.; Mizokami, M.; et al. Production of infectious hepatitis C virus in tissue culture from a cloned viral genome. Nat. Med. 2005, 11, 791–796. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Uprichard, S.L. Cell-based hepatitis C virus infection fluorescence resonance energy transfer (FRET) assay for antiviral compound screening. Curr. Protoc. Microbiol. 2010, 18, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Law, M.; Maruyama, T.; Lewis, J.; Giang, E.; Tarr, A.W.; Stamataki, Z.; Gastaminza, P.; Chisari, F.; Jones, I.M.; Fox, R.I.; et al. Broadly neutralizing antibodies protect against hepatitis C virus quasispecies challenge. Nat. Med. 2008, 14, 25–27. [Google Scholar] [CrossRef]
- Lindenbach, B.D.; Evans, M.J.; Syder, A.J.; Wölk, B.; Tellinghuisen, T.L.; Liu, C.C.; Maruyama, T.; Hynes, R.O.; Burton, D.R.; McKeating, J.A.; et al. Complete replication of hepatitis C virus in cell culture. Science 2005, 309, 623–626. [Google Scholar] [CrossRef] [Green Version]
- Sainz, B., Jr.; Chisari, F.V. Production of infectious hepatitis C virus by well-differentiated, growth-arrested human hepatoma-derived cells. J. Virol. 2006, 80, 10253–10257. [Google Scholar] [CrossRef] [Green Version]
- Raue, A.; Kreutz, C.; Maiwald, T.; Bachmann, J.; Schilling, M.; Klingmuller, U.; Timmer, J. Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics 2009, 25, 1923–1929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Funk, G.A.; Jansen, V.A.; Bonhoeffer, S.; Killingback, T. Spatial models of virus-immune dynamics. J. Theor. Biol. 2005, 233, 221–236. [Google Scholar] [CrossRef]
- Imle, A.; Kumberger, P.; Schnellbacher, N.D.; Fehr, J.; Carrillo-Bustamante, P.; Ales, J.; Schmidt, P.; Ritter, C.; Godinez, W.J.; Müller, B.; et al. Experimental and computational analyses reveal that environmental restrictions shape HIV-1 spread in 3D cultures. Nat. Commun. 2019, 10, 2144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iwami, S.; Takeuchi, J.S.; Nakaoka, S.; Mammano, F.; Clavel, F.; Inaba, H.; Kobayashi, T.; Misawa, N.; Aihara, K.; Koyanagi, Y.; et al. Cell-to-cell infection by HIV contributes over half of virus infection. eLife 2015, 4, e08150. [Google Scholar] [CrossRef]
- Toni, T.; Welch, D.; Strelkowa, N.; Ipsen, A.; Stumpf, M.P. Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. J. R. Soc. Interface 2009, 6, 187–202. [Google Scholar] [CrossRef] [Green Version]
- Klinger, E.; Rickert, D.; Hasenauer, J. pyABC: Distributed, likelihood-free inference. Bioinformatics 2018, 34, 3591–3593. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jagiella, N.; Rickert, D.; Theis, F.J.; Hasenauer, J. Parallelization and High-Performance Computing Enables Automated Statistical Inference of Multi-scale Models. Cell Syst. 2017, 4, 194–206.e9. [Google Scholar] [CrossRef] [Green Version]
- Costiniuk, C.T.; Jenabian, M.A. Cell-to-cell transfer of HIV infection: Implications for HIV viral persistence. J. Gen. Virol. 2014, 95, 2346–2355. [Google Scholar] [CrossRef]
- Ahmed, S.S.; Bundgaard, N.; Graw, F.; Fackler, O.T. Environmental Restrictions: A New Concept Governing HIV-1 Spread Emerging from Integrated Experimental-Computational Analysis of Tissue-Like 3D Cultures. Cells 2020, 9, 1112. [Google Scholar] [CrossRef] [PubMed]
- Fackler, O.T.; Murooka, T.T.; Imle, A.; Mempel, T.R. Adding new dimensions: Towards an integrative understanding of HIV-1 spread. Nat. Rev. Microbiol. 2014, 12, 563–574. [Google Scholar] [CrossRef]
- Sabahi, A.; Marsh, K.A.; Dahari, H.; Corcoran, P.; Lamora, J.M.; Yu, X.; Garry, R.F.; Uprichard, S.L. The rate of hepatitis C virus infection initiation in vitro is directly related to particle density. Virology 2010, 407, 110–119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Targett-Adams, P.; Boulant, S.; Douglas, M.W.; McLauchlan, J. Lipid metabolism and HCV infection. Viruses 2010, 2, 1195–1217. [Google Scholar] [CrossRef] [Green Version]
- Burlone, M.E.; Budkowska, A. Hepatitis C virus cell entry: Role of lipoproteins and cellular receptors. J. Gen. Virol. 2009, 90, 1055–1070. [Google Scholar] [CrossRef] [PubMed]
- Vieyres, G.; Pietschmann, T. HCV Pit Stop at the Lipid Droplet: Refuel Lipids and Put on a Lipoprotein Coat before Exit. Cells 2019, 8, 233. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kandathil, A.J.; Graw, F.; Quinn, J.; Hwang, H.S.; Torbenson, M.; Perelson, A.S.; Ray, S.; Thomas, D.L.; Ribeiro, R.; Balagopal, A. Use of laser capture microdissection to map hepatitis C virus-positive hepatocytes in human liver. Gastroenterology 2013, 145, 1404–1413.e10. [Google Scholar] [CrossRef] [Green Version]
- Wieland, S.; Makowska, Z.; Campana, B.; Calabrese, D.; Dill, M.T.; Chung, J.; Chisari, F.V.; Heim, M.H. Simultaneous detection of hepatitis C virus and interferon stimulated gene expression in infected human liver. Hepatology 2014, 59, 2121–2130. [Google Scholar] [CrossRef]
- Stiffler, J.D.; Nguyen, M.; Sohn, J.A.; Liu, C.; Kaplan, D.; Seeger, C. Focal distribution of hepatitis C virus RNA in infected livers. PLoS ONE 2009, 4, e6661. [Google Scholar] [CrossRef] [Green Version]
- Graw, F.; Balagopal, A.; Kandathil, A.J.; Ray, S.C.; Thomas, D.L.; Ribeiro, R.M.; Perelson, A.S. Inferring viral dynamics in chronically HCV infected patients from the spatial distribution of infected hepatocytes. PLoS Comput. Biol. 2014, 10, e1003934. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Starruß, J.; de Back, W.; Brusch, L.; Deutsch, A. Morpheus: A user-friendly modeling environment for multiscale and multicellular systems biology. Bioinformatics. 2014, 30, 1331–1332. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Catanese, M.T.; Loureiro, J.; Jones, C.T.; Dorner, M.; von Hahn, T.; Rice, C.M. Different requirements for scavenger receptor class B type I in hepatitis C virus cell-free versus cell-to-cell transmission. J. Virol. 2013, 87, 8282–8293. [Google Scholar] [CrossRef] [PubMed] [Green Version]
| Description | Parameter | Unit | Experiment | |
|---|---|---|---|---|
| Exp. A | Exp. B | |||
| Cell-to-Cell transmission rate (i.e., scaling factor) | βc | log10, min−1 intraRNA−1 | −4.19 (−6.24–−2.15) | −3.74 (−6.13–−2.02) |
| Cell-free transmission rate (i.e., scaling factor) | βf | log10, min−1 extraRNA−1 | −5.75 (−6.48–−5.05) | −3.87 (−4.46–−3.00) |
| Rate of anti-E2 usage/depletion due to neutralization of extracellular RNA | cE2 | log10, arbitrary unit min−1 | −0.98 (−1.95–0.62) | 0.33 (−0.27–0.95) |
| Specific infectivity for cell-to-cell transmission | τ | log10 | −3.15 (−3.27–−2.93) | −3.29 (−3.52–−3.07) |
| Viral diffusion coefficient * | D | log10, μm2/s | −1.68 (−1.96–−0.91) | −1.67 (−1.91–−1.27) |
| Treatment | Infected Cells (Mean) | Fraction of Cells Infected by CF | Fold Increase | Expected Fold Increase | |
|---|---|---|---|---|---|
| Experiment (Exp. A) | anti-E2 | 937.5 | - | 1 | - |
| untreated | 1559.5 | - | 1.66 | - | |
| Simulation * (ABM) | anti-E2 | 1028 | 0 | 1 | - |
| untreated | 1650 | 0.22 | 1.61 | 1.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Durso-Cain, K.; Kumberger, P.; Schälte, Y.; Fink, T.; Dahari, H.; Hasenauer, J.; Uprichard, S.L.; Graw, F. HCV Spread Kinetics Reveal Varying Contributions of Transmission Modes to Infection Dynamics. Viruses 2021, 13, 1308. https://doi.org/10.3390/v13071308
Durso-Cain K, Kumberger P, Schälte Y, Fink T, Dahari H, Hasenauer J, Uprichard SL, Graw F. HCV Spread Kinetics Reveal Varying Contributions of Transmission Modes to Infection Dynamics. Viruses. 2021; 13(7):1308. https://doi.org/10.3390/v13071308
Chicago/Turabian StyleDurso-Cain, Karina, Peter Kumberger, Yannik Schälte, Theresa Fink, Harel Dahari, Jan Hasenauer, Susan L. Uprichard, and Frederik Graw. 2021. "HCV Spread Kinetics Reveal Varying Contributions of Transmission Modes to Infection Dynamics" Viruses 13, no. 7: 1308. https://doi.org/10.3390/v13071308
APA StyleDurso-Cain, K., Kumberger, P., Schälte, Y., Fink, T., Dahari, H., Hasenauer, J., Uprichard, S. L., & Graw, F. (2021). HCV Spread Kinetics Reveal Varying Contributions of Transmission Modes to Infection Dynamics. Viruses, 13(7), 1308. https://doi.org/10.3390/v13071308






