Modeling within-Host SARS-CoV-2 Infection Dynamics and Potential Treatments
Abstract
1. Introduction
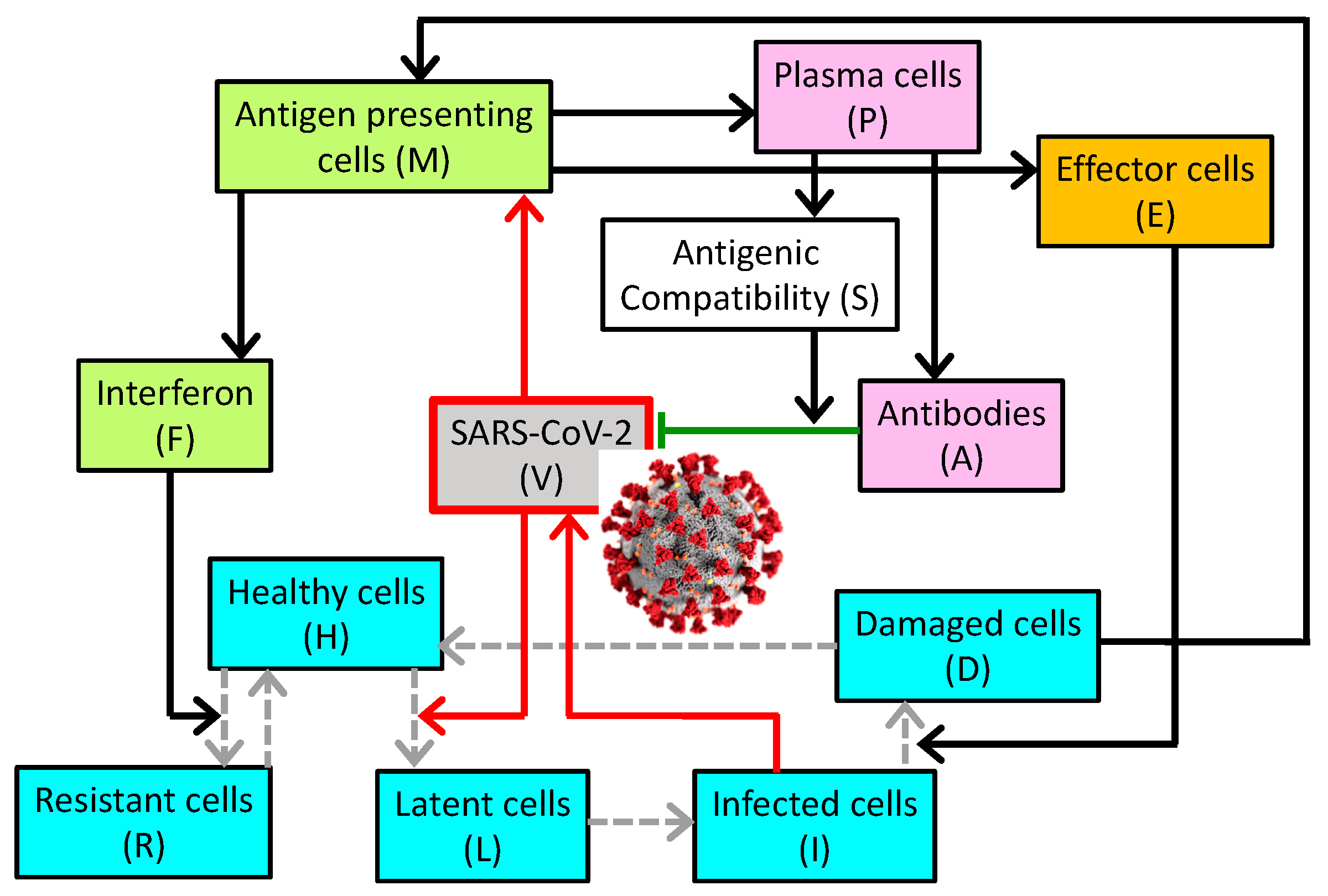
2. Materials and Methods
3. Results
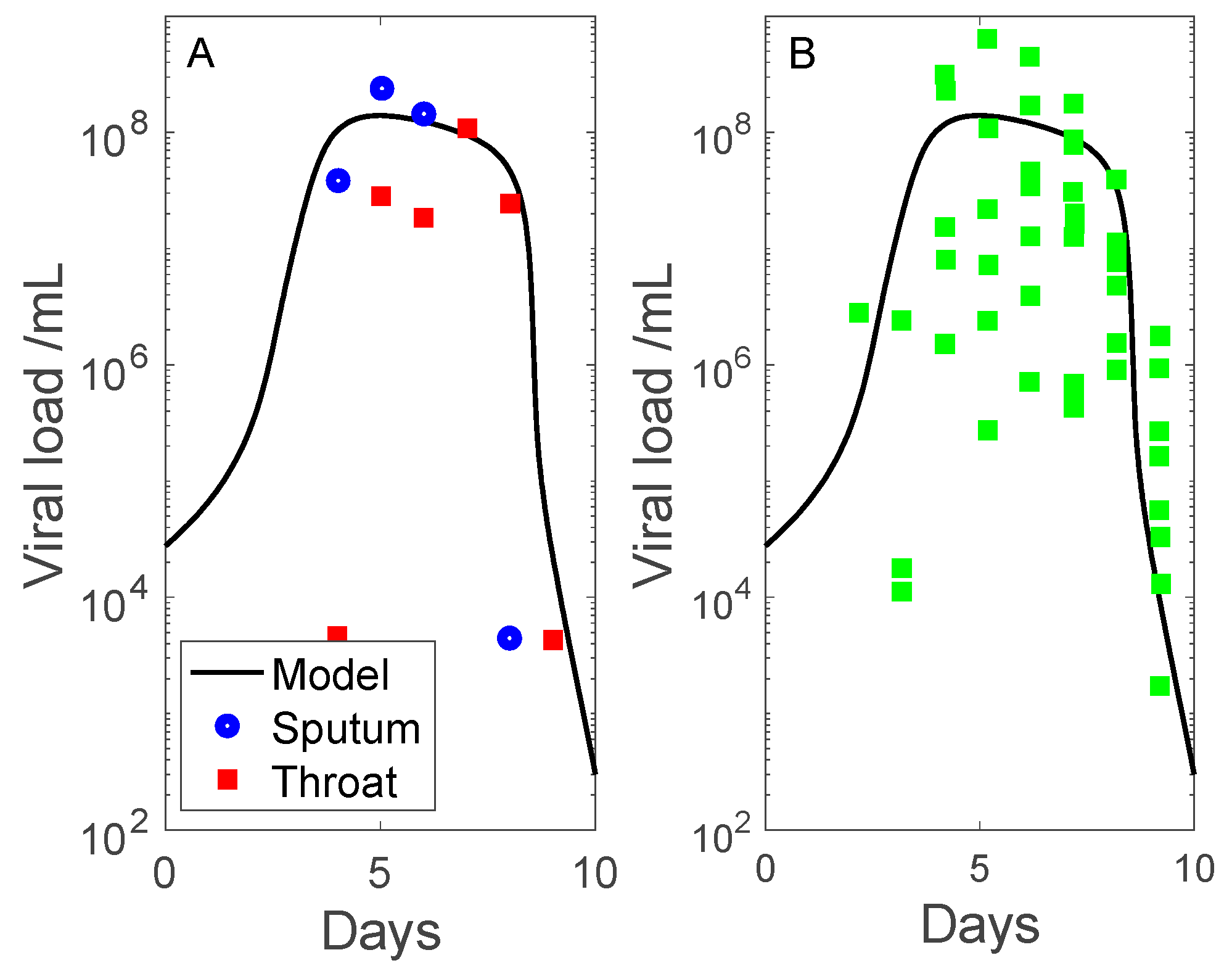
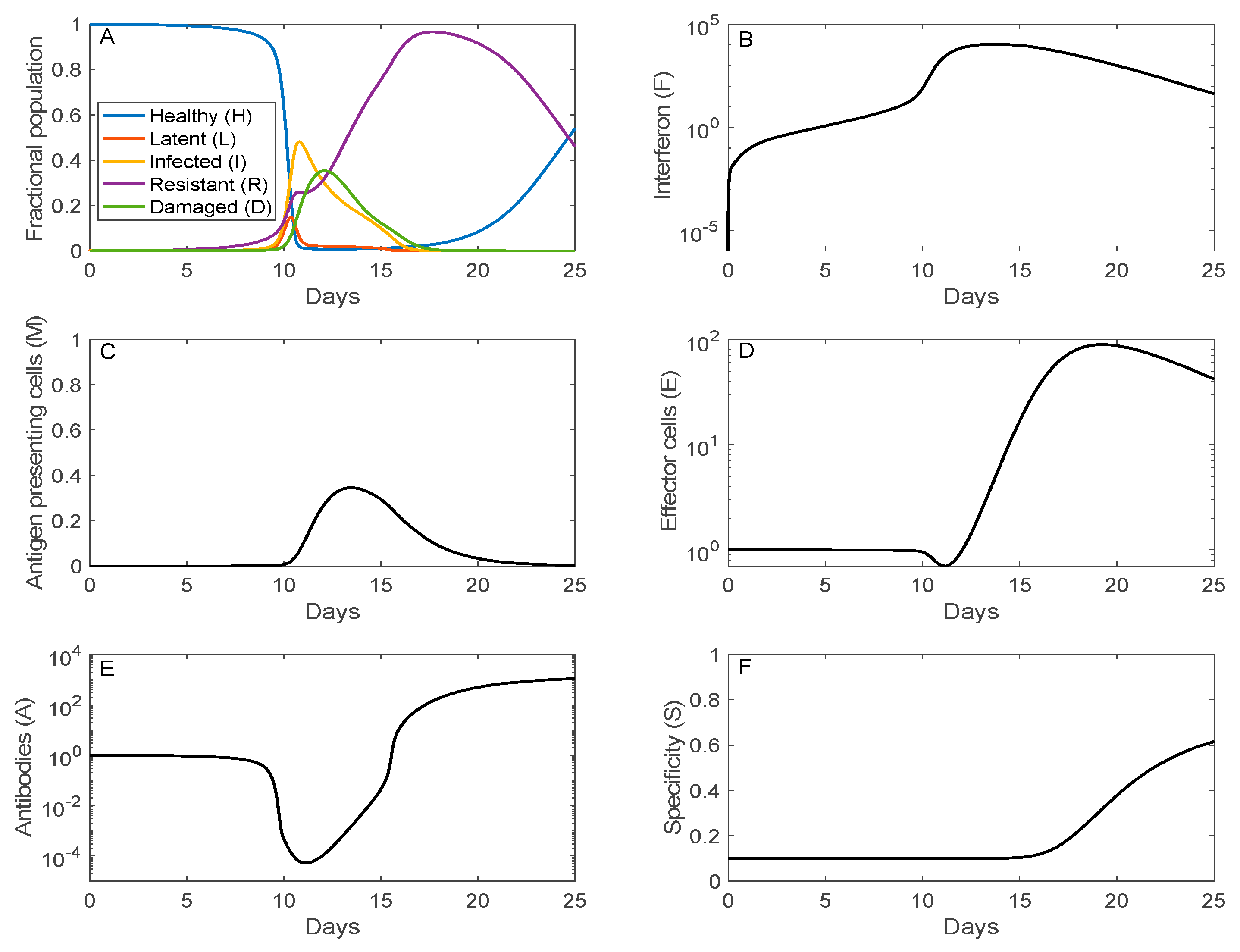
3.1. Simulation of SARS-CoV-2 Infection
3.2. Sensitivity Analysis
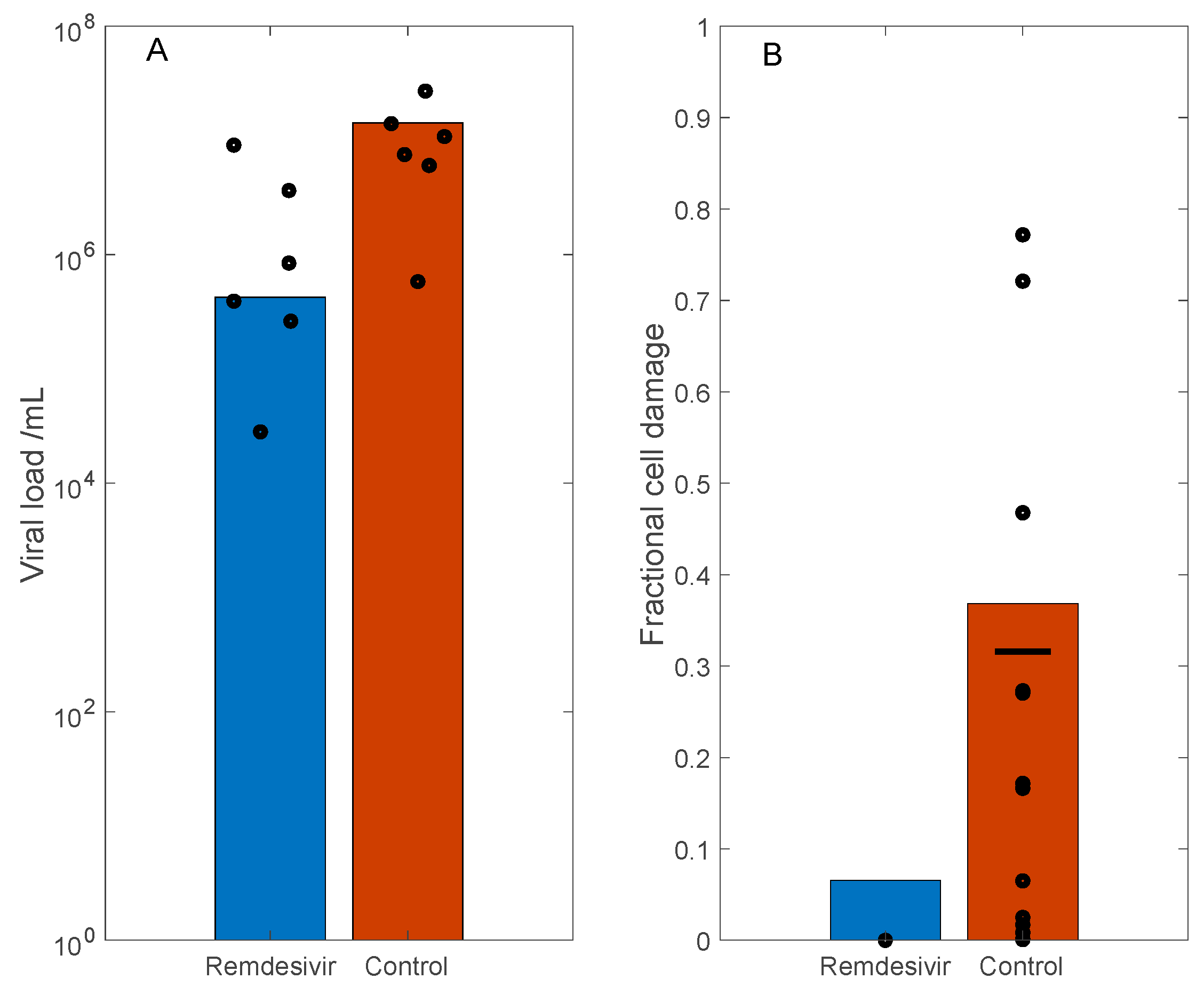
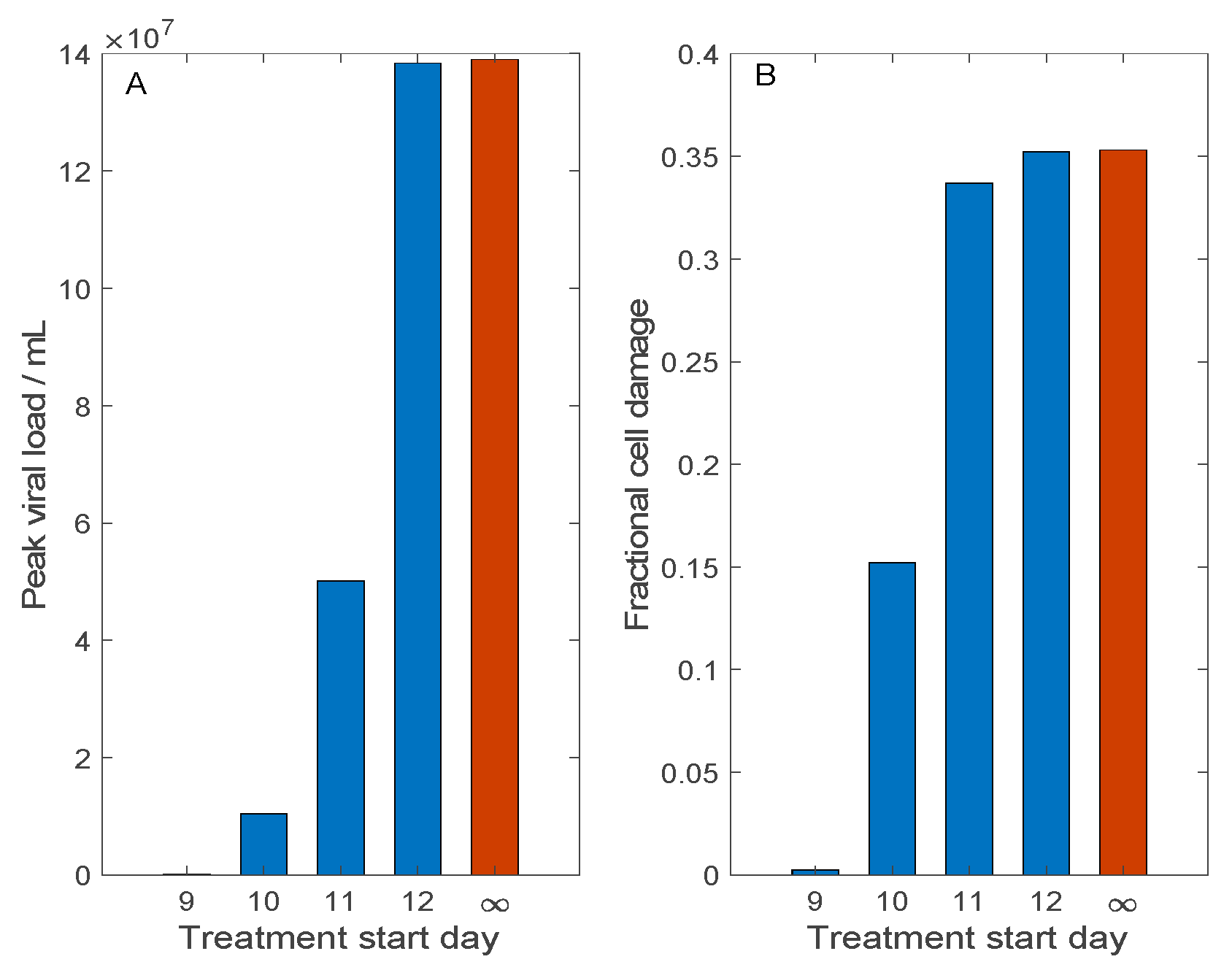
3.3. Simulation of Remdesivir
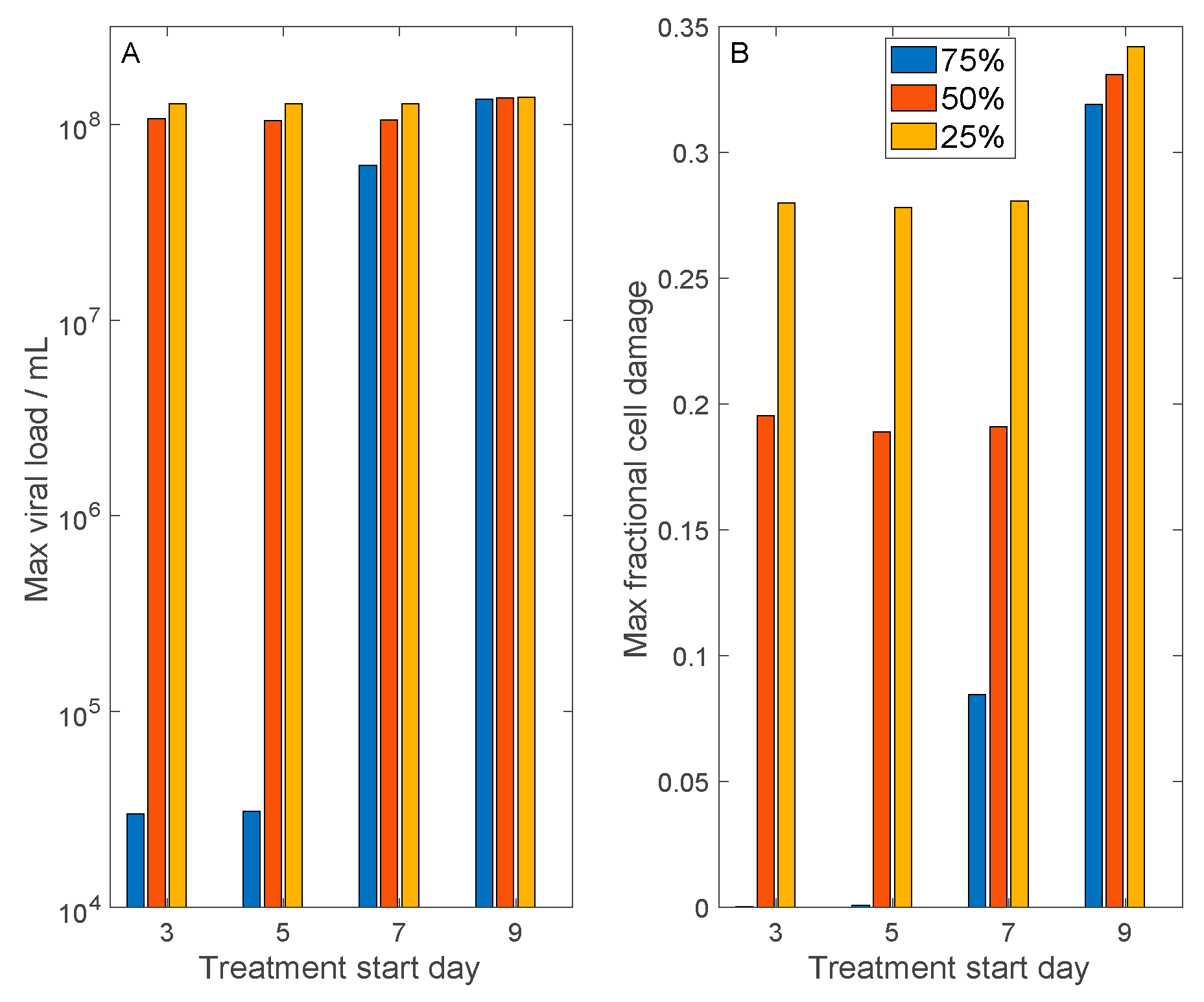
3.4. Host Cell Entry Inhibition
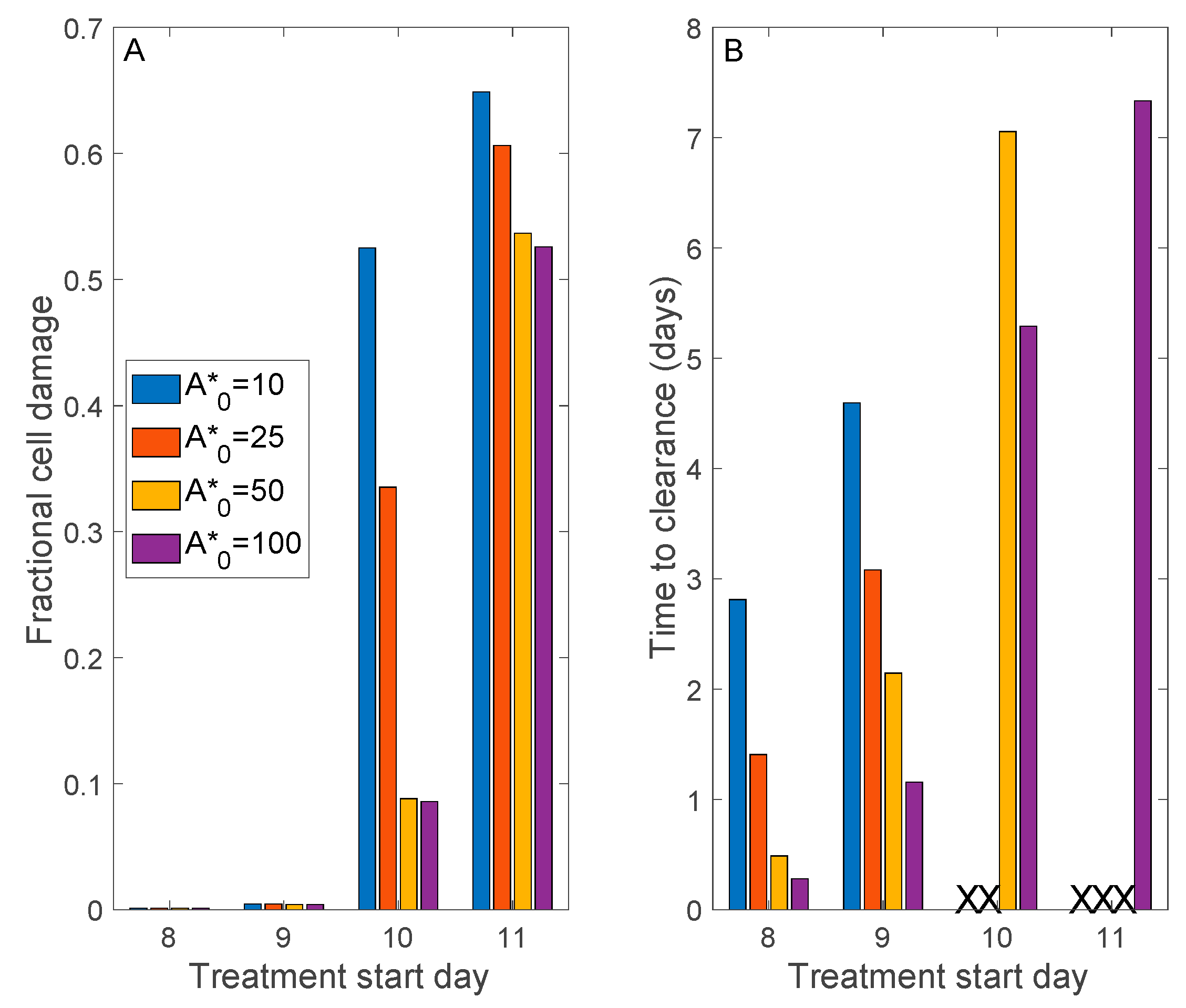
3.5. Convalescent Plasma Transfusion Therapy
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M.; Sun, F.; Jit, M.; Munday, J.D.; et al. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef]
- Peng, L.; Yang, W.; Zhang, D.; Zhuge, C.; Hong, L. Epidemic analysis of COVID-19 in China by dynamical modeling. arXiv 2020, arXiv:2002.06563. [Google Scholar]
- Hellewell, J.; Abbott, S.; Gimma, A.; Bosse, N.I.; Jarvis, C.I.; Russell, T.W.; Munday, J.D.; Kucharski, A.J.; Edmunds, W.J.; Sun, F. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob. Health 2020, 8, e488–e496. [Google Scholar] [CrossRef]
- Perelson, A.S. Modelling viral and immune system dynamics. Nat. Rev. Immunol. 2002, 2, 28–36. [Google Scholar] [CrossRef]
- Hancioglu, B.; Swigon, D.; Clermont, G. A dynamical model of human immune response to influenza A virus infection. J. Theor. Biol. 2007, 246, 70–86. [Google Scholar] [CrossRef]
- Wodarz, D.; Nowak, M.A. Mathematical models of HIV pathogenesis and treatment. BioEssays 2002, 24, 1178–1187. [Google Scholar] [CrossRef]
- Marchuk, G.I.; Petrov, R.V.; Romanyukha, A.A.; Bocharov, G.A. Mathematical model of antiviral immune response. I. Data analysis generalized picture construction and parameters evaluation for hepatitis B. J. Theor. Biol. 1991, 151, 1–40. [Google Scholar] [CrossRef]
- Neumann, A.U.; Lam, N.P.; Dahari, H.; Davidian, M.; Wiley, T.E.; Mika, B.P.; Perelson, A.S.; Layden, T.J. Differences in Viral Dynamics between Genotypes 1 and 2 of Hepatitis C Virus. J. Infect. Dis. 2000, 182, 28–35. [Google Scholar] [CrossRef]
- Ejima, K.; Kim, K.S.; Ito, Y.; Iwanami, S.; Ohashi, H.; Koizumi, Y.; Watashi, K.; Bento, A.I.; Aihara, K.; Iwami, S. Inferring Timing of Infection Using Within-host SARS-CoV-2 Infection Dynamics Model: Are “Imported Cases” Truly Imported? medRxiv 2020. [Google Scholar] [CrossRef]
- Kim, K.S.; Ejima, K.; Ito, Y.; Iwanami, S.; Ohashi, H.; Koizumi, Y.; Asai, Y.; Nakaoka, S.; Watashi, K.; Thompson, R.N.; et al. Modelling SARS-CoV-2 Dynamics: Implications for Therapy. medRxiv 2020. [Google Scholar] [CrossRef]
- Hernandez-Vargas, E.A.; Velasco-Hernandez, J.X. In-host Modelling of COVID-19 in Humans. medRxiv 2020. [Google Scholar] [CrossRef]
- Sahoo, S.; Hari, K.; Jhunjhunwala, S.; Jolly, M.K. Mechanistic modeling of the SARS-CoV-2 and immune system interplay unravels design principles for diverse clinicopathological outcomes. bioRxiv 2020. [Google Scholar] [CrossRef]
- Wölfel, R.; Corman, V.M.; Guggemos, W.; Seilmaier, M.; Zange, S.; Müller, M.A.; Niemeyer, D.; Jones, T.C.; Vollmar, P.; Rothe, C.; et al. Virological assessment of hospitalized patients with COVID-2019. Nature 2020, 581, 465–469. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, D.; Yang, P.; Poon, L.L.; Wang, Q. Viral load of SARS-CoV-2 in clinical samples. Lancet Infect. Dis. 2020, 20, 411–412. [Google Scholar] [CrossRef]
- Price, G.E.; Gaszewska-Mastarlarz, A.; Moskophidis, D. The Role of Alpha/Beta and Gamma Interferons in Development of Immunity to Influenza A Virus in Mice. J. Virol. 2000, 74, 3996–4003. [Google Scholar] [CrossRef]
- Lin, C.; Xiang, J.; Yan, M.; Li, H.; Huang, S.; Shen, C. Comparison of throat swabs and sputum specimens for viral nucleic acid detection in 52 cases of novel coronavirus (SARS-Cov-2)-infected pneumonia (COVID-19). Clin. Chem. Lab. Med. 2020, 58, 1089–1094. [Google Scholar] [CrossRef]
- Ada, G.L.; Jones, P.D. The Immune Response to Influenza Infection. In Current Topics in Microbiology and Immunology; Springer: Berlin/Heidelberg, Germany, 1986; pp. 1–54. [Google Scholar]
- Warren, T.K.; Jordan, R.; Lo, M.K.; Ray, A.S.; Mackman, R.L.; Soloveva, V.; Siegel, D.; Perron, M.; Bannister, R.; Hui, H.C.; et al. Therapeutic efficacy of the small molecule GS-5734 against Ebola virus in rhesus monkeys. Nature 2016, 531, 381–385. [Google Scholar] [CrossRef]
- Sheahan, T.P.; Sims, A.C.; Graham, R.L.; Menachery, V.D.; Gralinski, L.E.; Case, J.B.; Leist, S.R.; Pyrc, K.; Feng, J.Y.; Trantcheva, I.; et al. Broad-spectrum antiviral GS-5734 inhibits both epidemic and zoonotic coronaviruses. Sci. Transl. Med. 2017, 9, eaal3653. [Google Scholar] [CrossRef] [PubMed]
- De Wit, E.; Feldmann, F.; Cronin, J.; Jordan, R.; Okumura, A.; Thomas, T.; Scott, D.; Cihlar, T.; Feldmann, H. Prophylactic and therapeutic remdesivir (GS-5734) treatment in the rhesus macaque model of MERS-CoV infection. Proc. Natl. Acad. Sci. USA 2020, 117, 6771–6776. [Google Scholar] [CrossRef] [PubMed]
- Williamson, B.; Feldmann, F.; Schwarz, B.; Meade-White, K.; Porter, D.P.; Schulz, J.; Van Doremalen, N.; Leighton, I.; Yinda, C.K.; Pérez-Pérez, L.; et al. Clinical benefit of remdesivir in rhesus macaques infected with SARS-CoV-2. Nature 2020, 585, 273–276. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Cao, R.; Zhang, L.; Yang, X.; Liu, J.; Xu, M.; Shi, Z.; Hu, Z.; Zhong, W.; Xiao, G. Remdesivir and chloroquine effectively inhibit the recently emerged novel coronavirus (2019-nCoV) in vitro. Cell Res. 2020, 30, 269–271. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.; Wang, Z.; Zhao, F.; Yang, Y.; Li, J.; Yuan, J.; Wang, F.; Li, D.; Yang, M.; Xing, L.; et al. Treatment of 5 Critically Ill Patients With COVID-19 With Convalescent Plasma. JAMA 2020, 323, 1582. [Google Scholar] [CrossRef] [PubMed]
- Duan, K.; Liu, B.; Li, C.; Zhang, H.; Yu, T.; Qu, J.; Zhou, M.; Chen, L.; Meng, S.; Hu, Y.; et al. Effectiveness of convalescent plasma therapy in severe COVID-19 patients. Proc. Natl. Acad. Sci. USA 2020, 117, 9490–9496. [Google Scholar] [CrossRef] [PubMed]
- Bradburne, A.F. An investigation of the replication of coronaviruses in suspension cultures of L132 cells. Arch. Virol. 1972, 37, 297–307. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Lee, H.Y.; Topham, D.J.; Park, S.Y.; Hollenbaugh, J.; Treanor, J.; Mosmann, T.R.; Jin, X.; Ward, B.M.; Miao, H.; Holden-Wiltse, J.; et al. Simulation and Prediction of the Adaptive Immune Response to Influenza A Virus Infection. J. Virol. 2009, 83, 7151–7165. [Google Scholar] [CrossRef] [PubMed]
- Clarke, N.E.; Turner, A.J. Angiotensin-Converting Enzyme 2: The First Decade. Int. J. Hypertens. 2011, 2012, 1–12. [Google Scholar] [CrossRef]
- Cheng, Y.; Wong, R.; Soo, Y.O.Y.; Wong, W.S.; Lee, C.K.; Ng, M.H.L.; Chan, P.; Wong, K.C.; Leung, C.B.; Cheng, G. Use of convalescent plasma therapy in SARS patients in Hong Kong. Eur. J. Clin. Microbiol. Infect. Dis. 2004, 24, 44–46. [Google Scholar] [CrossRef]
- Zhou, B.; Zhong, N.; Guan, Y. Treatment with Convalescent Plasma for Influenza A (H5N1) Infection. New Engl. J. Med. 2007, 357, 1450–1451. [Google Scholar] [CrossRef]
- Hung, I.F.; To, K.K.; Lee, C.-K.; Lee, K.-L.; Chan, K.K.C.; Yan, W.-W.; Liu, R.; Watt, C.-L.; Chan, W.-M.; Lai, K.-Y.; et al. Convalescent Plasma Treatment Reduced Mortality in Patients with Severe Pandemic Influenza A (H1N1) 2009 Virus Infection. Clin. Infect. Dis. 2011, 52, 447–456. [Google Scholar] [CrossRef]
- Ko, J.-H.; Seok, H.; Cho, S.Y.; Ha, Y.E.; Baek, J.Y.; Kim, S.H.; Kim, Y.J.; Park, J.K.; Chung, C.R.; Kang, E.-S.; et al. Challenges of convalescent plasma infusion therapy in Middle East respiratory coronavirus infection: A single centre experience. Antivir. Ther. 2018, 23, 617–622. [Google Scholar] [CrossRef]
- Van Griensven, J.; Edwards, T.; De Lamballerie, X.; Semple, M.G.; Gallian, P.; Baize, S.; Horby, P.; Raoul, H.; Magassouba, N.; Antierens, A.; et al. Evaluation of Convalescent Plasma for Ebola Virus Disease in Guinea. N. Engl. J. Med. 2016, 374, 33–42. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Xiong, J.; Bao, L.; Shi, Y. Convalescent plasma as a potential therapy for COVID-19. Lancet Infect. Dis. 2020, 20, 398–400. [Google Scholar] [CrossRef]
- South, A.M.; Tomlinson, L.; Edmonston, D.; Hiremath, S.; Sparks, M.A. Controversies of renin–angiotensin system inhibition during the COVID-19 pandemic. Nat. Rev. Nephrol. 2020, 16, 305–307. [Google Scholar] [CrossRef] [PubMed]
- Leete, J.G.S.; Layton, A.T. Modeling Sex Differences in the Renin Angiotensin System and the Efficacy of Antihypertensive Therapies. Comput. Chem. Eng. 2018, 112, 253–264. [Google Scholar] [CrossRef]
- Sadria, M.; Layton, A.T. Use of Angiotensin-Converting Enzyme Inhibitors and Angiotensin II Receptor Blockers During the COVID-19 Pandemic: A Modeling Analysis. PLoS Comput. Biol. 2020, 16, e1008235. [Google Scholar] [CrossRef] [PubMed]
- Leete, J.; Layton, A.T. Sex-specific long-term blood pressure regulation: Modeling and analysis. Comput. Biol. Med. 2019, 104, 139–148. [Google Scholar] [CrossRef]
- Ahmed, S.; Layton, A.T. Sex-specific computational models for blood pressure regulation in the rat. Am. J. Physiol. Physiol. 2020, 318, F888–F900. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Li, S.; Liu, J.; Liang, B.; Wang, X.; Wang, H.; Li, W.; Tong, Q.; Yi, J.; Zhao, L.; et al. Longitudinal characteristics of lymphocyte responses and cytokine profiles in the peripheral blood of SARS-CoV-2 infected patients. EBioMedicine 2020, 55, 102763. [Google Scholar] [CrossRef]
- Lucas, C.; Team, Y.I.; Wong, P.; Klein, J.; Castro, T.B.R.; Silva, J.; Sundaram, M.; Ellingson, M.K.; Mao, T.; Oh, J.E.; et al. Longitudinal analyses reveal immunological misfiring in severe COVID-19. Nat. Cell Biol. 2020, 584, 463–469. [Google Scholar]
- Cheng, Y.; Luo, R.; Wang, K.; Zhang, M.; Wang, Z.; Dong, L.; Li, J.; Yao, Y.; Ge, S.; Xu, G. Kidney disease is associated with in-hospital death of patients with COVID-19. Kidney Int. 2020, 97, 829–838. [Google Scholar] [CrossRef]
- Layton, A.T.; Laghmani, K.; Vallon, V.; Edwards, A. Solute transport and oxygen consumption along the nephrons: Effects of Na+ transport inhibitors. Am. J. Physiol. Physiol. 2016, 311, F1217–F1229. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Xu, X.; Chen, Z.; Duan, J.; Hashimoto, K.; Yang, L.; Liu, C.; Yang, C. Nervous system involvement after infection with COVID-19 and other coronaviruses. Brain Behav. Immun. 2020, 87, 18–22. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Lian, J.S.; Hu, J.H.; Gao, J.; Zheng, L.; Zhang, Y.M.; Hao, S.R.; Jia, H.Y.; Cai, H.; Zhang, X.L.; et al. Epidemiological, clinical and virological characteristics of 74 cases of coronavirus-infected disease 2019 (COVID-19) with gastrointestinal symptoms. Gut 2020, 69, 1002–1009. [Google Scholar] [CrossRef]
- Chen, Z.; Wherry, E.J. T cell responses in patients with COVID-19. Nat. Rev. Immunol. 2020, 20, 529–536. [Google Scholar] [CrossRef]
- Li, Q.; McDonough, A.A.; Layton, H.E.; Layton, A.T. Functional implications of sexual dimorphism of transporter patterns along the rat proximal tubule: Modeling and analysis. Am. J. Physiol. Physiol. 2018, 315, F692–F700. [Google Scholar] [CrossRef]
- Ahmed, S.; Hu, R.; Leete, J.; Layton, A.T. Understanding sex differences in long-term blood pressure regulation: Insights from experimental studies and computational modeling. Am. J. Physiol. Circ. Physiol. 2019, 316, H1113–H1123. [Google Scholar] [CrossRef]
- Makinodan, T.; Kay, M.M. Age Influence on the Immune System. In Advances in Immunology; Elsevier: Amsterdam, The Netherlands, 1980; pp. 287–330. [Google Scholar]
- Layton, A.T.; Vallon, V. SGLT2 inhibition in a kidney with reduced nephron number: Modeling and analysis of solute transport and metabolism. Am. J. Physiol. Physiol. 2018, 314, F969–F984. [Google Scholar] [CrossRef]
- Layton, A.T.; Vallon, V.; Edwards, A. Predicted consequences of diabetes and SGLT inhibition on transport and oxygen consumption along a rat nephron. Am. J. Physiol. Physiol. 2016, 310, F1269–F1283. [Google Scholar] [CrossRef] [PubMed]
- Layton, A.T.; Vallon, V. Cardiovascular benefits of SGLT2 inhibition in diabetes and chronic kidney diseases. Acta Physiol. 2018, 222, e13050. [Google Scholar] [CrossRef]
| Symbol | Description | Value |
|---|---|---|
| Viral production by infected cells | 255 | |
| Elimination of virus by antibodies | 309.6 | |
| Virus entering healthy cells | 0.51 | |
| Virus degradation | 0.85 | |
| Maximal rate of virus removal | 50 | |
| Michaelis–Menten constant in virus removal | 23,000 | |
| Latent cells becoming fully infected | 6 | |
| Regeneration of epithelial cells | 2 | |
| Loss of viral resistance | 0.5 | |
| Rate of infection of cells by virus | 0.17 | |
| Susceptible cells becoming viral resistant | 0.005 | |
| Infected cells damaged by effector cells | 0.033 | |
| Infected cells death rate | 0.775 | |
| Stimulation of antigen presenting cells by damaged cells | 0.5 | |
| Stimulation of antigen presenting cells by virus | 0.00185 | |
| Antigen presenting cell natural death | 0.75 | |
| Interferon production rate per antigen presenting cell | 125,000 | |
| Interferon production rate per infected cell | 1000 | |
| Interferon binding to susceptible healthy cells | 8.5 | |
| Interferon natural decay | 4 | |
| Stimulation of effector cells | 4.15 | |
| Death of effector cells by infector cells | 1.36 | |
| Effector cell natural death | 0.2 | |
| Plasma cell production | 5.75 | |
| Plasma cell natural death | 0.2 | |
| Antibody production rate per plasma cell | 0.0225 | |
| Antibodies binding to viruses | 73.1 | |
| Antibody natural death | 0.0215 | |
| r | Change in antibody specificity | 0.000015 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadria, M.; Layton, A.T. Modeling within-Host SARS-CoV-2 Infection Dynamics and Potential Treatments. Viruses 2021, 13, 1141. https://doi.org/10.3390/v13061141
Sadria M, Layton AT. Modeling within-Host SARS-CoV-2 Infection Dynamics and Potential Treatments. Viruses. 2021; 13(6):1141. https://doi.org/10.3390/v13061141
Chicago/Turabian StyleSadria, Mehrshad, and Anita T. Layton. 2021. "Modeling within-Host SARS-CoV-2 Infection Dynamics and Potential Treatments" Viruses 13, no. 6: 1141. https://doi.org/10.3390/v13061141
APA StyleSadria, M., & Layton, A. T. (2021). Modeling within-Host SARS-CoV-2 Infection Dynamics and Potential Treatments. Viruses, 13(6), 1141. https://doi.org/10.3390/v13061141





