Time Intervals in Sequence Sampling, Not Data Modifications, Have a Major Impact on Estimates of HIV Escape Rates
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. A Sampling Method to Estimate Escape Rates without Data Modification
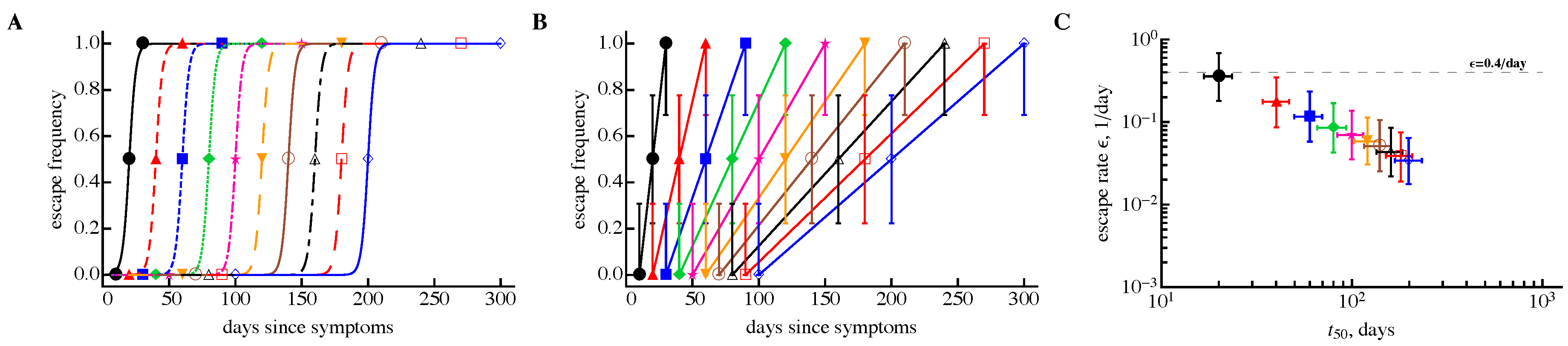
3.2. The Rate of HIV Escape Declines with Time since Infection
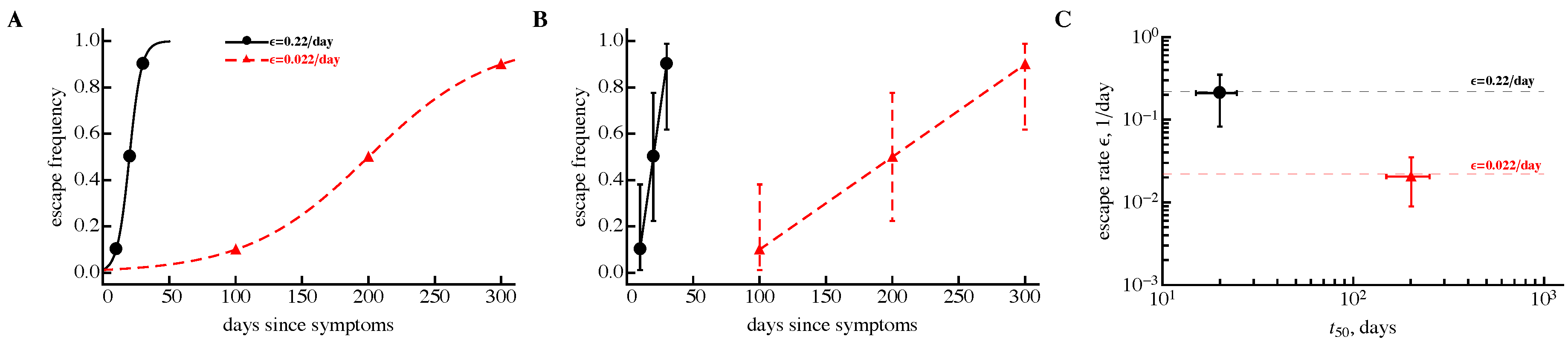
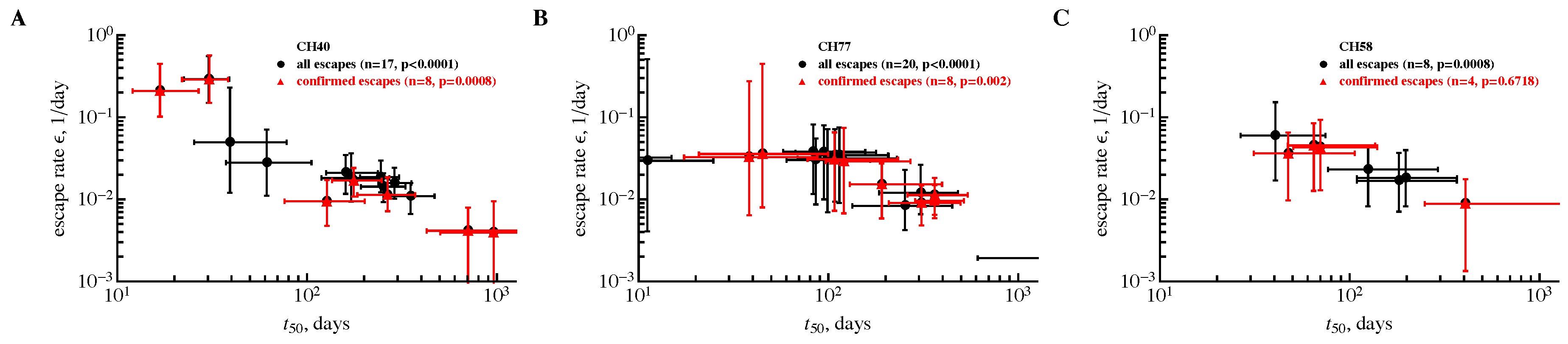
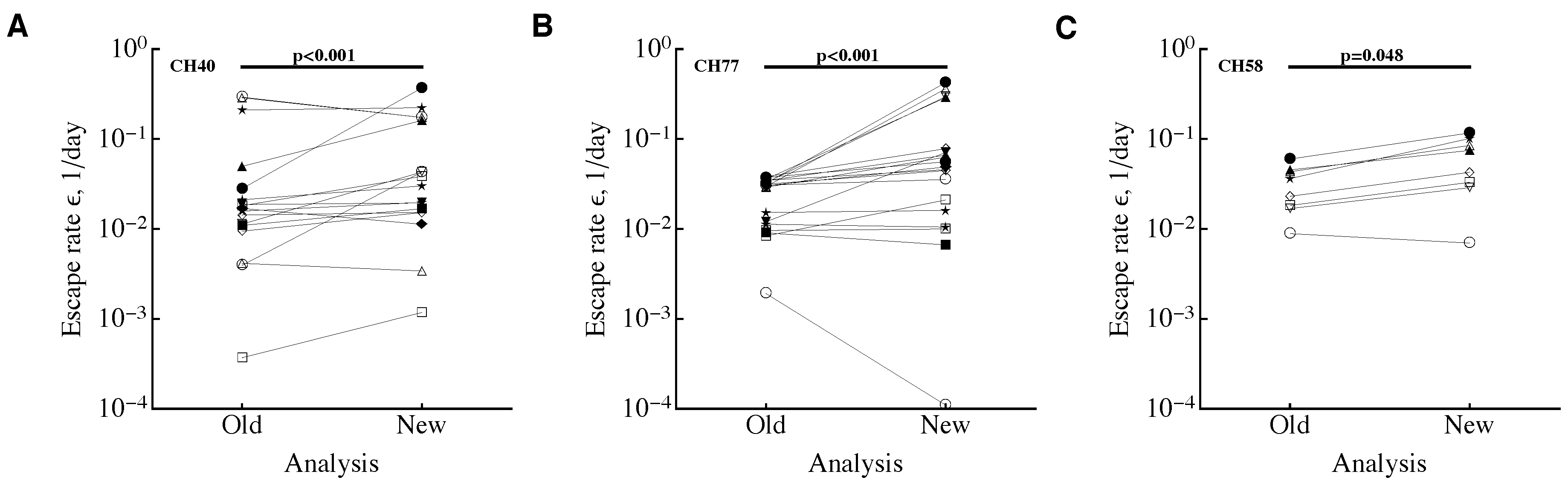
3.3. Time Frequency of Sampling Biases Estimates of the Escape Rate
4. Discussion
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mansky, L.M.; Temin, H.M. Lower in vivo mutation rate of human immunodeficiency virus type 1 than that predicted from the fidelity of purified reverse transcriptase. J. Virol. 1995, 69, 5087–5094. [Google Scholar] [PubMed]
- Mansky, L.M. Forward mutation rate of human immunodeficiency virus type 1 in a T lymphoid cell line. AIDS Res. Hum. Retroviruses 1996, 12, 307–314. [Google Scholar] [CrossRef] [PubMed]
- Mansky, L.M. Retrovirus mutation rates and their role in genetic variation. J. Gen. Virol. 1998, 79 Pt 6, 1337–1345. [Google Scholar] [CrossRef]
- SanjuÃn, R.; Nebot, M.R.; Chirico, N.; Mansky, L.M.; Belshaw, R. Viral mutation rates. J. Virol. 2010, 84, 9733–9748. [Google Scholar] [CrossRef] [PubMed]
- Geller, R.; Domingo-Calap, P.; Cuevas, J.M.; Rossolillo, P.; Negroni, M.; Sanjuán, R. The external domains of the hiv-1 envelope are a mutational cold spot. Nat. Commun. 2015, 6, 8571. [Google Scholar] [CrossRef] [PubMed]
- Cuevas, J.M.; Geller, R.; Garijo, R.; López-Aldeguer, J.; Sanjuán, R. Extremely high mutation rate of HIV-1 in vivo. PLoS Biol. 2015, 13, e1002251. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S. Modelling viral and immune system dynamics. Nat. Rev. Immunol. 2002, 2, 28–36. [Google Scholar] [CrossRef] [PubMed]
- Haase, A.T. Population biology of HIV-1 infection: Viral and CD4+ T cell demographics and dynamics in lymphatic tissues. Annu. Rev. Immunol. 1999, 17, 625–656. [Google Scholar] [CrossRef] [PubMed]
- Estes, J.D.; Kityo, C.; Ssali, F.; Swainson, L.; Makamdop, K.N.; Del Prete, G.Q.; Deeks, S.G.; Luciw, P.A.; Chipman, J.G.; Beilman, G.J.; et al. Defining total-body aids-virus burden with implications for curative strategies. Nat. Med. 2017, 23, 1271–1276. [Google Scholar] [CrossRef] [PubMed]
- Walker, B.D.; Korber, B.T. Immune control of HIV: the obstacles of HLA and viral diversity. Nat. Immunol. 2001, 2, 473–475. [Google Scholar] [CrossRef] [PubMed]
- Barouch, D.; Kunstman, J.; Kuroda, M.; Schmitz, J.; Santra, S.; Peyerl, F.; Krivulka, G.; Beaudry, K.; Lifton, M.; Gorgone, D.A.; et al. Eventual AIDS vaccine failure in a rhesus monkey by viral escape from cytotoxic T lymphocytes. Nature 2002, 415, 335–339. [Google Scholar] [CrossRef] [PubMed]
- Mullins, J.I.; Rolland, M.; Allen, T.M. Viral evolution and escape during primary human immunodeficiency virus-1 infection: Implications for vaccine design. Curr. Opin. HIV AIDS 2008, 3, 60–66. [Google Scholar] [CrossRef] [PubMed]
- Rolland, M.; Tovanabutra, S.; Decamp, A.C.; Frahm, N.; Gilbert, P.B.; Sanders-Buell, E.; Heath, L.; Magaret, C.A.; Bose, M.; Bradfield, A.; et al. Genetic impact of vaccination on breakthrough HIV-1 sequences from the STEP trial. Nat. Med. 2011, 17, 366–371. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Anderson, R.M.; McLean, A.R.; Wolfs, T.F.; Goudsmit, J.; May, R.M. Antigenic diversity thresholds and the development of AIDS. Science 1991, 254, 963–969. [Google Scholar] [CrossRef] [PubMed]
- Alizon, S.; Magnus, C. Modelling the course of an hiv infection: insights from ecology and evolution. Viruses 2012, 4, 1984–2013. [Google Scholar] [CrossRef] [PubMed]
- Goonetilleke, N.; Liu, M.K.; Salazar-Gonzalez, J.F.; Ferrari, G.; Giorgi, E.; Ganusov, V.V.; Keele, B.F.; Learn, G.H.; Turnbull, E.L.; Salazar, M.G.; et al. The first T cell response to transmitted/founder virus contributes to the control of acute viremia in HIV-1 infection. J. Exp. Med. 2009, 206, 1253–1272. [Google Scholar] [CrossRef] [PubMed]
- McMichael, A.J.; Borrow, P.; Tomaras, G.D.; Goonetilleke, N.; Haynes, B.F. The immune response during acute HIV-1 infection: Clues for vaccine development. Nat. Rev. Immunol. 2010, 10, 11–23. [Google Scholar] [CrossRef] [PubMed]
- Bar, K.J.; Tsao, C.-Y.; Iyer, S.S.; Decker, J.M.; Yang, Y.; Bonsignori, M.; Chen, X.; Hwang, K.-K.; Montefiori, D.C.; Liao, H.-X.; et al. Early Low-Titer Neutralizing Antibodies Impede HIV-1 Replication and Select for Virus Escape. PLoS Pathog. 2012, 8, e1002721. [Google Scholar] [CrossRef] [PubMed]
- Kijak, G.H.; Sanders-Buell, E.; Chenine, A.-L.; Eller, M.A.; Goonetilleke, N.; Thomas, R.; Leviyang, S.; Harbolick, E.A.; Bose, M.; Pham, P.; et al. Rare hiv-1 transmitted/founder lineages identified by deep viral sequencing contribute to rapid shifts in dominant quasispecies during acute and early infection. PLoS Pathog. 2017, 13, e1006510. [Google Scholar] [CrossRef]
- Liu, M.K.P.; Hawkins, N.; Ritchie, A.J.; Ganusov, V.V.; Whale, V.; Brackenridge, S.; Li, H.; Pavlicek, J.W.; Cai, F.; Rose-Abrahams, M.; et al. Vertical T cell immunodominance and epitope entropy determine HIV-1 escape. J. Clin. Investig. 2013, 123, 380–393. [Google Scholar] [CrossRef] [PubMed]
- Fernandez, C.; Stratov, I.; De Rose, R.; Walsh, K.; Dale, C.; Smith, M.; Agy, M.; Hu, S.; Krebs, K.; Watkins, D.I.; et al. Rapid viral escape at an immunodominant simian-human immunodeficiency virus cytotoxic T-lymphocyte epitope exacts a dramatic fitness cost. J. Virol. 2005, 79, 5721–5731. [Google Scholar] [CrossRef] [PubMed]
- Asquith, B.; Edwards, C.; Lipsitch, M.; McLean, A. Inefficient cytotoxic T lymphocyte-mediated killing of HIV-1-infected cells in vivo. PLoS Biol. 2006, 4, e90. [Google Scholar] [CrossRef] [PubMed]
- Ganusov, V.V.; De Boer, R.J. Estimating costs and benefits of CTL escape mutations in SIV/HIV Infection. PLoS Comput. Biol. 2006, 2, e24. [Google Scholar] [CrossRef] [PubMed]
- Fischer, W.; Ganusov, V.V.; Giorgi, E.E.; Hraber, P.T.; Keele, B.F.; Leitner, T.; Han, C.S.; Gleasner, C.D.; Green, L.; Lo, CC.; et al. Transmission of single HIV-1 genomes and dynamics of early immune escape revealed by ultra-deep sequencing. PLoS ONE 2010, 5, e12303. [Google Scholar] [CrossRef] [PubMed]
- Ganusov, V.V.; Goonetilleke, N.; Liu, M.K.P.; Ferrari, G.; Shaw, G.M.; McMichael, A.J.; Borrow, P.; Korber, B.T.; Perelson, A.S. Fitness Costs and Diversity of the Cytotoxic T Lymphocyte (CTL) Response Determine the Rate of CTL Escape during Acute and Chronic Phases of HIV Infection. J. Virol. 2011, 85, 10518–10528. [Google Scholar] [CrossRef] [PubMed]
- Kessinger, T.A.; Perelson, A.S.; Neher, R.A. Inferring HIV Escape Rates from Multi-Locus Genotype Data. Front. Immunol. 2013, 4, 252. [Google Scholar] [CrossRef] [PubMed]
- Leviyang, S. Constructing lower-bounds for ctl escape rates in early siv infection. J. Theor. Biol. 2014, 352, 82–91. [Google Scholar] [CrossRef] [PubMed]
- Asquith, B.; McLean, A. In vivo CD8+ T cell control of immunodeficiency virus infection in humans and macaques. Proc. Natl. Acad. Sci. USA 2007, 104, 6365–6370. [Google Scholar] [CrossRef] [PubMed]
- Leviyang, S.; Ganusov, V.V. Broad CTL Response in Early HIV Infection Drives Multiple Concurrent CTL Escapes. PLoS Comput. Biol. 2015, 11, e1004492. [Google Scholar] [CrossRef] [PubMed]
- Garcia, V.; Feldman, M.W.; Regoes, R.R. Investigating the Consequences of Interference between Multiple CD8+ T Cell Escape Mutations in Early HIV Infection. PLoS Comput. Biol. 2016, 12, e1004721. [Google Scholar] [CrossRef] [PubMed]
- Ganusov, V.V.; Neher, R.A.; Perelson, A.S. Modeling HIV escape from cytotoxic T lymphocyte responses. J. Stat. Mech. 2013, 2013, P01010. [Google Scholar] [CrossRef] [PubMed]
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap; Chapman & Hall: New York, NY, USA, 1993. [Google Scholar]
- Brown, L.; Cai, T.; DasGupta, A.; Agresti, A.; Coull, B.; Casella, G.; Corcoran, C.; Mehta, C.; Ghosh, M. Interval estimation for a binomial proportion. Stat. Sci. 2001, 16, 101–133. [Google Scholar]
- Yang, Y.; Ganusov, V.V. Kinetics of HIV-specic CTL responses plays a minimal role in determining HIV escape dynamics. Front. Immunol. 2018, 9, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Geldmacher, C.; Currier, J.R.; Herrmann, E.; Haule, A.; Kuta, E.; McCutchan, F.; Njovu, L.; Geis, S.; Hoffmann, O.; Maboko, L.; et al. CD8 T-cell recognition of multiple epitopes within specific Gag regions is associated with maintenance of a low steady-state viremia in human immunodeficiency virus type 1-seropositive patients. J. Virol. 2007, 81, 2440–2448. [Google Scholar] [CrossRef] [PubMed]
- Streeck, H.; Jolin, J.S.; Qi, Y.; Yassine-Diab, B.; Johnson, R.C.; Kwon, D.S.; Addo, M.M.; Brumme, C.; Routy, J.-P.; Little, S.; et al. Human immunodeficiency virus type 1-specific cd8+ t-cell responses during primary infection are major determinants of the viral set point and loss of cd4+ t cells. J. Virol. 2009, 83, 7641–7648. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ganusov, V.V. Time Intervals in Sequence Sampling, Not Data Modifications, Have a Major Impact on Estimates of HIV Escape Rates. Viruses 2018, 10, 99. https://doi.org/10.3390/v10030099
Ganusov VV. Time Intervals in Sequence Sampling, Not Data Modifications, Have a Major Impact on Estimates of HIV Escape Rates. Viruses. 2018; 10(3):99. https://doi.org/10.3390/v10030099
Chicago/Turabian StyleGanusov, Vitaly V. 2018. "Time Intervals in Sequence Sampling, Not Data Modifications, Have a Major Impact on Estimates of HIV Escape Rates" Viruses 10, no. 3: 99. https://doi.org/10.3390/v10030099
APA StyleGanusov, V. V. (2018). Time Intervals in Sequence Sampling, Not Data Modifications, Have a Major Impact on Estimates of HIV Escape Rates. Viruses, 10(3), 99. https://doi.org/10.3390/v10030099




