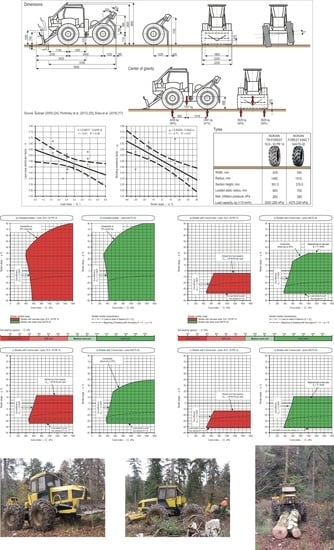
Mobility Range of a Cable Skidder for Timber Extraction on Sloped Terrain

1. Introduction

Terrain trafficability determines vehicle mobility and, for timber harvesting systems, terrain slope is still the most important terrain factor that affects vehicle stability when all wheels or tracks are “in conflict” with the same macro-topographic conditions. In timber extraction, vehicle mobility can be considered from two different aspects: (1) extraction on soils of limited bearing capacity and (2) extraction in hilly and mountainous forests where slope and ground obstacles define conditions for forestry vehicles.

For a long period of time, owing to the lack of understanding of the behaviour of the terrain and of the mechanics of the vehicle-terrain interactions, the development and design of off-road vehicles have been, by and large, guided by past experience and the “cut and try” methodology. In off-road operations, various types of terrain, ranging from sand through soft mud to fresh snow, may be encountered. An adequate knowledge of the mechanical properties of the terrain and an understanding of its response to vehicular loading are, therefore, essential to the rational development and design of off-road vehicles to meet specific operational environments [1].

The use of forestry vehicles in mechanised harvesting systems is still the most effective way of timber procurement [2,3], and forestry vehicles need to have high mobility to face various terrain conditions. Aside from vehicle mobility, optimal planning of how the skid roads and trails should be laid out is determined to a large degree by topography and soil bearing capacity [4]. The starting point for limiting the environmental impact of traffic is a good knowledge of the area involved, to calibrate interventions based on the susceptibility of the environment to damage and its resilience [5,6]. Cable skidding is the only method currently being used globally post motor-manual felling since stems are often scattered throughout the compartment [7]. Kulak et al. (2017) [8] stated that according to Gil (2000) [9] and Kocel (2013) [10] in Europe, semi-suspended skidding of timber is the most popular method, commonly engaged in the central and southern part of the continent. Planning of timber extraction operations is crucial since physical soil properties are often significantly impacted by harvesting operations, depending on logging method, and it may imply compaction and consequent restrictions to tree growth and natural regeneration [11].

Since vehicles in forestry are influenced by terrain conditions, it is crucial to know the factors affecting their mobility [12]. The same author states that the basis for the scientific research of the vehicle-terrain system was set up by Bekker in 1956 in the book “Theory of Land Locomotion”, which over time was complemented by many other authors and researchers. Wong (2014) [13] describes the dynamic behaviour of an off-road vehicle in terms of its performance (mobility), handling and ride. Performance characteristics refer to the ability of the vehicle to overcome motion resistance, to develop drawbar pull, to negotiate slope, to accelerate, and to decelerate. Handling behaviour is primarily concerned with the steering response of the vehicle to the driver’s commands. Ride quality is related to the vibration of the vehicle excited by surface irregularities and its effect on the driver or passenger.

The mobility of forest vehicles depends on the features defined during their construction, including (1) dimensions; (2) type of driving system; (3) vehicle mass and its axle distribution; and (4) center of gravity position. There are many indicators that determine the mobility of forest vehicles, and thus the range of their operational application: (1) the longitudinal and lateral stability angles of the vehicle [14,15]; (2) the boundary load in reference to the longitudinal stability of the vehicle [16]; (3) axle load distribution with respect to the terrain slope, the direction of vehicle movement (uphill or downhill) and load size [17,18]; (4) approach, ramp (break-over) and departure angles of the vehicle [19] and (5) environmental soundness expressed through nominal ground pressure and minimal cone index, but also wheel slip, which is one of the most important factors of the environmental impact assessment [20,21]. Vehicle maneuverability is determined by its ability to overcome terrain irregularities, wherein two geometrical systems i.e., geometry of the vehicle and of the terrain interact [22].

The core of planning timber harvesting is sustainability and promotion of a so called 5-E standards: economic, environmental, energy efficient, ergonomic and estetic. Development of region-specific, practically relevant performance criteria are highly desirable that meet local needs and maintain flexibility to evolve and be capable of incorporating ever-changing work environments and challenges [23].

The goal of this research is to give boundaries for planning purposes of timber extraction on sloped terrain by providing operational ranges of cable skidders considering terrain parameters, vehicle technical characteristics and load size relying on sustainability and eco-efficiency.

2. Materials and Methods

Analysis was based on Ecotrac 120 V skidder (Hittner Ltd., Bjelovar, Croatia) dimensions and centre of gravity [24], load mass distribution factor (k) and skidding resistance factor (μ_p) (Figure 1) during timber extraction on different terrain slopes and with different load masses. Analysis of most of parameters was done by equations given in

Table 1. Equations used in defining parameters during timber extraction by a cable skidder.

Downhill Skidding		Uphill Skidding		Directory
Adhesive weight (1)				α—Longitudinal terrain slope, % G—Skidder weight, kN Ga—Adhesive weight, kN G1—Load on front axle, kN G2—Load on rear axle, kN Fo—Thrust force, kN Fd—Drawbar pull, kN H—Horizontal component of rope force, kN V—Vertical component of rope force, kN Q—Load weight, kN f—Rolling resistance factor k—Load mass distribution factor μ—Net traction factor μp—Skidding resistance factor a—Distance from centre of gravity to rear axle b—Distance from centre of gravity to front axle c—Distance from horizontal rollers to rear end d—Height of horizontal rollers ht—Centre of gravity height
Ga = G cos α + V
Vertical component of rope force (2)
V = k Q cos α
Horizontal component of rope force (3) and (4)
H = Q (1 − k) cosα μp − Q sin α		H = Q (1 − k) cos α μp + Q sin α
Front axle load (5) and (6)
G1 = (G cos α a + G sin α ht − H d − V c)/L		G1 = (G cos α a − G sin α ht − H d − V c)/L
Rear axle load (7) and (8)
G2 = (G cos α b − G sin α ht + H d + V (L + c))/L		G2 = (G cos α b + G sin α ht + H d + V (L + c))/L
Angle of longitudinal stability (9) and (10)
tg α = (G b + Q (1 − k) μp d + k Q (L+c))/(Q d − G ht)		tg α = (G a − Q (1 − k) μp d − k Q c)/(Q d + G ht)
Critical load in reference to longitudinal stability (11) and (12)
Qcrit = (G (a cos α + ht sin α))/(d sin α + k c cos α + d (1 − k) μp cos α)		Qcrit = (G (a cos α − ht sin α))/(d sin α + k c cos α + d (1 − k) μp cos α)
Drawbar pull (13) and (14)
Fd = H − Ga sin α		Fd = H + Ga sin α
Net traction factor (15) and (16)
μ = Fd/Ga = (H − Ga sin α)/Ga		μ = Fd/Ga = (H + Ga sin α)/Ga
Brixius mobility model (17)–(19)				Tyre deflection (20) Δ = 0.008 + 0.001 (0.365 + (170/pi)) Gw
Nw = ((CI b d)/Gw) (1 + 5 (Δ/h))/(1 + 3 (b/d))	f = (1.0/Nw) + 0.04 + ((0.5 δ)/√Nw)		κ = 0.88 (1 − e−0.1 Nw) (1 − e−7.5 δ)

N_w—Wheel numeric; CI—Cone index, kPa; b—Tyre width, m; d—Tyre radius, m; G_w—Wheel load, kN; Δ—Tyre deflection, m; h—Section height, m; κ—Gross traction factor; δ—Wheel slip at 20%; f—Rolling resistance factor; p_i—Tyre inflation pressure, kPa.

. Poršinsky et al. (2012) [25] analysed load mass distribution factor as a function of (statistically and inversely correlated) load mass, load weight, number of logs per load, load volume, while skidding resistance factor was a function (statistically and inversely correlated) of terrain slope and direction of timber extraction i.e., uphill or downhill skidding (Figure 1). The skidder analysed in this research was a four-wheeled (4 × 4) articulated forestry vehicle, equipped with a hydraulic forest winch Hittner 2 × 80 (Hittner Ltd., Bjelovar, Croatia), of the nominal tractive force of 80 kN. It is driven by a 6-cylinder diesel DEUTZ (SDF group, Treviglio, Italy) engine with the nominal power of 84 kW at 2300 min⁻¹ and maximum torque of 400 Nm at 1500 min⁻¹.

Skidder mobility model was based on connecting two systems: vehicle-terrain (load distribution) and wheel-soil (skidder traction performance) with two mobility parameters:

• Maximal slope during uphill timber extraction by a cable skidder based on its traction performance (gradeability),
• Maximal slope during downhill timber extraction by a cable skidder when thrust force is equal to zero.

Skidder traction performance was based on the Brixius model (Equations (17)–(19)), regarding: (1) wheel numeric (N_w) for narrower tyres (Nokian TR Forest 16.9-30 PR 14, Nokian Tyres plc., Nokia, Finland) and wider tyres (Nokian Forest King T 540/70-30, Nokian Tyres plc., Nokia, Finland), (2) cone index (CI), and (3) wheel slip (δ) at 20%. Tyre deflection was calculated with Equation (20) [26]. In comparison to other authors, Brixius’ wheel numeric (Equation (17)) considers: (1) ratio of a tyre deflection and section height (Δ/h) and (2) ratio of a tyre width and radius (b/d) of a loaded wheel. Wheel numeric, which represents interaction between a loaded wheel and soil, is used in equations for predicting rolling resistance factor—f (Equation (18)) and gross traction factor—κ (Equation (19)). It should be stated that Brixius’ model defines net traction factor (μ) as a difference between gross traction factor and rolling resistance factor. The basic components of the Brixius’ model ensure wide application. Constant 0.88 limits the maximal torque moment on the wheel in contact with the soil up to 0.92 (0.88 + 0.04) which is achieved at higher wheel numeric i.e., wheel slip. Expression e^{−0.1 N}_w controls the maximal value of torque moment gained with higher wheel slip. Wheel numeric as torque moment increases with (1) increase of cone index (CI); (2) increase of tyre radius (d) and width (b); (3) decrease of wheel load (G_w); (4) increase of tyre deflection and section height ratio (Δ/h) and (5) decrease in tyre width and radius ratio (b/d). Constant parameter 7.5 in e^{−7.5 δ} defines the ruggedness of the surface, as it is below 7.5 on wet soils and significantly higher with use of chains or semi-tracks on wheels.

Brixius in his model for rolling resistance factor suggested it is influenced by (1) bending and friction of a tyre on a hard surface; (2) soil compaction during movement of a loaded wheel; (3) displacement of compressed soil on both sides of the wheel; and (4) side slip due to heterogeneity and viscosity of the soil.

Limiting terrain slope in uphill timber extraction is based on tractive performance and a loaded reference wheel on different slopes and with different loads. Net traction factor is levelled through load distribution and Bixius’ model considering cone index Equation (21). Gradeability was calculated for each value of the terrain slope and transported load (timber) regarding minimal cone index of the soil.

$$\frac{H+G_a·\sin \alpha }{G_a}=\left[0.88·\left(1-e^{-0.1·N_w}\right)·\left(1-e^{-7.5·\delta }\right)\right]-\left[\frac{1.0}{N_w}+0.04+\frac{0.5+\delta }{\sqrt{N_w}}\right]\to CI$$

(21)

Limiting terrain slope in downhill timber extraction when drawbar pull (F_d) is zero and the breaking force (F_br) appeared was also based on loaded reference wheel and different slopes and loads. Net traction factor become zero based on load distribution and Brixius’ model Equation (22).

$$\frac{H-G_a·\sin \alpha }{G_a}=0=\left[0.88·\left(1-e^{-0.1·N_w}\right)·\left(1-e^{-7.5·\delta }\right)\right]-\left[\frac{1.0}{N_w}+0.04+\frac{0.5+\delta }{\sqrt{N_w}}\right]\to CI$$

(22)

During skidder downhill movement, a new so-called braking force should be taken into account. With the assumption that the drawbar pull (F_d) and the braking force (F_br), with a positive wheel slip, are of the same course and that the mass moment of inertia will not be taken into account since they are unknown and the literature review does not give boundary values for their calculation, therefore, the braking force (including the safety factor) will be larger than the real one. The moment when the net traction factor (μ) changes to a braking factor (μ_br) is the moment when the horizontal component of rope force (H) is equal to adhesive weight (G_a) at a certain terrain slope (G_a sin α) as it is stated in Equation (23) i.e., the moment when the thrust force is equal to zero (F_o = 0). Then the net traction factor (μ) becomes zero, and by changing to a braking factor (μ_br) becomes negative in value.

$$H=G_a\sin \alpha \to \mu =0$$

(23)

Tractive performance of a skidder in downhill timber extraction is based on the assumption that the drawbar pull (F_d) and the braking force (F_br) are of the same course and the braking factor (μ_br) will be calculated as an absolute value according to Equation (24).

$${\mu }_{br }=\frac{F_{br}}{G_a}=\left|\frac{H-G_a\sin \alpha }{G_a}\right|$$

(24)

Wheel load of a skidder, depending on terrain slope and direction as well as load size, will assume equal distribution of axle load. Based on wheel load, a reference wheel will be determined (as the one with the highest load) and nominal ground pressure (NGP) according to Mellgren (1980) [27] will be calculated.

Proposed skidder mobility model will consider parameters from previous research:

• Unloading of the front axle (G₁) [28], whereas at least 10% of total dynamic load should be on the front axle (G₁ > 0.1 G_a), so the control of the vehicle is possible;
• Overload on the rear axle (G₂) [16], by which the load on the rear axle of the skidder must not be higher than the total weight of a skidder (G₂ < G);
• Maximal terrain slope [29] after which the load starts to push the skidder downhill, which is defined as the moment when horizontal component of rope force becomes zero (H = 0);
• Minimal soil bearing capacity [30] based on environmentally sound timber extraction depending on cone index and nominal ground pressure ratio (CI_min > 7.2 NGP);
• Allowed tyre load capacity (with different tyre sizes) regarding the recommended inflation pressures given by the manufacturer [31].

3. Results

Planning of timber extraction by a cable skidder was defined as an intersection area of (1) gradeability or dependence of maximal terrain slope for a cable skidder and cone index and (2) dependence of terrain slope and minimal cone index in which all other parameters besides gradeability of the skidder are included. Timber extraction by a cable skidder is characterised by different loads (from unloaded to 5 tonne load) and two types of tyres—standard narrower tyres (16.9-30 PR14, Nokian Tyres plc., Nokia, Finland) and optional wider tyres (540/70-30, Nokian Tyres plc., Nokia, Finland). Allowed tyre load capacity of narrower tyres is 3 tonnes per wheel at 260 kPa inflation pressure which results in 58.86 kN per axle. Allowed tyre load capacity of wider tyres is 4.375 tonnes per wheel at 240 kPa inflation pressure which amounts to 85.84 kN per axle.

When skidding timber on sloped terrain a shift in axle load develops due to effect of horizontal and vertical components of rope force, terrain slope and its direction (uphill or downhill skidding) and horizontal component of skidder weight (G sinα).

By skidding timber uphill there is an additional load to the rear axle due to shift of load from the front axle of a skidder because of the effect of the horizontal component of skidders’ weight (G sinα). When skidding timber downhill there is an opposite situation when the load shifts to the front axle of the vehicle.

Analysis showed that there are terrain slopes where loads on both axles become equal and are therefore in balance (G₁ = G₂). This develops at +25% terrain slope when skidder in unloaded, at 0% terrain slope when 1 tonne load is transported, at −16% terrain slope with 2 tonne load, at −27% terrain slope with 3 tonne load, at −35% terrain slope with 4 tonne load and at −41% terrain slope at 5 tonne load.

For analysed terrain slopes and different loads, defined criteria showed their influence:

• Unloading of the front axle (G₁ > 0.1 G_a)—this criterion did not show its influence up to 4 tonne load and terrain slope above +40% and with 5 tonne load at terrain slope higher than +25%.
• Overload on the rear axle (G₂ < G)—this criterion also did not show its influence up to 4 tonne load at terrain slope over +30% and with 5 tonne load at terrain slope beyond +11%.
• Allowed tyre load capacity of narrower tyres 16.9–30 PR14 (58.86 kN per axle)—narrower tyres did not impact timber transport up to 2 tonne load, but with 3 tonne load at +13% overload occurred. During 4 tonne load wheel overload is at –3% and by adding one more tonne overload starts at −13% of terrain slope.
• Allowed tyre load capacity of wider tyres 540/70-30 (85.84 kN per axle)—this criterion did not show its influence with loads up to 5 tonnes.

During driving of an unloaded skidder (Figure 2a,b) its mobility is determined by its tractive performance at 20%-wheel slip (gradeability) and environmental factor ratio of cone index and nominal ground pressure (CI_min = 7.2 NGP). It should be stated that during skidder movement uphill and above 25% of terrain slope, rear axle bears more load than the front axle (G₁ < G₂).

By adding load, different criteria start to affect skidder mobility and reduce the area of its efficiency in the stand regarding the soil bearing capacity and the terrain slope:

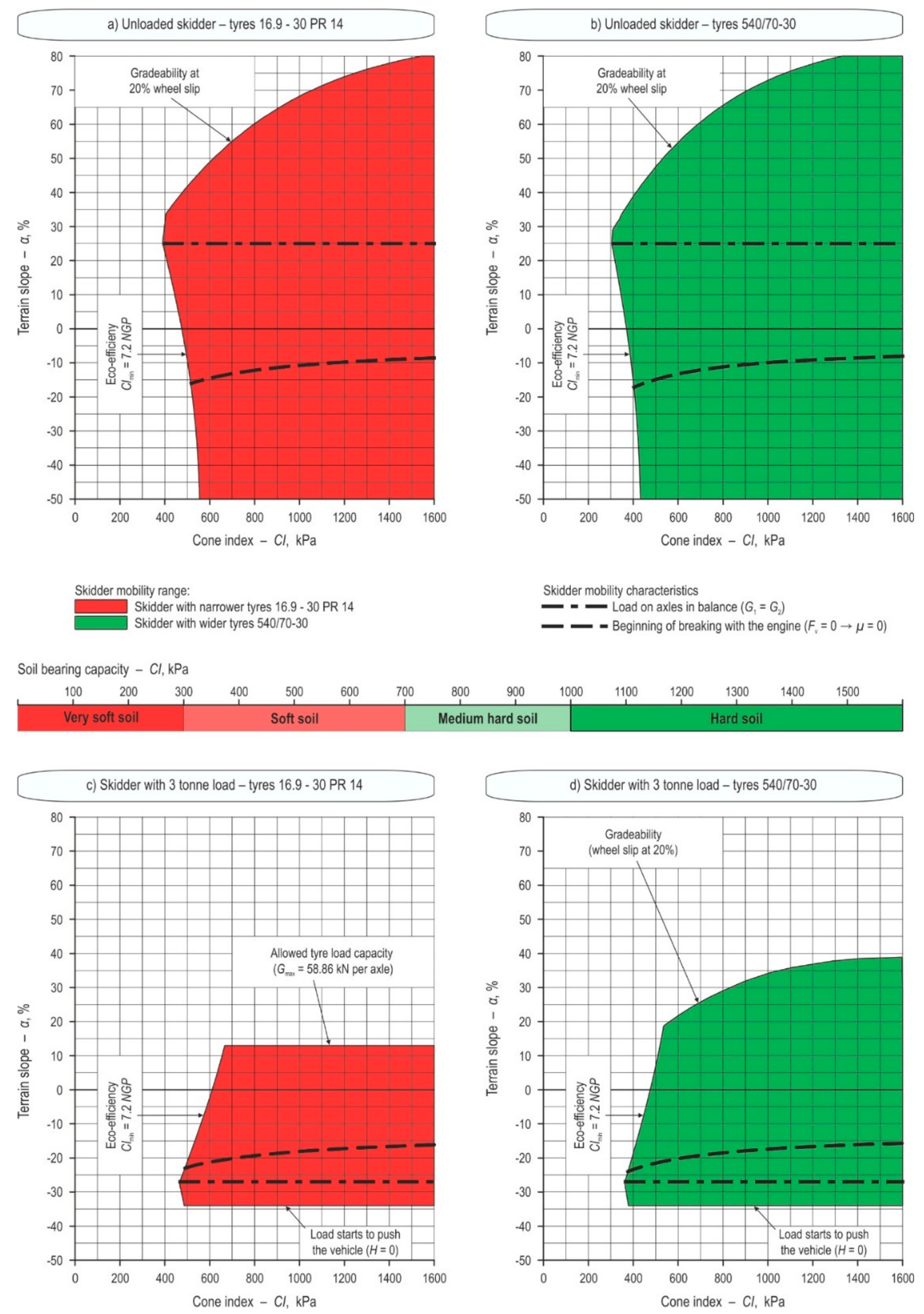
• During skidding of 1 tonne load uphill, skidder mobility is under influence of the gradeability (tractive performance) i.e., maximal terrain slope at +63% and minimal cone index at 1600 kPa. During downhill movement loss of drawbar pull is evident (net traction factor equals to zero) and at that moment the skidder will start to break with the engine at slopes between −10% and −15% even though transfer of load from rear to front axle is on 0% slope (G₁ > G₂). Downhill skidding should be up to −26% of terrain slope after which load starts to hit the rear protection plate.
• While skidding 2 tonne load, applicability of the uphill skidding is defined by gradeability where maximal reachable terrain slope with wider tyres is at 45% with minimal CI = 1100 kPa including environmental factor ratio (CI_min = 7.2 NGP). In downhill skidding, the beginning of braking with the engine correlates to the moment of load balance on both axles (G₁ = G₂) at −16% terrain slope. Maximal downhill slope is −30%, at which point horizontal component of rope force is equal to zero (H = 0) and load starts to hit the rear protection plate.
• When skidding 3 tonne load (Figure 2c,d) there is a clear difference between use of narrower and wider tyres on skidder performance uphill (Figure 2). For a skidder with narrower tyres allowed tyre load capacity (G_max = 58.86 kN per axle) showed its influence at +13% slope and by adding wider tyres performance rose up to +39% terrain slope. At +39% terrain slope gradeability (with a minimal CI = 800 kPa) showed influence on skidder mobility. Braking with the engine will start prior to balancing of load on both axles at −27% terrain slope, while the limiting slope for skidding load of 3 tonnes downhill is at −34%.
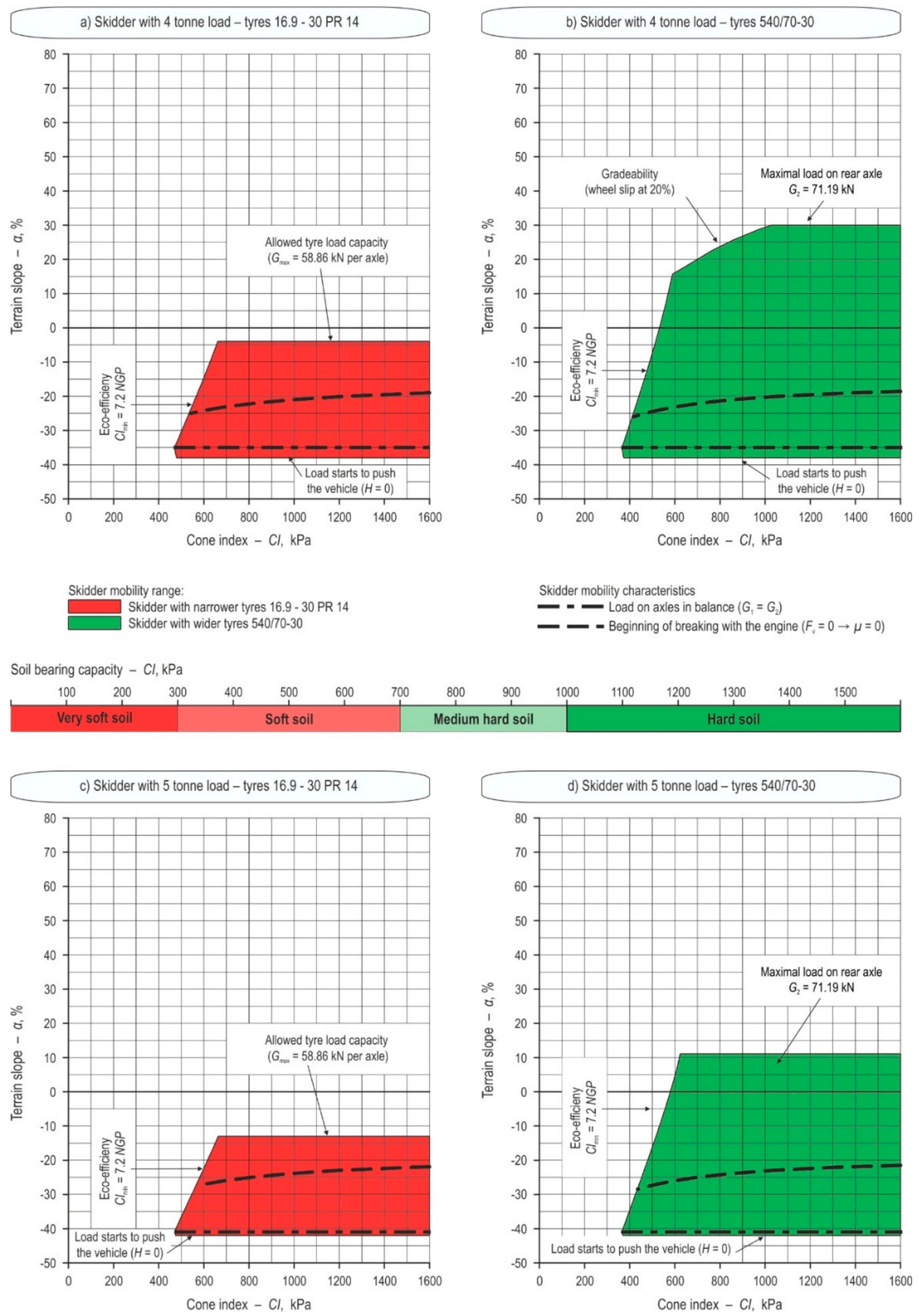
• If loading a skidder with a 4 tonne load (Figure 3a,b) its working range regarding terrain slope changes (Figure 3). With narrower tyres skidder should transport timber only downhill (below −4% slope) since allowed tyre load capacity (G_max = 58.86 kN per axle) shows its influence. When skidding downhill, a loss of drawbar pull at −25% slope is noticeable. Transfer of load from rear to front axle (G₁ > G₂) starts at terrain slope below −35% and the load starts to push the vehicle at −38% of terrain slope. By using wider tyres, working range of a cable skidder increases in uphill skidding up to +30% of terrain slope, at which point overload on the rear axle would occur G₂ = 71.19 kN.
• With adding one tonne more and transporting a total of 5 tonnes (Figure 3c,d), skidder could go further down the slope up to −42%. Loss of drawbar pull is between −20% to −25% of downhill skidding and the transfer of load from rear to front axle (G₁ > G₂) is at −41% of terrain slope. When using wider tyres, uphill timber transport would extend to +11% of terrain slope, after which overload on the rear axle will start G₂ = 71.19 kN.

4. Discussion

The basis of the skidder mobility model were its dimensional characteristics, center of gravity position of the Ecotrac 120 V skidder [24] and dependence of load mass distribution factor and skidding factor [25]. Many authors [32,33,34] have included load distribution during timber extraction in computer applications as well as tractive performance of vehicles (also based on Brixius’ model) in order to determine vehicles’ gradeabilty. Eichrodt (2003) [35] and Lubello (2008) [36] have connected vehicle mobility with GIS and created a Decision Support System (DSS) for planning of timber extraction on a tactical level. Nevertheless, it should be stated that most of the currently known skidder mobility models refer to uphill timber extraction. Simulation results of skidders’ load distribution, horizontal and vertical component of rope force, drawbar pull and net traction factor in dependence to terrain slope and direction (uphill or downhill extraction) and load size are in accordance to previous research [16,24,36,37,38,39,40,41].

The only firm limit in downhill skidding is the slope at which the load starts to hit the rear protection plate and to push the vehicle downhill [29]. Depending on load size this major point should be referred to as (1) a security measurement in downhill timber skidding, (2) a measure of vehicle protection during its use (life of machine in years) and (3) a planning information during building of a skid road network where allowed longitudinal slopes are between 20% and 25% and if that is exceeded pluvial erosion is possible [42].

During downhill skidding of timber, torque is used for braking and the skidder pulls the load by its weight and the transfer of power from the motor to the wheels is used for braking since there is a high influence of parallel component of skidder weight. Transfer of load from rear to front axle of the vehicle during downhill skidding (G₁ > G₂) can be described as the beginning of the use of brakes in the vehicle [43].

5. Conclusions

A skidder mobility model can be made by knowing its dimensions, and by connecting two approaches: (1) vehicle-terrain (distribution of forces and load on axles), and (2) wheel-soil (skidders’ tractive performance and wheel numeric) and by respecting limitations and recommendations from previous research. Creating a mobility model for an Ecotrac 120 V skidder was possible by knowing its characteristics, many of which are not visible in manufacturers’ prospectus such as (1) height and distance of center of gravity from front and rear axle and (2) height of horizontal rollers of the winch and its distance to rear axle. Therefore, it is recommended that dimensional characteristic needed for creating a mobility model become a standard part of vehicle tenders. The created skidder mobility model for skidding timber in a safe, sustainable and environmentally sound way included wide range of terrain slopes and both directions of skidding (uphill and downhill), different load sizes, soil bearing capacity, and using standard (narrower) or optional (wider) tyres. Even though skidding is possible on even greater terrain slopes than given in this research, the most important consideration in downhill skidding should be avoiding the blockage of the wheels which could lead to a vehicle slippage. If load pushes the vehicle downhill, due to the constant thrust of the timber at the back end of a skidder, in due time fatigue of the material and early damage to the vehicle is probable, not to mention work safety concerns and the negative influence on the psycho-physical state of the driver in such driving conditions.