Drought Sensitiveness on Forest Growth in Peninsular Spain and the Balearic Islands
Abstract
1. Introduction
2. Data and Methods
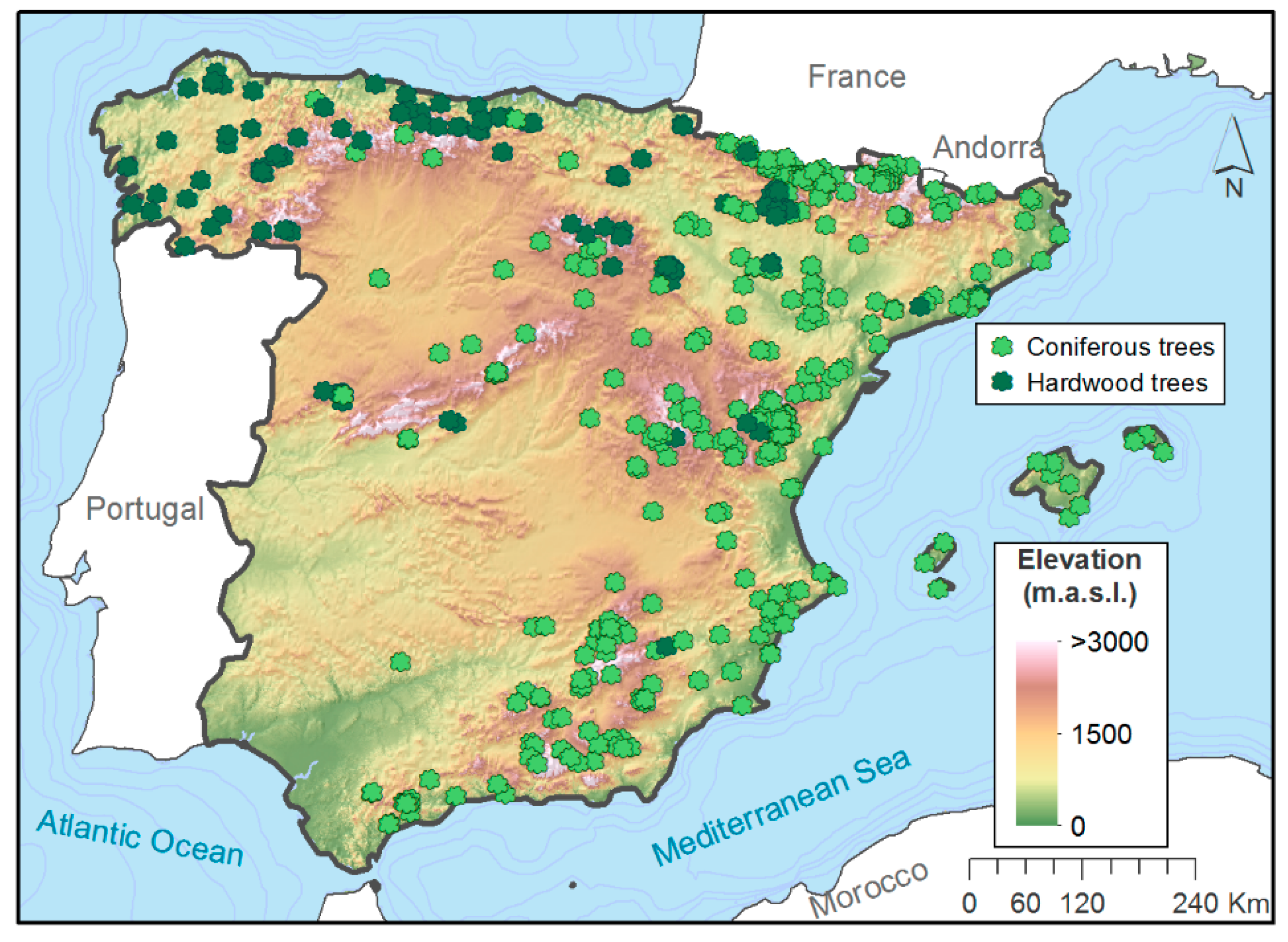
2.1. Datasets Description
2.2. NDVI Data
2.3. Tree-Ring Width Data
2.4. Drought Indices
2.4.1. Palmer Drought Severity Indices (PDSIs)
2.4.2. Standardized Precipitation Index (SPI)
2.4.3. Standardized Precipitation Evapotranspiration Index (SPEI)
2.4.4. Standardized Precipitation Drought Index (SPDI)
2.5. Statistical Methods
3. Results
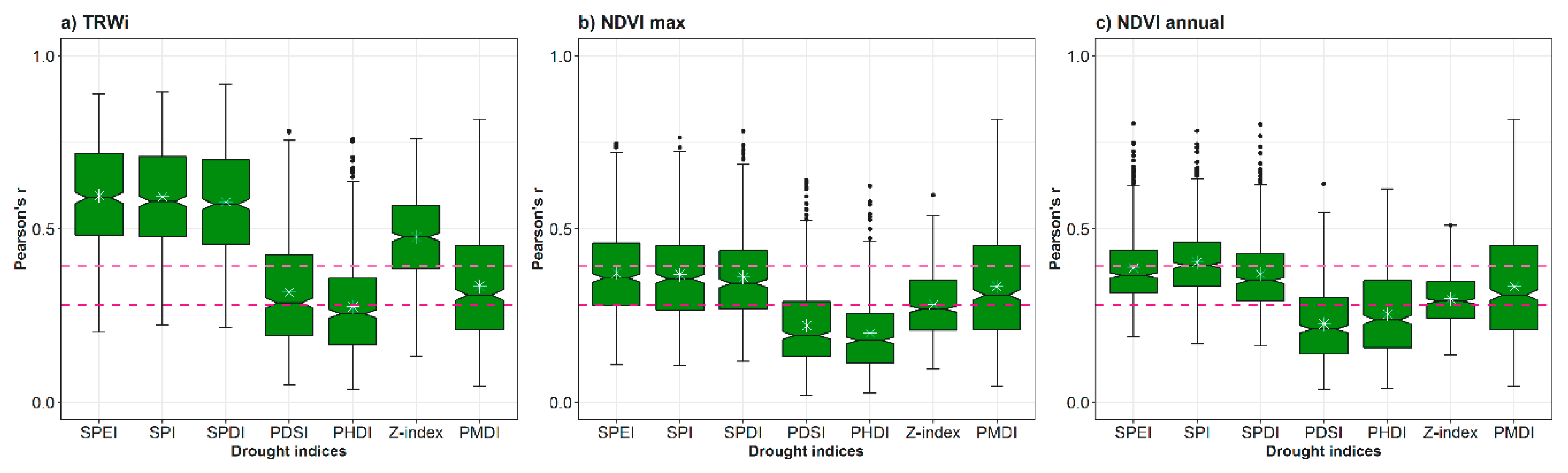
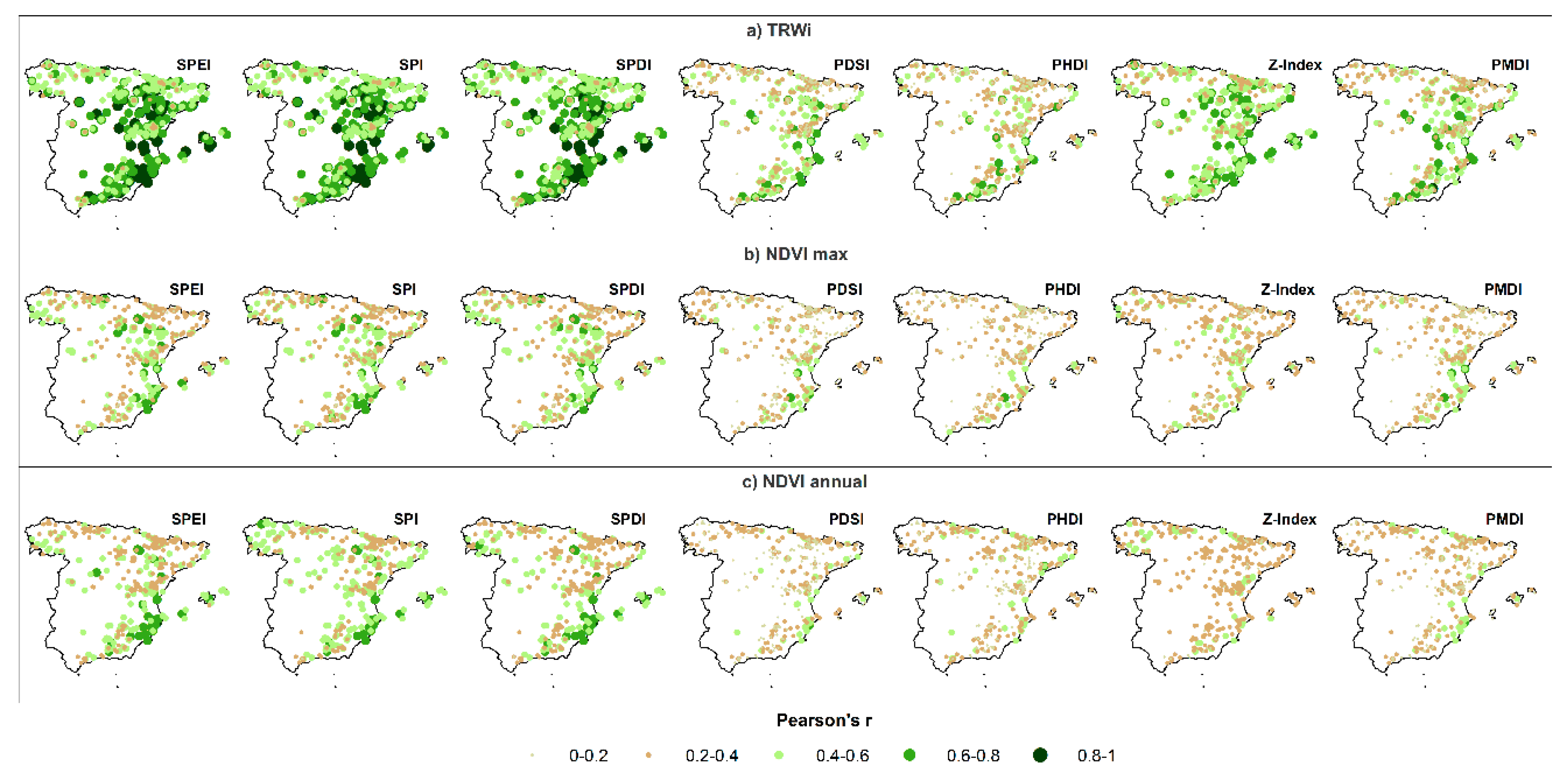
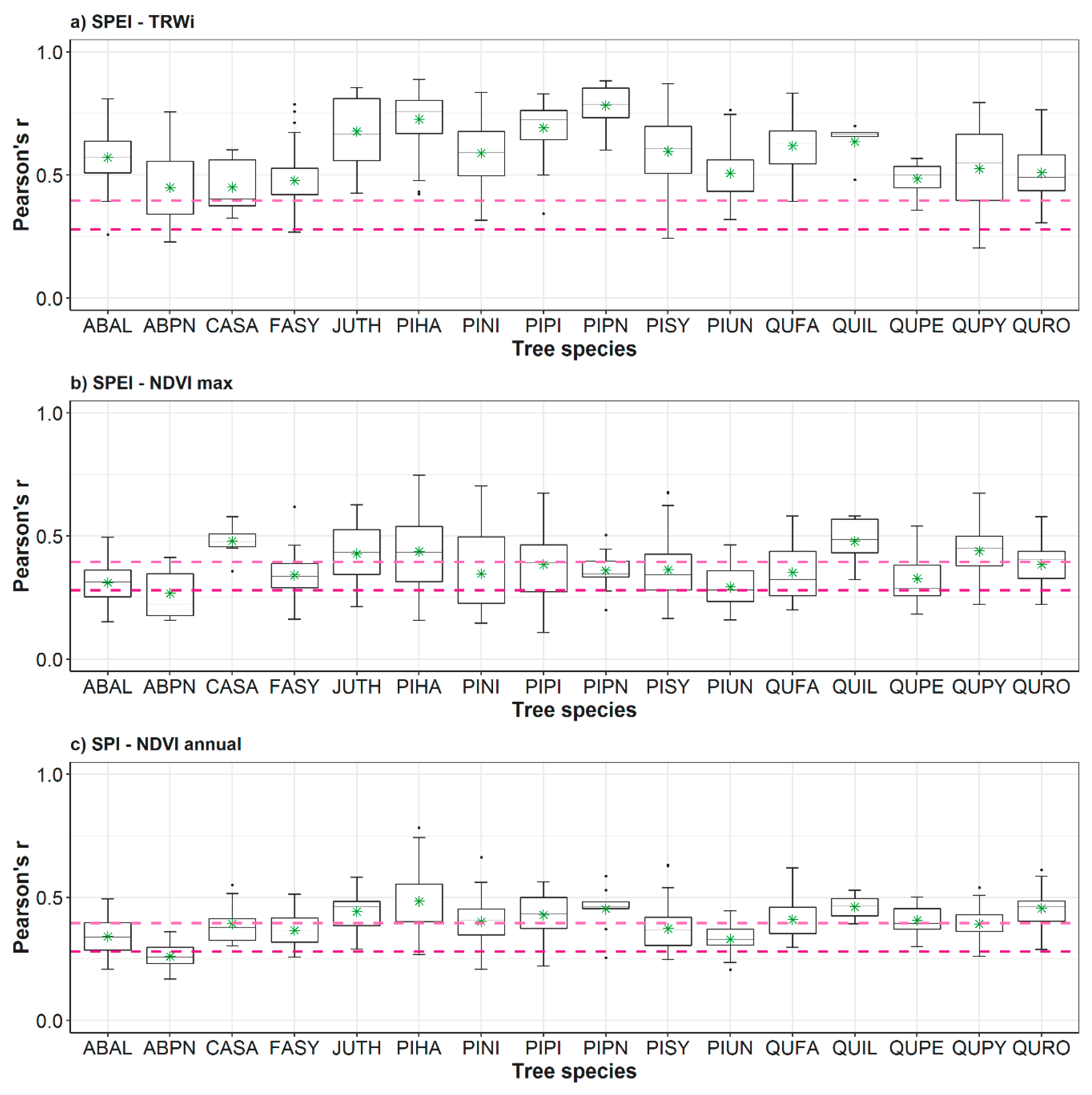
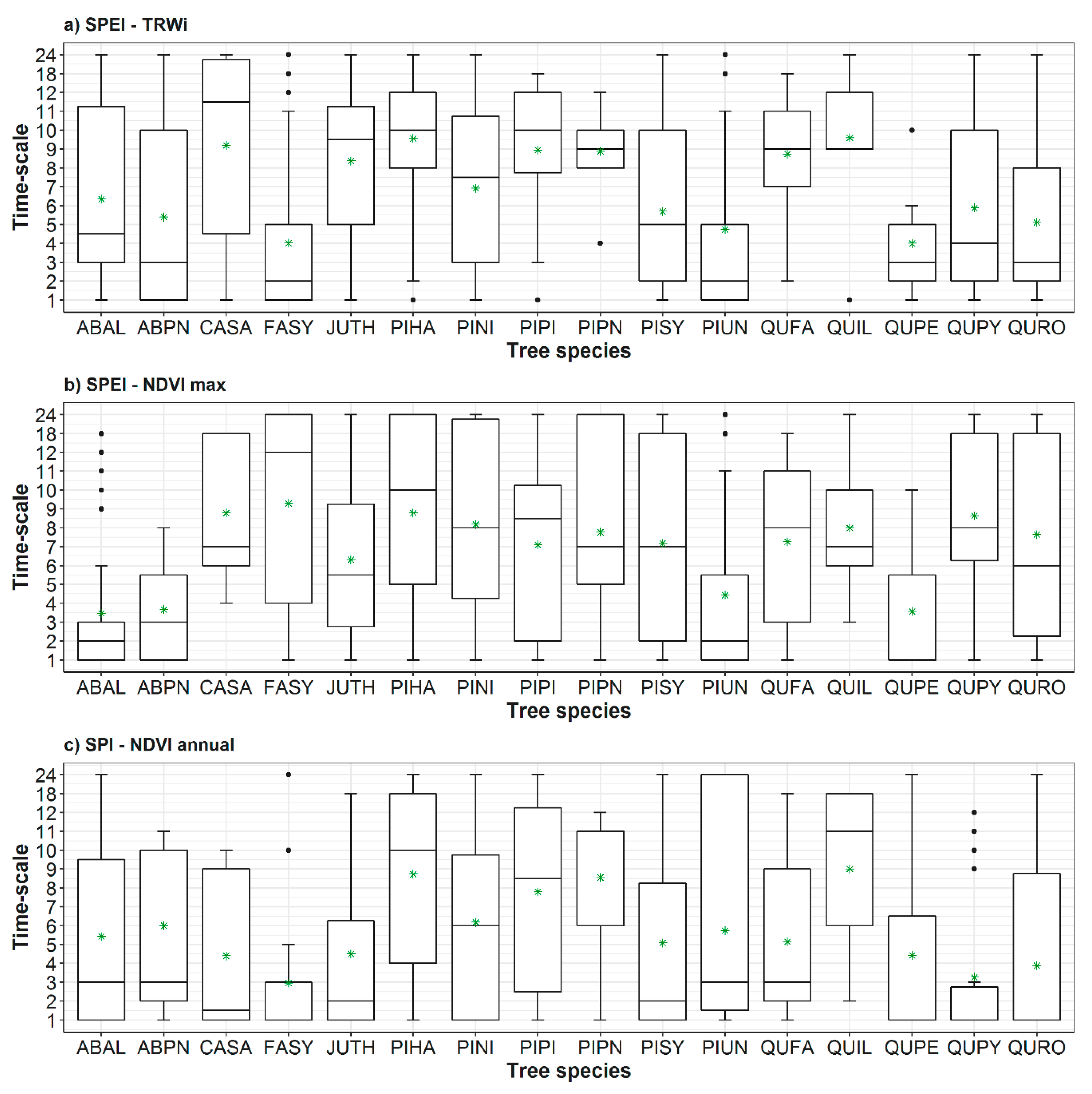
3.1. Spatial and Temporal Responses of Tree Variables to Drought
3.2. Relationship between Vegetation Variables and Drought by Species
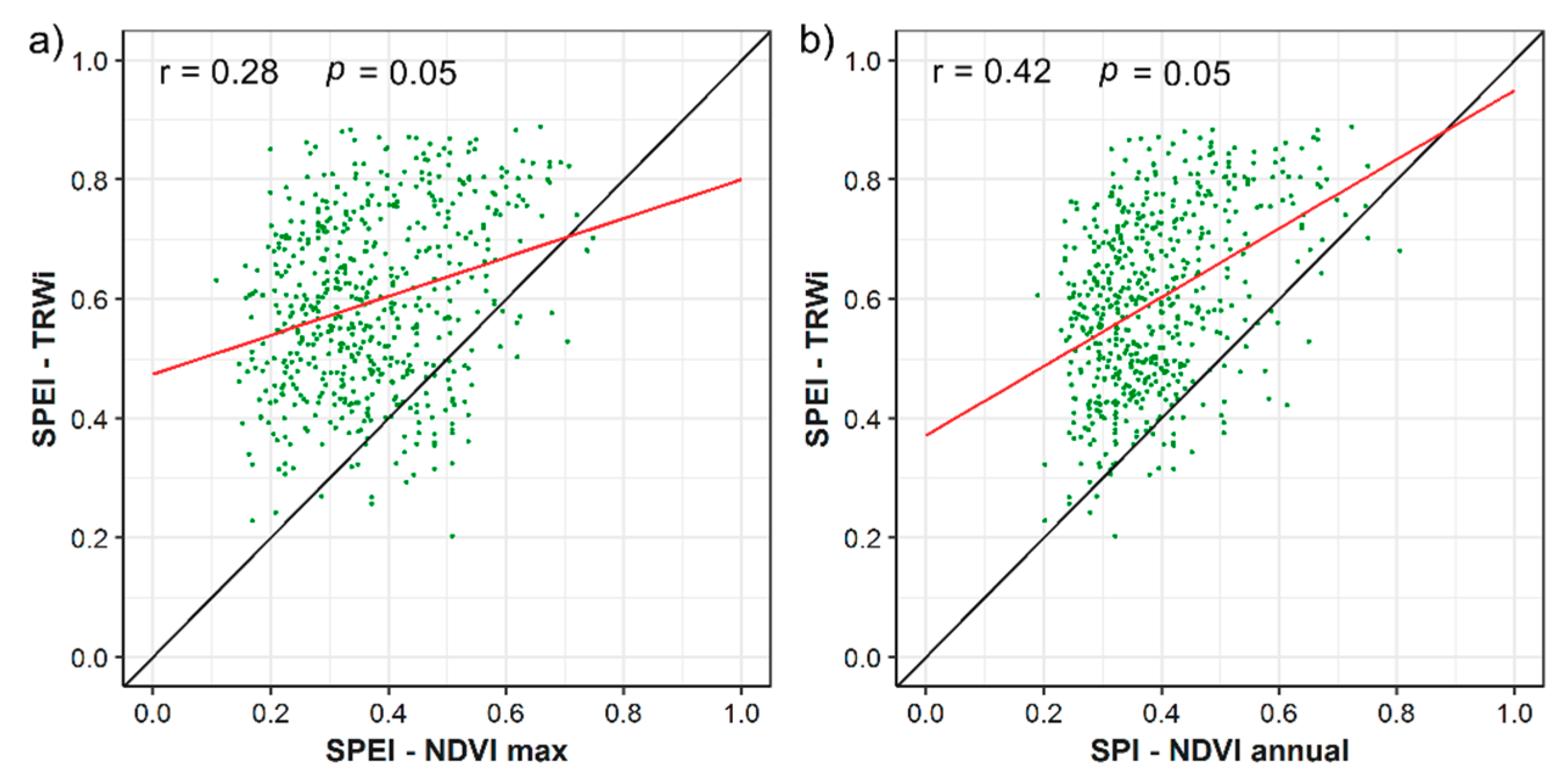
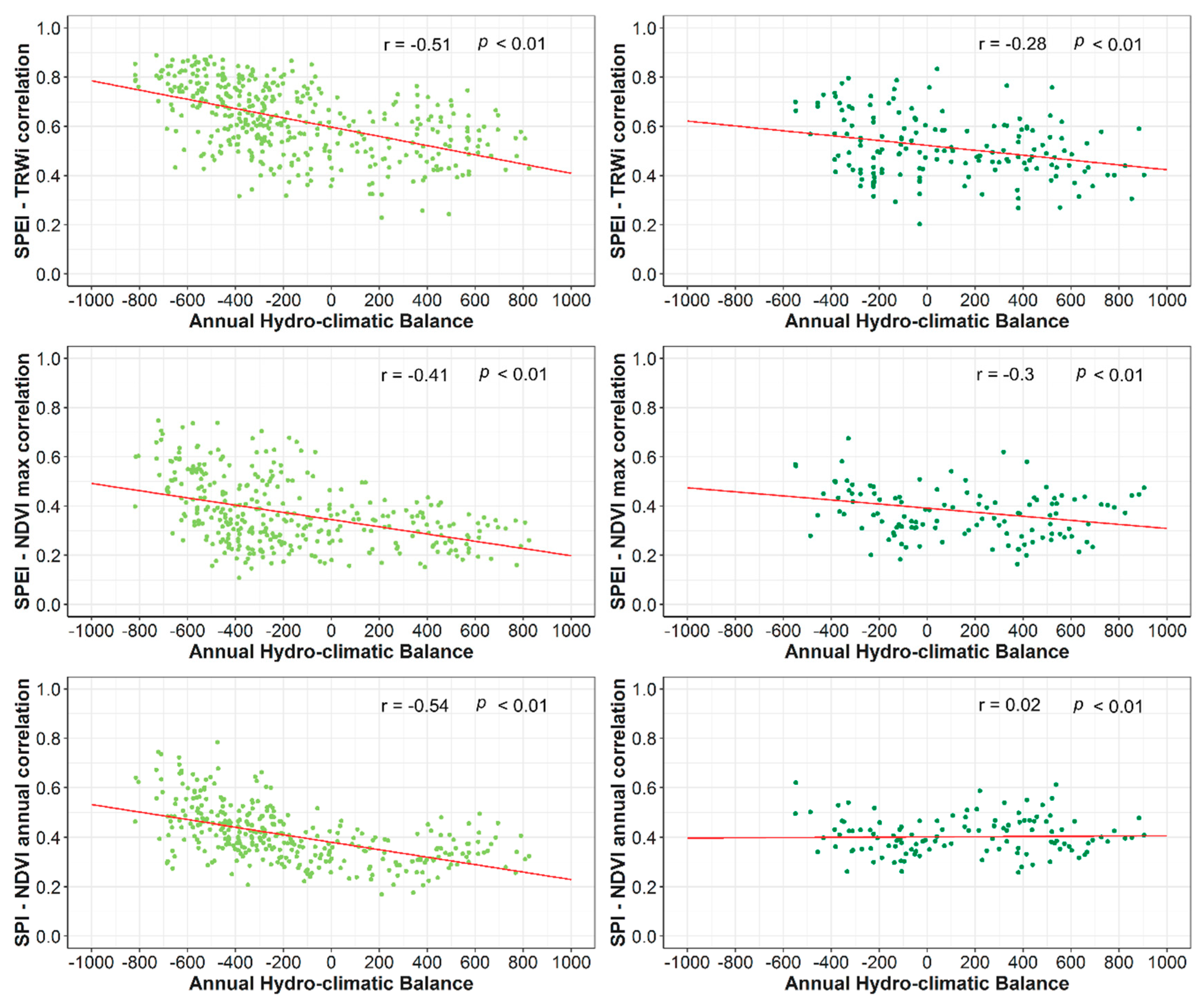
4. Discussion
5. Conclusions
- The multi-scalar drought indices (e.g., SPEI, SPI, and SPDI) perform better than uni-scalar indices (e.g., PDSI) to identify drought impacts on forests for different species.
- Among the multi-scalar indices, SPEI and SPI correlate better with TRWi and NDVI than the SPDI for most species.
- Albeit with the few differences in the magnitude of correlations between the SPEI and SPI, our results suggest a major role of the atmospheric evaporative demand in drought severity across forests located in dry Mediterranean areas.
- Droughts are more prone to impact forest secondary growth (TRWi) during summertime, and annual production and greenness (NDVI) during springtime.
- The response of the forests to drought is mainly driven by short time scales (1–3 months) in humid-temperate hardwood forests, compared to long to medium (>4 months) time scales in warm-dry conifer forests.
- Tree-ring growth seems a more reliable indicator of the response of forests to drought, due to its higher association with drought indices.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Wilhite, D.A.; Pulwarty, R.S. Drought and Water Crises: Integrating Science, Management, and Policy; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781138035645. [Google Scholar]
- Bachmair, S.; Kohn, I.; Stahl, K. Exploring the link between drought indicators and impacts. Nat. Hazards Earth Syst. Sci. 2015, 15, 1381–1397. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Svoboda, M.D.; Hayes, M.J. Understanding the complex impacts of drought: A key to enhancing drought mitigation and preparedness. Water Resour. Manag. 2007, 21, 763–774. [Google Scholar] [CrossRef]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.H.; et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Zhang, Q.; Shao, M.; Jia, X.; Wei, X. Relationship of Climatic and Forest Factors to Drought- and Heat-Induced Tree Mortality. PLoS ONE 2017, 12, e0169770. [Google Scholar] [CrossRef] [PubMed]
- Young, D.J.N.; Stevens, J.T.; Earles, J.M.; Moore, J.; Ellis, A.; Jirka, A.L.; Latimer, A.M. Long-term climate and competition explain forest mortality patterns under extreme drought. Ecol. Lett. 2017, 20, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Greenwood, S.; Ruiz-Benito, P.; Martínez-Vilalta, J.; Lloret, F.; Kitzberger, T.; Allen, C.D.; Fensham, R.; Laughlin, D.C.; Kattge, J.; Bönisch, G.; et al. Tree mortality across biomes is promoted by drought intensity, lower wood density and higher specific leaf area. Ecol. Lett. 2017, 20, 539–553. [Google Scholar] [CrossRef] [PubMed]
- Vicente-Serrano, S.M.; Lopez-Moreno, J.-I.; Beguería, S.; Lorenzo-Lacruz, J.; Sanchez-Lorenzo, A.; García-Ruiz, J.M.; Azorin-Molina, C.; Morán-Tejeda, E.; Revuelto, J.; Trigo, R.; et al. Evidence of increasing drought severity caused by temperature rise in southern Europe. Environ. Res. Lett. 2014, 9, 44001–44009. [Google Scholar] [CrossRef]
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Chang. 2013, 3, 52–58. [Google Scholar] [CrossRef]
- Pasho, E.; Camarero, J.J.; de Luis, M.; Vicente-Serrano, S.M. Impacts of drought at different time scales on forest growth across a wide climatic gradient in north-eastern Spain. Agric. For. Meteorol. 2011, 151, 1800–1811. [Google Scholar] [CrossRef]
- Gazol, A.; Camarero, J.J.; Anderegg, W.R.L.; Vicente-Serrano, S.M. Impacts of droughts on the growth resilience of Northern Hemisphere forests. Glob. Ecol. Biogeogr. 2017, 26, 166–176. [Google Scholar] [CrossRef]
- Sánchez-Salguero, R.; Navarro-Cerrillo, R.M.; Camarero, J.J.; Fernández-Cancio, Á. Selective drought-induced decline of pine species in southeastern Spain. Clim. Chang. 2012, 113, 767–785. [Google Scholar] [CrossRef]
- Arzac, A.; Rozas, V.; Rozenberg, P.; Olano, J.M. Water availability controls Pinus pinaster xylem growth and density: A multi-proxy approach along its environmental range. Agric. For. Meteorol. 2018, 250–251, 171–180. [Google Scholar] [CrossRef]
- Arzac, A.; García-Cervigón, A.I.; Vicente-Serrano, S.M.; Loidi, J.; Olano, J.M. Phenological shifts in climatic response of secondary growth allow Juniperus sabina L. to cope with altitudinal and temporal climate variability. Agric. For. Meteorol. 2016, 217, 35–45. [Google Scholar] [CrossRef]
- Forner, A.; Valladares, F.; Bonal, D.; Granier, A.; Grossiord, C.; Aranda, I. Extreme droughts affecting Mediterranean tree species’ growth and water-use efficiency: The importance of timing. Tree Physiol. 2018. [Google Scholar] [CrossRef] [PubMed]
- Peguero-Pina, J.J.; Sancho-Knapik, D.; Cochard, H.; Barredo, G.; Villarroya, D.; Gil-Pelegrin, E. Hydraulic traits are associated with the distribution range of two closely related Mediterranean firs, Abies alba Mill. and Abies pinsapo Boiss. Tree Physiol. 2011, 31, 1067–1075. [Google Scholar] [CrossRef] [PubMed]
- Martín Vide, J.; Olcina Cantos, J. Climas y Tiempos de España; Alianza Editorial: Madrid, Spain, 2001; ISBN 8420657778. [Google Scholar]
- Camarero, J.J.; Gazol, A.; Sangüesa-Barreda, G.; Cantero, A.; Sánchez-Salguero, R.; Sánchez-Miranda, A.; Granda, E.; Serra-Maluquer, X.; Ibáñez, R. Forest Growth Responses to Drought at Short- and Long-Term Scales in Spain: Squeezing the Stress Memory from Tree Rings. Front. Ecol. Evol. 2018, 6, 9. [Google Scholar] [CrossRef]
- Neumann, M.; Mues, V.; Moreno, A.; Hasenauer, H.; Seidl, R. Climate variability drives recent tree mortality in Europe. Glob. Chang. Biol. 2017, 23, 4788–4797. [Google Scholar] [CrossRef] [PubMed]
- Camarero, J.J.; Gazol, A.; Sangüesa-Barreda, G.; Oliva, J.; Vicente-Serrano, S.M. To die or not to die: Early warnings of tree dieback in response to a severe drought. J. Ecol. 2015, 103, 44–57. [Google Scholar] [CrossRef]
- Carnicer, J.; Coll, M.; Ninyerola, M.; Pons, X.; Sánchez, G.; Peñuelas, J. Widespread crown condition decline, food web disruption, and amplified tree mortality with increased climate change-type drought. Proc. Natl. Acad. Sci. USA 2011, 108, 1474–1478. [Google Scholar] [CrossRef] [PubMed]
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Frank, D.C.; Poulter, B.; Saurer, M.; Esper, J.; Huntingford, C.; Helle, G.; Treydte, K.; Zimmermann, N.E.; Schleser, G.H.; Ahlström, A.; et al. Water-use efficiency and transpiration across European forests during the Anthropocene. Nat. Clim. Chang. 2015, 5, 579–583. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W. Drought-Induced Reduction in Global Terrestrial Net Primary Production from 2000 Through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef] [PubMed]
- Gursoy, M.; Balkan, A.; Ulukan, H. Ecophysiological Responses to Stresses in Plants: A General Approach. Pak. J. Biol. Sci. 2012, 15, 506–516. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Cang, Z.; Jiao, F.; Bai, X.; Zhang, D.; Zhai, R. Influence of drought stress on photosynthetic characteristics and protective enzymes of potato at seedling stage. J. Saudi Soc. Agric. Sci. 2017, 16, 82–88. [Google Scholar] [CrossRef]
- Pinheiro, C.; Chaves, M.M. Photosynthesis and drought: can we make metabolic connections from available data? J. Exp. Bot. 2011, 62, 869–882. [Google Scholar] [CrossRef] [PubMed]
- Basu, S.; Ramegowda, V.; Kumar, A.; Pereira, A. Plant adaptation to drought stress. F1000Research 2016, 5. [Google Scholar] [CrossRef] [PubMed]
- Granda, E.; Escudero, A.; Valladares, F. More than just drought: Complexity of recruitment patterns in Mediterranean forests. Oecologia 2014, 176, 997–1007. [Google Scholar] [CrossRef] [PubMed]
- Lloret, F.; Escudero, A.; Iriondo, J.M.; Martínez-Vilalta, J.; Valladares, F. Extreme climatic events and vegetation: The role of stabilizing processes. Glob. Chang. Biol. 2012, 18, 797–805. [Google Scholar] [CrossRef]
- Vidal-Macua, J.J.; Ninyerola, M.; Zabala, A.; Domingo-Marimon, C.; Pons, X. Factors affecting forest dynamics in the Iberian Peninsula from 1987 to 2012. The role of topography and drought. For. Ecol. Manag. 2017, 406, 290–306. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Camarero, J.J.; Olano, J.M.; Martín-Hernández, N.; Peña-Gallardo, M.; Tomás-Burguera, M.; Gazol, A.; Azorin-Molina, C.; Bhuyan, U.; El Kenawy, A. Diverse relationships between forest growth and the Normalized Difference Vegetation Index at a global scale. Remote Sens. Environ. 2016, 187, 14–29. [Google Scholar] [CrossRef]
- Babst, F.; Poulter, B.; Trouet, V.; Tan, K.; Neuwirth, B.; Wilson, R.; Carrer, M.; Grabner, M.; Tegel, W.; Levanic, T.; et al. Site- and species-specific responses of forest growth to climate across the European continent. Glob. Ecol. Biogeogr. 2013, 22, 706–717. [Google Scholar] [CrossRef]
- Fritts, H.C. Tree Rings and Climate; Academic Press: Cambridge, MA, USA, 1976; ISBN 9780122684500. [Google Scholar]
- Gazol, A.; Sangüesa-Barreda, G.; Granda, E.; Camarero, J.J. Tracking the impact of drought on functionally different woody plants in a Mediterranean scrubland ecosystem. Plant Ecol. 2017, 218, 1009–1020. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Martín-Hernández, N.; Camarero, J.J.; Gazol, A.; Sánchez-Salguero, R.; Peña-Gallardo, M.; El Kenawy, A.; Domínguez-Castro, F.; Tomas-Burguera, M.; Gutiérrez, E.; et al. Spatial, temporal and climatic determinants of the responses of tree-ring growth to satellite-derived primary growth in multiple forest biomes. Sci. Total Environ. 2018. under review. [Google Scholar]
- Poulter, B.; Pederson, N.; Liu, H.; Zhu, Z.; D’Arrigo, R.; Ciais, P.; Davi, N.; Frank, D.; Leland, C.; Myneni, R.; Piao, S.; Wang, T. Recent trends in Inner Asian forest dynamics to temperature and precipitation indicate high sensitivity to climate change. Agric. For. Meteorol. 2013, 178–179, 31–45. [Google Scholar] [CrossRef]
- Wang, J.; Rich, P.M.; Price, K.P.; Kettle, W.D. Relations between NDVI and tree productivity in the central Great Plains. Int. J. Remote Sens. 2004, 25, 3127–3138. [Google Scholar] [CrossRef]
- Bochenek, Z.; Ziolkowski, D.; Bartold, M.; Orlowska, K.; Ochtyra, A. Monitoring forest biodiversity and the impact of climate on forest environment using high-resolution satellite images. Eur. J. Remote Sens. 2018, 51, 166–181. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Gouveia, C.; Camarero, J.J.; Beguería, S.; Trigo, R.; López-Moreno, J.I.; Azorín-Molina, C.; Pasho, E.; Lorenzo-Lacruz, J.; Revuelto, J.; et al. Response of vegetation to drought time-scales across global land biomes. Proc. Natl. Acad. Sci. USA 2013, 110, 52–57. [Google Scholar] [CrossRef] [PubMed]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Tucker, C.J.; Sellers, P.J. Satellite remote sensing of primary production. Int. J. Remote Sens. 1986, 7, 1395–1416. [Google Scholar] [CrossRef]
- Keyantash, J.; Dracup, J.A.; Keyantash, J.; Dracup, J.A. The Quantification of Drought: An Evaluation of Drought Indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- Shukla, S.; Steinemann, A.C.; Lettenmaier, D.P.; Shukla, S.; Steinemann, A.C.; Lettenmaier, D.P. Drought Monitoring for Washington State: Indicators and Applications. J. Hydrometeorol. 2011, 12, 66–83. [Google Scholar] [CrossRef]
- Lorenzo-Lacruz, J.; Vicente-Serrano, S.M.; López-Moreno, J.I.; Beguería, S.; García-Ruiz, J.M.; Cuadrat, J.M. The impact of droughts and water management on various hydrological systems in the headwaters of the Tagus River (central Spain). J. Hydrol. 2010, 386, 13–26. [Google Scholar] [CrossRef]
- Peña-Gallardo, M.; Vicente-Serrano, S.M.; Domínguez-Castro, F.; Quiring, S.M.; Svoboda, M.D.; Beguería-Portugués, S.; Hannaford, J. Effectiveness of drought indices in identifying impacts on major crops over the USA. Clim. Res. 2018, in press. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; Lorenzo-Lacruz, J.; Camarero, J.J.; López-Moreno, J.I.; Azorin-Molina, C.; Revuelto, J.; Morán-Tejeda, E.; Sanchez-Lorenzo, A.; Vicente-Serrano, S.M.; et al. Performance of Drought Indices for Ecological, Agricultural, and Hydrological Applications. Earth Int. 2012. [Google Scholar] [CrossRef]
- Kempes, C.P.; Myers, O.B.; Breshears, D.D.; Ebersole, J.J. Comparing response of Pinus edulis tree-ring growth to five alternate moisture indices using historic meteorological data. J. Arid Environ. 2008, 72, 350–357. [Google Scholar] [CrossRef]
- Bachmair, S.; Tanguy, M.; Hannaford, J.; Stahl, K. How well do meteorological indicators represent agricultural and forest drought across Europe? Environ. Res. Lett. 2018, 13, 034042. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Tomas-Burguera, M.; Beguería, S.; Reig, F.; Latorre, B.; Peña-Gallardo, M.; Luna, M.Y.; Morata, A.; González-Hidalgo, J.C. A High Resolution Dataset of Drought Indices for Spain. Data 2017, 2, 22. [Google Scholar] [CrossRef]
- Allen, R.G.; Rick, G. Food and Agriculture Organization of the United Nations. In Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Allen, R.G., Pereira, L.S., Raes, D., smith, M., Eds.; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; ISBN 9251042195. [Google Scholar]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.-M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Vicente-Serrano, M.; Martín-Hernández, N.; Camarero, J.J.; Gazol, A.; Sánchez-Salguero, R.; Peña-Gallardo, M.; El Kenawy, A.; Domínguez-Castro, F.; Tomás-Burquera, M.; Gutiérrez, E.; et al. Linking tree-ring growth and satellite-derived gross primary growth in multiple forest biomes. Temporal-scale matters. Sci. Total Environ. 2018. under review. [Google Scholar]
- Nagaraja Rao, C.R.; Zhang, N.; Sullivan, J.T. Inter-calibration of meteorological satellite sensors in the visible and near-infrared. Adv. Space Res. 2001, 28, 3–10. [Google Scholar] [CrossRef]
- Robel, J. NOAA KLM User’s Guide—Satellite and Data Description of NOAA’s Polar-Orbiting Satellites from NOAA-15 and Later. 2009. Available online: https://www1.ncdc.noaa.gov/pub/data/satellite/publications/podguides/N-15%20thru%20N-19/pdf/0.0%20NOAA%20KLM%20Users%20Guide.pdf (accessed on 28 August 2018).
- Riano, D.; Chuvieco, E.; Salas, J.; Aguado, I. Assessment of different topographic corrections in landsat-TM data for mapping vegetation types (2003). IEEE Trans. Geosci. Remote Sens. 2003, 41, 1056–1061. [Google Scholar] [CrossRef]
- Baena-Calatrava, R. Georreferenciación Automática de Imágenes NOAA-AVHRR; University of Jaén: Jaen, Spain, 2002. [Google Scholar]
- Azorin-Molina, C.; Baena-Calatrava, R.; Echave-Calvo, I.; Connell, B.H.; Vicente-Serrano, S.M.; López-Moreno, J.I. A daytime over land algorithm for computing AVHRR convective cloud climatologies for the Iberian Peninsula and the Balearic Islands. Int. J. Climatol. 2013, 33, 2113–2128. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurements. Tree-Ring Bull. 1983, 43, 69–78. [Google Scholar]
- Bunn, A.G. A dendrochronology program library in R (dplR). Dendrochronologia 2008, 26, 115–124. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; U.S. Department of Commerce: Washington, DC, USA, 1965.
- Alley, W.M. The Palmer Drought Severity Index: Limitations and Assumptions. J. Clim. Appl. Meteorol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- Doesken, N.J.; Garen, D. Drought monitoring in the Western United States using a surface water supply index. In Proceedings of the 7th Conference on Applied Climatology, Salt Lake City, UT, USA, 10–13 September 1991; Doesken, N.J., Mckee, T.B., Kleist, J., Eds.; Colorado State University: Fort Collins, CO, USA, 1991. [Google Scholar]
- Heim, R.R. A Review of Twentieth-Century Drought Indices Used in the United States. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1165. [Google Scholar] [CrossRef]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Svoboda, M.; Hayes, M.; Wood, D. Standardized Precipitation Index User Guide; World Meteorological Organization: Geneva, Swizerland, 2012. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I.; Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Ma, M.; Ren, L.; Yuan, F.; Jiang, S.; Liu, Y.; Kong, H.; Gong, L. A new standardized Palmer drought index for hydro-meteorological use. Hydrol. Process. 2014, 28, 5645–5661. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Van der Schrier, G.; Beguería, S.; Azorin-Molina, C.; Lopez-Moreno, J.-I. Contribution of precipitation and reference evapotranspiration to drought indices under different climates. J. Hydrol. 2015, 526, 42–54. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.; Cabello, D.; Tomás-Burguera, M.; Martín-Hernández, N.; Beguería, S.; Azorin-Molina, C.; Kenawy, A. Drought Variability and Land Degradation in Semiarid Regions: Assessment Using Remote Sensing Data and Drought Indices (1982–2011). Remote Sens. 2015, 7, 4391–4423. [Google Scholar] [CrossRef]
- Bian, J.; Li, A.; Deng, W. Estimation and analysis of net primary Productivity of Ruoergai wetland in China for the recent 10 years based on remote sensing. Procedia Environ. Sci. 2010, 2, 288–301. [Google Scholar] [CrossRef]
- Kuenzer, C.; Dech, S.W.; Wagner, W. Remote Sensing Time Series: Revealing Land Surface Dynamics; Springer: Berlin, Germany, 2015; ISBN 9783319159676. [Google Scholar]
- Gazol, A.; Camarero, J.J.; Vicente-Serrano, S.M.; Sánchez-Salguero, R.; Gutiérrez, E.; de Luis, M.; Sangüesa-Barreda, G.; Novak, K.; Rozas, V.; Tíscar, P.A.; Linares, J.C.; et al. Forest resilience to drought varies across biomes. Glob. Chang. Biol. 2018, 24, 2143–2158. [Google Scholar] [CrossRef] [PubMed]
- Tardieu, F.; Simonneau, T.; Muller, B. The Physiological Basis of Drought Tolerance in Crop Plants: A Scenario-Dependent Probabilistic Approach. Annu. Rev. Plant Biol. 2018, 69, 733–759. [Google Scholar] [CrossRef] [PubMed]
- Almeida, T.I.R.; Filho, D.S. Principal component analysis applied to feature-oriented band ratios of hyperspectral data: A tool for vegetation studies. Int. J. Remote Sens. 2004, 25, 5005–5023. [Google Scholar] [CrossRef]
- Rimkus, E.; Stonevicius, E.; Kilpys, J.; Maciulyte, V.; Valiukas, D. Drought identification in the eastern Baltic region using NDVI. Earth Syst. Dyn. 2017, 85194, 627–637. [Google Scholar] [CrossRef]
- He, J.; Shao, X. Relationships between tree-ring width index and NDVI of grassland in Delingha. Chin. Sci. Bull. 2006, 51, 1106–1114. [Google Scholar] [CrossRef]
- Bhuyan, U.; Zang, C.; Menzel, A. Different responses of multispecies tree ring growth to various drought indices across Europe. Dendrochronologia 2017, 44, 1–8. [Google Scholar] [CrossRef]
- Vilhar, U. Comparison of drought stress indices in beech forests: A modelling study. iForest 2016, 9, 635. [Google Scholar] [CrossRef]
- Aaltonen, H.; Lindén, A.; Heinonsalo, J.; Biasi, C.; Pumpanen, J. Effects of prolonged drought stress on Scots pine seedling carbon allocation. Tree Physiol. 2016, 37, 418–427. [Google Scholar] [CrossRef] [PubMed]
- McDowell, N.; Allen, C.D.; Anderson-Teixeira, K.; Brando, P.; Brienen, R.; Chambers, J.; Christoffersen, B.; Davies, S.; Doughty, C.; Duque, A.; et al. Drivers and mechanisms of tree mortality in moist tropical forests. New Phytol. 2018. [Google Scholar] [CrossRef] [PubMed]
- Rowland, L.; Lobo-do-Vale, R.L.; Christoffersen, B.O.; Melém, E.A.; Kruijt, B.; Vasconcelos, S.S.; Domingues, T.; Binks, O.J.; Oliveira, A.A.R.; Metcalfe, D.; et al. After more than a decade of soil moisture deficit, tropical rainforest trees maintain photosynthetic capacity, despite increased leaf respiration. Glob. Chang. Biol. 2015, 21, 4662–4672. [Google Scholar] [CrossRef] [PubMed]
- McDowell, N.G.; Fisher, R.A.; Xu, C.; Domec, J.C.; Hölttä, T.; Mackay, D.S.; Sperry, J.S.; Boutz, A.; Dickman, L.; Gehres, N.; et al. Evaluating theories of drought-induced vegetation mortality using a multimodel-experiment framework. New Phytol. 2013, 200, 304–321. [Google Scholar] [CrossRef] [PubMed]
- Rowland, L.; da Costa, A.C.L.; Galbraith, D.R.; Oliveira, R.S.; Binks, O.J.; Oliveira, A.A.R.; Pullen, A.M.; Doughty, C.E.; Metcalfe, D.B.; Vasconcelos, S.S.; et al. Death from drought in tropical forests is triggered by hydraulics not carbon starvation. Nature 2015, 528, 119. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Adiku, S.; Tenhunen, J.; Granier, A. On the relationship of NDVI with leaf area index in a deciduous forest site. Remote Sens. Environ. 2005, 94, 244–255. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices overcome the saturation problem in biomass estimation. Int. J. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
- Karl, T.R. The Sensitivity of the Palmer Drought Severity Index and Palmer’s Z-Index to their Calibration Coefficients Including Potential Evapotranspiration. J. Clim. Appl. Meteorol. 1986, 25, 77–86. [Google Scholar] [CrossRef]
- Quiring, S.M.; Ganesh, S. Evaluating the utility of the Vegetation Condition Index (VCI) for monitoring meteorological drought in Texas. Agric. For. Meteorol. 2010, 150, 330–339. [Google Scholar] [CrossRef]
- Jump, A.S.; Ruiz-Benito, P.; Greenwood, S.; Allen, C.D.; Kitzberger, T.; Fensham, R.; Martínez-Vilalta, J.; Lloret, F. Structural overshoot of tree growth with climate variability and the global spectrum of drought-induced forest dieback. Glob. Chang. Biol. 2017, 23, 3742–3757. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Xiao, J.; Zhou, Y.; Zheng, Y.; Li, J.; Xiao, H. Drought events and their effects on vegetation productivity in China. Ecosphere 2016, 7, e01591. [Google Scholar] [CrossRef]
- Irvine, J.; Perks, M.P.; Magnani, F.; Grace, J. The response of Pinus sylvestris to drought: stomatal control of transpiration and hydraulic conductance. Tree Physiol. 1998, 18, 393–402. [Google Scholar] [CrossRef] [PubMed]
- Klein, T.; Cohen, S.; Yakir, D. Hydraulic adjustments underlying drought resistance of Pinus halepensis. Tree Physiol. 2011, 31, 637–648. [Google Scholar] [CrossRef] [PubMed]
- Camarero, J.J.; Olano, J.M.; Parras, A. Plastic bimodal xylogenesis in conifers from continental Mediterranean climates. New Phytol. 2010, 185, 471–480. [Google Scholar] [CrossRef] [PubMed]
- Noormets, A.; McNulty, S.G.; DeForest, J.L.; Sun, G.; Li, Q.; Chen, J. Drought during canopy development has lasting effect on annual carbon balance in a deciduous temperate forest. New Phytol. 2008, 179, 818–828. [Google Scholar] [CrossRef] [PubMed]
| Gymnosperms | Angiosperms | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Tree Species | Abbreviation | Number of Sampled Forests Stands | Mean Annual Temperature (°C) | Annual Precipitation (mm) | Tree Species | Abbreviation | Number of Sampled Forests Stands | Mean Annual Temperature (°C) | Annual Precipitation (mm) |
| Abies alba | ABAL | 48 | 13.10 | 1439.98 | Fagus sylvatica | FASY | 51 | 14.36 | 1212.98 |
| Abies pinsapo | ABPN | 15 | 17.53 | 1467.33 | Quercus pyrenaica | QUPY | 34 | 16.20 | 878.27 |
| Pinus halepensis | PIHA | 119 | 19.93 | 599.87 | Quercus robur | QURO | 34 | 16.19 | 1484.53 |
| Pinus sylvestris | PISY | 76 | 14.80 | 958.32 | Quercus faginea | QUFA | 19 | 16.89 | 975.97 |
| Pinus nigra | PINI | 66 | 17.05 | 754.00 | Quercus ilex | QUIL | 5 | 17.32 | 786.00 |
| Pinus uncinata | PIUN | 39 | 10.11 | 1442.68 | Quercus petraea | QUPE | 7 | 15.58 | 1062.13 |
| Pinus pinaster | PIPI | 20 | 18.52 | 705.30 | Castanea sativa | CASA | 10 | 17.50 | 928.00 |
| Pinus pinea | PIPN | 9 | 19.98 | 550.89 | |||||
| Juniperus thurifera | JUTH | 16 | 17.22 | 690.59 | |||||
| TRWi | NDVI Max | NDVI Annual | |
|---|---|---|---|
| SPEI | 38.97 | 43.25 | 33.50 |
| SPI | 35.73 | 32.48 | 53.16 |
| SPDI | 25.30 | 24.27 | 13.33 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peña-Gallardo, M.; Vicente-Serrano, S.M.; Camarero, J.J.; Gazol, A.; Sánchez-Salguero, R.; Domínguez-Castro, F.; El Kenawy, A.; Beguería-Portugés, S.; Gutiérrez, E.; De Luis, M.; et al. Drought Sensitiveness on Forest Growth in Peninsular Spain and the Balearic Islands. Forests 2018, 9, 524. https://doi.org/10.3390/f9090524
Peña-Gallardo M, Vicente-Serrano SM, Camarero JJ, Gazol A, Sánchez-Salguero R, Domínguez-Castro F, El Kenawy A, Beguería-Portugés S, Gutiérrez E, De Luis M, et al. Drought Sensitiveness on Forest Growth in Peninsular Spain and the Balearic Islands. Forests. 2018; 9(9):524. https://doi.org/10.3390/f9090524
Chicago/Turabian StylePeña-Gallardo, Marina, Sergio M. Vicente-Serrano, J. Julio Camarero, Antonio Gazol, Raúl Sánchez-Salguero, Fernando Domínguez-Castro, Ahmed El Kenawy, Santiago Beguería-Portugés, Emilia Gutiérrez, Martin De Luis, and et al. 2018. "Drought Sensitiveness on Forest Growth in Peninsular Spain and the Balearic Islands" Forests 9, no. 9: 524. https://doi.org/10.3390/f9090524
APA StylePeña-Gallardo, M., Vicente-Serrano, S. M., Camarero, J. J., Gazol, A., Sánchez-Salguero, R., Domínguez-Castro, F., El Kenawy, A., Beguería-Portugés, S., Gutiérrez, E., De Luis, M., Sangüesa-Barreda, G., Novak, K., Rozas, V., Tíscar, P. A., Linares, J. C., Martínez del Castillo, E., Ribas Matamoros, M., García-González, I., Silla, F., ... Galván, J. D. (2018). Drought Sensitiveness on Forest Growth in Peninsular Spain and the Balearic Islands. Forests, 9(9), 524. https://doi.org/10.3390/f9090524












