Spatial and Temporal Patterns in Nonstationary Flood Frequency across a Forest Watershed: Linkage with Rainfall and Land Use Types
Abstract
:1. Introduction
2. Materials and Methods
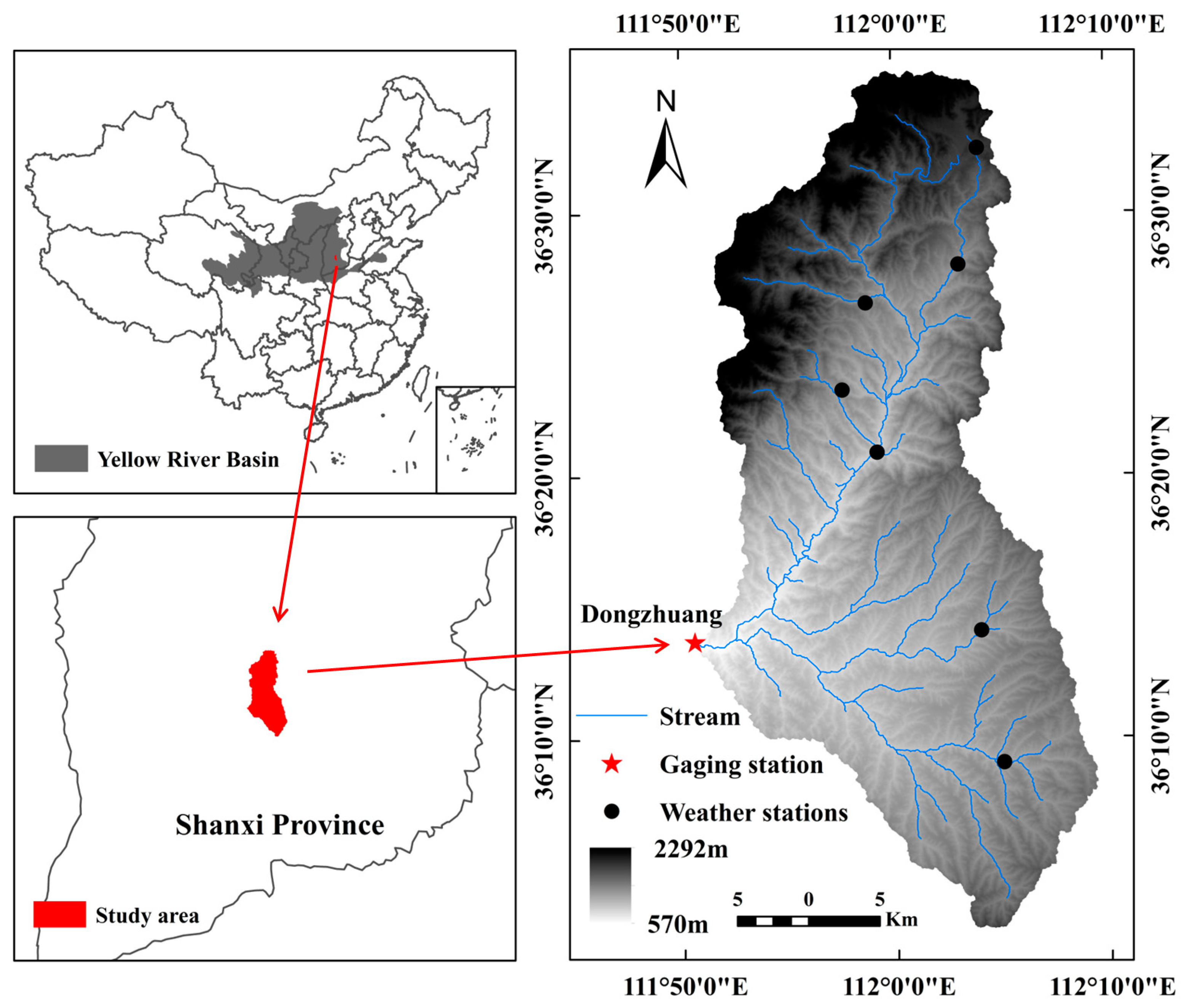
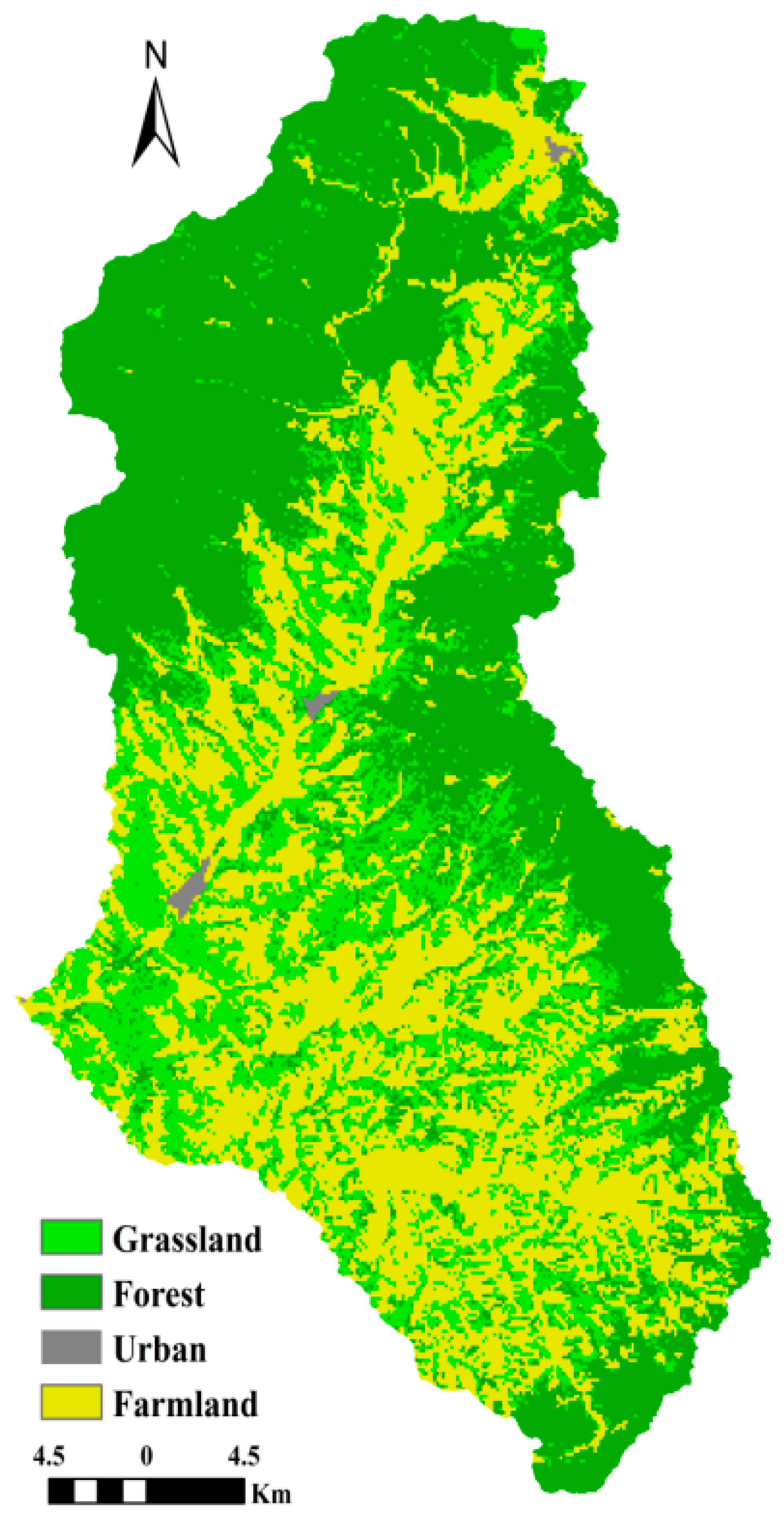
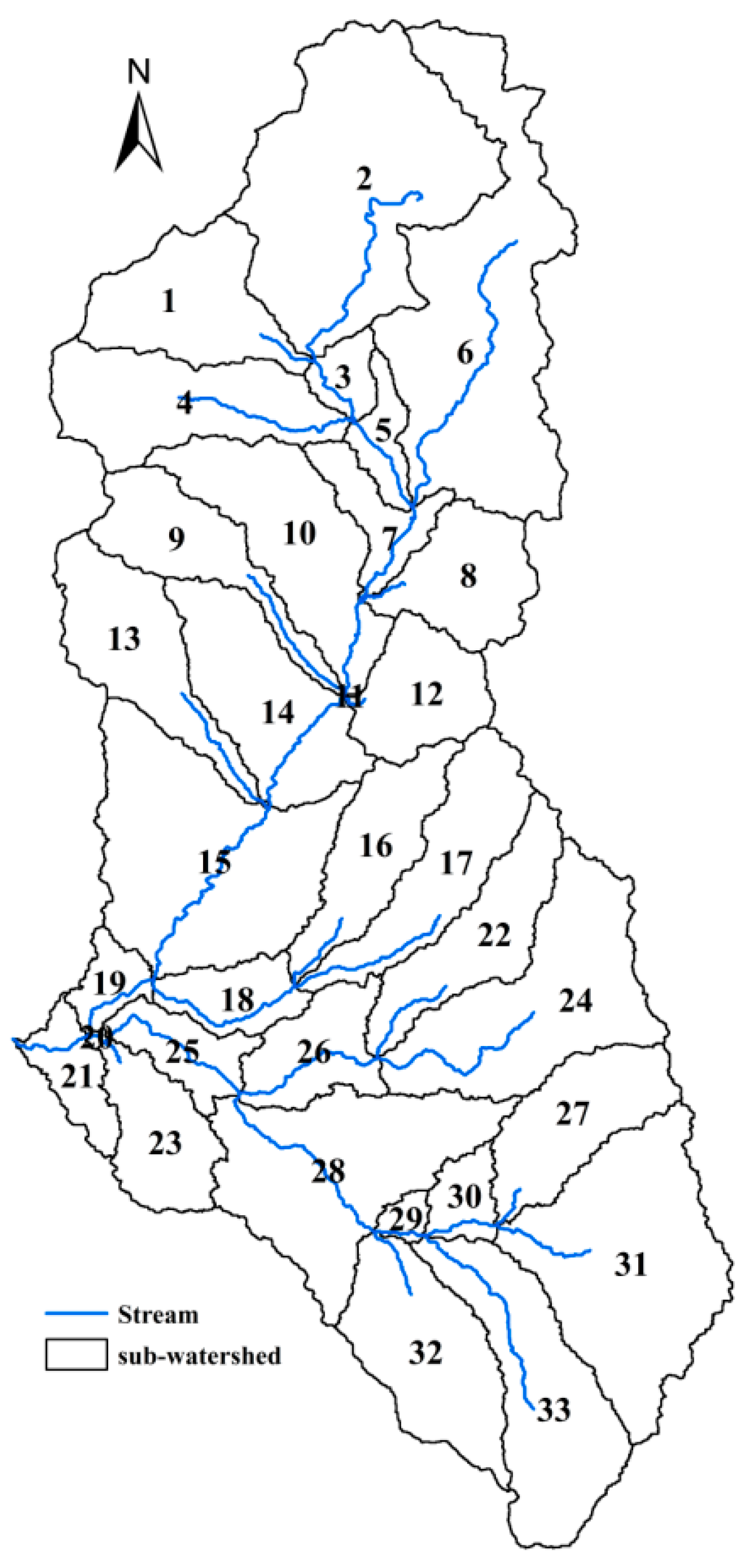
2.1. Study Area
2.2. Data Collection and Pretreatment
2.3. SWAT Model Calibration for Ungauged Sub-Watershed Streamflow
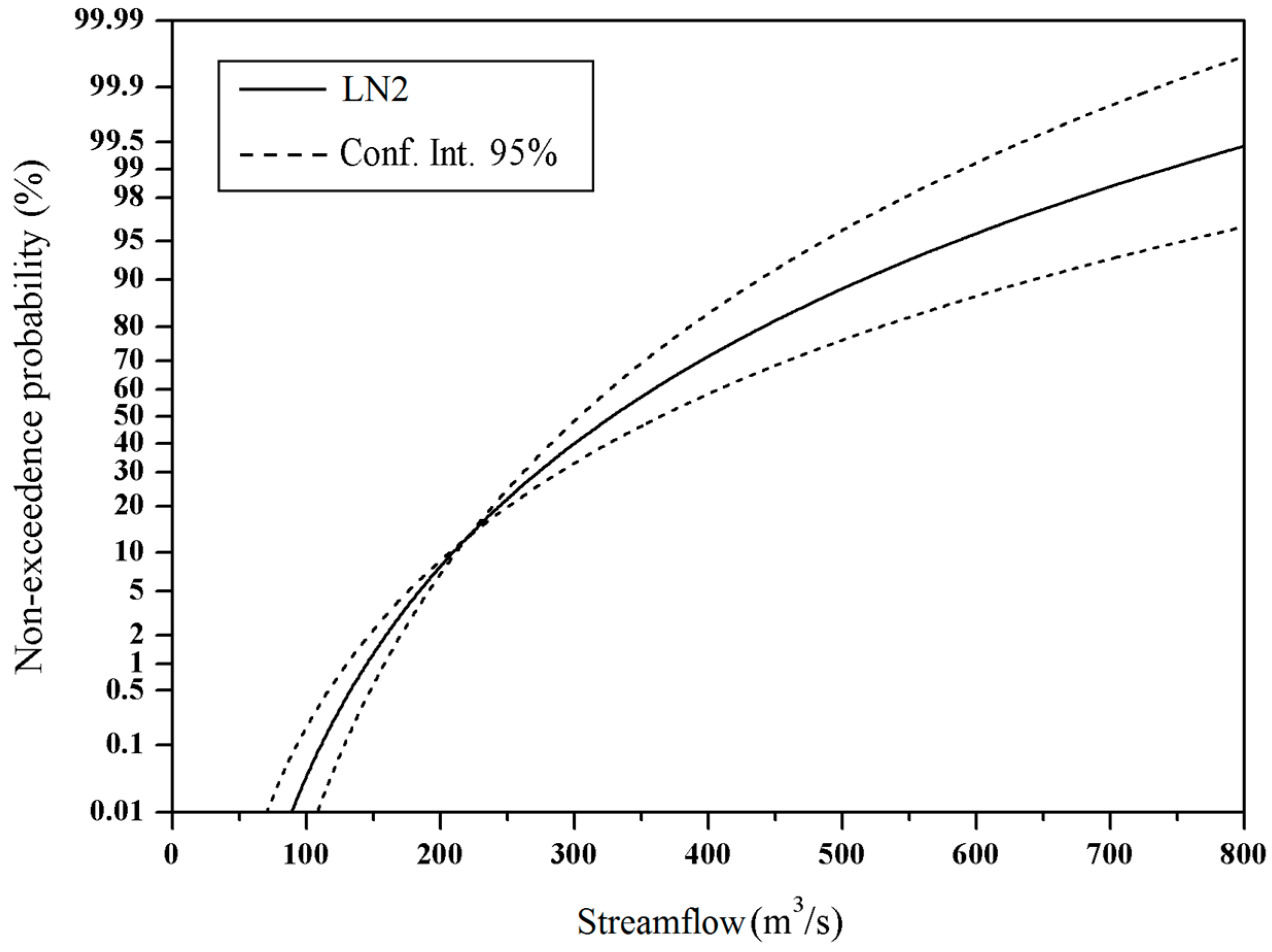
2.4. Evaluation of the Quantiles of Maximum Streamflow
2.5. Determination of Flood Events and Return Periods
3. Results
3.1. SWAT Model Calibration and Validation
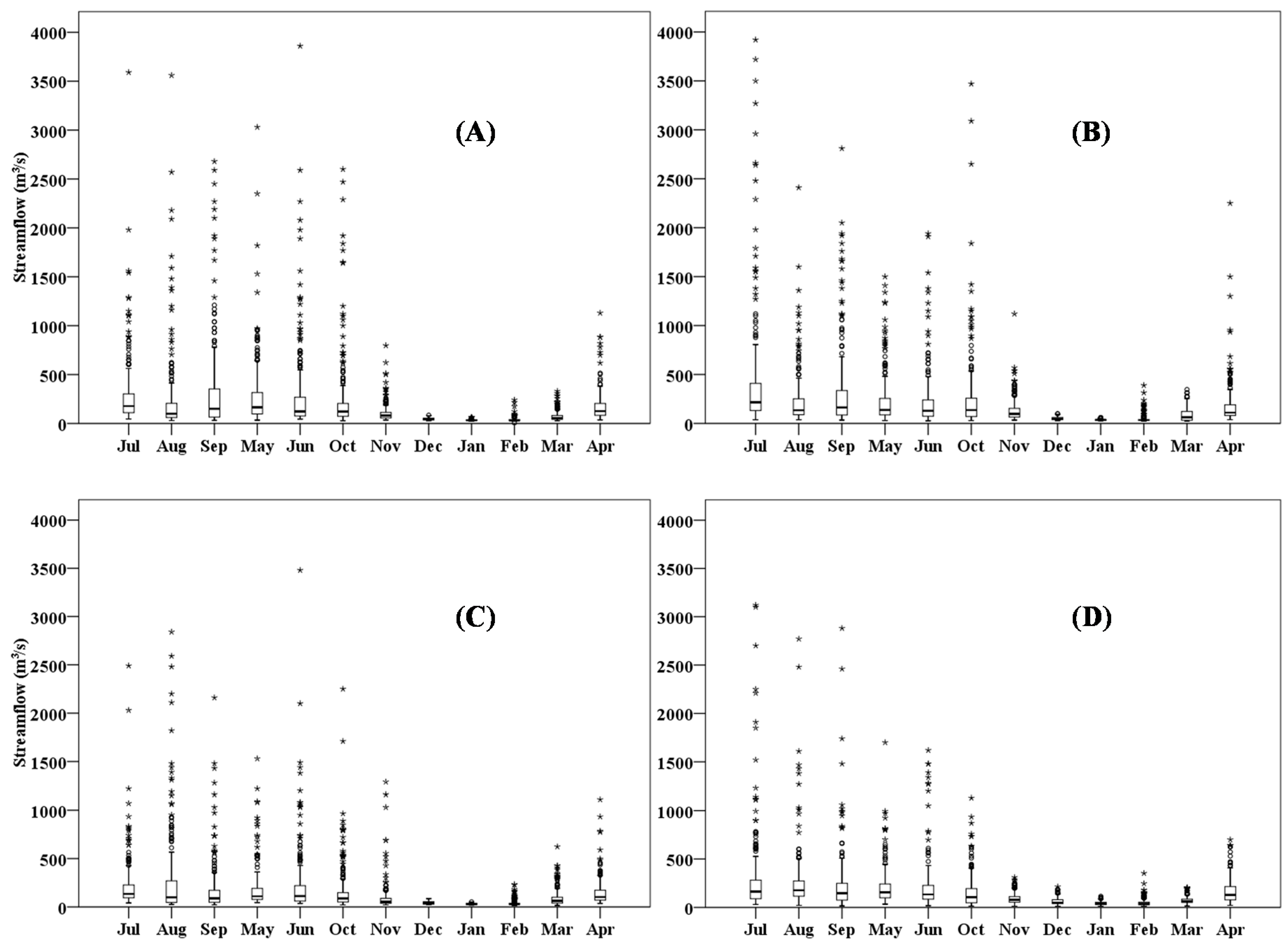
3.2. Annual Extreme Streamflow and Appropriate Distribution
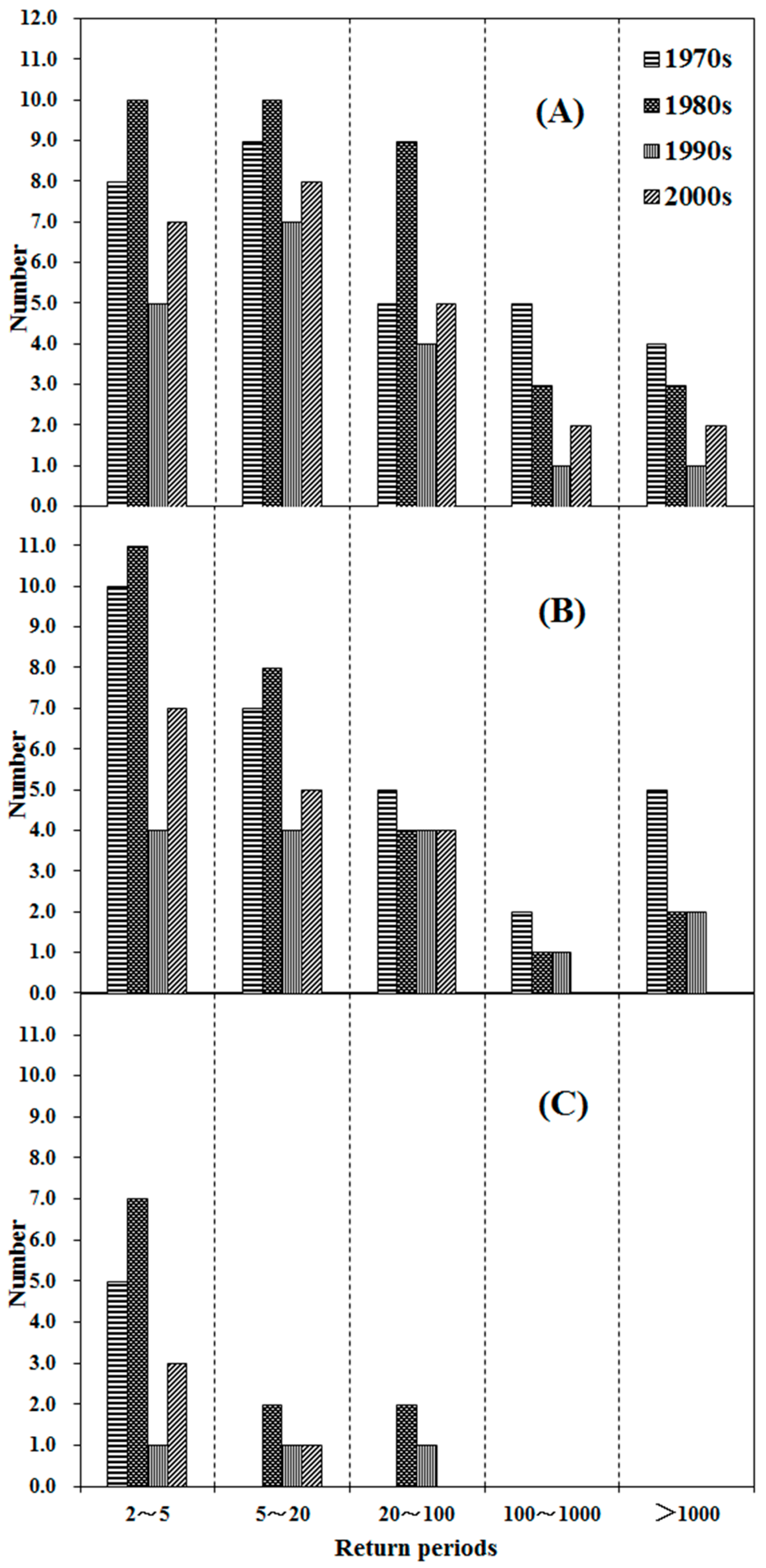
3.3. Nonstationary Regional Frequency Analysis
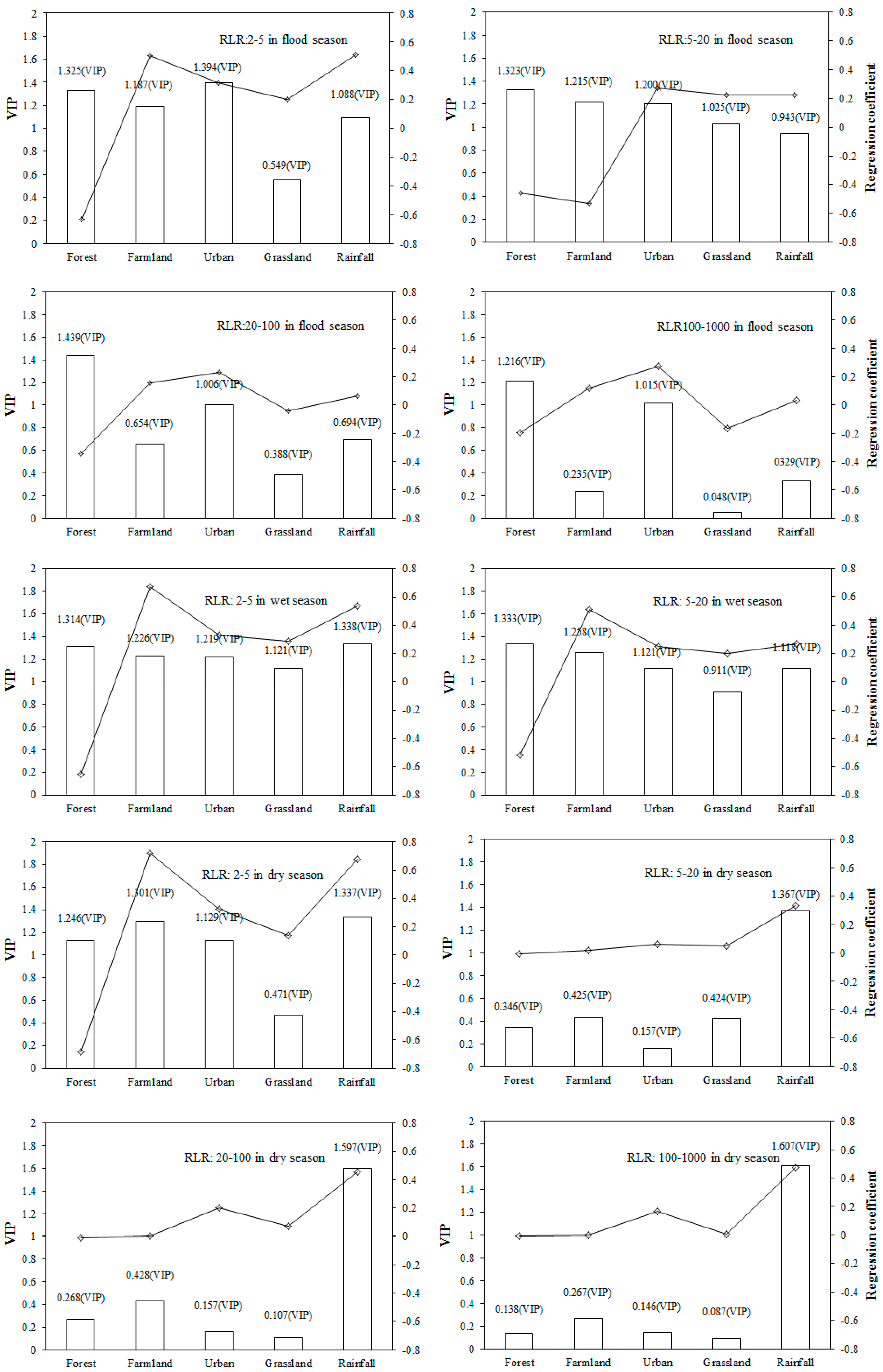
3.4. Contribution of Rainfall and Land Use to Flood Events
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Grubbs and Beck (1972) Statistical Test
Appendix A.2. Wald–Wolfowitz Test
Appendix A.3. Mann–Kendall Test
Appendix A.4. GEV Distributions
Appendix A.5. LN2
References
- Eagleson, P.S. Dynamics of flood frequency. Water Resour. Res. 1972, 8, 878–898. [Google Scholar] [CrossRef]
- Zaman, M.A.; Rahman, A.; Haddad, K. Regional flood frequency analysis in arid regions: A case study for Australia. J. Hydrol. 2012, 475, 74–83. [Google Scholar] [CrossRef]
- O’Brien, N.L.; Burn, D.H. A nonstationary index-flood technique for estimating extreme quantiles for annual maximum streamflow. J. Hydrol. 2014, 519, 2040–2048. [Google Scholar] [CrossRef]
- Haberlandt, U.; Radtke, I. Hydrological model calibration for derived flood frequency analysis using stochastic rainfall and probability distributions of peak flows. Hydrol. Earth Syst. Sci. 2014, 18, 353–365. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Gu, X.; Singh, V.P.; Xiao, M. Flood frequency analysis with consideration of hydrological alterations: Changing properties, causes and implications. J. Hydrol. 2014, 519, 803–813. [Google Scholar] [CrossRef]
- Rao, A.R.; Hamed, K.H. Flood Frequency Analysis; CRC Press: New York, NY, USA, 2000; p. 355. [Google Scholar]
- Wei, W.; Chen, L.D.; Fu, B.J.; Huang, Z.L.; Wu, D.P.; Gui, L.D. The effect of land uses and rainfall regimes on runoff and soil erosion in the semi-arid loess hilly area. China. J. Hydrol. 2007, 335, 247–258. [Google Scholar] [CrossRef]
- Yan, B.; Fang, N.F.; Zhang, P.C.; Shi, Z.H. Impacts of land use change on watershed streamflow and sediment yield: An assessment using hydrologic modelling and partial least squares regression. J. Hydrol. 2013, 484, 26–37. [Google Scholar] [CrossRef]
- Karim, F.; Hasan, M.; Marvanek, S. Evaluating annual maximum and partial duration series for estimating frequency of small magnitude floods. Water 2017, 9, 481. [Google Scholar] [CrossRef]
- Benkhaled, A.; Higgins, H.; Chebana, F.; Necir, A. Frequency analysis of annual maximum suspended sediment concentrations in Abiod wadi, Biskra (Algeria). Hydrol. Process. 2014, 28, 3841–3854. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J.; Ondo, J.C.; Gachon, P.; Bobée, B. Frequency analysis of a sequence of dependent and/or non-stationary hydro-meteorological observations: A review. J. Hydrol. 2006, 329, 534–552. [Google Scholar] [CrossRef]
- Schendel, T.; Thongwichian, R. Considering historical flood events in flood frequency analysis: Is it worth the effort? Adv. Water Resour. 2017, 105, 144–153. [Google Scholar] [CrossRef]
- Obeysekera, J.; Salas, J.D. Quantifying the uncertainty of design floods under nonstationary conditions. J. Hydrol. Eng. 2013, 19, 1438–1446. [Google Scholar] [CrossRef]
- She, D.X.; Xia, J.; Zhang, D.; Ye, A.Z.; Sood, A. Regional extreme-dry-spell frequency analysis using the L-moments method in the middle reaches of the Yellow River Basin, China. Hydrol. Process. 2014, 28, 4694–4707. [Google Scholar] [CrossRef]
- Tramblay, Y.; St–Hilaire, A.; Ouarda, T.B.M.J. Frequency analysis of maximum annual suspended sediment concentrations in North America. Hydrol. Sci. J. 2008, 53, 236–252. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Julio, B.; Malin, F.; Robert, M.H.; Zbigniew, W.K.; Dennis, P.L.; Ronald, J.S. Stationarity is dead: Whither water management. Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Harvey, K.D.; Hogg, W.D.; Yuzuk, T.R. Trends in Canadian streamflow. Water Resour. Res. 2001, 37, 987–999. [Google Scholar] [CrossRef]
- Leclerc, M.; Ouarda, T.B. Non-stationary regional flood frequency analysis at ungauged sites. J. Hydrol. 2007, 343, 254–265. [Google Scholar] [CrossRef]
- Kovalets, I.V.; Kivva, S.L.; Udovenko, O.I. Usage of the WRF/DHSVM model chain for simulation of extreme floods in mountainous areas: A pilot study for the Uzh River Basin in the Ukrainian Carpathians. Nat. Hazards 2014, 75, 2049–2063. [Google Scholar] [CrossRef]
- Behera, S.; Panda, R.K. Evaluation of management alternatives for an agricultural watershed in a sub-humid subtropical region using a physical process based model. Agric. Ecosyst. Environ. 2006, 113, 62–72. [Google Scholar] [CrossRef]
- Ryu, J.H.; Lee, J.H.; Jeong, S.; Park, S.K.; Han, K. The impacts of climate change on local hydrology and low flow frequency in the Geum River Basin, Korea. Hydrol. Process. 2011, 25, 3437–3447. [Google Scholar] [CrossRef]
- Huang, X.D.; Shi, Z.H.; Fang, N.F.; Li, X. Influences of land use change on baseflow in mountainous watersheds. Forests 2016, 7, 16. [Google Scholar] [CrossRef]
- Dessu, S.B.; Melesse, A.M. Modelling the rainfall-runoff process of the Mara River basin using the Soil and Water Assessment Tool. Hydrol. Process. 2012, 26, 4038–4049. [Google Scholar] [CrossRef]
- Artita, K.S.; Kaini, P.; Nicklow, J.W. Examining the possibilities: Generating alternative watershed-scale BMP designs with evolutionary algorithms. Water Resour. Manag. 2013, 27, 3849–3863. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, Y.; Chen, Y.; Xu, C.Y.; Gao, Y.; Du, J. Hydrological response to urbanization at different spatio-temporal scales simulated by coupling of CLUE-S and the SWAT model in the Yangtze River Delta region. J. Hydrol. 2013, 485, 113–125. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef] [Green Version]
- Buondonno, A.; Amenta, P.; Viscarra-Rossel, R.A.; Leone, A.P. Prediction of soil properties with plsr and vis-nir spectroscopy: Application to mediterranean soils from southern Italy. Curr. Anal. Chem. 2012, 8, 283–299. [Google Scholar]
- Geladi, P.; Sethson, B.; Nyström, J.; Lillhonga, T.; Lestander, T.; Burger, J. Chemometrics in spectroscopy. Spectrochim. Acta B At. Spectrosc. 2004, 59, 1347–1357. [Google Scholar] [CrossRef]
- Li, S.; Li, J.; Zhang, Q. Water quality assessment in the rivers along the water conveyance system of the Middle Route of the South to North Water Transfer Project (China) using multivariate statistical techniques and receptor modeling. J. Hazard. Mater. 2011, 195, 306–317. [Google Scholar] [CrossRef] [PubMed]
- Soil Survey Staff. Soil Taxonomy, A Basic System of Soil Classification for Making and Interpreting Soil Surveys, 2nd ed.; Agriculture Handbook No. 436; USDA Natural Resources Conservation Service, U.S. Government Printing 23 Office: Washington, DC, USA, 1999; pp. 160–162, 494–495.
- Duan, Q.D.; Gupta, V.K.; Sorooshian, S. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Grubbs, F.E.; Beck, G. Extension of sample sizes and percentage points for significance tests of outlying observations. Technometrics 1972, 14, 847–854. [Google Scholar] [CrossRef]
- Cunderlik, J.M.; Ouarda, T.B. Regional flood–duration–frequency modeling in the changing environment. J. Hydrol. 2006, 318, 276–291. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Cont. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Calenda, G.; Mancini, C.P.; Volpi, E. Selection of the probabilistic model of extreme floods: The case of the River Tiber in Rome. J. Hydrol. 2009, 371, 1–11. [Google Scholar] [CrossRef]
- Laio, F.; Di Baldassarre, G.; Montanari, A. Model selection techniques for the frequency analysis of hydrological extremes. Water Resour. Res. 2009, 45, W07416. [Google Scholar] [CrossRef]
- Sahu, N.; Behera, S.K.; Yamashiki, Y.; Takara, K.; Yamagata, T. IOD and ENSO impacts on the extreme stream-flows of Citarum river in Indonesia. Clim. Dynam. 2012, 39, 1673–1680. [Google Scholar] [CrossRef]
- Wang, G.Q.; Yang, H.; Wang, L.; Xu, Z.; Xue, B. Using the SWAT model to assess impacts of land use changes on runoff generation in headwaters. Hydrol. Process. 2014, 28, 1032–1042. [Google Scholar] [CrossRef]
- Seidou, O.; Ramsay, A.; Nistor, I. Climate change impacts on extreme floods I: Combining imperfect deterministic simulations and non-stationary frequency analysis. Nat. Hazards 2011, 61, 647–659. [Google Scholar] [CrossRef]
- Fu, C.; James, A.L.; Yao, H. SWAT-CS: Revision and testing of SWAT for Canadian Shield catchments. J. Hydrol. 2014, 511, 719–735. [Google Scholar] [CrossRef]
- Shi, Z.H.; Huang, X.D.; Ai, L.; Fang, N.F.; Wu, G.L. Quantitative analysis of factors controlling sediment yield in mountainous watersheds. Geomorphology 2014, 226, 193–201. [Google Scholar] [CrossRef]
- Shi, Z.H.; Ai, L.; Li, X.; Huang, X.D.; Wu, G.L.; Liao, W. Partial least-squares regression for linking land-cover patterns to soil erosion and sediment yield in watersheds. J. Hydrol. 2013, 498, 165–176. [Google Scholar] [CrossRef]
- Liu, H.M. The Runoff Simulation of SWAT Model Coupled with the ECMWF Dataset. Master Thesis, North China University of Water Resources and Electric Power, Zhengzhou, China, 2017. [Google Scholar]
- Koutroulis, A.G.; Tsanis, I.K.; Daliakopoulos, I.N. Seasonality of floods and their hydrometeorologic characteristics in the island of Crete. J. Hydrol. 2010, 394, 90–100. [Google Scholar] [CrossRef]
- Condon, L.E.; Gangopadhyay, S.; Pruitt, T. Climate change and non–stationary flood risk for the upper Truckee River basin. Hydrol. Earth Syst. Sci. 2015, 19, 159–175. [Google Scholar] [CrossRef]
- Döll, P. Vulnerability to the impact of climate change on renewable groundwater resources: A global-scale assessment. Environ. Res. Lett. 2009, 4, 035006. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Serinaldi, F.; Ntelekos, A.A. Analyses of seasonal and annual maximum daily discharge records for central Europe. J. Hydrol. 2011, 399, 299–312. [Google Scholar] [CrossRef]
- Magilligan, F.J.; Nislow, K.H. Long-term changes in regional hydrologic regime following impoundment in a humid-climate watershed. J. Am. Water Resour. As. 2001, 37, 1551–1569. [Google Scholar] [CrossRef]
- Ashraf, M.; Kahlown, M.A.; Ashfaq, A. Impact of small dams on agriculture and groundwater development: A case study from Pakistan. Agric. Water Manag. 2007, 92, 90–98. [Google Scholar] [CrossRef]
- Baratti, E.; Montanari, A.; Castellarin, A.; Salinas, J.L.; Viglione, A.; Bezzi, A. Estimating the flood frequency distribution at seasonal and annual time scales. Hydrol. Earth Syst. Sci. 2012, 16, 4651–4660. [Google Scholar] [CrossRef] [Green Version]
- Price, K. Effects of watershed topography, soils, land use, and climate on baseflow hydrology in humid regions: A review. Prog. Phys. Geogr. 2011, 35, 465–492. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Zhang, X.N.; Xia, D.Z.; You, J.S.; Rong, Y.S.; Bakir, M. Impacts of land–use and climate changes on hydrologic processes in the Qingyi River watershed, China. J. Hydrol. Eng. 2013, 18, 1495–1512. [Google Scholar] [CrossRef]
- Daniel, W.W. Applied Nonparametric Statistics, 2nd ed.; PWS-Kent: Boston, MA, USA, 1990. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Oxford Univ. Press: New York, NY, USA, 1975. [Google Scholar]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or the smallest member of a sample. Math. Proc. Camb. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Jenkinson, A.F. The frequency distributions of the annual maximum (or minimum) values of meteorological elements. Q. J. R. Meteorol. Soc. 1955, 81, 145–158. [Google Scholar] [CrossRef]
| Parameter | Definition | Calibrated Value | |
|---|---|---|---|
| basin.bsn | ESCO | Soil evaporation compensation factor | 0.19 |
| basin.bsn | EPCO | Plant water uptake compensation factor | 1 |
| basin.bsn | SURLAG | Surface runoff lag time | 4 |
| .GW | GW_DELAY | Groundwater delay | 31 |
| .GW | GW_REVAP | Groundwater revap | 0.06 |
| .GW | ALPHA_BF | Baseflow alpha factor | 0.043 |
| .soil | SOL_AWC | Available water capacity of the soil layer | 0.2 |
| .sub | CH_N1 | Manning’s ‘n’ value for tributary channels | 0.014 |
| .rte | CH_N2 | Manning’s ‘n’ value for the main channel | 0.014 |
| .mgt | CN2 | SCS curve number | 62 (Forest) |
| 77 (Grassland) | |||
| 78 (Farmland) | |||
| 79 (Urban) |
| Station | Period | ENSa | PBIASb | R2 |
|---|---|---|---|---|
| Monthly–Streamflow | Calibration (1972–1981) | 0.80 | –0.10 | 0.81 |
| Validation (1982–1991) | 0.77 | –0.09 | 0.87 | |
| Validation (1992–2001) | 0.75 | –0.13 | 0.80 | |
| Overall (1972–2001) | 0.77 | –0.11 | 0.83 | |
| Daily–Streamflow | Calibration (1971–1980) | 0.58 | –0.10 | 0.62 |
| Validation (1981–1990) | 0.56 | –0.09 | 0.67 | |
| Validation (1991–2000) | 0.52 | –0.11 | 0.62 | |
| Overall (1971–2000) | 0.55 | –0.10 | 0.64 |
| Distribution | AIC | BIC | ||
|---|---|---|---|---|
| LN2 a | GEV b | LN2 | GEV | |
| No. of sub-watersheds being selected | 26 | 7 | 27 | 6 |
| Percentage of sub-watersheds (%) | 78.8 | 21.2 | 81.8 | 18.2 |
| Response Y | R2 a | Component | Explained in Y (%) | Cumulative Explained in Y (%) | RMSECV b | |
|---|---|---|---|---|---|---|
| Seasons | Return Periods (Years) | |||||
| Flood | 2–5 | 0.81 | 1 | 74.3 | 74.3 | 0.89 |
| 2 | 6.9 | 81.2 | 0.80 | |||
| 3 | 0.1 | 81.3 | 0.81 | |||
| 5–20 | 0.79 | 1 | 71.8 | 71.8 | 4.17 | |
| 2 | 6.2 | 78.0 | 3.97 | |||
| 3 | 1.4 | 79.4 | 4.05 | |||
| 20–100 | 0.70 | 1 | 67.9 | 67.9 | 0.75 | |
| 2 | 2.4 | 70.3 | 0.73 | |||
| 3 | 0.1 | 70.4 | 0.74 | |||
| 100–1000 | 0.64 | 1 | 60.2 | 60.2 | 5.55 | |
| 2 | 3.1 | 63.3 | 5.28 | |||
| 3 | 0.8 | 64.1 | 5.47 | |||
| Wet | 2–5 | 0.82 | 1 | 75.1 | 75.1 | 0.71 |
| 2 | 5.6 | 80.7 | 0.64 | |||
| 3 | 1.3 | 82.0 | 0.61 | |||
| 4 | 0.4 | 82.4 | 0.65 | |||
| 5–20 | 0.79 | 1 | 71.3 | 71.3 | 0.85 | |
| 2 | 6.6 | 77.9 | 0.80 | |||
| 3 | 1.2 | 79.1 | 0.81 | |||
| Wet | 20–100 | 0.34 | 1 | 28.3 | 28.3 | 0.79 |
| 2 | 3.9 | 32.2 | 0.69 | |||
| 3 | 1.6 | 33.8 | 0.71 | |||
| 100–1000 | 0.27 | 1 | 22.2 | 22.2 | 0.65 | |
| 2 | 4.5 | 26.7 | 0.59 | |||
| 3 | 0.3 | 27.0 | 0.63 | |||
| Dry | 2–5 | 0.84 | 1 | 78.5 | 78.5 | 0.91 |
| 2 | 3.9 | 82.4 | 0.88 | |||
| 3 | 1.6 | 84.0 | 0.84 | |||
| 4 | 0.2 | 84.2 | 0.85 | |||
| 5–20 | 0.61 | 1 | 60.0 | 60.0 | 0.74 | |
| 2 | 0.9 | 60.9 | 0.68 | |||
| 3 | 0.1 | 61.0 | 0.69 | |||
| 20–100 | 0.69 | 1 | 67.2 | 67.2 | 0.65 | |
| 2 | 1.6 | 68.8 | 0.54 | |||
| 3 | 0.1 | 68.9 | 0.58 | |||
| 100–1000 | 0.76 | 1 | 74.2 | 74.2 | 0.54 | |
| 2 | 1.6 | 75.8 | 0.49 | |||
| 3 | 0.2 | 76.0 | 0.52 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.-d.; Wang, L.; Han, P.-p.; Wang, W.-c. Spatial and Temporal Patterns in Nonstationary Flood Frequency across a Forest Watershed: Linkage with Rainfall and Land Use Types. Forests 2018, 9, 339. https://doi.org/10.3390/f9060339
Huang X-d, Wang L, Han P-p, Wang W-c. Spatial and Temporal Patterns in Nonstationary Flood Frequency across a Forest Watershed: Linkage with Rainfall and Land Use Types. Forests. 2018; 9(6):339. https://doi.org/10.3390/f9060339
Chicago/Turabian StyleHuang, Xu-dong, Ling Wang, Pei-pei Han, and Wen-chuan Wang. 2018. "Spatial and Temporal Patterns in Nonstationary Flood Frequency across a Forest Watershed: Linkage with Rainfall and Land Use Types" Forests 9, no. 6: 339. https://doi.org/10.3390/f9060339
APA StyleHuang, X.-d., Wang, L., Han, P.-p., & Wang, W.-c. (2018). Spatial and Temporal Patterns in Nonstationary Flood Frequency across a Forest Watershed: Linkage with Rainfall and Land Use Types. Forests, 9(6), 339. https://doi.org/10.3390/f9060339




