Comparative Analysis of the Effects of Stem Height and Artificial Pruning on Seasonal Radial Growth Dynamics of Wild Cherry (Prunus avium L.) and Sycamore (Acer pseudoplatanus L.) in a Widely Spaced System
Abstract
1. Introduction
- Between tree species there are no differences in growth phenology and seasonal growth patterns [22]. Based on findings of previous studies [20,31], we assume the day of the maximum growth rate to be controlled by the photoperiod cycle and to occur approximately at the time of summer solstice with no differences between treatments and stem locations.
- Between the two stem locations there is no clear difference in annual radial growth [23,24]. Growth onset occurs earlier at higher locations of the stem due to an earlier allocation of auxin and photosynthetic assimilates to areas of the stem closer to the leaves [26] and therefore growth duration is longer at higher locations of the stem.
- Between pruning treatments there is a difference in annual radial growth due to the reduction of leaf mass in the crown of pruned trees, resulting in a temporarily reduced photosynthetic capacity leading to a lessened rate of biomass accumulation [8]. Therefore, we expect that the annual radial growth is smaller compared to un-pruned trees. The reduced growth rates after pruning treatment will also be reflected in a later growth onset and/or earlier growth cessation, as several studies found positive correlations between radial growth and the duration of cell production and cell enlargement [27,32,33,34]. The effect of pruning on growth dynamics also varies between the upper and the lower location of the stem [5].
2. Materials and Methods
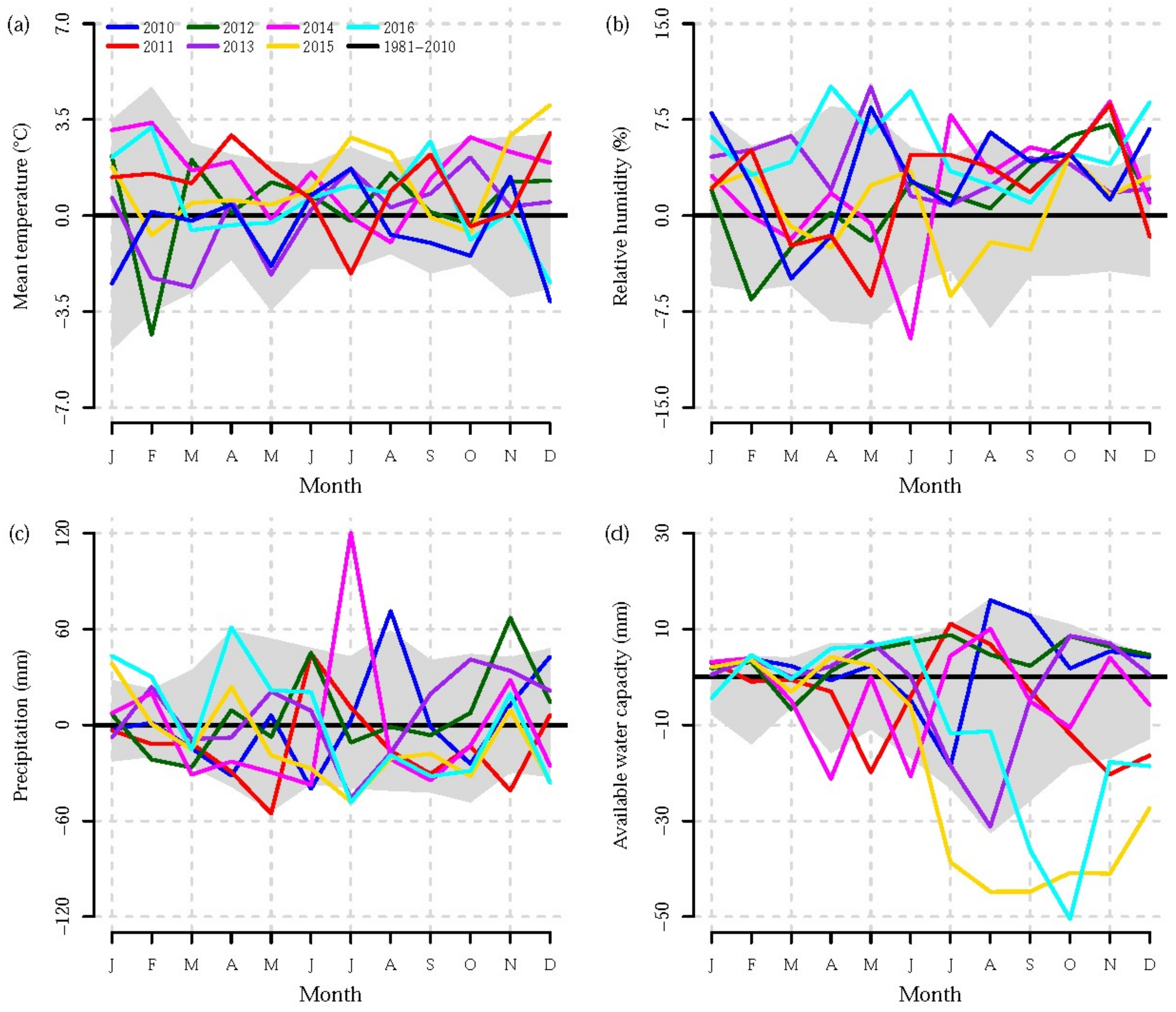
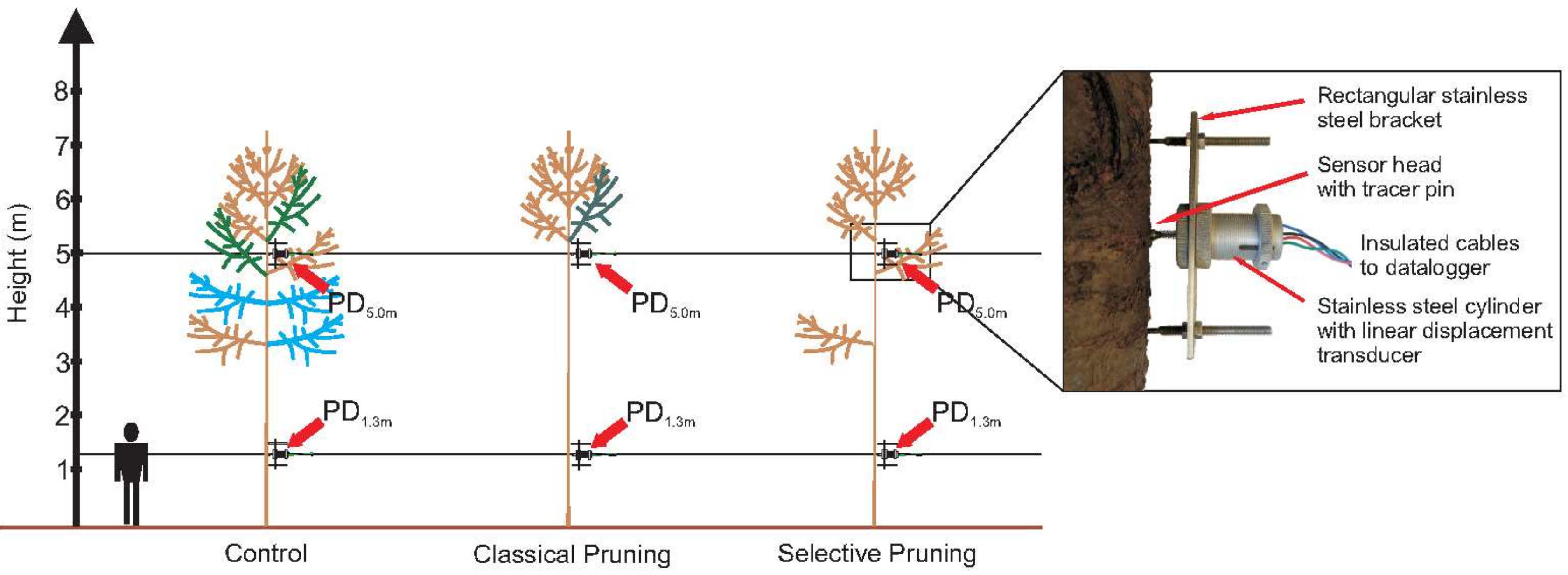
2.1. Study Area and Experimental Setup
2.2. Data Analysis and Statistical Methods
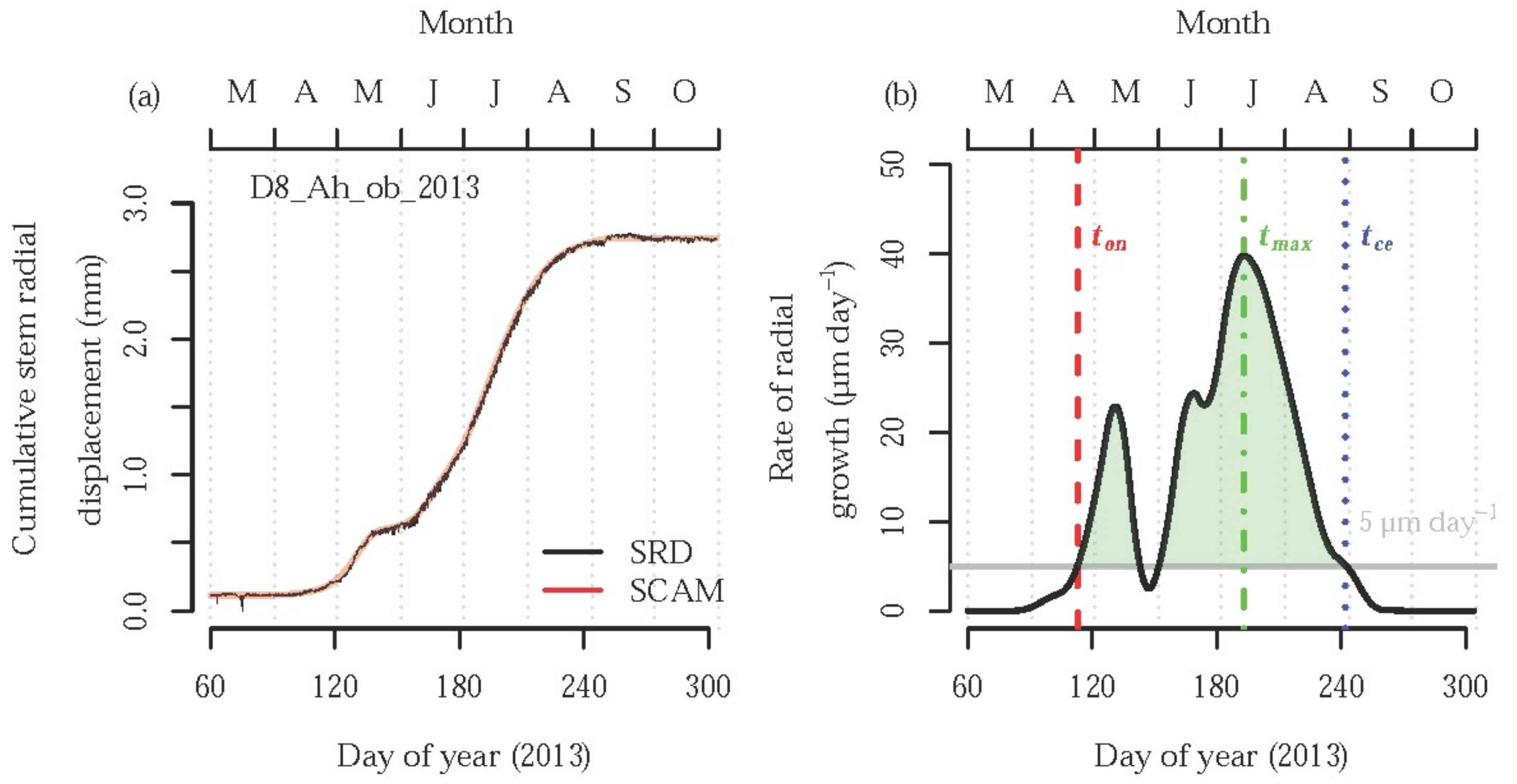
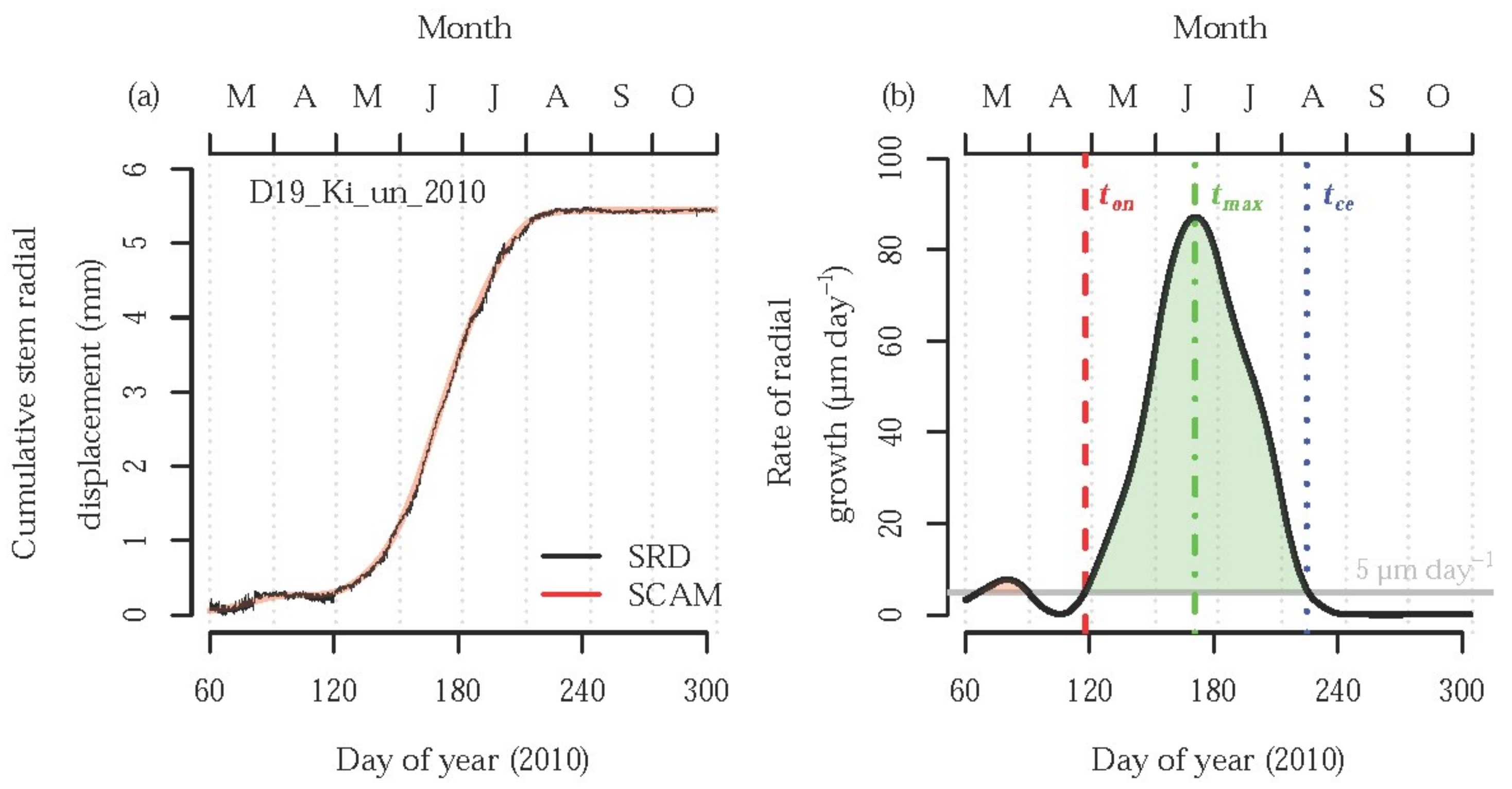
3. Results
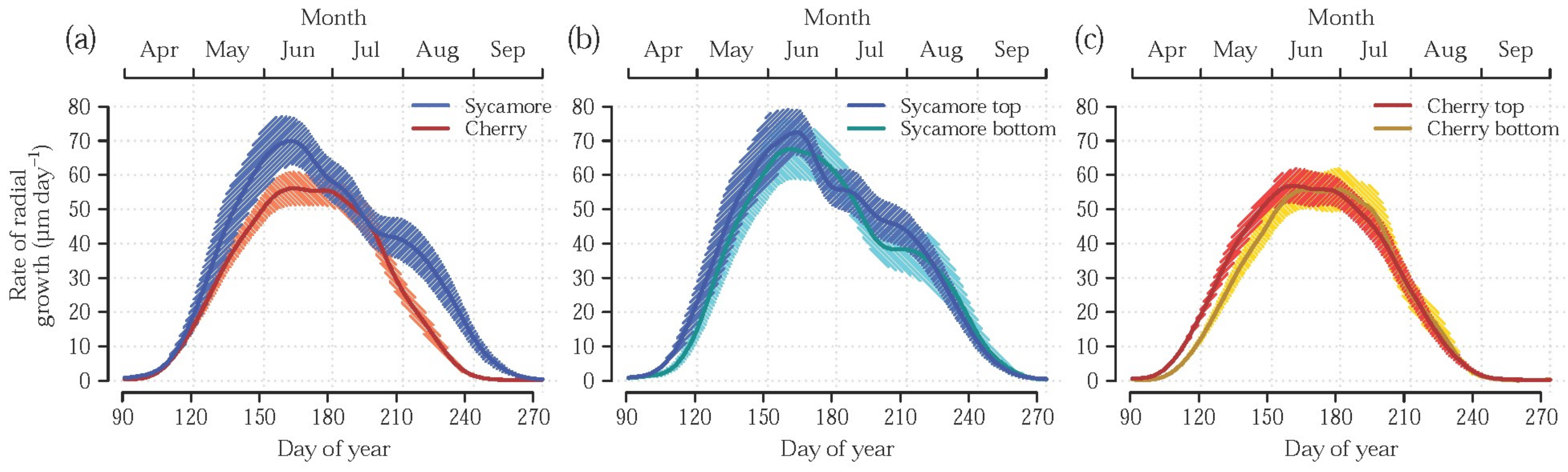
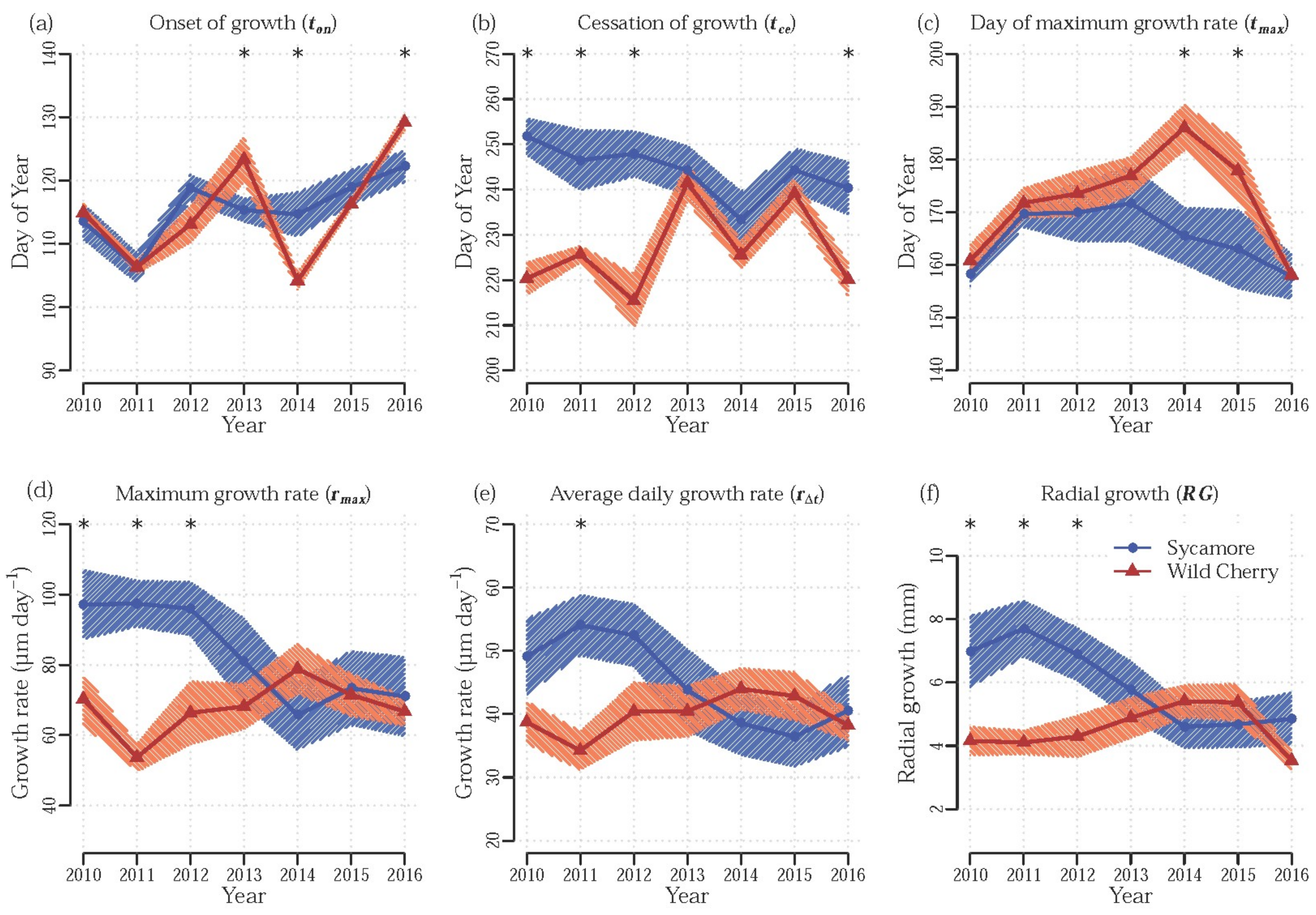
3.1. Effect of Tree Species
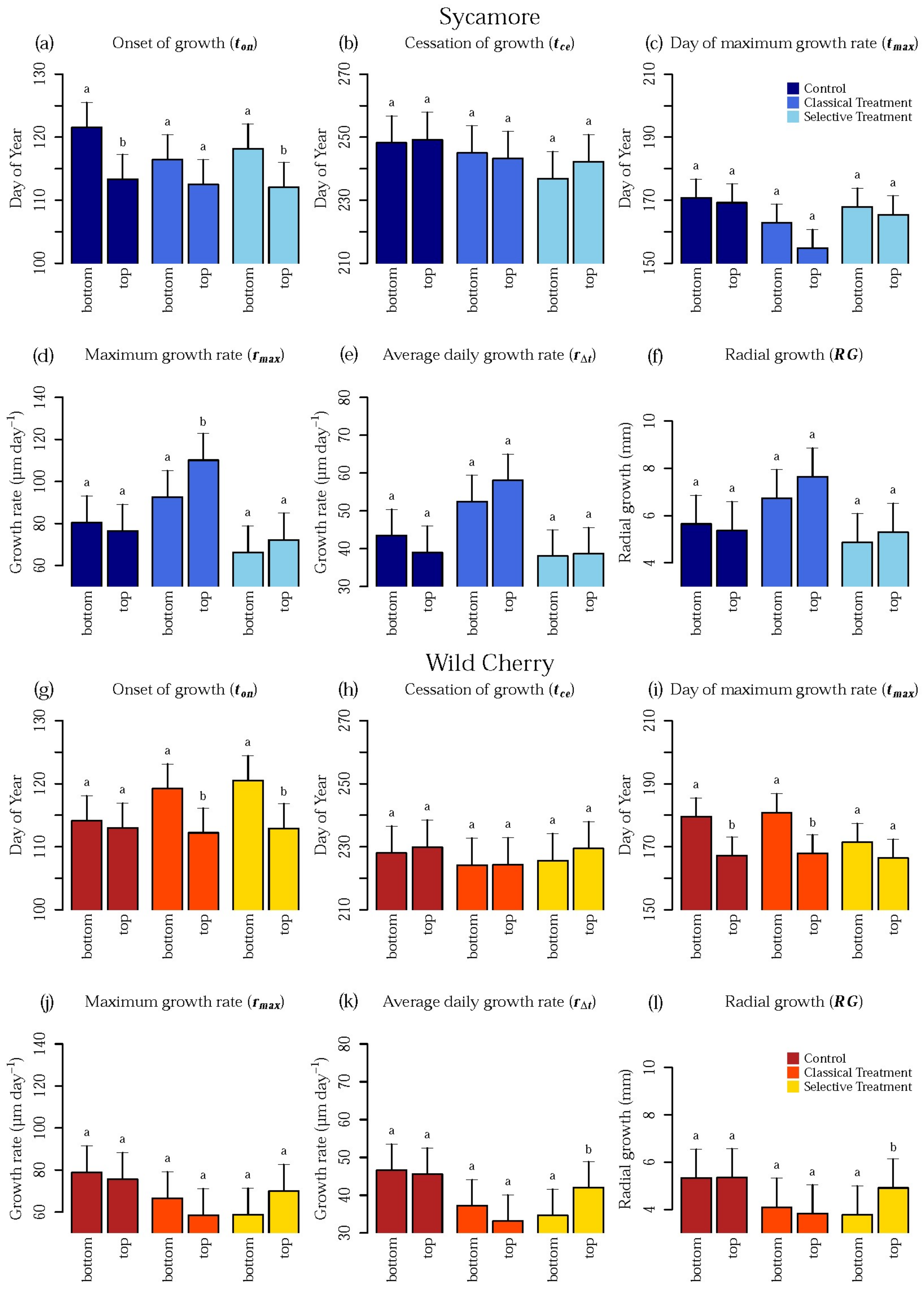
3.2. Effect of Stem Height
3.3. Effect of Treatment
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A

References
- Mantau, U.; Saal, U.; Prins, K.; Steierer, F.; Lindner, M.; Verherk, H.; Eggers, J.; Leek, N.; Olderburger, J.; Asikainen, A.; et al. Real Potential for Changes in Growth and Use of EU Forests; Centre of Wood Sciences, University of Hamburg: Hamburg, Germany, 2010. [Google Scholar]
- Becker, G.; Klädtke, J. Wood properties and wood processing of valuable broadleaved trees demonstrated with common ash and maple in southwest Germany. In Valuable Broadleaved Forests in Europe; Spiecker, H., Hein, S., Makkonen-Spiecker, K., Thies, M., Eds.; Brill: Leiden, The Netherlands; Boston, MA, USA, 2009; pp. 161–167. [Google Scholar]
- Spiecker, H. Minority tree species—A challenge for multi-purpose forestry. In Nature-Based Forestry in Central Europe: Alternatives to Industrial Forestry and Strict Preservation; Diaci, J., Ed.; Biotechnical Faculty, Department of Forestry and Renewable Forest Resources: Ljubljana, Slovenia, 2006; pp. 47–59. [Google Scholar]
- Pryor, S.N. The Silviculture and Yield of Wild Cherry; Her Majesty’s Stationery Office: London, UK, 1988. [Google Scholar]
- Springmann, S.; Rogers, R.; Spiecker, H. Impact of artificial pruning on growth and secondary shoot development of wild cherry (Prunus avium L.). For. Ecol. Manag. 2011, 261, 764–769. [Google Scholar] [CrossRef]
- Hein, S.; Spiecker, H. Controlling Diameter Growth of Common Ash, Sycamore and Wild Cherry. In Valuable Broadleaved Forests in Europe; Spiecker, H., Hein, S., Makkonen-Spiecker, K., Thies, M., Eds.; Brill: Leiden, The Netherlands; Boston, MA, USA, 2009; pp. 123–147. [Google Scholar]
- Spiecker, H. Zur Steuerung des Dickenwachstums und der Astreinigung von Trauben-und Stieleichen; Habilitation, Universität Freiburg, 1991; Selbstverlag Landesforstverwaltung Baden-Württemberg: Stuttgart, Germany, 1991. (In German) [Google Scholar]
- Morhart, C.; Sheppard, J.; Douglas, G.C.; Lunny, R.; Paris, P.; Spiecker, H.; Nahm, M. Management Guidelines for Valuable Wood Production in Agroforestry Systems; Chair of Forest Growth, University of Freiburg: Freiburg, Germany, 2015. [Google Scholar]
- Kupka, I. Growth reaction of young wild cherry (Prunus avium L.) trees to pruning. J. For. Sci. 2007, 53, 555–560. [Google Scholar] [CrossRef]
- Bulfin, M.; Radford, T. Effect of early formative shaping on newly planted broadleaves: Part 2: Height and diameter growth. Ir. For. 1998, 55, 52–61. [Google Scholar]
- Kerr, G.; Morgan, G. Does formative pruning improve the form of broadleaved trees? Can. J. For. Res. 2006, 36, 132–141. [Google Scholar] [CrossRef]
- Balandier, P. A method to evaluate needs and efficiency of formative pruning of fast-growing broad-leaved trees and results of an annual pruning. Can. J. For. Res. 1997, 27, 809–816. [Google Scholar] [CrossRef]
- Stangler, D.F.; Hamann, A.; Kahle, H.P.; Spiecker, H. A heat wave during leaf expansion severely reduces productivity and modifies seasonal growth patterns in a northern hardwood forest. Tree Physiol. 2017, 37, 47–59. [Google Scholar] [CrossRef]
- Duchesne, L.; Houle, D.; D’Orangeville, L. Influence of climate on seasonal patterns of stem increment of balsam fir in a boreal forest of Quebec, Canada. Agr. For. Meteorol. 2012, 162/163, 108–114. [Google Scholar] [CrossRef]
- Van der Maaten, E. Thinning prolongs growth duration of European beech (Fagus sylvatica L.) across a valley in southwestern Germany. For. Ecol. Manag. 2013, 306, 135–141. [Google Scholar] [CrossRef]
- Deslauriers, A.; Rossi, S.; Anfodillo, T. Dendrometer and intra-annual tree growth: What kind of information can be inferred? Dendrochronologia 2007, 25, 113–124. [Google Scholar] [CrossRef]
- Bresinsky, A.; Körner, C.; Kadereit, J.W.; Neuhaus, G.; Sonnewald, U. Strasburger’s Plant Sciences: Including Prokaryotes and Fungi; Springer: Berlin, Germany, 2013. [Google Scholar]
- Zweifel, R. The Rhythm of Trees: Water Storage Dynamics in Subalpine Norway Spruce. PhD Thesis, ETH Zürich, Zürich, Switzerland, 1999. [Google Scholar]
- Herzog, K.M.; Häsler, R.; Thum, R. Diurnal changes in the radius of a subalpine Norway spruce stem: Their relation to the sap flow and their use to estimate transpiration. Trees 1995, 10, 94–101. [Google Scholar] [CrossRef]
- Cuny, H.E.; Rathgeber, C.B.K.; Frank, D.C.; Fonti, P.; Mäkinen, H.; Prislan, P.; Rossi, S.; del Castillo, E.M.; Campelo, F.; Vavrčík, H.; et al. Woody biomass production lags stem-girth increase by over one month in coniferous forests. Nat. Plants 2015, 1, 15160. [Google Scholar] [CrossRef] [PubMed]
- Zweifel, R.; Häsler, R. Dynamics of water storage in mature subalpine Picea abies: Temporal and spatial patterns of change in stem radius. Tree Physiol. 2001, 21, 561–569. [Google Scholar] [CrossRef] [PubMed]
- Henhappl, G. Über die Stärkeänderungen der Peripheren Stammzone von Waldbäumen im Jahresablauf. Ph.D. Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg im Breisgau, Germany, 1965. (In German). [Google Scholar]
- Bouriaud, O.; Bréda, N.; Dupouey, J.-L.; Granier, A. Is ring width a reliable proxy for stem-biomass increment?: A case study in European beech. Can. J. For. Res. 2005, 35, 2920–2933. [Google Scholar] [CrossRef]
- Van der Maaten-Theunissen, M.J.C.; Bouriaud, O. Climate-growth relationships at different stem heights in silver fir and Norway spruce. Can. J. For. Res. 2012, 42, 958–969. [Google Scholar] [CrossRef]
- Chhin, S.; Hogg, E.H.T.; Lieffers, V.J.; Huang, S. Growth-climate relationships vary with height along the stem in lodgepole pine. Tree Physiol. 2010, 30, 335–345. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, U.; Möller, R.; Eckstein, D. Seasonal wood formation dynamics of beech (Fagus sylvatica L.) and black locust (Robinia pseudoacacia L.) as determined by the “pinning” technique. J. Appl. Bot. 2000, 74, 10–16. [Google Scholar]
- Hauser, S. Dynamik Hochaufgelöster Radialer Schaftveränderungen und des Dickenwachstums bei Buchen (Fagus sylvatica L.) der Schwäbischen Alb unter dem Einfluss von Witterung und Bewirtschaftung. Ph.D. Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg im Breisgau, Germany, 2003. (In German). [Google Scholar]
- Künstle, E. Beginn, Verlauf und Ende des Dickenwachstums von Solitär-Fichten auf dem Schauinsland bei Freiburg in den Jahren 1989 bis 1993. In Methoden der Permanent-Zuwachsmessung: 12 Beiträge zur Meßtechnik und Sensoranpassung im Seminar der Bayer. Landesanstalt für Wald und Forstwirtschaft “Waldklimastationen 4/94” am 12.09.1994; Preuhsler, T., Ed.; Frank: München, Germany, 1995; pp. 24–39. (In German) [Google Scholar]
- Lemay, A.; Krause, C.; Rossi, S.; Achim, A. Xylogenesis in stems and roots after thinning in the boreal forest of Quebec, Canada. Tree Physiol. 2017, 37, 1554–1563. [Google Scholar] [CrossRef] [PubMed]
- Thibeault-Martel, M.; Krause, C.; Morin, H.; Rossi, S. Cambial activity and intra-annual xylem formation in roots and stems of Abies balsamea and Picea mariana. Ann. Bot. 2008, 102, 667–674. [Google Scholar] [CrossRef] [PubMed]
- Rossi, S.; Deslauriers, A.; Anfodillo, T.; Morin, H.; Saracino, A.; Motta, R.; Borghetti, M. Conifers in cold environments synchronize maximum growth rate of tree-ring formation with day length. New Phytol. 2006, 170, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Rossi, S.; Anfodillo, T.; Čufar, K.; Cuny, H.E.; Deslauriers, A.; Fonti, P.; Frank, D.C.; Gričar, J.; Gruber, A.; King, G.M.; et al. A meta-analysis of cambium phenology and growth: Linear and non-linear patterns in conifers of the northern hemisphere. Ann. Bot. 2013, 112, 1911–1920. [Google Scholar] [CrossRef] [PubMed]
- Siegel, A. Optionen der Wachstumssteuerung von Gelbbirke und Zuckerahorn zur Überführung Exploitierter Laubmischwälder der Great Lakes-St. Lawrence Region (Kanada) in Naturnahen Wirtschaftswald. Ph.D. Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg im Breisgau, Germany, 2012. (In German). [Google Scholar]
- Rossi, S.; Morin, H.; Deslauriers, A. Causes and correlations in cambium phenology: Towards an integrated framework of xylogenesis. J. Exp. Bot. 2012, 63, 2117–2126. [Google Scholar] [CrossRef] [PubMed]
- Matzarakis, A.; Mayer, H.; Schindler, D.; Fritsch, J. Simulation des Wasserhaushaltes eines Buchenwaldes mit dem Forstlichen Wasserhaushaltsmodell WBS3; Meteorologisches Institut, Albert-Ludwigs-Universität Freiburg: Freiburg im Breisgau, Germany, 2000. (In German) [Google Scholar]
- Sheppard, J. Options for Management of High Value Timber within Temperate Agroforestry Systems. Ph.D. Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg im Breisgau, Germany, 2016. [Google Scholar]
- FAO. World Reference Base for Soil Resources 2006. A Framework for International Classification, Correlation and Communication; FAO: Rome, Italy, 2006. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2017. [Google Scholar]
- RStudio Team. RStudio Integrated Development Environment for R; RStudio Team: Boston, MA, USA, 2017. [Google Scholar]
- Pya, N.; Wood, S.N. Shape constrained additive models. Stat. Comput. 2015, 25, 543–559. [Google Scholar] [CrossRef]
- Stangler, D.F.; Mann, M.; Kahle, H.P.; Rosskopf, E.; Fink, S.; Spiecker, H. Spatiotemporal alignment of radial tracheid diameter profiles of submontane Norway spruce. Dendrochronologia 2016, 37, 33–45. [Google Scholar] [CrossRef]
- Mayer, D.G.; Butler, D.G. Statistical validation. Ecol. Model. 1993, 68, 21–32. [Google Scholar] [CrossRef]
- Cuny, H.E.; Rathgeber, C.B.K.; Kiessé, T.S.; Hartmann, F.P.; Barbeito, I.; Fournier, M. Generalized additive models reveal the intrinsic complexity of wood formation dynamics. J. Exp. Bot. 2013, 64, 1983–1994. [Google Scholar] [CrossRef] [PubMed]
- Mäkinen, H.; Seo, J.W.; Nöjd, P.; Schmitt, U.; Jalkanen, R. Seasonal dynamics of wood formation: A comparison between pinning, microcoring and dendrometer measurements. Eur. J. For. Res. 2008, 127, 235–245. [Google Scholar] [CrossRef]
- Swidrak, I.; Schuster, R.; Oberhuber, W. Comparing growth phenology of co-occurring deciduous and evergreen conifers exposed to drought. Flora 2013, 208, 609–617. [Google Scholar] [CrossRef]
- Rossi, S.; Deslauriers, A.; Morin, H. Application of the Gompertz equation for the study of xylem cell development. Dendrochronologia 2003, 21, 33–39. [Google Scholar] [CrossRef]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. J. Stat. Soft. 2015, 67. [Google Scholar] [CrossRef]
- Kuznetsova, A.; Brockhoff, P.B.; Christensen, R.H.B. lmerTest: Tests in Linear Mixed Effects Models. Available online: http://CRAN.R-project.org/package=lmerTest (accessed on 11 March 2016).
- Lenth, R.V.; Hervé, M. lsmeans: Least-Squares Means. Available online: http://CRAN.R-project.org/package=lsmeans (accessed on 11 March 2016).
- Schweingruber, F.H. Anatomie Europäischer Hölzer: Ein Atlas zur Bestimmung Europäischer Baum-, Strauch- und Zwergstrauchhölzer = Anatomy of European Woods: An Atlas for the Identification of European Trees, Shrubs and Dwarf Shrubs; Schweingruber, F.H., Baas, P., Eds.; Paul Haupt: Bern, Switzerland, 1990. (In German) [Google Scholar]
- Ladefoged, K. The Periodicity of Wood Formation; Biologiske Skrifter, Kgl; Dansk Videnskabernes Selskab: Kobenhavn, Denmark, 1952; Volume 7. [Google Scholar]
- Scherrer, D.; Bader, M.K.-F.; Körner, C. Drought-sensitivity ranking of deciduous tree species based on thermal imaging of forest canopies. Agric. For. Meteorol. 2011, 151, 1632–1640. [Google Scholar] [CrossRef]
- Teskey, R.; Wertin, T.; Bauweraerts, I.; Ameye, M.; McGuire, M.A.; Steppe, K. Responses of tree species to heat waves and extreme heat events. Plant Cell Environ. 2015, 38, 1699–1712. [Google Scholar] [CrossRef] [PubMed]
- Richardson, A.D.; Carbone, M.S.; Keenan, T.F.; Czimczik, C.I.; Hollinger, D.Y.; Murakami, P.; Schaberg, P.G.; Xu, X. Seasonal dynamics and age of stemwood nonstructural carbohydrates in temperate forest trees. New Phytol. 2013, 197, 850–861. [Google Scholar] [CrossRef] [PubMed]
- Vogel, M. Methodik und Ergebnisse von Zuwachsfeinmessungen auf Tharandter Intensivmeßflächen. In Methoden der Permanent-Zuwachsmessung: 12 Beiträge zur Meßtechnik und Sensoranpassung im Seminar der Bayer. Landesanstalt für Wald und Forstwirtschaft “Waldklimastationen 4/94” am 12.09.1994; Preuhsler, T., Ed.; Frank: München, Germany, 1995; pp. 64–75. (In German) [Google Scholar]
- Rossi, S.; Anfodillo, T.; Menardi, R. Trephor: A new tool for sampling microcores from tree stems. IAWA J. 2006, 27, 89–97. [Google Scholar] [CrossRef]
- Seo, J.W.; Eckstein, D.; Schmitt, U. The pinning method: From pinning to data preparation. Dendrochronologia 2007, 25, 79–86. [Google Scholar] [CrossRef]
- Thies, M.; Pfeifer, N.; Winterhalder, D.; Gorte, B.G.H. Three-dimensional reconstruction of stems for assessment of taper, sweep and lean based on laser scanning of standing trees. Scand. J. For. Res. 2004, 19, 571–581. [Google Scholar] [CrossRef]
- Larson, P.R. Wood Formation and the Concept of Wood Quality; Bulletin No. 74; School of Forestry, Yale University: New Haven, CT, USA, 1969. [Google Scholar]
- Brazier, J.D. The effect of forest practices on quality of the harvested crop. Forestry 1977, 50, 49–66. [Google Scholar] [CrossRef]
- King, G.M.; Fonti, P.; Nievergelt, D.; Büntgen, U.; Frank, D.C. Climatic drivers of hourly to yearly tree radius variations along a 6 °C natural warming gradient. Agric. For. Meteorol. 2013, 168, 36–46. [Google Scholar] [CrossRef]
- Zweifel, R.; Zimmermann, L.; Newbery, D.M. Modeling tree water deficit from microclimate: An approach to quantifying drought stress. Tree Physiol. 2005, 25, 147–156. [Google Scholar] [CrossRef] [PubMed]
- Duchesne, L.; Houle, D. Modelling day-to-day stem diameter variation and annual growth of balsam fir (Abies balsamea (L.) Mill.) from daily climate. For. Ecol. Manag. 2011, 262, 863–872. [Google Scholar] [CrossRef]
| ID | Species | Pruning Treatment | DBH (cm) | Tree Height (m) | Crown Length (m) | Crown Projection Area (m2) |
|---|---|---|---|---|---|---|
| 1 | Sycamore | Control | 19.5 | 14.6 | 12.7 | 38.71 |
| 2 | Sycamore | Control | 17.1 | 13.6 | 11.4 | 20.33 |
| 3 | Sycamore | Classical Treatment | 20.6 | 14.0 | 12.1 | 32.34 |
| 4 | Sycamore | Classical Treatment | 11.0 | 13.0 | 10.4 | 7.53 |
| 5 | Sycamore | Selective Treatment | 16.3 | 13.5 | 7.9 | 27.47 |
| 6 | Sycamore | Selective Treatment | 15.6 | 13.0 | 8.7 | 24.31 |
| 7 | Wild Cherry | Control | 27.3 | 19.8 | 18.7 | 53.19 |
| 8 | Wild Cherry | Control | 18.3 | 19.8 | 18.7 | 30.36 |
| 9 | Wild Cherry | Classical Treatment | 22.1 | 18.7 | 13.2 | 38.51 |
| 10 | Wild Cherry | Classical Treatment | 22.8 | 16.0 | 13.2 | 32.97 |
| 11 | Wild Cherry | Selective Treatment | 22.4 | 19.2 | 12.1 | 23.01 |
| 12 | Wild Cherry | Selective Treatment | 15.0 | 16.5 | 9.6 | 12.70 |
| Tree Species | Treatment | Modelling Efficiency | Mean Absolute Error | Mean Absolute Percentage Error |
|---|---|---|---|---|
| Sycamore | Control | 0.9999 | 12.22 | 0.45 |
| Classical Treatment | 0.9999 | 18.13 | 0.44 | |
| Selective Treatment | 0.9999 | 13.13 | 0.55 | |
| Wild Cherry | Control | 0.9998 | 21.42 | 0.71 |
| Classical Treatment | 0.9990 | 26.46 | 1.38 | |
| Selective Treatment | 0.9911 | 26.54 | 1.68 |
| Fixed Effect(s) | DF | Response | F-Value | p-Value | Response | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| S | 1 | ton | 0.02 | 0.886 | rmax | 2.53 | 0.163 |
| T | 2 | 0.04 | 0.959 | 0.81 | 0.490 | ||
| L | 1 | 27.72 | <0.001 | 2.18 | 0.144 | ||
| Y | 6 | 20.40 | <0.001 | 2.85 | 0.015 | ||
| S × T | 2 | 0.59 | 0.582 | 1.50 | 0.297 | ||
| S × L | 1 | 0.15 | 0.699 | 2.22 | 0.140 | ||
| T × L | 2 | 0.34 | 0.713 | 2.59 | 0.082 | ||
| S × Y | 6 | 5.43 | <0.001 | 9.32 | <0.001 | ||
| T × Y | 12 | 1.19 | 0.303 | 1.44 | 0.166 | ||
| L × Y | 6 | 1.05 | 0.398 | 0.25 | 0.958 | ||
| S × T × L | 2 | 2.15 | 0.123 | 3.54 | 0.034 | ||
| S × T × Y | 12 | 0.67 | 0.779 | 1.39 | 0.189 | ||
| S × L × Y | 6 | 1.20 | 0.314 | 0.52 | 0.793 | ||
| T × L × Y | 12 | 0.39 | 0.964 | 0.56 | 0.864 | ||
| S × T × L × Y | 12 | 0.47 | 0.925 | 0.82 | 0.632 | ||
| S | 1 | tce | 6.66 | 0.042 | r∆t | 0.86 | 0.389 |
| T | 2 | 0.25 | 0.786 | 0.60 | 0.580 | ||
| L | 1 | 1.35 | 0.248 | 0.24 | 0.629 | ||
| Y | 6 | 6.72 | <0.001 | 2.50 | 0.029 | ||
| S × T | 2 | 0.16 | 0.858 | 1.97 | 0.219 | ||
| S × L | 1 | 0.06 | 0.804 | 0.01 | 0.935 | ||
| T × L | 2 | 0.89 | 0.415 | 2.44 | 0.094 | ||
| S × Y | 6 | 8.71 | <0.001 | 8.38 | <0.001 | ||
| T × Y | 12 | 1.52 | 0.136 | 0.90 | 0.550 | ||
| L × Y | 6 | 1.14 | 0.348 | 0.43 | 0.856 | ||
| S × T × L | 2 | 0.16 | 0.851 | 4.08 | 0.021 | ||
| S × T × Y | 12 | 0.51 | 0.904 | 1.15 | 0.336 | ||
| S × L × Y | 6 | 1.69 | 0.136 | 0.71 | 0.645 | ||
| T × L × Y | 12 | 0.47 | 0.926 | 0.54 | 0.878 | ||
| S × T × L × Y | 12 | 0.72 | 0.729 | 0.66 | 0.780 | ||
| S | 1 | tmax | 3.30 | 0.119 | RG | 2.05 | 0.202 |
| T | 2 | 0.66 | 0.550 | 0.30 | 0.754 | ||
| L | 1 | 8.20 | 0.005 | 2.77 | 0.100 | ||
| Y | 6 | 4.59 | <0.001 | 4.88 | <0.001 | ||
| S × T | 2 | 1.21 | 0.361 | 0.97 | 0.430 | ||
| S × L | 1 | 1.53 | 0.219 | 0.01 | 0.915 | ||
| T × L | 2 | 0.61 | 0.544 | 1.96 | 0.148 | ||
| S × Y | 6 | 1.43 | 0.213 | 11.42 | <0.001 | ||
| T × Y | 12 | 0.81 | 0.638 | 0.89 | 0.556 | ||
| L × Y | 6 | 1.04 | 0.405 | 0.82 | 0.559 | ||
| S × T × L | 2 | 0.26 | 0.775 | 2.17 | 0.121 | ||
| S × T × Y | 12 | 0.57 | 0.861 | 0.79 | 0.656 | ||
| S × L × Y | 6 | 0.67 | 0.674 | 0.99 | 0.436 | ||
| T × L × Y | 12 | 1.15 | 0.337 | 0.57 | 0.862 | ||
| S × T × L × Y | 12 | 0.69 | 0.758 | 0.53 | 0.889 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sprengel, L.; Stangler, D.F.; Sheppard, J.; Morhart, C.; Spiecker, H. Comparative Analysis of the Effects of Stem Height and Artificial Pruning on Seasonal Radial Growth Dynamics of Wild Cherry (Prunus avium L.) and Sycamore (Acer pseudoplatanus L.) in a Widely Spaced System. Forests 2018, 9, 174. https://doi.org/10.3390/f9040174
Sprengel L, Stangler DF, Sheppard J, Morhart C, Spiecker H. Comparative Analysis of the Effects of Stem Height and Artificial Pruning on Seasonal Radial Growth Dynamics of Wild Cherry (Prunus avium L.) and Sycamore (Acer pseudoplatanus L.) in a Widely Spaced System. Forests. 2018; 9(4):174. https://doi.org/10.3390/f9040174
Chicago/Turabian StyleSprengel, Lars, Dominik Florian Stangler, Jonathan Sheppard, Christopher Morhart, and Heinrich Spiecker. 2018. "Comparative Analysis of the Effects of Stem Height and Artificial Pruning on Seasonal Radial Growth Dynamics of Wild Cherry (Prunus avium L.) and Sycamore (Acer pseudoplatanus L.) in a Widely Spaced System" Forests 9, no. 4: 174. https://doi.org/10.3390/f9040174
APA StyleSprengel, L., Stangler, D. F., Sheppard, J., Morhart, C., & Spiecker, H. (2018). Comparative Analysis of the Effects of Stem Height and Artificial Pruning on Seasonal Radial Growth Dynamics of Wild Cherry (Prunus avium L.) and Sycamore (Acer pseudoplatanus L.) in a Widely Spaced System. Forests, 9(4), 174. https://doi.org/10.3390/f9040174






