Next Article in Journal
Reconstructed Inter-Annual Variation in September–October Precipitation for the Upper Reaches of the Heihe River and Its Implications for Regional Drought Conditions
Previous Article in Journal
An Assessment of a Community-Based, Forest Restoration Programme in Durban (eThekwini), South Africa
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 8
Issue 8
10.3390/f8080269
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Allometric Equations for Estimating Biomass and Carbon Stocks in the Temperate Forests of North-Western Mexico

by
Benedicto Vargas-Larreta
1,*,
Carlos Antonio López-Sánchez
2,
José Javier Corral-Rivas
2,
Jorge Omar López-Martínez
3,
Cristóbal Gerardo Aguirre-Calderón
1 and
Juan Gabriel Álvarez-González
4
1
Instituto Tecnológico de El Salto, Mesa del Tecnológico s/n. 34942 El Salto, Durango, Mexico
2
Instituto de Silvicultura e Industria de la Madera, Universidad Juárez del Estado de Durango, Boulevard del Guadiana 501, Ciudad Universitaria, Torre de Investigación, 34120 Durango, Durango, Mexico
3
CONACYT-El Colegio de la Frontera Sur. Av. Centenario km 5.5, 77014 Chetumal, Quintana Roo, Mexico
4
Departamento de Ingeniería Agroforestal, Universidad de Santiago de Compostela, Escuela Politécnica Superior, 27002 Lugo, Spain
*
Author to whom correspondence should be addressed.
Forests 2017, 8(8), 269; https://doi.org/10.3390/f8080269
Submission received: 24 May 2017 / Revised: 17 July 2017 / Accepted: 27 July 2017 / Published: 28 July 2017
Browse Figures
Versions Notes

Abstract

:
This paper presents new equations for estimating above-ground biomass (AGB) and biomass components of seventeen forest species in the temperate forests of northwestern Mexico. A data set corresponding to 1336 destructively sampled oak and pine trees was used to fit the models. The generalized method of moments was used to simultaneously fit systems of equations for biomass components and AGB, to ensure additivity. In addition, the carbon content of each tree component was calculated by the dry combustion method, in a TOC analyser. The results of cross-validation indicated that the fitted equations accounted for on average 91%, 82%, 83% and 76% of the observed variance in stem wood and stem bark, branch and foliage biomass, respectively, whereas the total AGB equations explained on average 93% of the total observed variance in AGB. The inclusion of total height (h) or diameter at breast height2 × total height (d2h) as a predictor in the d-only based equations systems slightly improved estimates for stem wood, stem bark and total above-ground biomass, and greatly improved the estimates produced by the branch and foliage biomass equations. The predictive power of the proposed equations is higher than that of existing models for the study area. The fitted equations were used to estimate stand level AGB stocks from data on growing stock in 429 permanent sampling plots. Three machine-learning techniques were used to model the estimated stand level AGB and carbon contents; the selected models were used to map the AGB and carbon distributions in the study area, for which mean values of respectively 129.84 Mg ha−1 and 63.80 Mg ha−1 were obtained.

1. Introduction

Improved knowledge of carbon stocks and fluxes is needed in order to understand the current state of the carbon cycle and how it might evolve with changing land use and climatic conditions [1]. This has led to an increased interest in estimating forest biomass for practical forestry purposes and for scientific purposes. Tree biomass is an important component of the carbon pool in forests, and it can be estimated by using biomass expansion factors [2] or by relating biomass functions to tree-level data obtained in forest inventories [3]. In both cases, generic biomass functions are used to quantify the carbon in forests [4] because such functions improve the accuracy of carbon accounting systems and thus allow accurate planning of whole-tree and residual biomass utilization for bioenergy production.
Mexico is one of the largest emitters of CO2 due to deforestation and land degradation, which together account for 4.9 per cent (32 Mt CO2e) of the global emissions in the country [5]. Thus, most states in Mexico are implementing action plans aimed at mitigating the effects of climate change and accessing economic incentives that favour carbon sequestration in forests. Initiatives such as REDD+ (Reducing Emissions from Deforestation and Forest Degradation and enhancement of carbon stocks) are important efforts aimed at combating climate change; however, for effective implementation of such mechanisms, accurate estimation and monitoring of AGB and associated carbon stocks in forests is first required [6].
Several biomass equations and biomass expansion factors have been reported for forest species in Mexico. Acosta-Mireles et al. [7] generated allometric equations for six species of a mixed hardwood and oak forest in the northern Sierra of Oaxaca. All equations were of the form Y = bXk, where Y is the above-ground biomass (kg), X is diameter at breast height (cm), and b and k are the parameter estimates. Návar [8,9] developed diameter-based allometric biomass equations for nine species of pine and oak in temperate forests in Durango and Chihuahua. Rodríguez-Ortíz et al. [10] analyzed the effects of thinning on distribution and accumulated above-ground biomass content of Pinus patula in Ixtlán, Oaxaca. Silva-Arredondo and Návar-Cháidez [11] conducted research in northern Mexico to assess biomass components and biomass expansion factors by using classical allometric equations, and Villegas-Jiménez et al. [12] estimated above-ground biomass components in 13 Mexican provenances of P. greggii Engelm. in southern Mexico. Other similar studies have been carried out in Mexico by Díaz-Franco et al. [13], Mendoza-Ponce and Galicia [14], Búrquez et al. [15], Aguirre-Salado et al. [16], and Méndez-González et al. [17]. Rojas-García et al. [18] provide a comprehensive database with the above cited and other allometric equations applicable to a large number of tree and shrub species in Mexico. However, biomass equations were only available for nine tree species in the study area [8,9]. Moreover, these equations were developed using tree diameter as the only regressor, and they are not additive, one of the most important properties of biomass equations. Thus, there is still a need for research involving the accurate estimation of forest biomass and carbon stocks in these multi-species forests.
Temperate forests occupy 32,330,508 ha in Mexico, i.e., 17 per cent of the total land area. These are the richest ecosystems in Mexico with some 7000 plant species [19], of which ~150 are species of pines and 170 of oaks together representing more than 50 per cent of all known pine and oak species [20]. Durango is the most important forestry state in Mexico, with 10.5 million ha of forest cover and a timber production of 1.9 million m3 per year (32.8% of the national forest production [21]). Quantification of forest biomass and carbon stocks is important for management of these forests. Furthermore, mapping the spatial pattern of large-scale forest biomass can provide an overall picture of the carbon stocks within a region, which is of great scientific and political importance [22]. However, as pointed out in studies by Zianis and Mencuccini [23] and Walker et al. [24], although forest biomass can be measured directly, the method used (destructive sampling) is expensive and time-consuming and does not yield the continuous spatial distribution of biomass at large scales [25]. The difficulties associated with the direct estimation of biomass must be solved by quantitative satellite and remote sensing techniques, which represent the most promising methods for estimating biophysical features of forests, along with the development of parametric and nonparametric statistical methods for modelling stand variables [26]. Together these methods have enabled estimation of biomass at multiple scales with large spatial and temporal coverage [27,28].
The main objective of the present study was to develop species-specific systems of additive equations for predicting total above-ground biomass in the temperate forests of north-western Mexico. In addition, we used the new equations to model the forest biomass and carbon distribution at regional scale by applying remote sensing Landsat-5 TM imagery, terrain parameters and data from permanent research plots.

2. Materials and Methods

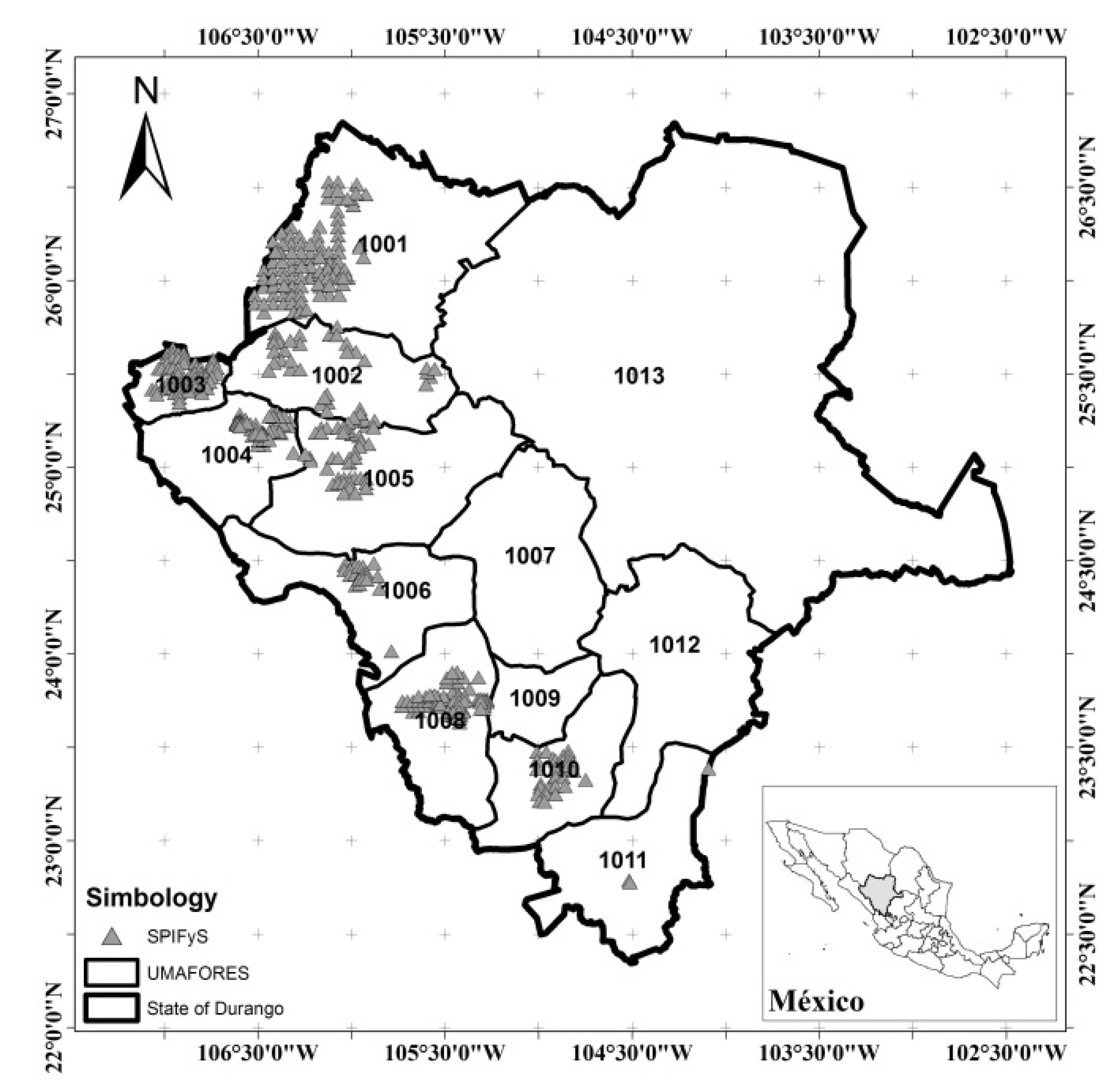
2.1. Study Area

The study was conducted in the uneven-aged and multi-species temperate forest of Durango (22°20′49″ to 26°46′33″ N; 103°46′38″ to 107°11′36″ W), which occupies about 23% of the Sierra Madre Occidental ecosystem (Figure 1). The study area is divided in Regional Forest Management Units (in Spanish, Unidades de Manejo Forestal Regional: UMAFORES). The elevation above sea level varies between 363 and 3200 m (average 2264 m). Precipitation ranges from 443 to 1452 mm, with an annual average of 917 mm, whereas the mean annual temperature varies from 8.2 to 26.2 °C, with an annual average of 13.3 °C. The predominant forest types are pine and uneven-aged pine-oak, with one or two pine species (usually P. cooperi and P. durangensis) dominating the overstorey and Q. sideroxyla dominating the understorey [29].

2.2. Biomass Data

Biomass estimates for stem wood, stem bark, branches and foliage were obtained from 1336 destructively sampled trees of 17 species: Pinus cooperi, P. durangensis, P. engelmannii, P. leiophylla, P. herrerae, P. teocote, P. lumholtzii, P. strobiformis, P. oocarpa, P. douglasiana, P. michoacana, Juniperus depeanna, Arbutus bicolor, Quercus sideroxyla, Q. rugosa, Q. durifolia and Q. crassifolia. As the number of specimens of P. michoacana and P. douglasiana was small, and as these species have similar morphological characteristics and are located in the same forest stands [30], the data for these species were combined in order to yield sufficient data for model fitting (Table 1). A generic equation was also developed for each biomass component for all pines and all oak trees.
For above-ground biomass measurement, the fieldwork included selection, measurement and felling of standing trees, collection of dimensional data, cutting and separating the tree components and weighing fresh components of each biomass component on site. The sample trees were subjectively selected to represent the complete range of diameter at breast height and total tree height; thus, the data were representative of the different growth and structure conditions in the study area. The number of trees sampled varied from a minimum of 30 in the case of P. douglasiana to a maximum of 130 trees of P. durangensis and Q. crassifolia. Diameter at breast height (d) and total height (h) were measured in each sample tree. The number of trees sampled per species depended on the distribution and abundance within the study area.
The following biomass components were considered: stem wood, stem bark, branches (including both wood and bark) and foliage (needles/leaves). Stems were divided into smaller sections to facilitate the weighing process. For each felled tree, stem diameter outside bark was measured at 0.3, 0.6, 1.3 m and thereafter every 2.5 m along the stem to take into account variations in moisture content. The total height of each felled tree was measured with a long fiberglass tape. The green weight of stem and branches was determined by weighing the logs and branches in the field by placing them on a 1000 kg balance (precision 100 g). Whole foliage was totally separated from the trunk and weighed on an analytical balance (precision 1 g). A disc of about 5 cm thick was cut from each log, and representative samples of branches and needles/leaves were weighed in the field (fresh weight) before being transported to the laboratory, where they were oven-dried at 70–85 °C to constant weight (dry weight, measured to the nearest 0.1 g). The time required to reach constant weight was 7–9, 3–4 and 2–3 days for wood discs, branches and foliage, respectively. The biomass of each tree component was calculated on the basis of the ratio of dry biomass to fresh biomass and then summed to produce the total AGB of each tree sampled. The carbon content of each tree component was determined by the dry combustion method, in a TOC analyser (Ol Analytical, College Station, Texas, USA). The number of observations used for tree biomass estimations and the basic description of the tree biomass components data for each species are summarized in Table 1.

2.3. Procedures for Developing the Species-Specific Biomass Equations

2.3.1. Basic Models

We used three basic model forms as starting points for model selection (Equations (1)–(3)).
w   =   α d β + ε i
w   =   α d β h γ + ε i
w   =   α d 2 h + ε i
where α, β, and γ are the equation parameters, w can be total tree AGB or any of the tree biomass components considered in the study, and ε i is the model error.
In a first step the models were linearized by using natural logarithms, and the stepwise variable selection approach was used to select the best set of independent variables for each biomass component equation. The significance level for entering and maintaining variables in the model was restricted to 0.001 [2]. In a second step, a species-specific system of equations with cross-equation constraints on the structural parameters and cross-equation error correlation was then defined for additive prediction of tree component and above-ground biomass [31,32].
The species-specific biomass equation system is formulated as follows:
W i   =   α i X j β i j   +   ε i
W t   =   ∑ i   =   1 n W i +   ε t
where Wi represents the tree biomass for the i-th component, Wt is the total tree AGB (i.e., the sum of all the tree biomass components), Xj are tree variables (j = d, h, d2h), αi, βij are parameters to be estimated in the fitting process, and εi, εt are inter-correlated error terms [32].

2.3.2. Simultaneous Fitting of Tree Biomass Components and Total AGB

Total tree AGB was formulated as the sum of the equations for each tree component, and the system of equations was fitted using the Generalized Method of Moments (GMM) in the PROC MODEL procedure of SAS/ETS® [33]. This method produces efficient parameter estimates under potentially heteroscedastic conditions, without specifying the nature of the heteroscedasticity [34], and it thus avoids estimating the heteroscedastic error variance. Bi et al. [32] and Castedo et al. [2] state that the GMM procedure of SAS overcomes the above-mentioned problem of the linear combination of the error terms of the tree biomass component equations by computing a generalized inverse of the variance covariance matrix (by setting part of the matrix for whole-tree biomass to zero) and that estimation of parameters by simultaneously fitting the biomass component equations guarantees that AGB will be the sum of the tree component estimates.

2.3.3. Comparison of Equations

Statistical and graphical analyses were used to compare the performance of the equations. Moreover, a 10-fold cross-validation approach was used to evaluate the predictive performance of the models. The root mean square error (RMSE) and the coefficient of determination (R2), calculated by Equations (6) and (7), were estimated using the residuals from the 10 fold cross-validation.
RMSE = ∑ i   =   1 n ( Y i j − Y ^ i j ) 2 n − p
R 2 =   1 − ∑ i = 1 n ( Y i j − Y ^ i j ) 2 ∑ i = 1 n ( Y i j − Y ¯ i j ) 2
where Yij and Y ^ i j are the j-th observed and predicted values of biomass for component i, Y ¯ i j is the mean of n observed values for the same component, and p is the number of parameters in the model.

2.4. Applying the Proposed Above-Ground Biomass Equations

A data set from a network of 429 permanent research sampling plots (Sitios Permanentes de Investigación Forestal y de Suelos: SPIFyS), distributed across the Sierra Madre Occidental in Durango was used to relate stand biomass and carbon stocks to variables obtained from remote sensors. The plots were installed between 2007 and 2011 using the protocol developed by [35]. The data from these permanent sample plots are used to monitor the growth and yield of the main types of forest in Durango. The plots are 50 × 50 m in size and they were distributed by systematic sampling, with a variable grid ranging from 3 to 5 km, depending on the size of the forest properties. The sampling plots are intended to be re-measured at five-year intervals. Among other variables, tag number, species code, breast height diameter (measured in cm at 1.3 m above ground level), total tree height (m), height to the live crown (m), azimuth (◦) and radius (m) from the centre of the plot to all trees equal or larger than 7.5 cm in diameter were recorded. The total AGB in each stand was calculated by applying the new tree-level biomass equations (to each tree), converted into carbon content by using the carbon proportion estimated for each component and expressed per unit area (ha). The species or group species-specific AGB models reported by Rojas-García et al. [18] were used to estimate total AGB for the tree species present in the permanent plots and for which no biomass equations were developed in this study.
The spectral data were derived from Landsat TM5 (Thematic Mapper) satellite images obtained during the same period that the SPIFyS were established (2007 to 2011) and are freely available from the National Landsat Archive Processing System (NLAPS). The Landsat 4-5 Thematic Mapper product, level 1 of surface reflectance (radiometrically and atmospherically corrected) was processed using the Standard Landsat Product Generation System (LPGS) via the Landsat Ecosystem Disturbance Adaptive Processing System (LEDAPS) algorithm (both available at [36]), which uses a 6S radiative transfer model to correct for atmospheric effects on a given date [37]. Landsat TM5 bands 1, 2, 3, 4, 5 and 7 were used. Band 6, which is designed for thermal mapping and determining soil moisture, was not considered because of its lower (120 m) spatial resolution [38]. Some common Vegetation Indexes (VI) and other derived parameters were computed from the atmospherically corrected image bands: the Normalized Difference Vegetation Index (NDVI); the Soil Adjusted Vegetation Index (SAVI) and its modification (MSAVI); the Enhanced Vegetation Index (EVI); the Normalized Burn Ratio using bands 4 and 7 (NBR1); the difference Normalized Burn Ratio 2 (NBR2) using bands 5 and 7; and the Normalized Difference Moisture Index (NDMI). These indices have been widely used as comprehensive indicators of the interaction between land cover and solar radiation in the visible and near-infrared regions of the electromagnetic spectrum [26,39,40,41].
The direct relationship between terrain variables and forest species composition, tree height growth and other stand variables enables these forest variables to be modelled [42,43]. First- and second-order terrain parameters were computed from a Digital Elevation Model (DEM) of the study area with a spatial resolution of 15 m [44]. Prior to these calculations, a low pass filter with a 5 × 5 moving window was applied to the original DEM in order to reduce the banding effects present in the original file. The first-order terrain parameters selected were elevation, slope, aspect, transformed aspect, profile curvature, plan curvature and curvature, while the second-order terrain parameters were terrain shape index and wetness index. These parameters are potentially related to key features for forest stand development, such as overall climate characteristics, insolation, evapotranspiration, run-off, infiltration, wind exposure and site productivity [42,45].
The sample plots were geolocated in order to extract the average pixel value with an associated buffer of 25 m for each potential predictor. The pixel data were extracted using R statistical software [46] and the “raster” package. Finally, a database was constructed with the mean biomass values for each plot; the corrected bands of the Landsat-5 TM sensor (6 bands: 1, 2, 3, 4, 5 and 7), the vegetation indexes (7 indexes) and the terrain variables derived from the DEM (9 variables).

2.5. Machine Learning Techniques (MLTs)

We compared the performance of three machine learning techniques for estimating the ABG and carbon at stand level: (i) the non-parametric Support Vector Machine (SVM) for Regression technique; (ii) Regression by Discretization based on Random Forest (RD-RF); and (iii) parametric multiple linear regression (MLR).
SVMs have proven useful in remote sensing of forest environments [47,48]. The Shevade et al. [49] modification of the Sequential Minimal Optimization (SMO) with a polynomial kernel and a trade-off parameter value of 1 was used in this study for SVM ensemble. On the other hand, RD-RF employed a classifier (random forest, in this case) on a copy of the data in which the response variable is discretized with equal width. The predicted value is the expected value of the mean class value for each discretized interval (based on the predicted probabilities for each interval). In this study, we used the random forest classification algorithm [50]. The success of this technique is based on the use of numerous trees developed with different independent variables that are randomly selected from the complete original set of variables. The number of bins for discretization was fixed at 10 and the number of trees fitted was established at 100. Finally, MLR—the technique most commonly used in this kind of study [51]—was used to select the best set of independent variables for the model. The equation was initially built on all descriptors, and descriptors with the smallest standardized regression coefficients were then removed step-wise from the model until no improvement was observed in the estimate of the average prediction error given by the Akaike information criterion [52]. WEKA open source software [53] was used to implement all three techniques used.
Several approaches can be used to test the accuracy of supervised learning algorithms. We used the common method of k-fold cross validation. In this process, the data set is divided into k subsets. In each application, one of the k subsets is used as the test set and the other k-1 subsets form the training set. Error statistics are calculated across all k trials. This provides a good indication of how well the classifier will perform on unseen data. We used k = 10 and computed several standard performance metrics to calculate the goodness-of-fit statistics for each technique. We compared the performance of the MLTs by using the root mean square error (RMSE), the coefficient of determination (R2) and a paired t-test (corrected) based on Student’s t-criterion. Finally, we used the selected MLT to generate above-ground biomass and carbon maps for the study area.

3. Results

3.1. Tree-Level Biomass Equations

Table 2 depicts the parameter estimates and goodness-of-fit statistics of cross-validation of the equations systems fitted for each species and groups of species. All the parameter estimates were significant at α = 0.05. Stem wood biomass and AGB estimates were the most accurate, as indicated by the R2 and RMSE values, whereas foliage and branch biomass estimates were the least accurate. The values of the goodness-statistics calculated using the residuals of cross-validation indicated that the selected equations performed well. The results of the coefficient of determination indicated that the fitted models explained between 57% and 98% of the observed biomass variance per component for all species, with mean values of 91%, 82%, 83% and 76% of the observed variance in stem wood and stem bark, branch and foliage biomass, respectively, whereas the total AGB equations explained on average 93% of the total observed variance in AGB. Nevertheless, as mentioned above, the explained variation was lower than 70% for three of the components: branch biomass in P. engelmannii (59%) and P. leiophylla (63%); foliage biomass in P. herrerae (60%), Q. crassifolia (64%) and Juniperus depeanna (67%); and stem bark biomass in Juniperus depeanna (57%).
The root mean square error (RMSE) for the cross-validation ranged between 22.81 and 140.91 kg for total above-ground biomass (Wt) (Table 2), whereas the values of these statistics for stem wood (Ww), stem bark (Wb) branch (Wbr) and foliage (Wf) biomass estimates were 15.11–127.6, 0.85–27.87, 3.02–67.38 and 1.72–16.67 kg, respectively. The RMSE of Wt for all pine and all oak species were 83.04 kg and 134.12 kg, respectively.
The allometric equation (Equation (1)) produced the best estimates of all biomass components of P. herrerae, P. lumholtzii, P. leiophylla, P. douglasiana, P. michoacana and P. oocarpa (except stem wood biomass), as well as for the branch and foliage biomass of P. leiophylla, foliage biomass of P. teocote, stem bark biomass of Q. rugosa, and stem bark and foliage biomass of all of the oak species.
A strong relationship between biomass components and total height was found for the groups of pine and oak species (Figure 2). The biomass equation including total height (h) as a predictor was the best equation for all biomass components of P. cooperi, P. durangensis, P. engelmannii, P. teocote (except foliage biomass), P. strobiformis, Arbutus bicolor, Q. sideroxyla, Q. rugosa (except stem bark biomass) and Q. durifolia, as well as for all of the pine species and for stem wood and branch biomass of all of the oak species. AGB and all biomass components of Juniperus depeanna, P. leiophylla and Q. crassifolia were best estimated using the combination of diameter at breast height and total height (d2h) (Equation (3)).
The biomass equation including total height (h) as a predictor was the best equation for all biomass components of P. cooperi, P. durangensis, P. engelmannii, P. teocote (except foliage biomass), P. strobiformis, Arbutus bicolor, Q. sideroxyla, Q. rugosa (except stem bark biomass) and Q. durifolia, as well as for all of the pine species and for stem wood and branch biomass of all of the oak species. AGB and all biomass components of Juniperus depeanna, P. leiophylla and Q. crassifolia were best estimated using the combination of diameter at breast height and total height (d2h) (Equation (3)).

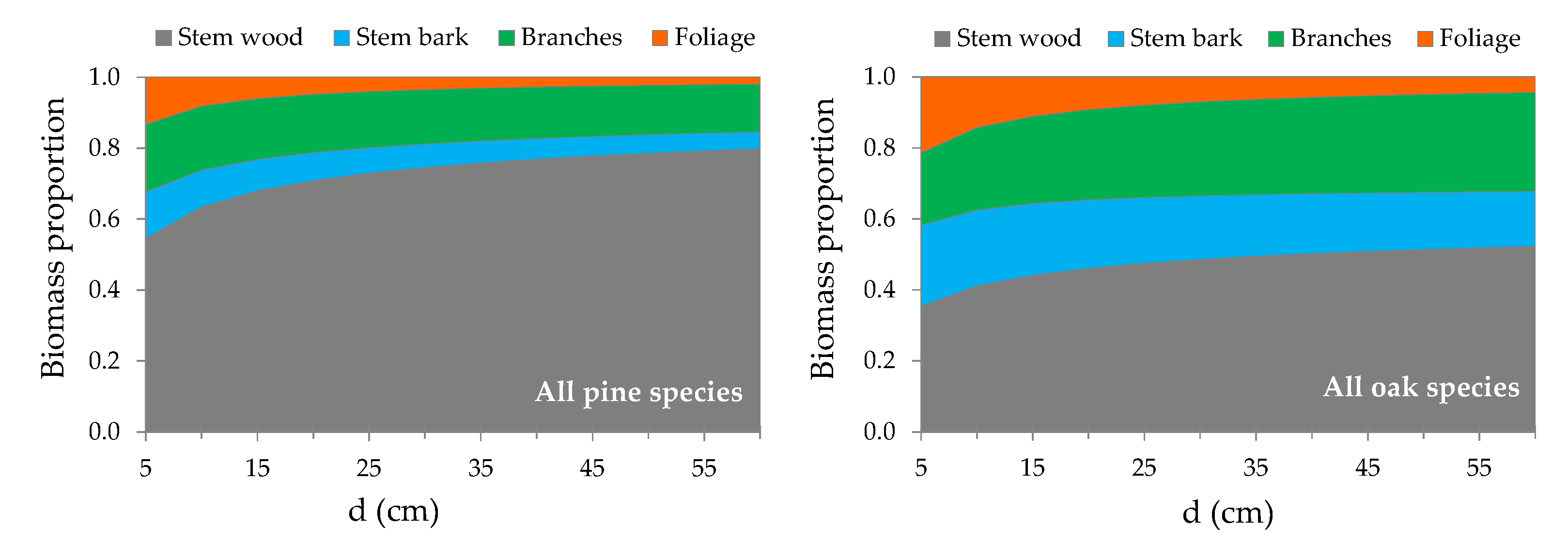
3.2. Above-Ground Biomass Allocation

Biomass distribution varied among tree components and between species. For all species, the largest amount of biomass was located in the stem wood (Figure 3). Stem wood biomass of pine ranged from 63% (P. oocarpa) to 80.9% (P. lumholtzii), while for oak species the values varied between 59.5% (Q. rugosa) and 65.3% (Q. durifolia). General equations for all pine and all oak species estimated stem wood biomass values of 92% and 78%, respectively.
The lowest values for stem bark, branches and foliage biomass were respectively 2.4% (J. depeanna), 11.6% (P. lumholtzii) and 2.4% (P. herrerae), and the highest values for these components were 18.7% (Q. rugosa), 30.5% (A. bicolor) and 7.1% (P. oocarpa), respectively. For all pine species pooled together, the highest quantity of biomass was contained in stem wood (75.4%); followed by branches (14.9%), stem bark (6.4%) and foliage (3.3%). For all oak species, the biomass values for the different components were respectively 62.9%, 22.2%, 10.9% and 4.0% (Figure 3).
The proportion of stem biomass in pine trees increased with d (exceeding 50% of AGB for all diameters); although the proportion of stem bark and foliage biomass decreased, it was fairly stable for branch biomass (Figure 4). In all of the oak species, stem wood and branch biomass increased from 0.25 and 0.14 for d = 5 cm to 0.42 and 0.23 for d > 50 cm, respectively. Stem bark of oaks decreased with d from 0.16 to about 0.10, while foliage biomass decreased from 0.13 to 0.03.

3.3. Carbon Fractions in Different Tree Components

The mean values of carbon fraction of the pine species were in all cases close to the value provided by IPCC [54] (0.5), except for oak species, in which the average proportion of carbon was 0.45. Sample size was 27 for all species (Table 3).

3.4. Biomass and Carbon Estimates in the Permanent Research Plots

The fitted equations were used to estimate the stand level total AGB and C contents in the 429 research plots. The total AGB ranged from 11.06 to 469.42 Mg ha−1 with a mean value of 129.84 Mg ha−1 and C contents ranged from 5.12 to 232.94 Mg ha−1 with a mean value of 63.80 Mg ha−1. The goodness-of-fit statistics obtained by the different machine learning methods used to model AGB and carbon contents of the 429 sample plots are shown in Table 4. The variables that were most important for estimating AGB and C contents by the MLT evaluated correspond to band 1 and band 7, the vegetation indices NDMI, NBR2 and EVI, and the terrain variables aspect and wetness index.
The best AGB estimates were obtained by using Support Vector Machine for Regression (SVM), whereas the best estimates of carbon content were obtained using Regression by Discretization based on Random Forest (RD-RF). However, the results of the paired t-test (corrected) based on Student’s t-criterion did not indicate any significant differences in the results produced by the three approaches considered (α = 0.05). A map of AGB and carbon distributions was elaborated using the SVM approach (Figure 5).

4. Discussion

4.1. The Allometric Equations

The equations were based on three model formulations (Equations (1)–(3)) used in previous studies [2,32,55,56,57]. Diameter at breast height was the main explanatory tree variable used to estimate the tree biomass components for all species. Several authors have noted that inclusion of total height does not usually lead to a substantial increase in the predictive ability of diameter-based biomass regressions, and they also assume that d is sufficient to yield a reliable tree biomass prediction [58,59,60]. However, other authors have found a significant improvement in model fits [61,62] or an increase in the accuracy of the biomass estimates [57,63] when h is also used as a predictor. In this study, d by itself was a good predictor of biomass, but the addition of h as a second variable improved the predictions for several species. A strong relationship between biomass components and total height was found for the groups of pine and oak species, and total height was a significant predictor of all tree biomass components and AGB of 12 out of 17 species and for the group of all pine species, as well as for stem wood and branch biomass of the oak species. The d and h based system of equations yielded poor fits for branch and foliage biomass of P. oocarpa and P. teocote. Lambert et al. [64], Bi et al. [65] and Zhao et al. [66] also found that inclusion of tree height improved the accuracy of predicting the stem biomass but not the crown (needles and branches) biomass components.
Feldpausch et al. [67] reported that the mean relative error in biomass estimates when h was included was 50% lower than when h was excluded. Similarly, we found that inclusion of total height in the biomass equations increased the accuracy of the biomass estimations (measured as RMSE) by between 10.4% (P. teocote) and 53.9% (P. durangensis) for stem wood biomass, by between 2.9% (A. bicolor) and 28.1% (P. strobiformis) for stem bark biomass, by between 13.1% (Q. durifolia) and 20.6% (P. strobiformis) for branch biomass, by between 1.1% (P. engelmannii) and 19.7% (Q. sideroxyla) for foliage biomass and by between 26.7% (Q. rugosa) and 55.9% (P. cooperi) for total tree AGB. These results are consistent with those of António et al. [55], who found that the use of height implied a decrease in the sum of squares of residuals by 72%, 8%, 12% and 10%, for stem wood, stem bark, leaves and branches, respectively. They are also consistent with the findings of Li and Zhao [68], who reported that inclusion of height improved model performance of the fitted equation especially for total above-ground biomass, stem wood biomass and stem bark biomass.
Branch and foliage biomass components are always difficult to estimate with the same accuracy as bole or total AGB. This is illustrated by the fact that inclusion of height in the model only improved the accuracy of branch and foliage biomass estimates by up to 21%. We assume, as Ter-Mikaelian and Parker [69] found, that the influence on height of stand density (i.e., competition), stand structure and site quality may account for some of this variation, and that these variables represent a large proportion of the small contribution of h to explaining the variance in these biomass components for some of the species evaluated. Nevertheless, this was not tested in the present study because the data does not enable discrimination of the effects of these factors or the different silvicultural treatments on the crown structure.
The combined variable d2h is usually used in biomass equations [70,71,72], and the accuracy of biomass estimation has been found to increase significantly (measured as R2) when h or d2h was also included, in addition to d. In fact, tree biomass is closely correlated with d2h, as shown by Parresol [73] and Carvalho and Parresol [74]. In the models developed by Parresol [73], height was a good predictor of stem wood but not of stem bark biomass, whereas Carvalho and Parresol [74] obtained the best estimates for stem, crown and total tree biomass of Pyrenean oak by including the variable d2h as the sole independent variable in the equation. Bi et al. [65] reached a similar conclusion, reporting that d2h performed better for predicting stem and bark components than diameter alone but not for branch and leaf components. In the present study, d2h yielded the best estimates of all biomass components and AGB for P. leiophylla, J. depeanna and Q. crassifolia. The results reported here suggest that the best equations for biomass estimation for most species are based on d and h; it is therefore possible to use the biomass equation systems developed for a specific species across different sites in the temperate forests of Durango, assuming that total height is included in the models and that the addition of this variable may take into account different levels of competition induced by different stand density conditions [55].
We found differences in biomass estimates yielded by the equations developed in this study and previously published biomass functions for nine species in northwest Mexico [8]. The predictive powers of the new biomass equations are higher than those of previous models developed by Návar [8,9], as noted for the evaluation using the RMSE. For the stem wood biomass component of all pine species pooled together, the RMSE of the new equation was lower (72.12 kg tree−1) than the value obtained for the previous equation (105.00 kg tree−1); the same behaviour was observed for the oak group, for which the RMSE values were 94.25 and 102.9 kg tree−1. For the total above-ground biomass, previous equations showed RMSE values of 131.8 and 156.96 kg tree−1 for pine and oaks, respectively; while the equations developed in this study yielded RMSE values of 83.04 and 134.12 kg tree−1, for these same groups of tree species. Differences relative to the biomass equations proposed by Návar [8,9] may be explained by the following: (i) the previous biomass equations were fitted using tree diameter as the only regressor; however, the inclusion of total height in allometric equations greatly improves the accuracy of individual tree biomass estimations [67,70,75,76], especially in mixed and uneven-aged stands, such as the stands analysed in this study. For example, different species, ages, sizes, crown types and tolerance levels co-exist in the stands under study and biomass equations based only on d cannot therefore describe all possible height-diameter relationships; and (ii) the biomass equations developed by Návar [8] are not additive, and additivity is one of the most important properties of biomass equations [31,74].

4.2. Contribution of Components to Total AGB

For all species evaluated, stem wood contributed most to the total AGB, followed by branches, stem bark and foliage. The fact that the highest proportion of the AGB is allocated in the stem has been widely documented, with the proportions ranging from 50% to 92% for different species [4,77,78]. Our results are within the same range, varying between 59.5% (Q. rugosa) and 80.9% (P. lumholtzii). The biomass allocation patterns observed are consistent with those reported by Blujdea et al. [56] for broadleaf species in Romania, Wirt et al. [4] for Norway spruce in Central Europe, Correia et al. [79] for P. pinea L. in Portugal, and by Pajtík et al. [80] for Picea abies [L.] Karst in Slovakia.
As expected, the proportion of biomass allocated to stem wood increased with increasing tree size, whereas the relative contribution of stem bark and foliage to AGB decreased. This is consistent with findings reported by Blujdea et al. [56] and Johansson [58]. The pattern was similar for pines and oaks, except for branch biomass. In oaks, branch biomass increased with d, whereas for pines it remained quite constant (around 15%) over the entire diameter range. The decrease in foliage biomass with increasing d can be attributed to competition for light among the trees; small branches and a smaller quantity of leaves occur in larger trees or those trees with a dominant position [81]. The foliage biomass of oaks decreased to below 3.5%, while for pines it decreased to about 2%.

4.3. Machine Learning Techniques (MLT)

The variables used to estimate AGB with the different machine learning algorithms evaluated can be classified into 2 different groups. In order of decreasing importance, the first group comprises the spectral bands (bands 1 and 7, are the most relevant) and the spectral indices (NDMI, NBR2 and EVI), and the second group comprises the first- and second-order terrain topographical variables (aspect and wetness index) derived from the DEM. Several studies have demonstrated that such variables are usually good predictors of AGB [26,82,83]. However, the results may also differ depending on the machine learning method used [26,84,85,86,87].
The SVM technique yielded the best fits, thus confirming that this type of technique is of great potential for improving biomass estimation, independently of the type of sensor to which it is applied, as demonstrated in recent studies [88]. However, no significant differences were found between this method and the other two approaches used.
The values of the goodness of fit statistics for the SVM technique obtained in the present study were slightly lower than those reported by Guo et al. [89], who estimated AGB in Picea crassifolia forests in China using Landsat TM data and two non-parametric methods (k-Nearest Neighbour kNN: R2 = 0.54 and RMSE = 26.62 Mg ha−1 and SVM: R2 = 0.51 and RMSE = 27.45 Mg ha−1). They were also lower than those reported by Tian et al. [90] (kNN: R2 = 0.59) and those obtained by López-Serrano et al. [26] for mixed and uneven-aged forests in the Sierra Madre Occidental of Mexico (R2 = 0.73 and RMSE = 22.59 Mg ha−1).

5. Conclusions

This study describes a set of simultaneous species-specific allometric equation systems for seventeen temperate species in north-western Mexico. Breast height diameter-only based equations proved best for predicting all biomass components of only four species. Including h or d2h as additional predictor in the equation systems only slightly improved stem wood, stem bark and above-ground biomass estimates, but greatly improved the predictions of branch and foliage biomass.
In all species, most of the biomass was allocated in stem wood, followed by branches, stem bark and foliage. The biomass allocation differed between tree components and among species; however, further study is required to clarify which factors affect the allocation patterns.
The proposed species-specific biomass equations can be applied to tree-level data in forest inventories and may also improve the quality of biomass estimates and verify changes in carbon stocks in the temperate uneven-aged multi-species forests in the study area. This research should be viewed as part of an ongoing process, and further sampling is required to provide data for a wider range of species with potentially different growth forms and biomass allocation patterns in order to improve our ability to estimate AGB and carbon for these forests.
The results of this study regarding the use of machine learning techniques to estimate AGB and C content from remote sensors indicate that moderate resolution sensors, such as the Landsat TM5, are potentially useful for monitoring these important variables in real time and at a low cost, because the spectral data are available free of charge. However, the use of new and more accurate biomass equations, such as the systems of equations fitted in this study, combined with high resolution remote sensing data (e.g., Sentinel satellites) to develop predictive machine learning models will enable more realistic and accurate prediction of biomass and carbon stocks at regional level by model-based inference.

Acknowledgments

This study was financially supported by the Mexican National Council for Science and Technology (CONACyT) and by the State of Durango Government (Project FOMIX- DGO-2011-C01-165681). The authors are grateful to the three anonymous reviewers and the academic editor for the constructive and insightful comments.

Author Contributions

B.V.-L. conceived the research design, conducted the field data collection, analysis, and wrote the manuscript. C.A.L.-S. conducted the analysis of satellite data. J.J.C.-R. and J.G.A.-G. analyzed the data and revised the manuscript. C.G.A.-C. and J.O.L.-M. assisted in analysis of the results and revised the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Data Availability

All codes and data are available and can be requested from the corresponding author.

References

  1. Hollinger, D. Defining a Landscape-Scale Monitoring Tier for the North American Carbon Program. In Field Measurements for Forest Carbon Monitoring; Hoover, C.M., Ed.; Springer: Dordrecht, The Netherlands, 2008; pp. 3–17. [Google Scholar] [CrossRef]
  2. Castedo-Dorado, F.; Gómez-García, E.; Diéguez-Aranda, U.; Barrio-Anta, M.; Crecente-Campo, F. Aboveground stand-level biomass estimation: A comparison of two methods for major forest species in northwest Spain. Ann. Forest Sci. 2012, 69, 735–746. [Google Scholar] [CrossRef]
  3. Hall, G.M.J.; Wiser, S.K.; Allen, R.B.; Beets, P.N.; Goulding, C.J. Strategies to estimate national forest carbon stocks from inventory data: The 1990 New Zealand baseline. Glob. Chang. Biol. 2001, 7, 389–403. [Google Scholar] [CrossRef]
  4. Wirth, C.; Schumacher, J.; Schulze, E.D. Generic biomass functions for Norway spruce in Central Europe—A meta-analysis approach toward prediction and uncertainty estimation. Tree Physiol. 2004, 24, 121–139. [Google Scholar] [CrossRef] [PubMed]
  5. Instituto Nacional de Ecología y Cambio Climático (INECC) y Secretaría de Medio Ambiente y Recursos Naturales (SEMARNAT). Primer Informe Bienal de Actualización ante la Convención Marco de las Naciones Unidas sobre el Cambio Climático; INECC/SEMARNAT: Mexico City, México, 2015. [Google Scholar]
  6. Salimon, C.I.; Putz, F.E.; Menezes-Filho, L.; Anderson, A.; Silveira, M.; Brown, I.F.; Oliveira, L.C. Estimating state-wide biomass carbon stocks for a REDD plan in Acre, Brazil. Forest Ecol. Manag. 2011, 262, 555–560. [Google Scholar] [CrossRef]
  7. Acosta-Mireles, M.; Vargas-Hernández, J.; Velázquez-Martínez, A.; Etchevers-Barra, J.D. Estimación de la biomasa aérea mediante el uso de relaciones alométricas en seis especies arbóreas en Oaxaca, México. Agrociencia 2002, 36, 725–736. [Google Scholar]
  8. Návar, J.J. Allometric equations for tree species and carbon stocks for forests of northwestern Mexico. Forest Ecol. Manag. 2009, 257, 427–434. [Google Scholar] [CrossRef]
  9. Návar-Cháidez, J.J. Biomass allometry for tree species of northwestern Mexico. Trop. Subtrop. Agroecosyst. 2010, 12, 507–519. Available online: https://www.cabdirect.org/cabdirect/abstract/20103282813 (accessed on 13 September 2015).
  10. Rodríguez-Ortíz, G.; Aldrete, A.; González-Hernández, V.A.; De los Santos-Posadas, H.M.; Gómez-Guerrero, A.; Fierros-González, A.M. ¿Afectan los aclareos la acumulación de biomasa aérea en una plantación de Pinus patula? Agrociencia 2011, 45, 719–732. [Google Scholar]
  11. Silva-Arredondo, F.M.; Návar-Cháidez, J.J. Estimación de factores de expansión de carbono en comunidades forestales templadas del norte de Durango, México. Rev. Chapingo Ser. Cienc. 2009, 15, 155–163. [Google Scholar]
  12. Villegas-Jiménez, D.E.; Rodríguez-Ortiz, G.; Velasco-Velasco, V.A.; Ruiz-Luna, J.; Carrillo-Rodríguez, J.C.; Ramírez-Sánchez, S.E. Partición de biomasa aérea en procedencias de Pinus greggii plantadas en el sur de México. Rev. Fitotec. Mex. 2013, 36, 421–427. [Google Scholar]
  13. Díaz-Franco, R.; Acosta-Mireles, M.; Carrillo, F.A.; Rodríguez, E.B.; Ayala, E.F.; Barra, J.D. Determinación de ecuaciones alométricas para estimar biomasa y carbono en Pinus patula Schl. et Cham. Madera Bosques 2007, 13, 25–34. [Google Scholar] [CrossRef]
  14. Mendoza-Ponce, A.; Galicia, L. Aboveground and belowground biomass and carbon pools in highland temperate forest landscape in Central Mexico. Forestry 2010, 83, 497–506. [Google Scholar] [CrossRef]
  15. Búrquez, A.; Martínez-Yrízar, A.; Núñez, S.; Quintero, T.; Aparicio, A. Aboveground biomass in three Sonoran Desert communities: Variability within and among sites using replicated plot harvesting. J. Arid. Environ. 2010, 74, 1240–1247. [Google Scholar] [CrossRef]
  16. Aguirre-Salado, C.A.; Treviño-Garza, E.J.; Aguirre-Calderón, O.A.; Jiménez-Pérez, J.; González-Tagle, M.A.; Miranda-Aragón, L.; Valdez-Lazalde, J.; Aguirre-Salado, A.; Sánchez-Díaz, G. Forest Cover Mapping in North-Central Mexico: A Comparison of Digital Image Processing Methods. GIScience Remote Sens. 2012, 49, 895–914. [Google Scholar] [CrossRef]
  17. Méndez-González, J.; Luckie-Navarrete, S.L.; Capo-Arteaga, M.A.; Nájera-Luna, J.A. Ecuaciones alométricas y estimación de incrementos en biomasa aérea y carbono en una plantación mixta de Pinus devoniana Lindl. y P. pseudostrobus Lindl., en Guanajuato, México. Agrociencia 2011, 45, 479–491. [Google Scholar]
  18. Rojas-García, F.; De Jong, B.J.; Martínez-Zurimendí, P.; Paz-Pellat, F. Database of 478 allometric equations to estimate biomass for Mexican trees and forests. Ann. Forest Sci. 2015, 72, 835–864. [Google Scholar] [CrossRef]
  19. Challenger, A. Utilización de los Ecosistemas Terrestres de México. Pasado, Presente y Future; Comisión Nacional para el Conocimiento y uso de la Biodiversidad (CONABIO): Mexico City, México, 1998. [Google Scholar]
  20. CONABIO. Estrategia Nacional Sobre Biodiversidad de México; Comisión Nacional para el Conocimiento y uso de la Biodiversidad: Mexico City, México, 2000. [Google Scholar]
  21. SEMARNAT. Anuario Estadístico de la Producción Forestal 2013; In Secretaría de Medio Ambiente y Recursos Naturales: Mexico City, México, 2014. [Google Scholar]
  22. Du, L.; Zhou, T.; Zou, Z.; Zhao, X.; Huang, K.; Wu, H. Mapping Forest Biomass Using Remote Sensing and National Forest Inventory in China. Forests 2014, 5, 1267–1283. [Google Scholar] [CrossRef]
  23. Zianis, D.; Mencuccini, M. On simplifying allometric analyses of forest biomass. Forest Ecol. Manag. 2004, 187, 311–332. [Google Scholar] [CrossRef]
  24. Walker, W.; Baccini, A.; Nepstad, M.; Horning, N.; Knight, D.; Braun, E.; Bausch, A. Guía de Campo para la Estimación de Biomasa y Carbono Forestal; Versión 1.0; Woods Hole Research Center: Falmouth, MA, USA, 2011. [Google Scholar]
  25. Brown, S. Measuring carbon in forests: Current status and future challenges. Environ. Pollut. 2002, 116, 363–372. [Google Scholar] [CrossRef]
  26. López-Serrano, P.; López-Sánchez, C.; Díaz-Varela, R.; Corral-Rivas, J.; Solís-Moreno, R.; Vargas-Larreta, B.; Alvarez-Gonzalez, J.G. Estimating biomass of mixed and uneven-aged forests using spectral data and a hybrid model combining regression trees and linear models. iForest 2015. [Google Scholar] [CrossRef]
  27. Hernández-Stefanoni, J.L.; Gallardo-Cruz, J.A.; Meave, J.A.; Dupuy, J.M. Combining geostatistical models and remotely sensed data to improve tropical plant richness mapping. Ecol. Indic. 2011, 11, 1046–1056. [Google Scholar] [CrossRef]
  28. Aguirre-Salado, C.A.; Treviño-Garza, E.J.; Aguirre-Calderón, O.A.; Jiménez-Pérez, J.; González-Taglel, M.A.; Valdéz-Lazalde, J.R.; Sánchez-Díaz, G.; Haapanen, R.; Aguirre-Salado, A.I.; Miranda-Aragón, L. Mapping aboveground biomass by integrating geospatial and forest inventory data through a k-nearest neighbour strategy in North Central Mexico. J. Arid Land 2014, 1, 80–96. [Google Scholar] [CrossRef]
  29. Hutchinson, M.E. Continent-wide data assimilation using thin plate smoothing splines. In Data assimilation systems; BMRC Research Report No.27; Jasper, J.D., Ed.; Bureau of Meteorology Research Centre: Melbourne, Australia, 1991; pp. 104–113. [Google Scholar]
  30. García-Arévalo, A.; González-Elizondo, S. Pináceas de Durango, 2nd ed.; Instituto de Ecología-Comisión Nacional Forestal: Durango, México, 2003. [Google Scholar]
  31. Parresol, B.R. Additivity of nonlinear biomass equations. Can. J. Forest Res. 2001, 31, 865–878. [Google Scholar] [CrossRef]
  32. Bi, H.; Long, Y.; Turner, J.; Lei, Y.; Snowdon, P.; Li, Y.; Harper, R.; Zerihun, A.; Ximenes, F. Additive prediction of aboveground biomass for Pinus radiata (D. Don) plantations. Forest Ecol. Manag. 2010, 259, 2301–2314. [Google Scholar] [CrossRef]
  33. Institute S. SAS/STAT 9.2. User´s Guide Release; SAS Institute Inc.: Cary, NC, USA, 2009. [Google Scholar]
  34. Greene, W.H. Econometric Analysis, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
  35. Corral-Rivas, J.J.; Vargas, B.; Wehenkel, C.; Aguirre, O.; Álvarez, J.; Rojo, A. Guía para el Establecimiento de Sitios de Inventario Periódico Forestal y de Suelos del Estado de Durango; Facultad de Ciencias Forestales, Universidad Juárez del Estado de Durango: Durango, México, 2009. [Google Scholar]
  36. ESPA Ordering Interface. Available online: https://espa.cr.usgs.gov (accessed on 8 May 2017).
  37. Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.-K. A Landsat Surface Reflectance Dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
  38. NASA. Landsat 7 Science Data Users Handbook; NASA: Washington, DC, USA, 2011.
  39. Rouse, J.W.; Haas, R.H.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. Remote Sens. 1974, 1, 309–313. [Google Scholar]
  40. Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
  41. Glenn, E.; Huete, A.; Nagler, P.; Nelson, S. Relationship between remotely-sensed Vegetation Indices, Canopy Attributes and Plant Physiological Processes: What Vegetation Indices Can and Cannot Tell Us About the Landscape. Sensors 2008, 8, 2136–2160. [Google Scholar] [CrossRef] [PubMed]
  42. McNab, W.H. Terrain Shape Index: Quantifying effect of minor landforms on tree height. Forest Sci. 1989, 35, 91–104. [Google Scholar]
  43. Moore, I.D.; Norton, T.W.; Williams, J.E. Modelling environmental heterogeneity in forested landscapes. J. Hydrol. 1993, 150, 717–747. [Google Scholar] [CrossRef]
  44. INEGI. Mexican Continuous Elevation 3.0 (CEM3.0). Available online: http://www.inegi.org.mx/geo/contenidos/datosrelieve/continental/descarga.aspx (accessed on 8 May 2015).
  45. Wilson, J.P.; Gallant, J.C. Digital terrain analysis. In Terrain Analysis: Principles and Applications; Wilson, J.P., Gallant, J.C., Eds.; John Wiley and Sons, Inc.: New York, NY, USA, 2000; pp. 1–26. [Google Scholar]
  46. R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
  47. Huang, D.; Knyazikhin, Y.; Wang, W.; Deering, D.W.; Stenberg, P.; Shabanov, N.; Tan, B.; Myneni, R.B. Stochastic transport theory for investigating the three-dimensional canopy structure from space measurements. Remote Sens. Environ. 2008, 11, 35–50. [Google Scholar] [CrossRef]
  48. Kuemmerle, T.; Hostert, P.; St-Louis, V.; Radeloff, V.C. Using image texture to map farmland field size: A case study in Eastern Europe. J. Land Use Sci. 2009, 4, 85–107. [Google Scholar] [CrossRef]
  49. Shevade, S.K.; Keerthi, S.S.; Bhattacharyya, C.; Murthy, K.R.K. Improvements to the SMO algorithm for SVM regression. Neural Networks. IEEE Trans. Neural Netw. 2000, 11, 1188–1193. [Google Scholar] [CrossRef] [PubMed]
  50. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  51. Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Kochf, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
  52. Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
  53. Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. SIGKDD Explor. 2009, 11, 10–18. [Google Scholar] [CrossRef]
  54. IPCC National Greenhouse Gas Inventories Programme. 2006 Guidelines for National Greenhouse Gas Inventories; Institute for Global Environmental Strategies (IGES): Hayama, Kanagawa, Japan, 2006. [Google Scholar]
  55. António, N.; Tomé, M.; Tomé, J.; Soares, P.; Fontes, L. Effect of tree, stand, and site variables on the allometry of Eucalyptus globulus tree biomass. Can. J. Forest Res. 2007, 37, 895–906. [Google Scholar] [CrossRef]
  56. Blujdea, V.N.B.; Pilli, R.; Dutca, I.; Ciuvat, L.; Abrudan, I.V. Allometric biomass equations for young broadleaved trees in plantations in Romania. Forest Ecol. Manag. 2012, 264, 172–184. [Google Scholar] [CrossRef]
  57. González-García, M.; Hevia, A.; Majada, J.; Barrio-Anta, M. Above-ground biomass estimation at tree and stand level for short rotation plantations of Eucalyptus nitens (Deane & Maiden) Maiden in Northwest Spain. Biomass Bioenergy 2013, 54, 147–157. [Google Scholar] [CrossRef]
  58. Johansson, T. Biomass equations for determining fractions of pendula and pubescent birches growing on abandoned farmland and some practical implications. Biomass Bioenergy 1999, 16, 223–238. [Google Scholar] [CrossRef]
  59. Porté, A.; Trichet, P.; Bert, D.; Loustau, D. Allometric relationships for branch and tree woody biomass of Maritime pine (Pinus pinaster Ait.). Forest Ecol. Manag. 2002, 158, 71–83. [Google Scholar] [CrossRef]
  60. Jenkins, J.; Chojnacky, D.S.; Birdsey, R. National scale biomass estimators for United States tree species. Forest Sci. 2003, 49, 12–35. [Google Scholar]
  61. Reed, D.; Tomé, M. Total aboveground biomass and net dry matter accumulation by plant component in young Eucalyptus globulus in response to irrigation. Forest Ecol. Manag. 1998, 103, 21–32. [Google Scholar] [CrossRef]
  62. Bartelink, H.H. Allometric relationships on biomass and needle area of Douglas-fir. Forest Ecol. Manag. 1996, 86, 193–203. [Google Scholar] [CrossRef]
  63. Menéndez-Miguélez, M.; Canga, E.; Barrio-Anta, M.; Majada, J.; Álvarez-Álvarez, P. A three level system for estimating the biomass of Castanea sativa Mill. coppice stands in north-west Spain. Forest Ecol. Manag. 2013, 291, 417–426. [Google Scholar] [CrossRef]
  64. Lambert, M.C.; Ung, C.H.; Raulier, F. Canadian national tree aboveground biomass equations. Can. J. Forest Res. 2005, 35, 1996–2018. [Google Scholar] [CrossRef]
  65. Bi, H.; Turner, J.; Lambert, M. Additive biomass equations for native eucalypt forest trees of temperate Australia. Trees 2004, 18, 467–479. [Google Scholar] [CrossRef]
  66. Zhao, D.; Kane, M.; Markewitz, D.; Teskey, R.; Clutter, M. Additive tree biomass equations for midrotation loblolly pine plantations. Forest Sci. 2015, 61, 613–623. [Google Scholar] [CrossRef]
  67. Feldpausch, T.R.; Lloyd, J.; Lewis, S.L.; Brienen, R.J.; Gloor, M.; Monteagudo Mendoza, A.; Lopez-Gonzalez, G.; Banin, L.; Abu Salim, K.; Affum-Baffoe, K.; et al. Tree height integrated into pantropical forest biomass estimates. Biogeosciences 2012, 9, 3381–3403. [Google Scholar] [CrossRef] [Green Version]
  68. Li, H.; Zhao, P. Improving the accuracy of tree-level aboveground biomass equations with height classification at a large regional scale. Forest Ecol. Manag. 2013, 289, 153–163. [Google Scholar] [CrossRef]
  69. Ter-Mikaelian, M.; Parker, W. Estimating biomass of white spruce seedlings with vertical photo imagery. New Forests 2000, 20, 145–162. [Google Scholar] [CrossRef]
  70. Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
  71. Schmidt, A.; Poulain, M.; Klein, D.; Krause, K.; Peña-Rojas, K.; Schmidt, H.; Schulte, A. Allometric above-belowground biomass equations for Nothofagus pumilio (Poepp. & Endl.) natural regeneration in the Chilean Patagonia. Ann. Forest Sci. 2009, 66, 513. [Google Scholar] [CrossRef]
  72. Zeng, W.; Tang, S.; Huag, G.; Zhang, M. Population classification and sample structure on modeling of single tree biomass equations for national biomass estimation in China. Forest Resour. Manag. 2010, 3, 16–23. [Google Scholar]
  73. Parresol, B.R. Assessing tree and stand biomass: A Review with examples and critical comparisons. Forest Sci. 1999, 45, 573–593. [Google Scholar]
  74. Carvalho, J.P.; Parresol, B.R. Additivity in tree biomass components of Pyrenean oak (Quercus pyrenaica Willd.). Forest Ecol. Manag. 2003, 179, 269–276. [Google Scholar] [CrossRef]
  75. Lima, A.; Suwa, R.; de Mello Ribeiro, G.; Kajimoto, T.; dos Santos, J.; da Silva, R.P.; de Souza, C.A.S.; de Barros, P.C.; Noguchi, H.; Ishizuka, M.; et al. Allometric models for estimating above- and below-ground biomass in Amazonian forests at São Gabriel da Cachoeira in the upper Rio Negro, Brazil. Forest Ecol. Manag. 2012, 277, 163–172. [Google Scholar] [CrossRef]
  76. Hunter, M.O.; Keller, M.; Victoria, D.; Morton, D.C. Tree height and tropical forest biomass estimation. Biogeosciences 2013, 10, 8385–8399. [Google Scholar] [CrossRef]
  77. Fonseca, W.; Rey, B.J.M.; Alice, F.E. Carbon accumulation in the biomass and soil of different aged secondary forests in the humid tropics of Costa Rica. Forest Ecol. Manag. 2011, 262, 1400–1408. [Google Scholar] [CrossRef]
  78. Redondo-Brenes, A.; Montagnini, F. Growth, productivity, aboveground biomass, and carbon sequestration of pure and mixed native tree plantations in the Caribbean lowlands of Costa Rica. Forest Ecol. Manag. 2006, 232, 168–178. [Google Scholar] [CrossRef]
  79. Correia, A.C.; Tomé, M.; Pacheco, C.A.; Faias, S.; Días, A.C.; Freire, J.; Carvalho, P.O.; Pereira, J.S. Biomass allometry and carbon factors for a Mediterranean pine (Pinus pinea L.) in Portugal. Forest Syst. 2010, 19, 418–433. [Google Scholar] [CrossRef]
  80. Pajtík, J.; Konôpka, B.; Lukac, M. Biomass functions and expansion factors in young Norway spruce (Picea abies [L.] Karst) trees. Forest Ecol. Manag. 2008, 256, 1096–1103. [Google Scholar] [CrossRef]
  81. Aquino-Ramírez, M.; Velázquez-Martínez, A.; Castellanos-Bolaños, J.F.; De los Santos-Posadas, H.M.; Etchevers-Barra, J.D. Partición de la biomasa aérea en tres especies arbóreas tropicales. Agrociencia 2015, 49, 299–314. [Google Scholar]
  82. Lu, D.; Chen, Q.; Wang, G.; Moran, E.; Batistella, M.; Zhang, M.; Vaglio Laurin, G.; Saah, D. Aboveground forest biomass estimation with Landsat and LiDAR data and uncertainty analysis of the estimates. Int. J. Forest Res. 2012, 2012, 1–16. [Google Scholar] [CrossRef]
  83. Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2014, 1–43. [Google Scholar] [CrossRef]
  84. López-Serrano, P.M.; López-Sánchez, C.A.; Álvarez-González, J.G.; García-Gutiérrez, J. A Comparison of Machine Learning Techniques Applied to Landsat-5 TM Spectral Data for Biomass Estimation. Can. J. Remote Sens. 2016, 42, 690–705. [Google Scholar] [CrossRef]
  85. López-Serrano, P.M.; Corral-Rivas, J.J.; Díaz-Varela, R.A.; Álvarez-González, J.G.; López-Sánchez, C.A. Evaluation of radiometric and atmospheric correction algorithms for aboveground forest biomass estimation using Landsat 5 TM data. Remote Sens. 2016, 8, 369. [Google Scholar] [CrossRef]
  86. López-Serrano, P.M.; López Sánchez, C.A.; Solís-Moreno, R.; Corral-Rivas, J.J. Geospatial Estimation of above Ground Forest Biomass in the Sierra Madre Occidental in the State of Durango, Mexico. Forests 2016, 7, 70. [Google Scholar] [CrossRef]
  87. López-Sánchez, C.A.; García-Ramírez, P.; Resl, R.; Hernández-Díaz, J.C.; López-Serrano, P.M.; Wehenkel, C. Modelling dasometric attributes of mixed and uneven-aged forests using Landsat-8 OLI spectral data in the Sierra Madre Occidental, Mexico. iForest 2017, 10, 288–295. [Google Scholar] [CrossRef]
  88. García-Gutiérrez, J.; Martínez-Álvarez, F.; Troncoso, A.; Riquelme, J.C. A comparison of machine learning regression techniques for LiDAR-derived estimation of forest variables. Neurocomputing 2015, 167, 24–31. [Google Scholar] [CrossRef]
  89. Guo, Z.D.; Hu, H.F.; Pan, Y.D.; Birdsey, R.A.; Fang, J.Y. Increasing biomass carbon stocks in trees outside forests in China over the last three decades. Biogeosciences 2014, 11, 4115–4122. [Google Scholar] [CrossRef]
  90. Tian, X.; Li, Z.; Su, Z.; Chen, E.; van der Tol, C.; Li, X.; Guo, Y.; Li, L.; Ling, F. Estimating montane forest above-ground biomass in the upper reaches of the Heihe River Basin using Landsat-TM data. Int. J. Remote Sens. 2014, 35, 7339–7362. [Google Scholar] [CrossRef]
Forests 08 00269 g001 550
Figure 1. Location of the study area. Triangles indicate the location of the 429 permanent sampling plots.
Figure 1. Location of the study area. Triangles indicate the location of the 429 permanent sampling plots.
Forests 08 00269 g001
Forests 08 00269 g002 550
Figure 2. Relationships between the total height (m) and the tree biomass components stem wood (Ww), stem bark (Wb), branches (Wbr) and foliage (Wf) (kg tree−1).
Figure 2. Relationships between the total height (m) and the tree biomass components stem wood (Ww), stem bark (Wb), branches (Wbr) and foliage (Wf) (kg tree−1).
Forests 08 00269 g002
Forests 08 00269 g003 550
Figure 3. Estimated relative contributions of the biomass components to total tree above-ground biomass (AGB) for pine and oak species in Durango state, Mexico.
Figure 3. Estimated relative contributions of the biomass components to total tree above-ground biomass (AGB) for pine and oak species in Durango state, Mexico.
Forests 08 00269 g003
Forests 08 00269 g004 550
Figure 4. Tree-level biomass allocation patterns of all pine and oak species as a function of individual tree size (d), estimated by the proposed biomass equation systems.
Figure 4. Tree-level biomass allocation patterns of all pine and oak species as a function of individual tree size (d), estimated by the proposed biomass equation systems.
Forests 08 00269 g004
Forests 08 00269 g005 550
Figure 5. Spatial distribution of total above-ground biomass (AGB) (a) and carbon content (b) in the Durango, Mexico forest study area estimated by the Support Vector Machine for Regression (SVM) approach.
Figure 5. Spatial distribution of total above-ground biomass (AGB) (a) and carbon content (b) in the Durango, Mexico forest study area estimated by the Support Vector Machine for Regression (SVM) approach.
Forests 08 00269 g005
Table
Table 1. Summary statistics of the felled trees and the main above-ground biomass components used to develop the biomass equations in the study.
Table 1. Summary statistics of the felled trees and the main above-ground biomass components used to develop the biomass equations in the study.
Tree Species (n)ValueVariableBiomass Component
dhWwWbWbrWfWt
Pinus cooperi (103)Max52.328.01586.5101.0317.828.81833.8
Min5.54.22.30.31.50.24.1
Mean28.917.1397.530.697.212.5537.8
SD10.95.0346.023.781.47.4444.3
P. durangensis (130)Max44.529.81027.589.2312.038.41319.0
Min8.76.98.91.33.00.414.4
Mean25.916.6269.237.2106.611.8424.8
SD8.54.4210.923.467.58.2294.5
P. engelmannii (89)Max51.827.81825.044.3308.330.42024.7
Min6.53.86.00.30.50.26.9
Mean27.715.0507.518.5107.011.8644.7
SD9.45.4421.711.558.96.9479.5
P. leiophylla (84)Max55.329.21129.889.7392.021.81614.6
Min8.45.45.70.51.10.47.7
Mean29.616.6329.523.2149.67.4509.7
SD12.05.4278.620.8111.35.7402.6
P. herrerae (97)Max46.431.01056.972.8139.431.81200.4
Min5.05.24.00.30.80.45.4
Mean27.816.3354.320.349.413.6437.6
SD9.24.9273.013.934.08.6319.2
P. teocote (81)Max45.024.7789.347.9161.334.8975.0
Min10.04.53.20.31.10.65.2
Mean29.615.6288.916.650.512.2368.2
SD9.44.0207.612.238.37.9261.7
P. lumholtzii (35)Max42.024.9832.237.686.937.0981.5
Min5.03.62.90.20.40.54.0
Mean22.414.7236.310.732.011.7290.7
SD8.64.3209.78.527.110.2252.7
P. strobiformis (98)Max49.026.61240.137.6211.340.41501.1
Min5.06.31.80.31.50.44.0
Mean27.116.2292.917.973.117.2401.3
SD9.84.8277.29.856.211.2354.4
P. oocarpa (37)Max35.718.7448.949.5173.138.0647.5
Min7.53.26.00.63.02.011.5
Mean21.612.9153.419.653.416.8243.3
SD6.33.6109.612.442.09.8167.3
P. douglasiana (30)Max39.025.6718.460.8124.231.2884.1
Min8.95.62.70.51.10.34.6
Mean25.017.5261.921.840.512.4336.6
SD7.24.4174.915.229.59.2224.9
P. michoacana (32)Max42.124.7866.756.2137.239.81073.5
Min12.913.548.84.012.94.269.9
Mean31.320.3416.627.464.621.4530.0
SD8.23.0232.513.536.69.2285.6
Juniperus deppeana (48)Max43.721.5357.021.856.327.5456.3
Min10.04.53.70.51.20.86.2
Mean32.911.4183.711.425.813.7234.7
SD7.93.192.74.815.86.9117.7
Arbutus bicolor (49)Max44.82.5236.19.6231.114.5375.6
Min7.92.43.80.23.10.27.2
Mean22.88.983.33.448.55.4140.6
SD7.82.953.92.446.83.797.6
Quercus sideroxyla (123)Max57.024.81018.0276.3308.329.61559.0
Min11.06.312.33.30.40.416.4
Mean30.714.6290.987.375.68.5462.2
SD9.73.7213.490.762.26.7331.9
Q. rugosa (61)Max41.320.2456.1129.8132.019.4648.6
Min9.33.34.21.63.21.514.3
Mean22.511.2107.240.651.119.2218.0
SD8.13.795.831.433.413.0166.2
Q. durifolia (131)Max45.522.1930.9118.4421.963.91526.3
Min7.05.46.41.32.10.310.2
Mean27.212.4344.432.5125.625.1527.6
SD8.83.5226.626.9109.618.3371.7
Q. crassifolia (108)Max43.118.8533.988.3274.635.5865.0
Min8.56.014.31.311.01.033.4
Mean25.511.2218.525.693.314.2351.5
SD7.72.6134.718.762.08.2212.5
where n = number of trees, d = diameter at breast height (cm), h = total height (m), Ww = stem wood biomass (kg tree−1), Wb = stem bark biomass (kg tree−1), Wbr = wood plus bark biomass of branches (kg tree−1), Wf = foliage (leaves/needles) biomass (kg tree−1), Wt = total above-ground biomass (Ww + Wb + Wbr + Wf) (kg tree−1).
Table
Table 2. Estimated parameters and goodness of fit statistics for the biomass equations for temperate forest species in Durango state, Mexico.
Table 2. Estimated parameters and goodness of fit statistics for the biomass equations for temperate forest species in Durango state, Mexico.
Tree Biomass Component EquationCross-ValidationTree Biomass Component EquationCross-Validation
R2RMSER2RMSE
Pinus cooperiP. douglasiana and P. michoacana
W w   =   0 . 031126 d 2.09355 h 0.768845 0.9741.22 W w   =   0 . 11997 d 2.34448 0.8968.85
W b   =   0 . 011361 d 1.676006 h 0.74627 0.8110.43 W b   =   0 . 03126 d 1.978201 0.776.94
W br   =   0 . 007965 d 1.599044 h 1.347388 0.8927.06 W br   =   0 . 014982 d 2.40887 0.9011.25
W f   =   0 . 049925 d 1.122846 h 0.600293 0.743.79 W f   =   0 . 01168 d 2.148631 0.834.24
W t   =   Σ W i 0.9487.21 W t   =   Σ W i 0.9176.01
P. durangensisJuniperus depeanna
W w   =   0 . 01204 d 1.76074 h 1.45047 0.9639.77 W w   =   0 . 01289 d 2 h 0.9128.98
W b   =   0 . 01706 d 1.37067 h 1.10922 0.878.44 W b   =   0 . 000772 d 2 h 0.573.15
W br   =   0 . 14589 d 1.64608 h 0.41109 0.7136.74 W br   =   0 . 00204 d 2 h 0.815.87
W f   =   0 . 00301 d 1.50863 h 1.15013 0.833.38 W f   =   0 . 00098 d 2 h 0.673.92
W t   =   Σ W i 0.9656.05 W t   =   Σ W i 0.9037.00
P. engelmanniiArbutus bicolor
W w   =   0 . 09798 d 1.67370 h 1.02867 0.91127.64 W w   =   0 . 06438 d 1.66448 h 0.86489 0.9315.11
W b   =   0 . 037974 d 1.11488 h 0.88389 0.981.64 W b   =   0 . 00328 d 1.51833 h 0.95083 0.870.85
W br   =   1 . 39092 d 1.25795 h 0.05199 0.5937.66 W br   =   0 . 02125 d 1.81216 h 0.8198 0.956.99
W f   =   0 . 069316 d 1.24804 h 0.34853 0.703.77 W f   =   0 . 00698 d 1.50325 h 0.84794 0.791.72
W t   =   Σ W i 0.92140.91 W t   =   Σ W i 0.9522.81
P. leiophyllaQuercus sideroxyla
W w   =   0 . 015582 d 2 h 0.9468.35 W w   =   0 . 033462 d 1.739234 h 1.111268 0.9065.75
W b   =   0 . 001074 d 2 h 0.896.92 W b   =   0 . 03022 d 1.66927 h 0.80238 0.7927.87
W br   =   0 . 007269 d 2 h 0.6367.38 W br   =   0 . 005154 d 1.92033 h 1.06618 0.8027.31
W f   =   0 . 000343 d 2 h 0.812.53 W f   =   0 . 00092 d 1.57684 h 1.34236 0.743.45
W t   =   Σ W i 0.92110.21 W t   =   Σ W i 0.9296.83
P. herreraeQ. rugosa
W w   =   0 . 06741 d 2.520356 0.82114.23 W w   =   0 . 01988 d 2.28684 h 0.52175 0.9029.42
W b   =   0 . 02468 d 1.98837 0.727.37 W b   =   0 . 05621 d 2.0764 0.7715.14
W br   =   0 . 05085 d 2.03574 0.7218.01 W br   =   0 . 11276 d 1.52164 h 0.53343 0.8612.56
W f   =   0 . 05437 d 1.64335 0.605.41 W f   =   0 . 0377 d 1.42193 h 0.70675 0.845.21
W t   =   Σ W i 0.85124.12 W t   =   Σ W i 0.9441.8
P. teocoteQ. durifolia
W w   =   0 . 04428 d 1.8953 h 0.84674 0.9258.5 W w   =   0 . 1254 d 1.7402 h 0.8114 0.9455.64
W b   =   0 . 00341 d 1.96215 h 0.66178 0.939.34 W b   =   0 . 00235 d 2.30073 h 0.68619 0.879.53
W br   =   0 . 0051 d 1.78757 h 1.12341 0.933.02 W br   =   0 . 00355 d 2.66464 h 0.56009 0.8935.50
W f   =   0 . 03041 d 1.78361 0.7316.67 W f   =   0 . 0073 d 2.05034 h 0.48685 0.866.87
W t   =   Σ W i 0.9576.11 W t   =   Σ W i 0.9580.97
P. lumholtziiQ. crassifolia
W w   =   0 . 078527 d 2.5043 0.9165.02 W w   =   0 . 02542 d 2 h 0.8356.45
W b   =   0 . 022809 d 1.93859 0.7616.98 W b   =   0 . 00305 d 2 h 0.818.12
W br   =   0 . 03461 d 2.1666 0.834.21 W br   =   0 . 01113 d 2 h 0.8225.96
W f   =   0 . 011642 d 2.16799 0.824.14 W f   =   0 . 00165 d 2 h 0.644.92
W t   =   Σ W i 0.9083.32 W t   =   Σ W i 0.9164.58
P. strobiformisAll pine species
W w   =   0 . 00716 d 2.02253 h 1.30938 0.9088.01 W w   =   0 . 0291 d 1.74165 h 1.16614 0.9272.12
W b   =   0 . 03088 d 1.10021 h 1.09925 0.886.34 W b   =   0 . 02029 d 1.33299 h 0.92887 0.6311.65
W br   =   0 . 01613 d 1.90578 h 0.70112 0.9315.24 W br   =   0 . 02508 d 1.83773 h 0.54626 0.6131.05
W f   =   0 . 03886 d 1.53515 h 0.31776 0.725.55 W f   =   0 . 05227 d 1.28231 h 0.43275 0.525.98
W t   =   Σ W i 0.9393.02 W t   =   Σ W i 0.9383.04
P. oocarpaAll oak species
W w   =   0 . 01753 d 1.8261 h 1.28397 0.9327.12 W w   =   0 . 11618 d 1.77395 h 0.68708 0.7894.25
W b   =   0 . 02898 d 2.08978 0.874.44 W b   =   0 . 00827 d 2.54589 0.6527.68
W br   =   0 . 00948 d 2.7493 0.8715.32 W br   =   0 . 0502 d 1.97638 h 0.34229 0.5753.64
W f   =   0 . 04163 d 1.93601 0.833.96 W f   =   0 . 08234 d 1.59396 0.2911.95
W t   =   Σ W i 0.9439.66 W t   =   Σ W i 0.82134.12
n = number of trees, d = diameter at breast height (cm), h = total height (m), Ww = stem wood biomass (kg tree−1), Wb = stem bark biomass (kg tree−1), Wbr = wood plus bark biomass of branches (kg tree−1), Wf = foliage (leaves/needles) biomass (kg tree−1), Wt = total above-ground biomass (Ww + Wb + Wbr + Wf) (kg tree−1), RMSE, root mean square error.
Table
Table 3. Specific mean carbon contents of the main tree components of pine and oak species in the study (standard deviation is given in brackets).
Table 3. Specific mean carbon contents of the main tree components of pine and oak species in the study (standard deviation is given in brackets).
SpeciesCarbon Proportion
WoodBarkLeaves/NeedlesTotal (s.d)
Pinus cooperi0.4850.5110.4710.489 (0.0020)
Pinus durangensis0.4890.5310.4870.505 (0.0030)
Pinus engelmannii0.4970.5310.4940.507 (0.0020)
Pinus leiophylla0.4950.5400.5150.516 (0.0023)
Pinus herrerae0.4790.5240.4800.512 (0.0025)
Pinus teocote0.4840.5390.5120.512 (0.0028)
Pinus lumholtzii0.4850.5320.4920.501 (0.0027)
Pinus strobiformis0.4940.5330.4920.506 (0.0023)
Pinus oocarpa0.4690.5280.4720.490 (0.0033)
Pinus douglasiana0.4830.5250.4940.500 (0.0021)
Pinus michoacana0.480.5080.4860.491 (0.0015)
Quercus sideroxyla0.4620.4620.4770.467 (0.0009)
Quercus rugosa0.4550.4660.4590.438 (0.0034)
Quercus durifolia0.4630.4280.4510.448 (0.0018)
Quercus crassifolia0.4600.4160.4590.445 (0.0025)
Juniperus depeanna0.5270.4380.4960.487 (0.0045)
Arbutus bicolor0.4670.3780.4790.441 (0.0055)
where Total: total carbon content, s.d = standard deviation.
Table
Table 4. Summary of the goodness-of-fit statistics for each machine learning method using 10-fold cross-validations for AGB and carbon content. The best results are highlighted in bold type.
Table 4. Summary of the goodness-of-fit statistics for each machine learning method using 10-fold cross-validations for AGB and carbon content. The best results are highlighted in bold type.
AGBCarbon
MLRDR-DFSVMMLRRD-RFSVM
R20.4650.4880.5120.4630.4910.510
RMSE51.04449.97149.77125.28224.63024.727
where MLR = Multiple Linear Regression, DR-DF = Regression by Discretization based on Random Forest, SVM = Support Vector Machine for Regression.

Share and Cite

MDPI and ACS Style

Vargas-Larreta, B.; López-Sánchez, C.A.; Corral-Rivas, J.J.; López-Martínez, J.O.; Aguirre-Calderón, C.G.; Álvarez-González, J.G. Allometric Equations for Estimating Biomass and Carbon Stocks in the Temperate Forests of North-Western Mexico. Forests 2017, 8, 269. https://doi.org/10.3390/f8080269

AMA Style

Vargas-Larreta B, López-Sánchez CA, Corral-Rivas JJ, López-Martínez JO, Aguirre-Calderón CG, Álvarez-González JG. Allometric Equations for Estimating Biomass and Carbon Stocks in the Temperate Forests of North-Western Mexico. Forests. 2017; 8(8):269. https://doi.org/10.3390/f8080269

Chicago/Turabian Style

Vargas-Larreta, Benedicto, Carlos Antonio López-Sánchez, José Javier Corral-Rivas, Jorge Omar López-Martínez, Cristóbal Gerardo Aguirre-Calderón, and Juan Gabriel Álvarez-González. 2017. "Allometric Equations for Estimating Biomass and Carbon Stocks in the Temperate Forests of North-Western Mexico" Forests 8, no. 8: 269. https://doi.org/10.3390/f8080269

APA Style

Vargas-Larreta, B., López-Sánchez, C. A., Corral-Rivas, J. J., López-Martínez, J. O., Aguirre-Calderón, C. G., & Álvarez-González, J. G. (2017). Allometric Equations for Estimating Biomass and Carbon Stocks in the Temperate Forests of North-Western Mexico. Forests, 8(8), 269. https://doi.org/10.3390/f8080269

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop