1. Introduction
The area of planted forests worldwide has been steadily growing, with an estimated 6.95% of total global forested area being plantations in 2010 [
1]. Tropical regions may be experiencing particularly rapid rates of plantation expansion [
2]. For example, the area of pine plantations in Brazil has dramatically risen in the last few decades to increase pulp and paper production. Currently ~20% of the total reforested area of Brazil is comprised of pine forest plantations [
2].
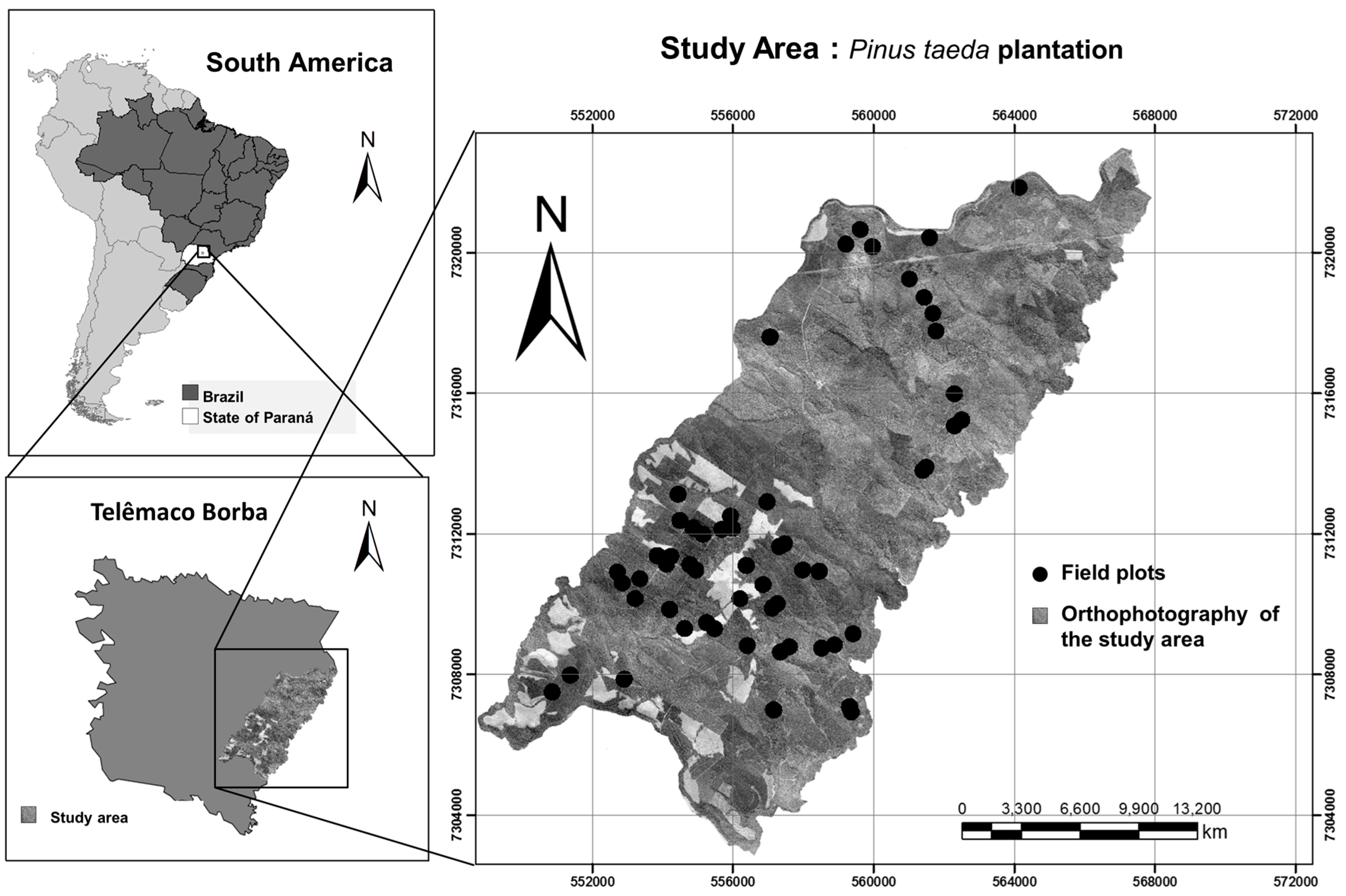
Most of the pine plantations are concentrated in South Brazil, with 34.1% and 42.4% of the total reforested area located in Paraná and Santa Catarina states [
2].
Pinus taeda L., also known as loblolly pine, is the most planted forest specie in these regions. It has high economic importance due to its high volumetric increment in the colder regions of the southern Brazil [
3]. It has fast growing rates presenting increments up to 50 m
3·ha
−1·year
−1 [
2]. Moreover,
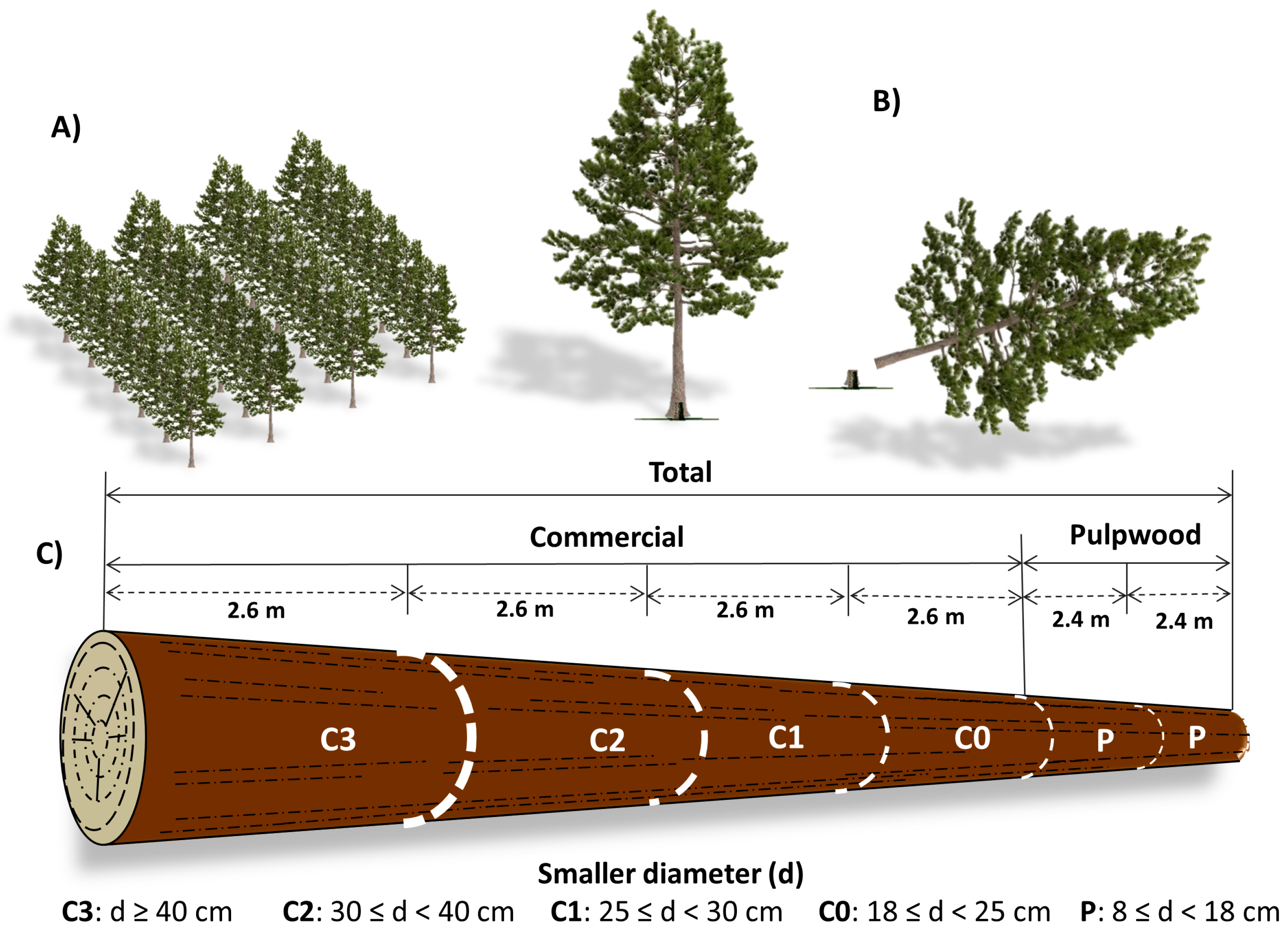
P. taeda is commonly managed for production of multiple types of wood such as stem total, saw logs, pulpwood and small-diameter logs and branches, which are used for energy. Saw logs and pulpwood can be further divided into different assortments that differ in size and therefore in economic value [
3].
Forest inventory in
P. taeda is currently based on field measurements and typically conducted annually to monitor forest growth in Brazil, allowing managers to identify problematic conditions during initial growth stages, and determine optimal harvest time [
4]. While field measurements are considered the most accurate approach for monitoring industrial forest plantations, measuring stem total and assortment volumes annually via traditional methods is an extremely time consuming and labor-intensive task, especially in large plantations where a huge number of plots need to be measured to characterize the variation [
5]. Hence, to improve plantation management there is a need to develop and implement accurate, repeatable, and economical remote sensing based methods that provide synoptic coverage at high spatial resolution.
Over the past few decades, lidar remote sensing has been established as one of the promising and primary tools for broad-scale analysis of forest systems. Lidar data can be used to characterize local to regional spatial extents with high enough resolution to quantify the three-dimensional structure of the forest with the support of efficiently collected field data and several statistical methods (e.g., [
6,
7,
8,
9,
10]). Lidar can be used to produce highly accurate retrievals of tree density, stem total and assortment volumes, basal area, aboveground carbon, and leaf area index, and thereby can be an effective way to predict and map forest attributes at unsampled locations (e.g., [
11,
12,
13,
14,
15,
16]). To parlay these attributes into improved forest management practices for wood and pulp production, it is often necessary to predict stem total and assortment volumes of pine plantations in operational and experimental scenarios, as these scenarios often include thinning cruises, mid-rotation cruises, genetic trials, and silviculture research tests [
17].
Current predictive modeling methods include parametric (e.g., multiple linear regression) and non-parametric (e.g., Random Forest) approaches (e.g., [
6,
7,
18]). Among the machine learning algorithms, the Random Forest (RF) modeling approach has gained popularity in estimating forest attributes from lidar data due to its flexibility and ability to maintain nonlinear dependences compared to parametric algorithms [
19]. The RF can be viewed as an improved version of classification and regression tree (CART) methods; data and variables can be randomly sampled by RF in an iterative bagging bootstrap procedure to generate a “forest” of regression trees [
20]. Also, incorporation of multiple decision trees and internal cross-validation has improved results, enhanced ease of use and reduced issues regarding over-fitting while performing this modeling approach [
21,
22]. In case of regression-type problems, RF acts as an arbitrary number of simple trees whose responses are averaged to obtain an estimate of dependent variables [
23]. Diversification of sample trees is primarily done in two ways, either through a balancing methodology where equal numbers of samples are drawn from minority classes and majority classes, or by assigning a higher weight (i.e., heavier penalty) on misclassified minority class and taking the majority voting of individual classification trees [
24]. As RF does not require any assumptions about the relationships between explanatory and response variables, they are considered well suited for analyzing complex non-linear and possibly hierarchical interactions in large datasets [
25]. In forest inventory, RF has been used for predicting and mapping forest attribute at the stand (e.g., [
19]) and individual tree levels [
23], in addition to disturbance evaluation (e.g., [
26]), mapping invasive plant species (e.g., [
27]), and vegetation classification (e.g., [
21]). Despite of the above-mentioned studies, to our knowledge, lidar and RF have been not yet been combined for predicting and mapping stem total, saw log and pulpwood volumes in industrial
P. taeda forest plantations at stand level.
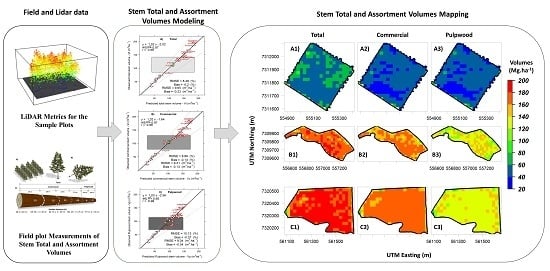
Timely monitoring of stem total and assortment volumes in P. taeda plantations with lidar data and RF would allow managers to determine the optimal time for harvest or other treatment activities to maximize economic return. Therefore, the development of robust frameworks for modeling and mapping stem total and assortment volumes at plot and stand levels is still needed to increase the efficiency in monitoring and managing wood and pulp productions in forest plantations. Moreover, efficient frameworks also play important role in helping lidar technology move from research to operational modes, especially in industrial forest plantation settings where lidar applications are relatively new. The aims of this study were to: (i) present a robust and efficient framework for modeling, predicting and mapping stem total volume (Vt), saw logs (in this study mentioned as commercial) volume (Vc) and pulpwood volume (Vp) in a P. taeda plantation in southern Brazil using airborne lidar data; (ii) evaluate the use of the RF machine learning algorithm for modeling stem total and assortment volumes; and (iii) generate maps representing the spatial distribution of Vt, Vc and Vp in differently aged plantations of P. taeda. This investigation was based on the hypothesis that lidar technology and Random Forest analysis can facilitate accurate and precise inferences of forest volumes in P. taeda plantations in southern Brazil.
4. Discussion
Detailed information on stem total and assortments volumes is required in industrial forest plantations to achieve production efficiency. For instance, incomplete or inaccurate forest information adds to the expense and challenge of forest operations (e.g., [
42]). Moreover, improving forest plantation productivity and efficiency are important for reducing harvest pressure on natural forests. To achieve efficiency gains in operational forest management, a wide range of forest inventory attributes are required to be measured accurately at high spatial resolution and landscape to regional extents [
34,
43]. More detailed inventory information can allow forest owners to make better decisions concerning the timing of timber sales, and allow forest companies to optimize their wood supply chain from forest to factory [
44]. In this study, we present a framework for predicting and mapping total, commercial and pulpwood volumes in industrial
P. taeda forest plantations using airborne lidar data and RF. While there have been previous studies exploring the use of lidar and non-parametric machine learning algorithm for forest inventory modeling (e.g., [
19,
34,
40,
45,
46,
47,
48]), no studies yet have demonstrated the potential of lidar and RF combined for predicting and mapping commercial and pulpwood volumes in industrial pine forest plantations.
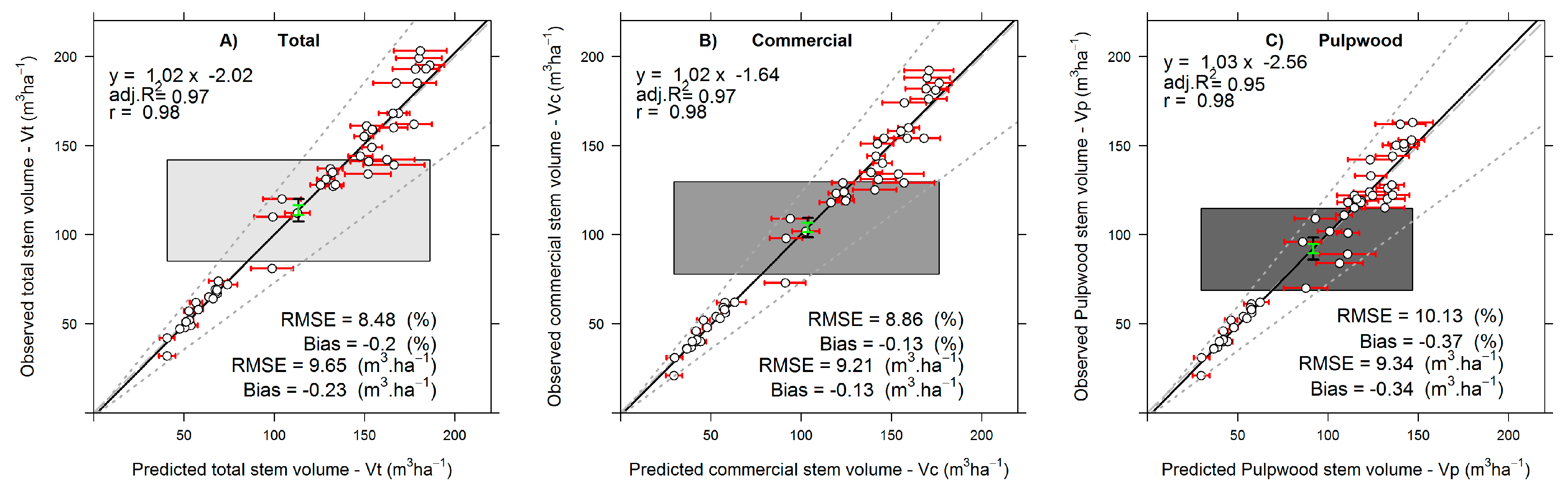
Stem total and assortment volumes are directly related to the supply of fiber to pulp and paper companies. Herein, the accuracy of lidar for retrieving Vt, Vc and Vp using RF models was clearly demonstrated through achieving a relative RMSE and Bias less than <15% both for modeling and for validation. As we are predicting forest attributes at a homogenous and single layered forest structure, our measures of precision and accuracy were similar to or higher than those who used lidar data for predicting stem volume through a RF framework in other forest types [
15,
16,
42,
44,
49]. Among prior studies, RF has generally showed better performance compared to other statistical approaches, such as multiple linear regression, boosting trees regression and support vector regression [
50,
51,
52,
53]. Lidar-derived stem total and saw log volumes and their estimation accuracies have previously been reported at the forest stand level (e.g., [
15,
16,
42,
54,
55]). For instance, in Eastern Finland in a typical Finnish southern boreal managed forest area, two studies used lidar data for estimating species-specific diameter distributions and saw log volumes [
15,
16]. Two years later, in Southern Wisconsin, USA, lidar data were used for predicting not only saw log volume, but also pulpwood volume [
55]; the models produced
R2 of ~0.65 for estimating both saw log and pulpwood volumes. While those authors have showed the great potential of lidar in retrieving assortment volumes, this specific application is still relatively novel and further studies, such as presented herein, still need to be carried out.
In this study, we showed that lidar measurements could be used as input data to predict and map stem total and assortment volumes through a RF framework. High levels of accuracy were found when predicting Vt, Vc and Vp volumes across variable stand ages of
P. taeda using only H99TH and HSKEW as predictor variables. Lidar-derived H99TH represents the top of the canopy (height at 99th percentile) and HSKEW is a measure of the asymmetry of height distribution, which is associated with the age of the stands because older trees are taller and cause a more positively skewed distribution. Skewness and height percentile variables are logical selections for distinguishing between different volume levels based on distributional shapes and height frequencies [
56]. In particular, these variables can explain changes in the volume distribution [
5], thus providing a solid justification for inclusion in the predictive model. Our results suggest that models based on variables describing the height of the canopy and the symmetry of the distribution of the returns are capable of predicting stem total and assortment volumes across different tree ages in industrial
P. taeda forest plantations. Height percentile lidar metrics, such as H99TH, and height distributional metrics, such as HSKEW, have been shown to be powerful metrics for modeling and predicting forest attributes (e.g., [
5,
6,
7,
33,
34,
48]).
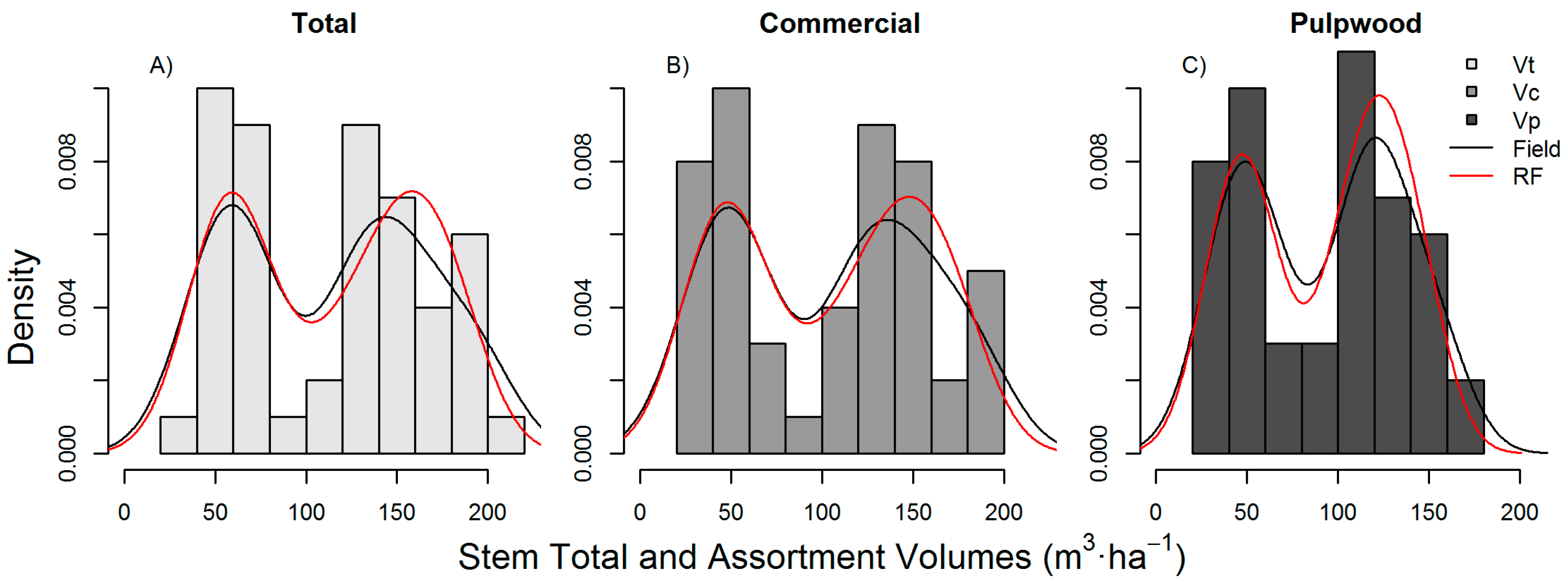
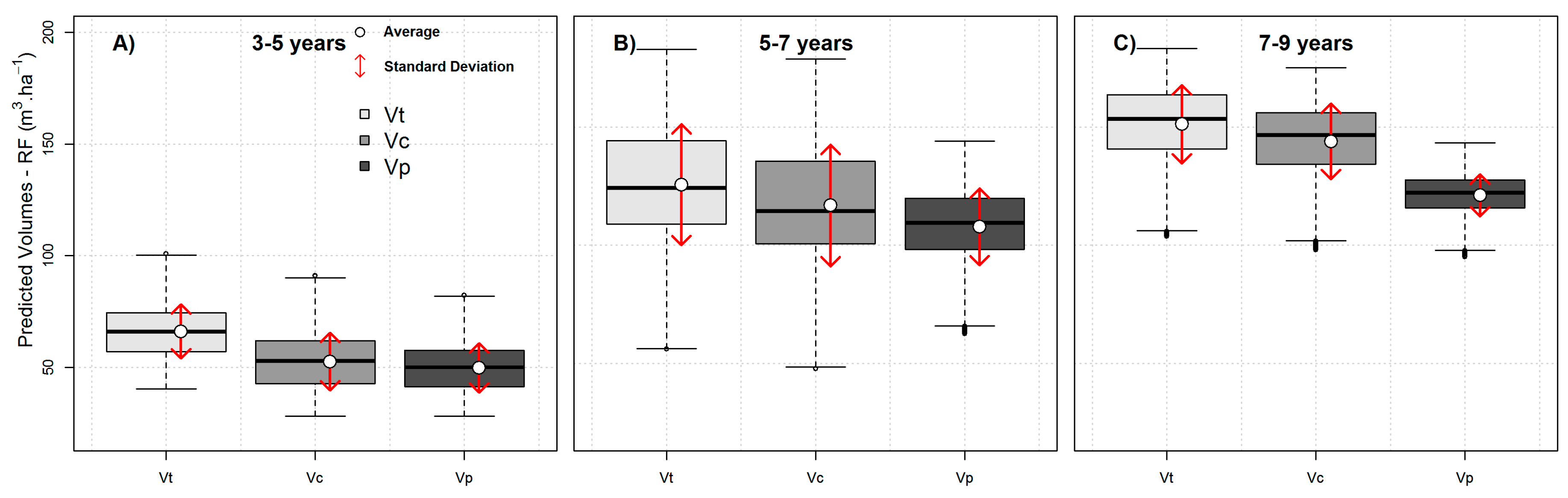
A disadvantage of using the RF framework presented here is that RF models do not extrapolate predictions beyond the trained data, and consequently, as found herein, reduce the variance compared to the observations (
Figure 5). However, an important advantage of non-parametric approaches, such as RF, is that they can model non-linear, complex relationships between the dependent and the independent variables more efficiently than parametric approaches [
46]. Furthermore, RF is insensitive to data skew, robust to a high number of variable inputs, and its implementation does not require pre-stratification by forest type [
20,
34,
46]. From an overall statistical perspective, the predicted and observed volumes were equivalent, although our RF model validations showed a systematic tendency to overestimate small values and underestimate high values. The same was found in previous studies (e.g., [
40,
57]). According to one study [
57], a possible cause might be that because the RF model estimates values by averaging the predictions of many decision trees, it might tend to underestimate when the predicted value is close to the maximum value of the training data. Similarly, when the estimated value is close to the minimum value of training data it might tend to overestimate. Other possible causes might be that we have a relatively small number of field plots, especially in the young and older stands.
Traditional forest inventory approaches are not effective in terms of costing and mobility especially in
P. taeda forest plantations, where there is a need to monitor annual forest growth and properties are very large. Lidar remote sensing constitutes an important step towards operational wood procurement planning and is of high current interest to forestry organizations. Such technology is of great interest owing to their spatial sampling capabilities within plantations, and have had great reliability in forest inventory work in countries such as Norway, Canada, or the USA (e.g., [
6,
7,
12,
58]). Moreover, the application of airborne lidar technology for Brazilian industrial management is relatively new. While some studies have showed that the cost of the forest inventory derived from lidar could be lower than conventional forest inventory [
59,
60], the cost of lidar data acquisition could still be high to monitor forest growth annually; however, lidar has the ability to provide wall-to-wall, accurate mapping of forest attributes at high spatial resolutions (e.g.,
Figure 7 and
Figure 8).
Traditional forest inventory approaches are based on sampling theory, and forest attributes measured at plot level are then used to infer inventory attributes for an entire stand [
5,
14]. We showed here that lidar and RF machine learning combined can be a powerful tool for mapping forest attributes in
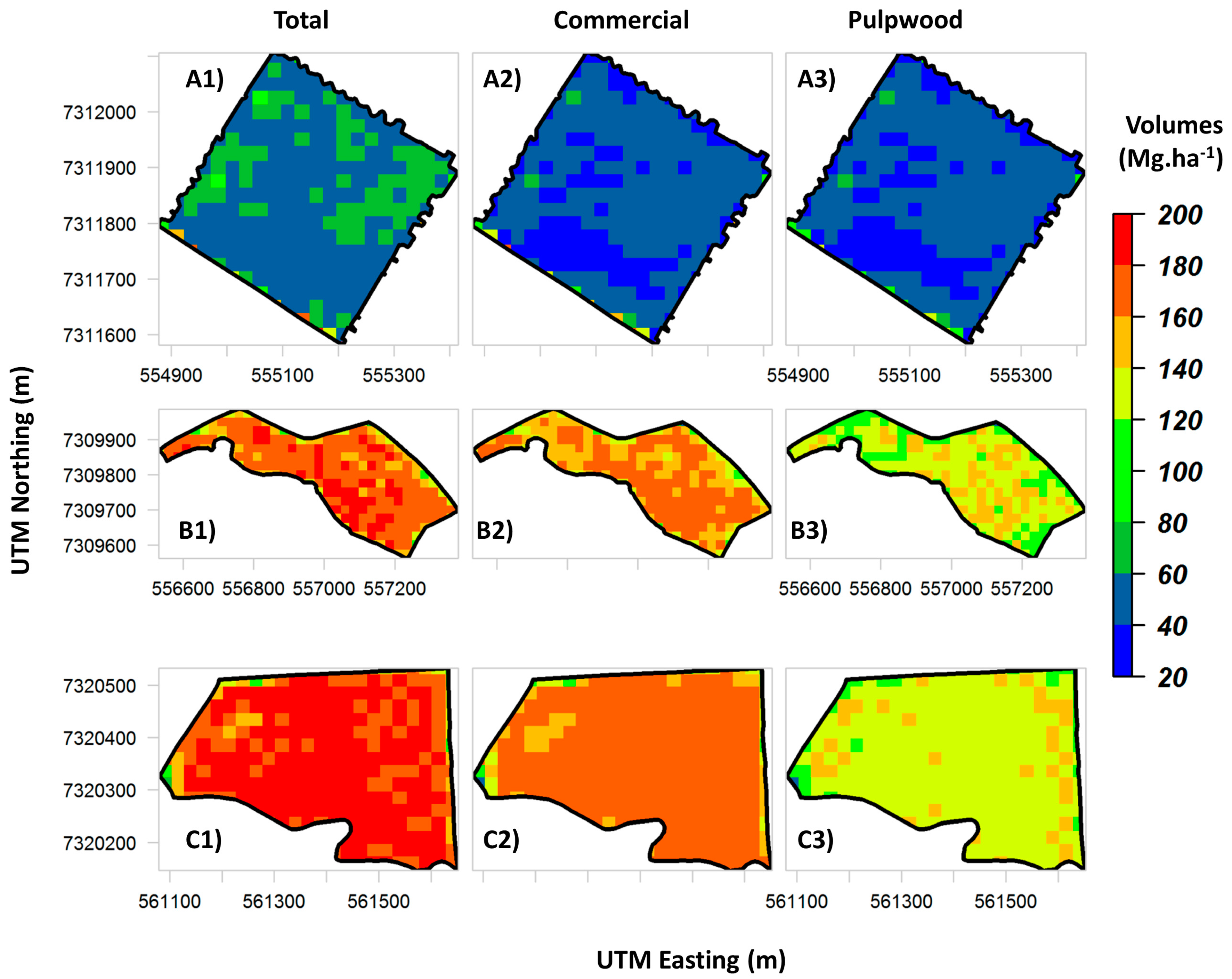
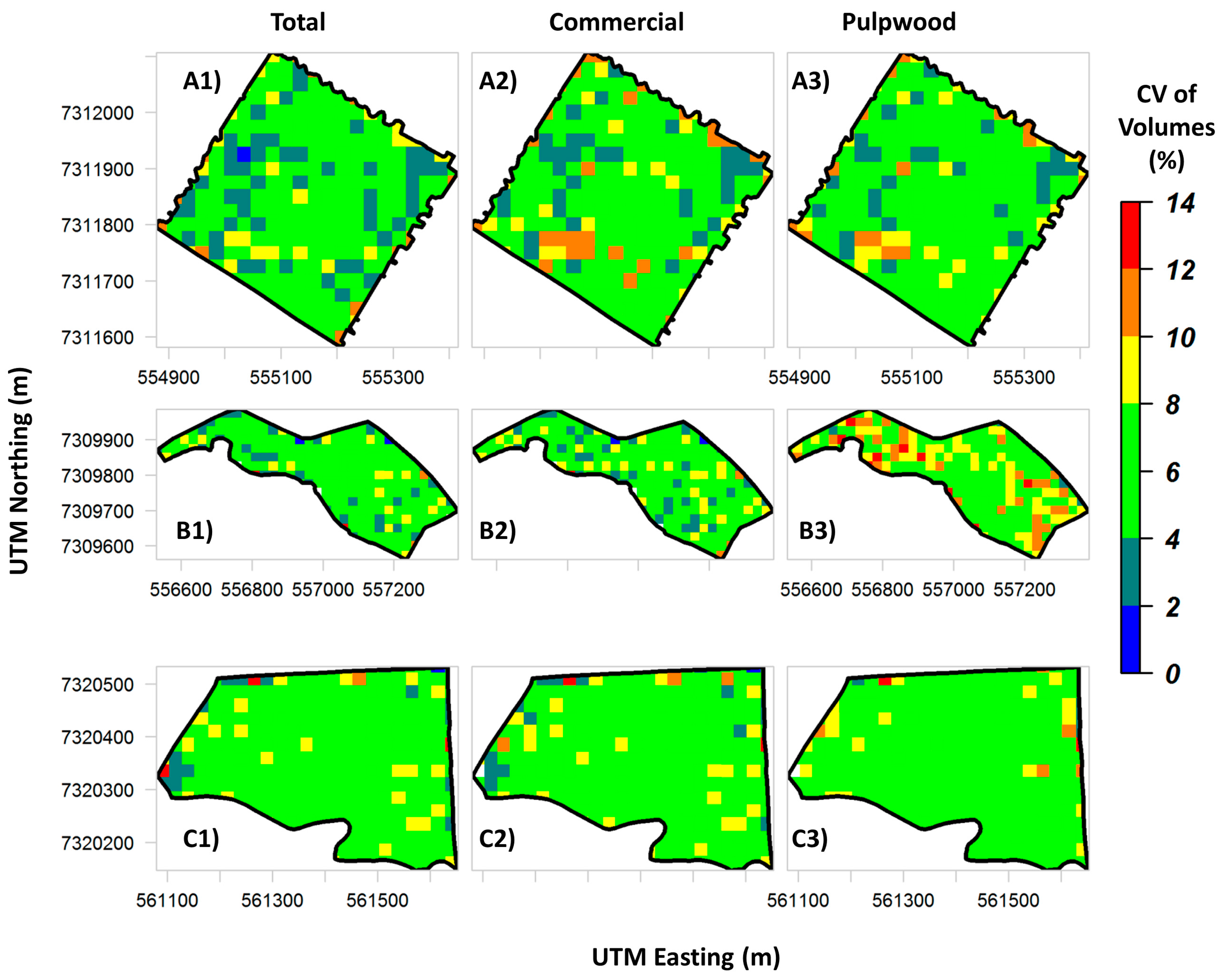
P. taeda forest plantations. In practice, lidar-derived maps of stem total and assortment volumes (
Figure 7 and
Figure 8) allow the owners to evaluate the production and forest structure variability within stands in a spatially explicit manner, which is not possible in a traditional forest inventory of
P. taeda. Also, such maps may allow managers to detect spatial patterns related to tree diseases, fire or forest clearing.
Recently, a study carried out in
Eucalyptus spp. forest plantations showed that lidar and RF could be combined to predict and map aboveground carbon at high spatial resolution (5 m), even if the models are calibrated using field plots with area larger than the cell size used for mapping [
34]. Therefore, future studies should be also test the ability of lidar and RF to map stem total and assortment volumes even at higher spatial resolution than presented in this study (e.g.,
Figure 7 and
Figure 8). Herein, we demonstrated the potential of combined lidar-derive metrics and RF to predict forest attributes through a lidar-plot based approach framework, however, to get even higher amount of details in
P. taeda forest plantations, RF could be also tested in a lidar-individual tree based approach. For instance, RF has been successfully used to impute individual tree height and volume in longleaf pine (
Pinus palustris Mill.) forest in Southern USA [
61]; therefore, lidar and RF could be also used to predict stem total and assortment volumes at an individual tree level in
P. taeda forest plantations, if carefully implemented.