Introducing a Non-Stationary Matrix Model for Stand-Level Optimization, an Even-Aged Pine (Pinus Sylvestris L.) Stand in Finland
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Growth Model
Model Parameter Estimation
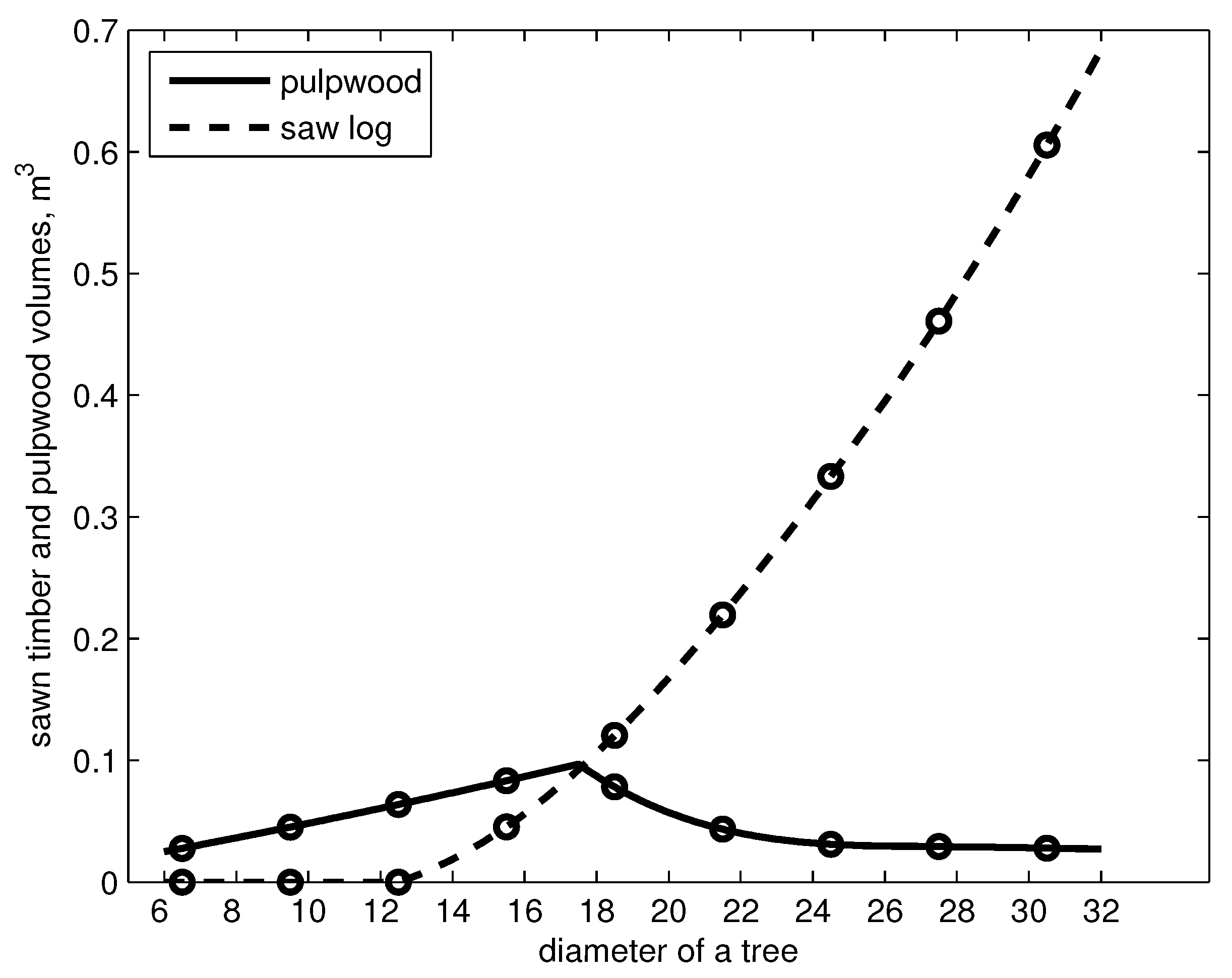
2.2. The Optimization Problem
Initial Data for Stand-Level Optimization
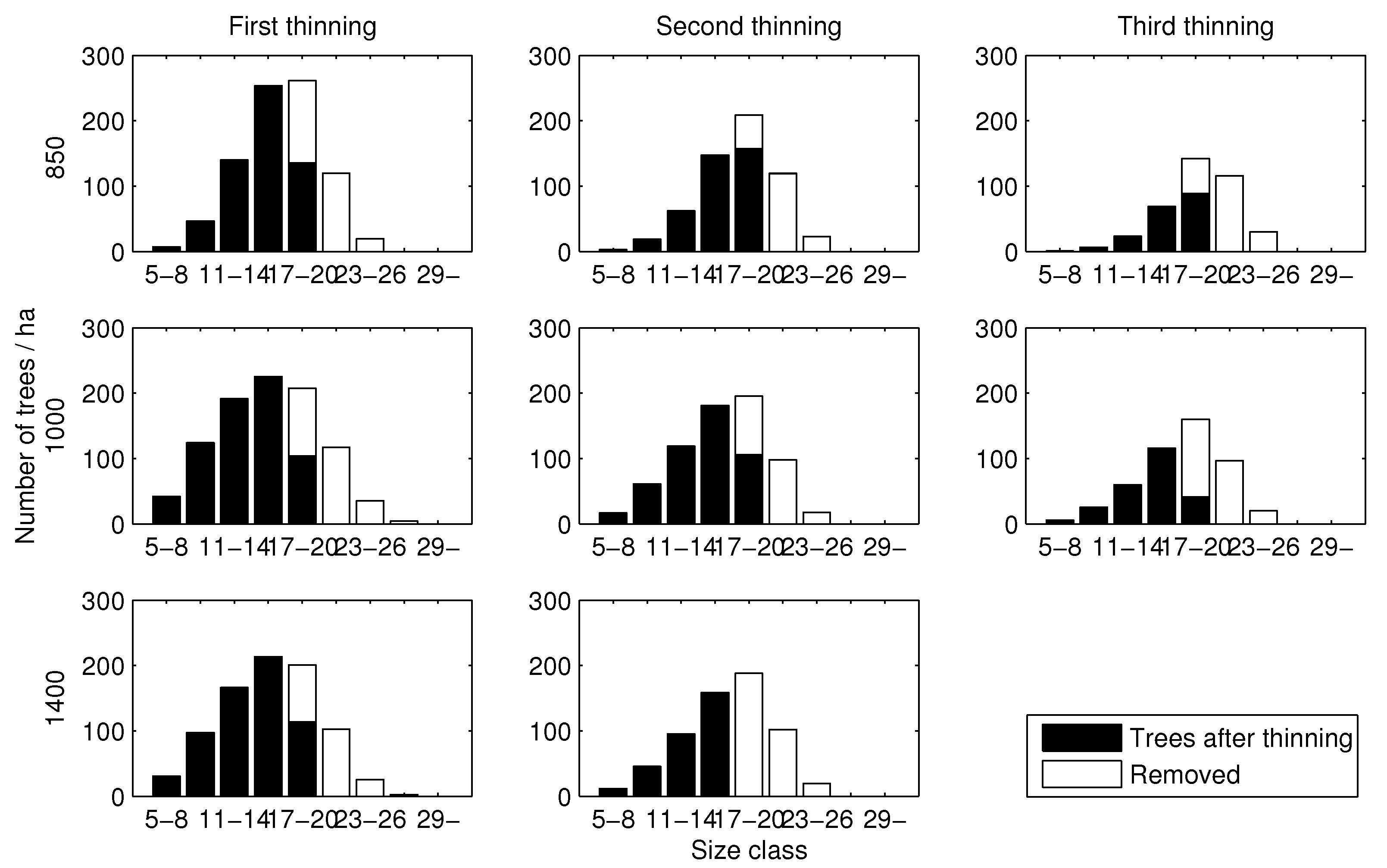
3. Results
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Liang, J.; Picard, N. Matrix model of forest dynamics: An overview and outlook. For. Sci. 2013, 59, 359–378. [Google Scholar] [CrossRef]
- Picard, N.; Mortier, F.; Chagneau, P. Influence of estimators of the vital rates in the stock recovery rate when using matrix models for tropical rainforests. Ecol. Model. 2008, 214, 349–360. [Google Scholar] [CrossRef]
- Hauser, C.E.; Cooch, E.G.; Lebreton, J.D. Control of structured populations by harvest. Ecol. Model. 2006, 196, 462–470. [Google Scholar] [CrossRef]
- Caswell, H. Matrix Population Models: Construction, Analysis and Interpretation, 2nd ed.; Sinauer Associates Inc. Publishers: Sunderland, MA, USA, 2001. [Google Scholar]
- Newman, K.B.; Buckland, S.T.; Morgan, B.J.T.; King, R.; Borchers, D.L.; Cole, D.J.; Besbeas, P.; Gimenez, O.; Thomas, L. Modelling Population Dynamics. Model Formulation, Fitting and Assessment Using State-Space Methods; Methods in Statistical Ecology; Springer: New York, NY, USA, 2014. [Google Scholar]
- Vanclay, J.K. Modeling Forest Growth and Yield: Applications to Mixed Tropical Forests; CAB International: Wallingford, UK, 1994. [Google Scholar]
- Porte, A.; Bartelink, H.H. Modelling mixed forest growth: A review of models for forest management. Ecol. Model. 2002, 150, 141–188. [Google Scholar] [CrossRef]
- Grimm, V. Ten years of individual-based modelling in ecology: What have we learned and what could we learn in the future? Ecol. Model. 1999, 115, 129–148. [Google Scholar] [CrossRef]
- Zuidema, P.A.; Jongejans, E.; Chien, P.D.; During, H.J.; Schieving, F. Integral projection models for trees: A new parametrization method and a validation of model output. J. Ecol. 2010, 98, 345–355. [Google Scholar] [CrossRef]
- Lee, C.-C.; Okuyama, T. Individual variation in stage duration in matrix population models: Problems and solutions. Biol. Control 2017, 110, 117–123. [Google Scholar] [CrossRef]
- Picard, N.; Liang, J. Matrix models for size-structured populations: Unrealistic fast growth or simply diffusion. PLoS ONE 2014, 9, e98254. [Google Scholar] [CrossRef] [PubMed]
- Salguero-Gomez, R.; Plotkin, J.B. Matrix dimensions bias demographic inferences: Implications for comparative plant demography. Am. Nat. 2010, 176, 710–722. [Google Scholar] [CrossRef] [PubMed]
- Picard, N.; Bar-Hen, A.; Guedon, Y. Modelling diameter class distribution with a second-order matrix model. For. Ecol. Manag. 2003, 180, 389–400. [Google Scholar] [CrossRef]
- Zhou, M.; Buongiorno, J. Nonlinearity and noise interaction in a model of forest growth. Ecol. Model. 2004, 180, 291–304. [Google Scholar] [CrossRef]
- Roth, G.; Caswell, H. Hyperstate matrix models: Extending demographic state spaces to higher dimensions. Methods Ecol. Evol. 2016, 7, 1438–1450. [Google Scholar] [CrossRef]
- Niinimäki, S.; Tahvonen, O.; Mäkelä, A. Applying a process-based model in Norway spruce management. For. Ecol. Manag. 2012, 265, 102–115. [Google Scholar] [CrossRef]
- Sable, S.E.; Rose, K.A. A comparison of individual-based and matrix models for simulating yellow perch population-dynamics in Oneida Lake, New York, USA. Ecol. Model. 2008, 215, 64–75. [Google Scholar] [CrossRef]
- Bollandsås, O.M.; Buongiorno, J.; Gobakken, T. Predicting the growth of stands of trees of mixed species and size: A matrix model for Norway. Scand. J. For. Res. 2008, 23, 167–178. [Google Scholar] [CrossRef]
- Tahvonen, O. Optimal choice between even- and uneven-aged forestry. Nat. Resour. Model. 2009, 22, 289–321. [Google Scholar] [CrossRef]
- Tahvonen, O.; Pukkala, T.; Laiho, O.; Lähde, E.; Niinimäki, S. Optimal management of uneven-aged Norway spruce stands. For. Ecol. Manag. 2010, 260, 106–115. [Google Scholar] [CrossRef]
- Lin, C.R.; Buongiorno, J.; Vasievich, M. A multi-species, density-dependent matrix growth model to predict tree diversity and income in northern hardwood stands. Ecol. Model. 1996, 91, 193–211. [Google Scholar] [CrossRef]
- Liang, J. Dynamics and management of Alaska boreal forest: An all-aged multi-species matrix growth model. For. Ecol. Manag. 2010, 260, 491–501. [Google Scholar] [CrossRef]
- Mäkinen, H.; Isomäki, A. Thinning intensity and growth of Scots pine stands in Finland. For. Ecol. Manag. 2004, 201, 311–325. [Google Scholar] [CrossRef]
- Tonteri, T.; Hotanen, J.P.; Kuusipalo, J. The Finnish forest site type approach: Ordination and classification studies of mesic forest sites in southern Finland. Vegetatio 1990, 87, 85–98. [Google Scholar] [CrossRef]
- Anonymous Statistical Yearbook of Forestry 2014, Table 1.5 at Page 51. Available online: http://www.metla.fi/metinfo/tilasto/julkaisut/vsk/2014/ (accessed on 9 May 2017).
- Venäläinen, A.; Tuomenvirta, H.; Pirinen, P.; Drebs, A. A Basic Finnish Climate Data Set 1961–2000—Description and Illustrations; Reports No. 2005:5; Finnish Meteorological Institute: Helsinki, Finland, 2005; pp. 1–27.
- Rämö, J.; Tahvonen, O. Economics of harvesting uneven-aged forest stands in Fennoscandia. Scand. J. For. Res. 2014, 29, 777–792. [Google Scholar] [CrossRef]
- Behforooz, H.G. A Comparison of the E(3) and Not-A-Knot Cubic Splines. Appl. Math. Comput. 1995, 72, 219–223. [Google Scholar]
- Siipilehto, J.; Mehtätalo, L. Parameter recovery vs. parameter prediction for the Weibull distribution validated for Scots pine stands in Finland. Silva Fenn. 2013, 47, 1–22. [Google Scholar] [CrossRef]
- Bailey, R.L.; Dell, T.R. Quantifying diameter distributions with the Weibull function. For. Sci. 1973, 19, 97–104. [Google Scholar]
- Näslund, M. Skogsförsöksanstaltens gallringsförsök i tallskog. Meddelanden från Statens Skogsförsöksanstalt 1936, 29, 169. [Google Scholar]
- Siipilehto, J.; Kangas, A. Näslundin pituuskäyrä ja siihen perustuvia malleja läpimitta-pituus riippuvuudesta suomalaisissa talousmetsissä. Metsätieteen Aikakauskirja 2015, 4, 215–316. [Google Scholar]
- Kojola, S. Kohti Hyvää Suometsien Hoitoa? Harvennusten Ja Kunnostusojitusten Vaikutus Ojitusaluemä NniköIden Puuntuotokseen Ja MetsäNkasvatuksen Taloustulokseen. Dissertationes Forestales 83. Ph.D. Thesis, University of Helsinki, Helsinki, Finland, 2009. (In Finnish with English summary). [Google Scholar]
- Van Mantegem, P.J.; Stephenson, N.L. The accuracy on matrix population model predictions for coniferous trees in the Sierra Nevada, California. J. Ecol. 2005, 93, 737–747. [Google Scholar] [CrossRef]
- Pukkala, T. Population-based methods in the optimization of stand management. Silva Fenn. 2009, 43, 261–274. [Google Scholar] [CrossRef]
- Cao, T. Silvicultural Decisions Based on Simulation-Optimization Systems. Dissertationes Forestales 103. Ph.D. Thesis, University of Helsinki, Helsinki, Finland, 2010. Available online: http://www.metla.fi/dissertationes/df103.htm (accessed on 9 May 2017).
- Arias-Rodil, M.; Pukkala, T.; Gonzalez-Conzalez, J.M; Barrio-Anta, M.; Dieguez-Aranda, U. Use of depth-first search and direct search methods to optimize even-aged stand management: A case study involving maritime pine in Asturias (northwest Spain). Can. J. For. Res. 2015, 45, 1269–1279. [Google Scholar] [CrossRef]
- Arias-Rodil, M.; Dieguez-Aranda, U.; Vazquez-Mendez, M.E. A differentiable optimization model for the management of single-species, even-aged stands. Can. J. For. Res. 2016, 47, 506–514. [Google Scholar] [CrossRef]
- Hyytiäinen, K.; Tahvonen, O.; Valsta, L. Optimum juvenile density, harvesting and stand structure in even-aged Scots pine stands. For. Sci. 2005, 51, 120–133. [Google Scholar]
- Tahvonen, O.; Pihlainen, S.; Niinimäki, S. On the economics of optimal timber production in boreal Scots pine stands. Can. J. For. Res. 2013, 43, 719–730. [Google Scholar] [CrossRef]
- Johansson, P.-O.; Löfgren, K.-G. The Economics of Forestry and Natural Resources; Basil Blackwell: Oxford, UK; New York, NY, USA, 1985. [Google Scholar]
- Pukkala, T.; Lähde, E.; Laiho, O. Optimizing the structure and management of uneven-sized stands of Finland. Forestry 2010, 83, 129–142. [Google Scholar] [CrossRef]
- Carson, S.; Garcia, O.; Hayes, J.D. Realized gain and prediction of yield with genetically improved Pinus radiata in New Zealand. For. Sci. 1999, 45, 186–200. [Google Scholar]
- Vergara, R.; White, T.L.; Shiver, B.D.; Rockwood, D.L. Estimated realized gains for first-generation slash pine (Pinus elliottii var. elliottii) tree improvement in the southeastern United States. Can. J. For. Res. 2004, 34, 2587–2600. [Google Scholar] [CrossRef]
- Kimberley, M.O.; Moore, J.R.; Dungey, H.S. Quantification of realised genetic gain in radiata pine and its incorporation into growth and yield modeling systems. Can. J. For. Res. 2015, 45, 1676–1687. [Google Scholar] [CrossRef]
- Cumbie, W.P.; Isik, F.; McKeand, S.E. Genetic improvement of sawtimber potential in Loblolly pine. For. Sci. 2012, 58, 168–177. [Google Scholar] [CrossRef]
- Kennedy, A.G.; Cameron, A.D.; Lee, S.J. Genetic relationships between wood quality traits and diameter growth of juvenile core wood in Sitka spruce. Can. J. For. Res. 2013, 43, 1–6. [Google Scholar] [CrossRef]
- Pfister, C.A; Wang, M. Beyond size: Matrix projection models for populations where size is an incomplete descriptor. Ecology 2005, 86, 2673–2683. [Google Scholar] [CrossRef]
- Jansson, G.; Hansen, J.K.; Haapanen, M.; Kvaalen, H.; Steffenrem, A. The genetic and economic gains from forest tree breeding programmes in Scandinavia and Finland. Scand. J. For. Res. 2017, 32, 273–286. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S J. Numerical Optimization; Springer: New York, NY, USA, 1999. [Google Scholar]
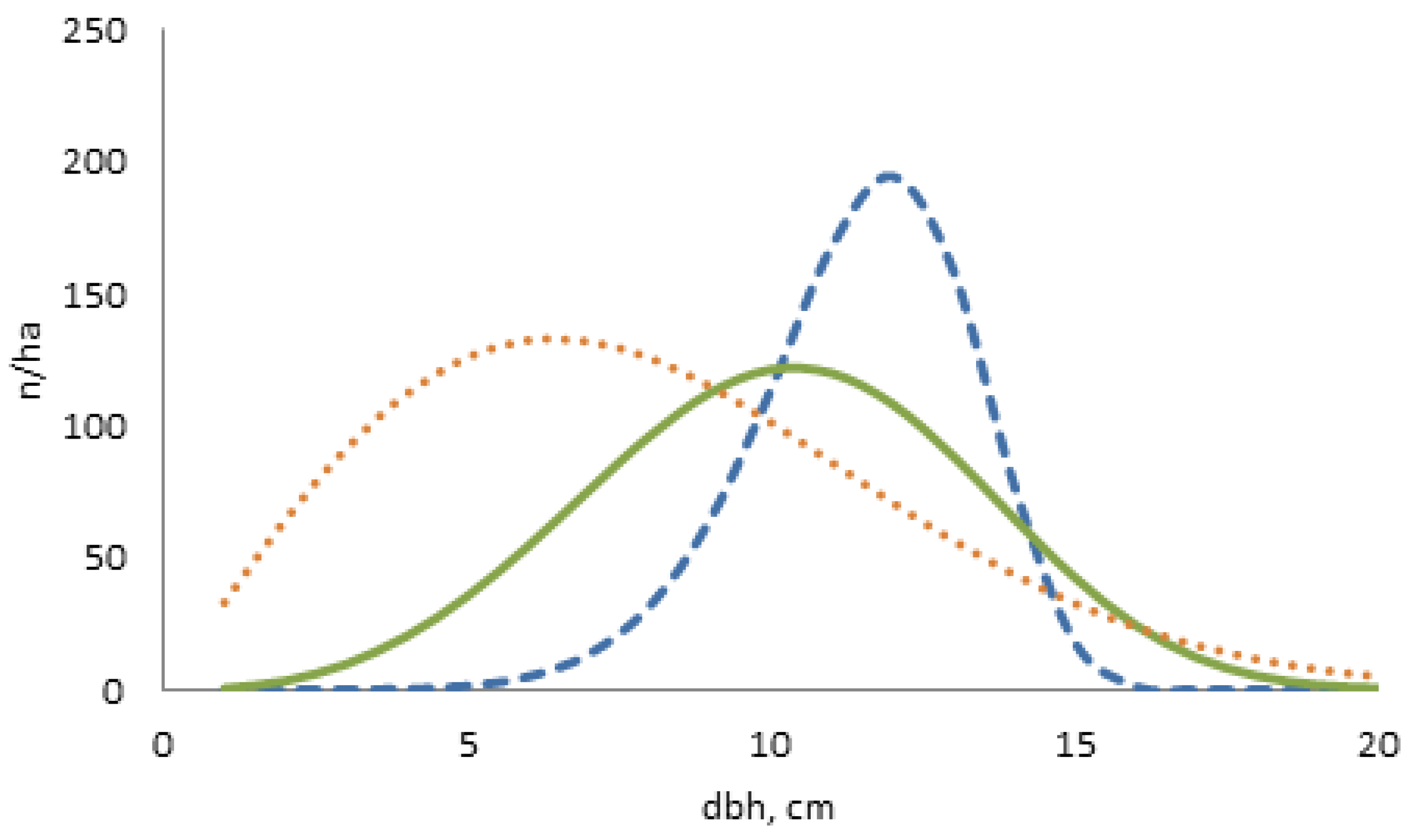
| Stand Age, Years | Basal Area, m ha | Number of Stems ha | Weighted Mean dbh, cm | Lorey’s Height, m | Dominant Height, m | Scale Parameter b | Shape Parameter c |
|---|---|---|---|---|---|---|---|
| 25 | 9 | 850 | 12 | 7.6 | 8.5 | 12.216 | 7.535 |
| 25 | 9 | 1000 | 12 | 7.6 | 8.5 | 11.352 | 3.612 |
| 25 | 9 | 1400 | 12 | 7.6 | 8.5 | 9.057 | 2.011 |
| Thinning | Age of the Stand (a) | Volume of Removed Trees (m ha) | Proportion of Saw log (%) | NPV (€ ha) | MAI (m ha year) |
|---|---|---|---|---|---|
| Sparse (Number of stems 850) | |||||
| First thinning | 45 | 63.7 | 75 | ||
| Second thinning | 55 | 50.0 | 80 | ||
| Third thinning | 65 | 52.3 | 81 | ||
| Final thinning | 95 | 73.7 | 90 | ||
| Total | 239.6 | 82 | 4042 | 2.52 | |
| Normal (Number of stems 1000) | |||||
| First thinning | 45 | 66.3 | 78 | ||
| Second thinning | 55 | 50.0 | 76 | ||
| Third thinning | 65 | 56.3 | 75 | ||
| Final thinning | 90 | 73.7 | 84 | ||
| Total | 246.3 | 79 | 4198 | 2.74 | |
| Dense (Number of stems 1400) | |||||
| First thinning | 45 | 54.9 | 78 | ||
| Second thinning | 55 | 71.4 | 72 | ||
| Final thinning | 85 | 95.1 | 85 | ||
| Total | 221.4 | 79 | 3713 | 2.60 | |
| Thinning | Age of the Stand (a) | Volume of Removed Trees (m ha) | Proportion of Saw log (%) | NPV (€ ha) | MAI (m ha year) |
|---|---|---|---|---|---|
| Interest rate 4% and minimum thinning removal 50 m ha | |||||
| First thinning | 40 | 61.4 | 70 | ||
| Second thinning | 50 | 50.2 | 67 | ||
| Final thinning | 75 | 109.3 | 78 | ||
| Total | 220.9 | 73 | 3168 | 2.95 | |
| Interest rate 5% and minimum thinning removal 50 m ha | |||||
| First thinning | 35 | 50.2 | 58 | ||
| Second thinning | 45 | 50.0 | 57 | ||
| Final thinning | 65 | 77.0 | 68 | ||
| Total | 177.2 | 62 | 2513 | 2.73 | |
| Interest rate 3% and minimum thinning removal 30 m ha | |||||
| First thinning | 35 | 36.9 | 66 | ||
| Second thinning | 45 | 38.6 | 68 | ||
| Third thinning | 55 | 30.0 | 80 | ||
| Fourth thinning | 65 | 36.5 | 86 | ||
| Fifth thinning | 75 | 30.2 | 88 | ||
| Sixth thinning | 85 | 43.1 | 88 | ||
| Final thinning | 105 | 41.2 | 88 | ||
| Total | 256.6 | 81 | 4355 | 2.44 | |
| Baseline optimal solution | |||||
| First thinning | 45 | 66.3 | 78 | ||
| Second thinning | 55 | 50.0 | 76 | ||
| Third thinning | 65 | 56.3 | 75 | ||
| Final thinning | 90 | 73.7 | 84 | ||
| Total | 246.3 | 79 | 4198 | 2.74 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pyy, J.; Ahtikoski, A.; Laitinen, E.; Siipilehto, J. Introducing a Non-Stationary Matrix Model for Stand-Level Optimization, an Even-Aged Pine (Pinus Sylvestris L.) Stand in Finland. Forests 2017, 8, 163. https://doi.org/10.3390/f8050163
Pyy J, Ahtikoski A, Laitinen E, Siipilehto J. Introducing a Non-Stationary Matrix Model for Stand-Level Optimization, an Even-Aged Pine (Pinus Sylvestris L.) Stand in Finland. Forests. 2017; 8(5):163. https://doi.org/10.3390/f8050163
Chicago/Turabian StylePyy, Johanna, Anssi Ahtikoski, Erkki Laitinen, and Jouni Siipilehto. 2017. "Introducing a Non-Stationary Matrix Model for Stand-Level Optimization, an Even-Aged Pine (Pinus Sylvestris L.) Stand in Finland" Forests 8, no. 5: 163. https://doi.org/10.3390/f8050163
APA StylePyy, J., Ahtikoski, A., Laitinen, E., & Siipilehto, J. (2017). Introducing a Non-Stationary Matrix Model for Stand-Level Optimization, an Even-Aged Pine (Pinus Sylvestris L.) Stand in Finland. Forests, 8(5), 163. https://doi.org/10.3390/f8050163







