A Mixed Application of Geographically Weighted Regression and Unsupervised Classification for Analyzing Latex Yield Variability in Yunnan, China
Abstract
:1. Introduction
1.1. Background
1.2. Literature Review
1.3. Research Questions
- (1)
- What are the determinants of latex yields at the level of Xishuangbanna prefecture as a whole?
- (2)
- How do their impacts vary over space at lower spatial levels within that prefecture?
- (3)
- In which parts of Xishuangbanna are potential yields the highest?
2. Data and Methods
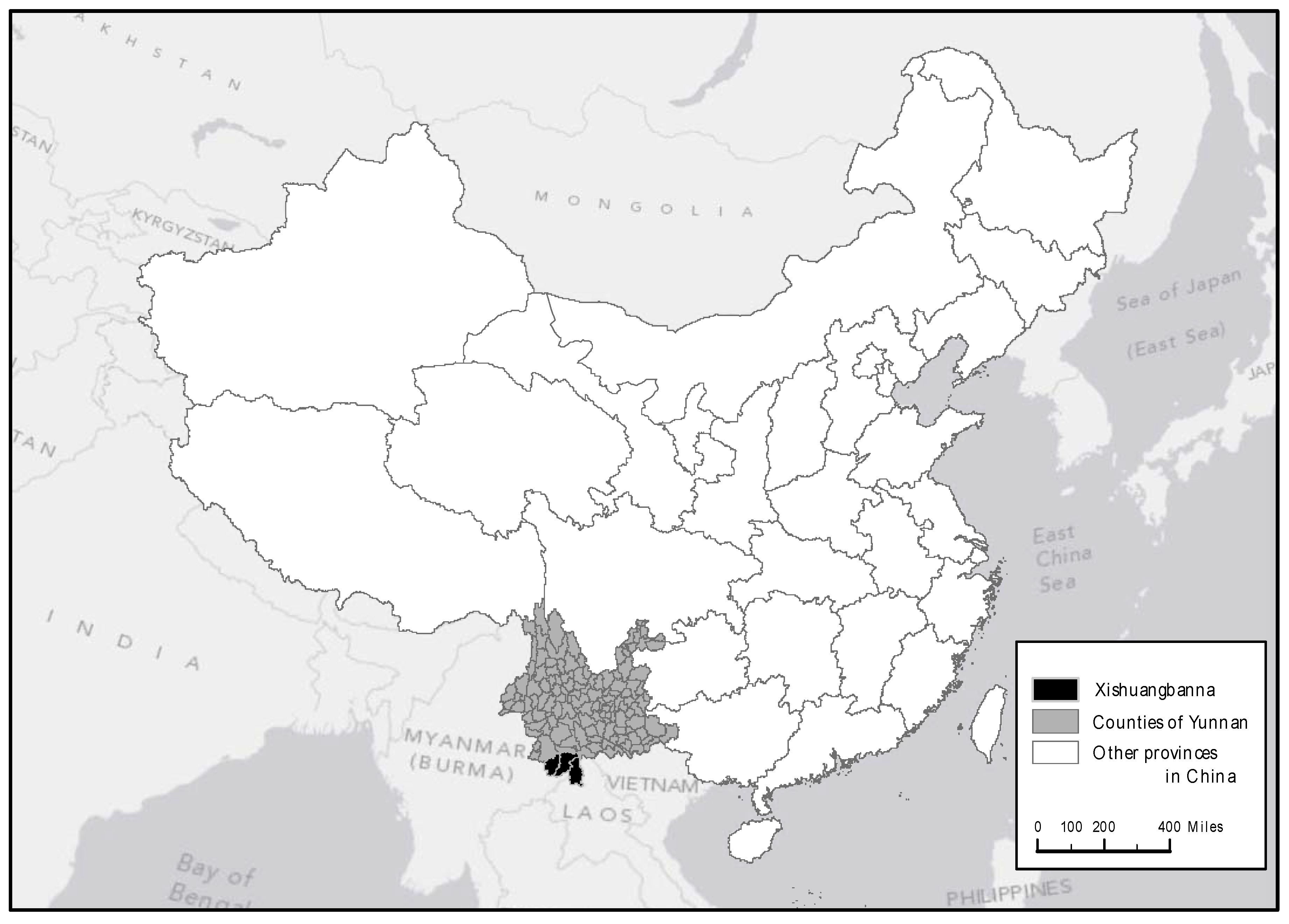
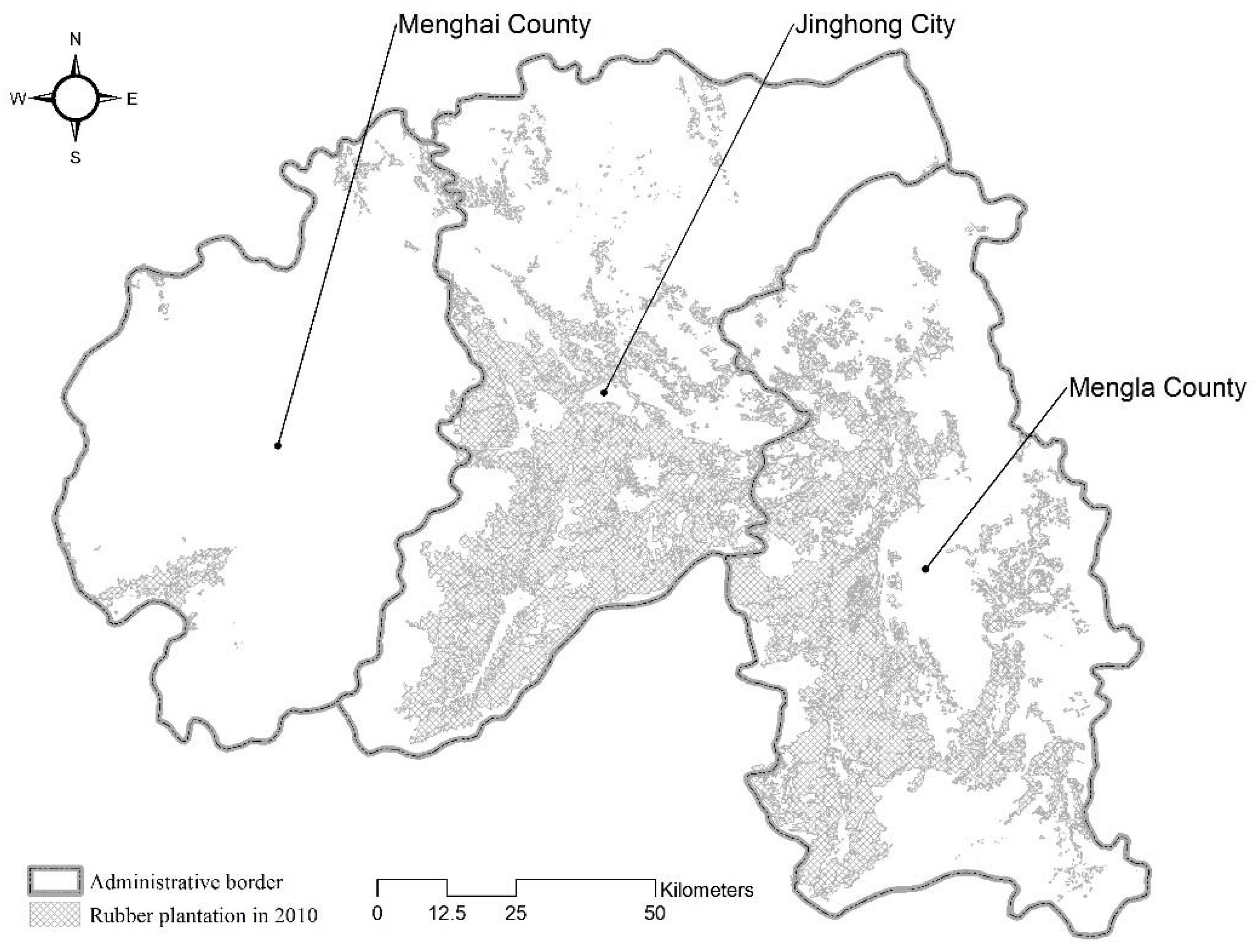
2.1. Study Area
2.2. Data
2.3. Methods
2.3.1. Geographically Weighted Regression
2.3.2. Iterative Self-Organizing Data Analysis Technique
3. Results
3.1. Global Model
3.2. Local Model
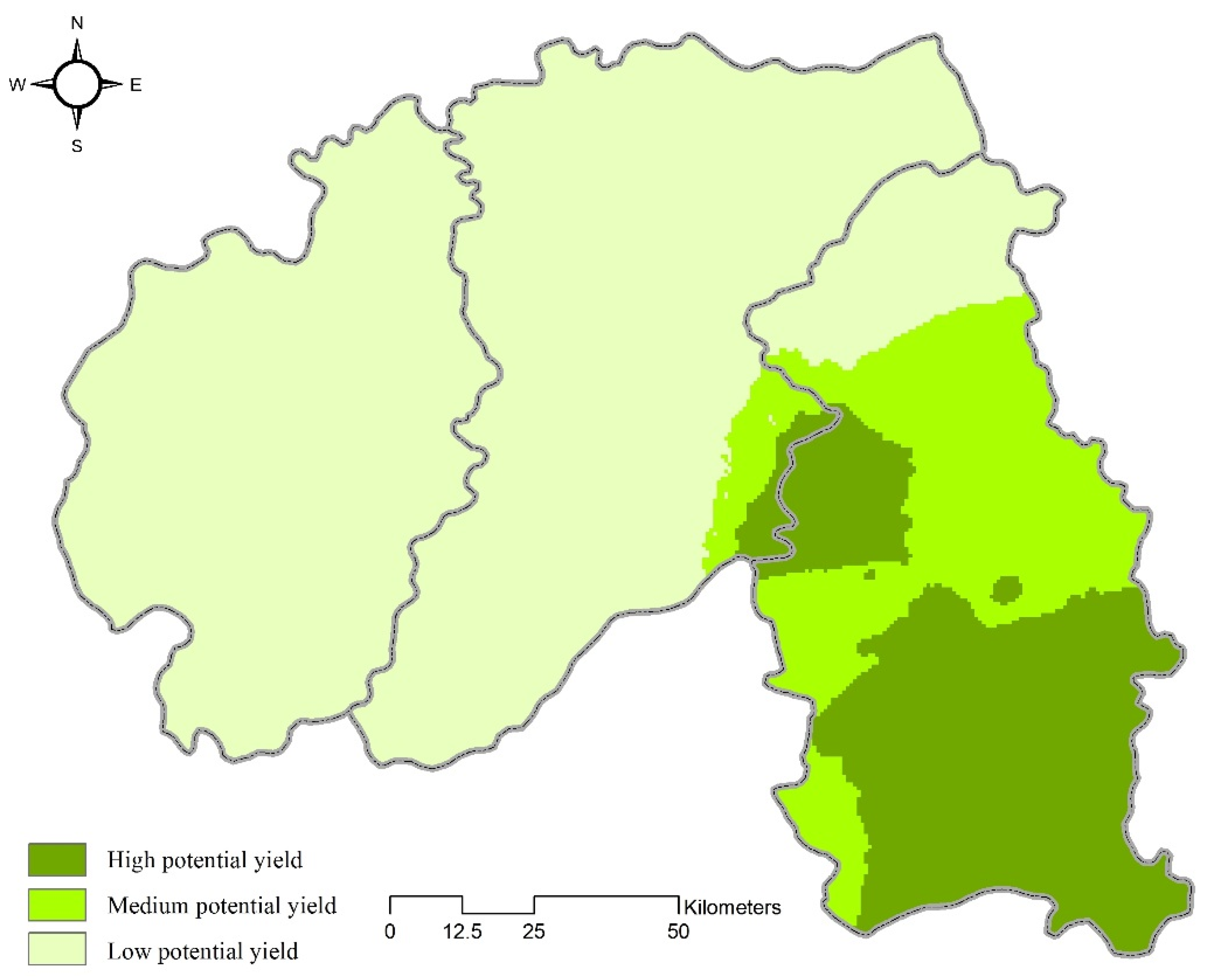
3.3. ISODATA
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gouyon, A. Eco-Certification as an Incentive to Conserve Biodiversity in Rubber Smallholder Agroforestry Systems: A Preliminary Study; World Agroforestry Centre (ICRAF): Bogor, Indonesia, 2003. [Google Scholar]
- Luan, N.K. Natural Rubber Industry Report 2013; FPT Securities Joint Stock Company: Ho Chi Minh, Vietnam, 2013. [Google Scholar]
- Ziegler, A.D.; Fox, J.M.; Xu, J. The rubber juggernaut. Science 2009, 324, 1024–1025. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Fox, J.M. Mapping rubber tree growth in mainland Southeast Asia using time-series MODIS 250 m NDVI and statistical data. Appl. Geogr. 2012, 32, 420–432. [Google Scholar] [CrossRef]
- Ahrends, A.; Hllingsworth, P.M.; Ziegler, A.D.; Fox, J.M.; Chen, H.; Su, Y.; Xu, J. Current trends of rubber plantation expansion may threaten biodiversity and livelihoods. Glob. Environ. Chang. 2015, 34, 48–58. [Google Scholar] [CrossRef]
- Xu, J.; Grumbine, R.E.; Beckschäfer, P. Landscape transformation through the use of ecological and socioeconomic indicators in Xishuangbanna, southwest China, Mekong region. Ecol. Indic. 2014, 36, 749–756. [Google Scholar] [CrossRef]
- Yi, Z.; Cannon, C.H.; Chen, J.; Ye, C.-X.; Swetnam, R.D. Developing indicators of economic value and biodiversity loss for rubber plantations in Xishuangbanna, southwest China: A case study from Menglun township. Ecol. Indic. 2013, 36, 788–797. [Google Scholar] [CrossRef]
- Kim, O.S.; Newell, J.P. The ‘Geographic Emission Benchmark’ model: A baseline approach to measuring emissions associated with deforestation and degradation. J. Land Use Sci. 2015, 10, 466–489. [Google Scholar] [CrossRef] [PubMed]
- Imran, M.; Stein, A.; Zurita-Milla, R. Using geographically weighted regression kriging for crop yield mapping in West Africa. Int. J. Geogr. Inf. Sci. 2015, 29, 234–257. [Google Scholar] [CrossRef]
- Qiu, B.; Zeng, C.; Chen, C.; Zhang, C.; Zhong, M. Vegetation distribution pattern along altitudinal gradient in subtropical mountainous and hilly river basin, China. J. Geogr. Sci. 2013, 23, 247–257. [Google Scholar] [CrossRef]
- Wang, J.; Kang, S.; Sun, J.; Chen, Z. Estimation of crop water requirement based on principal component analysis and geographically weighted regression. Chin. Sci. Bull. 2013, 58, 3371–3379. [Google Scholar] [CrossRef]
- Yang, Y.; Tong, X.; Zhu, J. A geographically weighted model of the regression between grain production and typical factors for the Yellow River Delta. Math. Comput. Model. 2013, 58, 582–587. [Google Scholar] [CrossRef]
- Gao, J.; Li, S.; Zhao, Z.; Cai, Y. Investigating spatial variation in the relationships between NDVI and environmental factors at multi-scales: A case study of Guizhou Karst Plateau, China. Int. J. Remote Sens. 2012, 33, 2112–2129. [Google Scholar] [CrossRef]
- Gao, Y.; Huang, J.; Li, S.; Li, S. Spatial pattern of non-stationarity and scale-dependent relationships between NDVI and climatic factors: A case study in Qinghai-Tibet Plateau, China. Ecol. Indic. 2012, 20, 170–176. [Google Scholar] [CrossRef]
- Qiu, B.; Zhong, M.; Zeng, C.; Tang, Z.; Chen, C. Effect of topography and accessibility on vegetation dynamic pattern in mountain-hill region. J. Mt. Sci. 2012, 9, 879–890. [Google Scholar] [CrossRef]
- Sharma, V.; Irmak, A.; Kabenge, I.; Irmak, S. Application of GIS and geographically weighted regression to evaluate the spatial nonstationarity relationships between precipitation vs. irrigated and rainfed maize and soybean yields. Trans. Am. Soc. Agric. Biol. Eng. 2011, 54, 953–972. [Google Scholar]
- Pineda Jaimes, N.B.; Bosque Sendra, J.; Gómez Delgado, M.; Franco Plata, R. Exploring the driving forces behind deforestation in the state of Mexico using geographically weighted regression. Appl. Geogr. 2010, 30, 576–591. [Google Scholar] [CrossRef]
- Zhao, N.; Yang, Y.; Zhou, X. Application of geographically weighted regression in estimating the effect of climate and site conditions on vegetation distribution in Haihe Catchment, China. Plant Ecol. 2010, 209, 349–359. [Google Scholar] [CrossRef]
- Clement, F.; Orange, D.; Williams, M.; Mulley, C.; Epprecht, M. Drivers of afforestation in Northern Vietnam: Assessing local variations using geographically weighted regression. Appl. Geogr. 2009, 29, 561–576. [Google Scholar] [CrossRef]
- Foody, G.M. Refining predictions of climate change impacts on plant species distribution through the use of local statistics. Ecol. Inform. 2008, 3, 228–236. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, P.; Ren, H.; Kakubari, Y. Spatiotemporal dynamics of forest net primary production in China over the past two decades. Glob. Planet. Chang. 2008, 61, 267–274. [Google Scholar] [CrossRef]
- Zhuang, Q.; Zhang, T.; Xiao, J.; Luo, T. Quantification of net primary production of Chinese forest ecosystems with spatial statistical approaches. Mitig. Adapt. Strateg. Glob. Chang. 2008, 14, 85–99. [Google Scholar] [CrossRef]
- Wang, Q.; Ni, J.; Tenhunen, J. Application of a geographically weighted regression analysis to estimate net primary production of Chinese forest ecosystems. Glob. Ecol. Biogeogr. 2005, 14, 379–393. [Google Scholar] [CrossRef]
- Foody, G.M. Geographical weighting as a further refinement to regression modelling: An example focused on the NDVI-rainfall relationship. Remote Sens. Environ. 2003, 88, 283–293. [Google Scholar] [CrossRef]
- Fotheringham, A.S. Trends in quantitative methods I: Stressing the local. Prog. Hum. Geogr. 1997, 21, 88–96. [Google Scholar] [CrossRef]
- Su, S.; Xiao, R. Spatially varying determinants of farmland conversion across Qiantang watershed, China. Environ. Manag. 2013, 52, 907–916. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.J.; Ng, C.N. Exploring spatio-temporal variations of habitat loss and its causal factors in the Shenzhen River cross-border watershed. Appl. Geogr. 2013, 39, 140–150. [Google Scholar] [CrossRef]
- Su, S.; Xiao, R.; Zhang, Y. Multi-scale analysis of spatially varying relationships between agricultural landscape patterns and urbanization using geographically weighted regression. Appl. Geogr. 2012, 32, 360–375. [Google Scholar] [CrossRef]
- Ali, A.; de Bie, C.A.J.M.; Skidmore, A.K.; Scarrott, R.G.; Lymberakis, P. Mapping the heterogeneity of natural and semi-natural landscapes. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 176–183. [Google Scholar] [CrossRef]
- Ivits, E.; Cherlet, M.; Horion, S.; Fensholt, R. Global Biogeographical pattern of ecosystem functional types derived from earth observation data. Remote Sens. 2013, 5, 3305–3330. [Google Scholar] [CrossRef]
- Metzger, M.J.; Bunce, R.G.H.; Jongman, R.H.G.; Sayre, R.; Trabucco, A.; Zomer, R. A high-resolution bioclimate map of the world: A unifying framework for global biodiversity research and monitoring. Glob. Ecol. Biogeogr. 2013, 22, 630–638. [Google Scholar] [CrossRef]
- Metzger, M.J.; Bunce, R.G.H.; Jongman, R.H.G.; Mücher, C.A.; Watkins, J.W. A climatic stratification of the environment of Europe. Glob. Ecol. Biogeogr. 2005, 14, 549–563. [Google Scholar] [CrossRef]
- Myers, N.; Mittermeier, R.A.; Mittermeier, C.G.; da Fonseca, G.A.; Kent, J. Biodiversity hotspots for conservation priorities. Nature 2000, 403, 853–858. [Google Scholar] [CrossRef] [PubMed]
- Xi, J. Valuation of Ecosystem Services in Xishuangbanna. Biodiversity Conservation Corridors Initiative Pilot Site, China; Asian Development Bank: Mandaluyong, Philippines, 2009. [Google Scholar]
- Food and Agriculture Organization (FAO). Global Forest Resources Assessment 2010: FAO Forestry Paper 163. 2010. Available online: http://www.fao.org/docrep/013/i1757e/i1757e00.htm (accessed on 3 May 2017).
- Food and Agriculture Organization (FAO). Global Forest Resources Assessment 2005: FAO Forestry Paper 147. 2006. Available online: http://www.fao.org/docrep/008/a0400e/a0400e00.htm (accessed on 3 May 2017).
- Food and Agriculture Organization (FAO). Global Forest Resources Assessment 2000: FAO Forestry Paper 140. 2001. Available online: http://www.fao.org/docrep/004/y1997e/y1997e00.htm (accessed on 3 May 2017).
- Li, H.; Ma, Y.; Aide, T.M.; Liu, W. Past, present and future land-use in Xishuangbanna, China, and the implications for carbon dynamics. For. Ecol. Manag. 2008, 255, 16–24. [Google Scholar] [CrossRef]
- Li, H.; Aide, T.M.; Ma, Y.; Liu, W.; Cao, M. Demand for rubber is causing the loss of high diversity rain forest in SW China. Biodivers. Conserv. 2007, 16, 1731–1745. [Google Scholar] [CrossRef]
- Information Office of the State Council of the People’s Republic of China. China’s Policies and Actions for Addressing Climate Change; Foreign Languages Press: Beijing, China, 2008.
- Murray, G.; Cook, I.G. The Greening of China; China Intercontinental Press: Beijing, China, 2004. [Google Scholar]
- Hyde, W.F.; Belcher, B.; Xu, J. (Eds.) China’s Forests: Global Lessons from Market Reforms; Resource for The Future (RFF); Center for International Forestry Research (CIFOR): Washington, DC, USA, 2003. [Google Scholar]
- Xu, J.; Ma, E.T.; Tashi, D.; Fu, Y.; Lu, Z.; Melick, D. Integrating sacred knowledge for conservation: Cultures and landscapes in Southwest China. Ecol. Soc. 2006, 10, 1–25. [Google Scholar] [CrossRef]
- Li, H.; Ma, Y.; Liu, W.; Liu, W. Clearance and fragmentation of tropical rain forest in Xishuangbanna, SW, China. Biodivers. Conserv. 2009, 18, 3421–3440. [Google Scholar] [CrossRef]
- Qiu, J. Where the rubber meets the garden. Nature 2009, 457, 246–247. [Google Scholar] [CrossRef] [PubMed]
- Kim, O.S. A Spatially Explicit Approach to Measuring Carbon Dynamics for Reducing Emissions from Deforestation and Forest Degradation: A Case Study of Chinese Forests. Ph.D. Thesis, University of Southern California, Los Angeles, CA, USA, 2013. [Google Scholar]
- Chen, H.; Yi, Z.; Schmidt-Vogt, D.; Ahrends, A.; Beckschäfer, P.; Kleinn, C.; Ranjitkar, S.; Xu, J. Pushing the limits: the pattern and dynamics of rubber monoculture expansion in Xishuangbanna, SW China. PLoS ONE 2016, 11, e0150062. [Google Scholar] [CrossRef] [PubMed]
- National Aeronautics and Space Administration (NASA). Precipitation Measurement Missions; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2015.
- Jones, P.D.; Lister, D.H.; Osborn, T.J.; Harpham, C.; Salmon, M.; Morice, C.P. Hemispheric and large-scale land-surface air temperature variations: An extensive revision and an update to 2010. J. Geophys. Res. 2012, 117, D05127. [Google Scholar] [CrossRef]
- Ministry of Economy, Trade, and Industry of Japan; The United States National Aeronautics and Space Administration (NASA). Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Global Digital Elevation Map (GDEM); Ministry of Economy, Trade, and Industry of Japan: Tokyo, Japan, 2011.
- Dobson, J.E.; Bright, E.A.; Coleman, P.R.; Worley, B.A. LandScan: A global population database for estimating populations at risk. Photogramm. Eng. Remote Sens. 2000, 66, 849–857. [Google Scholar]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M.E. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley and Sons: New York, NY, USA, 2002. [Google Scholar]
- Bivand, R.; Yu, D.; Nakaya, T.; Garcia-Lopez, M.-A. Package ‘spgwr’. 2015. Available online: https://cran.r-project.org/web/packages/spgwr/spgwr.pdf (accessed on 27 December 2016).
- Nakaya, T.; Charlton, M.; Lewis, P.; Brunsdon, C.; Yao, J.; Fotheringham, S. GWR4 User Manual. 2014. Available online: http://gwr.maynoothuniversity.ie/wp-content/uploads/2013/04/GWR4_Manual.pdf (accessed on 27 December 2016).
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression–modelling spatial non-stationarity. J. R. Stat. Soc. Ser. D Stat. 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Ball, G.H.; Hall, D.J. ISODATA, A Novel Method of Data Analysis and Pattern Classification; Stanford Research Institute: Menlo Park, CA, USA, 1965. [Google Scholar]
- Kim, O.S. A determinant analysis on natural latex yield using geographically weighted regression: A case study of Xishuangbanna, Yunnan, China. J. Korean Cartogr. Assoc. 2015, 15, 67–77. (In Korean) [Google Scholar] [CrossRef]
- Wheeler, D.; Tiefelsdorf, M. Multicollinearity and correlation among local regression coefficients in geographically weighted regression. J. Geogr. Syst. 2004, 7, 161–187. [Google Scholar] [CrossRef]
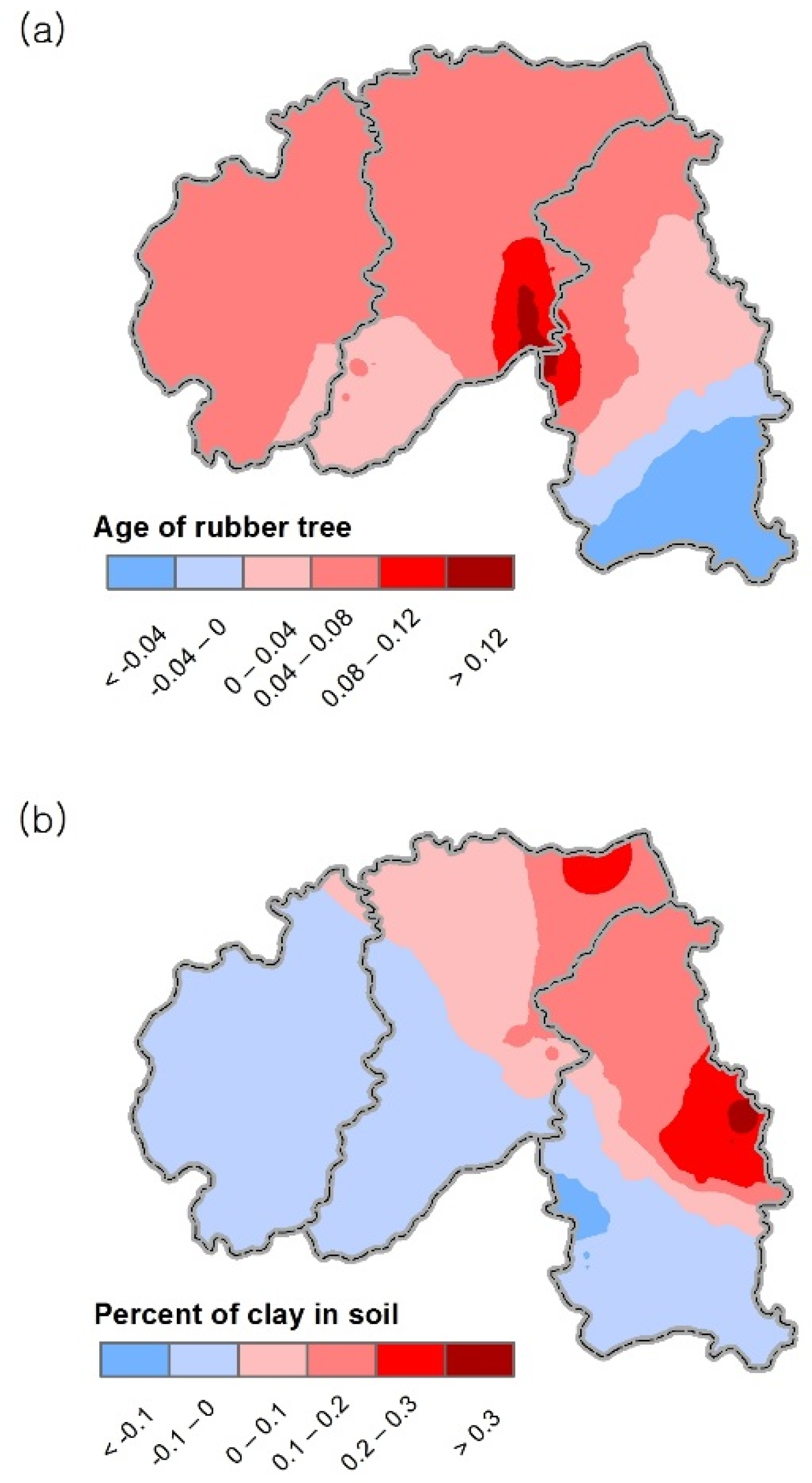
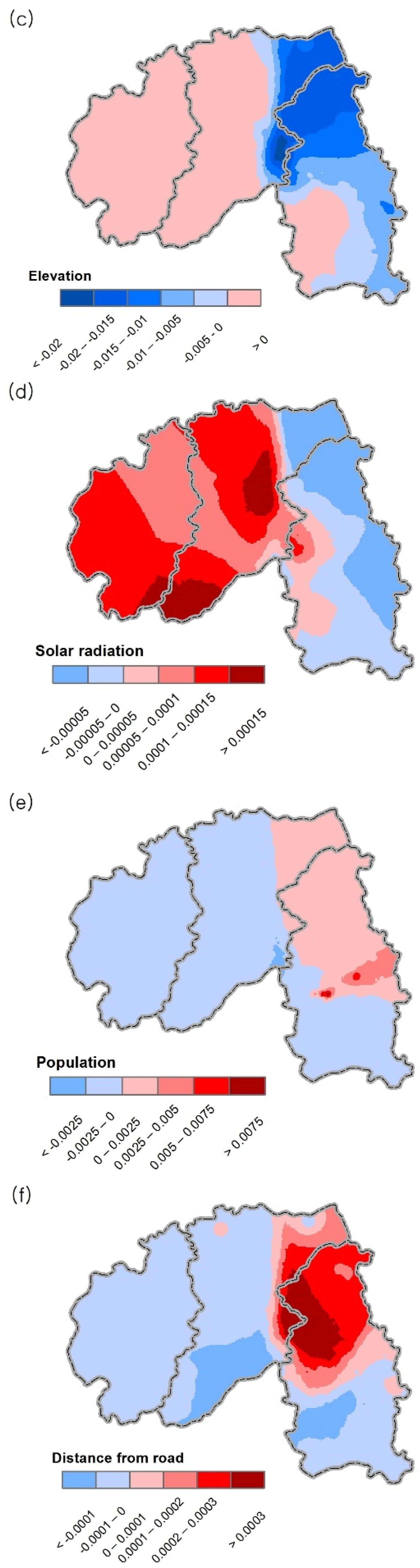
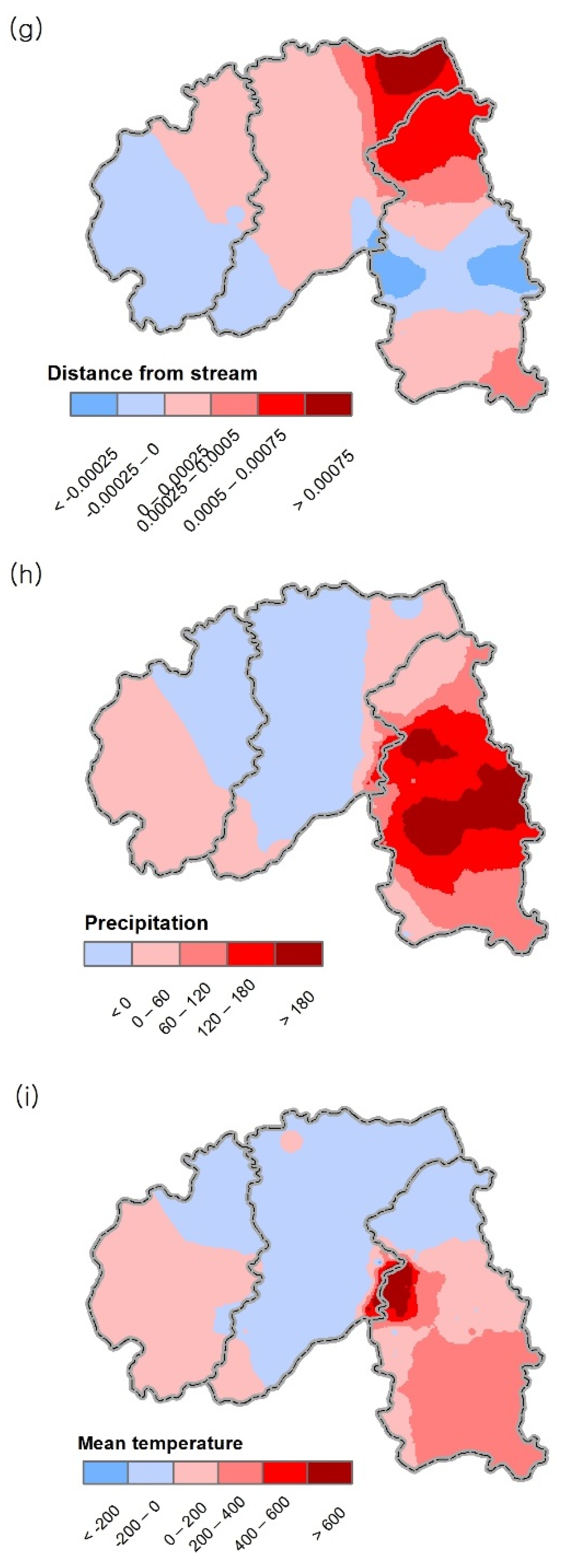
| Variable | Parameter Estimates | p-Value |
|---|---|---|
| (Intercept) | −273.50 | 0.00 |
| Age of rubber tree | 0.02 | 0.02 |
| Percent of clay in soil | 0.13 | 0.00 |
| Soil pH | ||
| Elevation | −0.01 | 0.00 |
| Slope | ||
| Aspect | ||
| Solar radiation | 0.00 | 0.04 |
| Population | −0.00 | 0.02 |
| Distance from road | 0.00 | 0.00 |
| Distance from stream | 0.00 | 0.10 |
| Nature reserve (dummy) | ||
| Precipitation | 35.13 | 0.00 |
| Mean temperature | 30.87 | 0.00 |
| Maximum temperature | ||
| Minimum temperature | ||
| Squared age of rubber tree | ||
| Squared percent of clay in soil | −0.00 | 0.00 |
| Squared soil pH | ||
| Squared elevation | 0.00 | 0.00 |
| Squared slope | ||
| Squared aspect | ||
| Squared solar radiation | −0.00 | 0.10 |
| Squared population | 0.00 | 0.10 |
| Squared distance from road | −0.00 | 0.00 |
| Squared distance from stream | −0.00 | 0.06 |
| Squared precipitation | ||
| Squared mean temperature | −0.86 | 0.00 |
| Squared maximum temperature | ||
| Squared minimum temperature | ||
| Interaction (Percent of clay in soil and Precipitation) | ||
| Interaction (Percent of clay in soil and Distance from stream) | ||
| Interaction (Population and Slope) | ||
| Interaction (Population and Distance from road) |
| Variable | Minimum | Mean | Median | Maximum |
|---|---|---|---|---|
| (Intercept) | −7964.84 | −1484.24 | −1291.43 | 2310.32 |
| Age of rubber tree | −0.11 | 0.03 | 0.04 | 0.13 |
| Percent of clay in soil | −0.12 | 0.02 | −0.02 | 0.32 |
| Elevation | −0.03 | −0.00 | −0.00 | 0.01 |
| Solar radiation | −0.00 | 0.00 | 0.00 | 0.00 |
| Population | −0.00 | −0.00 | −0.00 | 0.01 |
| Distance from road | −0.00 | 0.00 | −0.00 | 0.00 |
| Distance from stream | −0.00 | 0.00 | 0.00 | 0.00 |
| Precipitation | −27.89 | 86.33 | 89.94 | 242.54 |
| Mean temperature | −262.04 | 163.78 | 139.31 | 894.24 |
| Squared percent of clay in soil | −0.00 | −0.00 | 0.00 | 0.00 |
| Squared elevation | −0.00 | −0.00 | −0.00 | 0.00 |
| Squared solar radiation | −0.00 | 0.00 | 0.00 | 0.00 |
| Squared population | −0.00 | 0.00 | 0.00 | 0.00 |
| Squared distance from road | −0.00 | 0.00 | 0.00 | 0.00 |
| Squared distance from stream | −0.00 | 0.00 | 0.00 | 0.00 |
| Squared mean temperature | −25.13 | −4.53 | −3.86 | 7.47 |
| Statistics | Global Model | Local Model |
|---|---|---|
| R2 | 0.53 | 0.76 |
| Adjusted R2 | 0.52 | 0.74 |
| CV | 2.48 | 2.64 |
| AIC | 4351.13 | 3673.84 |
| AICc | 4351.13 | 3686.53 |
| BIC | 4442.34 | 4092.56 |
| Moran’s i | 0.47 | 0.15 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, O.S.; Nugent, J.B.; Yi, Z.-F.; Newell, J.P.; Curtis, A.J. A Mixed Application of Geographically Weighted Regression and Unsupervised Classification for Analyzing Latex Yield Variability in Yunnan, China. Forests 2017, 8, 162. https://doi.org/10.3390/f8050162
Kim OS, Nugent JB, Yi Z-F, Newell JP, Curtis AJ. A Mixed Application of Geographically Weighted Regression and Unsupervised Classification for Analyzing Latex Yield Variability in Yunnan, China. Forests. 2017; 8(5):162. https://doi.org/10.3390/f8050162
Chicago/Turabian StyleKim, Oh Seok, Jeffrey B. Nugent, Zhuang-Fang Yi, Joshua P. Newell, and Andrew J. Curtis. 2017. "A Mixed Application of Geographically Weighted Regression and Unsupervised Classification for Analyzing Latex Yield Variability in Yunnan, China" Forests 8, no. 5: 162. https://doi.org/10.3390/f8050162
APA StyleKim, O. S., Nugent, J. B., Yi, Z.-F., Newell, J. P., & Curtis, A. J. (2017). A Mixed Application of Geographically Weighted Regression and Unsupervised Classification for Analyzing Latex Yield Variability in Yunnan, China. Forests, 8(5), 162. https://doi.org/10.3390/f8050162





