A Basal Area Increment-Based Approach of Site Productivity Evaluation for Multi-Aged and Mixed Forests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
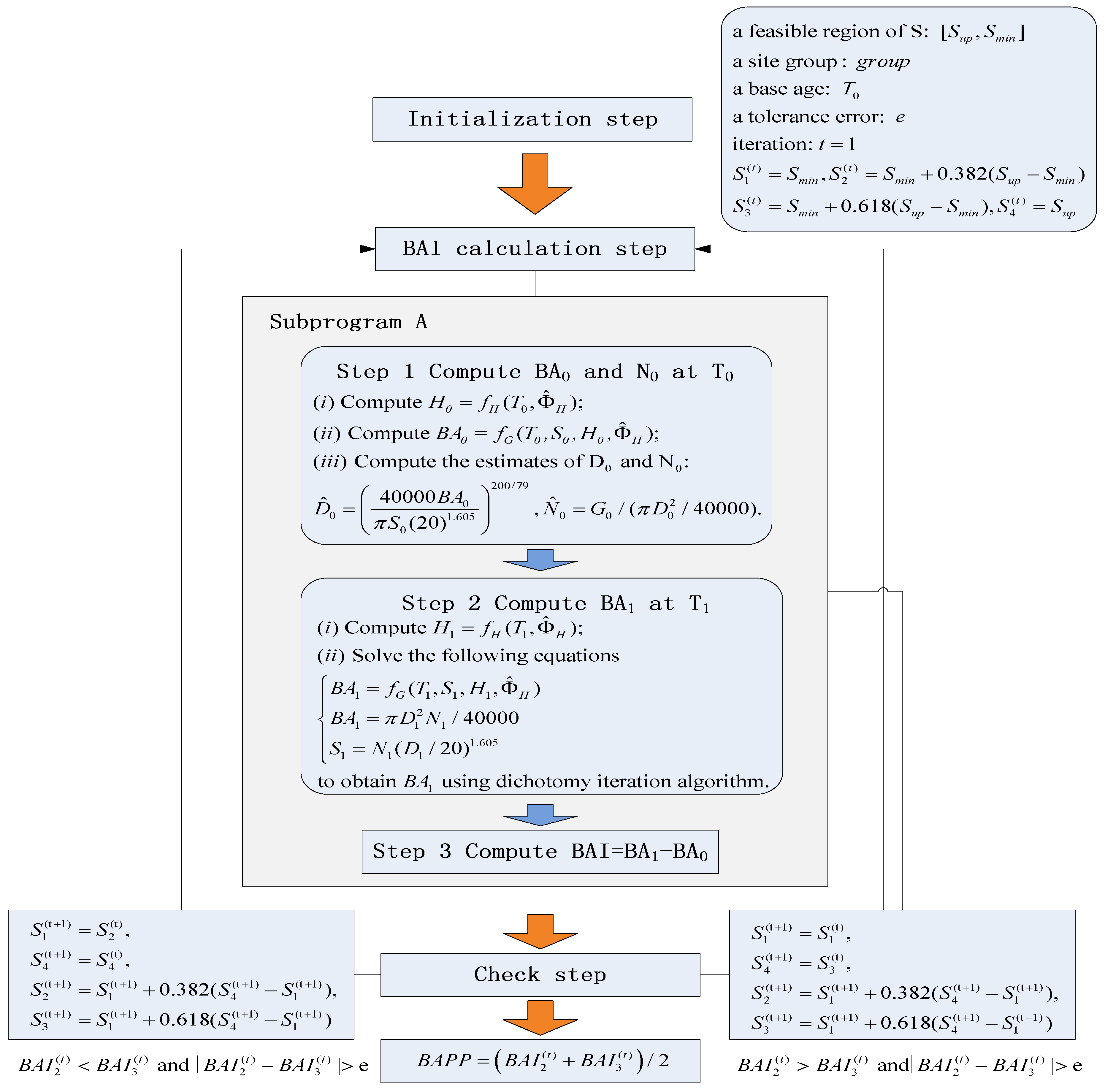
2.2. Basal Area Potential Productivity Index
- (i)
- Stability: BAPP is dependent on site type, stand type, and T. Thus, when these variables are quantified, BAPP can be determined.
- (ii)
- Maximization: BAPP reflects the maximum mean annual BAI of a particular site type, stand type, and T; therefore, the mean annual BAI of a stand is always less than or equal to BAPP. However, in theory, the mean annual BAI can be close, or even equal to BAPP for an appropriately managed stand.
Computational Conditions for BAPP
2.2.1. The GS&DIA Procedure
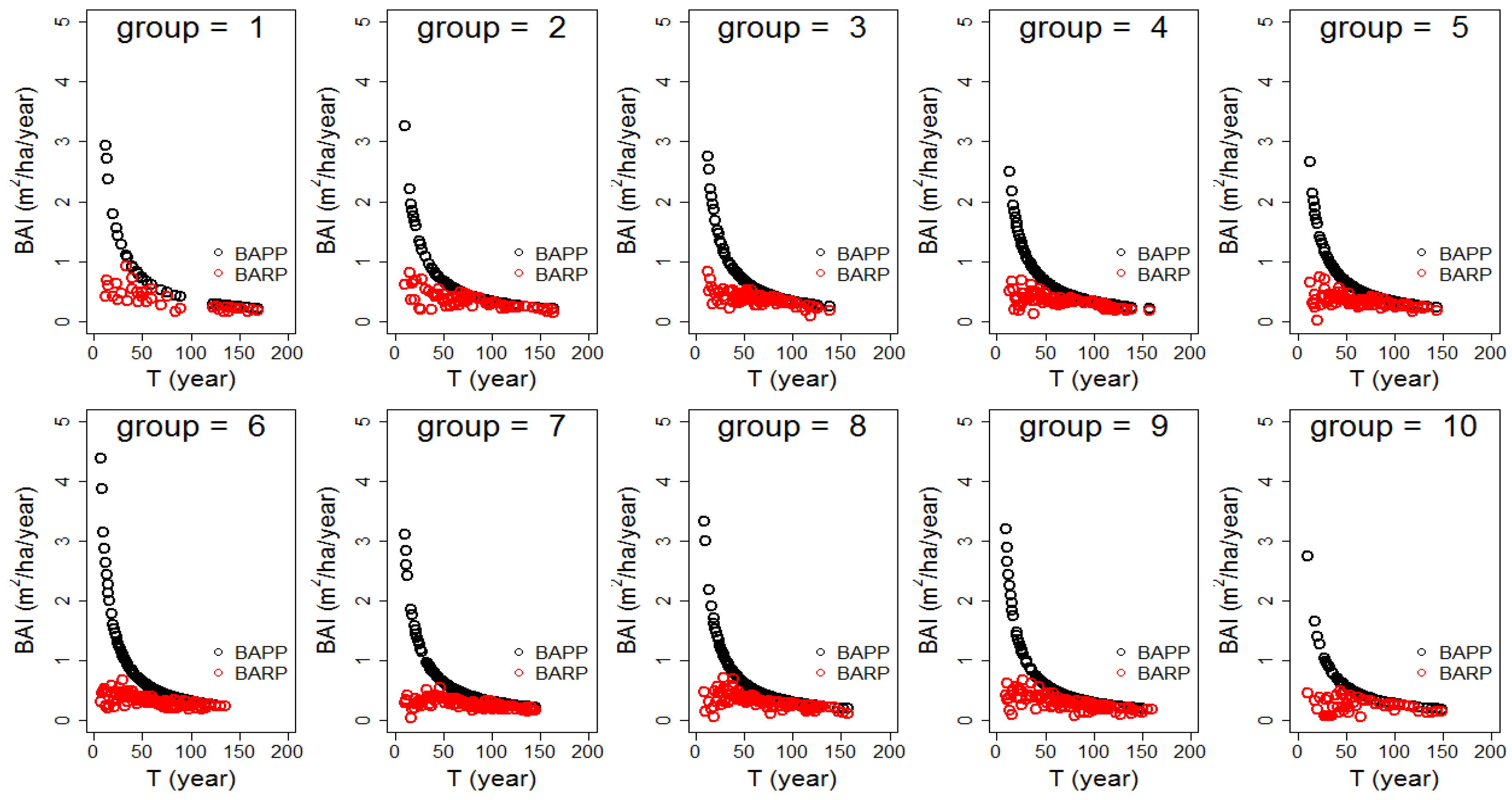
2.3. BARP
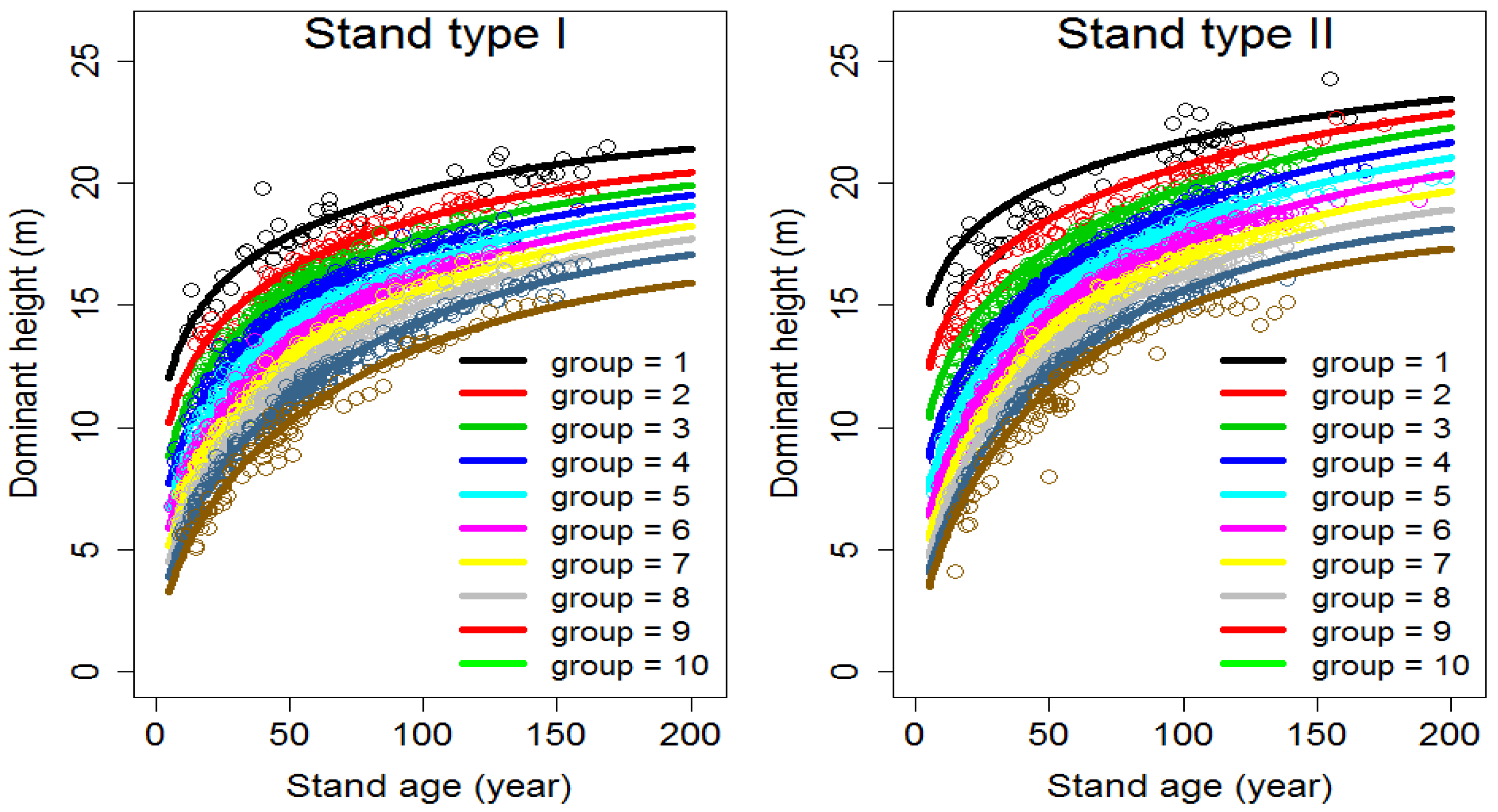
2.4. Stand Mean Height and Stand Basal Area Growth Models
3. Results
3.1. Parameter Estimation
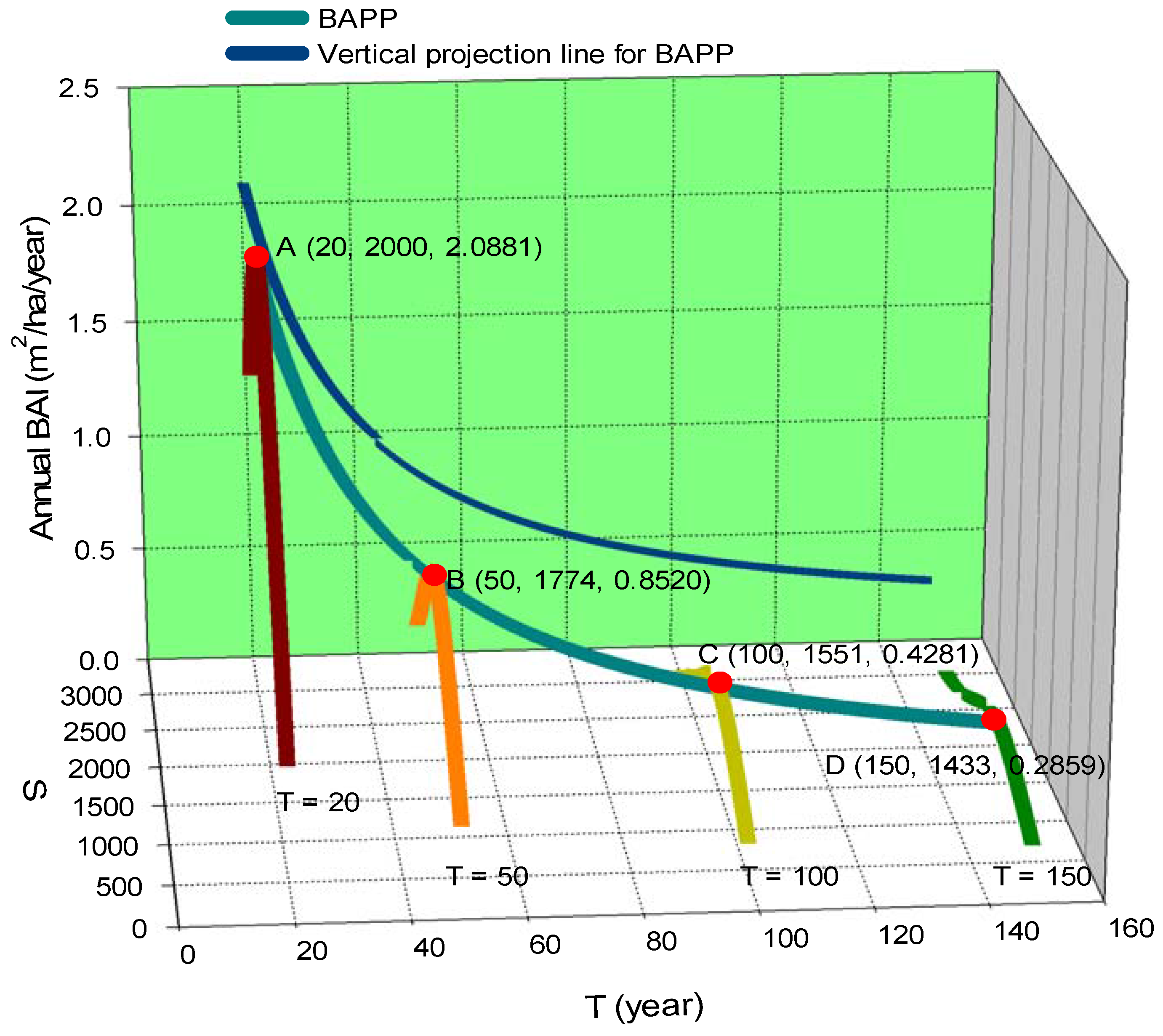
3.2. BAPP Calculation
- (i)
- Equation (12) was used as a growth model, and its parameter estimates are given in Table 2;
- (ii)
- Equation (13) was used as a growth model, and its parameter estimates are listed in Table 2;
- (iii)
- Ten site groups denoted by were applied.
- (iv)
- The feasible range of ranged from 10 to 150 years.
- (v)
- A 50-year base age () was used.
- (vi)
- The feasible region of ranged from 30 to 3000.
3.3. BAPP Verification
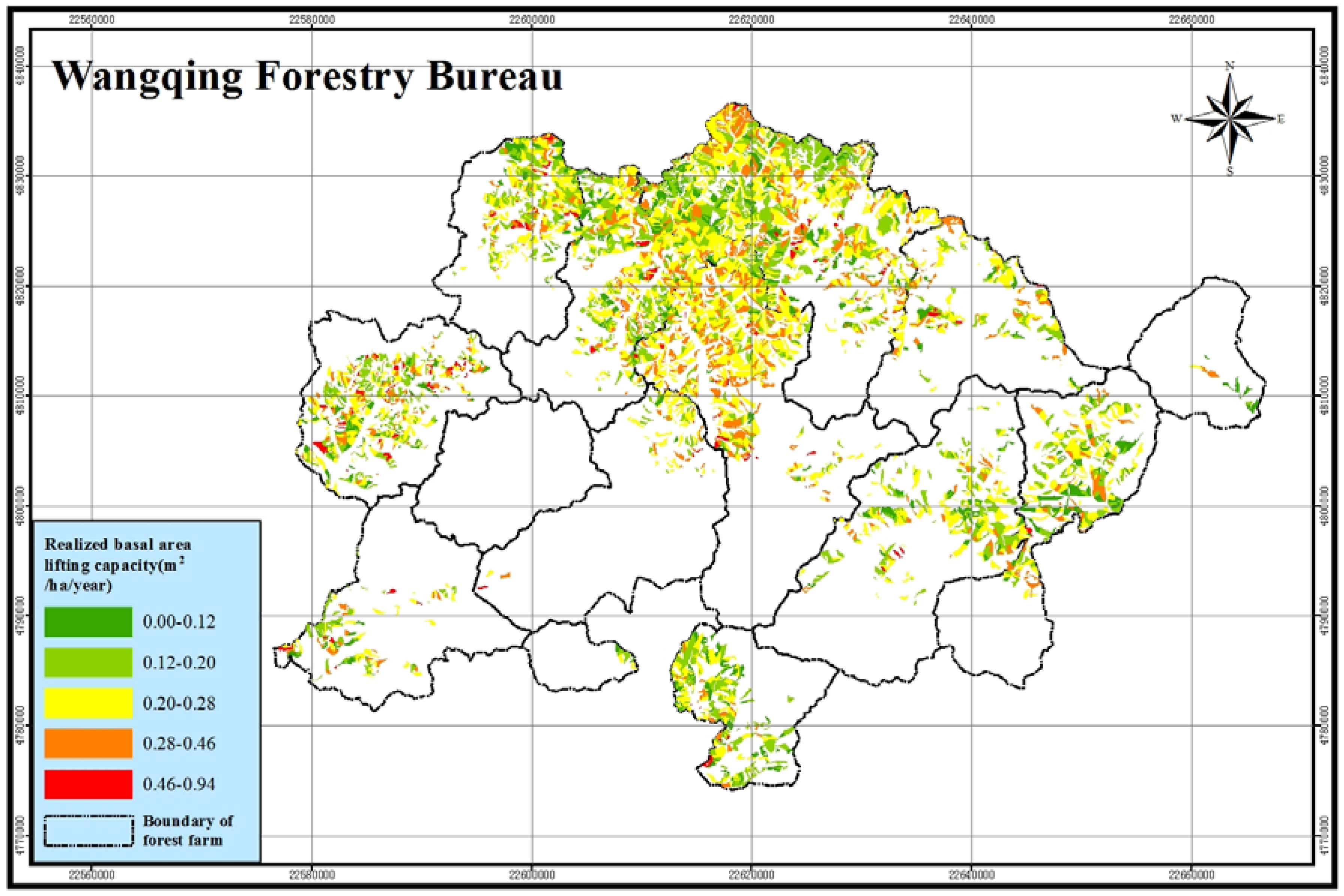
3.4. Application of BAPP in Forest Management
4. Discussion
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Skovsgaard, J.P.; Vanclay, J.K. Forest site productivity: A review of the evolution of dendrometric concepts for even-aged stands. Forestry 2008, 81, 13–31. [Google Scholar] [CrossRef]
- Jiang, H.; Radtke, P.J.; Weiskittel, A.R.; Coulston, J.W.; Guertin, P.J. Climate- and soil-based models of site productivity in eastern US tree species. Can. J. For. Res. 2015, 45, 325–342. [Google Scholar] [CrossRef]
- Del Río, M.; Pretzsch, H.; Alberdi, I.; Bielak, K.; Bravo, F.; Brunner, A.; Condés, S.; Ducey, M.J.; Fonseca, T.; von Lüpke, N.; et al. Characterization of the structure, dynamics, and productivity of mixed-species stands: Review and perspectives. Eur. J. For. Res. 2016, 135, 23–49. [Google Scholar] [CrossRef]
- Schnur, G.L. Yield, Stand, and Volume Tables for Even-Aged Upland Oak Forests; USDA Technical Bulletin 560; US Department of Agriculture: Washington, DC, USA, 1937.
- Carmean, W.H. Forest site quality evaluation in the United States. Adv. Agron. 1975, 27, 209–267. [Google Scholar]
- Vanclay, J.K. Assessing site productivity in tropical moist forests. For. Ecol. Manag. 1992, 54, 257–287. [Google Scholar] [CrossRef]
- Pokharel, B.; Dech, J.P. An ecological land classification approach to modeling the production of forest biomass. For. Chron. 2011, 87, 23–32. [Google Scholar] [CrossRef]
- Sharma, R.P.; Brunner, A.; Eid, T. Site index prediction from site and climate variables for Norway spruce and Scots pine in Norway. Scand. J. For. Res. 2012, 27, 619–636. [Google Scholar] [CrossRef]
- Sharma, R.P.; Brunner, A.; Eid, T.; Øyen, B.-H. Modelling dominant height growth from national forest inventory individual tree data with short time series and large age errors. For. Ecol. Manag. 2011, 262, 2162–2175. [Google Scholar] [CrossRef]
- Berrill, J.; O’Hara, K.L. Estimating site productivity in irregular stand structures by indexing the basal area or volume increment of the dominant species. Can. J. For. Res. 2014, 44, 92–100. [Google Scholar] [CrossRef]
- Monserud, R.A. Height growth and site index curves for inland Douglas-fir based on stem analysis data and forest habitat type. For. Sci. 1984, 30, 943–965. [Google Scholar]
- Huang, S.; Titus, S.J. An index of site productivity for uneven-aged or mixed-species stands. Can. J. For. Res. 1993, 23, 558–562. [Google Scholar] [CrossRef]
- Peng, C. Growth and yield models for uneven-aged stands: Past, present and future. For. Ecol. Manag. 2000, 132, 259–279. [Google Scholar] [CrossRef]
- Pokharel, B.; Froese, R.E. Representing site productivity in the basal area increment model for FVS-Ontario. For. Ecol. Manag. 2009, 258, 657–666. [Google Scholar] [CrossRef]
- Aertsen, W.; Kint, V.; Van Orshoven, J.; Özkan, K.; Muys, B. Comparison and ranking of different modelling techniques for prediction of site index in Mediterranean mountain forests. Ecol. Model. 2010, 221, 1119–1130. [Google Scholar] [CrossRef]
- Herrera-Fernández, J.J.; Campos, J.J.; Kleinn, C. Site productivity estimation using height-diameter relationships in Costa Rican secondary forests. Investig. Agrar. Sist. Recur. Fo. r 2004, 13, 295–303. [Google Scholar]
- Diaci, J.; Kerr, G.; O’Hara, K. Twenty-first century forestry: Integrating ecologically based, uneven-aged silviculture with increased demands on forests. Forestry 2011, 84, 463–465. [Google Scholar] [CrossRef]
- State Forestry Administration of China (SFA). Technical Regulation on Sample Collections for Tree Biomass Modeling; China Standard Press: Beijing, China, 2015; 11p. (In Chinese) [Google Scholar]
- Chen, Y.F. Research on standard age affecting analysis of site quality evaluation. For. Res. 2010, 23, 283–287, (In Chinese with English Abstract). [Google Scholar]
- Shen, C.C.; Lei, X.D.; Liu, H.Y.; Wang, L.L.; Liang, W.J. Potential impacts of regional climate change on site productivity of Larixolgensis plantations in Northeast China. iForest 2015, 8, 642–651. [Google Scholar] [CrossRef]
- Zhao, L.; Ni, C.C.; Nigh, G. Generalized algebraic difference site index model for ponderosa pine in British Columbia, Canada. Sci. Silva. Sin. 2012, 48, 74–81, (In Chinese with English Abstract). [Google Scholar]
- Raulier, F.; Lambert, M.; Pothier, D.; Ung, C. Impact of dominant tree dynamics on site index curves. For. Ecol. Manag. 2003, 184, 65–78. [Google Scholar] [CrossRef]
- Rozas, V. Tree age estimates in Fagus sylvatica and Quercusrobur: Testing previous and improved methods. Plant. Ecol. 2003, 167, 193–212. [Google Scholar] [CrossRef]
- Reineke, L.H. Perfecting a stand-density index for even-aged forests. J. Agric. Res. 1933, 46, 627–638. [Google Scholar]
- Tang, S.; Meng, C.H.; Meng, F.; Wang, Y.H. A growth and self-thinning model for pure even-age stands: Theory and applications. For. Ecol. Manag. 1994, 70, 67–73. [Google Scholar] [CrossRef]
- Zhu, G. Site Quality Classification and Site Productivity Evaluation for Forest Lands in Jilin Province; Postdoctoral Research Report; Chinese Academy of Forestry: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Lou, M.; Zhang, H.; Lei, X.; Li, C.; Zang, H. Spatial Autoregressive Models for Stand Top and Stand Mean Height Relationship in Mixed Quercus mongolica Broadleaved Natural Stands of Northeast China. Forests 2016, 7, 43. [Google Scholar] [CrossRef]
- Schwefel, P.H.P. Evolution and Optimum Seeking: The Sixth Generation; John Wiley & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Tang, S.Z.; Li, Y.; Fu, L.Y. Statistical Foundation for Bio-Mathematical Models, 2nd ed.; Higher Education Press: Beijing, China, 2015; 435p. (In Chinese) [Google Scholar]
- Tang, S.; Lang, K.; Li, H. Statistical and Biological Mathematical Model (ForStat Tutorial); Science Press: Beijing, China, 2008; 584p. (In Chinese) [Google Scholar]
- Tang, S. Integrated stand growth model of Masson pine (Pinusmassoniana Lamb.) and its application. For. Res. 1991, 4, 8–14, (In Chinese with English Abstract). [Google Scholar]
- Adame, P.; Cañellas, I.; Roig, S.; Río, M.D. Modelling dominant height growth and site index curves for rebollo oak (Quercuspyrenaica Willd.). Ann. For. Sci. 2006, 63, 929–940. [Google Scholar] [CrossRef]
- Sturtevant, B.R.; Seagle, S.W. Comparing estimates of forest site quality in old secon-growth oak forests. Forest Ecol. Manag. 2004, 191, 311–328. [Google Scholar] [CrossRef]
- Smith, V.G. Asymptotic site-index curves, fact or artifact? For. Chron. 1984, 60, 150–156. [Google Scholar] [CrossRef]
- Alemdag, I.S. National site-index and height-growth curves for white spruce growing in natural stands in Canada. Can. J. For. Res. 1991, 21, 1466–1474. [Google Scholar] [CrossRef]
- Meng, S.X.; Huang, S. Improved calibration of nonlinear mixed-effects models demonstrated on a height growth function. For. Sci. 2009, 55, 239–248. [Google Scholar]
- Fu, L.Y.; Li, Y.C.; Li, C.M.; Tang, S.Z. Study of the dominant height for Chinese Fir plantation using two-level nonlinear mixed effects model. For. Res. 2011, 24, 720–726, (In Chinese with English Abstract). [Google Scholar]
- Tang, S.; Meng, F.; Meng, C. The impact of initial stand density and site index on maximum stand density index and self-thinning index in a stand self-thinning model. For. Ecol. Manag. 1995, 75, 61–68. [Google Scholar] [CrossRef]
- Cañellas, I.; Del Río, M.; Roig, S.; Montero, G. Growth response to thinning in Quercuspyrenaica Willd. coppice stands in Spanish central mountain. Ann. For. Sci. 2004, 61, 243–250. [Google Scholar] [CrossRef]
- Knutti, R. Should we believe model predictions of future climate change? Philos. Trans. R. Soc. 2008, 366, 4647–4664. [Google Scholar] [CrossRef] [PubMed]
- Wang, C. Biomass allometric equations for 10 co-occurring tree species in Chinese temperate forests. For. Ecol. Manag. 2006, 222, 9–16. [Google Scholar] [CrossRef]
- Leng, W.; He, H.S.; Bu, R.; Dai, L.; Hu, Y.; Wang, X. Predicting the distributions of suitable habitat for three larch species under climate warming in Northeastern China. For. Ecol. Manag. 2008, 254, 420–428. [Google Scholar] [CrossRef]
- Lei, X.; Yu, L.; Hong, L. Climate-sensitive integrated stand growth model (CS-ISGM) of Changbai larch (Larixolgensis) plantations. For. Ecol. Manag. 2016, 376, 265–275. [Google Scholar] [CrossRef]


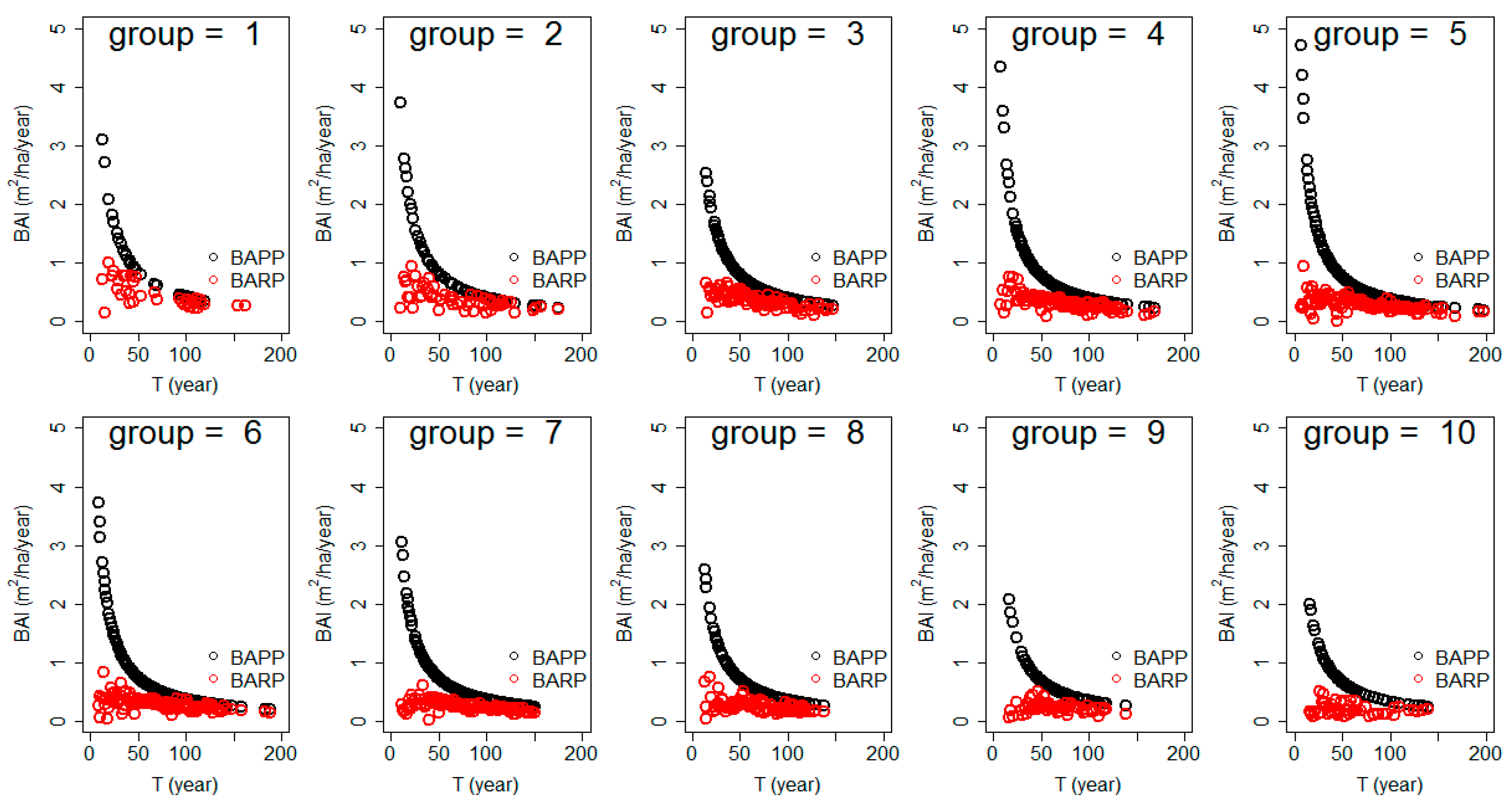

| Stand Type | Variable | Max. | Min. | Mean | Std. |
|---|---|---|---|---|---|
| I | (m2 ha−1) | 61.19 | 0.21 | 20.87 | 10.30 |
| 1857.97 | 10.45 | 731.24 | 321.56 | ||
| T (year) | 169 | 6 | 59 | 29 | |
| H (m) | 21.51 | 5.04 | 13.51 | 2.71 | |
| II | (m2 ha−1) | 55.47 | 0.07 | 18.93 | 9.15 |
| 1541.27 | 3.90 | 651.37 | 279.07 | ||
| T (year) | 198 | 7 | 63 | 31 | |
| H (m) | 24.24 | 4.11 | 15.08 | 2.81 |
| Stand Type | Site Group | Equation (12) | Equation (13) | |||||
|---|---|---|---|---|---|---|---|---|
| I | 22.8815 | 0.0059 | 0.1818 | 57.3370 | 54.4206 | 5.4439 | 0.1843 | |
| 22.0010 | 0.0063 | 0.2216 | 68.0126 | 54.4206 | 5.4439 | 0.1843 | ||
| 21.5656 | 0.0067 | 0.2615 | 66.6466 | 54.4206 | 5.4439 | 0.1843 | ||
| 21.2149 | 0.0070 | 0.3013 | 72.8284 | 54.4206 | 5.4439 | 0.1843 | ||
| 20.8084 | 0.0074 | 0.3412 | 62.8744 | 54.4206 | 5.4439 | 0.1843 | ||
| 20.4139 | 0.0078 | 0.3810 | 60.2647 | 54.4206 | 5.4439 | 0.1843 | ||
| 19.9569 | 0.0082 | 0.4209 | 64.6764 | 54.4206 | 5.4439 | 0.1843 | ||
| 19.3855 | 0.0086 | 0.4607 | 67.7971 | 54.4206 | 5.4439 | 0.1843 | ||
| 18.6787 | 0.0090 | 0.5006 | 65.6484 | 54.4206 | 5.4439 | 0.1843 | ||
| 17.4138 | 0.0094 | 0.5404 | 65.4586 | 54.4206 | 5.4439 | 0.1843 | ||
| II | 27.5375 | 0.0016 | 0.1253 | 70.1663 | 11.6575 | 5.1463 | 0.1919 | |
| 26.5008 | 0.0028 | 0.1767 | 83.1320 | 11.6575 | 5.1463 | 0.1919 | ||
| 25.4642 | 0.0040 | 0.2280 | 80.1126 | 11.6575 | 5.1463 | 0.1919 | ||
| 24.4275 | 0.0052 | 0.2794 | 83.9506 | 11.6575 | 5.1463 | 0.1919 | ||
| 23.3909 | 0.0064 | 0.3308 | 78.3488 | 11.6575 | 5.1463 | 0.1919 | ||
| 22.3542 | 0.0076 | 0.3822 | 76.4004 | 11.6575 | 5.1463 | 0.1919 | ||
| 21.3175 | 0.0088 | 0.4335 | 86.6588 | 11.6575 | 5.1463 | 0.1919 | ||
| 20.2809 | 0.0100 | 0.4849 | 73.0883 | 11.6575 | 5.1463 | 0.1919 | ||
| 19.2442 | 0.0113 | 0.5363 | 90.4887 | 11.6575 | 5.1463 | 0.1919 | ||
| 18.2075 | 0.0125 | 0.5877 | 74.8134 | 11.6575 | 5.1463 | 0.1919 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, L.; Sharma, R.P.; Zhu, G.; Li, H.; Hong, L.; Guo, H.; Duan, G.; Shen, C.; Lei, Y.; Li, Y.; et al. A Basal Area Increment-Based Approach of Site Productivity Evaluation for Multi-Aged and Mixed Forests. Forests 2017, 8, 119. https://doi.org/10.3390/f8040119
Fu L, Sharma RP, Zhu G, Li H, Hong L, Guo H, Duan G, Shen C, Lei Y, Li Y, et al. A Basal Area Increment-Based Approach of Site Productivity Evaluation for Multi-Aged and Mixed Forests. Forests. 2017; 8(4):119. https://doi.org/10.3390/f8040119
Chicago/Turabian StyleFu, Liyong, Ram P. Sharma, Guangyu Zhu, Haikui Li, Lingxia Hong, Hong Guo, Guangshuang Duan, Chenchen Shen, Yuancai Lei, Yutang Li, and et al. 2017. "A Basal Area Increment-Based Approach of Site Productivity Evaluation for Multi-Aged and Mixed Forests" Forests 8, no. 4: 119. https://doi.org/10.3390/f8040119
APA StyleFu, L., Sharma, R. P., Zhu, G., Li, H., Hong, L., Guo, H., Duan, G., Shen, C., Lei, Y., Li, Y., Lei, X., & Tang, S. (2017). A Basal Area Increment-Based Approach of Site Productivity Evaluation for Multi-Aged and Mixed Forests. Forests, 8(4), 119. https://doi.org/10.3390/f8040119








