Evaluation of Bent Trees in Juvenile Teak (Tectona grandis L.f.) Plantations in Costa Rica: Effects on Tree Morphology and Wood Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Studied Plantations
2.2. Sampling Procedures
2.3. Information Collected
2.4. Analysis of Field Data
2.5. Destructive Study in Site 6 (54-Month-Old Plantation)
3. Results
3.1. Morphological Characteristics of the Trees and Stand Density in Sampled Plantations
3.2. Incidence of Bent Trees and Bending Height
3.3. Relationship between the Morphological Characteristics and Bending Height
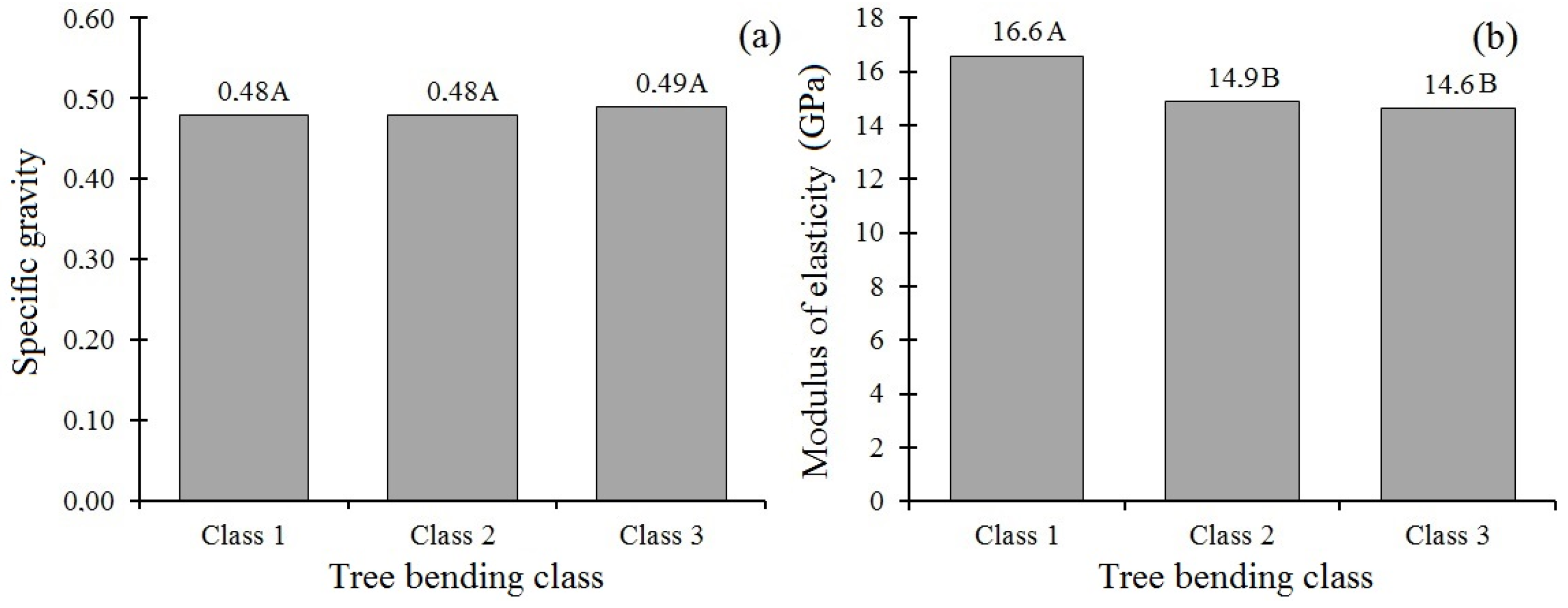
3.4. Destructive Study in the Plantation Site 6 (54-Month-Old Plantation)
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kollert, W.; Cherubini, L. Teak Resources and Market Assessment 2010. FAO Planted Forests and Trees Working Paper FP/47/E, Rome. 2012. Available online: http://www.fao.org/forestry/plantedforests/67508@170537/en/ (accessed on 22 November 2016).
- Moya, R.; Bond, B.; Quesada-Pineda, H. A review of heartwood properties of Tectona grandis trees from fast-growth plantations. Wood Sci. Technol. 2014, 48, 411–433. [Google Scholar] [CrossRef]
- Keogh, R. The Future of Teak and the High-Grade Tropical Hardwood Sector: Planted Forests and Trees Working Paper FP/44E. 2009. Available online: http://www.fao.org/forestry/site/10368/en/ (accessed on 24 November 2016).
- Kumar, B.M.; Long, J.N.; Kumar, P. A density management diagram for teak plantations of Kerala in peninsular India. For. Ecol. Manag. 1995, 74, 125–131. [Google Scholar] [CrossRef]
- Bhat, K.M.; Priya, P.B.; Rugmini, P. Characterisation of juvenile wood in teak. Wood Sci. Technol. 2001, 34, 517–532. [Google Scholar] [CrossRef]
- Cassidy, M.; Palmer, G.; Smith, R.G.B. The effect of wide initial spacing on wood properties in plantation grown Eucalyptus pilularis. New For. 2013, 44, 919–936. [Google Scholar] [CrossRef]
- Pérez, D.; Kanninen, M. Stand growth scenarios for Tectona grandis plantations in Costa Rica. For. Ecol. Manag. 2005, 210, 425–441. [Google Scholar] [CrossRef]
- Tewari, V.P.; Álvarez-González, J.G.; García, O. Developing a dynamic growth model for teak plantations in India. For. Ecosyst. 2014, 1, 1–9. [Google Scholar] [CrossRef]
- Boše, M.; Konôpka, B.; Šebeň, V.; Vladovič, J.; Tobin, B. Modelling height to diameter ratio—An opportunity to increase Norway spruce stand stability in the Western Carpathians. For. J. 2014, 60, 71–80. [Google Scholar] [CrossRef]
- Nunes, L.; Gower, S.T.; Monteiro, M.L.; Lopes, D.; Rego, F.C. Growth dynamics and productivity of pure and mixed Castanea sativa Mill. and Pseudotsuga menziesii (Mirb.) Franco plantations in northern Portugal. iFor. Biogeosci. For. 2014, 7, 93–107. [Google Scholar]
- Opio, C.; Jacob, N.; Coopersmith, D. Height to diameter ratio as a competition index for young conifer plantations in northern British Columbia, Canada. For. Ecol. Manag. 2000, 137, 245–252. [Google Scholar] [CrossRef]
- Shibuya, M.; Koizumi, A.; Torita, H. Tree shape and resistance to uprooting: A simple model analysis. Eurasian J. For. Res. 2014, 17, 11–17. [Google Scholar]
- James, K.R.; Haritos, N.; Ades, P.K. Mechanical stability of trees under dynamic loads. Am. J. Bot. 2006, 93, 1522–1530. [Google Scholar] [CrossRef] [PubMed]
- Cucchi, V.; Meredieu, C.; Stokes, A.; Berthier, S.; Bert, D.; Najar, M.; Denis, A.; Lastennet, R. Root anchorage of inner and edge trees in stands of Maritime pine (Pinus pinaster Ait.) growing in different podzolic soil conditions. Trees 2004, 18, 460–466. [Google Scholar] [CrossRef]
- Mitchell, S.J. Wind as a natural disturbance agent in forests: A synthesis. Forestry 2013, 86, 147–157. [Google Scholar] [CrossRef]
- Kilpatrick, D.J.; Sanderson, J.M.; Savill, P.S. The influence of five early respacing treatments on the growth of Sitka spruce. Forestry 1981, 54, 17–29. [Google Scholar] [CrossRef]
- Cremer, K.W.; Borough, C.J.; McKinnel, F.H.; Carter, P.R. Effects of stocking and thinning on wind damage in plantations. N. Z. J. For. Sci. 1982, 12, 244–268. [Google Scholar]
- Moore, J.R. Differences in maximum resistive bending moments of Pinus radiata trees grown on a range of soil types. For. Ecol. Manag. 2000, 135, 63–71. [Google Scholar] [CrossRef]
- Jones, T.G.; Downes, G.M.; Watt, M.S.; Kimberley, M.O.; Culvenor, D.S.; Ottenschlaeger, M.; Xue, J. Effect of stem bending and soil moisture on the incidence of resin pockets in radiata pine. N. Zeal. J. For. Sci. 2013, 43, 10. [Google Scholar]
- Van Gelder, H.A.; Poorter, L.; Sterck, F.J. Wood mechanics, allometry, and life-history variation in a tropical rain forest tree community. New Phytol. 2006, 171, 367–378. [Google Scholar] [CrossRef] [PubMed]
- Anten, N.P.; Schieving, F. The role of wood mass density and mechanical constraints in the economy of tree architecture. Am. Nat. 2009, 175, 250–260. [Google Scholar] [CrossRef] [PubMed]
- Braz, R.L.; da Silva Oliveira, J.T.; Rosado, A.M.; Vidaurre, G.B.; Paes, J.B. Parâmetros dendrométricos e resistência mecânica das arvores de clones de Eucalyptus em áreas sujeitas a ação dos ventos. Ciência Florestal 2014, 24, 945–956. [Google Scholar] [CrossRef]
- Monteuuis, O.; Goh, D.K.; Garcia, C.; Alloysius, D.; Gidiman, J.; Bacilieri, R.; Chaix, G. Genetic variation of growth and tree quality traits among 42 diverse genetic origins of Tectona grandis planted under humid tropical conditions in Sabah, East Malaysia. Tree Genet. Gen. 2011, 7, 1263–1275. [Google Scholar] [CrossRef]
- Chaix, G.; Monteuuis, O.; Garcia, C.; Alloysius, D.; Gidiman, J.; Bacilieri, R.; Goh, D.K. Genetic variation in major phenotypic traits among diverse genetic origins of teak (Tectona grandis L.f.) planted in Taliwas, Sabah, East Malaysia. Ann. For. Sci. 2011, 68, 1015–1026. [Google Scholar] [CrossRef]
- Ladrach, W. Alternativas para el raleo de plantaciones de teca (Tectona grandis L.). Rev. For. Mesoam. 2012, 6, 6–15. [Google Scholar]
- Frankie, G.W.; Baker, H.G.; Opler, P.A. Comparative phenological studies of trees in tropical wet and dry forests in the lowlands of Costa Rica. J. Ecol. 1974, 62, 881–919. [Google Scholar] [CrossRef]
- Jaouen, G.; Alméras, T. How to determine sapling buckling risk with only a few measurements. Am. J. Bot. 2007, 94, 1583–1593. [Google Scholar] [CrossRef] [PubMed]
- American Society for Testing and Materials (ASTM). ASTM D-4442–92 (Reproved 2003), Standard Test Methods for Direct Moisture Content Measurements of Wood and Wood-Base Materials; ASTM: West Conshohocken, PA, USA, 2003. [Google Scholar]
- American Society for Testing and Materials (ASTM). ASTM D-1036–99 (Reproved 2003), Standard Test Methods of Static Tests of Wood Poles; ASTM: West Conshohocken, PA, USA, 2003. [Google Scholar]
- Sparks, D.L. Methods of Soil Analysis. Part 3, Chemical Methods; Soil Science Society of America: Madison, WI, USA, 1996; p. 356. [Google Scholar]
- Pérez, D. Growth and volume equations developed from stem analysis for Tectona grandis in Costa Rica. J. Trop. For. Sci. 2008, 20, 66–75. [Google Scholar]
- Víquez, E.; Pérez, D. Effect of pruning on tree growth, yield, and wood properties of Tectona grandis plantations in Costa Rica. Silva Fenn. 2005, 39, 381–390. [Google Scholar] [CrossRef]
- James, K.R.; Hallam, C.; Spencer, C. Measuring tilt of tree structural root zones under static and wind loading. Agric. For. Met. 2013, 168, 160–167. [Google Scholar] [CrossRef]
- Toky, O.P.; Bisht, R.P. Observations on the rooting patterns of some agroforestry trees in an arid region of north-western India. Agrofor. Syst. 1992, 18, 245–263. [Google Scholar] [CrossRef]
- James, K.R.; Hallam, C.; Spencer, C. Tree stability in winds: Measurements of root plate tilt. Biosyst. Eng. 2013, 115, 324–331. [Google Scholar] [CrossRef]
- Thulasidas, P.K.; Bhat, K.M. Log characteristics and sawn timber recovery of home-garden teak from wet and dry localities of Kerala, India. Small Scale For. 2008, 8, 15–24. [Google Scholar] [CrossRef]
- Malik, J.; Hopewell, G.P. Sawing Recovery of several sawmill in Jepara. J. Penelit. Has. Hutan 2011, 29, 331–342. [Google Scholar] [CrossRef]
- Saunderson, S.E.; England, A.H.; Baker, C.J. A dynamic model of the behaviour of Sitka spruce in high winds. J. Theor. Biol. 1999, 200, 249–259. [Google Scholar] [CrossRef]
- Baker, C.J. The development of a theoretical model for the wind throw of plants. J. Theor. Biol. 1995, 175, 355–372. [Google Scholar] [CrossRef]
- Guitard, G.E.; Castera, P. Experimental analysis and mechanical modelling of wind-induced tree sways. In Wind and Trees; Coutts, M.P., Grace, J., Eds.; Cambridge University Press: Cambridge, UK, 1995; pp. 182–194. [Google Scholar]
- Telewski, F.W. Wind induced physiological and developmental responses in trees. In Wind and Trees; Coutts, M.P., Grace, J., Eds.; Cambridge University Press: Cambridge, UK, 1995; pp. 237–263. [Google Scholar]
- Alméras, T.; Costes, E.; Salles, J.C. Identification of biomechanical factors involved in stem shape variability between apricot tree varieties. Ann. Bot. 2004, 93, 455–468. [Google Scholar] [CrossRef]
- Mattheck, C. Why they grow, how they grow: The mechanics of trees. Arboricult. J. 1990, 14, 1–17. [Google Scholar] [CrossRef]
- Skatter, S.; Kucera, B. Tree breakage from torsional wind loading due to crown asymmetry. For. Ecol. Manag. 2000, 135, 97–103. [Google Scholar] [CrossRef]
- Lasserre, J.P.; Mason, E.G.; Watt, M.S. Influence of the main and interactive effects of site, stand stocking and clone on Pinus radiata D. Don corewood modulus of elasticity. For. Ecol. Manag. 2008, 255, 3455–3459. [Google Scholar] [CrossRef]
- Grey, R.; Kyanka, G. Potassium fertilization effects on the static bending properties of red pine wood. For. Prod. J. 1974, 24, 92–96. [Google Scholar]
- Kjaer, E.; Kajornsrichon, S.; Lauridsen, E. Heartwood, calcium and silica content in five provenances of teak (Tectona grandis L.f.). Silvae Genet. 1998, 48, 1–3. [Google Scholar]
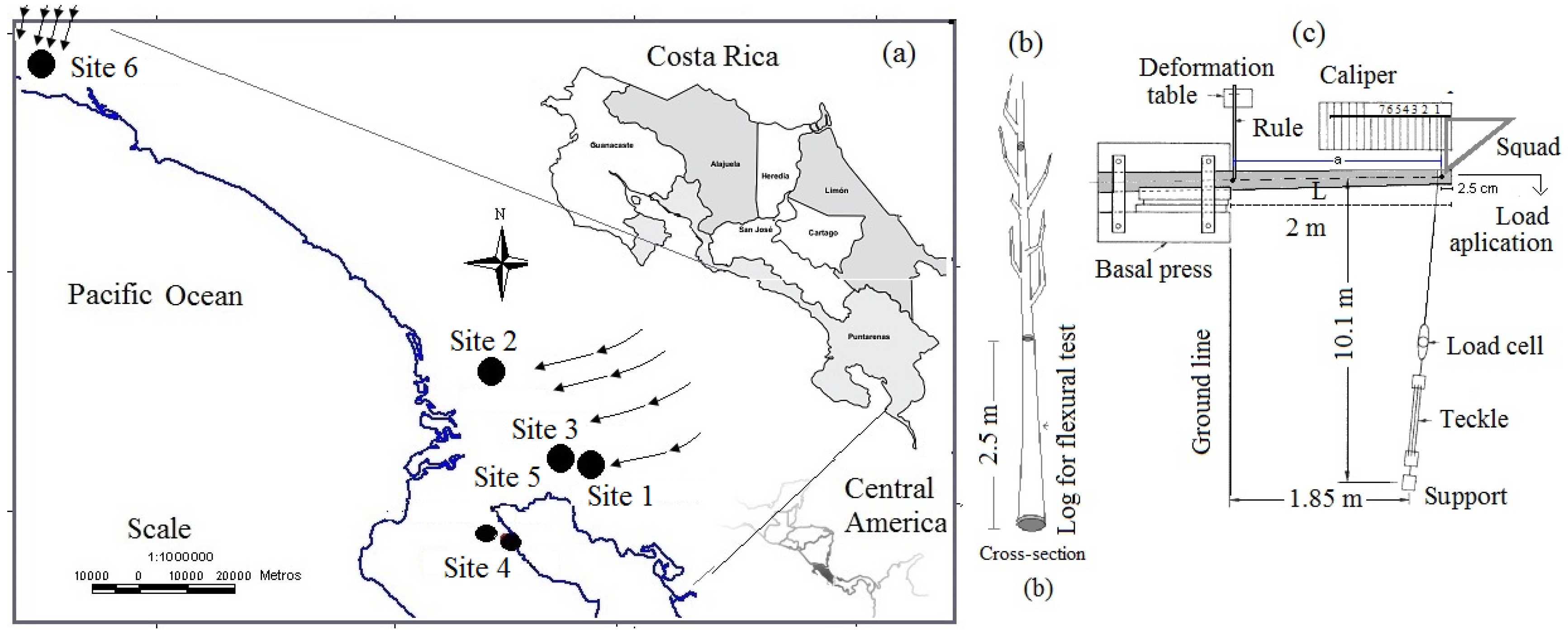

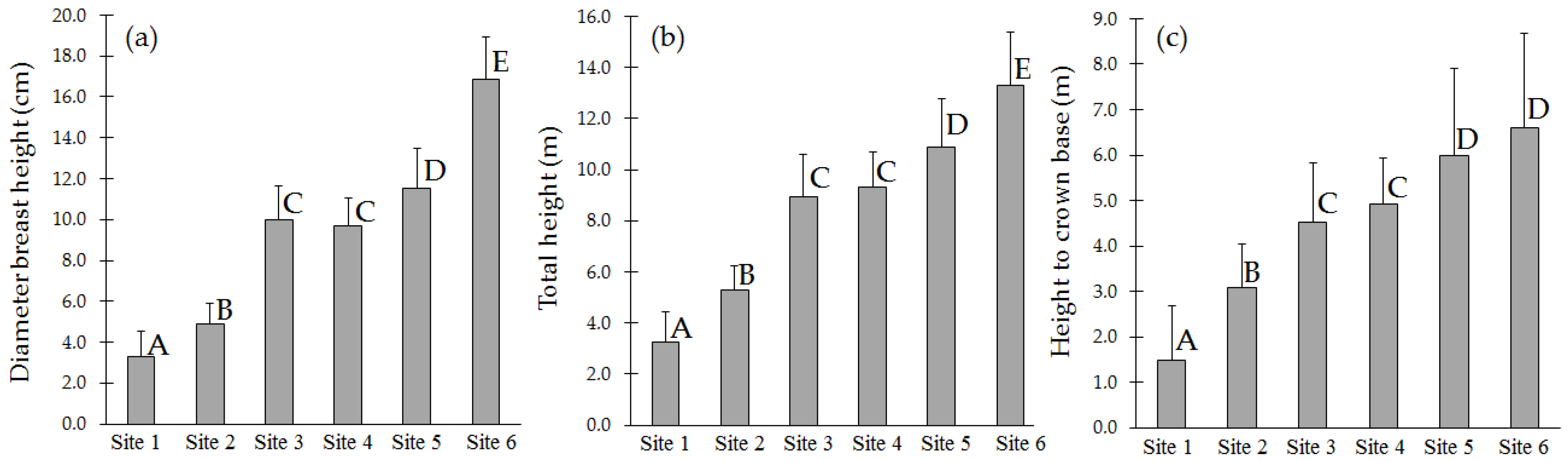
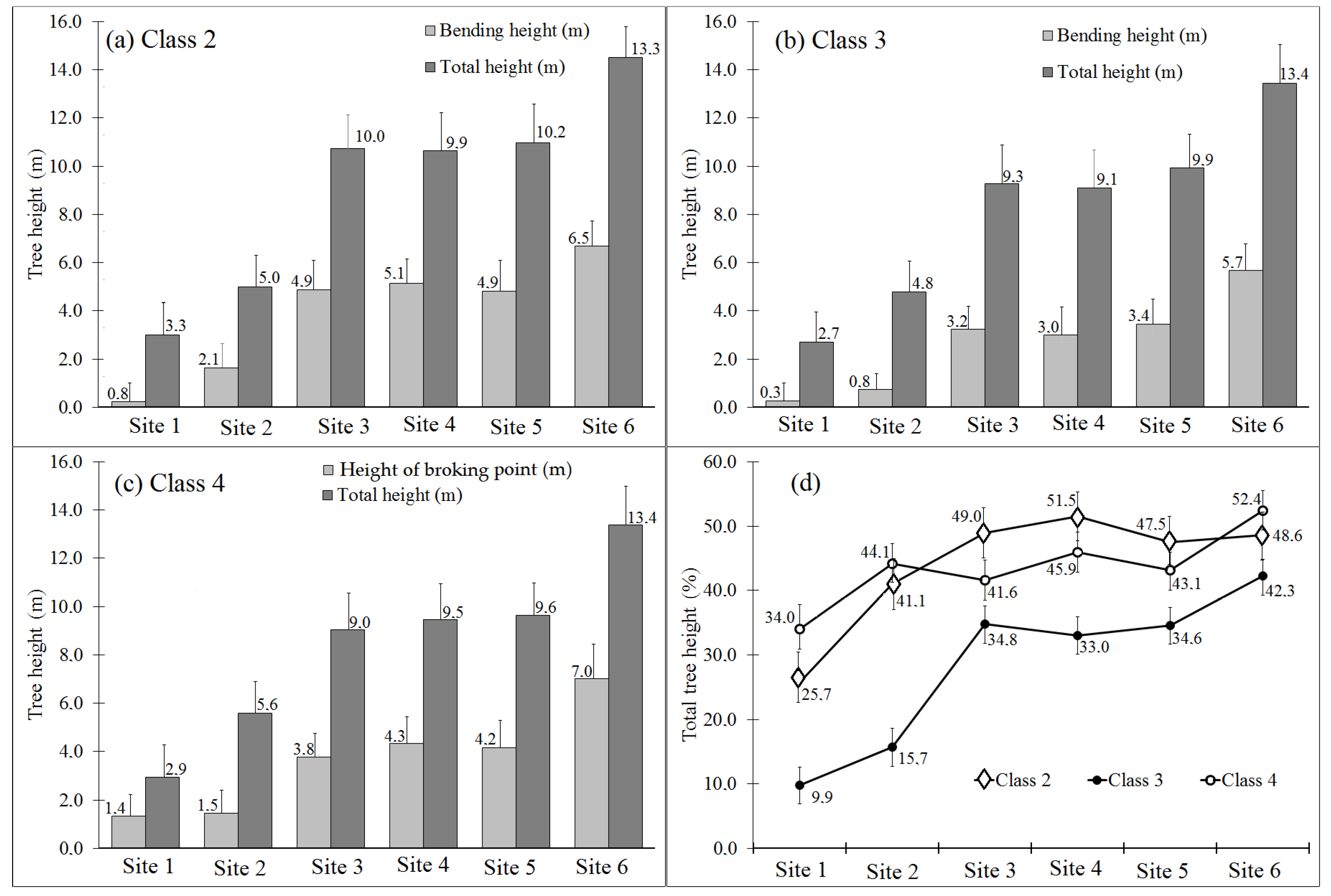
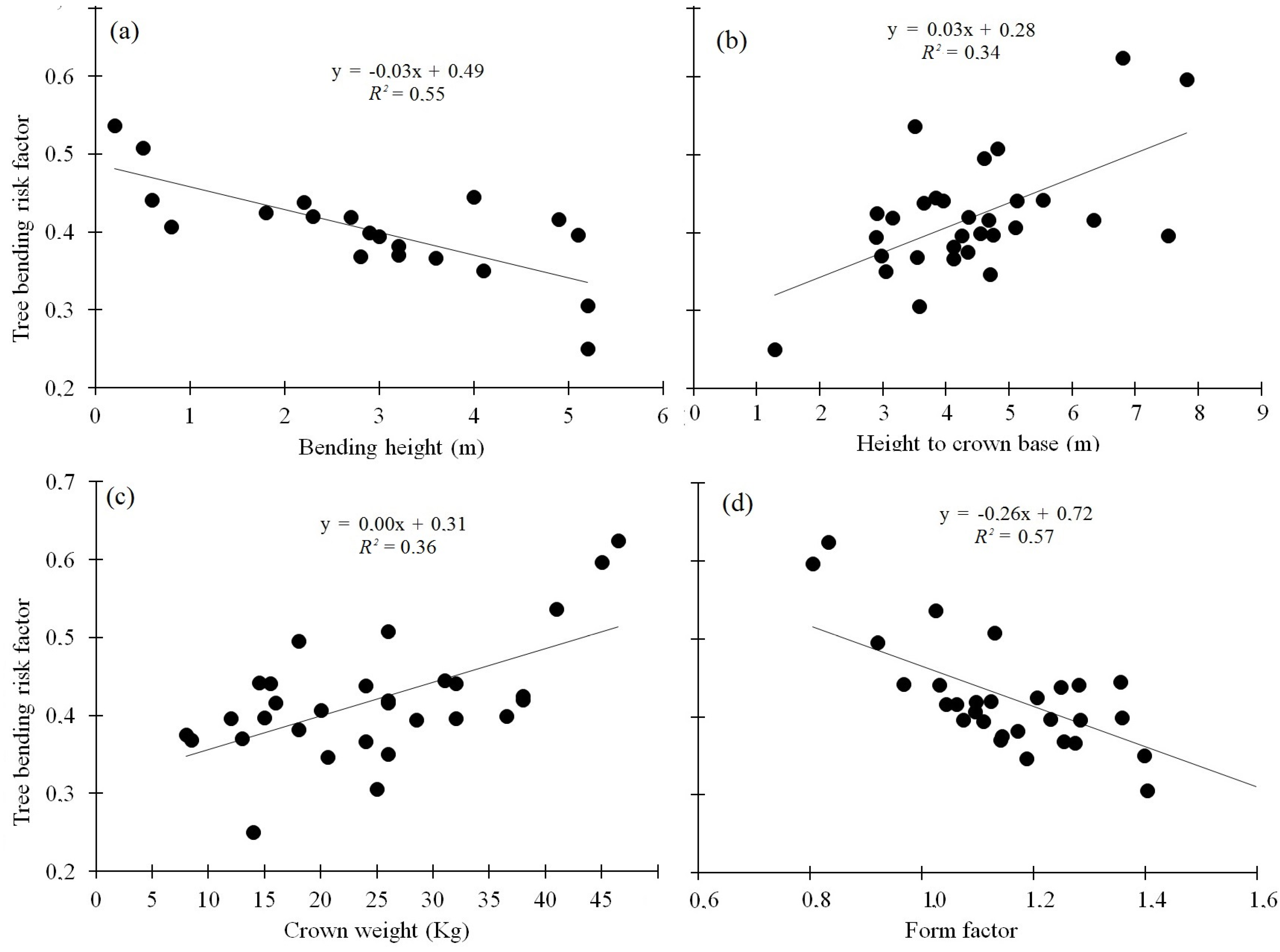
| Site and Tree Age | Soil Description | Elevation and Life Zone | Description of Topography and Climate |
|---|---|---|---|
| Site 6, 54-month-old | Soils are characterized by having little development of horizons. | 100 meters above sea level and tropical moist forest with transition to per-humid | The topography is flat. Average precipitation varies from 3000 to 3200 mm per year. The rainiest months are September and October. |
| Site 1 and 3, 8- and 27- month-old | Soils are characterized by having little development of horizons. | 100 meters above sea level and basal tropical wet forest. | The topography is flat. Annual rainfall is 4852 mm. Most rainfall occurs in September and October. |
| Site 2, 17-month-old | Soils are characterized by clay presence, with less than 35% base saturation, generally deep and well drained with relatively low fertility. | 200 meters above sea level and basal tropical wet forest. | The topography is rugged in some sectors and in others is flat. The annual average rainfall is 4000 mm, with an average of three dry months from January to March. |
| Site 4 and 6, 28- and 31- month-old | Soil is younger, with a second horizon. | 0 meters above sea level and basal tropical wet forest. | The topography is flat. The annual average rainfall is 4000 mm. The rainfall is concentrated from May to November. |
| Site | Age and Plantation | Total Area (ha) | Plantation Density (n·ha−1) | Sampled Area (ha) | Number of Plots (n) | Sampling Intensity % |
|---|---|---|---|---|---|---|
| 1 | 8-month-old | 35.8 | 932 | 6.8 | 115 | 19.1 |
| 2 | 17-month-old | 113.2 | 939 | 19.1 | 31 | 16.9 |
| 3 | 27-month-old | 24.5 | 897 | 4.7 | 94 | 19.2 |
| 4 | 28-month-old | 7.3 | 935 | 1.1 | 34 | 15.2 |
| 5 | 31-month-old | 35.5 | 944 | 6.2 | 26 | 17.6 |
| 6 | 54-month-old | 32.4 | 432 | 5.8 | 22 | 17.8 |
| Plantation | Tree | |||
|---|---|---|---|---|
| Class 1 | Class 2 | Class 3 | Class 4 | |
| Site 1 | 97.8 (±0.029) | 0.6 (±0.015) | 0.3 (±0.010) | 1.3 (±0.022) |
| Site 2 | 93.2 (±0.054) | 2.9 (±0.033) | 1.8 (±0.026) | 1.9 (±0.027) |
| Site 3 | 71.7 (±0.096) | 11.9 (±0.069) | 10.9 (±0.066) | 3.7 (±0.040) |
| Site 4 | 77.3 (±0.082) | 5.5 (±0.045) | 9.4 (±0.057) | 4.9 (±0.042) |
| Site 5 | 74.2 (±0.086) | 5.8 (±0.046) | 10.6 (±0.060) | 7.7 (±0.053) |
| Site 6 | 78.0 (±0.088) | 13.4 (±0.073) | 4.5 (±0.044) | 1.6 (±0.026) |
| Morphological Variable | Site 1 | Site 2 | Site 3 | Site 4 | Site 5 | Site 6 |
|---|---|---|---|---|---|---|
| n | 11 | 74 | 750 | 154 | 212 | 446 |
| d | 0.38 NS | 0.26 * | 0.42 ** | 0.23 ** | 0.50 ** | 0.13 NS |
| Ht | 0.41 NS | 0.45 ** | 0.54 ** | 0.50 ** | 0.44 ** | 0.03 NS |
| Hcb | 0.43 NS | 0.66 ** | 0.54 ** | 0.63 ** | 0.62 ** | 0.37 ** |
| d/Ht ratio | 0.18 NS | −0.25 * | −0.20 ** | −0.33 ** | 0.01 NS | 0.09 NS |
| Hcb/Ht ratio | 0.24 NS | 0.46 ** | 0.28 ** | 0.52 ** | 0.53 ** | 0.31 ** |
| Morphological Variable | Site 1 | Site 2 | Site 3 | Site 4 | Site 5 | Site 6 |
|---|---|---|---|---|---|---|
| R2 multiple | 0.28 | 0.47 | 0.47 | 0.48 | 0.47 | 0.15 |
| 1st parameter | Hcb R2 = 0.18 NS | Hcb R2 = 0.43 ** | Hcb R2 = 0.29 ** | Hcb R2 = 0.39 ** | Hcb R2 = 0.39 ** | Hcb R2 = 0.13 ** |
| 2nd parameter | Ht R2 = 0.10 NS | Hcb/ht ratio R2 = 04 NS | Ht R2 = 0.16 ** | Ht R2 = 0.08 ** | d R2 = 0.07 ** | d R2 = 0.01 NS |
| 3rd parameter | Hcb/ht ratio R2 = 0.02 ** | D R2 = 0.10 NS | Hcb/ht ratio R2 = 0.01 NS |
| Variable | Average | ||
|---|---|---|---|
| Class 1 | Class 2 | Class 3 | |
| d (cm) | 8.38 A | 9.69 A | 9.41 A |
| Ht (m) | 9.26 A | 9.91 A | 9.16 A |
| Hcb (m) | 5.59 A | 4.02 B | 3.58 C |
| Wc (kg) | 15.10 A | 23.25 B | 27.85 C |
| N (%) | 2.26 A | 2.59 A | 2.56 A |
| P (%) | 0.16 A | 0.23 A | 0.22 A |
| Ca (%) | 1.21 A | 1.65 B | 1.61 B |
| Mg (%) | 0.09 A | 0.22 B | 0.15 B |
| K (%) | 1.28 A | 1.16 A | 1.19 A |
| S (%) | 0.15 A | 0.16 A | 0.16 A |
| Fe (mg/kg) | 56.00 A | 63.00 A | 59.67 A |
| Cu (mg/kg) | 13.33 A | 16.00 A | 14.00 A |
| Zn (mg/kg) | 28.33 A | 31.00 A | 29.67 A |
| Mn (mg/kg) | 23.00 A | 33.67 A | 35.00 A |
| B (mg/kg) | 8.33 A | 11.67 A | 16.67 A |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guzmán, N.; Moya, R.; Murillo, O. Evaluation of Bent Trees in Juvenile Teak (Tectona grandis L.f.) Plantations in Costa Rica: Effects on Tree Morphology and Wood Properties. Forests 2017, 8, 79. https://doi.org/10.3390/f8030079
Guzmán N, Moya R, Murillo O. Evaluation of Bent Trees in Juvenile Teak (Tectona grandis L.f.) Plantations in Costa Rica: Effects on Tree Morphology and Wood Properties. Forests. 2017; 8(3):79. https://doi.org/10.3390/f8030079
Chicago/Turabian StyleGuzmán, Nancy, Roger Moya, and Olmán Murillo. 2017. "Evaluation of Bent Trees in Juvenile Teak (Tectona grandis L.f.) Plantations in Costa Rica: Effects on Tree Morphology and Wood Properties" Forests 8, no. 3: 79. https://doi.org/10.3390/f8030079
APA StyleGuzmán, N., Moya, R., & Murillo, O. (2017). Evaluation of Bent Trees in Juvenile Teak (Tectona grandis L.f.) Plantations in Costa Rica: Effects on Tree Morphology and Wood Properties. Forests, 8(3), 79. https://doi.org/10.3390/f8030079







