1. Introduction
Tree species, diameter-at-breast-height (dbh), and height are the most common individual tree attributes measured or determined in the field [
1,
2]. Dbh is the most fundamental of tree measurements and is defined as the outside-bark-stem diameter of a tree at a point on the stem that is 1.3 m above the ground from the base of the tree [
1,
3]. In forestry, the word “diameter” implies that the trees would have circular cross-sections. Yet, several studies have proved that exact circularity is rare and the form of a cross-section is more like a closed convex [
4,
5,
6,
7]. The most common methods for the field measurements of dbh are the use of calipers or diameter tapes. Diameter tapes are more commonly employed for permanent sample plots because they are perceived as being more consistent for repeated measures [
8]. However, calipers are often used and preferred for dbh measurements in temporary plots or when measuring a large number of trees, as they are quick and efficient to use [
9]. With calipers, the dbh is measured by placing the two arms of the caliper on perpendicular sides of the tree at the height of 1.3 m. One arm is fixed at the origin of the measurement scale and the other one can be moved along the scale beam of the caliper. When the two arms are pressed together against the tree trunk, a 90° angle must be formed with the scale beam. Thereafter, the diameter can be read from the scale. Although measurement of dbh using calipers is straightforward, it includes many sources of error that can cause variation in measurements. For example, when calipers are not oriented perpendicularly to the vertical axis of the stem, or when branches and other anomalies such as gnarls, wounds or branch bumps are located exactly at height of 1.3 m. Site conditions must also be considered, such as when there are steep slopes. In this context, dbh should be measured halfway between the measure at 1.3 m height on the slope’s upper and lower sides. In addition, there may be variation in how personnel use the calipers for the measurements. Conventionally, a minimum dbh threshold for measurement is specified and only those trees in a sample plot with a dbh greater than this minimum threshold are measured. The trees with a diameter less than the specified threshold often will have little effect on the derived forest attribute estimates, such as total volume or basal area, and the measurement of these small trees can be extremely time consuming and can substantially add to the plot costs [
10].
Tree height is defined as the distance between the base and the top of a standing tree [
1]. Clinometers are instruments used to measure individual tree height [
1]. These instruments are based on simple trigonometric relationships between the known planimetric distance from the instrument to the tree and the angles from the instrument to the base and top of the tree, which must be clearly visible when performing measurements [
11]. A vertex clinometer is one of the most popular instruments for measuring tree height because it is efficient, easy to calibrate, and automatically measures the distance to the tree [
1]. Height measurements in sample plots are time consuming, so it is typical to measure a sub-sample of tree heights within the sample plot; e.g., [
12,
13,
14,
15], rather than all trees in the plot [
16,
17,
18]. If only a sub-sample of tree heights is measured, the sample must be representative of the dbh frequency distribution within the plot. The heights of the unmeasured trees can then be estimated through species-specific dbh-height regression models developed from the measured sub-sample e.g., [
19,
20,
21].
Attributes of individual trees, usually collected from sample plots, are used in many forest inventory and modeling applications. A forest inventory could—in principle—be based on measuring every tree in a given area, but this would be time consuming, expensive, and unnecessarily impractical for most applications in forestry [
22]. Thus, the acquisition of forest resource information is often more efficiently based on sampling, measuring, and modeling [
1]. The most common sample units are a single tree and a plot, while the most commonly measured tree attribute is stem dbh. Some examples of the most frequently used models in forest mensuration are models for tree height or stem volume; see e.g., [
19,
20,
21,
23]. To obtain estimates over large areas, individual tree measures are summed at the sample-plot level and then sample plots are used in deriving stand-, landscape-, regional- and even global-scale estimates of forest resources [
22]. Due to this hierarchy and the capacity to propagate and exaggerate small errors through multipliers, it is highly important to measure individual tree attributes accurately and precisely. In addition, when new measurement techniques, such as terrestrial or mobile laser scanning [
24,
25,
26,
27], close-range photogrammetry [
28,
29] and mobile phone applications [
30,
31], for tree attributes are developed, their measurements are often compared to conventional caliper and clinometer measurements, which are considered as a baseline.
There have been several studies on the precision of tree dbh and height measurements. Different measurement techniques and tools have also been compared to each other. The precision and variation between several re-measurements of dbh and height have been reported for example in [
32,
33,
34,
35,
36,
37,
38]. The results of these studies have been reported using various means (e.g., mean, absolute and relative standard deviation, and bias) and straightforward comparisons of the resulting precision are not possible in all cases. In addition, the amount of measured trees and the number of repeat measurements varied widely amongst the studies, and these studies all used diameter tapes for dbh measurements instead of calipers. When collecting reference data for research and in operational use, the calipers are often preferred instead of diameter tape and thus characterizing the precision of caliper measurements is useful information for benchmarking emerging alternative measurement tools.
In non-destructive measurements, there are no unambiguous instructions for determining the reference value for dbh or tree height and the problem has been approached differently in previous studies. For example, in [
37], the author’s own measurements of dbh and height were used as the true value in the study and were assumed to be error free when compared to measurements conducted by others, whereas Hyppönen and Roiko-Jokela [
33] admitted that measurement bias could not be calculated since it was not possible to obtain the exact dbh. Furthermore, Kitahara et al. [
39] have noted that in tree height measurements, educated and experienced mensurationists provide more precise results than beginners with only basic knowledge.
In addition to studies where the measurements are repeated using the same instruments, there have been studies that have compared the measurements of the same trees using several devices, such as a caliper and diameter tape, or a laser height finder and a clinometer, but no major differences in precision have been reported; e.g., [
4,
40,
41,
42]. Guillemette and Lambert [
43] found no significant difference in dbh measured with calipers and diameter tape and recommended against the mixing of models and databases developed using either instrument. They also stated that evaluation of the most precise method is extremely difficult without destructive sampling.
In forest mensuration, the vast majority of dbh and height measurements are carried out non-destructively with standing trees, which was the case in this study as well. In this context, and considering that the previous studies, especially in Finland, are dated and consequently were not carried out with modern versions of measurement devices, there is a need for a current investigation of the precision of individual tree dbh and height measurements in boreal forest conditions when caliper and clinometer measurements are used. The objective of this study was to determine the degree of precision for tree dbh and height measurements when four experienced mensurationists complete the same measurements on the same sample trees in conditions that are typical when collecting operational forest resource information in boreal Finland. In addition, we explore whether the use of dbh cross-measurements, where dbh is the mean of two dbh measurements from perpendicular directions (hereafter, dbhobs), would have an effect on the precision of the measurements.
3. Results
Based on our analysis, there were no statistically significant differences between the measurements from the four members of the field crew for either dbh
obs or height (
α = 0.05). For dbh
obs measurements, it was assumed that the means of the dbh
obs measurements by all mensurationists (dbh
obsm) are equal to each other (Equation (3)).
The assumption of equality was supported by the results of the variance analysis (
p = 0.911;
Table 2). When performing the same analysis separately for tree species with the same assumptions of equal dbh
obs-means, the
p-values were 0.952, 0.975 and 0.993 for pine, spruce, and birch, respectively.
In measurements for tree height, it was assumed that the means of the height measurements by each mensurationist (height
m) were equal to each other:
The assumption of equality was supported by the variance analysis with a
p-value of 0.140 (
Table 3). The
p-values for tree species with the same assumption were 0.342, 0.686 and 0.647 for pine, spruce, and birch, respectively.
The largest difference between measured dbh
obs (i.e., 0.55 cm) was observed for spruce, whereas the largest difference between measured height values was observed for birch (0.82 m), but the differences were not significant (
Table 4).
The mean dbh
obs and the mean height of all the sample trees were 20.5 cm and 18.8 m, respectively. The means of standard deviations for all dbh
obs and height measurements were 0.3 cm (1.5%) and 0.5 m (2.9%), respectively (
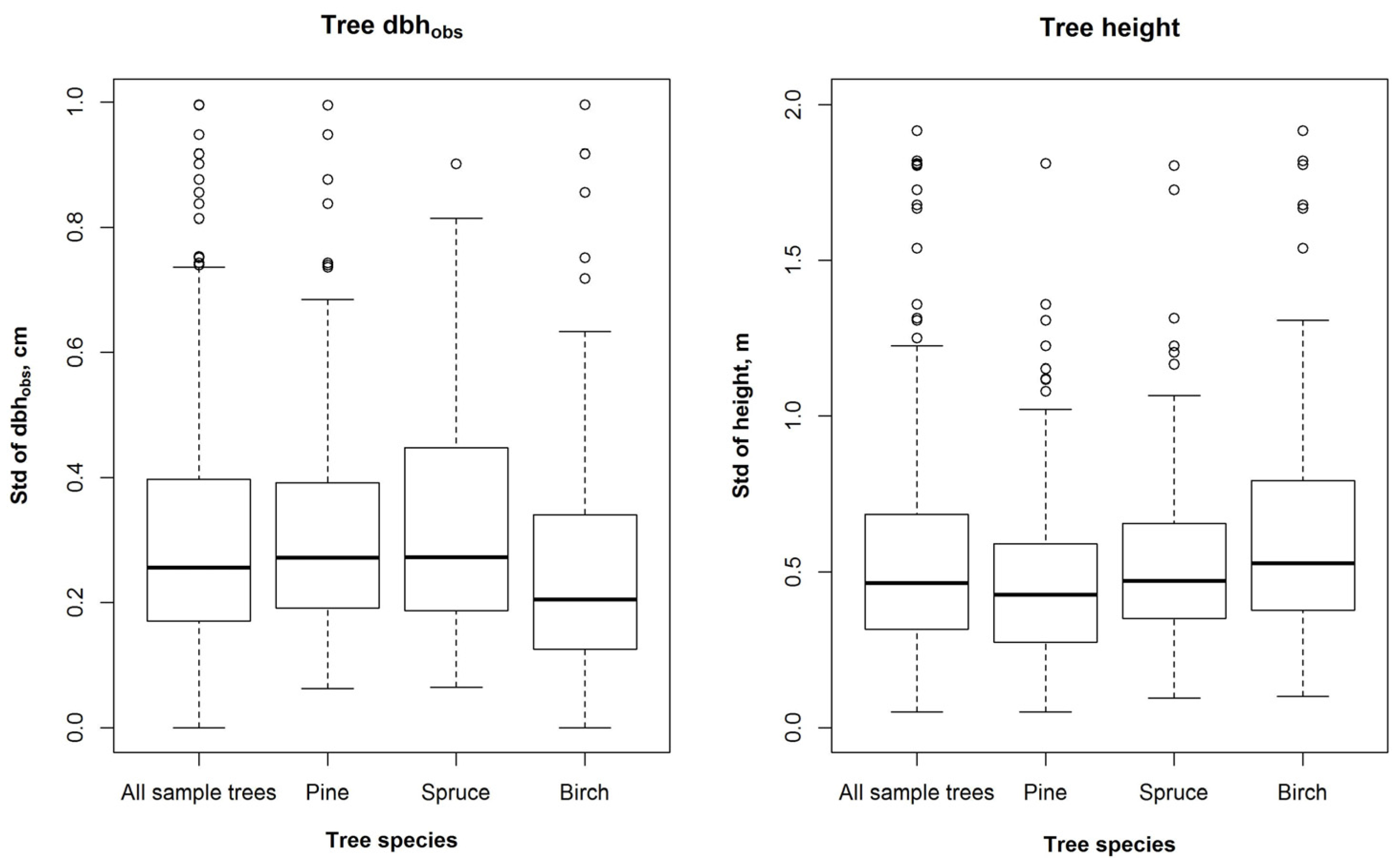
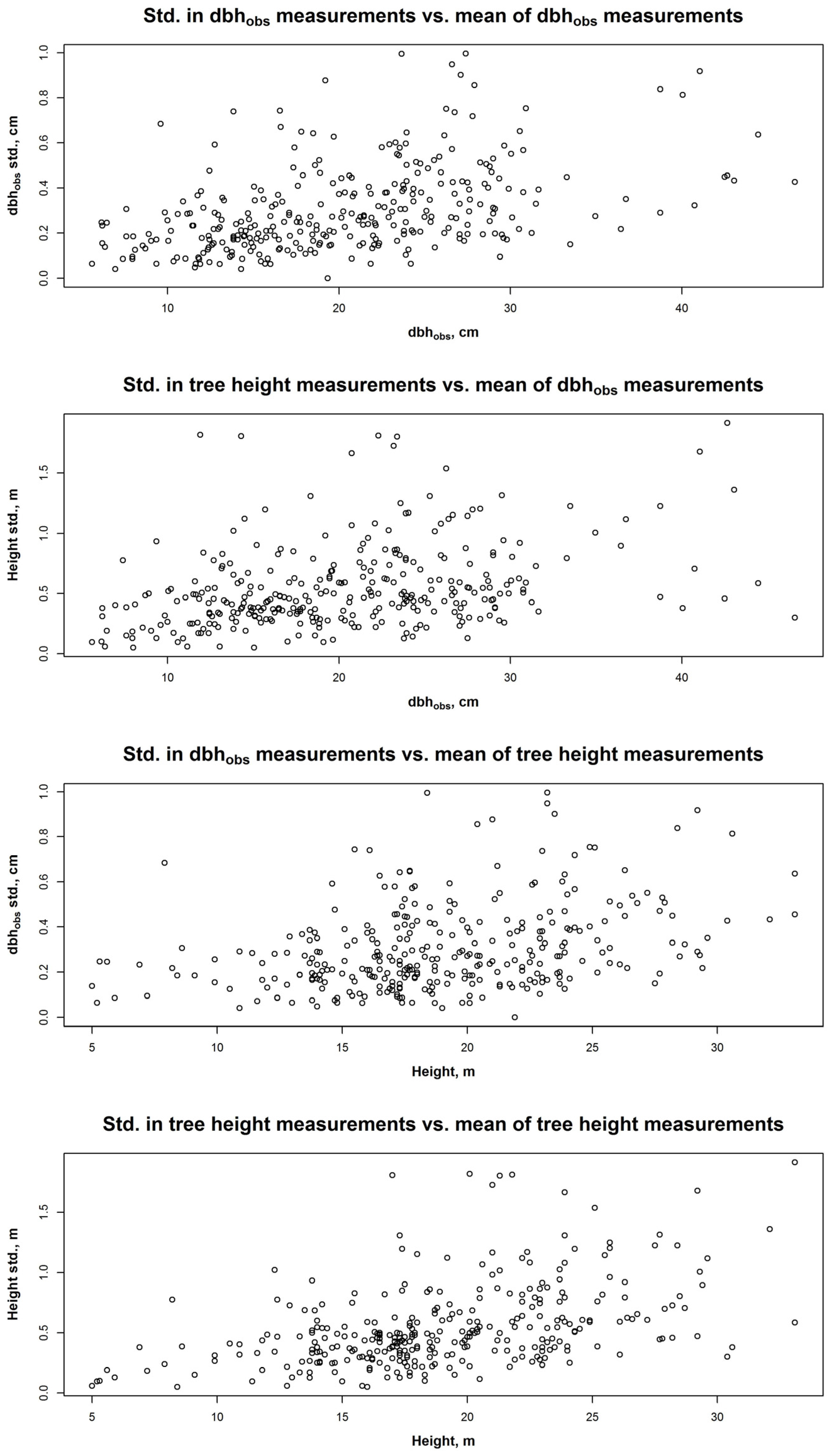
Table 5). Analyzed tree-by-tree, the standard deviation in dbh
obs measurements varied from 0 cm to 1.0 cm and in height measurements from 0.1 m to 1.9 m (
Figure 2). The relative standard deviation in the dbh
obs and height measurements was smallest for Norway spruce although the absolute standard deviation was smallest for birch in dbh
obs and Scots pine in height (
Table 5).
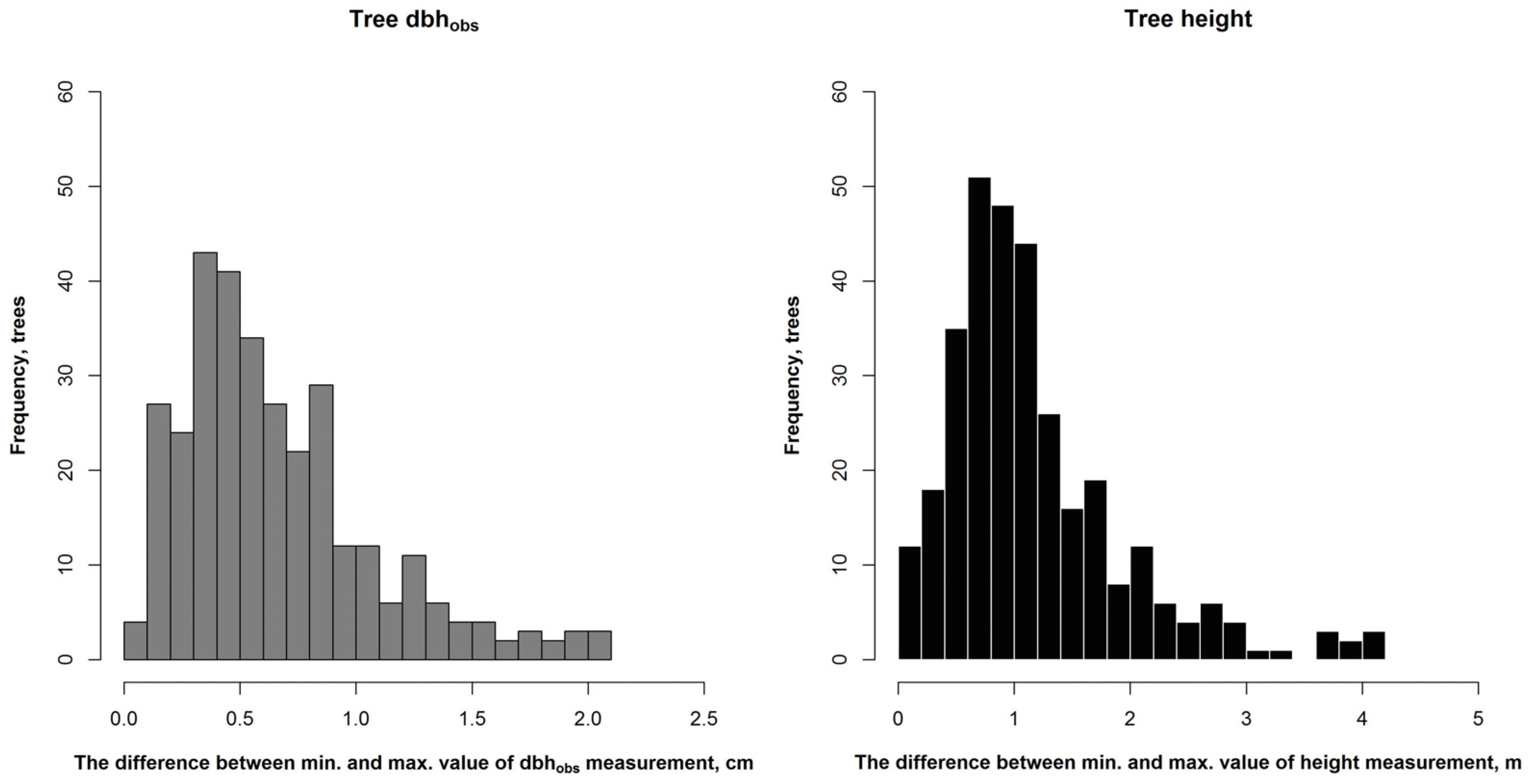
The difference between the lowest and highest dbh
obs values from the same tree among the four measures varied in range from 0 cm to 2.1 cm (
Figure 3). For 80.6% of the 319 trees measured, the range in variation remained less than 1.0 cm and for 94.0% less than 1.5 cm. For height, the difference between minimum and maximum values of the four individual measurements from the same tree was from 0.1 m to 4.2 m, respectively (
Figure 3). For 73.3% of the trees, the largest difference within the height observations from the same tree was less than 1.5 m.
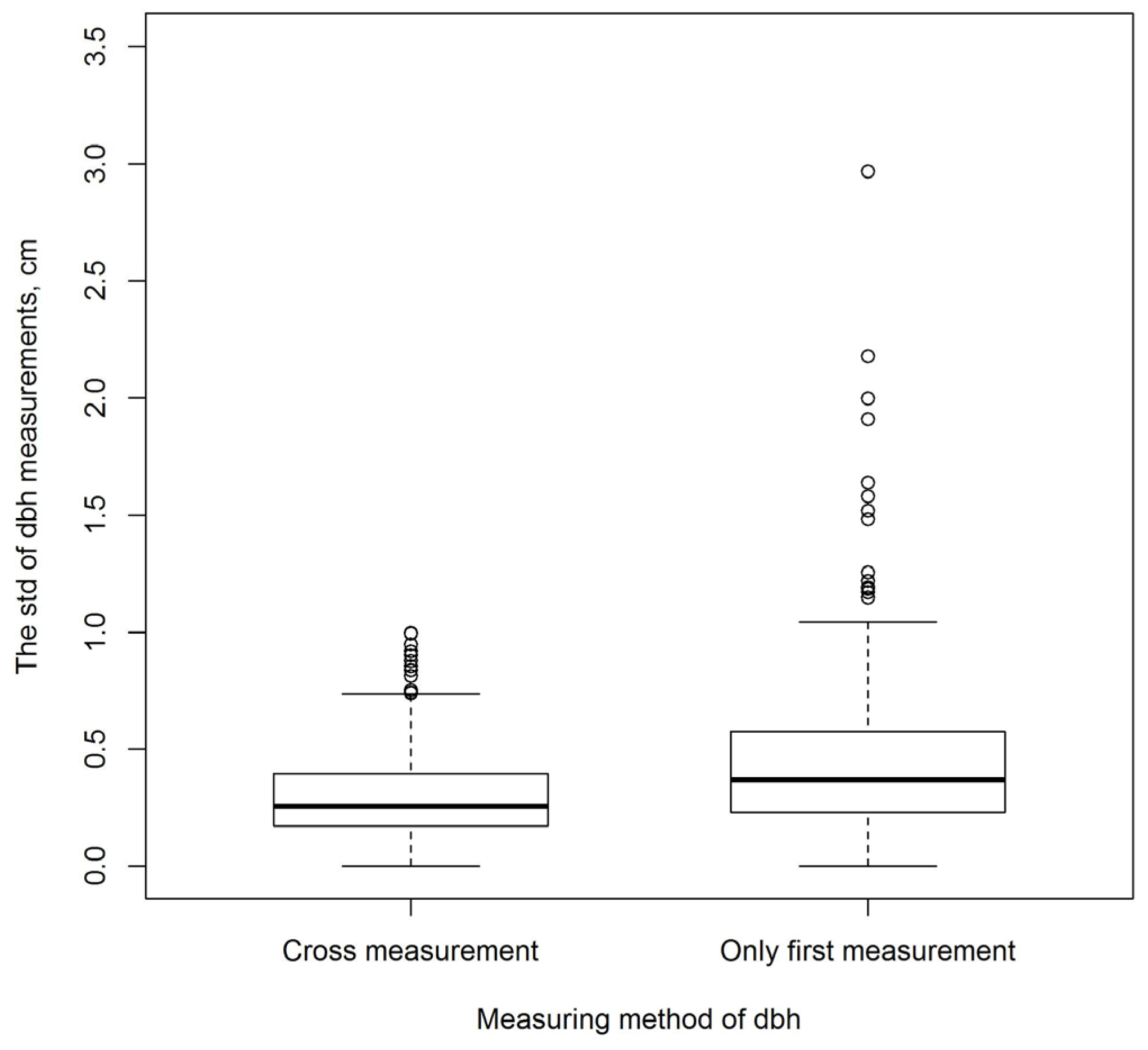
When only the first dbh measurement from each mensurationist was used for the analysis instead of the dbh
obs, the standard deviation of the measurements was 0.5 cm (2.2%) (
Figure 4). Likewise, the standard deviation was 0.5 cm for all tree species. The difference between the smallest and largest measured dbh value from the same tree varied from 0 cm to 6.6 cm; for 93.4% of the trees, the range of dbh measurements remained less than 2.0 cm.
The standard deviation of dbh
obs measurements varied between 0.2 cm and 0.4 cm (from 1.4% to 1.9%) in the five dbh-classes and between 0.2 cm and 0.4 cm (from 1.3% to 1.9%) within the five height classes (
Table 6 and
Table 7). The absolute standard deviation values increased as the dbh increased. The reversed trend was detected with relative standard deviations (
Table 6).
The standard deviation of the height measurements varied between 0.4 m and 0.7 m (from 2.6% to 3.1%) within the five dbh classes and from 0.4 m to 0.7 m (from 2.6% to 3.4%) between the five height classes (
Table 6 and
Table 7). The standard deviations of dbh
obs and height measurements by tree size are plotted in
Figure 5.
4. Discussion
There is a need to characterize the precision of field measurements, such as individual tree dbh and height, using modern calipers and a clinometer. These measurement devices are routinely used for collecting forest resource information in boreal forests. Currently, close-range remote sensing techniques such as terrestrial and mobile laser scanning techniques are actively being developed in conjunction with photogrammetry to provide fully automatic sample plot or tree measurements. To assess accuracy, these and other remote sensing-based modes of measurement are often compared to traditional caliper and clinometer measurements of dbh and height. Thus, our aim with this study was to characterize the precision afforded by these conventional measures in order to provide baseline information for assessment of these new measurement tools and methods.
In order to describe the possible variation between the mensurationists, both the amount of sample trees and the number of mensurationists used in this study are large. In earlier studies, attention has been paid to one of these factors, e.g., Elzinga et al. [
32] studied the observed variation of dbh measurements with 879 sample trees and two mensurationists, whereas McRoberts et al. [
35] investigated the variation with 61 sample trees and eight or nine repeat measurements. The aim in this study was to have several mensurationists (4) and a large number of sample trees (319).
Although we found no statistically significant differences in dbh or height as measured by our four mensurationists, the results showed variation. For example, the largest difference between two cross-measured dbh measurements (i.e., dbhobs) from the same tree was 2.1 cm. For tree height, the respective difference was 4.2 m. Despite the relatively large maximum differences, it should be noted that for 80.6% of the trees, the range in the dbhobs measurements was less than 1.0 cm.
In dbh
obs measurements, there seemed to be very little variation over the entire data set, since the relative standard deviation was only 1.5% which is in line with the results of Hyppönen and Roiko-Jokela [
33] who obtained 1.4% standard deviation in dbh measurements. Päivinen et al. [
38] have also studied the precision of dbh measurements performed by several mensurationists; the standard deviation for dbh in their study was 0.69 cm (2.8%). In both of the previous studies mentioned, the number of unique trees in the data set was relatively small when compared to this study (
n = 319 trees), since the data consisted of only 38 [
33] and 64 [
38] unique trees. In those studies, the measurements were then repeated several times, to get the total amount of dbh measurements to 540 and 520 measurements, respectively. In our study, spruce had the lowest relative standard deviation in dbh measurements which is supported by the findings of Päivinen et al. [
38]. One possible reason for the greater precision found in this study can be related to the nature of spruce bark, since spruce bark is more homogenous than the outer surface of pine or birch trees. In [
37], 95% of measured diameters were within 5 cm of the control measurements when the mean dbh was 52.7 cm, whereas Elzinga et al. [
32] reported that in dbh measurements, errors greater than 5% may be expected in 5% of measurements. In general, the design of different studies may restrict the comparison of the results to each other if different kinds of measurement devices are used; if the diameter is acquired with single or cross measurement; or if the cardinal directions for caliper measurements are undefined, as it was in this study; or if the height of 1.3 m is marked on the tree or not.
The dbh values used in the analysis of this study are based on cross measurements, that is, two measurements from each tree from perpendicular directions. The results of this study indicate that even though cross measurements are slightly more time consuming than single caliper measurements, the greater precision they yield is worth the effort and the use of cross measurements is therefore recommended. The standard deviation of dbh measurements was approximately 1.5 times greater when using only one measurement from each tree (1.5% vs. 2.2%), and thus cross measurements improved precision notably.
Laser technology has also been used to measure dbh. In these studies, calipers have been used as a reference data and thus, comparison with these studies is not straightforward. The reported accuracy in dbh measurements has varied from 0.8 cm to 1.6 cm (standard error) with the laser-relascope [
47], and from 0.88 cm to 1.43 cm with laser-dendrometers [
48,
49]. With camera-based systems, the accuracies have varied from 0.7 cm to 2.3 cm [
30,
50,
51,
52]. Terrestrial laser scanning (TLS) is also used for dbh measurements. Several studies have reported measurement accuracies (RMSE) between 0.9 cm and 8.9 cm [
27,
53,
54,
55,
56,
57,
58,
59]. Vastaranta et al. [
60] compared several of the methods mentioned earlier and reported standard errors of 0.83 cm, 0.85 cm and 1.43 cm in dbh measurements with the TLS, laser-camera, and laser-relascope, respectively.
The standard deviation of 0.5 m (2.9%) reported for the height measurements is on the same level with the previous studies: Hyppönen and Roiko-Jokela [
33] reported standard deviations of 0.8 m and 0.56 m for height measurements done with two different models of Suunto clinometers. Päivinen et al. [
38] measured tree heights with Suunto clinometer as well, and reported standard deviation of 0.67 m. The advantage of our study is to report the precision of a modern clinometer, which is rather different from the viewpoint of a user than the clinometer used in earlier studies. The Vertex clinometer used in this study measures distance based on ultrasound, which allows flexible measuring distance. This is in contrast to the Suunto clinometer, which requires a fixed measuring distance. However, the Vertex clinometer requires calibration, and if a user fails to calibrate the instrument, the results may not be reliable and accurate. The laser-relascope has been found to measure the tree height with standard error between 0.49 m to 0.99 m [
47,
60]. In Omule [
37], the variation in height measurements among the crew was reported to be 21.8% with a mean tree height of 32.3 m.
Based on our results, the precision of height measurements varied somewhat more between the three tree species than the dbh measurements did. For pine and spruce, the relative standard deviations in height measurements were within 0.1 percentage points (2.7% and 2.6%, respectively), but for birch, the value was 3.6%. Most probably, the reason for the lower precision of birch measurements is that when measuring the height of birch trees, observing the exact end point of the tree top can be more difficult than with the coniferous trees. In Päivinen et al. [
38], the precision of pine, spruce and birch height measurements were 0.71 m, 0.55 m and 0.79 m, but no significant differences between the species were reported in the study.
We found that the size of the tree (dbh or height) did not impact the precision of field measurements (
Figure 5). There was little variation in relative standard deviation for tree height between the groups of different sized trees in both dbh- and height-based size classes. However, the variation falls within one percentage point in both classifications and no trend can be seen from the results. Hyppönen and Roiko-Jokela [
33] also noticed that the height of the tree had no effect on the standard deviation of tree height measurements.
In general, there was more imprecision in measuring tree height than dbh. According to Larjavaara and Muller-Landau [
61], the tree height is difficult to measure accurately for standing trees in the field. When measuring the tree height, the mensurationist needs to operate from a distance, whereas for dbh measurements, the measurement is performed while standing next to the tree stem. When using clinometers for height measurements, it can also be difficult to see and define the exact end point of the tree top—especially in very dense forests or in other areas with restricted visibility. Moreover, there is always a risk of error from optical illusion if a tree is leaning, even if the mensurationist always selects the best possible measurement direction. Furthermore, there is always some randomness and variation when the measurements are performed by using steel calipers and by different mensurationists. Most importantly, for dbh measurements, different methods of defining the measuring height of 1.3 m above the base and the cardinal directions for the caliper cross-measurement cause variation between the observations. A standard measure can be used for determining the exact measuring height, as it was done in this study. In addition, the asymmetrical form of the tree stem and the occasional irregularity of the tree bark may cause differences in measurement results. Non-circular stem form was taken into account by utilizing two dbh measurements from perpendicular directions.
The measurements were carried out independently by the four mensurationist which could have caused bias as the sample trees were not identified together. Nevertheless, they had the stem maps of all sample plots for recognizing the sample trees to be measured. We did not determine one reference dbh and height value to which other measurements were compared. Therefore, the results do not reveal the possible bias in the measurements; however, this is a realistic scenario that is often encountered in operational context.