Individual-Tree Diameter Growth Models for Mixed Nothofagus Second Growth Forests in Southern Chile
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Description
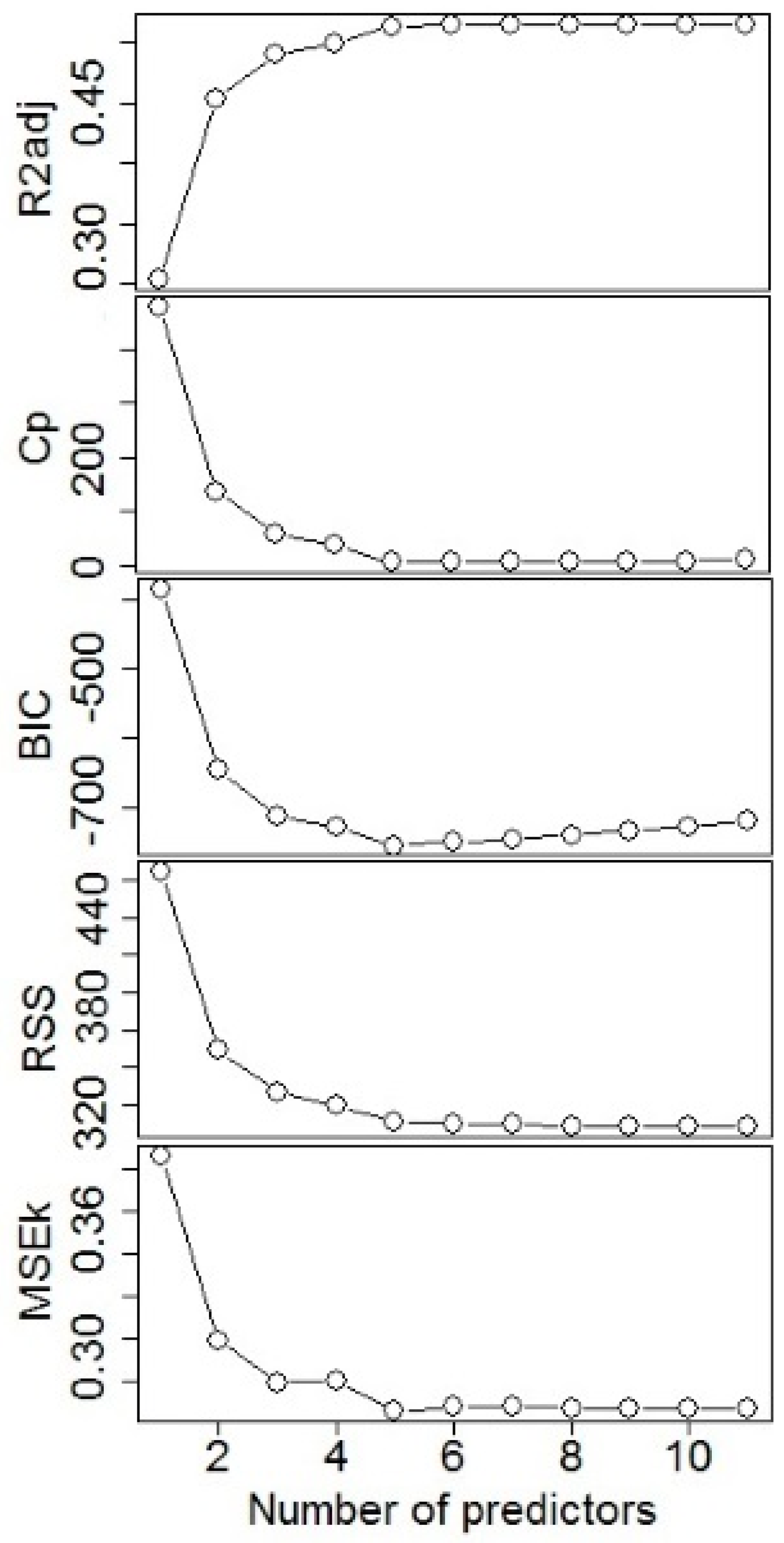
2.2. Model Fitting
3. Results
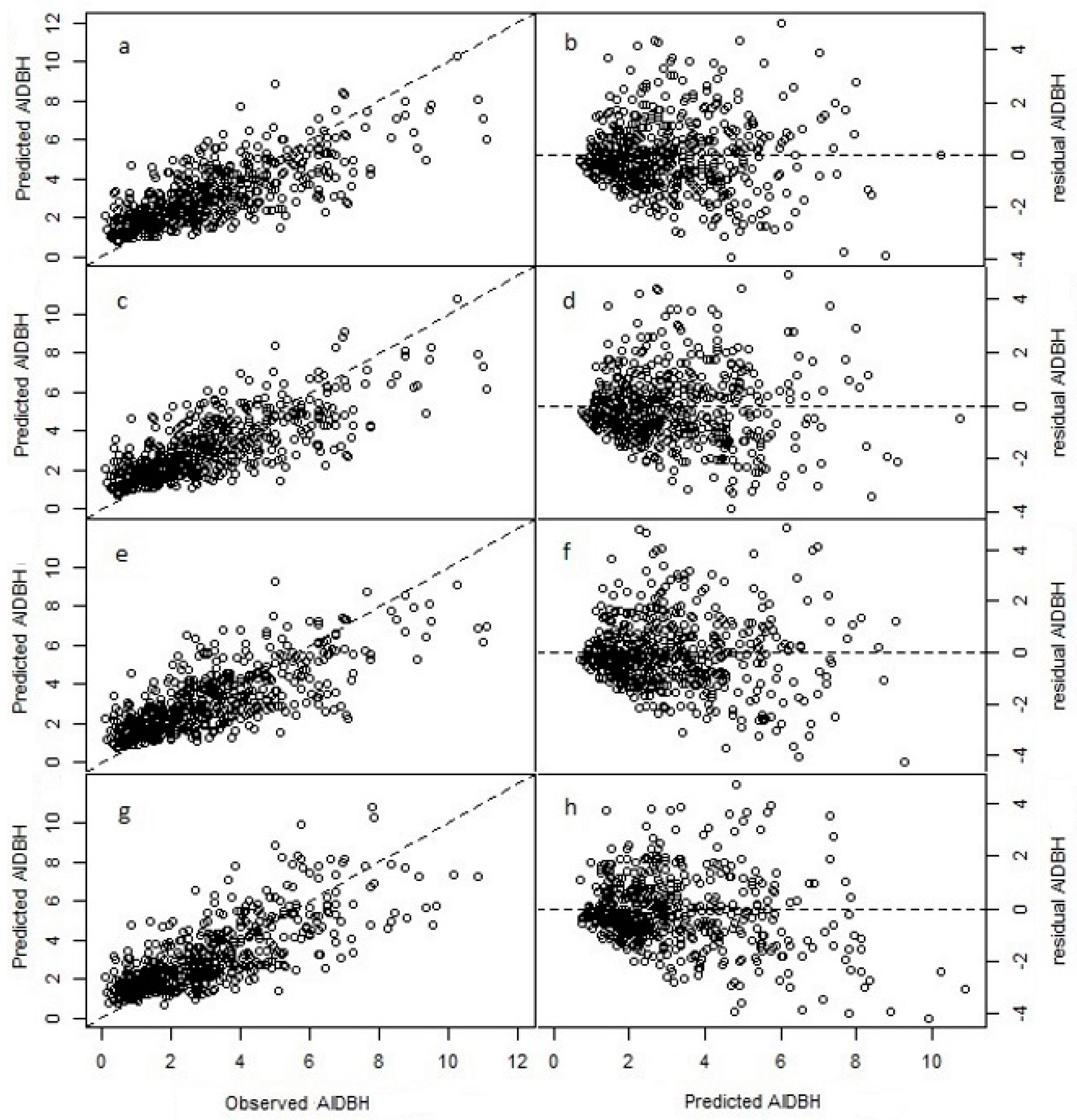
3.1. Model Fitting
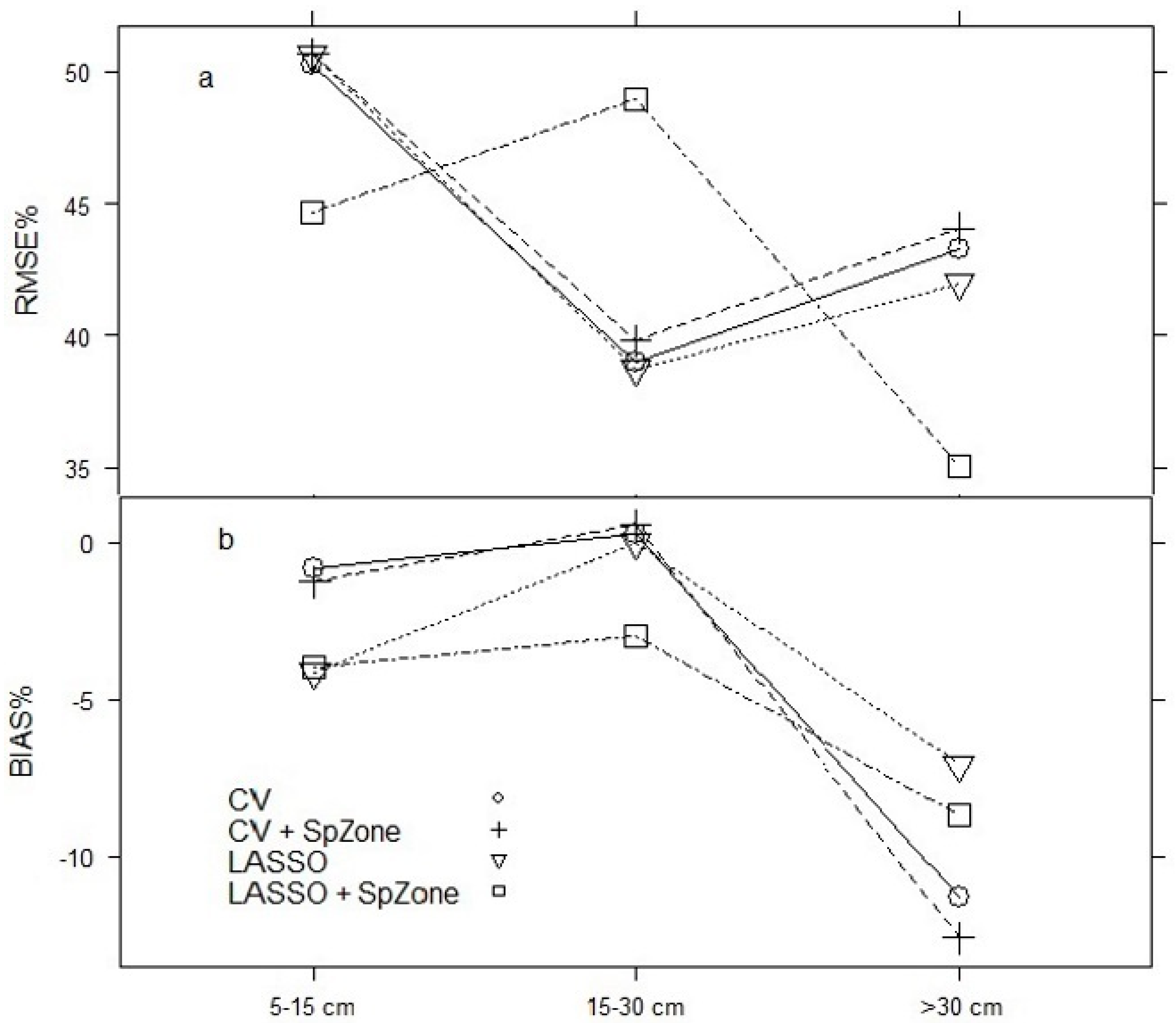
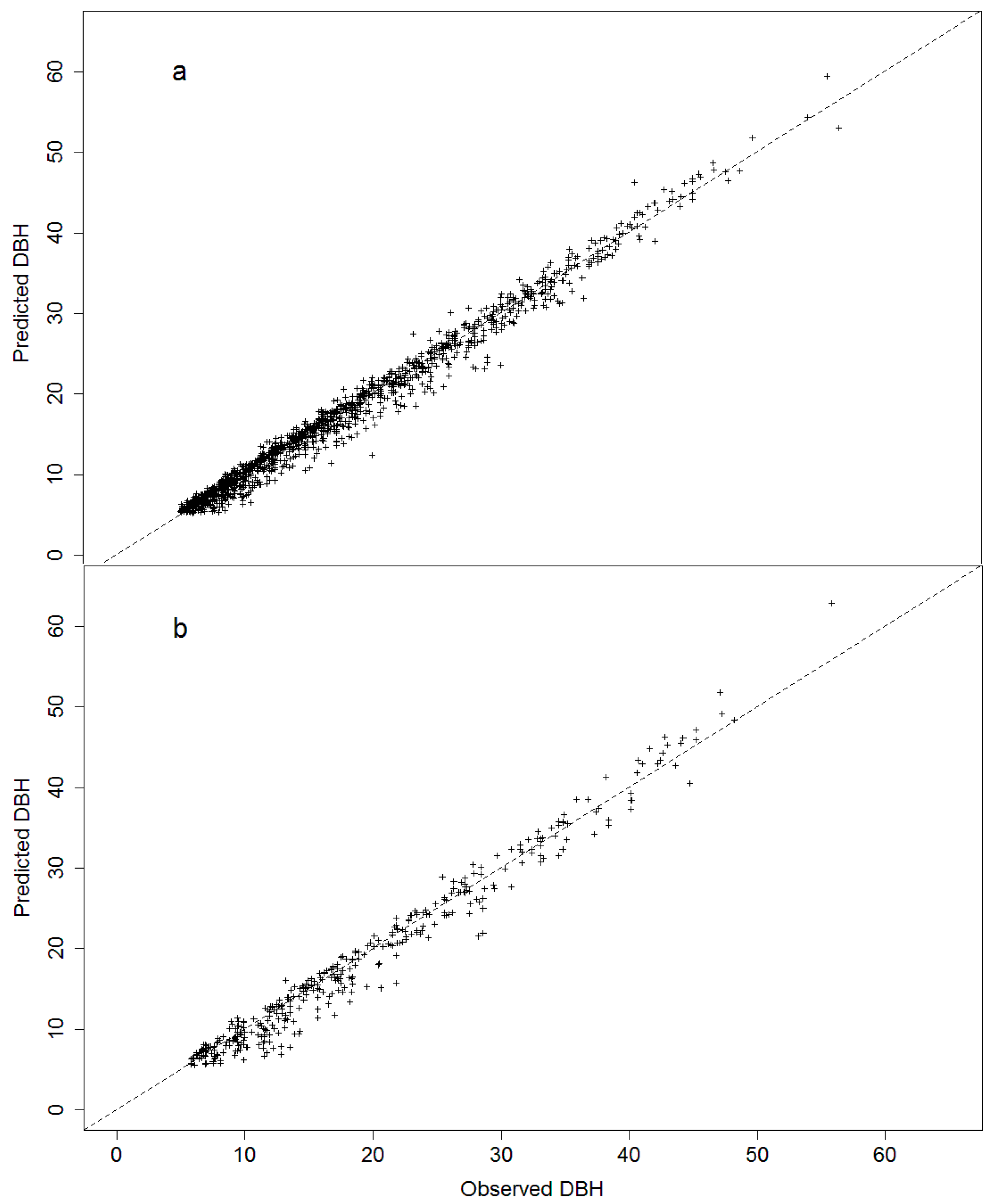
3.2. Model Projection
3.3. Selected Model
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Donoso, C. Variación natural en especies de Nothofagus en Chile. Bosque 1987, 8, 85–97. Available online: http://mingaonline.uach.cl/pdf/bosque/v8n2/art03.pdf (accessed on 15 July 2017). [CrossRef]
- Donoso, C. Bosques Templados de Chile y Argentina: Variación, Estructura y Dinámica; Editorial Universitaria: Santiago, Chile, 1993. [Google Scholar]
- Corporación Nacional Forestal (CONAF). Catastro de los Recursos Vegetacionales Nativos de Chile. Monitoreo de Cambios y Actualizaciones. Periodo 1997–2011; Ministerio de Agricultura: Santiago, Chile, 2011.
- Instituto Forestal (INFOR). Bosque nativo 12; Ministerio de Agricultura: Santiago, Chile, 2016.
- Donoso, C.; Premoli, A.; Gallo, L.; Ipinza, R. Variación Intraespecífica en las Especies Arbóreas de los Bosques Templados de Chile y Argentina; Editorial Universitaria: Santiago, Chile, 2004. [Google Scholar]
- Gezan, S.A.; Ortega, A.; Andenmatten, E. Diagramas de manejo de densidad para renovales de roble, raulí y coigüe en Chile. Bosque 2007, 28, 97–105. [Google Scholar] [CrossRef]
- Moreno, P.C. Individual-Tree Diameter Growth Models and Variability of Mixed Nothofagus Second Growth Forests in Southern Chile. Master’s Thesis, University of Florida, Gainesville, FL, USA, 2017. [Google Scholar]
- Instituto Forestal (INFOR). Rentabilidad Económica de Distintas Propuestas Silvícolas para Renovales de Nothofagus en el Centro sur de Chile. Informe Técnico 193; Ministerio de Agricultura: Santiago, Chile, 2013.
- Echeverrıa, C.; Lara, A. Growth patterns of secondary Nothofagus oblique—N. alpina forests in southern Chile. For. Ecol. Manag. 2004, 195, 29–43. [Google Scholar] [CrossRef]
- Donoso, P.; Donoso, C.; Sandoval, V. Proposición de zonas de crecimiento de renovales de roble (Nothofagus obliqua) y raulí (Nothofagus alpina) en su rango de distribución natural. Bosque 1993, 14, 37–55. Available online: http://mingaonline.uach.cl/pdf/bosque/v14n2/art06.pdf (accessed on 19 July 2017). [CrossRef]
- Gezan, S.A.; Moreno, P.C. Establecimiento y medición de una red de parcelas permanentes para renovales de roble (Nothofagus obliqua), raulí (Nothofagus alpina) y coigüe (Nothofagus dombeyi). Bosque Nativo. 1999, 22, 9–11. [Google Scholar]
- Shortt, J.S.; Burkhart, H.E. A comparison of loblolly pine plantation growth and yield models for inventory updating. South J. Appl. For. 1996, 20, 15–22. [Google Scholar]
- Moreno, P.C. Proposición Preliminar de Curvas de Índice de Sitio para Renovales de Raulí. Ph.D. Thesis, Universidad de Chile, Santiago, Chile, 2001. [Google Scholar]
- Salas, C.; García, O. Modelling height development of mature Nothofagus obliqua. For. Ecol. Manag. 2006, 229, 1–6. [Google Scholar] [CrossRef]
- Ugalde, G.A. Crecimiento en Altura de Renovales de Lenga (Nothofagus pumilio (Poepp. et endl.) Krasser) en Monte alto (XII región) en Función de la Calidad del Sitio. Ph.D. Thesis, Universidad de Chile, Santiago, Chile, 2006. [Google Scholar]
- Birdsey, R. Updating Methods for Forest Inventories: An Overview; USDA Forest Service General Technical Report; PNW-GTR-Pacific Northwest Research Station: Washington, DC, USA, 1990. [Google Scholar]
- Blanco, J.A.; González de Andrés, E.; San Emeterio, L.; Lo, Y.H. Modelling mixed forest stands: Methodological challenges and approaches. In Advanced Modelling Techniques Studying Global Changes in Environmental Sciences; Lek, S., Park, Y.S., Baehr, C., Jorgensen, S.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 187–213. [Google Scholar]
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Vanclay, J.K. Modelling Forest Growth and Yield: Applications to Mixed Tropical Forests; CAB International: Wallingford, UK, 1994. [Google Scholar]
- Gonzalez-Benecke, C.A.; Gezan, S.A.; Leduc, D.J.; Martin, T.A.; Cropper, W.P.; Samuelson, L.J. Modeling survival, yield, volume partitioning and their response to thinning for longleaf pine plantations. Forests 2012, 3, 1104–1132. [Google Scholar] [CrossRef]
- Harrison, W.C.; Burk, T.E.; Beck, D.E. Individual tree basal area increment and total height equations for Appalachian mixed hardwoods after thinning. South. J. Appl. For. 1986, 10, 99–104. [Google Scholar]
- Murphy, P.A.; Graney, D.L. Individual-tree basal area growth, survival, and total height models for upland hardwoods in the Boston mountains of Arkansas. South. J. Appl. For. 1998, 22, 184–192. [Google Scholar]
- Huang, S.; Titus, S.J. Estimating a system of nonlinear simultaneous individual tree models for white spruce in boreal mixed-species stands. Can. J. For. Res. 1999, 29, 1805–1811. [Google Scholar] [CrossRef]
- Andreassen, K.; Tomter, S.M. Basal area growth models for individual trees of norway spruce, scots pine, birch and other broadleaves in Norway. For. Ecol. Manag. 2003, 180, 11–24. [Google Scholar] [CrossRef]
- Pukkala, T.; Lähde, E.; Laiho, O. Growth and yield models for uneven-sized forest stands in Finland. For. Ecol. Manag. 2009, 258, 207–216. [Google Scholar] [CrossRef]
- Nunes, L.; Tomé, J.; Tomé, M. Prediction of annual tree growth and survival for thinned and unthinned even-aged maritime pine stands in Portugal from data with different time measurement intervals. For. Ecol. Manag. 2011, 262, 1491–1499. [Google Scholar] [CrossRef]
- Ma, W.; Lei, X. Nonlinear simultaneous equations for individual-tree diameter growth and mortality model of natural mongolian oak forests in northeast China. Forests 2015, 6, 2261–2280. [Google Scholar] [CrossRef]
- Burkhart, H.E. Suggestions for choosing an appropriate level for modelling forest stands. In Modelling Forest Systems; Amaro, A., Reed, D., Soares, P., Eds.; CAB International: Wallingford, UK, 2003; pp. 3–10. [Google Scholar]
- Buckman, R.E. Growth and Yield of Red Pine in Minnesota; Technical Bulletin 1272; US Department of Agriculture: Washington, DC, USA, 1962.
- Huang, S.; Titus, S.J. An individual tree diameter increment model for white spruce in Alberta. Can. J. For. Res. 1995, 25, 1455–1465. [Google Scholar] [CrossRef]
- Welham, S.J.; Gezan, S.A.; Clark, S.; Mead, A. Statistical Methods in Biology: Design and Analysis of Experiments and Regression; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B. 1996, 58, 267–288. Available online: http://www.jstor.org/stable/2346178 (accessed on 5 July 2017).
- Kyung, M.; Gill, J.; Ghosh, M.; Casella, G. Penalized regression, standard errors, and bayesian lassos. Bayesian Anal. 2010, 5, 369–411. [Google Scholar] [CrossRef]
- Wu, T.T.; Chen, Y.F.; Hastie, T.; Sobel, E.; Lange, K. Genome-wide association analysis by lasso penalized logistic regression. Bioinformatics 2009, 25, 714–721. [Google Scholar] [CrossRef] [PubMed]
- Lockhart, R.; Taylor, J.; Tibshirani, R.J.; Tibshirani, R. A significance test for the lasso. Ann. Stat. 2014, 42, 413–468. [Google Scholar] [CrossRef] [PubMed]
- Ortega, A.; Gezan, S.A. Cuantificación de crecimiento y proyección de calidad en Nothofagus. Bosque 1998, 19, 123–126. Available online: http://mingaonline.uach.cl/scielo.php?pid=S0717-92001998000100013&script=sci_arttext&tlng=es (accessed on 25 July 2017). [CrossRef]
- Corporación Nacional Forestal (CONAF); Comisión Nacional del Medio Ambiente (CONAMA); Banco Internacional de Reconstrucción y Fomento (BIRF); Universidad Austral de Chile; Pontificia Universidad Católica de Chile; Universidad Católica de Temuco. Proyecto Catastro y Evaluación de los Recursos Vegetacionales Nativos de Chile; Ministerio de Agricultura: Santiago, Chile, 1999.
- Avery, T.E.; Burkhart, H. Forest Measurements, 5th ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Pukkala, T.; Lähde, E.; Laiho, O. Using optimization for fitting individual-tree growth models for uneven-aged stands. Eur. J. For. Res. 2011, 130, 829–839. [Google Scholar] [CrossRef]
- Lumley, T.; Miller, A. Leaps: Regression Subset Selection. R Package Version 3.0. 2017. Available online: https://cran.r-project.org/web/packages/leaps/index.html (accessed on 5 July 2017).
- Baskerville, G. Use of logarithmic regression in the estimation of plant biomass. Can. J. For. Res. 1972, 2, 49–53. [Google Scholar] [CrossRef]
- Ahlburg, D.A. Forecast evaluation and improvement using theil’s decomposition. J. Forecast. 1984, 3, 345–351. [Google Scholar] [CrossRef]
- Blanco, J.A.; Seely, B.; Welham, C.; Kimmins, J.; Seebacher, T.M. Testing the performance of a forest ecosystem model (forecast) against 29 years of field data in a pseudotsuga menziesii plantation. Can. J. For. Res. 2007, 37, 1808–1820. [Google Scholar] [CrossRef]
- Fox, J.; Monette, G. Generalized collinearity diagnostics. J. Am. Stat. Assoc. 1992, 87, 178–183. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015; Available online: http://www.r-project.org (accessed on 3 January 2017).
- Friedman, J.; Hastie, T.; Simon, N.; Tibshirani, R. Glmnet: Lasso and Elastic-Net Regularized Generalized Linear Models. R Package Version 1.9-5; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Peng, C. Growth and yield models for uneven-aged stands: Past, present and future. For. Ecol. Manage. 2000, 132, 259–279. Available online: http://flash.lakeheadu.ca/~chpeng/reprint_uneven-age.pdf (accessed on 9 July 2017). [CrossRef]
- Cubillos, D. Modelos de crecimiento diametral para algunos renovales de raulí. Cienc. Investig. For. 1987, 1, 67–76. [Google Scholar]
- Monserud, R.A.; Sterba, H. A basal area increment model for individual trees growing in even-and uneven-aged forest stands in Austria. For. Ecol. Manag. 1996, 80, 57–80. [Google Scholar] [CrossRef]
- Coomes, D.A.; Allen, R.B. Effects of size, competition and altitude on tree growth. J. Ecol. 2007, 95, 1084–1097. [Google Scholar] [CrossRef]
- Richardson, S.J.; Hurst, J.M.; Easdale, T.A.; Wiser, S.K.; Griffiths, A.D.; Allen, R.B. Diameter growth rates of beech (Nothofagus) trees around New Zealand. N. Z. J. For. 2011, 56, 3–11. Available online: http://nzjf.org.nz/free_issues/NZJF56_1_2011/9B1010A2-B122-4805-9290-E4144A6738D1.pdf (accessed on 18 July 2017).
- Ivancich, H.S.; Martínez Pastur, G.J.; Lencinas, M.V.; Cellini, J.M.; Peri, P.L. Proposals for Nothofagus antarctica diameter growth estimation: Simple vs. Global models. J. For. Sci. 2014, 60, 307–317. Available online: http://ri.conicet.gov.ar/bitstream/handle/11336/5497/CONICET_Digital_Nro.6975_D.pdf?sequence=5&isAllowed=y (accessed on 1 July 2017).
- Lusk, C.H.; Ortega, A. Vertical structure and basal area development in second-growth Nothofagus stands in Chile. J. Appl. Ecol. 2003, 40, 639–645. [Google Scholar] [CrossRef]
- Moreno-Chacón, M.; Lusk, C.H. Vertical distribution of fine root biomass of emergent Nothofagus dombeyi and its canopy associates in a Chilean temperate rainforest. For. Ecol. Manag. 2004, 199, 177–181. [Google Scholar] [CrossRef]
- Donoso, P.J.; Lusk, C.H. Differential effects of emergent Nothofagus dombeyi on growth and basal area of canopy species in an old-growth temperate rainforest. J. Veg. Sci. 2007, 18, 675–684. [Google Scholar] [CrossRef]
- Donoso, P.J.; Soto, D.P. Does site quality affect the additive basal area phenomenon? Results from Chilean old-growth temperate rainforests. Can. J. For. Res. 2016, 46, 1330–1336. [Google Scholar] [CrossRef]
- Schlatter, J.; Gerding, V.; Adriazola, J. Sistema de Ordenamiento de la Tierra. Herramienta para la Planificación Forestal, Aplicada a las Regiones VII, VIII y IX; Serie Técnica; Facultad Ciencias Forestales, Universidad Austral de Chile: Valdivia, Chile, 1994. [Google Scholar]
- Schlatter, J.; Gerding, V.; Adriazola, J. Sistema de Ordenamiento de la Tierra. Herramienta para la Planificación Forestal, Aplicada para la X Región; Serie técnica; Facultad Ciencias Forestales, Universidad Austral de Chile: Valdivia, Chile, 1995. [Google Scholar]
- Chauchard, L.; Sbrancia, R. Modelos de crecimiento diamétrico para Nothofagus obliqua. Bosque 2003, 24, 3–16. [Google Scholar] [CrossRef]
- Thiers, O.; Gerding, V.; Hildebrand, E. Renovales de Nothofagus obliqua en centro y sur de Chile: Factores de sitio relevantes para su productividad. In Libro de Actas de eco Reuniones. Segunda Reunión Sobre los Nothofagus en la Patagonia; Bava, J., Picco, O., Pildaín, M., López, P., Orellana, I., Eds.; Centro de Investigación y Extensión Forestal Andino Patagónico (CIEFAP): Esquel, Argentina, 2008; pp. 255–260. [Google Scholar]
- Gezan, S.A.; Moreno, P.; Ortega, A. Modelos fustales para renovales de roble, raulí y coigüe en Chile. Bosque 2009, 30, 61–69. [Google Scholar] [CrossRef]
- Esse, C.; Donoso, P.J.; Gerding, V.; Encina-Montoya, F. Determination of homogeneous edaphoclimatic zones for the secondary forests of Nothofagus dombeyi in central-southern chile. Cienc. Investig. Agrar. 2013, 40, 351–360. [Google Scholar] [CrossRef]
- Wykoff, W.R. A basal area increment model for individual conifers in the northern Rocky Mountains. For. Sci. 1990, 36, 1077–1104. [Google Scholar]
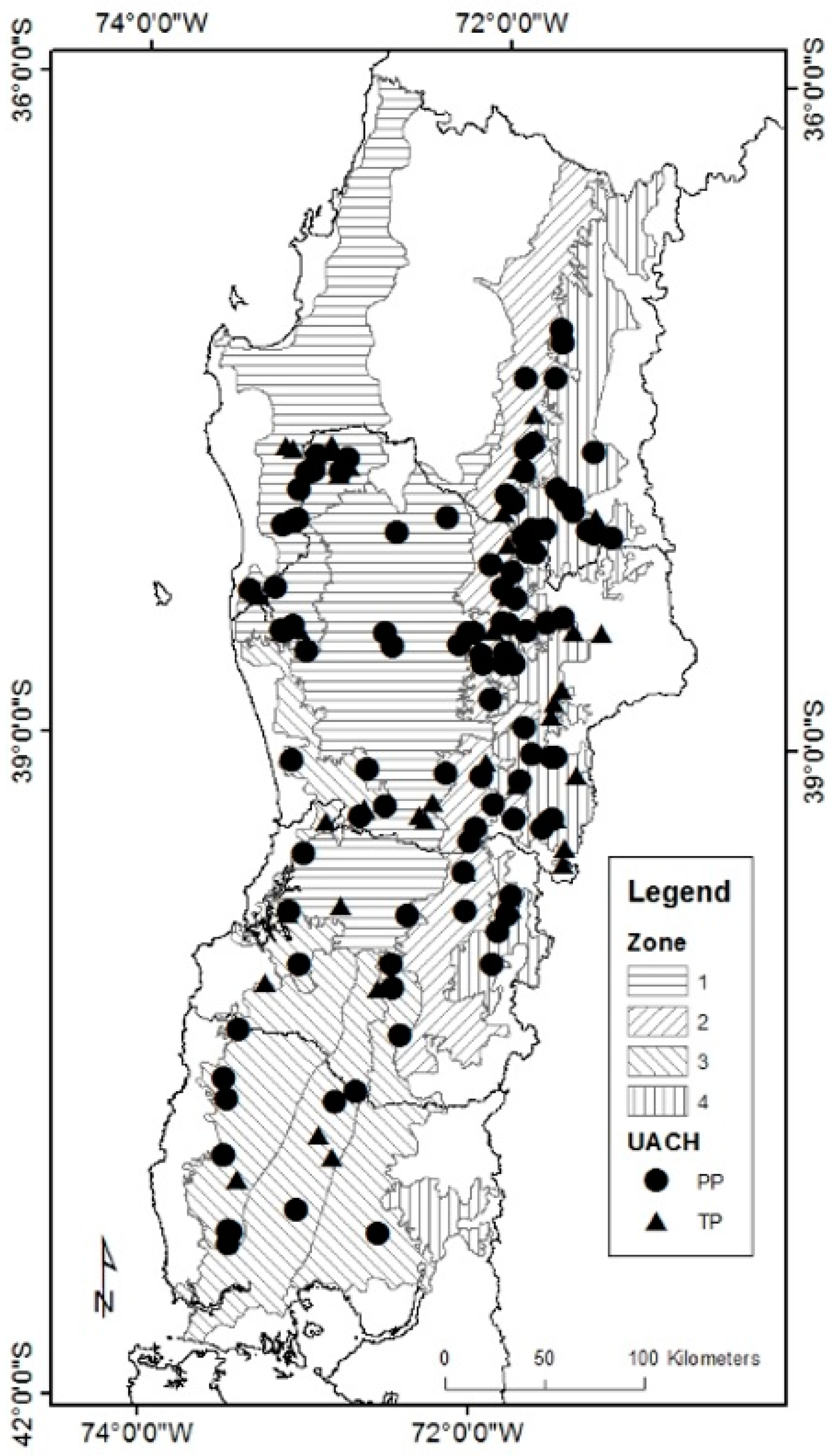
| Tree Species | Nothofagus alpina | Nothofagus obliqua | Nothofagus dombeyi | ||||||||||||
| Tree Variables | n | Mean | SD | Min | Max | n | Mean | SD | Min | Max | n | Mean | SD | Min | Max |
| DBH | 202 | 16.7 | 9.8 | 5.0 | 42.7 | 627 | 17.0 | 10.0 | 5.0 | 62.1 | 279 | 19.3 | 11.3 | 5.0 | 60.2 |
| H | 202 | 15.2 | 6.6 | 4.2 | 34.5 | 627 | 16.1 | 7.3 | 3.5 | 45.0 | 279 | 16.2 | 6.1 | 4.2 | 34.5 |
| A | 202 | 36.7 | 14.2 | 11.0 | 104.0 | 627 | 30.6 | 14.6 | 8.0 | 95.0 | 279 | 32.5 | 13.2 | 9.0 | 80.0 |
| BAL | 202 | 26.0 | 16.8 | 0.0 | 83.4 | 627 | 19.0 | 14.0 | 0.0 | 65.1 | 279 | 28.0 | 20.6 | 0.0 | 92.4 |
| BALn | 202 | 20.9 | 15.0 | 0.0 | 82.3 | 627 | 15.7 | 12.3 | 0.0 | 54.9 | 279 | 20.6 | 16.6 | 0.0 | 82.2 |
| SS | 202 | 2.3 | 1.1 | 1.0 | 4.0 | 627 | 2.3 | 1.0 | 1.0 | 4.0 | 279 | 2.2 | 1.0 | 1.0 | 4.0 |
| BALr | 202 | 0.6 | 0.3 | 0.0 | 1.0 | 627 | 0.6 | 0.3 | 0.0 | 1.0 | 279 | 0.6 | 0.3 | 0.0 | 1.0 |
| AIDBH | 202 | 2.6 | 1.6 | 0.2 | 7.7 | 627 | 3.0 | 2.1 | 0.2 | 12.1 | 279 | 3.6 | 2.2 | 0.1 | 10.2 |
| Dominant Specie | Nothofagus alpina | Nothofagus obliqua | Nothofagus dombeyi | ||||||||||||
| Stand Variables | n | Mean | SD | Min | Max | n | Mean | SD | Min | Max | n | Mean | SD | Min | Max |
| BA | 24 | 46.7 | 13.8 | 10.8 | 72.3 | 87 | 35.7 | 13.0 | 9.5 | 71.5 | 47 | 55.2 | 17.8 | 23.4 | 98.4 |
| N | 24 | 2564 | 1184 | 320 | 5000 | 87 | 2378 | 1119 | 320 | 4640 | 47 | 2900 | 1357 | 880 | 5600 |
| QD | 24 | 16.4 | 4.8 | 8.5 | 30.5 | 87 | 15.4 | 6.2 | 6.8 | 33.3 | 47 | 16.9 | 5.4 | 8.4 | 30.4 |
| Hd | 24 | 21.2 | 5.7 | 10.2 | 35.1 | 87 | 20.8 | 7.0 | 7.8 | 42.4 | 47 | 20.8 | 5.9 | 9.9 | 34.1 |
| Ad | 24 | 47.5 | 10.9 | 23.0 | 77.0 | 87 | 36.6 | 14.7 | 12.7 | 86.8 | 47 | 40.2 | 13.1 | 21.3 | 85.1 |
| SI | 24 | 10.3 | 3.9 | 4.1 | 24.3 | 87 | 12.5 | 3.9 | 2.0 | 22.9 | 47 | 11.4 | 3.4 | 3.9 | 18.4 |
| BAN | 24 | 37.6 | 12.4 | 10.8 | 59.7 | 87 | 30.4 | 11.5 | 8.8 | 57.8 | 47 | 46.5 | 18.7 | 8.0 | 89.6 |
| SDI | 24 | 1212 | 336 | 406 | 1944 | 87 | 956 | 258 | 410 | 1674 | 47 | 1400 | 361 | 640 | 2305 |
| RS | 24 | 0.1 | 0.0 | 0.1 | 0.2 | 87 | 0.1 | 0.0 | 0.1 | 0.3 | 47 | 0.1 | 0.0 | 0.1 | 0.2 |
| Parameter | Estimate | SE | p-Value | VIF* | Parameter | Estimate | VIF* |
|---|---|---|---|---|---|---|---|
| CV (Equation (8)) | LASSO (Equation (9)) | ||||||
| 2.410 × 100 | 2.173 × 10−1 | <0.001 | - | −3.098 × 10−1 | - | ||
| −7.062 × 10−3 | 2.064 × 10−3 | <0.001 | 1.74 | −7.255 × 10−3 | 3.20 | ||
| 2.745 × 10−4 | 6.787 × 10−5 | <0.001 | 1.22 | 2.215 × 10−4 | 1.40 | ||
| 9.046 × 10−1 | 6.798 × 10−2 | <0.001 | 3.29 | 7.892 × 10−1 | 5.28 | ||
| −1.138 × 100 | 7.488 × 10−2 | <0.001 | 2.26 | −1.073 × 100 | 6.73 | ||
| −1.336 × 10−1 | 3.149 × 10−2 | <0.001 | 2.22 | −1.325 × 10−1 | 2.44 | ||
| - | - | - | - | −4.318 × 10−2 | 5.36 | ||
| - | - | - | - | 9.792 × 100 | 6.59 | ||
| CV + SpZone (Equation (10)) | LASSO + SpZone (Equation (11)) | ||||||
| 2.702 × 100 | 2.562 × 10−1 | <0.001 | 2.09 | −1.387 × 100 | - | ||
| 2.908 × 100 | 2.345 × 10−1 | <0.001 | 2.09 | 6.790 × 10−2 | 2.28 | ||
| 3.065 × 100 | 2.397 × 10−1 | <0.001 | 2.09 | −2.507 × 10−1 | 2.28 | ||
| 2.538 × 100 | 2.120 × 10−1 | <0.001 | 2.09 | −1.702 × 10−1 | 2.28 | ||
| 2.587 × 100 | 2.219 × 10−1 | <0.001 | 2.09 | −1.955 × 10−1 | 2.28 | ||
| 2.841 × 100 | 2.272 × 10−1 | <0.001 | 2.09 | 3.455 × 10−2 | 2.28 | ||
| 2.678 × 100 | 2.329 × 10−1 | <0.001 | 2.09 | 5.922 × 10−2 | 2.28 | ||
| 2.946 × 100 | 2.298 × 10−1 | <0.001 | 2.09 | −7.117 × 10−3 | 3.30 | ||
| 2.948 × 100 | 2.680 × 10−1 | <0.001 | 2.09 | 8.700 × 10−5 | 2.07 | ||
| 2.941 × 100 | 2.353 × 10−1 | <0.001 | 2.09 | 7.699 × 10−1 | 6.21 | ||
| 2.902 × 100 | 2.358 × 10−1 | <0.001 | 2.09 | −1.096 × 100 | 7.30 | ||
| −6.517 × 10−3 | 2.002 × 10−3 | 0.0012 | 1.82 | −1.293 × 10−1 | 2.53 | ||
| 9.307 × 10−1 | 6.970 × 10−2 | <0.001 | 3.82 | −2.250 × 10−2 | 5.56 | ||
| −1.175 × 100 | 7.797 × 10−2 | <0.001 | 2.61 | 1.419 × 10−1 | 6.91 | ||
| −1.401 × 10−1 | 3.092 × 10−2 | <0.001 | 2.29 | - | - | ||
| n | R2emp | RMSE | RMSE% | BIAS | BIAS% | U2 | |
|---|---|---|---|---|---|---|---|
| Zone | 551 | 0.55 | 1.37 | 44.82 | −0.07 | −2.29 | 0.37 |
| Sp | 551 | 0.56 | 1.36 | 44.49 | −0.07 | −2.29 | 0.37 |
| Zone + Sp | 551 | 0.55 | 1.38 | 45.14 | −0.07 | −2.29 | 0.37 |
| SpZone | 551 | 0.56 | 1.36 | 44.49 | −0.06 | −1.96 | 0.37 |
| Model | n | R2emp | RMSE | RMSE% | BIAS | BIAS% | U2 |
|---|---|---|---|---|---|---|---|
| CV | 551 | 0.56 | 1.35 | 44.16 | −0.06 | −1.96 | 0.37 |
| LASSO | 551 | 0.57 | 1.35 | 44.16 | −0.09 | −2.94 | 0.37 |
| CV + SpZone | 551 | 0.56 | 1.36 | 44.49 | −0.07 | −2.29 | 0.37 |
| LASSO + SpZone | 551 | 0.54 | 1.36 | 45.13 | −0.13 | −4.31 | 0.38 |
| Projection = 6 Years | ||||||||||
| CV | CV + SpZone | |||||||||
| n | R2emp | RMSE% | BIAS% | U2 | n | R2emp | RMSE% | BIAS% | U2 | |
| Total | 1455 | 0.98 | 7.32 | 0.18 | 0.06 | 1455 | 0.98 | 7.44 | 0.54 | 0.06 |
| DBH (5–15) | 777 | 0.88 | 10.06 | −0.42 | 0.10 | 777 | 0.89 | 9.75 | 0.00 | 0.09 |
| DBH (15–30) | 510 | 0.88 | 6.94 | 0.94 | 0.07 | 510 | 0.87 | 7.27 | 1.46 | 0.07 |
| DBH (>30) | 168 | 0.97 | 4.11 | 0.46 | 0.04 | 168 | 0.97 | 4.19 | 0.32 | 0.04 |
| Nothofagus | 943 | 0.99 | 6.33 | −0.26 | 0.06 | 943 | 0.99 | 6.48 | 0.31 | 0.06 |
| Companion | 512 | 0.96 | 10.47 | 1.46 | 0.09 | 512 | 0.96 | 10.47 | 1.20 | 0.09 |
| LASSO | LASSO + SpZone | |||||||||
| n | R2emp | RMSE% | BIAS% | U2 | n | R2emp | RMSE% | BIAS% | U2 | |
| Total | 1455 | 0.99 | 7.26 | 0.36 | 0.06 | 1455 | 0.98 | 7.32 | 0.60 | 0.06 |
| DBH (5–15) | 777 | 0.88 | 9.96 | −0.52 | 0.10 | 777 | 0.89 | 9.85 | −0.31 | 0.09 |
| DBH (15–30) | 510 | 0.88 | 6.94 | 1.13 | 0.07 | 510 | 0.88 | 7.12 | 1.51 | 0.07 |
| DBH (>30) | 168 | 0.97 | 3.96 | 0.13 | 0.04 | 168 | 0.97 | 4.02 | −0.03 | 0.04 |
| Nothofagus | 943 | 0.99 | 6.28 | −0.05 | 0.06 | 943 | 0.99 | 6.38 | 0.36 | 0.06 |
| Companion | 512 | 0.96 | 10.29 | 1.54 | 0.09 | 512 | 0.96 | 10.38 | 1.29 | 0.09 |
| Projection = 12 Years | ||||||||||
| CV | CV + SpZone | |||||||||
| n | R2emp | RMSE% | BIAS% | U2 | n | R2emp | RMSE% | BIAS% | U2 | |
| Total | 389 | 0.97 | 9.66 | 1.75 | 0.08 | 389 | 0.97 | 9.82 | 2.34 | 0.09 |
| DBH (5–15) | 177 | 0.58 | 17.07 | 5.03 | 0.16 | 177 | 0.59 | 16.87 | 6.02 | 0.16 |
| DBH (15–30) | 151 | 0.83 | 8.39 | 2.10 | 0.08 | 151 | 0.81 | 8.86 | 2.70 | 0.09 |
| DBH (>30) | 61 | 0.89 | 5.55 | 1.36 | 0.05 | 61 | 0.89 | 5.60 | 1.00 | 0.05 |
| Nothofagus | 295 | 0.98 | 7.93 | −0.29 | 0.07 | 295 | 0.97 | 8.17 | 0.53 | 0.07 |
| Companion | 94 | 0.83 | 18.45 | 12.49 | 0.17 | 94 | 0.83 | 18.20 | 11.92 | 0.17 |
| LASSO | LASSO + SpZone | |||||||||
| n | R2emp | RMSE% | BIAS% | U2 | n | R2emp | RMSE% | BIAS% | U2 | |
| Total | 389 | 0.97 | 9.50 | 1.96 | 0.08 | 389 | 0.97 | 9.50 | 2.39 | 0.08 |
| DBH (5–15) | 177 | 0.58 | 17.07 | 4.74 | 0.16 | 177 | 0.59 | 16.87 | 5.13 | 0.16 |
| DBH(15–30) | 151 | 0.83 | 8.30 | 2.42 | 0.08 | 151 | 0.82 | 8.49 | 2.80 | 0.08 |
| DBH (>30) | 61 | 0.90 | 5.30 | 0.79 | 0.05 | 61 | 0.90 | 5.27 | 0.37 | 0.05 |
| Nothofagus | 295 | 0.98 | 7.74 | 0.05 | 0.07 | 295 | 0.98 | 7.83 | 0.62 | 0.07 |
| Companion | 94 | 0.83 | 18.45 | 12.41 | 0.17 | 94 | 0.83 | 18.04 | 11.76 | 0.16 |
| N. alpina | N. obliqua | N. dombeyi | |
|---|---|---|---|
| Zone 1 | 0.794 (0.125) abcd | 0.652 (0.057) a | 1.020 (0.079) cd |
| Zone 2 | 0.996 (0.072) cd | 0.697 (0.053) ab | 1.027 (0.154) abcd |
| Zone 3 | - | 0.948 (0.063) bcd | 1.034 (0.090) cd |
| Zone 4 | 1.153 (0.086) d | 0.784 (0.069) abc | 0.960 (0.087) abcd |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno, P.C.; Palmas, S.; Escobedo, F.J.; Cropper, W.P.; Gezan, S.A. Individual-Tree Diameter Growth Models for Mixed Nothofagus Second Growth Forests in Southern Chile. Forests 2017, 8, 506. https://doi.org/10.3390/f8120506
Moreno PC, Palmas S, Escobedo FJ, Cropper WP, Gezan SA. Individual-Tree Diameter Growth Models for Mixed Nothofagus Second Growth Forests in Southern Chile. Forests. 2017; 8(12):506. https://doi.org/10.3390/f8120506
Chicago/Turabian StyleMoreno, Paulo C., Sebastian Palmas, Francisco J. Escobedo, Wendell P. Cropper, and Salvador A. Gezan. 2017. "Individual-Tree Diameter Growth Models for Mixed Nothofagus Second Growth Forests in Southern Chile" Forests 8, no. 12: 506. https://doi.org/10.3390/f8120506
APA StyleMoreno, P. C., Palmas, S., Escobedo, F. J., Cropper, W. P., & Gezan, S. A. (2017). Individual-Tree Diameter Growth Models for Mixed Nothofagus Second Growth Forests in Southern Chile. Forests, 8(12), 506. https://doi.org/10.3390/f8120506






