Spatial Genetic Structure within and among Seed Stands of Pinus engelmannii Carr. and Pinus leiophylla Schiede ex Schltdl. & Cham, in Durango, Mexico
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Genetic Analysis
2.3. Spatial Structural Analysis of AFLP Data
2.4. Kruskal Wallis Test
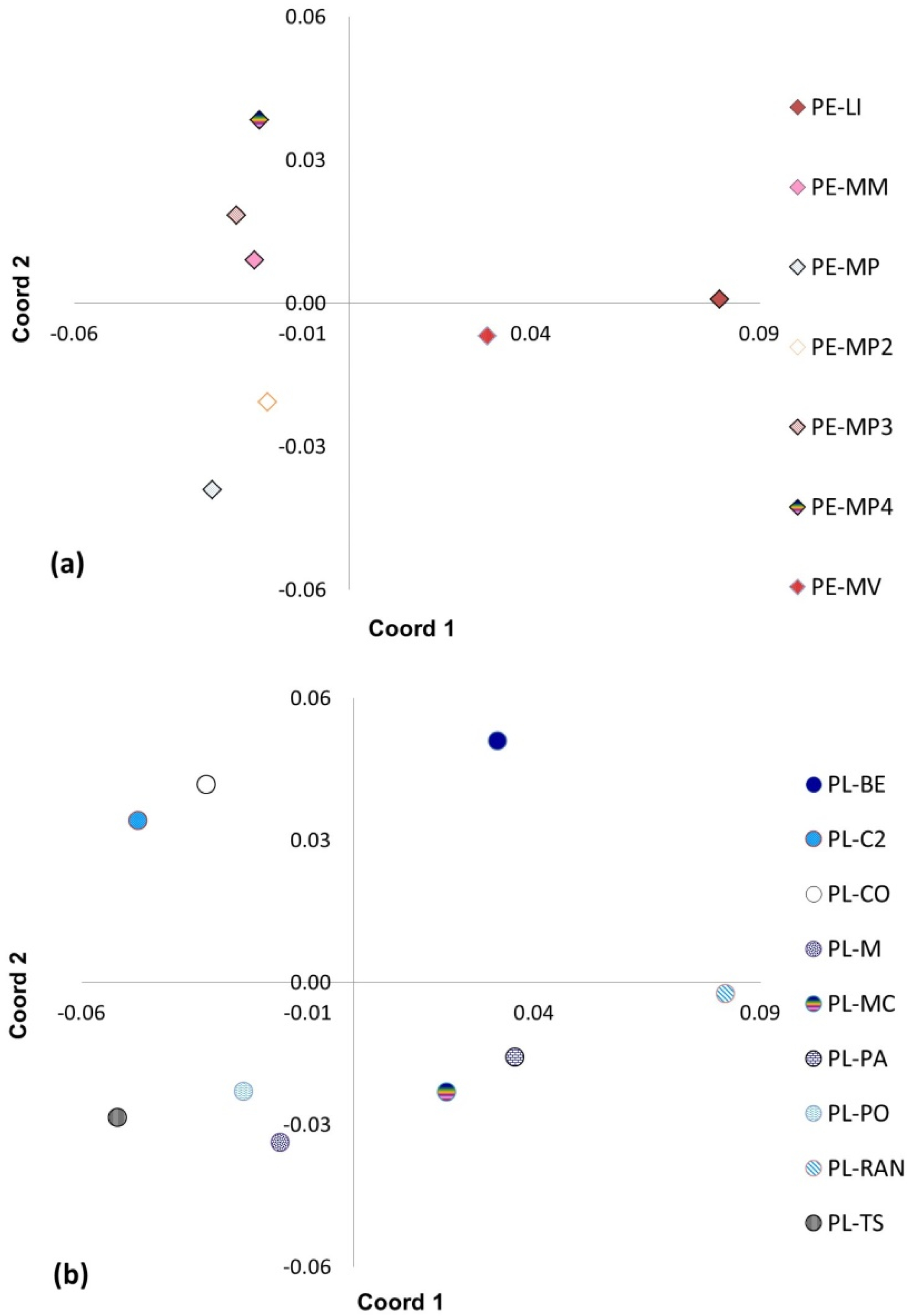
2.5. Principal Coordinate Analysis
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vekemans, X.; Hardy, O.J. New insights from fine-scale spatial genetic structure analyses in plant populations. Mol. Ecol. 2004, 13, 921–935. [Google Scholar] [CrossRef] [PubMed]
- Van Rossum, F.; Triest, L. Fine-Scale genetic structure of the common Primula elatior (Primulaceae) at an early stage of population fragmentation. Am. J. Bot. 2006, 93, 1281–1288. [Google Scholar] [CrossRef] [PubMed]
- Ledoux, J.B.; Garrabou, J.; Bianchimani, O.; Drap, P.; FÉRAL, J.P.; Aurelle, D. Fine-Scale genetic structure and inferences on population biology in the threatened Mediterranean red coral, Corallium rubrum. Mol. Ecol. 2010, 19, 4204–4216. [Google Scholar] [CrossRef] [PubMed]
- Segelbacher, G.; Cushman, S.A.; Epperson, B.K.; Fortin, M.J.; Francois, O.; Hardy, O.J.; Holderegger, R.; Taberlet, P.; Waits, L.P.; Manel, S. Applications of landscape genetics in conservation biology: Concepts and challenges. Conserv. Genet. 2010, 11, 375–385. [Google Scholar] [CrossRef]
- Degen, B.; Petit, R.; Kremer, A. SGS—Spatial Genetic Software: A Computer Program for Analysis of Spatial Genetic and Phenotypic Structures of Individuals and Populations. J. Hered. 2001, 92, 447–449. [Google Scholar] [CrossRef] [PubMed]
- Reyes-Murillo, C.A.; Hernández-Díaz, J.C.; Heinze, B.; Prieto-Ruiz, J.Á.; López-Sánchez, C.A.; Wehenkel, C. Spatial genetic structure in seed stands of Pinus lumholtzii BL Rob. & Fernald in Durango, Mexico. Tree Genet. Genomes 2016, 12, 1–10. [Google Scholar]
- Mueller, U.G.; Wolfenbarger, L.L. AFLP genotyping and fingerprinting. Trends Ecol. Evol. 1999, 14, 389–394. [Google Scholar] [CrossRef]
- Hardy, I.C.W.; Goubault, M.; Batchelor, T.P. Hymenopteran contests and agonistic behaviour. In Animal Contests; Hardy, I.C.W., Briffa, M., Eds.; Cambridge University Press: Cambridge, UK, 2013; pp. 147–177. [Google Scholar]
- Hardy, O.J. Estimation of pairwise relatedness between individuals and characterization of isolation-by-distance processes using dominant genetic markers. Mol. Ecol. 2003, 12, 1577–1588. [Google Scholar] [CrossRef] [PubMed]
- Krauss, S.L.; Sinclair, E.A.; Bussell, J.D.; Hobbs, R.J. An ecological genetic delineation of local seed-source provenance for ecological restoration. Ecol. Evol. 2013, 3, 2138–2149. [Google Scholar] [CrossRef] [PubMed]
- Parker, K.C.; Hamrick, J.L.; Parker, A.J.; Nason, J.D. Fine-Scale genetic structure in Pinus clausa (Pinaceae) populations: Effects of disturbance history. Heredity 2001, 87, 99–113. [Google Scholar] [CrossRef] [PubMed]
- Epperson, B.K.; Gi Chung, M. Spatial genetic structure of allozyme polymorphisms within populations of Pinus strobus (Pinaceae). Am. J. Bot. 2001, 88, 1006–1010. [Google Scholar] [CrossRef] [PubMed]
- Quiñones-Pérez, C.Z.; Simental-Rodríguez, S.L.; Sáenz-Romero, C.; Jaramillo-Correa, J.P.; Wehenkel, C. Spatial genetic structure in the very rare and species-rich Picea chihuahuana tree community (Mexico). Silvae. Genet. 2014, 63, 149–159. [Google Scholar]
- Hernández-Velasco, J.; Hernández-Díaz, J.C.; Fladung, M.; Cañadas-López, A.; Prieto-Ruíz, J.A.; Wehenkel, C. Spatial genetic structure in four Pinus species in the Sierra Madre Occidental, Durango, México. Can. J. For. Res. 2016. [Google Scholar] [CrossRef]
- Rzedowski, J.; Huerta, L. Vegetación de México. Available online: http://www.biodiversidad.gob.mx/publicaciones/librosDig/pdf/VegetacionMxPort.pdf (accessed on 6 January 2017).
- Comisión Nacional Forestal (CONAFOR). Inventario Nacional Forestal y de Suelos de México 2004–2009, 1st ed.; CONAFOR: Zapopan, Mexico, 2009; p. 206. [Google Scholar]
- Rodríguez-Banderas, A.; Vargas-Mendoza, C.F.; Buonamici, A.; Vendramin, G.G. Genetic diversity and phylogeographic analysis of Pinus leiophylla: A post-glacial range expansion. J. Biogeogr. 2009, 36, 1807–1820. [Google Scholar] [CrossRef]
- Ávila-Flores, I.J.; Hernández-Díaz, J.C.; González-Elizondo, M.S.; Prieto-Ruíz, J.A.; Wehenkel, C. Pinus engelmannii Carr. In Northwestern Mexico: A Review. Pak. J. Bot. 2016, 5. in press. [Google Scholar]
- González Elizondo, M.S.; González Elizondo, M.; Márquez Linares, M.A. Vegetación y Ecorregiones de Durango; Plaza y Valdés Editores-Instituto Politécnico Nacional: Distrito Federal, Mexico, 2007; p. 220. [Google Scholar]
- González-Elizondo, M.S.; González-Elizondo, M.; Ruacho-González, L.; López-Enríquez, L.; Retana-Rentería, F.I.; Tena-Flores, J.A. Ecosystems and Diversity of the Sierra Madre Occidental. Available online: https://www.fs.fed.us/rm/pubs/rmrs_p067/rmrs_p067_204_211.pdf (accessed on 6 January 2017).
- Silva-Flores, R.; Pérez-Verdín, G.; Wehenkel, C. Patterns of tree species diversity in relation to climatic factors on the Sierra Madre Occidental, Mexico. PLoS ONE 2014, 9, e105034. [Google Scholar] [CrossRef] [PubMed]
- Wehenkel, C.; Corral-Rivas, J.J.; Hernández-Díaz, J.C.; von Gadow, K. Estimating balanced structure areas in multi-species forests on the Sierra Madre Occidental, Mexico. Ann. For. Sci. 2011, 68, 385–394. [Google Scholar] [CrossRef]
- Wehenkel, C.; Simental-Rodríguez, S.L.; Silva-Flores, R.; Hernández-Díaz, J.C.; López-Sánchez, C.A.; Antúnez, P. Discrimination of 59 seed stands of various Mexican pine species based on 43 dendrometric, climatic, edaphic and genetic traits. Forstarchiv 2015, 86, 194–201. [Google Scholar]
- Farjon, A. Pinus engelmannii. The IUCN Red List of Threatened Species. Available online: http://www.iucnredlist.org/details/42362/0 (accessed on 14 June 2016).
- Farjon, A. Pinus leiophylla. The IUCN Red List of Threatened Species. Available online: http://www.iucnredlist.org/details/42376/0 (accessed on 22 July 2016).
- Mejía-Bojorquez, J.M.; Prieto-Ruíz, J.Á.; García-Cuevas, X.; García-Rodríguez, J.L.; Muñoz-Flores, H.J; Rosales-Mata, S. Evaluación de plantaciones comerciales en el Estado de Durango. In Evaluación de reforestaciones en la Sierra Madre Occidental; Muñoz-Flores, H.J., Prieto-Ruíz, J.A., Ruedas-Sánchez, A., Alarcón-Bustamante, M., Eds.; Campo experimental Valle del Guadiana, CIRNOC.INIFAP: Durango, Mexico, 2011; pp. 57–86. [Google Scholar]
- Castelán-Muñoz, N. Fisiología de Plántulas de Pinus Leiophylla Sometidas a Estrés Hídrico. Master’s Thesis, Colegio de Postgraduados, Texcoco, Mexico, 2014. [Google Scholar]
- Wehenkel, C.; Cruz-Cobos, F.; Carrillo, A.; Lujan-Soto, J.E. Estimating bark volumes for 16 native tree species on the Sierra Madre Occidental, Mexico. Scand. J. For. Res. 2012, 27, 578–585. [Google Scholar] [CrossRef]
- Slavov, G.T.; Howe, G.T.; Adams, W.T. Pollen contamination and mating patterns in a Douglas-fir seed orchard as measured by simple sequence repeat markers. Can. J. For. Res. 2005, 35, 1592–1603. [Google Scholar] [CrossRef]
- Vos, P.; Hogers, R.; Bleeker, M.; Reijans, M.; Van Lee, T.; Hornes, M.; Frijters, A.; Pot, J.; Zabeau, M. AFLP: A new technique for DNA fingerprinting. Nucleic Acids Res. 1995, 23, 4407–4414. [Google Scholar] [CrossRef] [PubMed]
- Ávila-Flores, I.J.; Hernández-Díaz, J.C.; González-Elizondo, M.S.; Prieto-Ruíz, J.A.; Wehenkel, C. Spatial genetic structure and degree of hybridization in seed stands of Pinus engelmannii Carr. in the Sierra Madre Occidental, Durango, Mexico. PLoS ONE 2015, 11, e0152651. [Google Scholar]
- Krauss, S.L. Accurate gene diversity estimates from amplified fragment length polymorphism (AFLP) markers. Mol. Ecol. 2000, 9, 1241–1245. [Google Scholar] [CrossRef] [PubMed]
- Bonin, A.; Bellemain, E.; Bronken, E.P.; Pompanon, F. How to track and assess genotyping errors in population genetics studies. Mol. Ecol. 2004, 13, 3261–3273. [Google Scholar] [CrossRef] [PubMed]
- Deichsel, G.; Trampisch, H.J. Cluster Analyse und Diskriminanz Analyse; Gustav Fischer Verlag: Stuttgart, Germany, 1985; p. 880. [Google Scholar]
- Huff, D.R.; Peakall, R.; Smouse, P.E. RAPD variation within and among natural populations of outcrossing buffalo grass Buchloe dactyloides (Nutt) Engelm. Theor. Appl. Genet. 1993, 86, 927–934. [Google Scholar] [CrossRef] [PubMed]
- Peakall, R.; Smouse, P.E. GenAlEx 6.5: Genetic analysis in Excel. Population genetic software for teaching and research-an update. Bioinformatics 2012, 28, 2537–2539. [Google Scholar] [CrossRef] [PubMed]
- Doligez, A.; Joly, H.I. Genetic diversity and spatial structure within a natural stand of a tropical forest tree species, Carapa procera (Meliaceae), in French Guiana. Heredity 1997, 79, 72–82. [Google Scholar] [CrossRef]
- Manly, B.F. Randomization Bootstrap and Monte Carlo Methods in Biology, 3rd ed.; Chapman and Hall/CRC: London, UK, 1997; p. 480. [Google Scholar]
- Hochberg, Y. A sharper Bonferroni procedure for multiple tests of significance. Biometrika 1988, 75, 800–802. [Google Scholar] [CrossRef]
- Hardy, O.J.; Vekemans, X. SPAGeDi: A versatile computer program to analyse spatial genetic structure at the individual or population levels. Mol. Ecol. Notes 2002, 2, 618–620. [Google Scholar] [CrossRef]
- SPAGeDi software ver. 1.4. 2016. Available online: http://ebe.ulb.ac.be/ebe/Software.html (accessed on 10 August 2016).
- Rousset, F. Inbreeding and relatedness coefficients: What do they measure? Heredity 2002, 88, 371–380. [Google Scholar] [CrossRef] [PubMed]
- Kruskal, W.H.; Wallis, W.A. Use of Ranks in One-Criterion Variance Analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Sachs, L. Angewandte Statistik; Springer: Belin, Germany, 1997; p. 155. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Pohlert, T. The Pairwise Multiple Comparison of Mean Ranks Package (PMCMR). 2014. Available online: https://cran.r-project.org/web/packages/PMCMR/vignettes/PMCMR.pdf (accessed on 11 February 2014).
- Nei, M. Genetic distance between populations. Amer. Nat. 1972, 106, 283–392. [Google Scholar] [CrossRef]
- Nei, M. Estimation of average heterozygosity and genetic distance from a small number of individuals. Genetics 1978, 89, 583–590. [Google Scholar] [PubMed]
- Epperson, B.K.; Alvarez-Buylla, E.R. Limited seed dispersal and genetic structure in life stages of Cecropia obtusifolia. Evolution 1997, 51, 275–282. [Google Scholar] [CrossRef]
- Hamrick, J.L.; Murawski, D.A.; Nason, J.D. The influence of seed dispersal mechanisms on the genetic structure of tropical tree populations. Vegetatio 1993, 107–108, 281–297. [Google Scholar]
- Fuchs, E.J.; Hamrick, J.L. Spatial genetic structure within size classes of the endangered tropical tree Guaiacum sanctum (Zygophyllaceae). Am. J. Bot. 2010, 97, 1200–1207. [Google Scholar] [CrossRef] [PubMed]
- Hamrick, J.L.; Nason, J.D. Consequences of dispersal in plants. In Population Dynamics in Ecological Space and Time; Rhodess, O.E., Jr., Chesser, R.K., Smith, M.H., Eds.; University of Chicago Press: Chicago, IL, USA, 1996; pp. 203–236. [Google Scholar]
- Jordano, P.; Garcia, C.; Godoy, J.A.; Garcia-Castano, J.L. Differential contribution of frugivores to complex seed dispersal patterns. Proc. Natl. Acad. Sci. USA 2007, 104, 3278–3288. [Google Scholar] [CrossRef] [PubMed]
- Wright, S. Isolation by distance. Genetics 1943, 28, 114–138. [Google Scholar] [PubMed]
- Peterson, M.A.; Denno, R.F. The influence of dispersal and diet breadth on patterns of genetic isolation by distance in phytophagous insects. Amer. Nat. 1998, 152, 428–446. [Google Scholar] [CrossRef] [PubMed]
- Prescher, F. Seed Orchards–Genetic Considerations on Function, Management and Seed Procurement. Ph.D. Thesis, Swedish University of Agricultural Sciences, Uppsala, Sweden, 2007. [Google Scholar]
- Varis, S.; Pakkanen, A.; Galofré, A.; Pulkkinen, P. The extent of south-north pollen transfer in Finnish Scots pine. Silva Fenn. 2009, 43, 717–726. [Google Scholar] [CrossRef]
- Williams, C.G. Long-Distance pine pollen still germinates after meso-scale dispersal. Am. J. Bot. 2010, 97, 846–855. [Google Scholar] [CrossRef] [PubMed]
- Robledo-Arnuncio, J.J. Wind pollination over mesoscale distances: An investigation with Scots pine. New Phytol. 2011, 190, 222–233. [Google Scholar] [CrossRef] [PubMed]
- Ivanek, O.; Procházková, Z.; Matĕjka, K. Analysis of the genetic structure of a model Scots pine (Pinus sylvestris) seed orchard for development of management strategies. J. For. Sci. 2013, 59, 377–385. [Google Scholar]
- Vander Mijnsbrugge, K.; Bischoff, A.; Smith, B. A question of origin: Where and how to collect seed for ecological restoration. Basic Appl. Ecol. 2010, 11, 300–311. [Google Scholar] [CrossRef]
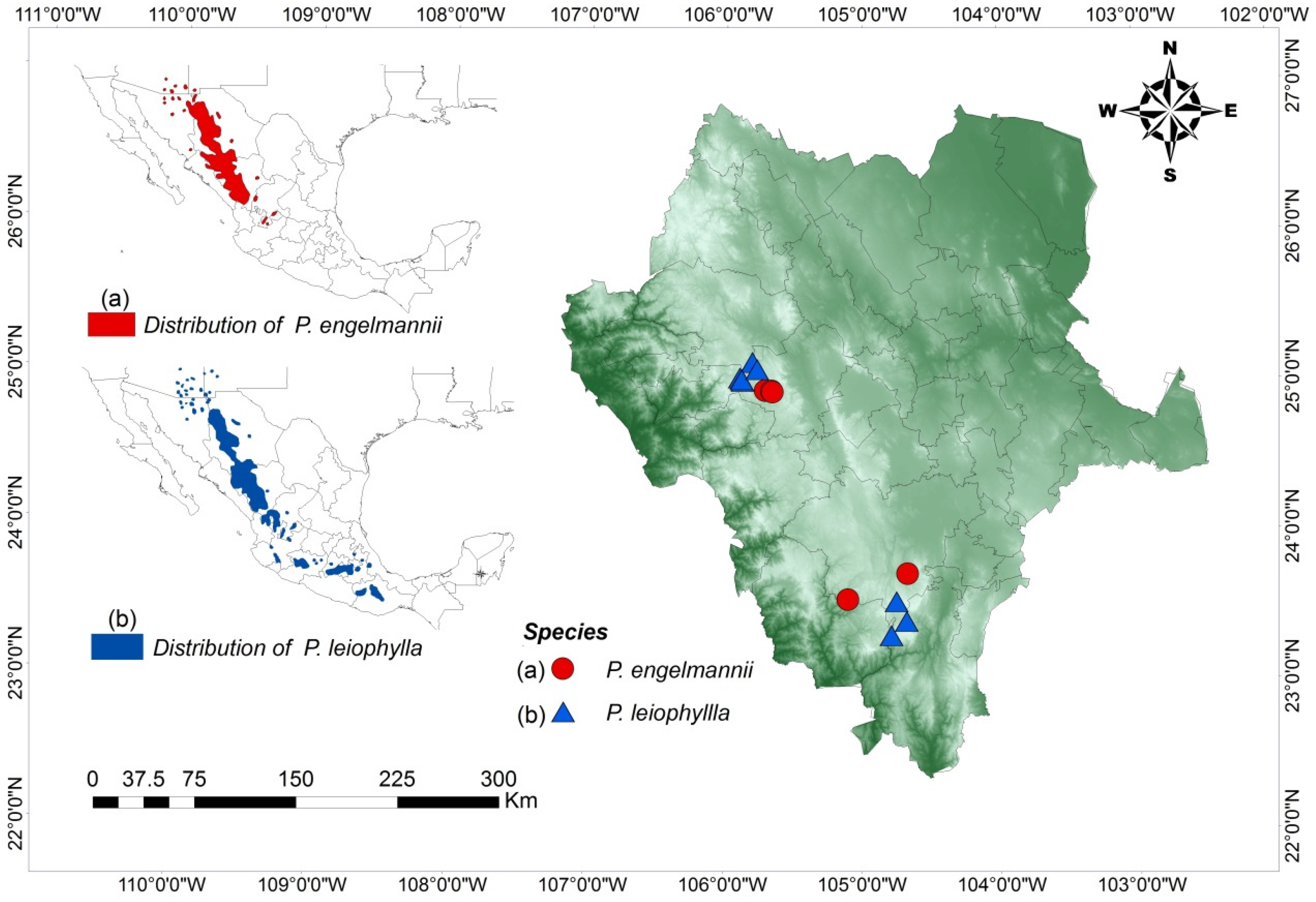

| Code | SP | N | Location | Municipality | Latitude (North) | Longitude (West) | E (m) | MD (m) | CE |
|---|---|---|---|---|---|---|---|---|---|
| PE-Li | PE | 35 | La Lisuda | Pueblo Nuevo | 23°32′11″ | 105°06′00″ | 2523 | 35.56 | 1.070 |
| PE-MM | PE | 35 | Mesa de Mingarreta | Santiago Papasquiaro | 24°55′48″ | 105°42′25″ | 2418 | 55.15 | 1.121 |
| PE-MP | PE | 35 | Mesa de Perdederos 1 | Santiago Papasquiaro | 24°55′15″ | 105°39′36″ | 2420 | 57.78 | 0.984 |
| PE-MP2 | PE | 35 | Mesa de Perdederos 2 | Santiago Papasquiaro | 24°55′27″ | 105°39′41″ | 2443 | 52.22 | 1.201 |
| PE-MP3 | PE | 34 | Mesa de Perdederos 3 | Santiago Papasquiaro | 24°55′36″ | 105°39′38″ | 2424 | 61.48 | 1.354 |
| PE-MP4 | PE | 35 | Mesa de Perdederos 4 | Santiago Papasquiaro | 24°55′08″ | 105°39′15″ | 2424 | 53.74 | 0.98 |
| PE-MV | PE | 35 | La Mesa de Veracruz | Durango | 23°42′34″ | 104°40′04″ | 2390 | 66.49 | 1.257 |
| PL-BE | PL | 23 | Bajío | Mezquital | 23°23′27″ | 104°40′27″ | 2551 | 64.09 | 1.225 |
| PL-C2 | PL | 35 | Coloradas | Mezquital | 23°17′49″ | 104°47′08″ | 2451 | 41.58 | 0.970 |
| PL-CO | PL | 34 | Cócono | Durango | 23°31′28″ | 104°44′51″ | 2742 | 40.07 | 0.969 |
| PL-M | PL | 35 | Maguey | Santiago Papasquiaro | 25°07′05″ | 105°48′06″ | 2518 | 47.5 | 0.873 |
| PL-MC | PL | 34 | Mesa de Cristo | Santiago Papasquiaro | 24°59′29″ | 105°52′24″ | 2575 | 38.27 | 0.916 |
| PL-PA | PL | 35 | Patio | Santiago Papasquiaro | 25°00′48″ | 105°53′38″ | 2500 | 30.36 | 0.689 |
| PL-PO | PL | 33 | Polvorín | Santiago Papasquiaro | 25°00′05″ | 105°52′47″ | 2508 | 31.18 | 0.940 |
| PL-RAN | PL | 35 | Rancho | Santiago Papasquiaro | 25°00′05″ | 105°52′47″ | 2475 | 26.15 | 1.034 |
| PL-TS | PL | 34 | Tijera de Salsipuedes | Santiago Papasquiaro | 25°04′17″ | 105°46′05″ | 2541 | 99.86 | 0.872 |
| Spatial Genetic Software | ||||||
|---|---|---|---|---|---|---|
| Code | N | MD | TD | P(TD) < (−CI) | P(TD) > (+CI) | MT |
| PE-LI | 35 | 35.56 | 0.4533 | 0.857 (150–300) | 0.965 (300–450) | 49 (600–750) |
| PE-MM | 34 | 57.78 | 0.5119 | 0.727 (0–150) | 0.681 (300–450) | 38 (450–600) |
| PE-MP | 35 | 55.15 | 0.5072 | 0.836 (600–750) | 0.753 (300–450) | 40 (600–750) |
| PE-MP2 | 35 | 52.22 | 0.4928 | 0.772 (0–150) | 0.885 (450–600) | 48 (450–600) |
| PE-MP3 | 35 | 61.48 | 0.5088 | 0.984 (150–300) | 0.968 (600–750) | 37 (600–750) |
| PE-MP4 | 35 | 53.74 | 0.4594 | 0.950 (150–300) | 0.983 (450–600) | 63 (600–750) |
| PE-MV | 29 | 70.77 | 0.4909 | 0.885 (0–150) | 0.813 (450–600) | 61 (600–750) |
| PL-BE | 23 | 64.09 | 0.4946 | 0.837 (150–300) | 0.902 (300–450) | 41 (0–150) |
| PL-C2 | 35 | 41.58 | 0.5499 | 0.911 (0–150) | 0.833 (300–450) | 64 (450–600) |
| PL-CO | 34 | 40.07 | 0.5150 | 0.994 (150–300) | 0.9999 + (300–450) | 146 (0–150) |
| PL-M | 35 | 47.5 | 0.4854 | 0.994 (0–150) | 0.941 (300–450) | 143 (0–150) |
| PL-MC | 34 | 38.27 | 0.4956 | 0.988 (0–150) | 0.766 (150–300) | 40 (450–600) |
| PL-PA | 35 | 30.36 | 0.4998 | 0.812 (150–300) | 0.973 (450–600) | 35 (600–750) |
| PL-PO | 33 | 31.18 | 0.5595 | 0.986 (150–300) | 0.983 (0–150) | 43 (300–450) |
| PL-RAN | 35 | 26.15 | 0.4928 | 0.856 (0–150) | 0.988 (300–450) | 85 (300–450) |
| PL-TS | 34 | 99.86 | 0.5343 | 0.868 (1050–1200) | 0.914 (0–150) | 32 (0–150, 1050–1200) |
| Code | N | MD | TD | P(TD) < (−CI) | P(TD) > (+CI) | MT | Classes |
|---|---|---|---|---|---|---|---|
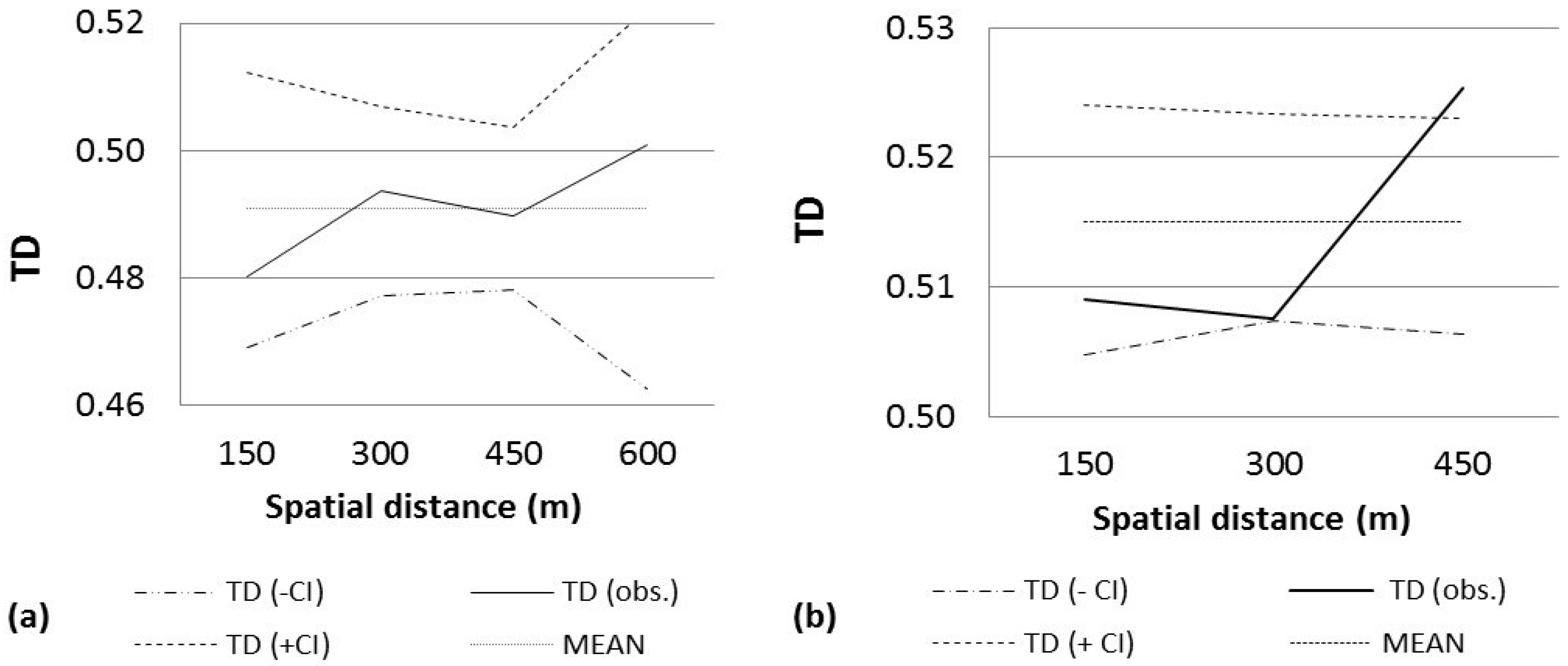
| NORTH | 140 | 55.68 | 0.5047 | 0.9999 (0–160) + | 0.9999 (320–480) + | 32 (0–160) | 10 |
| 0.9999 (160–320) + | 0.9999 (480–640) + | ||||||
| 0.9999 (960–1120) + | 0.9999 (640–800) + | ||||||
| SOUTH | 64 | 51.51 | 0.4837 | 0.9999 (0–24) + | 0.9549 (24–48) | 997 (24–48) | 2 |
| Code | N | MD | TD | P(TD) < (−CI) | P(TD) > (+CI) | MT | Classes |
|---|---|---|---|---|---|---|---|
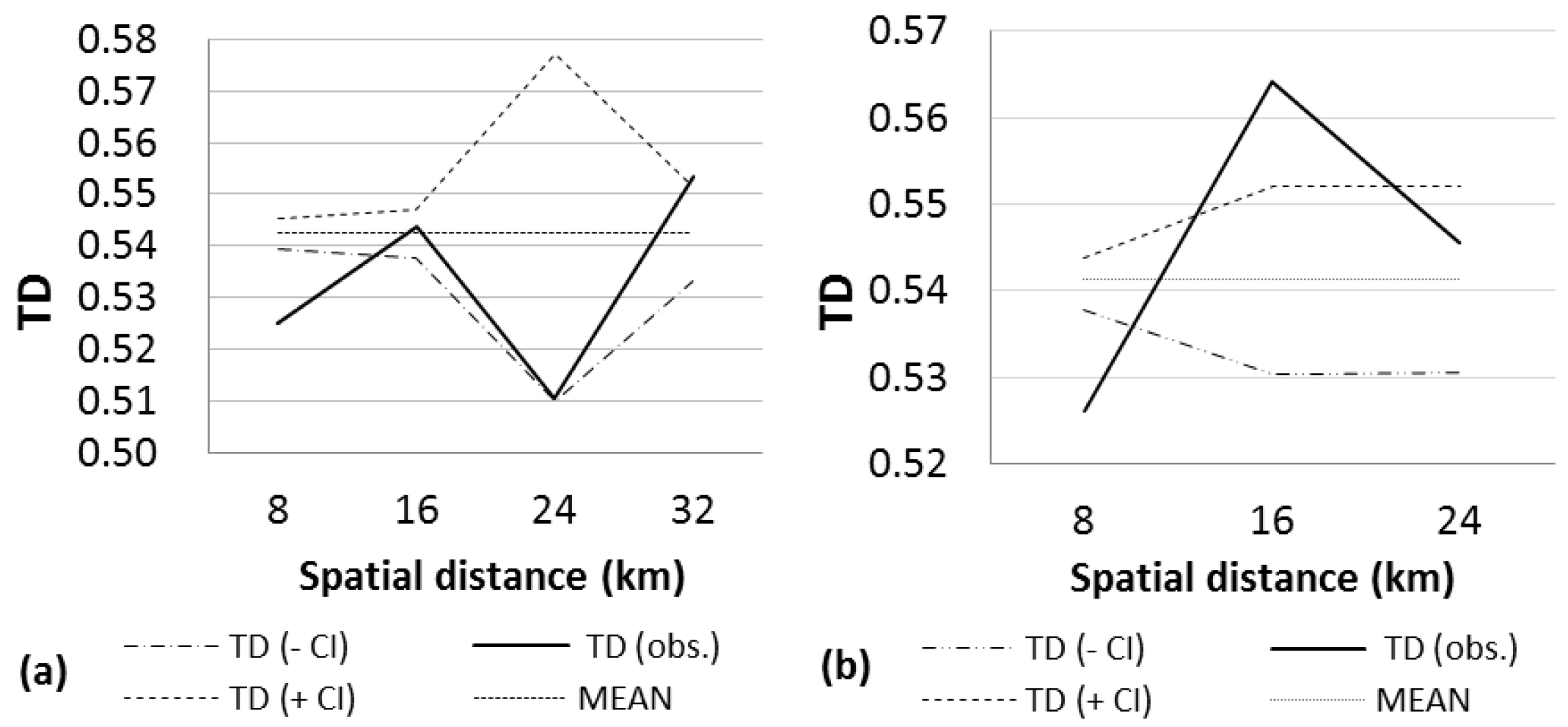
| NORTH | 206 | 45.47 | 0.5425 | 0.9999 (0–8) + | 0.9976 (24–32) | 2349 (28–35) | 4 |
| 0.9999 (16–24) + | |||||||
| SOUTH | 92 | 46.65 | 0.5413 | 0.9999 (0–8) + | 0.9999 (8–16) + | 732 (8–16) | 3 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ortiz-Olivas, M.E.; Hernández-Díaz, J.C.; Fladung, M.; Cañadas-López, Á.; Prieto-Ruíz, J.Á.; Wehenkel, C. Spatial Genetic Structure within and among Seed Stands of Pinus engelmannii Carr. and Pinus leiophylla Schiede ex Schltdl. & Cham, in Durango, Mexico. Forests 2017, 8, 22. https://doi.org/10.3390/f8010022
Ortiz-Olivas ME, Hernández-Díaz JC, Fladung M, Cañadas-López Á, Prieto-Ruíz JÁ, Wehenkel C. Spatial Genetic Structure within and among Seed Stands of Pinus engelmannii Carr. and Pinus leiophylla Schiede ex Schltdl. & Cham, in Durango, Mexico. Forests. 2017; 8(1):22. https://doi.org/10.3390/f8010022
Chicago/Turabian StyleOrtiz-Olivas, María Elena, José Ciro Hernández-Díaz, Matthias Fladung, Álvaro Cañadas-López, José Ángel Prieto-Ruíz, and Christian Wehenkel. 2017. "Spatial Genetic Structure within and among Seed Stands of Pinus engelmannii Carr. and Pinus leiophylla Schiede ex Schltdl. & Cham, in Durango, Mexico" Forests 8, no. 1: 22. https://doi.org/10.3390/f8010022
APA StyleOrtiz-Olivas, M. E., Hernández-Díaz, J. C., Fladung, M., Cañadas-López, Á., Prieto-Ruíz, J. Á., & Wehenkel, C. (2017). Spatial Genetic Structure within and among Seed Stands of Pinus engelmannii Carr. and Pinus leiophylla Schiede ex Schltdl. & Cham, in Durango, Mexico. Forests, 8(1), 22. https://doi.org/10.3390/f8010022







