Next Article in Journal / Special Issue
Predictive Modeling of Black Spruce (Picea mariana (Mill.) B.S.P.) Wood Density Using Stand Structure Variables Derived from Airborne LiDAR Data in Boreal Forests of Ontario
Previous Article in Journal
The Effect of Harvest on Forest Soil Carbon: A Meta-Analysis
Previous Article in Special Issue
Enhancing Forest Growth and Yield Predictions with Airborne Laser Scanning Data: Increasing Spatial Detail and Optimizing Yield Curve Selection through Template Matching
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 7
Issue 12
10.3390/f7120307
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Forest Inventory Attribute Prediction Using Lightweight Aerial Scanner Data in a Selected Type of Multilayered Deciduous Forest

by
Ivan Sačkov
1,*,
Giovanni Santopuoli
2,
Tomáš Bucha
1,
Bruno Lasserre
2 and
Marco Marchetti
2
1
National Forest Centre-Forest Research Institute Zvolen, T. G. Masaryka 22, Zvolen 96092, Slovakia
2
Department of Biosciences and Territory, University of Molise, C.da Fonte Lappone, Pesche 86090, Italy
*
Author to whom correspondence should be addressed.
Forests 2016, 7(12), 307; https://doi.org/10.3390/f7120307
Submission received: 7 September 2016 / Revised: 30 November 2016 / Accepted: 1 December 2016 / Published: 7 December 2016
(This article belongs to the Special Issue LiDAR Remote Sensing of Forest Resources)
Browse Figures
Versions Notes

Abstract

:
Airborne laser scanning is a promising technique for efficient and accurate, remote-based forest inventory, due to its capacity for direct measurement of the three-dimensional structure of vegetation. The main objective of this study was to test the usability and accuracy of an individual tree detection approach, using reFLex software, in the evaluation of forest variables. The accuracy assessment was conducted in a selected type of multilayered deciduous forest in southern Italy. Airborne laser scanning data were taken with a YellowScan Mapper scanner at an average height of 150 m. Point density reached 30 echoes per m2, but most points belonged to the first echo. The ground reference data contained the measured positions and dimensions of 445 trees. Individual tree-detection rates were 66% for dominant, 48% for codominant, 18% for intermediate, and 5% for suppressed trees. Relative root mean square error for tree height, diameter, and volume reached 8.2%, 21.8%, and 45.7%, respectively. All remote-based tree variables were strongly correlated with the ground data (R2 = 0.71–0.79). At the stand-level, the results show that differences ranged between 4% and 17% for stand height and 22% and 40% for stand diameter. The total growing stock differed by −43% from the ground reference data, and the ratios were 64% for dominant, 58% for codominant, 36% for intermediate, and 16% for suppressed trees.

1. Introduction

Forests are one of Europe’s most important renewable resources, and provide multiple benefits to society and the economy. Providing information on the state and trends of forest resources is one of the most important challenges at a global level. Although a great deal of effort has been made for monitoring, assessing, and reporting on forest ecosystems [1,2], several challenges remain because forest cover is increasing, and, in addition, due to the national and international commitments to biodiversity conservation and renewable energy, which require even more information on forests and on Sustainable Forest Management (SFM). The current trend of afforestation and natural succession of abandoned lands [3,4] have increased the EU’s forest area by around 0.4% per year in recent decades [5]. As a result, on the one hand, there is an increase of forest cover, while, on the other hand, there is a strong interest in assessing the productivity of forests and the trade-off between the production of wood and non-wood forest products, and other ecosystem services, derived from forest resources [6]. For this reason, many efforts have been made in assessing the progress towards SFM, testing, implementing [7,8], and developing (see [9]) new SFM indicators to enable the support of policy and decision makers, in order to discover strategies to foster forest resilience and adaptation to climate change.
Traditional inventories, based on field measurement, are the most direct way to estimate a forest biomass pool, and are considered statistically highly accurate. However, they are expensive, time consuming [10], and difficult to implement (i.e., steeped, rocked, and ownership regimes hinder practical implementation). Furthermore, Andersen et al. [11] highlighted that field samplings are (typically) based on a relatively limited inventory of stand attributes, and that they will be subject to sampling errors, and will be unable to capture variations in stand structure at fine spatial scales over the landscape.
In the last few decades, however, innovative tools and methodologies, such as airborne Light Detection And Ranging (LiDAR), also referred to as Airborne Laser Scanning (ALS), have been developed and implemented at local, landscape/watershed, and regional scales [12,13,14]. Basically, LiDAR represents a powerful tool for deriving relevant forest inventory information; however, its derived products can never reveal certain tree patterns that are measured in the field, such as suppressed trees, grouped trees in dense forests, and understory [15,16,17]. This is even more evident in the Mediterranean forest ecosystems [18], where the complexity of forest structures, which are affected by, for example, the excessive fragmentation of ownership regimes, and the traditional forest management systems, make it more difficult to obtain realistic representation through ALS data of some forest components such as deadwood, suppressed trees, understory vegetation, and tree regeneration. On the other hand, use of LiDAR technologies have gained greater importance, not only for estimating forest attributes, but also for estimating the biomass pool of trees outside forests and for urban trees [19,20], which play an important role in the provision of ecosystem services.
One of the current challenges for forest researchers and forest decision makers is therefore to identify effective remote-based approach that enable proper estimation of the individual tree numbers, tree height, tree diameter, tree crown boundaries, spatial (i.e., vertical and horizontal) variability of plant density, biomass pool, carbon sequestration, and their changes over the years, in order of forest inventory as well as for defining the management strategies to better adapt to climate change. For this reason, several studies are focused on algorithm calibration and accuracy assessment [19] within Area-Based Approaches (ABA) or Individual Tree Detection approaches (ITD). Recent studies report that the use of smoothed canopy height models [21,22], segmented laser point clouds [23,24], or hybrid techniques that combine the ALS data with different types of geo-data and a variety of a priori information [25,26] have produced encouraging results over coniferous forests, but similar performances have not been assessed for broadleaved woodlands or multi-layered forest canopies, which are characterized by complex plant morphology with overlapping crowns [14,27,28]. Furthermore, most of these studies use a processed point cloud and so some information, which can be supportive to predict forest inventory variables, is lost by transforming the ALS data.
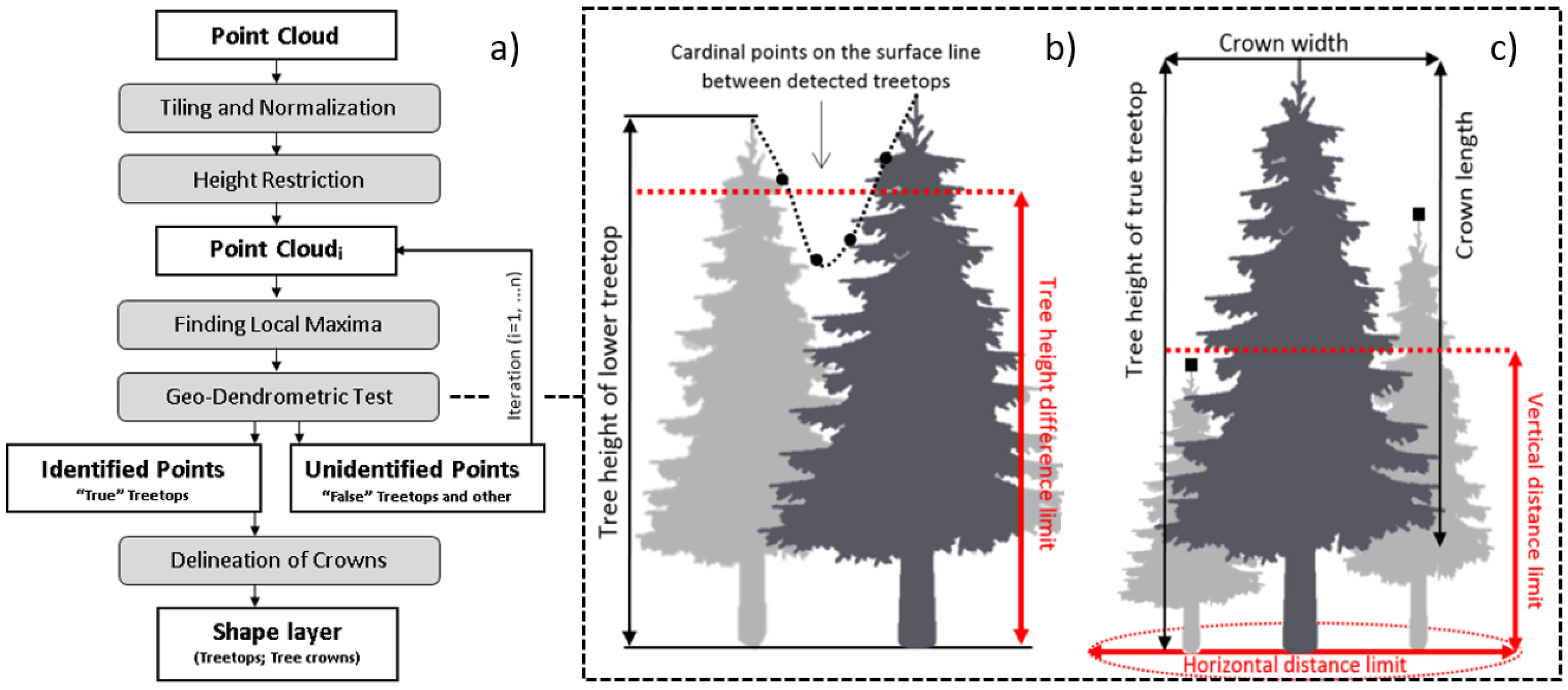
The purpose of this study is to assess the usability and accuracy of our own single-tree detection algorithm within remote-based forest inventory, using airborne LiDAR data acquired with a lightweight scanner in a selected type of Italy’s multilayered deciduous forest. Main forestry tree and stand characteristics, such as number of trees, tree height, tree diameter, and volume, were evaluated separately. We were particularly interested in identifying the benefits of the algorithm which uses the complete information contained in original ALS data in all procedures, and each iteration of single tree detection includes tests for treetops authenticity based on tree allometry rules. The following section reports the material and methods used to carry out the study. Section 3 shows the results, followed by Section 4 and Section 5, which describe the discussion and conclusions, respectively.

2. Materials and Methods

2.1. Data Sources

2.1.1. Ground Reference Data

Ground data were obtained by a terrestrial survey using Field-Map technology [29] in the reference square plot, with the total area of one hectare (Figure 1). Field-Map is an integrated tool designed for computer aided field data collection, consisting of the laser rangefinder with a distance accuracy of 3–5 cm, the electronic compass with azimuth accuracy of ±0.3°, and the field computer. Separately, Vertex system [30] was used for measuring the tree heights. The vertical accuracy is expected to be ±1.0 m. The GPS Trimble GeoXT with Hurricane Antenna was used for recording the coordinates of the origin of the plot in order to allow the shifting from local to global coordinates, fostering the overlay with ALS data and other cartographic layers. The horizontal accuracy after real-time correction is expected to be ±1.5 m.
A total of 614 trees with Diameter at Breast Height (DBH) higher than 2.5 cm were measured for stem position, species, height, diameter, crown length, crown projection, and vitality. However, for this study, only trees with a diameter greater than 7 cm were used. Therefore, the final sample size included 445 trees.
Forest composition was dominated by European beech (Fagus sylvatica L.), Italian Maple (Acer obtusatum Mill.), and Turkey oak (Quercus cerris L.), at 43%, 26%, and 20% of the tree number, respectively. The other deciduous trees were European hornbeam (Carpinus betulus L.) at 4%, Manna ash (Fraxinus ornus L.) at 3%, and other deciduous trees, which accounted for less than 1% of the tree number. Crown canopy closure was close to 100%. The ground reference data included 12% codominant, 22% dominant, 15% intermediate, and 51% suppressed trees. Almost 96% of trees were found to have great vitality.

2.1.2. ALS Data

ALS data were acquired for the study area for scientific purposes related to the FRESh LIFE project—demonstrating remote sensing integration in sustainable forest management under largely leaf-off canopy conditions—in November 2015. A light conventional helicopter was used. The LiDAR instrument was a YellowScan Mapper [31], which reaches absolute accuracy of ±15 cm, and records a maximum of three echoes per laser pulse (multiple pulses in air is not available). The sensor was set with a maximum scan angle of ±50° (FOV: field of view), and a pulse frequency of 20 kHz, resulting in an average density of 30 pulses/m2 for single strip-run.

2.2. Remote-Based Forest Inventory

2.2.1. Tree Detection and Tree Height Evaluation

The treetops, tree crowns, and tree heights were obtained, based on the reFLex algorithm, which includes several tree allometry rules on permissible tree heights and crown dimensions in order to increase the likelihood that real trees are detected [27,32,33]. A simplified workflow of treetops detection, tree crown delineation and tree height evaluation is shown in Figure 2a.
The initial procedures are applied to divide the points into a three-dimensional regular tiles, calculate the absolute height above ground for each point, and reduce the number of points in the input file by applying a minimum tree height threshold. These operations produce a point cloud that is further used in an iterative search for treetops and tree crowns.
A moving-window analysis is applied to iteratively search for the local maxima [34,35]. Because there are reasons to assume that a part of the local maxima identified in the previous operation may not be indicative of real treetops, an additional geo-dendrometric test is applied.
The geo-dendrometric test is done iteratively, and each iteration includes three subtests for treetops authenticity which is based on tree allometry rules. First, the height differences between local maxima located in the testing area are evaluated. The simplified base of this test is that if the surface line between the two detected treetops is convex [36], and such treetops represent true trees (Figure 2b). Second, the horizontal and vertical distances between all local maxima are evaluated. The horizontal distances depend on tree crown diameter and are tested to eliminate false treetops situated in the crowns of other trees. The vertical distances depend on tree crown length and are tested to eliminate false treetops situated in the crowns of other trees, and to capture trees situated under the canopy (Figure 2c). Finally, all tested local maxima are classified as true treetops or false treetops.
The final procedures are applied to delineate the tree crowns. First, each true treetop is assigned a central crown part. Then, the peripheral crown parts are repeatedly assigned to the central crown part. Finally, all crown parts assigned to the true treetop are merged to create a single crown object, and the borderline of this object is smoothed using Bezier interpolation to create a realistic crown shape.
After the treetop detection and crown delineation phases are completed, tree height is recorded and ratio of the forest floor covered by the delineated vertical crown projection and the whole stand area (crown coverage) is calculated. Finally, the outputs of all procedures are exported to point and polygon vector files in ESRI shp format.
The parameters used for algorithm calibration in this study were estimated based on field reference data for a tile size of three meters. A minimum tree height parameter was set, with respect to the conventional forest definitions by IUFRO and FAO, to 5 m. The ratio of mean crown radius to tree height was 17%, the ratio of mean tree height differences to tree height was 12%, the ratio of maximum crown width to tree height was 63%, and the ratio of maximum crown length to tree height was 52%.

2.2.2. Tree Diameter Derivation

The diameters of the detected trees were derived based on nonlinear regression models. Using ground reference data, the function with highest correlation between tree height and diameter was selected. The statistical significance of the regression model was assessed using the F-test at a significance level of α = 0.05. The model predictors were tree species and height.
For each detected single tree using the reFLex algorithm, the tree species was taken from a paired measured tree; tree height was evaluated directly from a point cloud as well. Then, DBH derivation was applied. Finally, in the case that systematic errors exist, the outputs of derivation were corrected by using a bias value. Stand diameter evaluation was obtained as the average of the tree data.

2.2.3. Tree Volume Calculation

The volume of trees was calculated based on models introduced by Federici et al. [37]. The model predictors were tree species, height, and diameter.
The tree species were taken from paired measured trees. Tree height was evaluated directly from a point cloud using the reFLex algorithm. The tree diameter was derived using regression models. Finally, in case that systemic errors exist, the outputs of the calculation were corrected using a bias value. The stand volume calculation was obtained by summing the tree data.

2.3. Accuracy Assessment

2.3.1. Tree Level

An accuracy assessment was carried out by comparing of the pairs of identical trees, measured in the field (GR), and trees detected using ALS data (RS). The matching process was carried out by visual analysis of a human interpreter based on normalized digital surface models. With respect to the accuracy of field measurement (e.g., tree location, tree height), the matching results were classified into four classes: (i) correctly assigned (true positive); (ii) correctly not assigned (true negative); (iii) wrongly assigned (false positive); and (iv) wrongly not assigned (false negative). Only detected trees within a distance of 5 m and height difference of ±2 m to the reference trees were candidates for correctly assigned trees.
The mean difference (e) was calculated as an average of individual differences, and used as an indicator of systematic errors (i.e., under- or overestimation). First, the shape of the distribution of differences was evaluated using the Shapiro-Wilk W test to allow for a proper selection of the statistical test (Student’s or Wilcoxon paired test). Simultaneously, the relative mean difference (e%) was calculated. The relative random error component (se%) was used to assess the dispersion of individual differences around their mean values. The relative root mean square error (RMSE%) was used to aggregate both the systematic and the random error components.
Detection rate (DR) was used to assess the ratio of tree numbers measured on the ground to the remotely-detected and matched single trees, with respect to omission and commission errors. The omission error contains the reference trees that could not be linked to any treetop detected using the algorithm based on ALS data. The commission error contains detected treetops that could not be linked to any tree measured in the field (Equation (1)).
DR = (TP/GR) × 100
where DR—Detection Rate (%), TP—True Positive (matched single trees), GR—Ground Reference data.

2.3.2. Stand Level

The sample size for accuracy assessment on the stand level included all measured (GR) and detected (RS) trees.
An accuracy assessment of stand height and diameter were carried out by comparing the mean as well as top heights and diameters of measured trees with the mean heights and diameters of detected trees. The following factors were compared: (i) Quadratic mean height/diameter of all measured trees (GRhs, GRds) versus Arithmetic mean height/diameter of all detected trees (RShs, RSds); and (ii) Quadratic mean height/diameter of 10%, as well as 20%, of measured trees with the largest diameters (GRh10, GRh20, GRd10, GRd20) versus Arithmetic mean heights/diameters of all detected trees (RShs, RSds).
Stand volume was compared to the total volume calculated, based on measured (GRv) and detected (RSv) trees, for accuracy assessment.

3. Results

3.1. Accuracy of Tree Number Detection

The proportion of trees found in the sample plot was about 24%, 36%, and 48%, for all trees, trees higher than 16 m, and trees higher than 21 m, respectively. Selected height intervals (trees higher than 16 m and 21 m) related to the height variability of points in the point cloud (two and one standard deviation). Simultaneously, we found quite a low commission rate (false positive detection) of approximately 4%–9% (Table 1).
As expected, the detection rate has a significant relationship with the social position of trees and dropped when trees were occluded by taller or bigger trees. The detection rates for dominant, codominant, intermediate, and suppressed trees are 66%, 48%, 18%, and 5%, respectively (Table 2).

3.2. Accuracy of Tree Height Evaluation

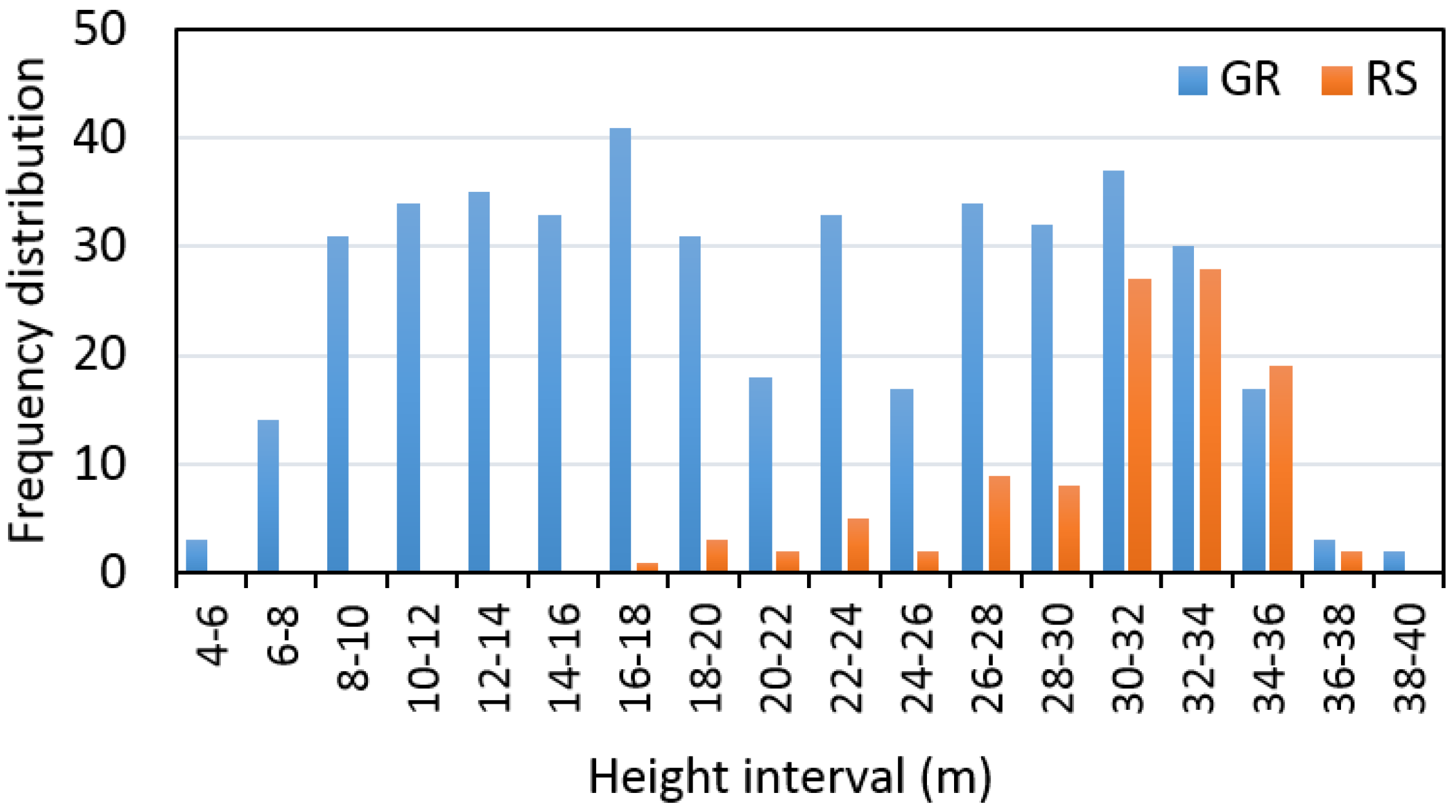
The distribution of trees measured on the ground and remotely-sensed trees within the 2-m height intervals are presented in Figure 3.
The results of the accuracy assessment for the evaluation of tree and stand height, based on airborne LiDAR data, are shown in Table 3.
Based on the sample size, which contains pairs of measured and detected trees, the remote-based approach overestimated tree height by 3% ± 9%, and the RMSE% was ±8%. At the same time, we found that the tree height evaluated, based on ALS data, provided an output with differences that were statistically significant relative to the ground data (α = 0.05). 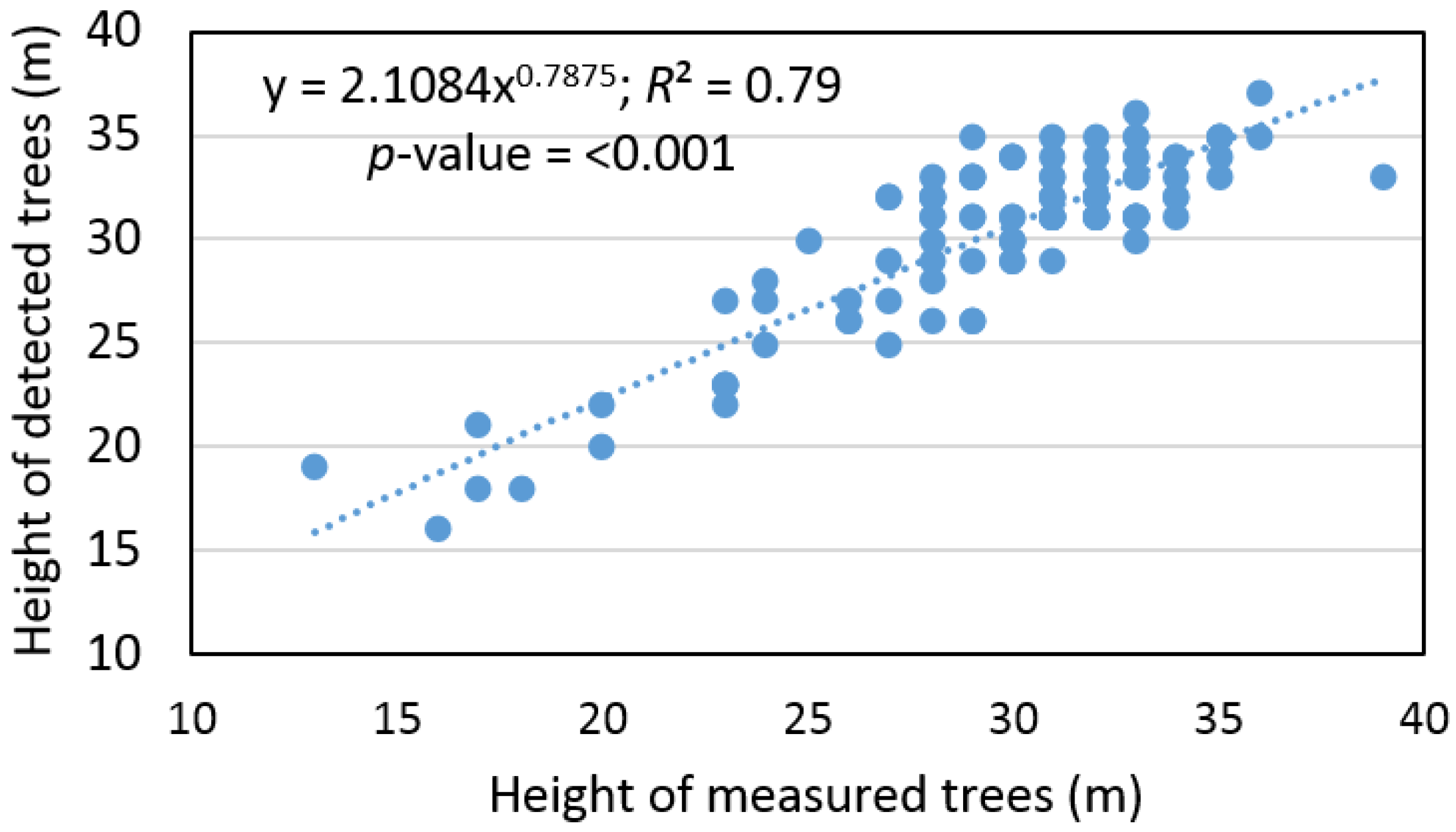On other hand, we found a significant relationship (R2 = 0.79) between the height of measured and detected trees (Figure 4).
While the stand height, calculated based on remotely detected trees, reached a value of 30.3 m, the stand heights calculated based on measured trees were 25.9 m, 32.1 m, and 31.6 m, for mean height, mean height of 10% trees with the largest diameters, and mean height of 20% trees with the largest diameters, respectively.

3.3. Accuracy of Tree Diameter Derivation

General information of all significant regression models for predicting tree diameter from tree height is presented per tree species in Table 4. We found that the derived tree diameter using the regression model was systematically underestimated in the case of dominant trees and systematically overestimated in the cases of trees from other social positions (α = 0.05). Therefore, all results of derivation were corrected with respect to a bias value for dominant, codominant, intermediate, and suppressed tress.
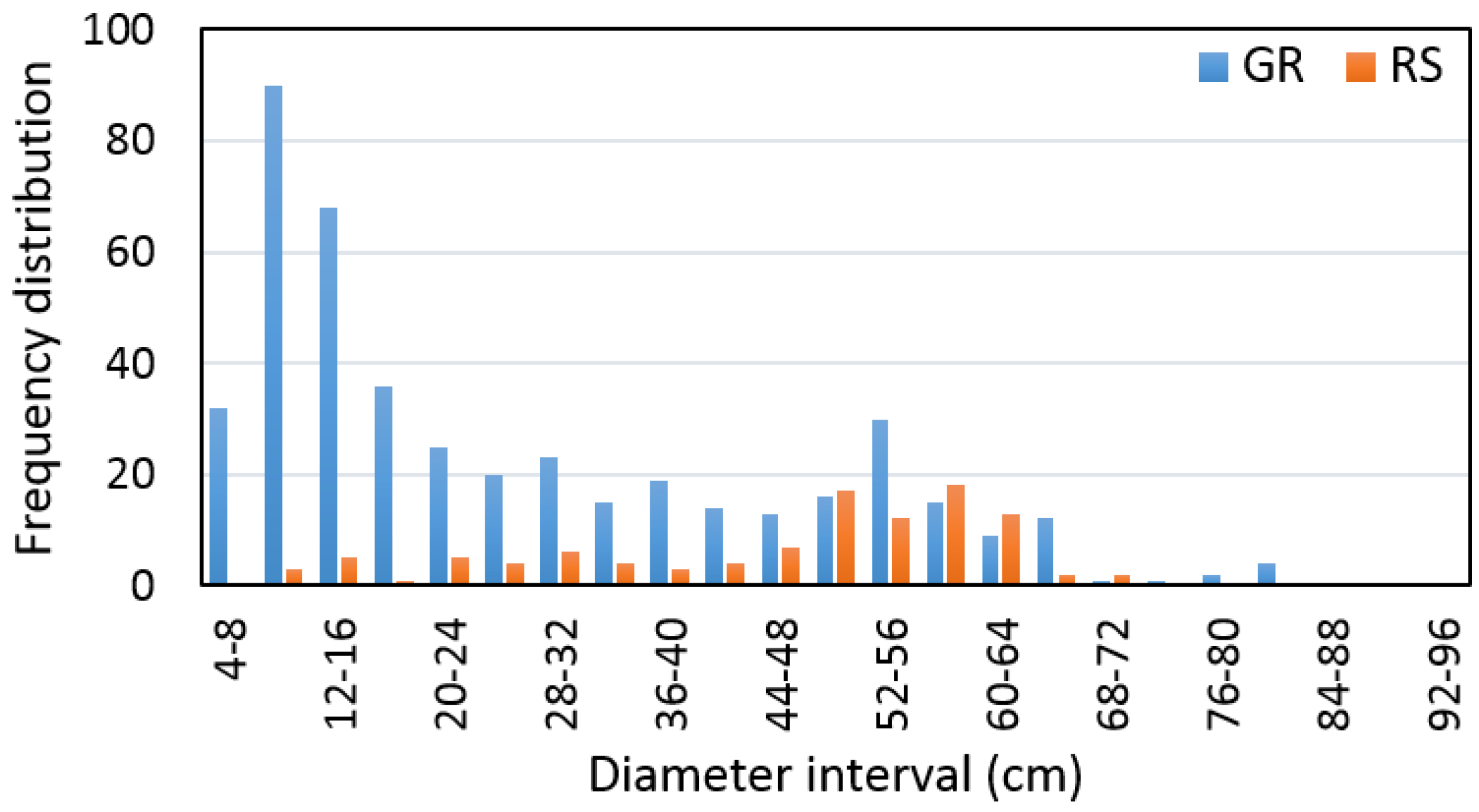
The distribution of trees measured on the ground and remotely-sensed trees within the 4-cm diameter interval are presented in Figure 5.
The results of the accuracy assessment for tree and stand diameter derivation, based on airborne LiDAR data, are shown in Table 5.
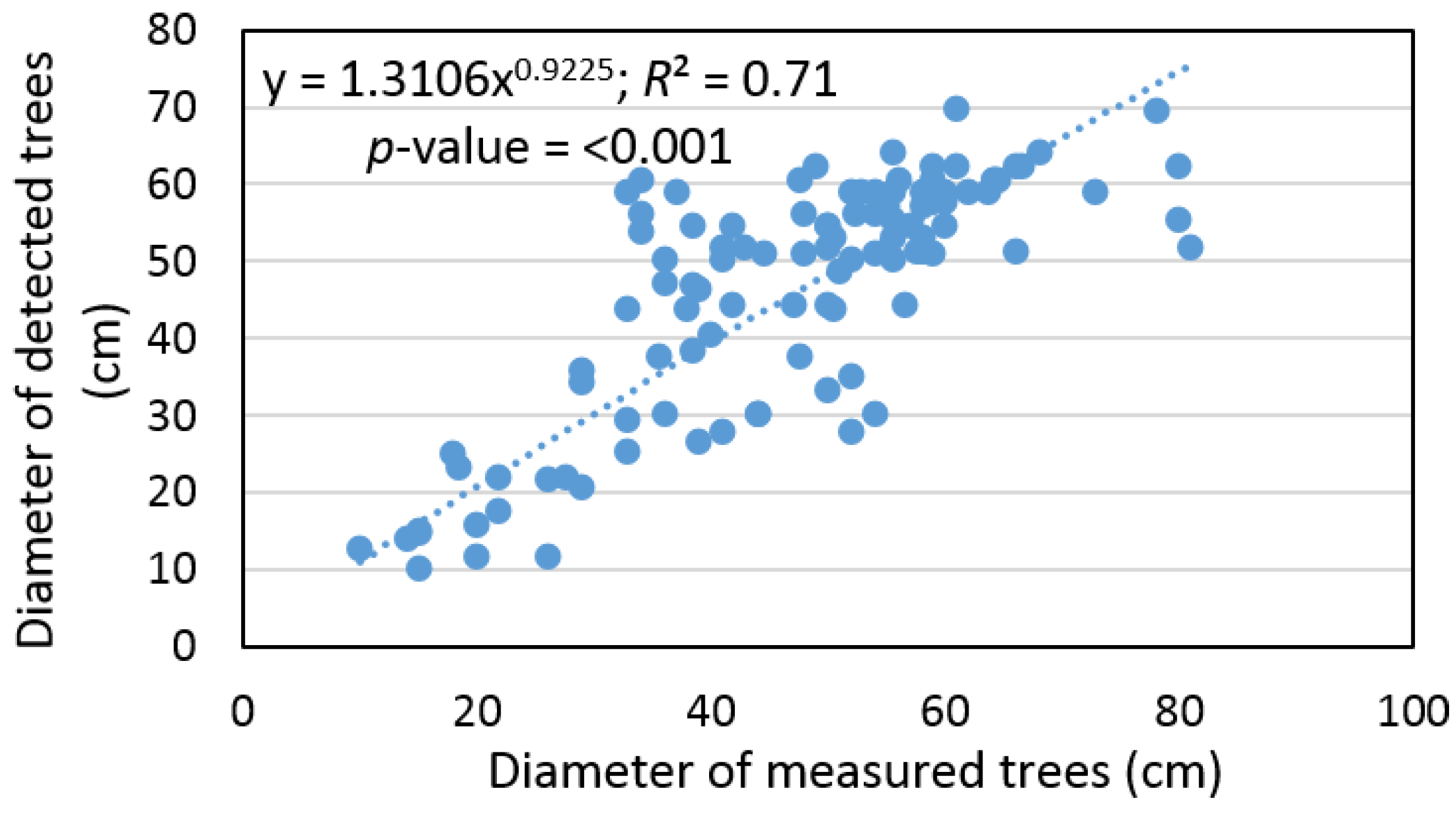
Based on the sample size, which contains pairs of measured and detected trees, the remote-based approach was corrected using a bias value that underestimated tree diameter by 1% ± 25% and the RMSE% was ±22%. At the same time, we found that tree diameter, detected based on ALS data, provided an output with a difference that was not statistically significant relative to the ground data (α = 0.05). In addition, we found a significant relationship (R2 = 0.71) between the diameter of measured and detected trees (Figure 6).
While stand diameter calculated based on remotely-sensed trees reached a value of 46.1 cm, the stand diameters calculated based on measured trees were 32.9 cm, 63.7 cm, and 58.7 cm, for the mean diameter of all trees, mean diameter of 10% of trees with the largest diameters, and mean diameter of 20% of trees with the largest diameters, respectively.

3.4. Accuracy of Tree Volume Calculation

As was the case for the tree diameter derivation, the results of volume calculation were under- or overestimated. However, the bias value was not significant and, therefore, the results of calculation were not corrected.
Distribution of trees measured on the ground and remotely-sensed trees within the 1-m3 volume interval are presented in Figure 7.
The results of the accuracy assessment for tree and stand volume calculation, based on airborne LiDAR data, are shown in Table 6.
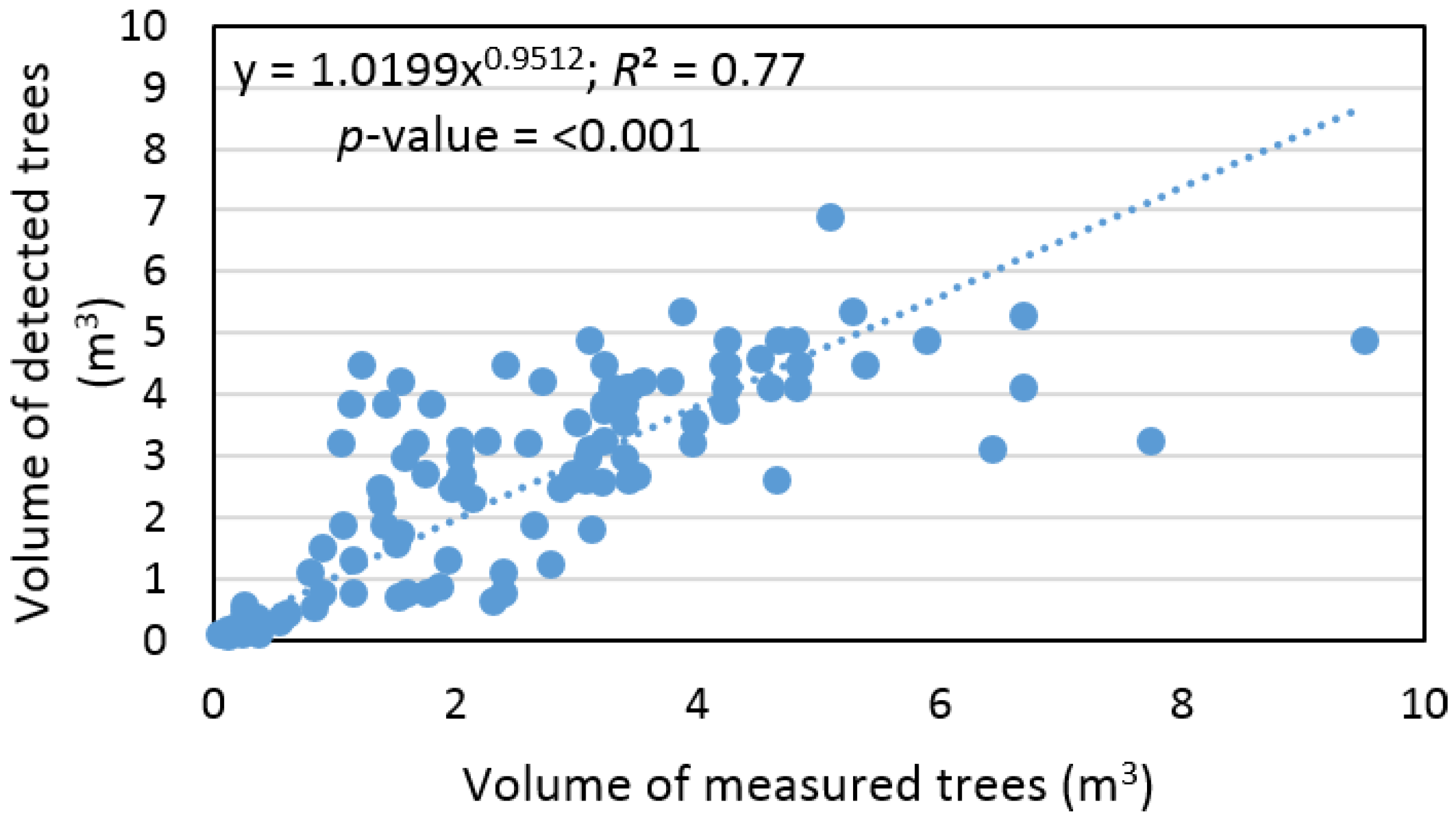
Based on sample size, which contains pairs of measured and detected trees, the remote-based approach overestimated tree volume by 1% ± 61% and the RMSE% was ±46%. At the same time, we found that tree volume, calculated based on ALS data, provided an output with a difference that was not statistically significant relative to ground data (α = 0.05). In addition, we found a significant relationship (R2 = 0.77) between volume of measured and detected trees (Figure 8).
While the stand volume calculated based on remotely-sensed trees reached a value of 289.7 m3, the stand volume calculated based on measured trees was 507.0 m3. The total growing stock differed by −43% from the ground reference data, and detection rate was 64% for dominant, 58% for codominant, 36% for intermediate, and 16% for suppressed trees.

4. Discussion

In this study, we explored the opportunities using lightweight aerial scanner for the estimation of main forestry variables with a single-tree detection algorithm over a selected type of multilayered deciduous forest. In the following sections, we discuss the findings, compare our results with other studies, and outline methods to improve performance. Archived results, however, could be different under other conditions, where there may be other forest types or data sources. It should be also noted that measurement errors, related to the accuracy of measurement equipment, play an important role in presented results.

4.1. Single-Tree Detection

Our findings indicated that the single-tree detection algorithm, with optimal settings for local conditions, can capture approximately 66% dominant, 48% codominant, 18% intermediate, and 5% suppressed trees. False positive detection (commission rate) was relatively low, and ranged between 4% and 9%.
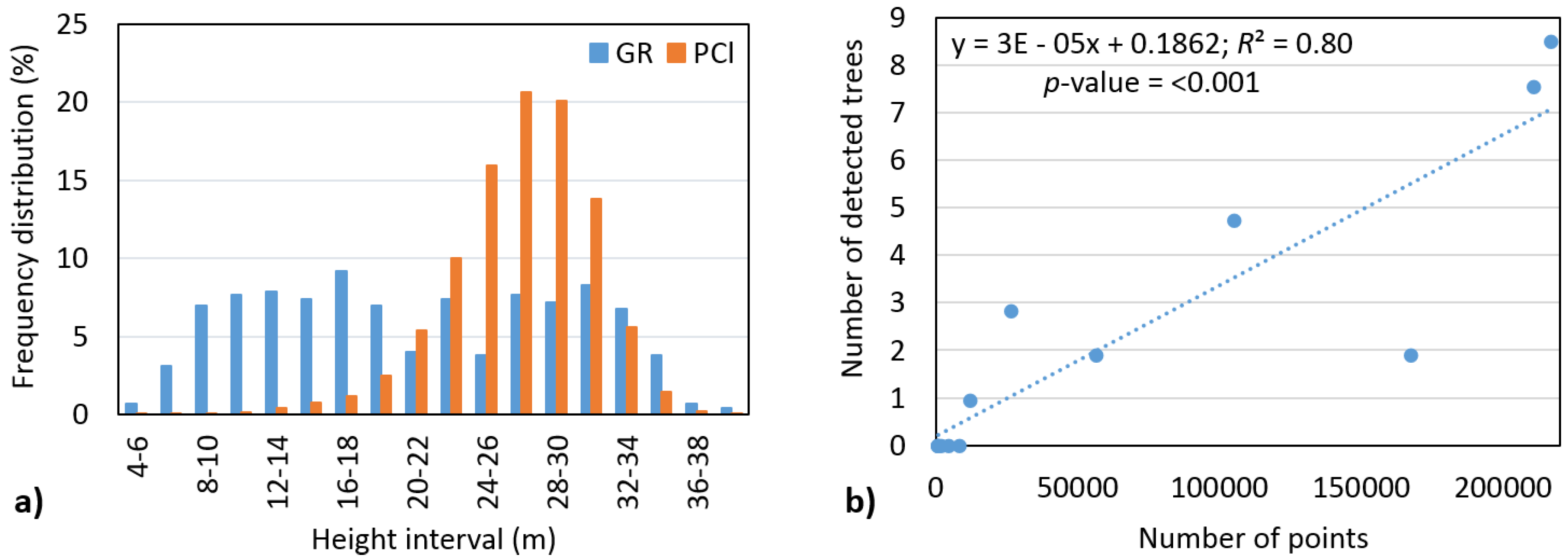
There are several factors that could have affected the accuracy of tree number detection in our assessment, which should be considered when interpreting our findings. First, clearly, the individual tree detection algorithm is best suited to finding dominant trees; however, the ground reference data include only 12% dominant and 22% codominant trees. Second, most of the points in the point cloud are related to height ranges of 16–36 m (95% of points) and 21–31 m (68% of points), respectively (Figure 9a). For example, only 5% from all points is situated in the 2–20 m space, but it accounts for 59% of trees. This means that, based on objective reasons, identification of these trees is very difficult. Therefore, we then investigated the effect of number of points on number of detected trees in the height range of 2–20 m. We found a significant relationship (α = 0.05) with a strong correlation (R2 = 0.80) (Figure 9b). Thus, having more points from intermediate echoes causes a significant increase in the detection rate of trees below the main canopy layer.
In similar conditions, such a detection rate has also been reported by other authors, and relates to the crown morphology of deciduous species with indistinct treetops. Furthermore, a dense crown canopy also causes most of the points from a LiDAR point cloud to be concentrated within the main canopy layer. Therefore, detection of understory trees is difficult. International research has suggested that detection rates fluctuated around 50%, and RMSE% varied from 45% to 89% (e.g., [38,39,40,41]). On the other hand, the commission error of our own method did exceed the accuracy reported by other research. For example, within the single tree detection benchmark inside the NEWFOR project [42], the commission rate varied from 7% to 141%. Thus, the geo-dendrometric criteria included in the presented algorithm has been successful in suppressing most false treetops, such as protruding branches, multiple terminals, and other morphological patterns that can be present in tree crowns.
With respect to the density of the 30 hits per square meter used in this study, we do not assume that an increase in scanning density could improve the accuracy of detection of dominant and codominant trees. However, the combination of ALS data, from the leaf-on and leaf-off seasons, may be appropriate for increases the chance that more points could penetrate the canopy, and that the detection rate of trees growing under the canopy could increase with a higher scanning density.

4.2. Tree Height Evaluation

Related to the individual tree height, ALS data generally provide remote-based measurements that are highly correlated with field-based measurements. Although the precision of field measurements of tree height in deciduous forests with a dense canopy layer is limited, which influences total accuracy, we confirmed the relationship by a strong correlation with an R2 value of 0.8. We also found that the tree height evaluated by the algorithm was systematically overestimated relative to the testing data, and total accuracy in terms of RMSE reached 2.4 m (8%). In the case of stand height, the differences between measured and evaluated values were in the range of −1.8 m (−6%)–4.5 m (17%), for top and mean height, respectively. The mean height, evaluated based on ALS data, was most similar to the mean height of 20% of measured trees with the largest diameter.
A similar approach for tree height evaluation to that in our study was used by Brandtberg et al. [43] and Gaveau and Hill [44], where evaluated LiDAR tree heights acquired in leaf-off conditions over a deciduous forest reached an overall standard error of 1.1 m, or canopy surface height was underestimated by 0.91 m in shrub canopies, and 1.27 in tree canopies. Chávez and Tullis [45] evaluated tree height using ALS data and a spectral predictor over full-canopy oak-hickory forests with an average error of 1.67–2.99 m, RMSE of 2.2 m, and the correlation coefficient ranged between 0.42 and 0.51.

4.3. Tree Diameter Derivation

Although our model for tree diameter derivation is relatively simple (one-parameter nonlinear function), and not as accurate as those used by other studies that specialize on this topic (e.g., [46,47]) regression between pairs of identical detected and measured trees is encouraging (R2 = 0.71). After bias correction, the overall accuracy reached 10.2 cm (22%). In the case of stand diameter, the differences between measured and derived values were in the range of −17.6 cm (−28%) to 13.2 cm (40%) for top and mean diameter, respectively. The mean diameter, evaluated based on ALS data, was most similar to mean diameter of 20% of measured trees with the largest diameters.
Several authors [48,49] have provided extensive research on predicting stem diameter using ALS data in a temperate forest. The proposed regression models included multilinear regression, least square boosting decision trees, random forest, and ε-support vector regression. As LiDAR metrics were used, variables, such as tree height, crown area, crown height, and crown volume, were extracted based on the ITD approach. These studies achieved accuracies of 15%–23%, in terms of RMSE%.

4.4. Tree Volume Calculation

Our findings indicated that the presented approach captured approximately 57% of the stand volume in the study area. The calculated volume was distributed as 64%, 58%, 36%, and 16%, for dominant, codominant, intermediate, and suppressed trees, respectively. No significant differences were found between stem volumes of pairs of measured and detected trees. Therefore, volume calculation was executed without statistical correction, and we found a RMSE% of 1.2 m3 (46%) and a correlation with an R2 value of 0.8.
While the presented ITD approach for volume calculation is based on tree height and diameter, several studies also used a combination of tree and stand variables. For example, Naesset [50], in a mature forest area, used a percentile of pulse laser heights and canopy density, with an R2 that ranged from 0.83 to 0.86. The approach by Tesfamichael et al. [51] combined a LiDAR-derived height variables, stems per hectare, as well as stand age, and the level of association between estimated and observed volume in eucalyptus plantations was relatively high (R2 = 0.82–0.94) with negative biases and a RMSE ranging in the order of 20%–43%. Many authors have also reported methods for volume estimation, based on the ABA approach. In these cases, the biophysical forest variables are regressed against ALS metrics, and such a statistical relationship can be approximated by, for example, linear models [52], non-parametric approaches, including nearest neighbors imputation [53], linear mixed effects models with random stand-level intercepts [54], or Bayesian methods [55].
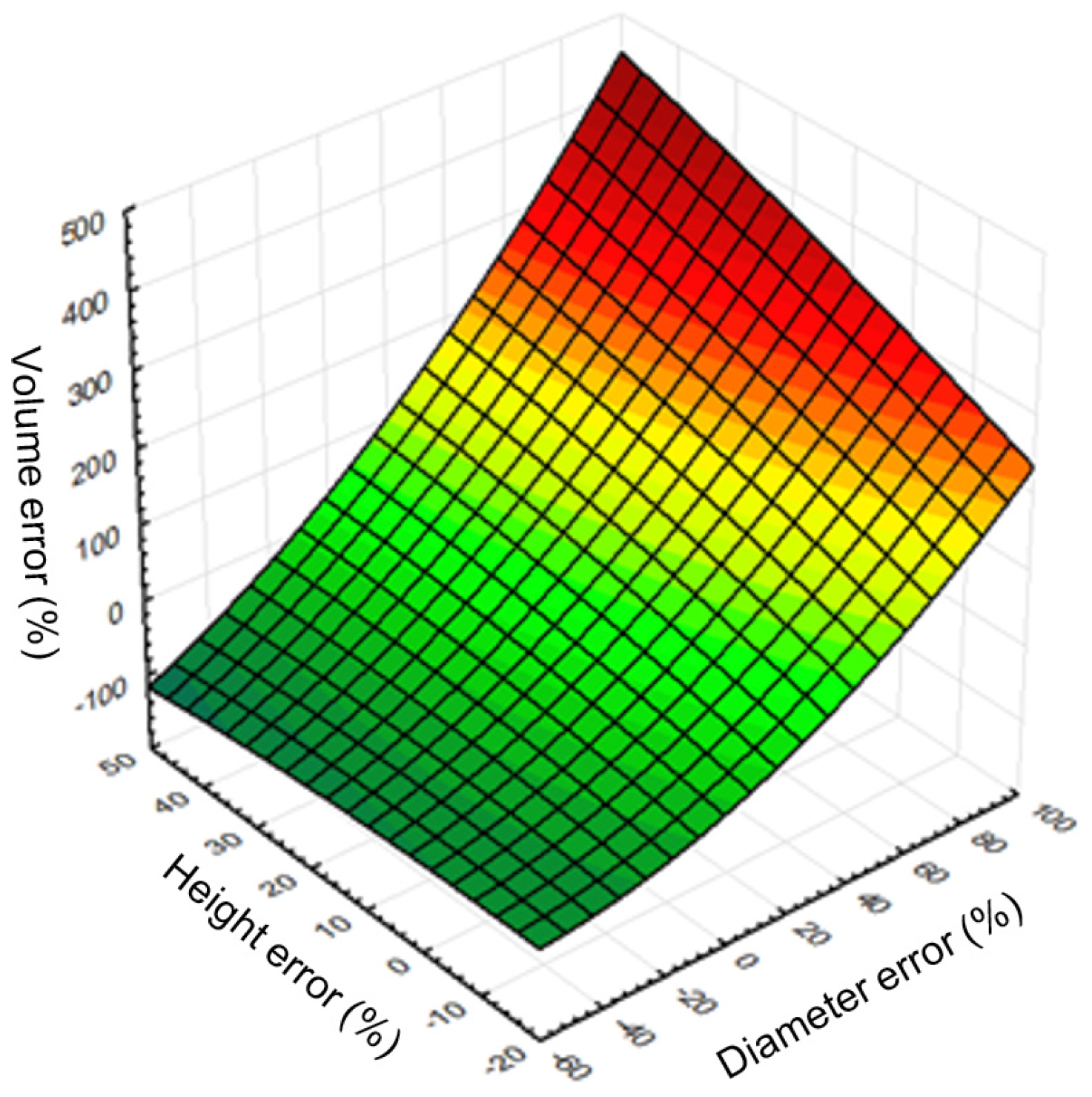
Accuracy of assessment of tree and stand volume using the ITD approach ultimately depends on the accuracy of the underlying characteristics, and is affected by the accumulation of errors from single tree detection, tree height evaluation, tree species classification, and diameter derivation [56,57,58]. In our study, we confirmed multiple significant and strong relationships (R2 = 0.96) between relative mean errors of remote-based volume, tree height, and tree diameter (Figure 10). In general, a method for increasing the accuracy of stem volume calculation lies in improving the methods of detection, feature extraction, and estimation for each underlying characteristic.

5. Conclusions

The main objective of this study was to assess the usability and accuracy of our own single-tree detection algorithm within a remote-based forest inventory, using LiDAR data from lightweight aerial scanner for a selected type of multilayered deciduous forest.
Results show that this approach can be used for detecting single trees and measuring (or derivation of) various biophysical tree variables, such as height, diameter, and volume. With respect to other studies, our findings also indicated that airborne LiDAR data are suitable, mainly for the evaluation of tree height. The algorithm has less success for tree detection, tree diameter derivation, and volume calculation. In this context, the detection rate of understory trees typically depends on point density across a point cloud, and the accuracy of stem diameter derivation depends on the model used. Finally, it is important to note that the results of accuracy assessment depend on the accuracy of reference data as well.
Therefore, future research should be concerned with building more precise models for stem diameter derivation and developing algorithms for tree-species classification. Future research should also be carried out to apply the presented approach within a praxis of forest inventories under different ecosystems and data quality.

Acknowledgments

This research was supported by the LIFE program and the Italian Academy of Forest Sciences, in the framework of the project “FRESh LIFE—Demonstrating Remote Sensing integration in sustainable forest management” (LIFE14 ENV/IT/000414). Support has also been provided by the Slovak Research and Development Agency, in the framework of the project “Innovations in the forest inventories based on progressive technologies of remote sensing” (APVV-15-0393). The authors are grateful to the staff of Oben srl (www.oben.it) for providing ALS data and for their comments.

Author Contributions

Ivan Sačkov was involved in the whole study (algorithm construction, data analysis and writing the manuscript). Giovanni Santopuoli contributed to remote sensing and field data collection. Tomáš Bucha, Bruno Lasserre, Marco Marchetti provided the theoretical background. All the co-authors improved the article at various stages of the reviewing and writing process.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
EUEuropean Union
ESRI shpEnvironmental Systems Research Institute Shapefile
IUFROInternational Union of Forest Research Organizations
FAOFood and Agriculture Organization of the United Nations References

References

  1. Forest Europe. State of Europe’s Forests 2015. In Proceedings of the Ministerial Conference on the Protection of Forests in Europe, Madrid, Spain, 20–21 October 2015; Julián Camarillo: Madrid, Spain, 2015; p. 314. [Google Scholar]
  2. The Food and Agricultural Organization of the United Nations. Global Forest Resources Assessment 2015; FAO Forestry Paper No. 1; FAO: Rome, Italy, 2015; p. 253. [Google Scholar]
  3. Herrando, S.; Brotons, L.; Anton, M.; Paramo, F.; Villero, D.; Titeux, N.; Stefanescu, C. Assessing impacts of land abandonment on Mediterranean biodiversity using indicators based on bird and butterfly monitoring data. Environ. Conserv. 2016, 43, 69–78. [Google Scholar] [CrossRef]
  4. Sallustio, L.; Quatrini, V.; Geneletti, D.; Corona, P.; Marchetti, M. Assessing land take by urban development and its impact on carbon storage: Findings from two case studies in Italy. Environ. Impact Assess. Rev. 2015, 54, 80–90. [Google Scholar] [CrossRef] [Green Version]
  5. European Commission. Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions. A New EU Forest Strategy: For Forests and the Forest-Based Sector; European Commission: Brussels, Belgium, 2013. [Google Scholar]
  6. Verkerk, P.J.; Mavsar, R.; Giergiczny, M.; Lindner, M.; Edwards, D.; Schelhaas, M.J. Assessing impacts of intensified biomass production and biodiversity protection on ecosystem services provided by European forests. Ecosyst. Serv. 2014, 9, 155–165. [Google Scholar] [CrossRef]
  7. Baycheva-Merger, T.; Wolfslehner, B. Evaluating the implementation of the Pan-European Criteria and indicators for sustainable forest management—A SWOT analysis. Ecol. Indic. 2016, 60, 1192–1199. [Google Scholar] [CrossRef]
  8. Santopuoli, G.; Ferranti, F.; Marchetti, M. Implementing Criteria and Indicators for Sustainable Forest Management in a Decentralized Setting: Italy as a Case Study. J. Environ. Policy Plan. 2016, 18, 177–196. [Google Scholar] [CrossRef]
  9. De Cinti, B.; Bombi, P.; Ferretti, F.; Cantiani, P.; Di Salvatore, U.; Simončič, P.; Matteucci, G. From the experience of LIFE+ ManFor C. BD to the Manual of Best Practices in Sustainable Forest Management. Ital. J. Agron. 2016, 11, 1–175. [Google Scholar] [CrossRef]
  10. Maselli, F.; Chiesi, M.; Mura, M.; Marchetti, M.; Corona, P.; Chirici, G. Combination of optical and LiDAR satellite imagery with forest inventory data to improve wall-to-wall assessment of growing stock in Italy. Int. J. Appl. Earth Observ. Geoinf. 2014, 26, 377–386. [Google Scholar] [CrossRef]
  11. Andersen, H.E.; McGaughey, R.J.; Reutebuch, S.E. Estimating forest canopy fuel parameters using LiDAR data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
  12. Nelson, R.; Krabill, W.; MacLean, G. Determining forest canopy characteristics using airborne laser data. Remote Sens. Environ. 1984, 15, 201–212. [Google Scholar] [CrossRef]
  13. Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. LiDAR Remote Sensing for Ecosystem Studies LiDAR, An emerging remote sensing technology that directly measures the three-dimensional distribution of plant canopies, can accurately estimate vegetation structural attributes and should be of particular interest to forest, landscape, and global ecologists. BioScience 2002, 52, 19–30. [Google Scholar]
  14. Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef]
  15. Popescu, S.C.; Zhao, K. A voxel-based LiDAR method for estimating crown base height for deciduous and pine trees. Remote Sens. Environ. 2008, 112, 767–781. [Google Scholar] [CrossRef]
  16. Zhao, K.; Popescu, S.; Nelson, R. LiDAR remote sensing of forest biomass: A scale-invariant estimation approach using airborne lasers. Remote Sens. Environ. 2009, 113, 182–196. [Google Scholar] [CrossRef]
  17. Forzieri, G.; Guarnieri, L.; Vivoni, E.R.; Castelli, F.; Preti, F. Multiple attribute decision making for individual tree detection using high-resolution laser scanning. For. Ecol. Manag. 2009, 258, 2501–2510. [Google Scholar] [CrossRef]
  18. Guerra-Hernández, J.; Görgens, E.B.; García-Gutiérrez, J.; Carlos, L.; Rodriguez, E.; Tomé, M.; González-Ferreiro, E. Comparison of ALS based models for estimating aboveground biomass in three types of Mediterranean forest. Eur. J. Remote Sens. 2016, 49, 185–204. [Google Scholar] [CrossRef]
  19. Johnson, K.D.; Birdsey, R.; Cole, J.; Swatantran, A.; O’Neil-Dunne, J.; Dubayah, R.; Lister, A. Integrating LiDAR and forest inventories to fill the trees outside forests data gap. Environ. Monit. Assess. 2015, 187, 1–8. [Google Scholar] [CrossRef]
  20. Nowak, D.J.; Greenfield, E.J.; Hoehn, R.E.; Lapoint, E. Carbon storage and sequestration by trees in urban and community areas of the United States. Environ. Pollut. 2013, 178, 229–236. [Google Scholar] [CrossRef] [PubMed]
  21. Jakubowski, M.K.; Li, W.; Guo, Q.; Kelly, M. Delineating Individual Trees from Lidar Data: A Comparison of Vector- and Raster-based Segmentation Approaches. Remote Sensing. 2013, 5, 4163–4186. [Google Scholar] [CrossRef]
  22. Koch, B.; Heyder, U.; Weinecker, H. Detection of individual tree crowns in airborne LiDAR data. Photogramm. Eng. Remote Sens. 2006, 4, 357–363. [Google Scholar] [CrossRef]
  23. Hirschmugl, M.; Ofner, M.; Raggam, J.; Schardt, M. Single tree detection in very high resolution remote sensing data. Remote Sens. Environ. 2007, 110, 533–544. [Google Scholar] [CrossRef]
  24. Pirotti, F. Assessing a template matching approach for tree height and position extraction from LiDAR-derived canopy height models of Pinus pinaster stands. Forests 2010, 1, 194–208. [Google Scholar] [CrossRef]
  25. Heinzel, J.; Weinecker, H.; Koch, B. Prior-knowledge based single tree extraction. Int. J. Remote Sens. 2010, 32, 4990–5020. [Google Scholar] [CrossRef]
  26. Ene, L.; Næsset, E.; Gobakken, T. Single tree in heterogeneous boreal forests using airborne laser scanning and area-based stem number estimates. Int. J. Remote Sens. 2012, 33, 5171–5193. [Google Scholar] [CrossRef]
  27. Kulla, L.; Sačkov, I.; Juriš, M. Test of airborne laser scanning ability to refine and streamline growing stock estimations by yield tables in different stand structures. For. J. 2016, 62, 39–47. [Google Scholar] [CrossRef]
  28. Maltamo, M.; Packalén, P.; Yu, X.; Eerikäinen, K.; Hyyppä, J.; Pitkänen, J. Identifying and quantifying structural characteristics of heterogeneous boreal forests using laser scanner data. For. Ecol. Manag. 2005, 216, 41–50. [Google Scholar] [CrossRef]
  29. What Is Field-Map? Available online: http://www.fieldmap.cz/?page=fmsoftware (accessed on 25 October 2016).
  30. VERTEX IV. Available online: http://www.haglofcg.com/index.php/en/products/instruments/height/341-vertex-iv (accessed on 25 October 2016).
  31. YellowScan Mapper. Available online: http://www.yellowscan.fr/products/yellowscan-mapper (accessed on 25 October 2016).
  32. Sačkov, I.; Bucha, T.; Király, G.; Brolly, G.; Raši, R. Individual tree and crown identification in the Danube floodplain forests based on airborne laser scanning data. In Proceedings of the 34th EARSeL Symposium, Warsaw, Poland, 17–18 June 2014; Zagajevski, B., Kycko, M., Reuter, R., Eds.; EARSeL and University of Warsaw: Warsaw, Poland, 2014; pp. 6.20–6.26. [Google Scholar]
  33. Sačkov, I.; Sedliak, M.; Kulla, L.; Bucha, T. Integration of remote sensing data into forest inventory in close-to-nature forests: An initial case of study in Smolnícka osada, Slovakia. In Proceedings of the 3rd Workshop of the SIG on Forestry, Krakow, Poland, 15–16 September 2016; EARSeL and University of Agriculture in Krakow: Krakow, Poland, 2016. in print. [Google Scholar]
  34. Longley, P.A.; Goodchild, M.F.; Maguire, D.J.; Rhind, D.W. Geographic Information Systems and Science, 3rd ed.; John Wiley: Chichester, UK, 2005; p. 560. [Google Scholar]
  35. Kwak, D.; Lee, W.K.; Lee, J.; Biging, G.; Gong, P. Detection of individual trees and estimation of tree height using LiDAR data. J. For. Res. 2007, 12, 425–434. [Google Scholar] [CrossRef]
  36. Webster, R. Convexity; Oxford University Press: Oxford, UK, 1995; p. 464. [Google Scholar]
  37. Federici, S.; Vitullo, M.; Tulipano, S.; De Lauretis, R.; Seufert, G. An approach to estimate carbon stocks change in forest carbon pools under the UNFCCC: The Italian case. iForest Biogeosci. For. 2008, 1, 86–95. [Google Scholar] [CrossRef]
  38. Morsdorf, F.; Meier, E.; Kötz, B.; Itten, K.I.; Dobbertin, M.; Allgöwer, B. LIDAR-based geometric reconstruction of boreal type forest stands at single tree level for forest and wildland fire management. Remote Sens. Environ. 2004, 92, 353–362. [Google Scholar] [CrossRef]
  39. Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkänen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.M.; et al. Comparative testing of single-tree detection algorithms under different types of forest. Forestry 2011, 85, 27–40. [Google Scholar] [CrossRef]
  40. Kaartinen, H.; Hyyppä, J.; Yu, X.; Vastaranta, M.; Hyyppä, H.; Kukko, A.; Holopainen, M.; Heipke, C.H.; Hirschmugl, M.; Morsdorf, F.; et al. An International Comparison of Individual Tree Detection and Extraction Using Airborne Laser Scanning. Remote Sens. 2012, 4, 950–974. [Google Scholar] [CrossRef] [Green Version]
  41. Koch, B.; Kattenborn, T.; Straub, C.H.; Vauhkonen, J. Segmentation of forest to tree objects. In Forestry Application of Airborne Laser Scanning: Concept and Case Studies; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 1–16. [Google Scholar]
  42. Eysn, L.; Hollaus, M.; Monnet, J.-M.; Dalponte, M.; Kobal, M.; Pellegrini, M.; Lindberg, E.; Mongus, D.; Berger, F. NEWFOR—Single Tree Detection Benchmark—Report; NEWFOR: Wien, Austria, 2014; p. 87. [Google Scholar]
  43. Brandtberg, T.; Warner, T.; Landenberger, R.; McGraw, J. Detection and analysis of individual leaf-off tree crowns in small-footprint, high sampling density LiDAR data from eastern deciduous forest in North America. Remote Sens. Environ. 2003, 85, 290–303. [Google Scholar] [CrossRef]
  44. Gaveau, D.L.A.; Hill, R.A. Quantifying canopy height underestimation by laser pulse penetration in small-footprint airborne laser scanning data. Can. J. Remote Sens. 2003, 29, 650–657. [Google Scholar] [CrossRef]
  45. Chávez, J.S.; Tullis, J.S. Deciduous Forest Structure Estimated with LiDAR-Optimized Spectral Remote Sensing. Remote Sens. 2013, 5, 155–182. [Google Scholar] [CrossRef]
  46. Hirata, Y.; Tsubota, Y.; Sakai, A. Allometric models of DBH and crown area derived from QuickBird panchromatic data in Cryptomeria japonica and Chamaecyparis obtusa stands. Int. J. Remote Sens. 2009, 30, 5071–5088. [Google Scholar] [CrossRef]
  47. Salas, C.H.; Ene, L.; Gregoire, T.G.; Næsset, E.; Gobakken, T. Modelling tree diameter from airborne laser scanning derived variables: A comparison of spatial statistical models. Remote Sens. Environ. 2010, 14, 1277–1285. [Google Scholar] [CrossRef]
  48. Yu, X.; Hyyppä, J.; Vastaranta, M.; Holopainen, M. Predicting individual tree attributes from airborne laser point clouds based on random forest technique. ISPRS J. Photogramm. Remote Sens. 2011, 66, 28–37. [Google Scholar] [CrossRef]
  49. Wu, J.; Yao, W.; Choi, S.; Park, T.; Myneni, R.B. A comparative study of predicting DBH and stem volume of individual trees in a temperate forest using airborne waveform LiDAR. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2267–2271. [Google Scholar] [CrossRef]
  50. Næsset, E. Practical large-scale forest stand inventory using a small-footprint airborne scanning laser. Scand. J. For. Res. 2004, 19, 164–179. [Google Scholar] [CrossRef]
  51. Tesfamichael, S.G.; Aardt, J.A.N.; Ahmed, F. Estimating plot-level tree height and volume of Eucalyptus grandis plantations using small-footprint, discrete return LiDAR data. Prog. Phys. Geogr. 2010, 34, 515–540. [Google Scholar] [CrossRef]
  52. Means, J.E.; Acker, S.S.; Fitt, B.J.; Renslow, M.; Emerson, L.; Hendrix, C.J. Predicting forest stand characteristics with airborne scanning LiDAR. Photogramm. Eng. Remote Sens. 2000, 66, 1367–1371. [Google Scholar]
  53. Andersen, H.E.; Strunk, J.; Temesgen, H.; Atwood, D.; Winterberger, K. Using multi-level remote sensing and ground data to estimate forest biomass resources in remote regions: A case study in the boreal forests of interior Alaska. Can. J. Remote Sens. 2011, 37, 596–611. [Google Scholar] [CrossRef]
  54. Vauhkonen, J.; Mehtätalo, L.; Packalén, P. Combining tree height samples produced by airborne laser scanning and stand management records to estimate plot volume in Eucalyptus plantations. Can. J. For. Res. 2011, 41, 1649–1658. [Google Scholar] [CrossRef]
  55. Hernandez-Marin, S.; Wallace, A.M.; Gibson, G.J. Bayesian Analysis of LiDAR Signals with Multiple Returns. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 2170–2180. [Google Scholar] [CrossRef] [PubMed]
  56. Rossmann, J.; Schluse, M.; Bücken, A.; Krahwinkler, P. Using airborne laser scanner data in forestry management: A novel approach to single tree delination. In Proceedings of the ISPRS Workshop on Laser Scanning 2007 and SilviLaser 2007, Espoo, Finland, 12–14 September 2007; Rönnholm, P., Hyyppä, H., Hyyppä, J., Eds.; ISPRS Working Groups: Espoo, Finland, 2007; pp. 350–354. [Google Scholar]
  57. Heurich, M. Automatic recognition and measurement of single trees based on data from airborne laser scanning over the richly structured natural forests of the Bavarian Forest National Park. For. Ecol. Manag. 2008, 255, 2416–2433. [Google Scholar] [CrossRef]
  58. Maltamo, M.; Packalén, P.; Suvanto, A.; Korhonen, K.T.; Mehtätalo, P. Combining ALS and NFI training data for forest management planning: A case study in Kuortane, Western Finland. Eur. J. For. Res. 2009, 128, 305–317. [Google Scholar] [CrossRef]
Forests 07 00307 g001 550
Figure 1. Location of the study area (a); Reference plot—point cloud 3D frame and 2D profile (b); Reference plot—normalized Digital Surface Model (nDSM) (c).
Figure 1. Location of the study area (a); Reference plot—point cloud 3D frame and 2D profile (b); Reference plot—normalized Digital Surface Model (nDSM) (c).
Forests 07 00307 g001
Forests 07 00307 g002 550
Figure 2. Workflow of treetops’ detection, tree crown delineation and tree height evaluation (a); The iterations of geo-dendrometric test are performed to remove the false treetops using tree allometry rules: If all cardinal points on the surface line between detected treetops (black points) are higher than the limit for height difference, the lower treetop is false (b); If any detected treetops (black squares) is within horizontal distance limit and higher than vertical distance limit, the lower treetop is false (c).
Figure 2. Workflow of treetops’ detection, tree crown delineation and tree height evaluation (a); The iterations of geo-dendrometric test are performed to remove the false treetops using tree allometry rules: If all cardinal points on the surface line between detected treetops (black points) are higher than the limit for height difference, the lower treetop is false (b); If any detected treetops (black squares) is within horizontal distance limit and higher than vertical distance limit, the lower treetop is false (c).
Forests 07 00307 g002
Forests 07 00307 g003 550
Figure 3. Frequency distribution of field-measured trees (GR) and remotely-sensed trees (RS) within the height intervals.
Figure 3. Frequency distribution of field-measured trees (GR) and remotely-sensed trees (RS) within the height intervals.
Forests 07 00307 g003
Forests 07 00307 g004 550
Figure 4. Regression between heights of field-measured trees and remotely-sensed trees. The figure contains regression functions, coefficients of determination (R2), and F-test of statistical significance of the regression model (p-value).
Figure 4. Regression between heights of field-measured trees and remotely-sensed trees. The figure contains regression functions, coefficients of determination (R2), and F-test of statistical significance of the regression model (p-value).
Forests 07 00307 g004
Forests 07 00307 g005 550
Figure 5. Frequency distribution of field-measured trees (GR) and remotely-sensed trees (RS) within the diameter intervals.
Figure 5. Frequency distribution of field-measured trees (GR) and remotely-sensed trees (RS) within the diameter intervals.
Forests 07 00307 g005
Forests 07 00307 g006 550
Figure 6. Regression between diameters of field-measured trees and remotely-sensed trees. The figure contains regression functions, coefficients of determination (R2), and F-test of statistical significance of the regression model (p-value).
Figure 6. Regression between diameters of field-measured trees and remotely-sensed trees. The figure contains regression functions, coefficients of determination (R2), and F-test of statistical significance of the regression model (p-value).
Forests 07 00307 g006
Forests 07 00307 g007 550
Figure 7. Frequency distribution of field-measured trees (GR) and remotely-sensed trees (RS) within the volume intervals.
Figure 7. Frequency distribution of field-measured trees (GR) and remotely-sensed trees (RS) within the volume intervals.
Forests 07 00307 g007
Forests 07 00307 g008 550
Figure 8. Regression between volumes of field-measured trees and remotely-sensed trees. The figure contains regression functions, coefficients of determination (R2), and F-test of statistical significance of the regression model (p-value).
Figure 8. Regression between volumes of field-measured trees and remotely-sensed trees. The figure contains regression functions, coefficients of determination (R2), and F-test of statistical significance of the regression model (p-value).
Forests 07 00307 g008
Forests 07 00307 g009 550
Figure 9. Frequency distribution of number of points (PCl) and number of field-measured trees (GR) at height intervals (a); and regression between number of points and number of remotely-sensed trees in the height interval of 2–20 m. The figure contains regression functions, coefficients of determination (R2), and F-test of statistical significance of the regression model (p-value) (b).
Figure 9. Frequency distribution of number of points (PCl) and number of field-measured trees (GR) at height intervals (a); and regression between number of points and number of remotely-sensed trees in the height interval of 2–20 m. The figure contains regression functions, coefficients of determination (R2), and F-test of statistical significance of the regression model (p-value) (b).
Forests 07 00307 g009
Forests 07 00307 g010 550
Figure 10. Relationship between relative mean error for calculated volume (z-axis) and relative mean error for evaluated tree height (y-axis) and derived tree diameter (x-axis).
Figure 10. Relationship between relative mean error for calculated volume (z-axis) and relative mean error for evaluated tree height (y-axis) and derived tree diameter (x-axis).
Forests 07 00307 g010
Table
Table 1. Number of field-measured trees (GR) and remotely-sensed trees (RS) for different tree heights.
Table 1. Number of field-measured trees (GR) and remotely-sensed trees (RS) for different tree heights.
VariableGRRS
TotalTotalTruePosFalsePosFalseNegDR (%)
Tree (all)4451171061133924
Tree (>16 m)2951171061118936
Tree (>21 m)210105101410948
Note: TruePos—correct identification; FalsePos—commission error; FalseNeg—omission error; DR—detection rate.
Table
Table 2. Number of field-measured trees (GR), remotely-sensed trees (RS), and detection rates (DR) for different social position of trees.
Table 2. Number of field-measured trees (GR), remotely-sensed trees (RS), and detection rates (DR) for different social position of trees.
VariableGRRSDR (%)
Dominant trees533566
Codominant trees994848
Intermediate trees671218
Suppressed trees226115
Table
Table 3. Differences between heights of field-measured trees (GR) and remotely-sensed trees (RS).
Table 3. Differences between heights of field-measured trees (GR) and remotely-sensed trees (RS).
Compared VariablesTree HeightStand Height
e%se%RMSE%Normality TestPaired TestRShs-GRhs (%)RShs-GRh10 (%)RShs-GRh20 (%)
Wp-ValueZp-Value
RS vs. GR2.88.88.20.950.001 *3.370.001 *17.2−5.6−4.2
Note: e%—relative mean error; se%—relative standard deviation of mean error; RMSE%—relative root mean square error; * null hypothesis is rejected at α = 0.05, Sample size n = 106; hs—mean height of all trees; h10—mean height of 10% trees with the largest diameter; h20—mean height of 20% trees with the largest diameter.
Table
Table 4. Regression models used for derivation of tree diameter based on tree height.
Table 4. Regression models used for derivation of tree diameter based on tree height.
Tree SpeciesModelnRR2 SdSd (%)c (%)
European beechd = 4.4973 × exp(0.0745 × h)1930.910.828.1840.67Dominant−13.67
Adriatic oakd = 21.429 × exp(0.0285 × h)910.400.1610.9135.35Codominant3.34
European hornbeamd = 4.2836 × exp(0.0791 × h)190.850.724.8850.46Intermediate11.77
Italian Mapled = 3.8658 × exp(0.0728 × h)1170.860.745.3130.72Suppressed31.13
Manna ashd = 2.6696 × exp(0.0965 × h)180.810.654.8024.03
Note: n—sample size; R—correlation coefficient; R2—coefficient of determination; Sd—accuracy of model; Sd%—relative accuracy of model; c (%)—relative bias used for correction of outputs.
Table
Table 5. Differences between diameters of field-measured trees (GR) and remotely-sensed trees (RS).
Table 5. Differences between diameters of field-measured trees (GR) and remotely-sensed trees (RS).
Compared VariablesTree DiameterStand Diameter
e%se%RMSE%Normality TestPaired TestRSds-GRds (%)RSds-GRd10 (%)RSds-GRd20 (%)
Wp-Valuetp-Value
RS vs. GR−1.224.721.80.980.1800.550.58640.0−27.60−21.5
Note: e%—relative mean error; se%—relative standard deviation of mean error; RMSE%—relative root mean square error; sample size n = 106; ds—mean diameter of all trees; d10—mean diameter of 10% trees with the largest diameters; d20—mean diameter of 20% trees with the largest diameters.
Table
Table 6. Differences between volumes of field-measured trees (GR) and remotely-sensed trees (RS).
Table 6. Differences between volumes of field-measured trees (GR) and remotely-sensed trees (RS).
Compared VariablesTree VolumeStand Volume
e%se%RMSE%Normality TestPaired TestRSv-GRv (%)
Wp-ValueZp-Value
RS vs. GR1.161.445.70.940.001 *0.590.556−42.9
Note: e%—relative mean error; se%—relative standard deviation of mean error; RMSE%—relative root mean square error; * null hypothesis is rejected at α = 0.05, sample size n = 106; v—total volume.

Share and Cite

MDPI and ACS Style

Sačkov, I.; Santopuoli, G.; Bucha, T.; Lasserre, B.; Marchetti, M. Forest Inventory Attribute Prediction Using Lightweight Aerial Scanner Data in a Selected Type of Multilayered Deciduous Forest. Forests 2016, 7, 307. https://doi.org/10.3390/f7120307

AMA Style

Sačkov I, Santopuoli G, Bucha T, Lasserre B, Marchetti M. Forest Inventory Attribute Prediction Using Lightweight Aerial Scanner Data in a Selected Type of Multilayered Deciduous Forest. Forests. 2016; 7(12):307. https://doi.org/10.3390/f7120307

Chicago/Turabian Style

Sačkov, Ivan, Giovanni Santopuoli, Tomáš Bucha, Bruno Lasserre, and Marco Marchetti. 2016. "Forest Inventory Attribute Prediction Using Lightweight Aerial Scanner Data in a Selected Type of Multilayered Deciduous Forest" Forests 7, no. 12: 307. https://doi.org/10.3390/f7120307

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop