Evaluation of Whole Tree Growth Increment Derived from Tree-Ring Series for Use in Assessments of Changes in Forest Productivity across Various Spatial Scales
Abstract
:1. Introduction
2. Materials and Methods
2.1. Stem Analysis Data Collection and Measurement
2.2. Stem Analysis Growth Estimates
2.3. Model-Based Growth Estimates
2.3.1. Height Estimation
2.3.2. Volume Estimation
2.4. Comparison of Estimates
2.5. Inter-Annual Variation
2.6. Stand-Level Example Application
3. Results
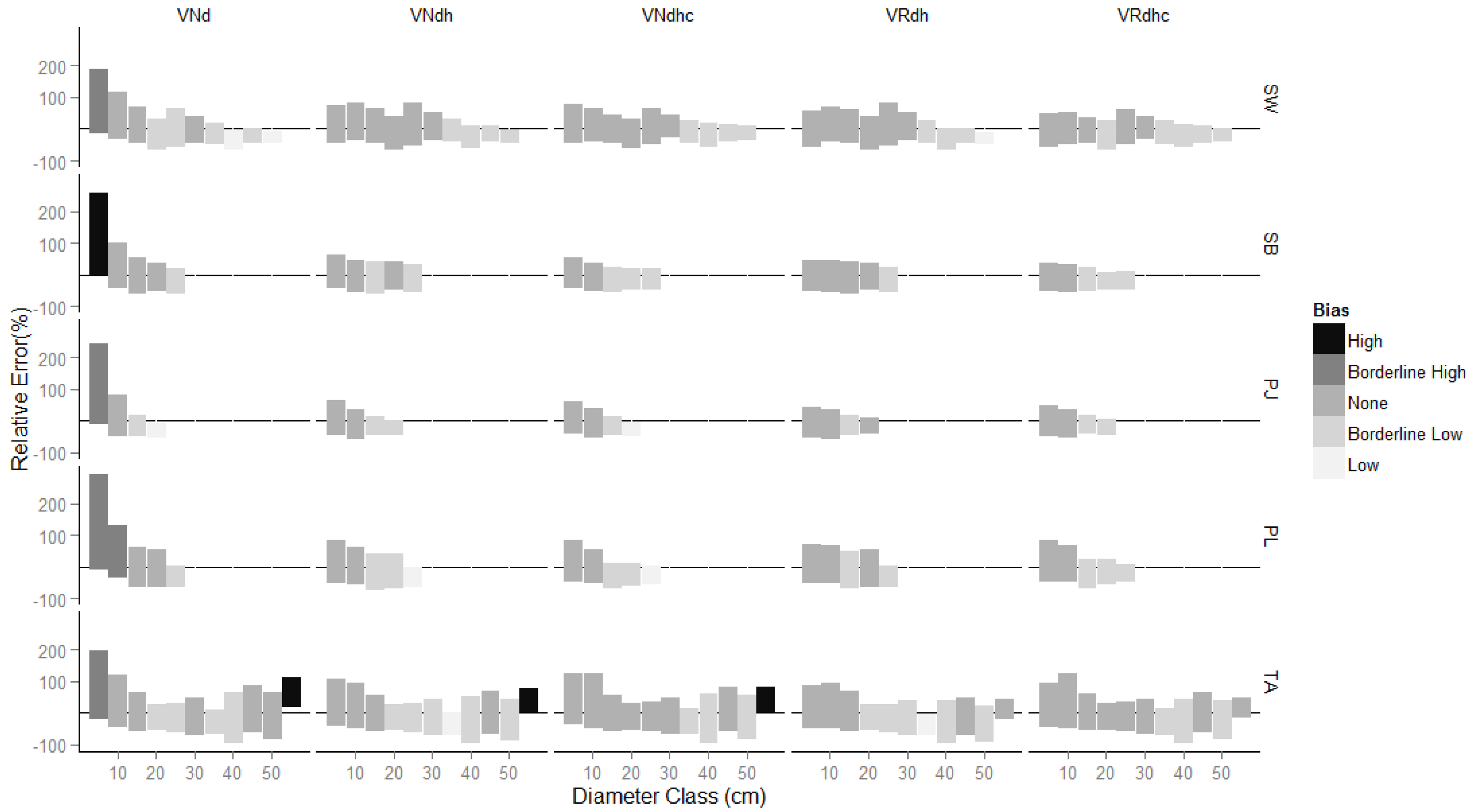
3.1. Comparison of Estimates
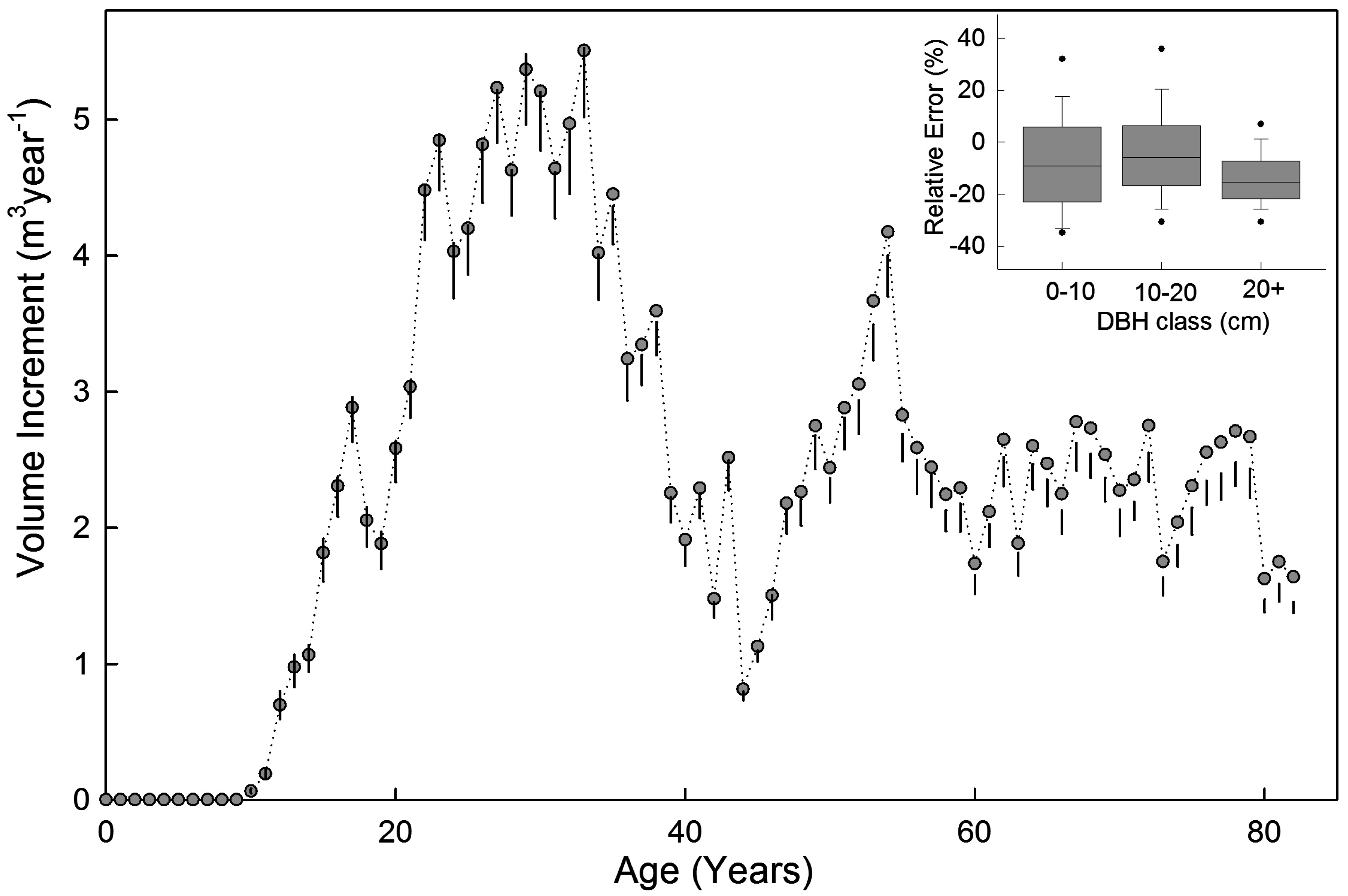
3.2. Inter-Annual Variation
3.3. Example Application
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Luo, Y.; Keenan, T.F.; Smith, M. Predictability of the terrestrial carbon cycle. Glob. Chang. Biol. 2015, 21, 1737–1751. [Google Scholar] [CrossRef] [PubMed]
- Metsaranta, J.M.; Lieffers, V.J. Using dendrochronology to obtain annual data for modelling stand development: A supplement to permanent sample plots. Forestry 2009, 82, 163–173. [Google Scholar] [CrossRef]
- Metsaranta, J.M.; Kurz, W.A. Inter-annual variability of ecosystem production in boreal jack pine forests (1975–2004) estimated from tree-ring data using CBM-CFS3. Ecol. Mod. 2012, 224, 111–123. [Google Scholar] [CrossRef]
- Hember, R.A.; Kurz, W.A.; Metsaranta, J.M.; Black, T.A.; Coops, N.C.; Guy, R.D. Accelerated regrowth of temperate-maritime forests due to environmental change. Glob. Chang. Biol. 2012, 18, 2026–2040. [Google Scholar] [CrossRef]
- Babst, F.; Alexander, M.R.; Szejner, P.; Bouriaud, O.; Klesse, S.; Roden, J.; Ciais, P.; Poulter, B.; Frank, D.; Moore, D.J.P.; et al. A tree-ring perspective on the terrestrial carbon cycle. Oecologia 2014, 176, 307–322. [Google Scholar] [CrossRef] [PubMed]
- Graumlich, L.J.; Brubaker, L.B.; Grier, C.C. Long-term trends in forest net primary productivity: Cascade Mountains, Washington. Ecology 1989, 70, 405–410. [Google Scholar] [CrossRef]
- Babst, F.; Bouriaud, O.; Alexander, R.; Trouet, V.; Frank, D. Toward consistent measurement of carbon accumulation: A multi-site assessment of biomass and basal area increment across Europe. Dendrochronologia 2014, 32, 153–161. [Google Scholar] [CrossRef]
- Fang, O.; Wang, Y.; Shao, X. The effect of climate on the net primary production (NPP) of Pinus koraiensis in the Changbai Mountains over the past 50 years. Trees 2016, 30, 281–294. [Google Scholar] [CrossRef]
- Bunn, A.G.; Hughes, M.K.; Kirdyanov, A.V.; Losleben, M.; Shishov, V.V.; Berner, L.T.; Oltchev, A.; Vaganov, E.A. Comparing forest measurements from tree rings and a space based index of vegetation activity in Siberia. Environ. Res. Lett. 2013, 8, 035034. [Google Scholar] [CrossRef]
- Babst, F.; Bouriaud, O.; Papale, D.; Gielen, B.; Jansenns, I.A.; Nikinmaa, E.; Ibrom, A.; Wu, J.; Bernhofer, C.; Köstner, B.; et al. Above-ground woody carbon sequestration measured from tree rings is coherent with net ecosystem productivity at five eddy-covariance sites. New Phytol. 2014, 201, 1289–1303. [Google Scholar] [CrossRef] [PubMed]
- LeBlanc, D.C. Relationship between breast-height and whole-stem growth indices for red spruce on Whiteface Mountain, New York. Can. J. For. Res. 1990, 20, 1399–1407. [Google Scholar] [CrossRef]
- Newton, P.F. A stem analysis computational algorithm for estimating volume growth and its empirical evaluation under various sampling strategies. Comput. Electron. Agric. 2004, 44, 21–31. [Google Scholar] [CrossRef]
- Bouriaud, O.; Breda, N.; Dupouey, J.-L.; Granier, A. Is ring width a reliable proxy for stem-biomass increment? A case study in European beech. Can. J. For. Res. 2005, 35, 2920–2933. [Google Scholar] [CrossRef]
- Chhin, S.; Hogg, E.H.; Lieffers, V.J.; Huang, S. Growth–climate relationships vary with height along the stem in lodgepole pine. Tree Phys. 2010, 30, 335–345. [Google Scholar] [CrossRef] [PubMed]
- Van der Maaten-Theunissen, M.; Bouriaud, O. Climate-growth relationships at different stem heights in silver fir and Norway spruce. Can. J. For. Res. 2012, 42, 958–969. [Google Scholar] [CrossRef]
- Duff, G.H.; Nolan, N.J. Growth and morphogenesis in the Canadian forest species: I. The controls of cambial and apical activity in Pinus resinosa. Can. J. Bot. 1957, 31, 471–513. [Google Scholar] [CrossRef]
- Shea, S.R.; Armson, K.A. Stem analysis of jack pine (Pinus banksiana Lamb.): Techniques and concepts. Can. J. For. Res. 1972, 2, 392–406. [Google Scholar] [CrossRef]
- Dyer, M.E.; Bailey, R.L. A test of six methods for estimating true height from stem analysis data. For. Sci. 1987, 33, 3–13. [Google Scholar]
- Halliwell, D.H.; Apps, M.J. BOReal Ecosystem-Atmosphere Study (BOREAS) Biometry and Auxiliary Sites: Overstory and Understory Data; Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre: Edmonton, AB, Canada, 1997.
- Varem-Sanders, T.M.L.; Cambpell, I.D. BOReal Ecosystem-Atmosphere Study (BOREAS) Biometry and Auxiliary Sites: X-ray Densitometry of Tree Allometry Samples; Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre: Edmonton, AB, Canada, 1998.
- Varem-Sanders, T.M.L.; Cambell, I.D. DendroScan: A Tree-Ring Width and Density Measurement System; UBC Press: Vancouver, BC, Canada, 1996. [Google Scholar]
- Martin, A.J. Testing volume equation accuracy with water displacement techniques. For. Sci. 1984, 30, 41–50. [Google Scholar]
- Figueiredo-Filho, A.; Schaaf, L.B. Comparison between predicted volumes estimated by taper equations and true volumes obtained by the water displacement technique (xylometer). Can. J. For. Res. 1999, 29, 451–461. [Google Scholar] [CrossRef]
- Biging, G.S.; Wensel, L.C. The effect of eccentricity on the estimation of basal area and basal area increment of coniferous trees. For. Sci. 1988, 34, 621–633. [Google Scholar]
- Bakker, J.D. A new, proportional method for reconstructing historical tree diameters. Can. J. For. Res. 2005, 35, 2515–2520. [Google Scholar] [CrossRef]
- Ung, C.H.; Guo, X.J.; Fortin, M. Canadian national taper models. For. Chron. 2014, 89, 211–224. [Google Scholar] [CrossRef]
- Kozak, A. A variable-exponent taper equation. Can. J. For. Res. 1988, 18, 1362–1368. [Google Scholar] [CrossRef]
- Gál, J.; Bella, I.E. New Stem Taper Functions for 12 Saskatchewan Timber Species; Information Report NOR-X-338; Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre: Edmonton, AB, Canada, 1994.
- Klos, R. Ecologically Based Taper Equations for Major Tree Species in Manitoba. Master’s Thesis, Lakehead University, Thunder Bay, ON, Canada, 2004. [Google Scholar]
- Huang, S. Ecologically Based Individual Tree Volume Estimation for Major Alberta Tree Species Report #1 Individual Tree Volume Estimation Procedures for Alberta: Methods of Formulation and Statistical Foundations; Alberta Sustainable Resource Development, Public Lands and Forests Division: Edmonton, AB, Canada, 1994.
- Huang, S. Ecologically Based Individual Tree Volume Estimation for Major Alberta Tree Species Report #2 Ecologically Based Individual Tree Height-Diameter Models for Major Alberta Tree Species; Alberta Sustainable Resource Development, Public Lands and Forests Division: Edmonton, AB, Canada, 1994.
- Metsaranta, J.M.; Shaw, C.H.; Kurz, W.A.; Boisvenue, C.; Morken, S. Uncertainty of inventory-based estimates of the carbon dynamics of Canada’s managed forest (1990–2014). Can. J. For. Res. 2016. in review. [Google Scholar]
- Metsaranta, J.M.; Lieffers, V.J.; Wein, R.W. Dendrochronological reconstruction of jack pine snag and downed log dynamics in Saskatchewan and Manitoba, Canada. For. Ecol. Manag. 2008, 255, 1262–1270. [Google Scholar] [CrossRef]
- Hasenauer, H.; Monserud, R.A. Biased predictions for tree height increment models developed from smoothed ‘data’. Ecol. Mod. 1997, 98, 13–22. [Google Scholar] [CrossRef]
- Sumida, A.; Miyaura, T.; Torii, H. Relationships of tree height and diameter at breast height revisited: Analysis of stem growth using 20-year data of an even-aged Chamaecyparis obtuse stand. Tree Phys. 2013, 33, 106–118. [Google Scholar] [CrossRef] [PubMed]
- Lambert, M.C.; Ung, C.H.; Raulier, F. Canadian national tree aboveground biomass equations. Can. J. For. Res. 2005, 35, 1996–2018. [Google Scholar] [CrossRef]
- Ung, C.H.; Bernier, P.; Guo, X.J. Canadian national biomass equations: New parameter estimates that include British Columbia data. Can. J. For. Res. 2008, 38, 1123–1132. [Google Scholar] [CrossRef]
- Weiskittel, A.R.; MacFarlane, D.W.; Radtke, P.J.; Affleck, D.L.R.; Temesgen, H.; Woodall, C.W.; Westfall, J.A.; Coulston, J.W. A call to improve methods for estimating tree biomass for regional and national assessments. J. For. 2015, 113, 414–424. [Google Scholar] [CrossRef]
- Garcia, O. Sampling for tree-ring analysis. In Presented at Integrating Forest Information Over Space and Time, Canberra, Australia, 13–17 January 1992; pp. 110–128.
- Osawa, A.; Abaimov, A.P.; Kajimoto, T. Feasibility of estimating total stem volume and aboveground biomass from measurement on the largest trees in even-aged pure stands. Can. J. For. Res. 2001, 31, 2042–2048. [Google Scholar] [CrossRef]
- Mérian, P.; Bert, D.; Lebourgeois, F. An approach for quantifying and correcting sample size-related bias in population estimates of climate-tree growth relationships. For. Sci. 2013, 59, 444–452. [Google Scholar] [CrossRef]
- Nehrbass-Ahles, C.; Babst, F.; Klesse, S.; Nöttzli, M.; Bouriaud, O.; Neukom, R.; Dobbertin, M.; Frank, D. The influence of sampling design on tree-ring based quantification of forest growth. Glob. Chang. Biol. 2014, 20, 2867–2885. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.; Zhang, S.Y. Height-diameter models using stand characteristics for Pinus banksiana and Picea mariana. Scand. J. For. Res. 2004, 19, 442–451. [Google Scholar] [CrossRef]
- Sharma, M.; Zhang, S.Y. Variable-exponent taper equations for jack pine, black spruce and balsam fir in eastern Canada. For. Ecol. Manag. 2004, 198, 39–53. [Google Scholar] [CrossRef]
- Sharma, M.; Parton, J. Modelling stand density effects on taper for jack pine and black spruce plantations using dimensional analysis. For. Sci. 2009, 55, 268–282. [Google Scholar]
- Almedag, I.S.; Stiell, W.M. Spacing and Age Effects on Biomass Production in Red Pine Plantations. For. Chron. 1982, 58, 220–224. [Google Scholar] [CrossRef]
| Species | DBH (cm) | Height (m) | Age (Years) | Year Sampled (Year (n)) |
|---|---|---|---|---|
| White spruce (SW) (Picea glauca) | 23.0 (6.2, 51.4) | 18.7 (6.7, 33.7) | 86 (15, 226) | 1994 (5) |
| 2005 (4) | ||||
| 2006 (11) | ||||
| 2010 (8) | ||||
| Black spruce (SB) (Picea mariana) | 11.8 (5.0, 24.6) | 10.8 (6.4, 20.9) | 89 (18, 222) | 1994 (26) |
| 2005 (19) | ||||
| 2006 (16) | ||||
| 2010 (7) | ||||
| Trembling aspen (TA) (Populus tremuloides) | 21.4 (5.3, 54.8) | 17.7 (6.5, 35.6) | 69 (19, 176) | 1994 (9) |
| 2005 (15) | ||||
| 2010 (7) | ||||
| Jack pine (PJ) (Pinus banksiana) | 13.1 (7.0, 18.6) | 12.3 (8.5, 15.8) | 64 (52, 76) | 1994 (15) |
| Lodgepole pine (PL) (Pinus contorta) | 15.3 (4.2, 27.0) | 14.7 (5.8, 28.1) | 77 (14, 153) | 2005 (24) |
| 2006 (6) |
| Metric | Comparison | Description | References for Equations and Parameters |
|---|---|---|---|
| (A) Volume | (1) National DBH | (1.1) Volume is estimated from DBH only, using a national equation | [26] |
| (2) National DBH and HT | (2.1) Volume is estimated from DBH and uncorrected height (HTr), using a national equation. | [26]; heights as in B1.1 or B1.2 | |
| (2.2) Volume is estimated from DBH and corrected height (HTc) using a national volume equation | |||
| (3) Regional DBH and HT | (3.1) Volume is estimated from DBH and uncorrected height (HTr), using a regional equation. | [27] for the equation formulation, Regional parameters from published sources for Saskatchewan [28], Manitoba [29], Alberta [30], and the Northwest Territories [30]. Heights estimated as in B1.1 or B1.2 | |
| (3.2) Volume is estimated from DBH and corrected height (HTc) using a regional equation | |||
| (B) Tree height | (1) HT DBH model | (1.1) Heights estimated from diameters reconstructed on the breast height sample are compared to heights interpolated between stem analysis sections. | (1.1 and 1.2) Provincial parameter sets for trees in Manitoba [29]. Alberta parameter sets for other provinces (NWT, SK, and AB) [31] |
| (1.2) Heights estimated as above, but a correction factor is calculated from the difference between measured and predicted height at time of sampling, and applied to the rest of the height time series. |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Metsaranta, J.M.; Bhatti, J.S. Evaluation of Whole Tree Growth Increment Derived from Tree-Ring Series for Use in Assessments of Changes in Forest Productivity across Various Spatial Scales. Forests 2016, 7, 303. https://doi.org/10.3390/f7120303
Metsaranta JM, Bhatti JS. Evaluation of Whole Tree Growth Increment Derived from Tree-Ring Series for Use in Assessments of Changes in Forest Productivity across Various Spatial Scales. Forests. 2016; 7(12):303. https://doi.org/10.3390/f7120303
Chicago/Turabian StyleMetsaranta, Juha M., and Jagtar S. Bhatti. 2016. "Evaluation of Whole Tree Growth Increment Derived from Tree-Ring Series for Use in Assessments of Changes in Forest Productivity across Various Spatial Scales" Forests 7, no. 12: 303. https://doi.org/10.3390/f7120303
APA StyleMetsaranta, J. M., & Bhatti, J. S. (2016). Evaluation of Whole Tree Growth Increment Derived from Tree-Ring Series for Use in Assessments of Changes in Forest Productivity across Various Spatial Scales. Forests, 7(12), 303. https://doi.org/10.3390/f7120303





