Occurrence of Density-Dependent Height Repression within Jack Pine and Black Spruce Populations
Abstract
:1. Introduction
2. Experimental Section
2.1. Detecting Density-Dependent Height Development
2.1.1. Nelder Plot Structure and Measurements
2.1.2. Stand Density-Height Regression Relationships
3. Results
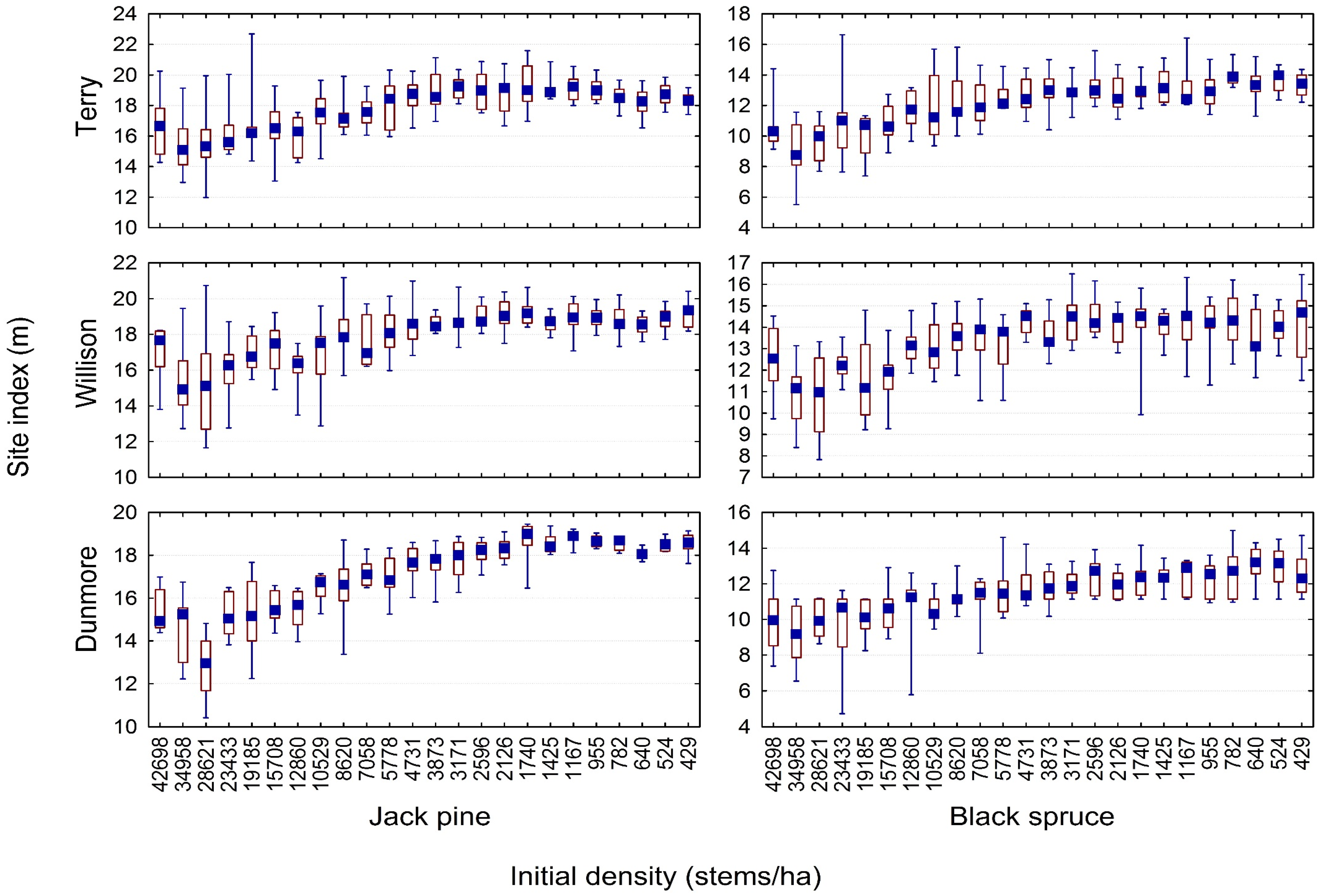
3.1. Experimental Evidence of a Density-Dependent Height Repression Effect
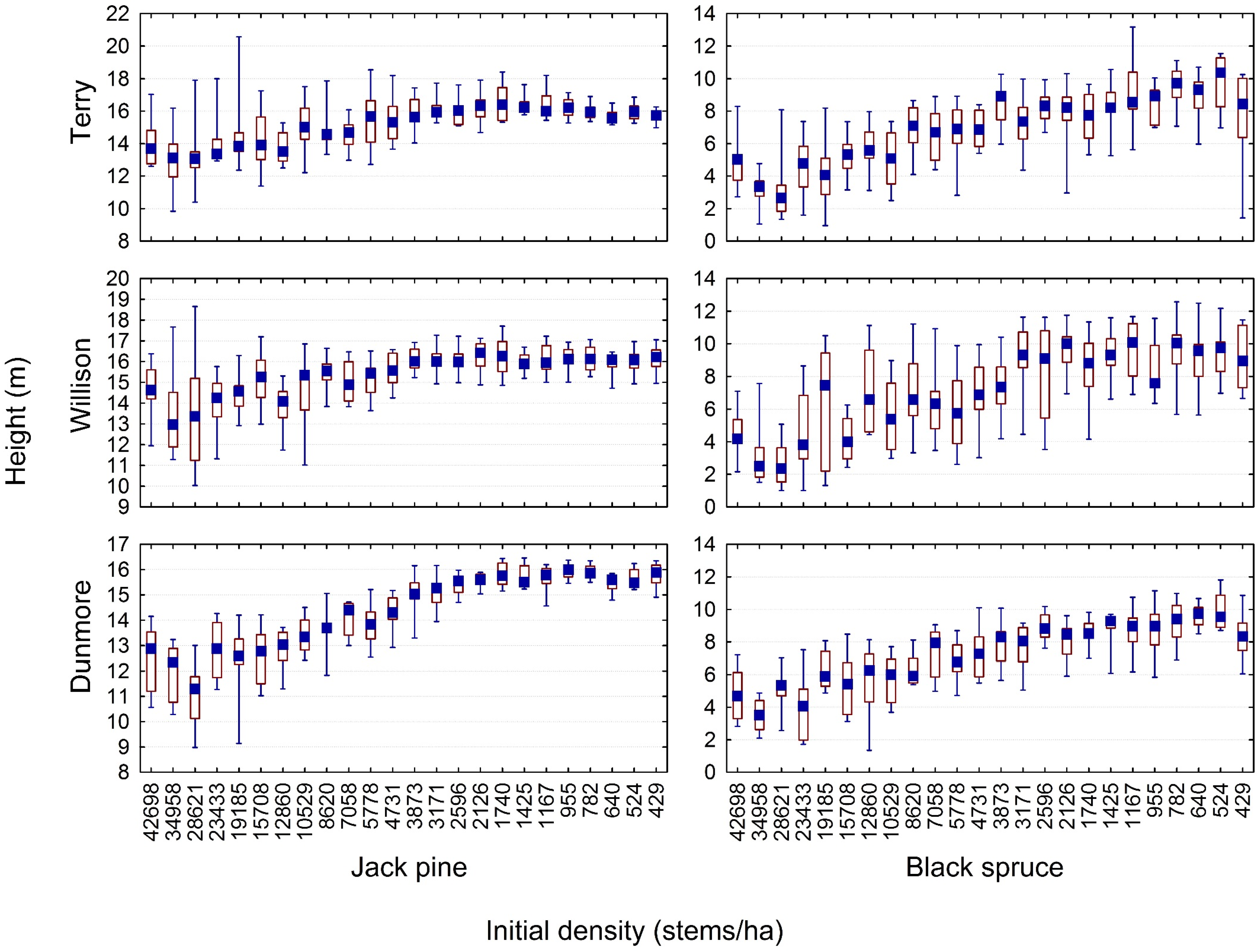
3.2. Quantifying the Density-Dependent Height Repression Effect
| Species | Age | Nelder Plot Series | Spatial Autocorrelation Detection via Time Series Statistics a | Spatial Autocorrelation Detection via Regression Statistics b | ||
|---|---|---|---|---|---|---|
| Frequency of significant partial autocorrelation coefficients (ns/nt) | Spatial lag | Frequency of significant density-dependent height repression effects (n’s/nt) | Frequency of significant spatial autocorrelation (n’’s/n’s) | |||
| Jack | 16 | Dunmore | 1/10 | 1st | 3/10 | 1/3 |
| Pine | Willison | 3/9 | 1st | 6/9 | 0/6 | |
| Terry | 1/9 | 1st | 5/9 | 0/5 | ||
| 20 | Dunmore | 1/10 | 1st | 3/10 | 1/3 | |
| Willison | 2/9 | 1st | 7/9 | 0/7 | ||
| Terry | 5/9 | 1st | 6/9 | 1/6 | ||
| 40 | Dunmore | 3/10 | 1st | 8/10 | 0/8 | |
| Willison | 2/9 | 1st | 8/9 | 2/8 | ||
| Terry | 4/8 | 1st | 8/8 | 1/8 | ||
| Black | 41 | Dunmore | 3/10 | 1st | 8/10 | 0/8 |
| Spruce | Willison | 3/9 | 1st | 8/9 | 0/8 | |
| Terry | 3/8 | 1st | 8/8 | 0/8 | ||
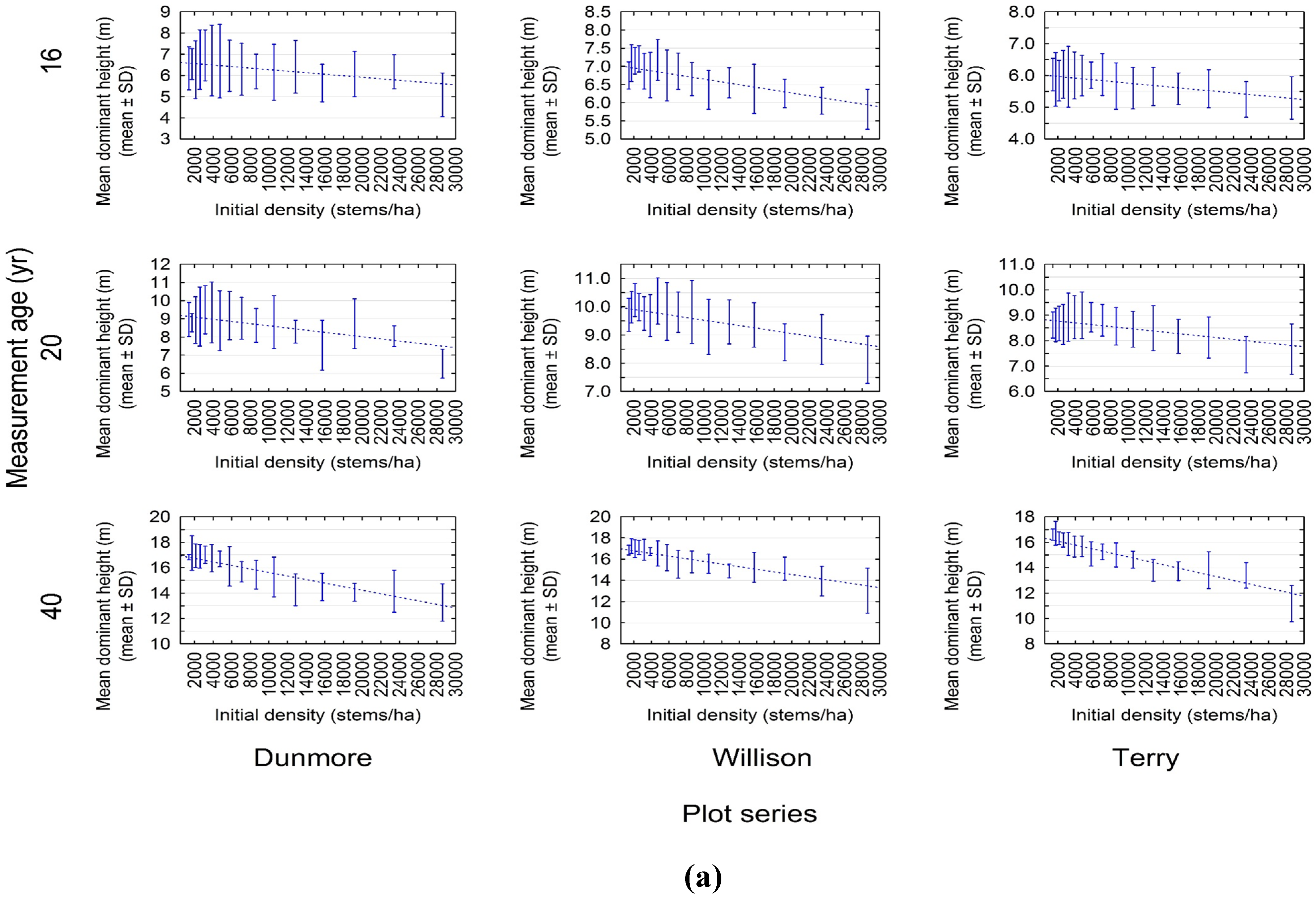
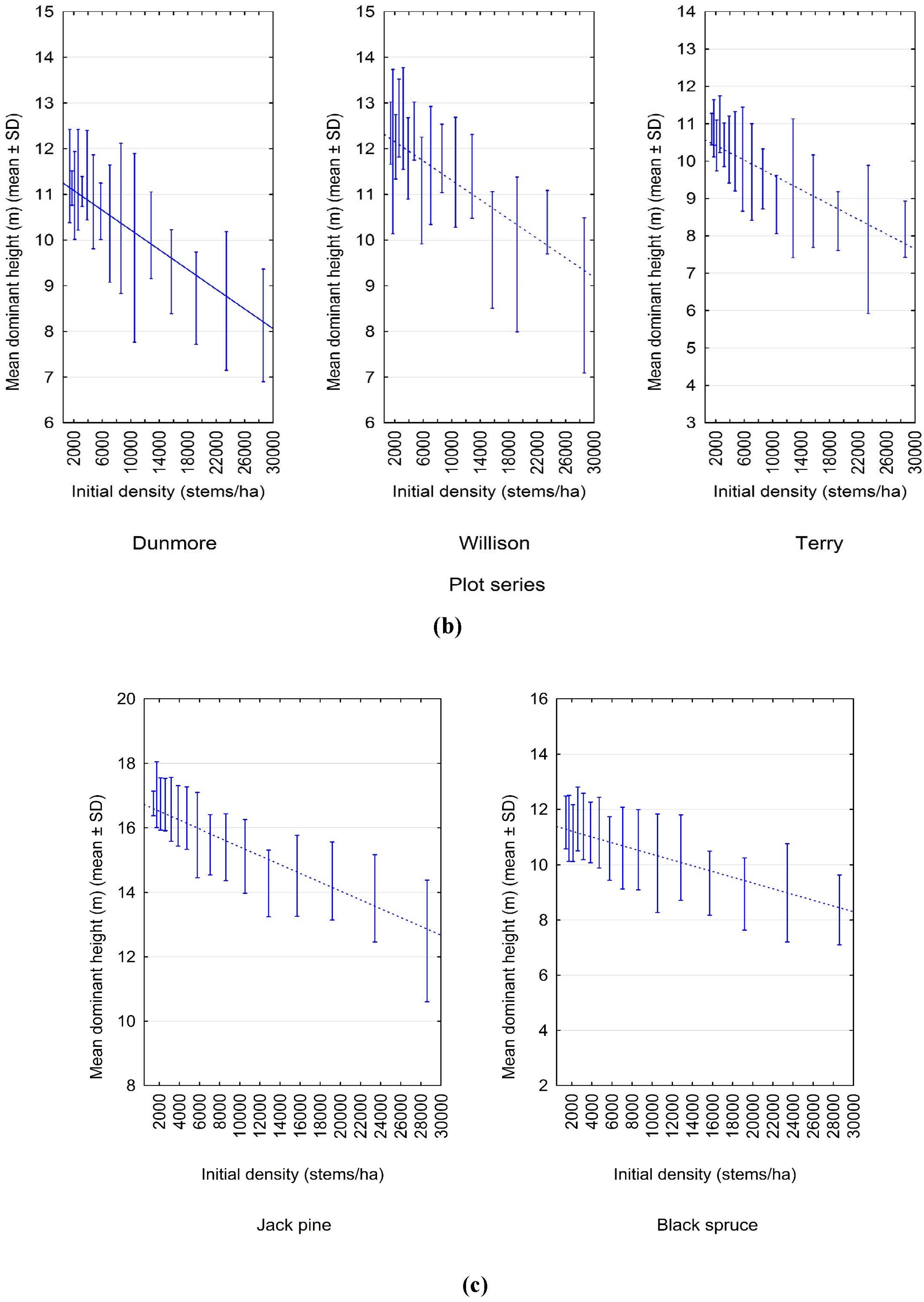
| Species | Age | Plot Series | n | Intercept | Density-Dependent Height Repression Coefficient a | ||
|---|---|---|---|---|---|---|---|
| 95% CI-L | 95% CI-U | ||||||
| Jack Pine | 16 | Dunmore | 3 | 6.634 | −0.000130 | −0.000036 | 0.000058 |
| Willison | 6 | 7.028 | −0.000080 | −0.000038 | 0.000004 | ||
| Terry | 5 | 6.019 | −0.000059 | −0.000026 | 0.000007 | ||
| Combined | 14 | 6.563 | −0.000050 | −0.000031 | −0.000012 | ||
| 20 | Dunmore | 3 | 9.215 | −0.000216 | −0.000060 | 0.000096 | |
| Willison | 7 | 9.993 | −0.000094 | −0.000047 | 0.000000 | ||
| Terry | 6 | 8.840 | −0.000077 | −0.000036 | 0.000005 | ||
| Combined | 16 | 9.384 | −0.000067 | −0.000042 | −0.000018 | ||
| 40 | Dunmore | 8 | 17.007 | −0.000256 | −0.000139 | −0.000021 | |
| Willison | 8 | 17.032 | −0.000232 | −0.000124 | −0.000017 | ||
| Terry | 8 | 16.385 | −0.000286 | −0.000154 | −0.000023 | ||
| Combined | 24 | 16.789 | −0.000200 | −0.000137 | −0.000078 | ||
| Black Spruce | 41 | Dunmore | 8 | 11.300 | −0.000202 | −0.000108 | −0.000015 |
| Willison | 8 | 12.367 | −0.000198 | −0.000106 | −0.000014 | ||
| Terry | 8 | 10.624 | −0.000185 | −0.000099 | −0.000014 | ||
| Combined | 24 | 11.429 | −0.000150 | −0.000104 | −0.000059 | ||
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
Appendix
| Species | Age | Nelder Plot Series | Plot No. | Parameter Estimates a | Regression Statistics b | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intercept | Slope (height-repression coefficient) | DF | r2 | SEE (m) | F-ratio | |||||||
| Estimate | SE | Estimate | 95% CL | nreg, nres | ||||||||
| Lower | Upper | |||||||||||
| Jack Pine | 16 | Dunmore | 1 | 7.20 | 0.143 | −0.0000450 | −0.0000696 | −0.0000205 | 1,14 | 0.525 | 0.371 | 15.5 * |
| 5 | 7.65 | 0.175 | −0.0000554 | −0.0000856 | −0.0000253 | 1,14 | 0.526 | 0.455 | 15.5 * | |||
| 9 | 5.25 | 0.150 | −0.0000281 | −0.0000539 | −0.0000022 | 1,14 | 0.279 | 0.390 | 5.4 * | |||
| Willison | 11 | 7.83 | 0.115 | −0.0000612 | −0.0000809 | −0.0000415 | 1,14 | 0.760 | 0.298 | 44.2 * | ||
| 12 | 6.91 | 0.114 | −0.0000260 | −0.0000459 | −0.0000061 | 1,13 | 0.381 | 0.296 | 8.0 * | |||
| 13 | 7.32 | 0.134 | −0.0000378 | −0.0000607 | −0.0000149 | 1,13 | 0.495 | 0.342 | 12.8 * | |||
| 14 | 6.97 | 0.164 | −0.0000593 | −0.0000876 | −0.0000310 | 1,14 | 0.590 | 0.427 | 20.2 * | |||
| 16 | 6.60 | 0.131 | −0.0000433 | −0.0000659 | −0.0000207 | 1,14 | 0.547 | 0.341 | 16.9 * | |||
| 17 | 6.99 | 0.125 | −0.0000450 | −0.0000666 | −0.0000234 | 1,14 | 0.588 | 0.326 | 20.0 * | |||
| Terry | 22 | 7.18 | 0.112 | −0.0000399 | −0.0000593 | −0.0000205 | 1,14 | 0.582 | 0.292 | 19.5 * | ||
| 23 | 5.88 | 0.108 | −0.0000265 | −0.0000451 | −0.0000079 | 1,14 | 0.401 | 0.280 | 9.4 * | |||
| 25 | 5.55 | 0.092 | −0.0000205 | −0.0000363 | −0.0000046 | 1,14 | 0.354 | 0.239 | 7.7 * | |||
| 26 | 5.56 | 0.073 | −0.0000314 | −0.0000440 | −0.0000188 | 1,14 | 0.671 | 0.190 | 28.5 * | |||
| 28 | 6.05 | 0.093 | −0.0000250 | −0.0000407 | −0.0000093 | 1,13 | 0.476 | 0.232 | 11.8 * | |||
| 20 | Dunmore | 1 | 9.64 | 0.209 | −0.0000604 | −0.0000965 | −0.0000243 | 1,14 | 0.479 | 0.544 | 12.9 * | |
| 5 | 10.53 | 0.283 | −0.0001142 | −0.0001629 | −0.0000654 | 1,14 | 0.643 | 0.736 | 25.2 * | |||
| 9 | 7.88 | 0.193 | −0.0000495 | −0.0000827 | −0.0000162 | 1,14 | 0.421 | 0.501 | 10.2 * | |||
| Willison | 11 | 10.99 | 0.188 | −0.0000848 | −0.0001171 | −0.0000525 | 1,14 | 0.693 | 0.488 | 31.7 * | ||
| 12 | 9.87 | 0.129 | −0.0000287 | −0.0000512 | −0.0000062 | 1,13 | 0.369 | 0.335 | 7.6 * | |||
| 13 | 10.29 | 0.161 | −0.0000435 | −0.0000709 | −0.0000161 | 1,13 | 0.475 | 0.410 | 11.8 * | |||
| 14 | 10.11 | 0.181 | −0.0000930 | −0.0001241 | −0.0000619 | 1,14 | 0.746 | 0.469 | 41.1 * | |||
| 15 | 10.87 | 0.241 | −0.0000655 | −0.0001070 | −0.0000240 | 1,14 | 0.450 | 0.626 | 11.5 * | |||
| 16 | 9.06 | 0.152 | −0.0000611 | −0.0000873 | −0.0000349 | 1,14 | 0.640 | 0.396 | 24.9 * | |||
| 17 | 9.90 | 0.160 | −0.0000694 | −0.0000969 | −0.0000418 | 1,14 | 0.676 | 0.416 | 29.2 * | |||
| Terry | 22 | 10.33 | 0.214 | −0.0000606 | −0.0000975 | −0.0000237 | 1,14 | 0.470 | 0.557 | 12.4 * | ||
| 23 | 8.78 | 0.125 | −0.0000367 | −0.0000582 | −0.0000151 | 1,14 | 0.487 | 0.325 | 13.3 * | |||
| 25 | 8.46 | 0.084 | −0.0000610 | −0.0000755 | −0.0000466 | 1,14 | 0.854 | 0.218 | 82.0 * | |||
| 26 | 8.52 | 0.126 | −0.0000579 | −0.0000796 | −0.0000362 | 1,14 | 0.700 | 0.327 | 32.7 * | |||
| 28 | 8.92 | 0.120 | −0.0000227 | −0.0000430 | −0.0000025 | 1,13 | 0.312 | 0.298 | 5.9 * | |||
| 29 | 8.72 | 0.146 | −0.0000481 | −0.0000732 | −0.0000230 | 1,14 | 0.547 | 0.378 | 16.9 * | |||
| 40 | Dunmore | 1 | 17.55 | 0.392 | −0.0001911 | −0.0002585 | −0.0001236 | 1,14 | 0.725 | 1.018 | 36.9 * | |
| 2 | 16.68 | 0.321 | −0.0001829 | −0.0002396 | −0.0001261 | 1,13 | 0.788 | 0.833 | 48.5 * | |||
| 3 | 17.16 | 0.337 | −0.0001396 | −0.0001992 | −0.0000799 | 1,13 | 0.663 | 0.875 | 25.6 * | |||
| 4 | 18.31 | 0.471 | −0.0001326 | −0.0002184 | −0.0000469 | 1,13 | 0.462 | 1.221 | 11.2 * | |||
| 6 | 17.63 | 0.288 | −0.0001510 | −0.0002006 | −0.0001013 | 1,14 | 0.753 | 0.748 | 42.6 * | |||
| 7 | 16.51 | 0.230 | −0.0001383 | −0.0001779 | −0.0000988 | 1,14 | 0.801 | 0.597 | 56.2 * | |||
| 8 | 16.26 | 0.406 | −0.0001199 | −0.0001897 | −0.0000500 | 1,14 | 0.492 | 1.054 | 13.5 * | |||
| 10 | 16.59 | 0.489 | −0.0001166 | −0.0002008 | −0.0000324 | 1,14 | 0.387 | 1.270 | 8.8 * | |||
| Willison | 11 | 18.16 | 0.353 | −0.0001393 | −0.0002002 | −0.0000785 | 1,14 | 0.633 | 0.918 | 24.1 * | ||
| 12 | 17.41 | 0.288 | −0.0000896 | −0.0001397 | −0.0000395 | 1,13 | 0.535 | 0.746 | 14.9 * | |||
| 13 | 17.64 | 0.235 | −0.0001261 | −0.0001661 | −0.0000861 | 1,13 | 0.781 | 0.599 | 46.4 * | |||
| 14 | 16.84 | 0.381 | −0.0001350 | −0.0002007 | −0.0000694 | 1,14 | 0.582 | 0.990 | 19.5 * | |||
| 16 | 16.58 | 0.286 | −0.0001943 | −0.0002435 | −0.0001451 | 1,13 | 0.848 | 0.737 | 72.7 * | |||
| 17 | 16.84 | 0.293 | −0.0001993 | −0.0002551 | −0.0001434 | 1,13 | 0.821 | 0.749 | 59.4 * | |||
| 18 | 16.63 | 0.333 | −0.0001078 | −0.0001657 | −0.0000499 | 1,13 | 0.554 | 0.863 | 16.1 * | |||
| 19 | 17.25 | 0.376 | −0.0001349 | −0.0001996 | −0.0000702 | 1,13 | 0.610 | 0.968 | 20.3 * | |||
| Terry | 23 | 17.11 | 0.448 | −0.0001933 | −0.0002705 | −0.0001160 | 1,14 | 0.673 | 1.165 | 28.8 * | ||
| 24 | 15.94 | 0.438 | −0.0001668 | −0.0002422 | −0.0000914 | 1,14 | 0.616 | 1.138 | 22.5 * | |||
| 25 | 16.48 | 0.267 | −0.0002068 | −0.0002527 | −0.0001608 | 1,14 | 0.869 | 0.693 | 93.1 * | |||
| 26 | 16.46 | 0.229 | −0.0001492 | −0.0001908 | −0.0001075 | 1,13 | 0.821 | 0.593 | 59.8 * | |||
| 27 | 16.54 | 0.168 | −0.0001339 | −0.0001630 | −0.0001047 | 1,13 | 0.883 | 0.434 | 98.4 * | |||
| 28 | 17.10 | 0.264 | −0.0002240 | −0.0002694 | −0.0001785 | 1,14 | 0.889 | 0.685 | 111.8 * | |||
| 29 | 16.19 | 0.388 | −0.0001184 | −0.0001872 | −0.0000496 | 1,13 | 0.515 | 1.009 | 13.8 * | |||
| 30 | 16.36 | 0.347 | −0.0001500 | −0.0002092 | −0.0000909 | 1,13 | 0.698 | 0.886 | 30.0 * | |||
| Black Spruce | 41 | Dunmore | 1 | 11.33 | 0.210 | −0.0001484 | −0.0001867 | −0.0001101 | 1,13 | 0.844 | 0.545 | 70.2 * |
| 2 | 10.84 | 0.142 | −0.0000723 | −0.0000968 | −0.0000479 | 1,14 | 0.742 | 0.369 | 40.2 * | |||
| 4 | 13.04 | 0.433 | −0.0001076 | −0.0001821 | −0.0000331 | 1,14 | 0.407 | 1.124 | 9.6 * | |||
| 6 | 12.11 | 0.311 | −0.0001176 | −0.0001712 | −0.0000640 | 1,14 | 0.613 | 0.809 | 22.1 * | |||
| 7 | 11.13 | 0.338 | −0.0001390 | −0.0001972 | −0.0000808 | 1,14 | 0.652 | 0.878 | 26.2 * | |||
| 8 | 10.90 | 0.256 | −0.0001135 | −0.0001576 | −0.0000695 | 1,14 | 0.686 | 0.665 | 30.5 * | |||
| 9 | 10.95 | 0.370 | −0.0001124 | −0.0001761 | −0.0000487 | 1,14 | 0.506 | 0.961 | 14.3 * | |||
| 10 | 11.26 | 0.253 | −0.0001806 | −0.0002243 | −0.0001370 | 1,14 | 0.849 | 0.658 | 78.9 * | |||
| Willison | 11 | 13.09 | 0.435 | −0.0001188 | −0.0001938 | −0.0000438 | 1,14 | 0.452 | 1.131 | 11.6 * | ||
| 12 | 12.67 | 0.375 | −0.0001805 | −0.0002451 | −0.0001159 | 1,14 | 0.720 | 0.975 | 35.9 * | |||
| 14 | 11.33 | 0.465 | −0.0001129 | −0.0001930 | −0.0000328 | 1,14 | 0.395 | 1.209 | 9.1 * | |||
| 15 | 13.04 | 0.178 | −0.0000712 | −0.0001019 | −0.0000405 | 1,14 | 0.639 | 0.463 | 24.7 * | |||
| 16 | 12.95 | 0.179 | −0.0001717 | −0.0002023 | −0.0001412 | 1,13 | 0.919 | 0.457 | 147.8 * | |||
| 17 | 11.37 | 0.407 | −0.0000943 | −0.0001644 | −0.0000243 | 1,14 | 0.373 | 1.057 | 8.3 * | |||
| 18 | 12.97 | 0.290 | −0.0001332 | −0.0001831 | −0.0000833 | 1,14 | 0.701 | 0.753 | 32.8 * | |||
| 19 | 12.92 | 0.473 | −0.0001140 | −0.0001954 | −0.0000325 | 1,14 | 0.391 | 1.229 | 9.0 * | |||
| Terry | 23 | 10.61 | 0.290 | −0.0000926 | −0.0001425 | −0.0000427 | 1,14 | 0.531 | 0.752 | 15.9 * | ||
| 24 | 10.78 | 0.293 | −0.0001468 | −0.0001973 | −0.0000963 | 1,14 | 0.735 | 0.762 | 38.8 * | |||
| 25 | 10.23 | 0.538 | −0.0001838 | −0.0002765 | −0.0000911 | 1,14 | 0.564 | 1.399 | 18.1 * | |||
| 26 | 10.72 | 0.222 | −0.0001025 | −0.0001402 | −0.0000648 | 1,13 | 0.726 | 0.563 | 34.5 * | |||
| 27 | 10.19 | 0.261 | −0.0001130 | −0.0001578 | −0.0000681 | 1,14 | 0.676 | 0.677 | 29.2 * | |||
| 28 | 11.05 | 0.303 | −0.0000735 | −0.0001258 | −0.0000213 | 1,14 | 0.394 | 0.789 | 9.1 * | |||
| 29 | 11.33 | 0.355 | −0.0000989 | −0.0001601 | −0.0000378 | 1,14 | 0.462 | 0.923 | 12.0 * | |||
| 30 | 11.17 | 0.339 | −0.0000947 | −0.0001532 | −0.0000363 | 1,14 | 0.463 | 0.882 | 12.1 * | |||
References
- Rowe, J.S. Forest Regions of Canada; Publication No. 1300; Government of Canada, Department of Environment, Canadian Forestry Service: Ottawa, ON, Canada, 1972.
- OMNR (Ontario Ministry of Natural Resources). State of Ontario’s Forests; Queens Printer for Ontario: Toronto, ON, Canada, 2012; p. 73. [Google Scholar]
- OMNRF (Ontario Ministry of Natural Resources and Forestry). Forest Management Guide to Silviculture in the Great Lakes-St. Lawrence and Boreal Forests of Ontario; Queens Printer for Ontario: Toronto, ON, Canada, 2015; p. 394. [Google Scholar]
- McKinnon, L.M.; Kayahara, G.J.; White, R.G. Biological Framework for Commercial Thinning Even-aged Single-Species Stands of Jack Pine, White Spruce, and Black Spruce in Ontario. 2006. Available online: http://www.forestresearch.ca/images/stories/pdf/tr-046.pdf (accessed on 8 July 2015).
- Bell, W.F.; Parton, J.; Joyce, D.; Reid, D.; Wester, M.; Stinson, A.; Kayahara, G.; Towill, B. Developing a silvicultural framework and definitions for use in forest management planning and practice. For. Chron. 2008, 84, 678–692. [Google Scholar] [CrossRef]
- Newton, P.F. Development of an integrated decision-support model for density management within jack pine stand-types. Ecol. Model. 2009, 220, 3301–3324. [Google Scholar] [CrossRef]
- Newton, P.F. A decision-support system for density management within upland black spruce stand-types. Environ. Model. Softw. 2012, 35, 171–187. [Google Scholar] [CrossRef]
- Lanner, R.M. On the insensitivity of height growth to spacing. For. Ecol. Manag. 1985, 13, 143–148. [Google Scholar] [CrossRef]
- Bontemps, J.D.; Bouriaud, O. Predictive approaches to forest site productivity: Recent trends, challenges and future perspectives. Forestry 2014, 87, 109–128. [Google Scholar] [CrossRef]
- Lynch, D.W. Effects of Stocking on Site Measurement and Yield of Second-Growth Ponderosa Pine in the Inland Empire; USDA Forest Service Research Paper No. 56; USDA Forest Service Research: Washington, DC, USA, 1958.
- Knowe, S.A. Effect of competition control treatments on height-age and height-diameter relationships in young Douglas-fir plantations. For. Ecol. Manag. 1994, 67, 101–111. [Google Scholar] [CrossRef]
- MacFarlane, D.W.; Green, E.J.; Burkhart, H.E. Population density influences assessment and application of site index. Can. J. For. Res. 2000, 30, 1472–1475. [Google Scholar] [CrossRef]
- Sharma, M.; Burkhart, H.E.; Amateis, R.L. Modeling the effect of density on the growth of Loblolly Pine trees. South. J. Appl. For. 2002, 26, 124–133. [Google Scholar]
- Cieszewski, C.J.; Bella, I.E. Modeling density-related lodgepole pine height growth, using Czarnowski’s stand dynamics theory. Can. J. For. Res. 1993, 23, 2499–2506. [Google Scholar] [CrossRef]
- Farnden, C.; Herring, L. Severely repressed lodgepole pine responds to thinning and fertilization: 19-year results. For. Chron. 2002, 78, 404–414. [Google Scholar] [CrossRef]
- Nelder, J.A. New kinds of systematic designs for spacing experiments. Biometrics 1962, 18, 283–307. [Google Scholar] [CrossRef]
- García, O. Estimating top height with variable plot sizes. Can. J. For. Res. 1998, 28, 1509–1517. [Google Scholar] [CrossRef]
- Magnussen, S. Effect of plot size on estimates of top height in Douglas-fir. West. J. Appl. For. 1999, 14, 17–27. [Google Scholar]
- Affleck, D.L.R. A Comparative Study of Spatial Analysis Methods for Forestry Nelder Experiments. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 2001. [Google Scholar]
- Gujarati, D.N. Essential of Econometrics, 3rd ed.; McGraw-Hill/Irwin Inc.: New York, NY, USA, 2006; p. 838. [Google Scholar]
- Hedges, L.V.; Olkin, I. Statistical Methods for Meta-Analysis; Academic Press: New York, NY, USA, 1985; p. 369. [Google Scholar]
- Becker, B.J.; Wu, M.J. The synthesis of regression slopes in meta-analysis. Stat. Sci. 2007, 22, 414–429. [Google Scholar] [CrossRef]
- Carmean, W.H.; Niznowski, G.P.; Hazenberg, G. Polymorphic site index curves for jack pine in Nothern Ontario. For. Chron. 2001, 77, 141–150. [Google Scholar] [CrossRef]
- Carmean, W.H.; Hazenberg, G.; Deschamps, K.C. Polymorphic site index curves for black spruce and trembling aspen in northwest Ontario. For. Chron. 2006, 82, 231–242. [Google Scholar] [CrossRef]
- Neter, J.; Wasserman, W.; Kutner, M.H. Applied Linear Statistical Models, 3rd ed.; Irwin: Boston, MA, USA, 1990; p. 878. [Google Scholar]
- Newton, P.F. Forest production model for upland black spruce stands—Optimal site occupancy levels for maximizing net production. Ecol. Model. 2006, 190, 190–204. [Google Scholar] [CrossRef]
- Alexander, R.R.; Tackle, D.; Dahms, W.G. Site Indexes for Lodgepole Pine with Corrections for Stand Density: Methodology; USDA, Forest Service Research Paper RM-29; USDA Forest Service Research: Washington, DC, USA, 1967.
- Sharma, M.; Subedi, N.; Ter-Mikaelian, M.; Parton, J. Modeling climatic effects on stand height/site index of plantation grown jack pine and black spruce trees. For. Sci. 2015, 61, 25–34. [Google Scholar]
- Niklas, K.J. Plant Allometry: Scaling of Form and Process; University of Chicago Press: Chicago, IL, USA, 1994; p. 395. [Google Scholar]
- Newton, P.F. Evaluating the ecological integrity of structural stand density management models developed for boreal conifers. Forests 2015, 6, 992–1030. [Google Scholar] [CrossRef]
- Penner, M.; Woods, M.; Parton, J.; Stinson, A. Validation of empirical yield curves for natural-origin stands in boreal Ontario. For. Chron. 2008, 84, 704–717. [Google Scholar] [CrossRef]
- Weiskittel, A.R.; Hann, D.W.; Kershaw, J.A.; Vanclay, J.K. Forest Growth and Yield Modeling; John Wiley and Sons: West Sussex, UK, 2011; p. 415. [Google Scholar]
- Huang, S.; Monserud, R.A.; Braun, T.; Lougheed, H.; Bakowsky, O. Comparing site productivity of mature fire-origin and post-harvest juvenile lodgepole pine stands in Alberta. Can. J. For. Res. 2004, 34, 1181–1191. [Google Scholar] [CrossRef]
- Newton, P.F. Quantifying growth responses of black spruce and jack pine to thinning within the context of density management decision-support systems. Open J. For. 2015, 5, 409–421. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Newton, P.F. Occurrence of Density-Dependent Height Repression within Jack Pine and Black Spruce Populations. Forests 2015, 6, 2450-2468. https://doi.org/10.3390/f6072450
Newton PF. Occurrence of Density-Dependent Height Repression within Jack Pine and Black Spruce Populations. Forests. 2015; 6(7):2450-2468. https://doi.org/10.3390/f6072450
Chicago/Turabian StyleNewton, Peter F. 2015. "Occurrence of Density-Dependent Height Repression within Jack Pine and Black Spruce Populations" Forests 6, no. 7: 2450-2468. https://doi.org/10.3390/f6072450
APA StyleNewton, P. F. (2015). Occurrence of Density-Dependent Height Repression within Jack Pine and Black Spruce Populations. Forests, 6(7), 2450-2468. https://doi.org/10.3390/f6072450





