1. Introduction
The use of remote sensing data and related methods (
i.e., biomass estimation, delineation of forested areas) has become a standard in forest management [
1,
2,
3]. Large area applications such as, for example, harvesting planning or forest stand mapping based on remote sensing products are now widely operational, especially in the northern European countries [
4,
5,
6]. This development enables high-precision forest management, which is a prerequisite for the sustainable use of one of the key resources within the context of renewable energy. In mountainous regions, and particularly in the Alps, the use of forest resources in remote areas has decreased as valorization is hampered by accessibility constraints that prevent efficient mapping, management, and harvesting. To develop strategies to tackle this shortcoming, the research project NEWFOR (NEW technologies for a better mountain FORest timber mobilization) [
7] was introduced to the Alpine Space program of the European Territorial Cooperation. The project aims at enhancing the wood supply chain within the Alpine Space (Alps core area and surrounding foothills/lowlands) to improve forest timber evaluation and mobilization using new remote sensing technologies such as airborne laser scanning (ALS), also referred to as Lidar.
When processing ALS remote sensing data for forest applications, area-based approaches [
8,
9,
10] as well as single-tree based methods [
11,
12,
13] can be found in the literature. Area-based methods provide statistically calibrated maps of forest stand parameters such as growing stock, stem density, and stand height, which are useful for large-area forest inventory and long term management planning. They can also be sufficient for harvesting planning in the case of simple forests such as plantations. Meanwhile, in complex alpine forests single tree information is highly valuable. Irregular stands are frequent, and silviculture is driven by the largest trees [
14], which might also be used as intermediate support to optimize cable yarding. The spatial distribution of trees and their characteristics (height, species, crown size) are required inputs for growth simulation models [
15], for the evaluation of the forest protection effect against rockfalls [
16], or even to identify trees with high biodiversity value [
17]. Field inventories (FI) provide the required high level of local detailed information, but the high labor cost as well as accessibility constraint advocate for remote sensing solutions.
To gain such detailed information from ALS data, many studies on single tree detection were carried out by the research community [
18,
19,
20,
21,
22,
23]. Thus, many different methods are available for operational or scientific use. To gain deeper knowledge about the performance of different single tree detection methods, an international benchmark was carried out from 2005 to 2008 by the European Spatial Data Research Organization (EuroSDR), the International Society for Photogrammetry and Remote Sensing (ISPRS), and the Finnish Geodetic Institute (FGI). The study was published by Kaartinen
et al. [
24,
25]. The benchmark was carried out using homogeneous ALS data and FI data from two study areas in southern Finland. A different benchmark based on ALS data from different types of forest was carried out in 2012 by Vauhkonen
et al. [
26] to test six different algorithms under different forest conditions. The investigated study areas are located in Norway, Sweden, Germany, and Brazil. Both studies had a great influence on understanding the performance of single tree detection based on ALS data. While the benchmark of Kaartinen
et al. [
24] focused on the performance of different methods using quite homogeneous dataset from one region, the benchmark of Vauhkonen
et al. [
26] focused on the effect of different study areas and forest types on the detection results of different algorithms. Vauhkonen
et al. [
26] used a very heterogeneous dataset which spans from a plantation of monospecies forest in Brazil to natural mixed forests in Europe.
For the Alps, the previously published benchmark results are only partly applicable as forests in Central Europe are different from forests in Northern Europe or Brazil. For this reason, the present study focuses on testing ALS-based single tree detection methods established in the Alpine Space. Based on a unique dataset covering different study areas, forest types, and structures from different regions in the Alpine Space, different methods are tested and analyzed in a clear and reproducible way. The focus is on the performance of the methods. Investigations on the effect of the heterogeneity of the ALS data (
i.e., different point density) on the detection results are not in the scope of this study. To the authors’ best knowledge, this is the first benchmark ever performed for different forests within the Alps. This study is based on the single tree detection benchmark carried out within the project NEWFOR [
7]. Detailed results are published in the project’s final report [
27]. The presented study summarizes the findings of the report and provides a discussion of the results.
The dataset used in this study is presented in
Section 2.
Section 3 provides a brief description of the tested methods as well as a detailed description of the matching procedure and evaluation of the results. In
Section 4 results are presented in different levels of information while
Section 5 contains the discussion. Finally, conclusions are drawn in
Section 6.
4. Results
All participants were able to apply their method to the provided dataset. All submitted detection results were checked using the matching procedure described in
Section 3.2. In total, 168 results consisting of 10987 detected potential tree positions were investigated.
4.1. Validation of the Matching Procedure
A subset of 699 Test trees, randomly selected from the submitted results, was manually interpreted and classified. The resulting error matrix and descriptive measures are presented in
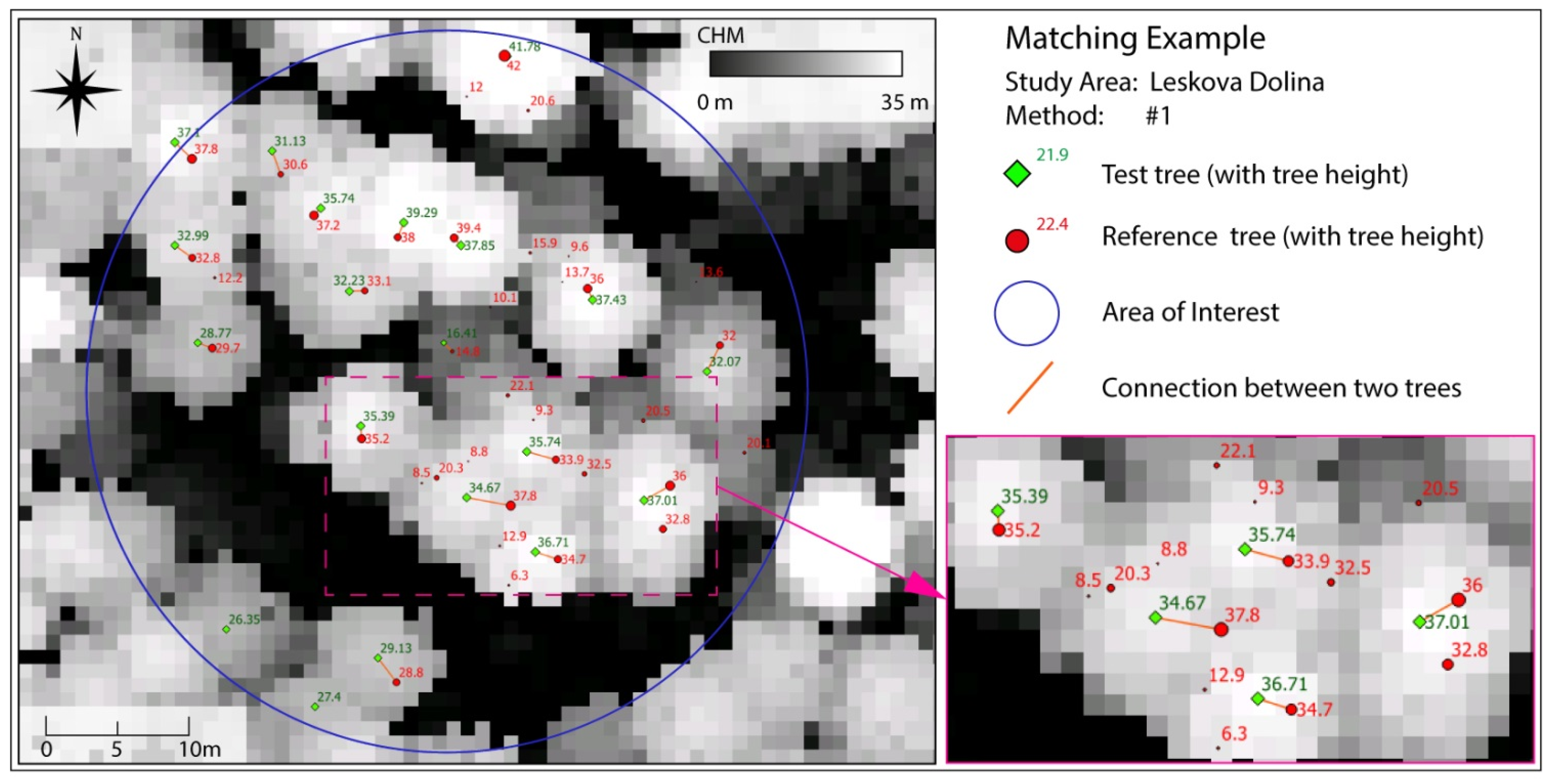
Table 5. An example of a visualized matching result displayed in Quantum GIS 2.8.1 [
29] is presented in
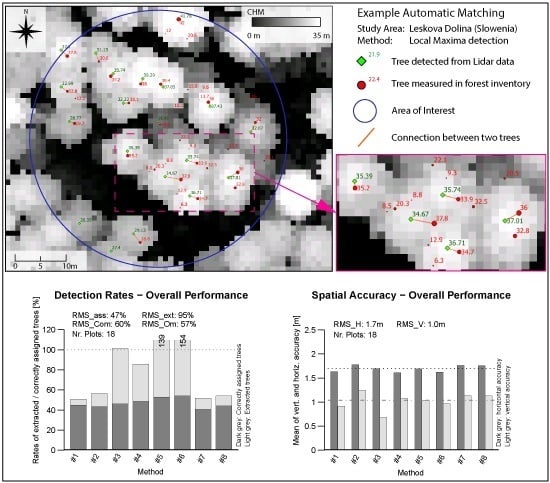
Figure 4. Nearby trees with matching tree heights get correctly connected in most cases. From the validated tree sample, only 3% were wrongly treated within the matching procedure. The obtained quality of the matching process shows an overall accuracy of 97% and a Kappa of 0.94.
Table 5.
Error matrix and descriptive measures for the matching quality check.
Table 5.
Error matrix and descriptive measures for the matching quality check.
| | Reference—Manual Interpretation |
|---|
| Matching Result | Match | No Match | Totals | User’s Accuracy |
| Match | 307 | 8 | 315 | 97% |
| No match | 14 | 370 | 384 | 96% |
| Totals | 321 | 378 | 699 | |
| Producer’s accuracy | 96% | 98% | | |
| Overall accuracy: 97% | | Kappa: 0.94 | | |
4.2. Matching Results at Method Level
The matching results per method indicate how well a method performed for all study areas. In
Table 6, the resulting statistical values are summarized.
The highest extraction rate (RMSextr: 154%) was obtained by Method #6 (LM 3 × 3), while the lowest rate was found by Method #1 (LM + Filtering), showing a value of 51%. Regarding the matching rates, the highest rate (RMSass: 54%) was found by Method #6. In contrast, the lowest rate was obtained by Method #7 (LM 5 × 5). Speaking about incorrect detections, the highest commission rate (RMSCom) with a value of 113% was produced by Method #6. The best RMSCom rate with a value of 9% was found for Method #1. The highest omission rate (RMSOm) was found for Method #7, which missed 63% of the given reference trees. The lowest and therefore best omission rates (RMSOm: 51%) were found for Methods #5 and #6.
In the spatial accuracy section, the best positional accuracy with a RMSH of 1.6 m was obtained by Methods #1, #4, and #6. The best height accuracy with a RMSV value of 0.7 m was found for Method #3.
Table 6.
Summarized detection results per method: RMS of selected indicators for all plots.
Table 6.
Summarized detection results per method: RMS of selected indicators for all plots.
| ID | Method | RMSextr. (%) Extraction Rate | RMSass. (%) Matching Rate | RMSCom (%) Commission Rate | RMSOm (%) Omission Rate | RMSH (m) Height Accuracy | RMSV (m) Planar Accuracy |
|---|
| 1 | LM + Filtering | 51 | 45 | 9 | 59 | 1.6 | 0.9 |
| 2 | LM + Region Growing | 57 | 43 | 20 | 61 | 1.8 | 1.2 |
| 3 | LM + Multi CHM | 101 | 46 | 61 | 57 | 1.7 | 0.7 |
| 4 | LM + Watershed | 86 | 49 | 49 | 55 | 1.6 | 1.1 |
| 5 | Segment. + Clustering | 139 | 53 | 95 | 51 | 1.7 | 1.0 |
| 6 | LM 3 × 3 | 154 | 54 | 113 | 51 | 1.6 | 0.9 |
| 7 | LM 5 × 5 | 52 | 41 | 16 | 63 | 1.8 | 1.1 |
| 8 | Polyn. Fitting + Watersh. | 54 | 44 | 13 | 59 | 1.8 | 1.1 |
Table 7 shows the matching results (
RMSass values) in different height layers. For the layers 2–5 m and 5–10 m, Method #5 shows the best performance with values of 15% and 17%, respectively, while all other methods detected only half or even a quarter of the trees. For the layer from 10 to 15 m, the clear lead of Method #5 gets lost as Methods #3 and #6 show comparable values. For the uppermost two layers, the performance difference between the different methods is reduced. In the uppermost layer greater than 20 m,
RMSass values from 66% to 82% are found.
Table 7.
Root mean square of matching rate per method in different heights.
Table 7.
Root mean square of matching rate per method in different heights.
| ID | Method | RMSass. 2–5 m | RMSass. 5–10 m | RMSass. 10–15 m | RMSass. 15–20 m | RMSass. > 20 m |
|---|
| 1 | LM + Filtering | 0% | 3% | 16% | 35% | 72% |
| 2 | LM + Region Growing | 0% | 5% | 15% | 30% | 72% |
| 3 | LM + Multi CHM | 0% | 3% | 32% | 46% | 68% |
| 4 | LM + Watershed | 4% | 7% | 20% | 36% | 76% |
| 5 | Segment + Clustering | 15% | 17% | 32% | 45% | 76% |
| 6 | LM 3 × 3 | 4% | 6% | 28% | 44% | 82% |
| 7 | LM 5 × 5 | 2% | 4% | 14% | 24% | 66% |
| 8 | Polyn. Fitting + Watersh | 2% | 9% | 16% | 40% | 73% |
4.3. Matching Results by Forest Type
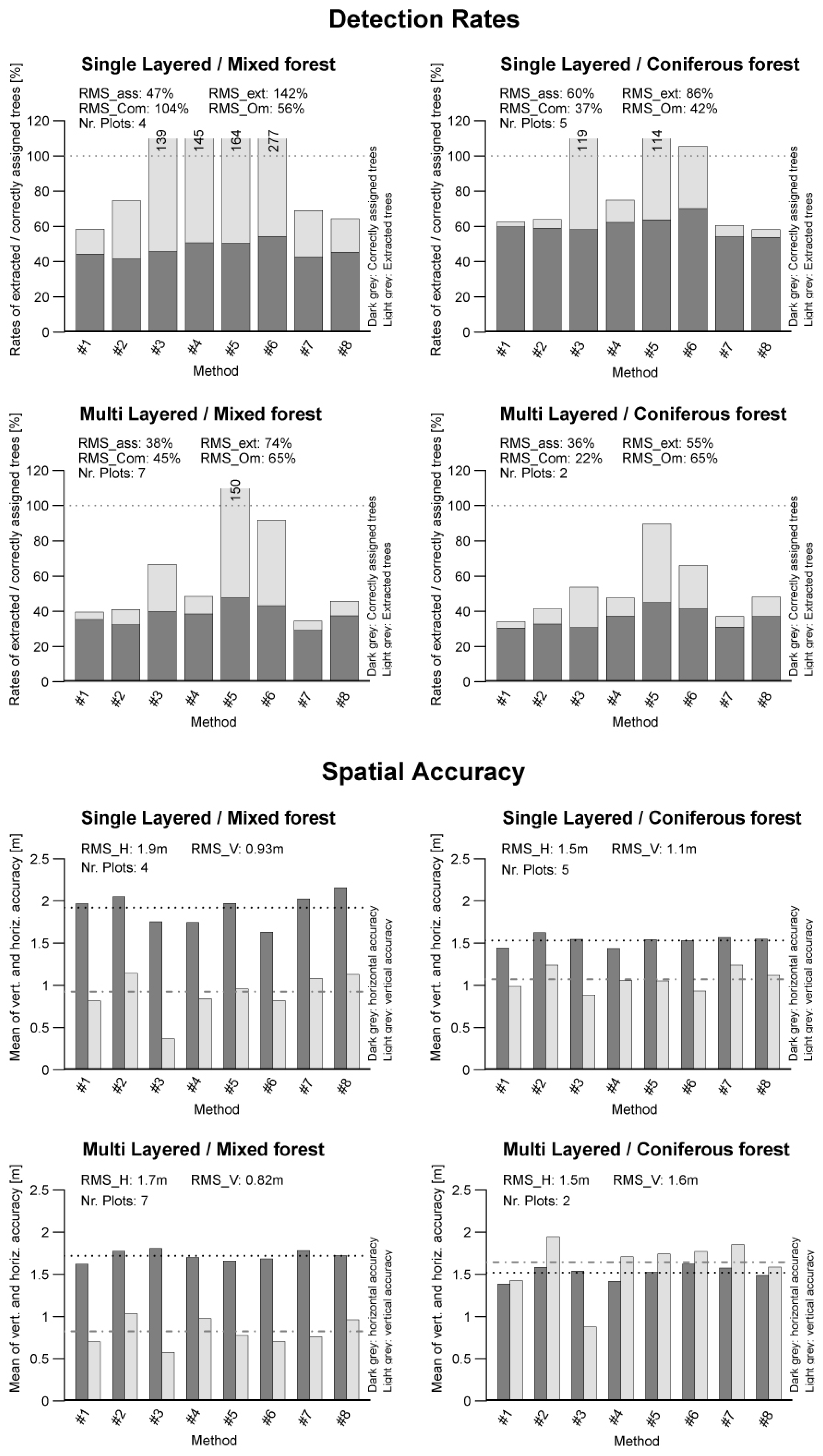
The detailed matching results by forest type indicate how well the different methods performed for different forest types. A graphical preparation of the matching results sorted to forest type is presented in
Figure 6. In
Table 8, the statistical parameters are summarized.
The highest extraction rate (RMSextr) of 142% was found for single-layered mixed forests, while the lowest rate of 55% was found for multi-layered coniferous forests (ML/C).
For the matching rates, the highest RMSass rate of 86% was found for single-layered coniferous forests. The lowest matching rate (47%) was found for single-layered mixed forests.
Figure 6.
Bar graphs of detection rates and accuracies of the different forest types.
Figure 6.
Bar graphs of detection rates and accuracies of the different forest types.
The highest commission rate (RMSCom) of 104% was found for single-layered mixed forests. The lowest RMSCom rate was found for multi-layered coniferous forests with 22%.
The highest omission rate (RMSOm) was found for both types of multi-layered forests, with a value of 65%. The lowest rate was found for single-layered coniferous forests with a value of 37%.
In the spatial accuracy section, the best positional accuracy with a RMSH of 1.5 m was obtained for coniferous forests. The best height accuracy with a RMSV value of 0.8 m was found for multi-layered mixed forests.
Table 8.
Summarized matching results by forest type—statistical parameters. Forest type: single or multi-layered (SL or ML)/mixed or coniferous (M/C).
Table 8.
Summarized matching results by forest type—statistical parameters. Forest type: single or multi-layered (SL or ML)/mixed or coniferous (M/C).
| Type | Nr. Plots | RMSextr. | RMSass. | RMSCom | RMSOm | RMSH | RMSV |
|---|
| SL/M | 4 | 142% | 47% | 104% | 56% | 1.9 m | 0.9 m |
| SL/C | 5 | 86% | 60% | 37% | 42% | 1.5 m | 1.1 m |
| ML/M | 7 | 74% | 38% | 45% | 65% | 1.7 m | 0.8 m |
| ML/C | 2 | 55% | 35% | 22% | 65% | 1.5 m | 1.6 m |
4.4. Overall Performance
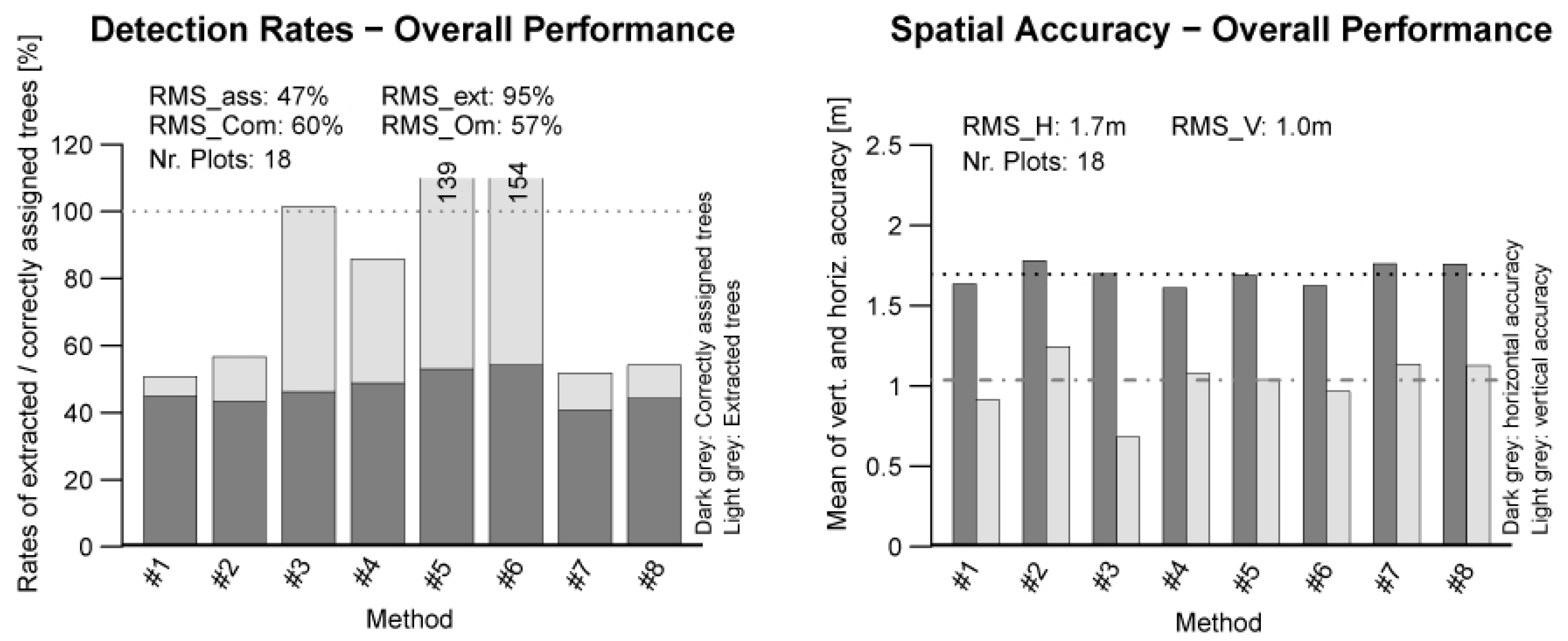
In this section, the overall performance of the matching results of all eight methods is put together. A graphical preparation of the result is presented in
Figure 7. The overall matching rate
RMSass shows a value of 47%. This means that statistically 47% of all available Reference trees could be successfully matched. For the extraction rate
RMSext, a value of 95% was found. The commission error and omission error show values of 60% and 57%, respectively.
Figure 7.
Overall performance of the tested methods.
Figure 7.
Overall performance of the tested methods.
5. Discussion
5.1. Input Data
For some study areas, the time gap between the ALS flight and the field survey is quite important. In the case of a field survey conducted after the ALS flight, the following errors can be expected:
- -
false omission errors due to tree growth in diameter (small trees reaching the caliper threshold between the ALS and the field surveys);
- -
false commission errors due to tree removal;
- -
false commission errors combined with false omission errors due to tree growth in height, which exceeds the matching threshold.
The opposite errors can be expected when the ALS flight is made afterwards. The time gap is two years in Montafon and Tyrol and six years in Berner Jura. It is one year or less in the other study areas. In mountain areas, tree growth is quite slow so that this factor has a limited impact on the matching process. Indeed the height growth of dominant trees during two years is likely to be lower than the vertical accuracy, which is already handled by the matching process. Besides, the proportion of trees reaching the caliper threshold in between the ALS and field survey is very low, except for young, dense stands. In all plots, the mean diameter exceeds the diameter threshold by more than 10 cm. Unless the diameter distribution is bimodal, the proportion of trees with a diameter close to the threshold is small. In Berner Jura, the forest is a dense, mature stand with no understory, so that the caliper threshold and height growth are not an issue. Regarding tree harvesting or mortality, no changes were reported by the partners who provided the data.
The difference in caliper threshold might also influence the matching results. The smallest trees represent a minor proportion of basal area but a major proportion of omission errors. Foresters usually set the caliper threshold by taking into consideration the inventory objective, the forest structure, and the required field effort. In this benchmark, the caliper thresholds were not a posteriori set to the highest value (12 cm in Berner Jura) because this would not be suitable to describe some young, dense plots. When comparing the detection results at the forest type level, it should nevertheless be taken into consideration.
Accurate georeferencing of the input data in a pre-processing step is a prerequisite for correctly comparing remotely sensed data with FI ground truth data. Three main error sources exist when comparing these data. These error sources are (
A) positional errors due to inaccurate measurements (georeferencing); (
B) irregularities of the local forest (
i.e., tilted trees, complex crowns); and (
C) errors originating from the detection algorithm. To minimize error source
A, forest inventory data is ideally acquired by using a survey grade GNSS system or a total station. A positional check by manually co-registering the inventory data to the remote sensing data in a post-processing step is necessary in most cases. Automated co-registration methods [
44,
45,
46] can help to support the co-registration process. The reported performance of automated methods varies from 68% up to 92% and depends mainly on the input data and the variability of the forest stands [
45]. In the presented study, error
A was minimized by using manually co-registered datasets, with an estimated planar accuracy of ±2.0 m. and ±1.0 m for the vertical accuracy. The errors
B and
C are handled within the matching procedure by allowing flexible matching connections with a search radius depending on tree heights. The used FI data are heterogeneous due to different acquisition guidelines and methods. Therefore the data can be considered as imperfect compared to a local standardized FI. However, imperfect data should not have disadvantaged one of the detection methods as all participants faced the same conditions.
The presented matching procedure enables interpreter-independent and reproducible results in a short amount of time. The automatic matching took a few minutes while the manual interpretation within the validation process of the subset took several hours. The Overall Accuracy of 97% indicates that the matching procedure worked sufficiently for the presented dataset.
5.2. Matching Results
In general, the vertical structure of the forest (vertical distribution of tree heights) seems to have a major impact on the detection/matching results of the different methods. This finding is also reported by Vauhkonen
et al. [
26]. The more vertically distributed the trees are, the lower the matching rates are. The matching rates in different height layers indicate that especially in the lower height layers more advanced methods like point cloud-driven 3D clustering (Method #5) can detect more trees than methods that rely on local maximum detection based on a rasterized canopy height model. This finding was also reported in the benchmark study of Kaartinen
et al. [
24]. Method #5 achieved the highest number of small trees extracted.
Matching results combining a high matching rate with a low commission rate indicate a good matching result. The best detection result was obtained within the study area of Berner Jura, which consists of an old forest stand with high trees and no understory vegetation. The lowest detection result was obtained within plot #5 in Pellizzano, which consists of a multi-layered forest with a high amount of trees in different height layers. Only 15% of trees smaller than 10 m could be correctly extracted by the best performing method. In a summarized view, the results show that multi-layered forests are challenging for all tested methods. Maybe new methods as e.g., presented in Vega
et al. [
47] or Kandare
et al. [
48] will help to improve this issue in the future. Vega
et al. [
47] reported an overall performance of 75% for mixed multi-layered mountainous forest in the French Alps, with a 58% detection rate in the dominated tree layer.
Regarding the detection of small trees, it can be assumed that small trees in subdominant layers theoretically get mapped more efficiently at a higher ALS point density. This can be linked to a potentially higher canopy penetration rate. Kaartinen and Hyyppä [
25] and Reitberger
et al. [
49] conclude that the laser point density has less impact on the individual tree detection. In contrast Wallace, Lucieer, and Watson [
43] conclude that high point densities are more significant for single tree detection than the method used. Wallace
et al. studied a very young, planted stand of Eucalyptus trees using high-resolution UAV Lidar data, which is not comparable to the dataset of the Alpine Space. Therefore, it is assumed that the different point densities given in the presented study should not significantly influence the detection results. Within the pilot area Pellizzano, a maximum ALS point density of 121 pts/m
2 is given and the inventory data show a high vertical distribution of trees. Even at this high point density, only the worst detection result of all tested areas could be obtained. All study areas have point densities higher than 10/m
2, except Berner Jura and Tyrol. Both of these have plots of single-layered, mature stands so that the smaller point density is probably not a limiting factor for tree detection. However, investigating the effect of different point density on the detection results was not in the scope of this study.
5.3. Matching Results per Method
The best ratio between a high matching rate and a low commission rate was found for Method #1, which consists of a local maximum search in a canopy height model using a moving window approach. The fact that the algorithm parameters were automatically optimized for this purpose on an independent dataset seems to be an advantage compared to methods where parameters are set according to the user appreciation. In the lower height layers up to 10 m tree height, only up to 3% of the extracted trees could be correctly matched. Since the method relies on a rasterized canopy height model and filtering of trees smaller than 7.5 m, this rather low value was expected. For the spatial accuracy, the obtained values for the location are comparable to the results of the other tested methods. For the height component, the second best value was achieved with a RMS value of 0.9 m, which is comparable to the values obtained for the best models in the benchmark of Kaartinen
et al. [
24].
Method #2 shows comparable matching rates to Method #1, but with a commission rate twice as high. In the lower height layers up to 10 m tree height, only up to 5% of the extracted trees could be correctly matched. In contrast to Method #1, trees down to a height of 2.5 m could be detected, which might lead to the slightly higher percentage value. However, the method is based on rasterized ALS data and therefore the rather low matching rate in the lower height layers was expected. The spatial accuracy of the method is comparable to the results of Method #1.
High commission rates in the results of Methods #3, #5, and #6 indicate that these methods tend to over-perform, which means they show high commission rates. Methods #3 and #5 are based on 3D operations in multiple canopy height models or directly in the 3D point cloud, while Method #6 is based on local maximum detection in a canopy height model, which uses a small local maxima kernel (3 × 3 pixels) and no preliminary smoothing. The small kernel tends to find local irregularities in the canopy height model and since these irregularities can be located even inside a single tree crown, the small kernel tends to detect too many potential trees. The result is the highest commission rate within this benchmark. The alternative Method #7 shows better results in terms of commission rate as the rate of the 5 × 5 kernel is seven times lower than the one from the 3 × 3 kernel. Methods #3 and #5 seem to be too sensitive in the detection process and the 3D clustering especially tends to detect multiple trees within a given single tree crown. Beside the fact of high commission rates for these methods, Method #5 shows up to 17% of correctly matched trees in the lower layers up to 10 m tree height. Compared to other methods, this is clearly the best result. Method #3 shows the best height accuracy with a RMS value of 0.7 m. Both Method #7 and #3 show the lowest matching rates in the uppermost height layer with trees taller than 20 m. In total, Method #7 shows comparable results to results of Method #1 and is counted as one of the best results within this benchmark.
Method #4 shows a relatively high matching rate of 49% (RMS) but in contrast the commission rate is high. This indicates that the method found many trees that could not be linked to the reference data. In the lower layers below 10 m tree height, up to 7% (RMS) of the available reference trees were correctly matched, while up to 40% (RMS) of the detected trees are sorted to commission errors. The rather low matching value can be explained by the methodology. It uses a smoothed rasterized canopy model, which follows the upper canopy and therefore the detection rate of smaller trees in subdominant layers is believed to be low. In the highest height layer with trees taller than 20 m, a matching rate of 76% (RMS) could be obtained, which is one of the highest values in this benchmark for this height class. The spatial accuracy of the method is comparable to that from Method #1. In general, the spatial accuracy of all methods does not differ very much.
Method #8 shows a high matching rate of 44% paired with a low commission rate of 13%. Based on these values, the results of Method #8 are close to the results of Method #1 and among the best within this benchmark. In the lower levels with tree heights up to 10 m, the method obtained a matching rate of up to 9%, which counts, together with Method #4 and #5, as the best obtained results. In general, a 9% matching rate in lower height intervals is, compared to the other methods, a good result, but from an overall perspective such a low detection rate is unsatisfying. Like other methods that rely on maximum search in a rasterized canopy height model of the uppermost canopy, the low rate can be explained by the methodology.
5.4. Matching Results per Forest Type
The class of single-layered coniferous forests shows the best results of all tested classes as a high matching rate of 60% combined with a low commission rate of 37% is given. This result seems feasible as coniferous trees have, in most cases, a clearly defined tree crown shape. This means that the tree top appears as a clear peak in the canopy height model. Since most of the tested methods within this benchmark rely on local maximum detection on the canopy height model, the good result for single-layered coniferous forests was expected. The best performing methods for this forest type were Methods #1, #3, and #4.
The class of multi-layered coniferous forest as well as the class of multi-layered mixed forest show the lowest matching rates in this benchmark. Only a matching rate of up to 38% (RMS) could be obtained. The commission rate of the multi-layered mixed forest is twice as high as the rate found for the multi-layered coniferous forest, which shows a value of 22% RMS. The low matching rate can be explained by the methodology of the tested methods. Trees in lower layers are challenging for all tested methods. The higher commission rate for the multi-layered mixed forest can be linked to more complex crowns for deciduous trees, which results in over performing detection results. The best results for the multi-layered coniferous forest were obtained by Methods #2, #4, and #10. For the multi-layered deciduous forest, the best results were obtained by Methods #1, #4, and #8.
The single-layered mixed forest shows a matching rate of 47%, which is the second best matching rate for the classified results. In contrast, a very high commission rate of 104% is given. The high rate can be explained by the fact that deciduous tree crowns tend to be more complex than coniferous ones. Single tree crowns may consist of multiple local peaks in the canopy height model, which may be correctly detected as local maximum but do not represent the tree stem. The best performing methods for this forest type are Methods #1 and #8.
In general, it can be seen that the single-layered forest types show better results than the multi-layered ones. This was expected as forest structure has a significant influence on the results. Between the single-layered coniferous and mixed class, a considerable difference in the matching rates as well as commission rates is noticeable. This confirms the findings of Vauhkonen
et al. [
26], who tested the performance within coniferous and deciduous plots in Germany
. 5.6. Perspectives
The trade-off between omission and commission errors turns out to be a critical point regarding tree detection. Some detection methods are probably intrinsically more efficient because they are able to extract more relevant information from the point cloud, as is expected from point cloud-based methods. However, as exemplified by Methods #6 and #7, which differ only by the LM kernel size, it turns out that the choice of algorithm parameters such as raster resolution, kernel size, and horizontal or vertical exclusion thresholds may have a major impact on detection results. From the image processing point of view, extracting trees is basically separating the signal from the noise. Depending on the forest structure (and on the caliper threshold, which defines the tree object) and on the acquisition parameters, the filters required for tree extraction have to be chosen or at least tuned specifically. In order to improve the detection algorithm available for forest practitioners, it seems important to A) have datasets that allow us to test the robustness of algorithms on a wide range of forest structures, and B) design algorithms able to optimize their setting, either based on internal (Lidar itself) or external (tree allometry) data. For the comparison of results, an automated matching procedure like that presented in this paper is of high relevance. Moreover, the choice of a trade-off criterion between the omission and commission errors would make comparisons easier, but it has to be application-oriented.
6. Conclusions
This study demonstrated that Forest Inventory data can be automatically matched to single tree detection results obtained from airborne laser scanning data. Furthermore, eight single tree detection methods were tested based on a unique dataset of different forest types originating from eight areas within the Alpine Space. The proposed method for automatically matching forest inventory data and remotely sensed data worked efficiently. In general, all tested methods achieve comparable results for the matching rates, but do differ for the extraction rates and omission/commission rates. The tree detection rates show a higher variation than the estimated tree heights. A method based on local maxima detection within a canopy height model using variable-sized moving windows is rated as the best performing algorithm. Complex multi-layered forests were challenging for all tested methods. A point cloud clustering-based method gained the best results for trees in subdominant layers, which is rated as an advantage over raster-based methods. The best detection results were obtained for single-layered coniferous forests.
Future studies should investigate the effect of different point densities on the detection results. Multiple datasets of the same area acquired with different flight parameters (
i.e., viewing angles, heights above ground, footprint size) would be necessary to perform this analysis robustly. Such datasets are rarely available. Automated absolute georeferencing between FI data and ALS data (co-registration) as well as an automated classification of FI plots in different forest types (
i.e., single-/multi-layered forests) based on the ALS data would help us to overcome the manual steps performed in the presented study. Finally, the performance of novel, point cloud-driven single tree detection methods [
47] should be tested on the unique dataset from the Alpine Space presented herein.