Evaluating the Ecological Integrity of Structural Stand Density Management Models Developed for Boreal Conifers
Abstract
:1. Introduction
SSDMMs and Their Evaluation
2. Experimental Section
| Input Parameter | Denotations and (or) Value |
|---|---|
| Stand-type | Natural-origin Stands (n., subscripted by N) |
| Natural Upland Black Spruce (PImUN) | |
| Natural Jack Pine (PNbN) | |
| Natural Black Spruce and Jack Pine Mixtures (PImPNbN) | |
| Natural Lowland Black Spruce (PImLN) | |
| Plantations (n., subscripted by M) | |
| Managed Upland Black Spruce (PImUM) | |
| Managed Jack Pine (PNbM) | |
| Site Index (SI) | SI ranging from 11 to 19 by 2 m intervals across all 6 stand-types. Note, Ontario-based stand-type-specific SI models were used. For the upland black spruce stand-types (PImUN and PImUM), the SI model developed by Carmean [22] was utilized. For the jack pine stand-types ( PNbN and PNbM), the SI model developed by Carmean [23] was employed. For the mixed black spruce and jack pine stand-type (PImPNbN), the SI models developed by Carmean [22,23] were used in combination. Lastly, for the lowland black spruce stand-types (PImLN), the SI model developed by Newton [24] was used. |
| Rotation Age (RA) | Varied by stand-type and SI. Specifically, for natural-origin stands (PImUN, PNbN, PImPNbN and PImLN): (1) if SI < 15 then RA ranged from 100 to 120 by 10 year intervals; or (2) if SI ≥ 15 then RA ranged from 80 to 100 by 10 year intervals. For plantations (PImM and PNbM): (1) if SI < 15 then RA ranged from 70 to 90 by 10 year intervals; or (2) if SI ≥ 15 then RA ranged from 50 to 70 by 10 year intervals. |
| Initial Density (NI) | Varied by stand-type. Specifically, for natural-origin stands (PImUN, PNbN, PImPNbN and PImLN), NI ranged from 3000 to 10,000 stems/ha by 1000 stems/ha intervals. For plantations (PImM and PNbM), NI ranged from 1500 to 3500 stems/ha by 500 stems/ha intervals. |
| Thinning | Varied by stand-type. |
| Treatments | Specifically, for natural-origin stands (PImUN, PNbN, PImPNbN and PImLN), a single PCT treatment was applied with the following conditions: |
| Time of Thinning (TA) = 10 years | |
| Thinning Type (TY) = PCT for Regimes 2 and 3 (TY =1) | |
| Thinning Response Model: varied by Regime. Specifically, the maximum response model was used in Regime 2 whereas the minimum response model was used in Regime 3. | |
| Thinning Removal: varied by the stand density existing at the time of thinning: residual target density post-PCT = 2000 to 3000 stems/ha. | |
| For plantations (PImM and PNbM), a single CT treatment was applied. | |
| TA = RA-25 for Regimes 2 and 3 | |
| TY: CT for Regimes 2 and 3 (TY = 2) | |
| Thinning Units: %BA | |
| Thinning Removal = 35% basal area | |
| Merchantable | Length of pulplog (m) = 2.59 |
| Specifications | Length of sawlog (m) = 5.03 |
| Minimum small-end inside-bark diameter for pulplogs (cm) = 10 | |
| Minimum small-end inside-bark diameter for sawlogs (cm) = 14 | |
| Minimum small-end inside-bark diameter for merchantable volume (cm) = 4 | |
| Operational | 0.01%/year |
| Adjustment Factor | |
| Genetic Worth | Plantations only. |
| Effects | Genetic worth (GW) and selection age (GA): (1) for black spruce plantations (PImM), GW was set at 10% and GA at 15 years; and (2) for jack pine plantations (PNbM), GW was set at 7% and GA at 20 years. |
| Genetic worth response model: (1) Regimes 1 (Control) and 2 utilized a Type 1 response model initiating from the specified selection age; and (2) Regime 3 utilized a Type 2 response model initiating at the time of planting. |
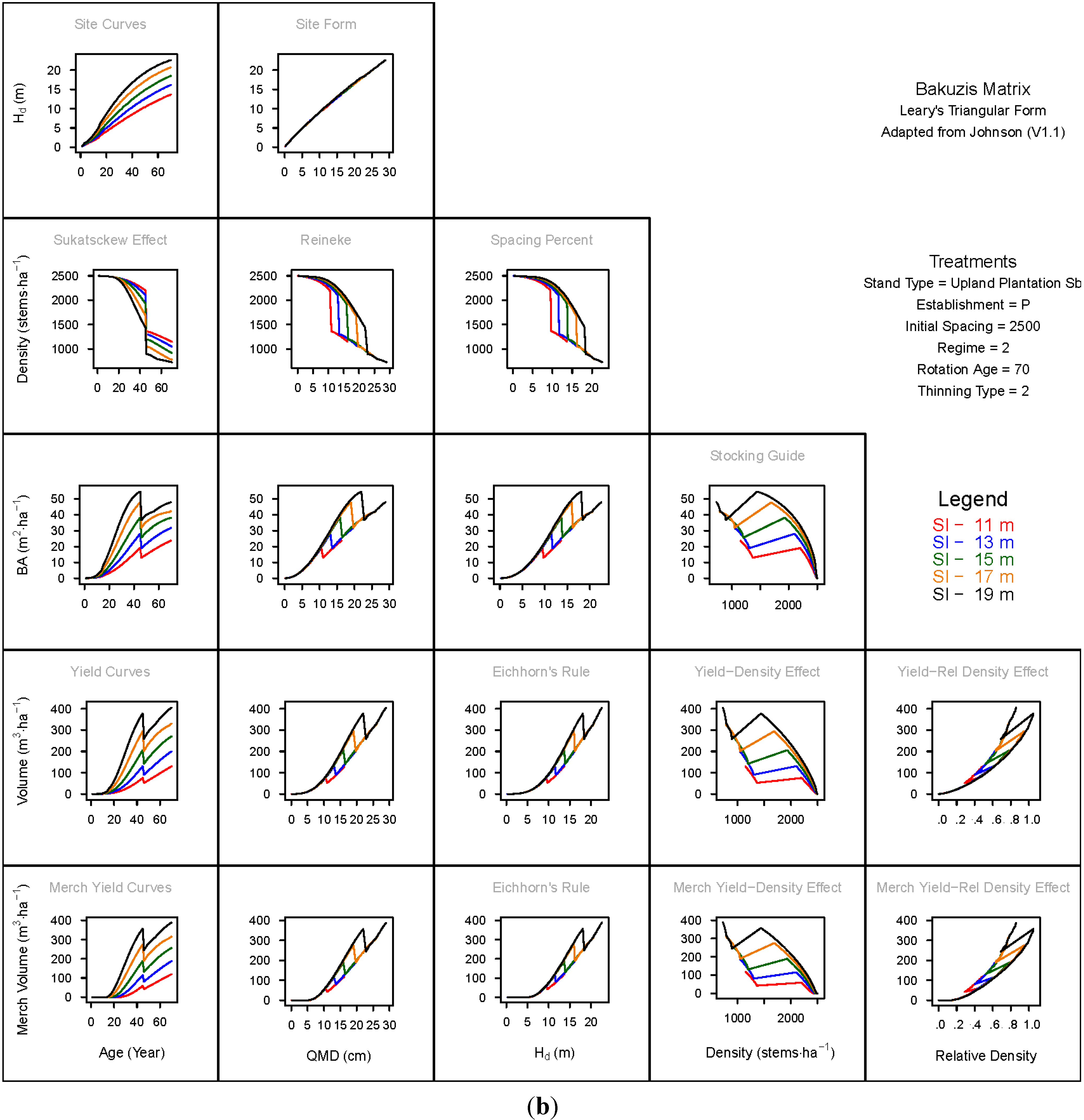
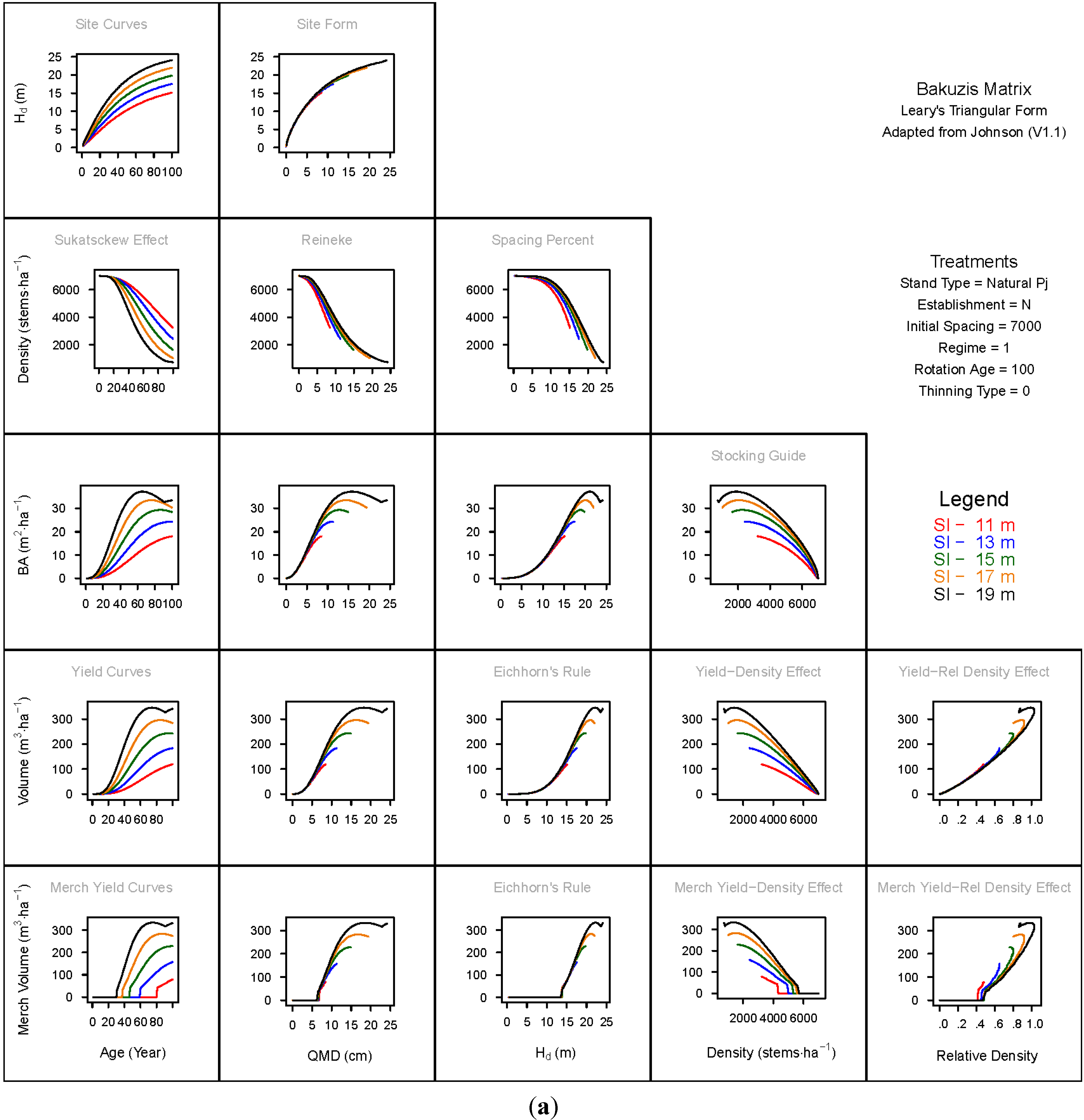
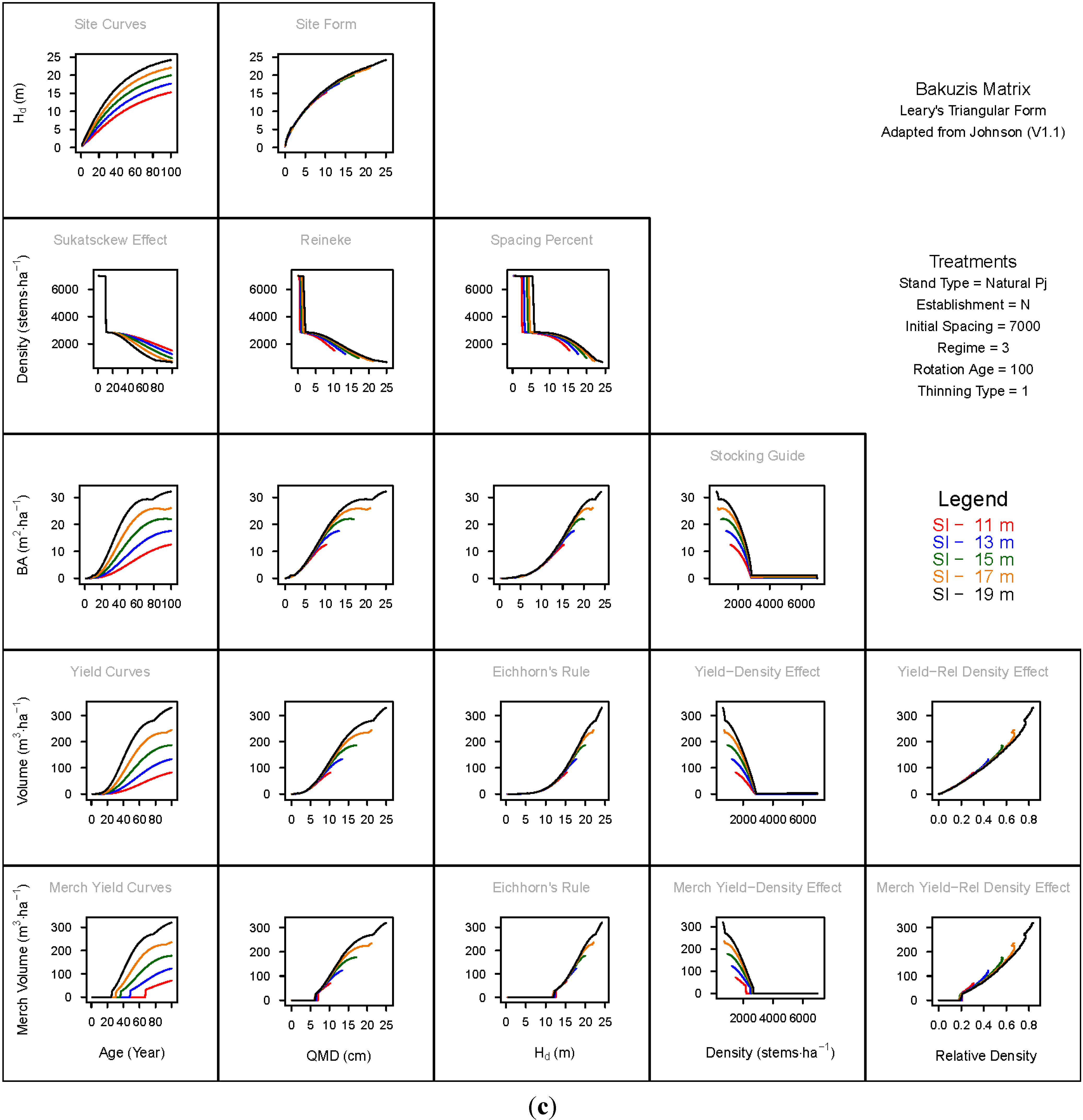
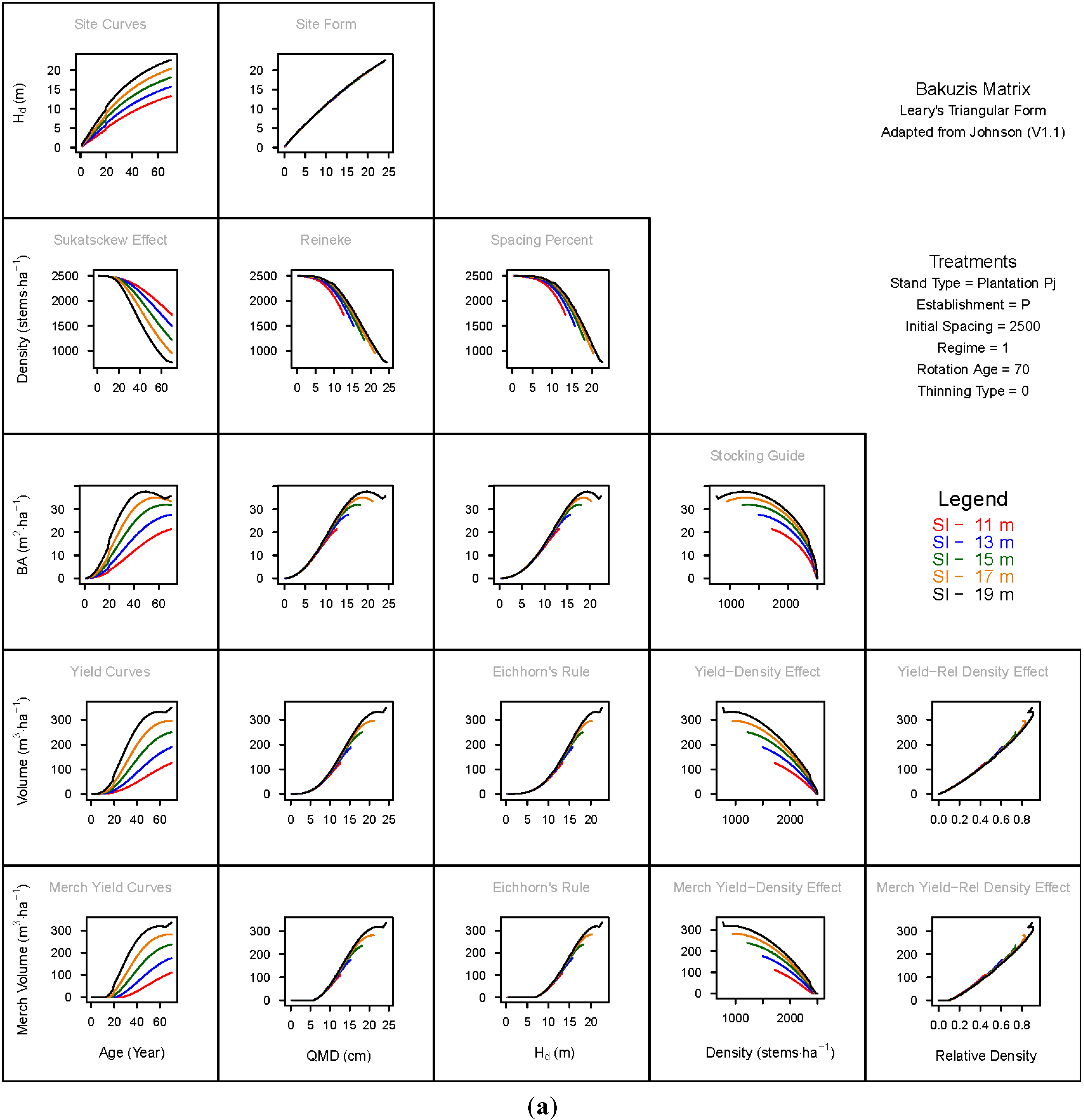
3. Results and Discussion
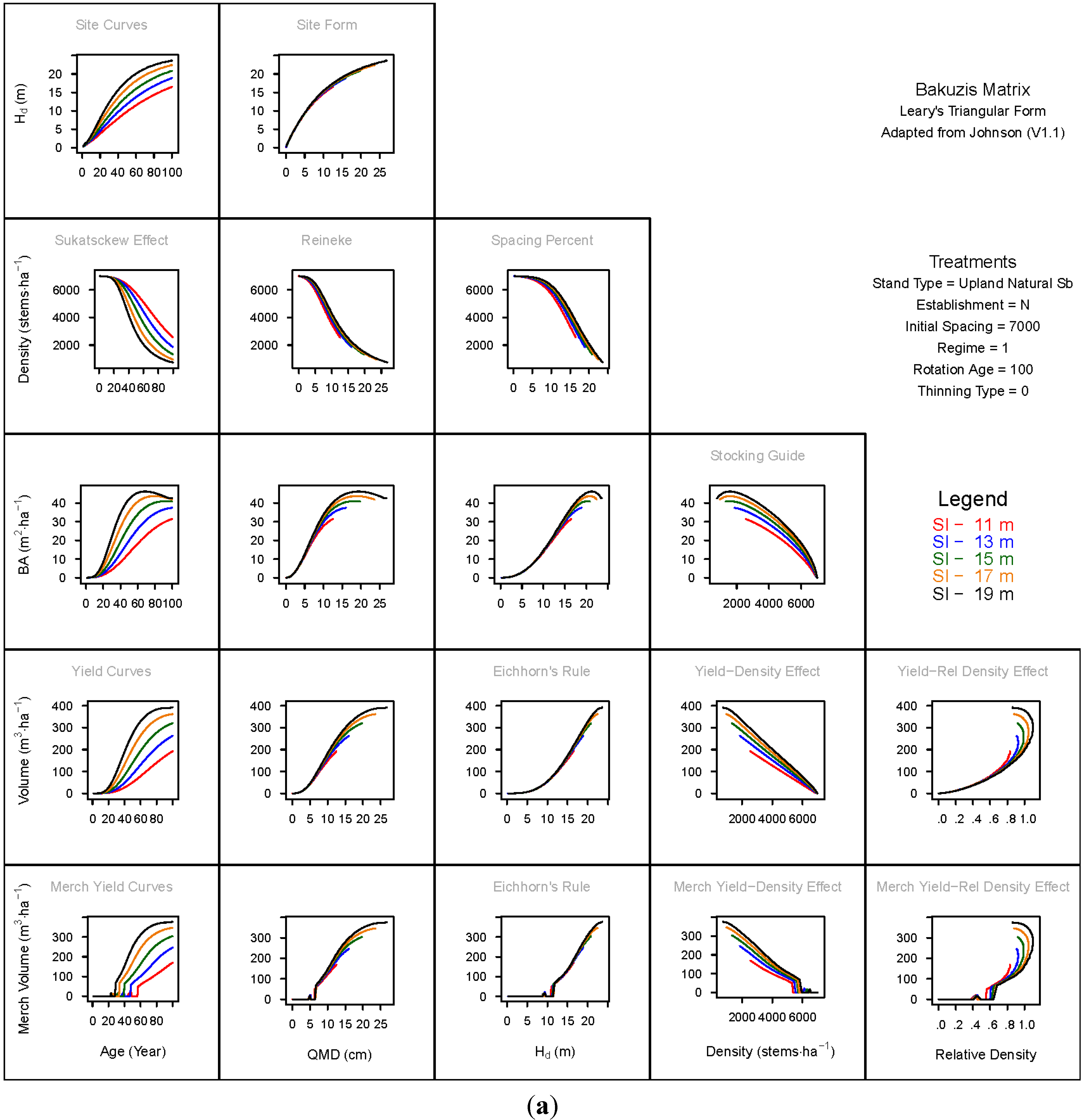
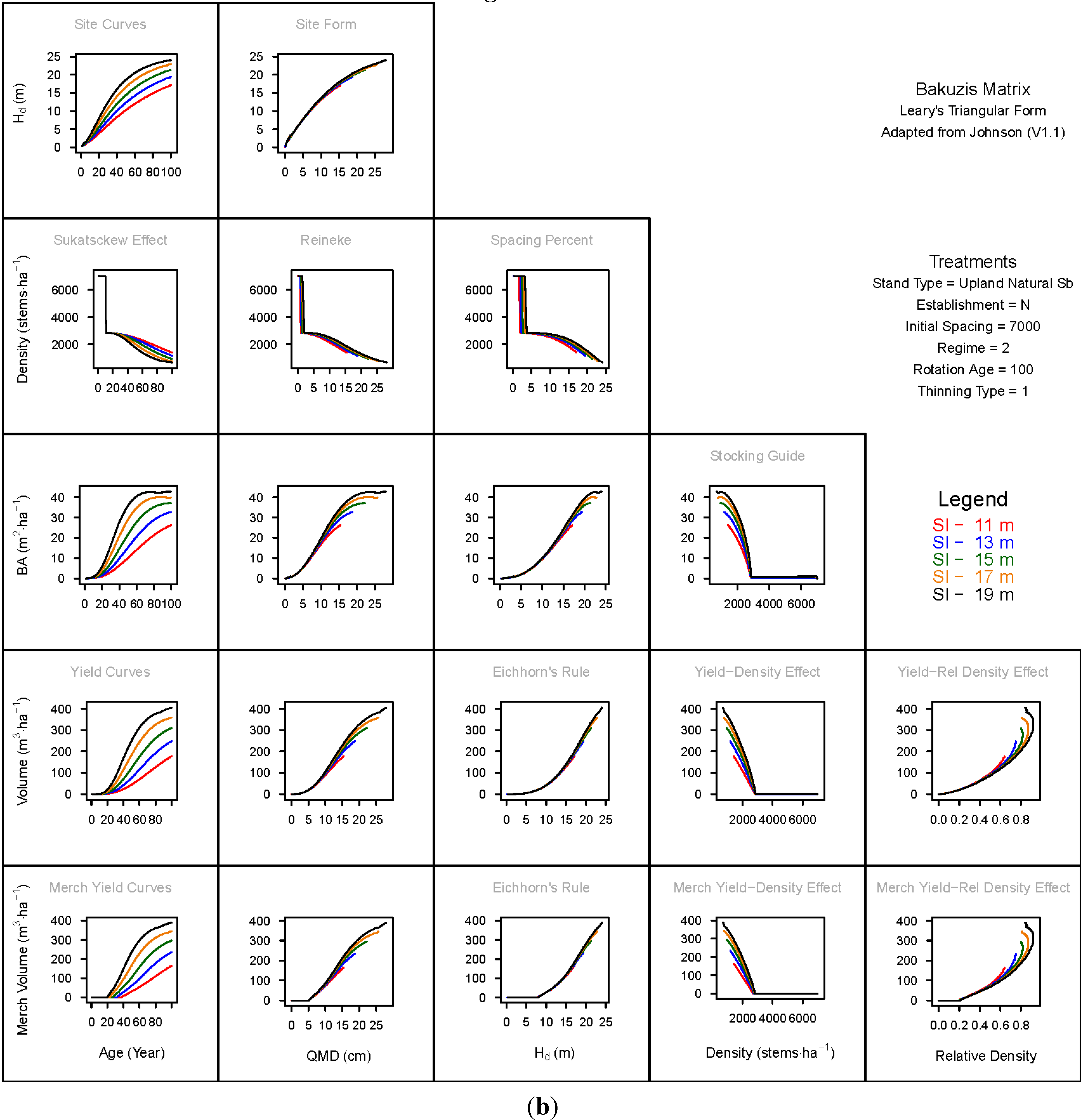
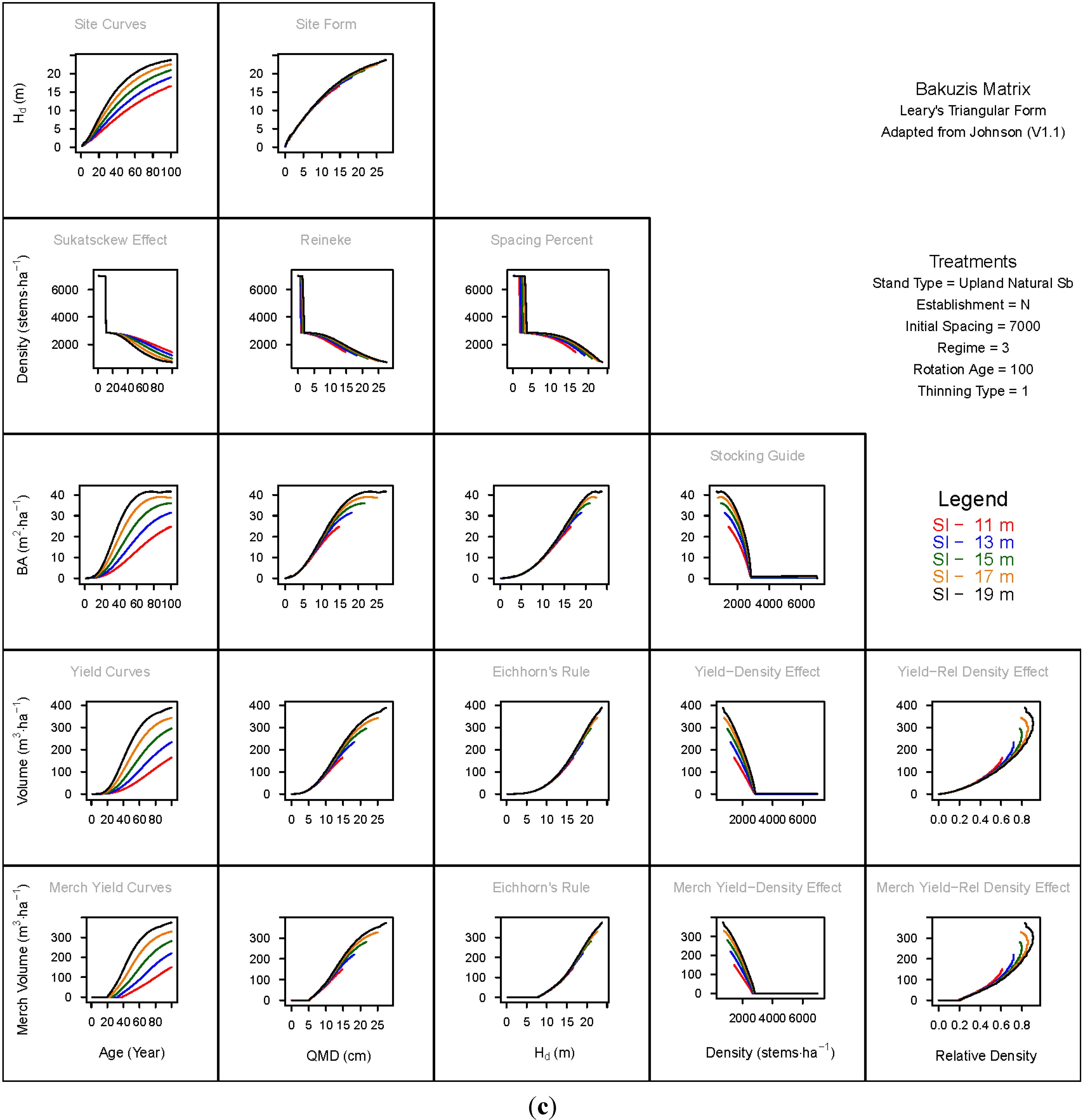
3.1. Principal Relationships Examined
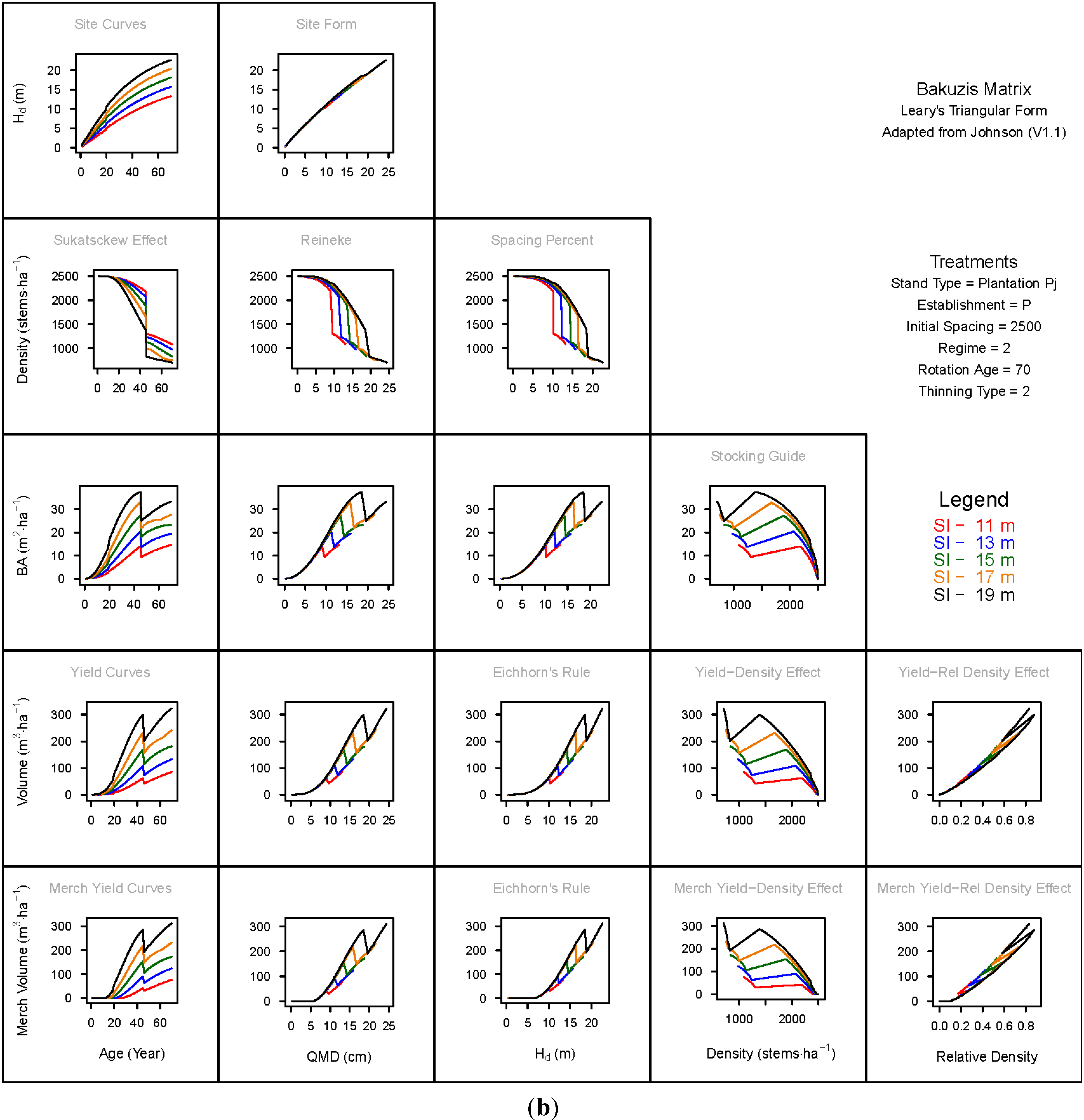
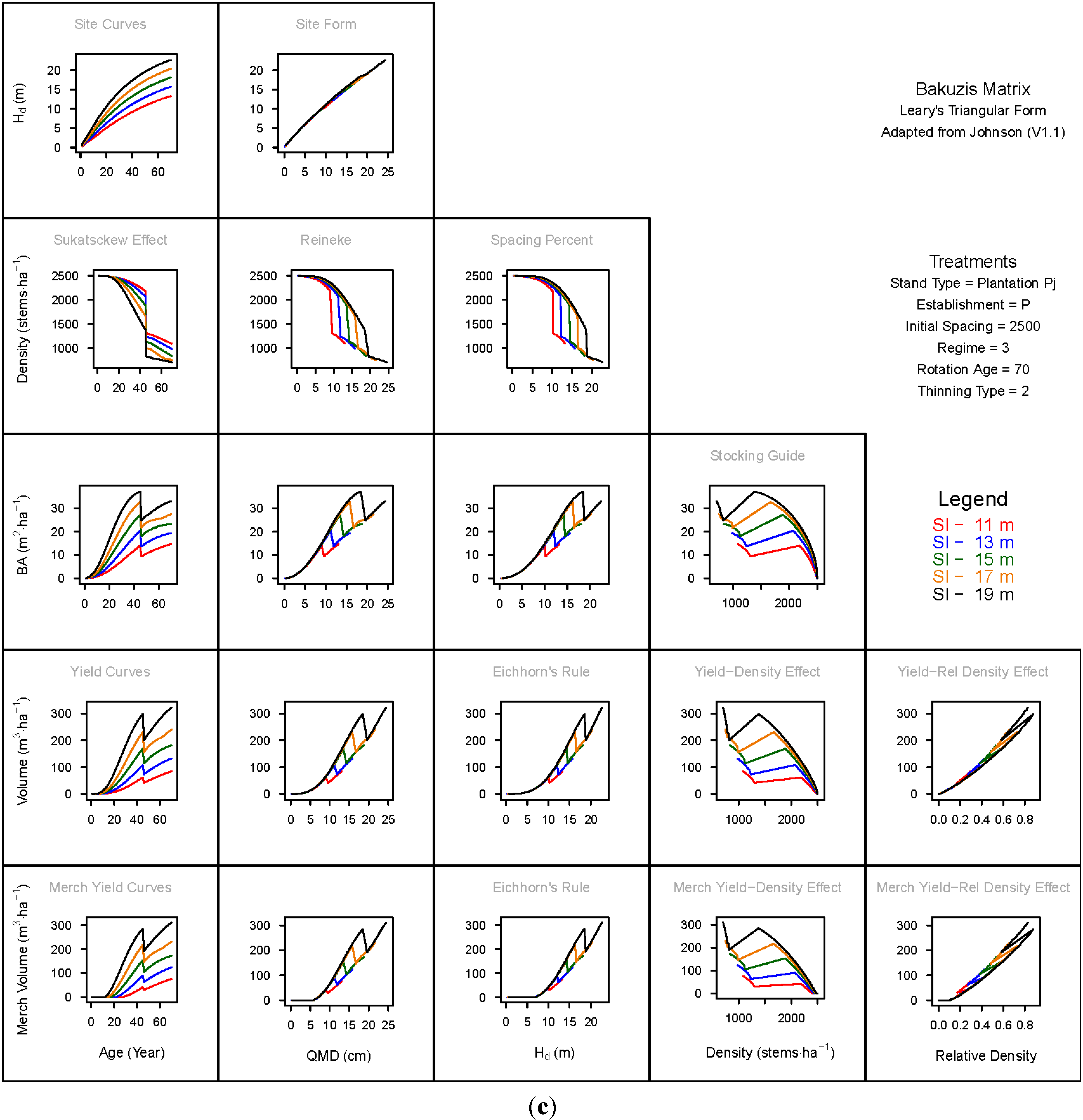
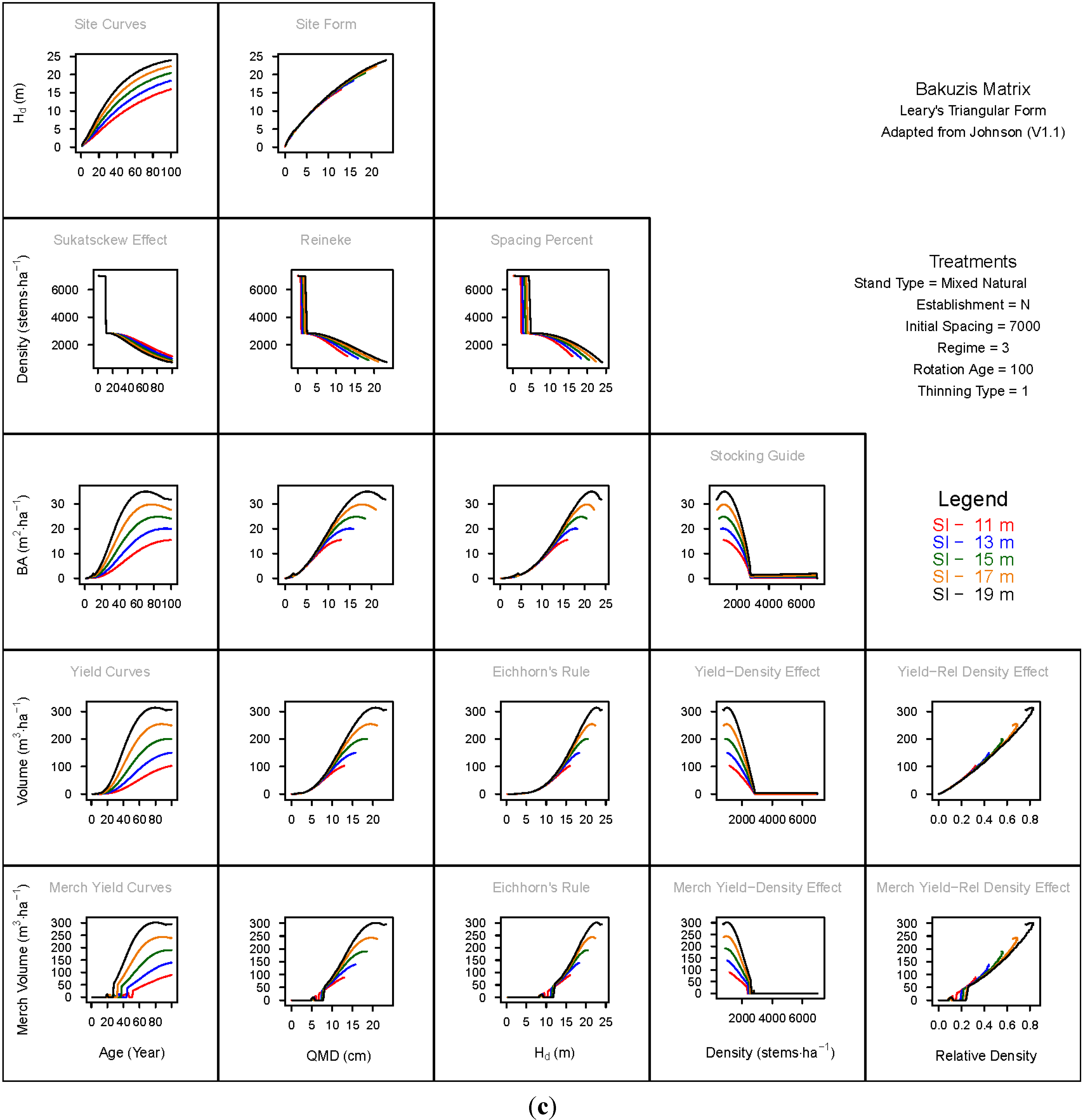
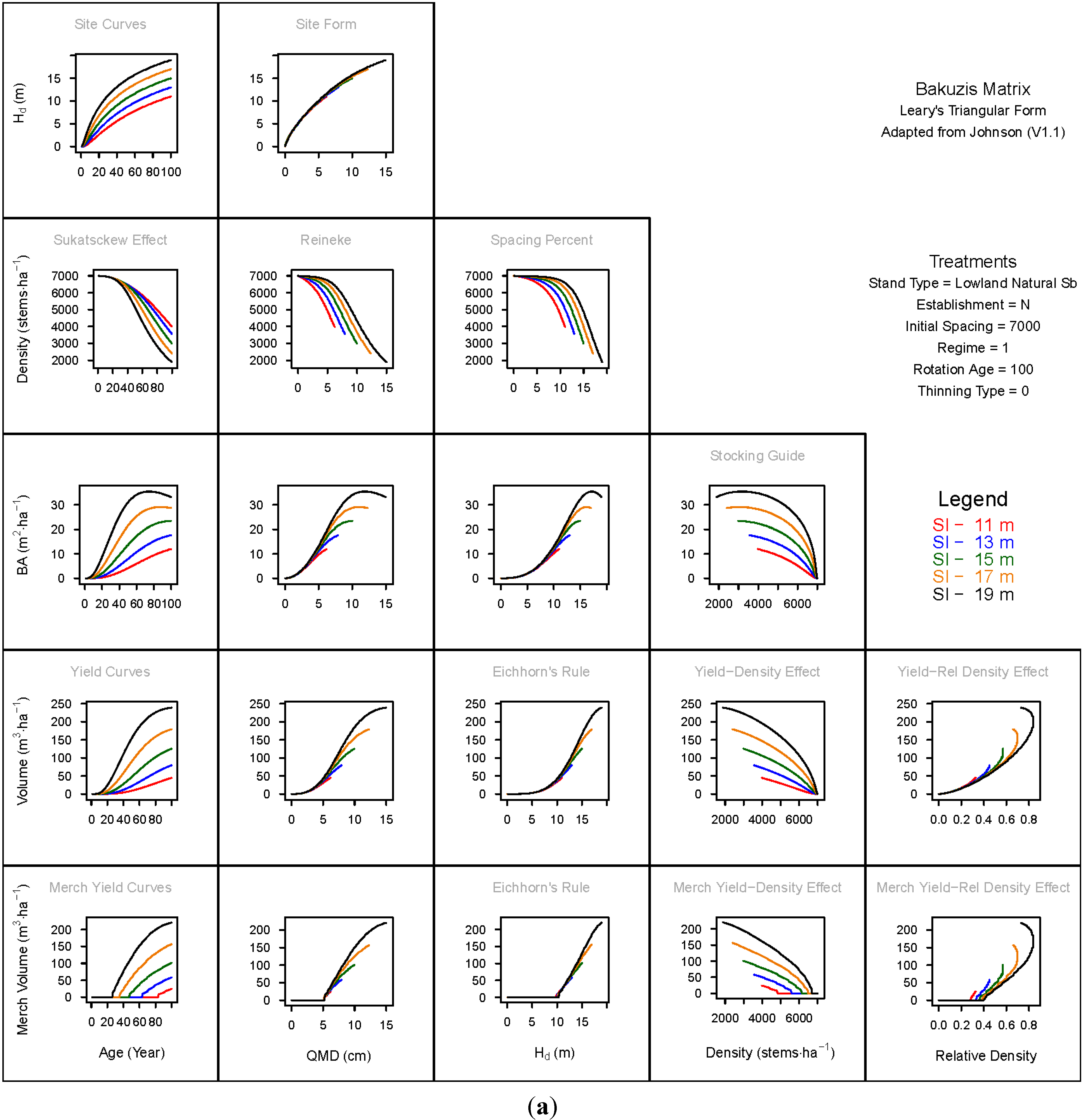
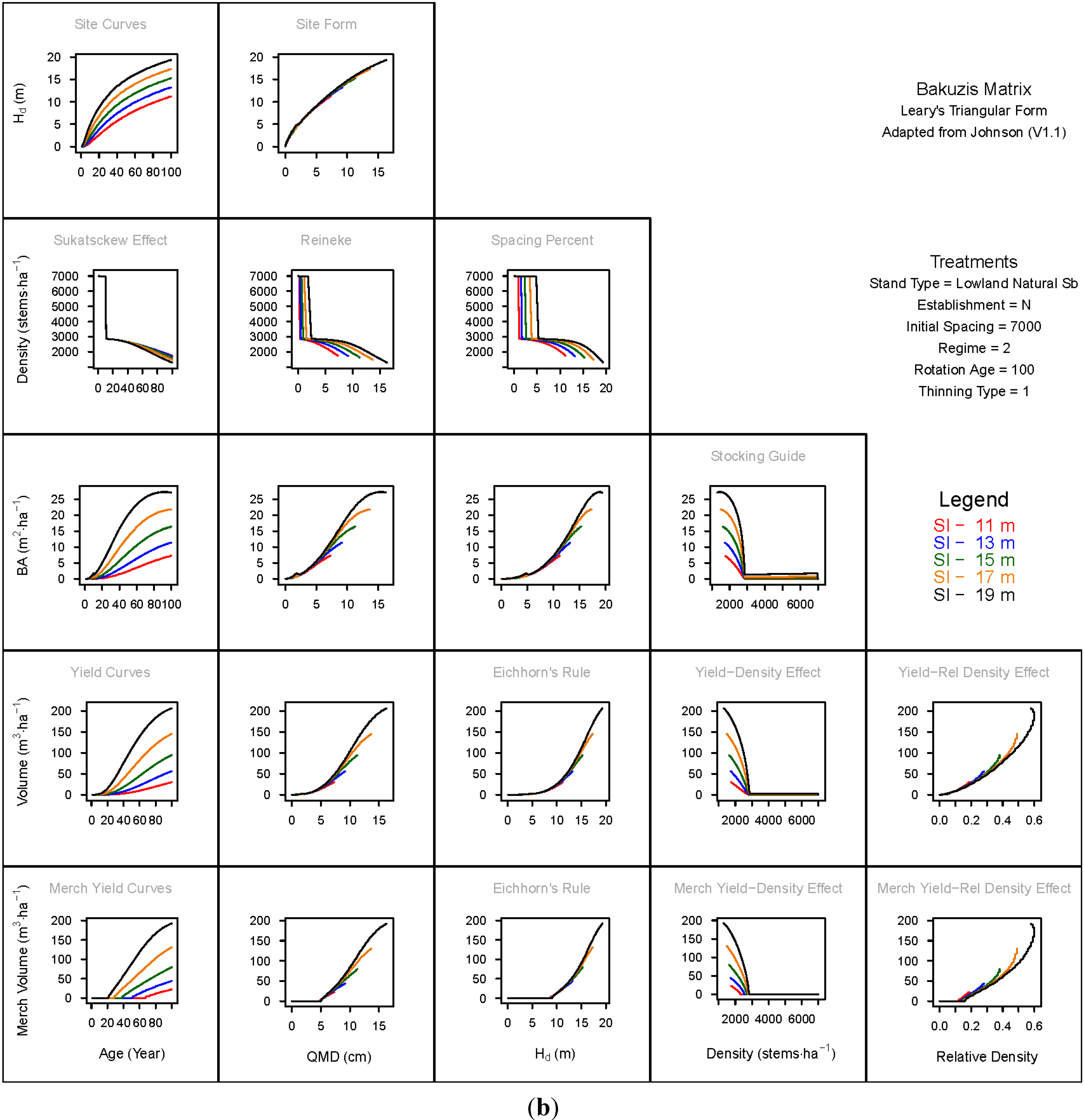
3.1.1. Mean Dominant Height–Age Developmental Patterns (1:1)
3.1.2. Site Form: Mean Dominant Height-Quadratic Mean Diameter Relationship (1:2)
3.1.3. Sukatsckew Effect: Density–Stand Age Relationship (2:1)
3.1.4. Reineke’s Stand Density Index: Density–Quadratic Mean Diameter Relationship (2:2)
3.1.5. Spacing Percent: Density–Mean Diameter Height Relationship (2:3)
3.1.6. Temporal Production Patterns: Basal Area (3:1), Total Volume (4:1) and Merchantable Volume (5:1)–Age
3.1.7. Yield Interrelationships: Basal Area (3:2), Total Volume (4:2) and Merchantable Volume (5:2)—Quadratic Mean Diameter
3.1.8. Eichhorn’s Rule: Basal Area (3:3), Total Volume (4:3) and Merchantable Volume (5:3)–Mean Dominant Height
3.1.9. Reciprocal Yield Effect Relationships: Basal Area (3:4), Total Volume (4:4) and Merchantable Volume (5:4)—Stand Density
3.1.10. Density-dependent Effects on Volumetric Production: Total Volume (4:5) and Merchantable Volume (5:5)–Relative Density Index.
3.2. Site-Dependent Occupancy Effects on Productivity
3.3. Ecological Integrity of SDMD-Type Models: A Broader Discussion
4. Conclusions
Acknowledgments
Appendix
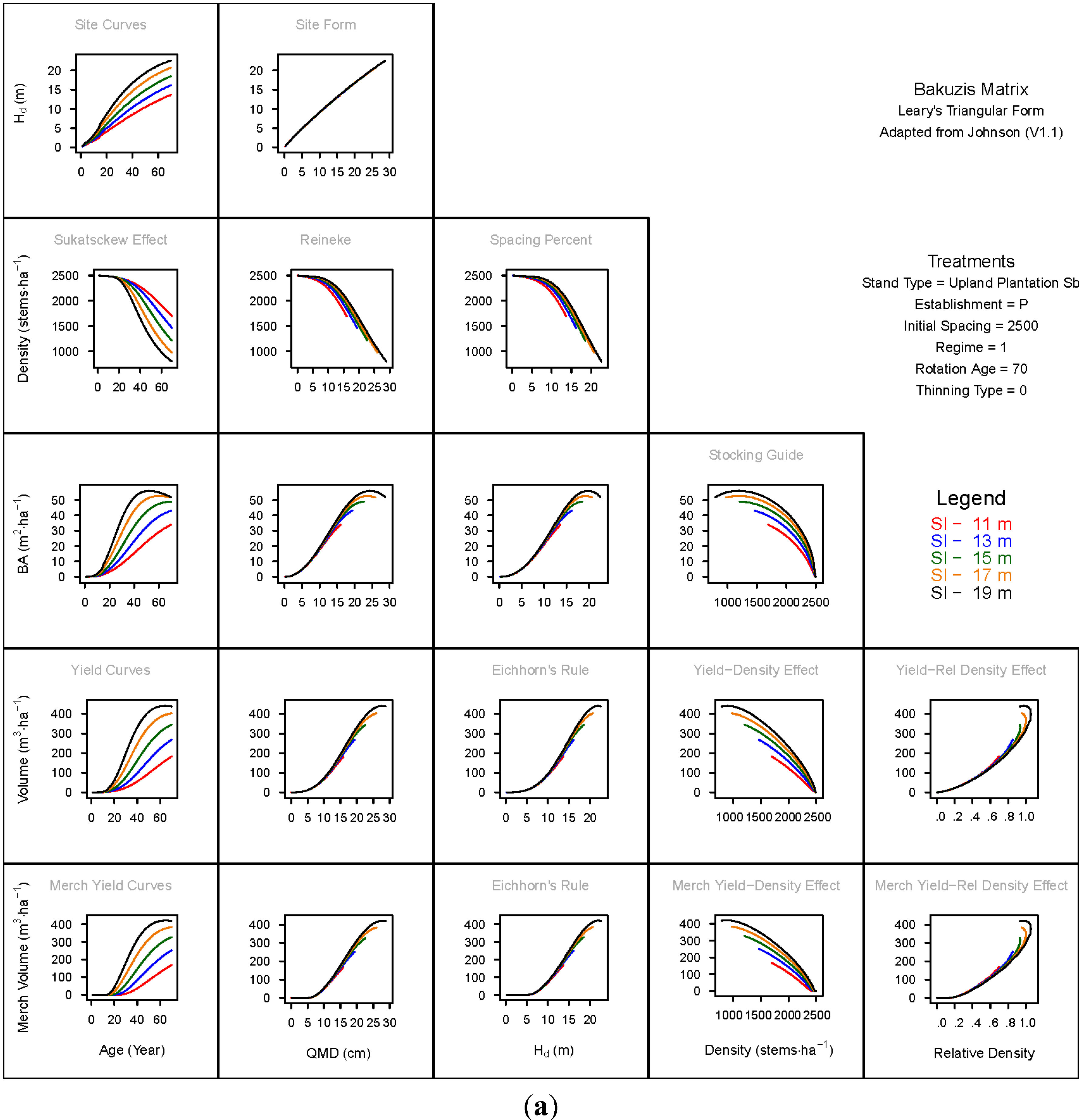





Conflicts of Interest
References
- Ando, T. Growth analysis on the natural stands of Japanese red pine (Pinus densiflora Sieb. et. Zucc.). II. Analysis of stand density and growth. Government of Japan. Bull. Govern. For. Exp. Stat. 1962, 147, 77. (In Japanese) [Google Scholar]
- Drew, T.J.; Flewelling, J.W. Stand density management: An alternative approach and its application to Douglas-fir plantations. For. Sci. 1979, 25, 518–532. [Google Scholar]
- Newton, P.F. Stand density management diagrams: Review of their development and utility in stand-level management planning. For. Ecol. Manag. 1997, 98, 251–265. [Google Scholar] [CrossRef]
- Porté, A.; Barlelink, H.H. Modelling mixed forest growth: A review of models for forest management. Ecol. Model. 2002, 150, 141–188. [Google Scholar] [CrossRef]
- Newton, P.F. Yield prediction errors of a stand density management program for black spruce and consequences for model improvement. Can. J. For. Res. 2003, 33, 490–499. [Google Scholar] [CrossRef]
- Barbour, R.J.; Kellogg, R.M. Forest management and end-product quality: A Canadian perspective. Can. J. For. Res. 1990, 20, 405–414. [Google Scholar] [CrossRef]
- Emmett, B. Increasing the value of our forest. For. Chron. 2006, 82, 3–4. [Google Scholar] [CrossRef]
- Newton, P.F. Development of an integrated decision-support model for density management within jack pine stand-types. Ecol. Model. 2009, 220, 3301–3324. [Google Scholar] [CrossRef]
- Newton, P.F. Development and utility of an ecological-based decision-support system for managing mixed coniferous forest stands for multiple objectives. In Ecological Modeling; Zhang, W.-J., Ed.; Nova Science Publishers Inc.: New York, NY, USA, 2012; pp. 100–160. [Google Scholar]
- Newton, P.F. A silvicultural decision-support algorithm for density regulation within peatland black spruce stands. Comput. Electron. Agric. 2012, 80, 115–125. [Google Scholar] [CrossRef]
- Newton, P.F. A decision-support system for density management within upland black spruce stand-types. Environ. Model. Softw. 2012, 35, 171–187. [Google Scholar] [CrossRef]
- Jack, S.B.; Long, J.N. Linkages between silviculture and ecology: An analysis of density management diagrams. For. Ecol. Manag. 1996, 86, 205–220. [Google Scholar] [CrossRef]
- Vanclay, J.K.; Henry, N.B. Assessing site productivity of indigenous cypress pine forest in southern Queensland. Commonw. For. Rev. 1988, 67, 53–64. [Google Scholar]
- Leary, R.A. Testing models of unthinned red pine plantation dynamics using a modified Bakuzis matrix of stand properties. Ecol. Model. 1997, 98, 35–46. [Google Scholar] [CrossRef]
- Kira, T.; Ogawa, H.; Sakazaki, N. Intraspecific competition among higher plants. I. Competition-yield-density interrelationship in regularly dispersed populations. J. Instit. Polytechn. Ser. D 1953, 4, 1–16. [Google Scholar]
- Shinozaki, K.; Kira, T. Intraspecific competition among higher plants. VII. Logistic theory of the C-D effect. J. Instit. Polytechn. Ser. 1956, 12, 69–82. [Google Scholar]
- Yoda, K.; Kira, T.; Ogawa, H.; Hozumi, K. Self-thinning in overcrowded pure stands under cultivated and natural-origin conditions. J. Biol. 1963, 14, 107–129. [Google Scholar]
- Newton, P.F. Asymptotic size–density relationships within self-thinning black spruce and jack pine stand-types: Parameter estimation and model reformulations. For. Ecol. Manag. 2006, 226, 49–59. [Google Scholar] [CrossRef]
- Newton, P.F.; Amponsah, I.G. Comparative evaluation of five height–diameter models developed for black spruce and jack pine stand-types in terms of goodness-of-fit, lack-of-fit and predictive ability. For. Ecol. Manag. 2007, 247, 149–166. [Google Scholar] [CrossRef]
- Newton, P.F.; Amponsah, I.G. Evaluation of Weibull-based parameter prediction equation systems for black spruce and jack pine stand types within the context of developing structural stand density management diagrams. Can. J. For. Res. 2005, 35, 2996–3010. [Google Scholar] [CrossRef]
- Lambeth, C.M. Juvenile-mature correlations in Pincaceae and implications for early selection. For. Sci. 1980, 26, 571–580. [Google Scholar]
- Carmean, W.H.; Hazenberg, G.; Deschamps, K.C. Polymorphic site index curves for black spruce and trembling aspen in northwest Ontario. For. Chron. 2006, 82, 231–242. [Google Scholar] [CrossRef]
- Carmean, W.H.; Niznowski, G.P.; Hazenberg, G. Polymorphic site index curves for jack pine in Nothern Ontario. For. Chron. 2001, 77, 141–150. [Google Scholar] [CrossRef]
- Newton, P.F. Base-age invariant polymorphic height growth and site index equations for peatland black spruce stands. North. J. Appl. For. 2008, 25, 202–210. [Google Scholar]
- R-Development Core Team. R: A Language and Environment for Statistical Computing. Available online: http://www.R-project.org/ (accessed on 1 February 2014).
- Johnson, G.; Hamlin, D. Bakuzis Matrix Graphing Package. 2007. Available online: http://www.growthmodel.org/papers/followup/followup.htm#Greg_Johnson_12_05 (accessed on 1 September 2013).
- Vanclay, J.K.; Skovsgaard, J.P. Evaluating forest growth models. Ecol. Model. 1997, 98, 1–12. [Google Scholar] [CrossRef]
- Wang, G.G. Is height of dominant trees at a reference diameter an adequate measure of site quality? For. Ecol. Manag. 1998, 112, 49–54. [Google Scholar] [CrossRef]
- Harper, J.L. Population Biology of Plants; Academic Press: London, UK, 1977; p. 892. [Google Scholar]
- Khil’mi, G.F. Theoretical Forest Biogeophysics; Academy of Sciences of the USSR (Translated from Russian by the National Science Foundation): Washington, DC, USA, 1957. [Google Scholar]
- Reineke, L.H. Perfecting a stand-density index for even-aged forests. J. Agric. Res. 1933, 46, 627–638. [Google Scholar]
- Weiskittel, A.; Gound, P.; Temesgen, H. Source of variation in the self-thinning boundary line for three species with varying levels of shade tolerance. For. Sci. 2009, 55, 84–93. [Google Scholar]
- Wilson, F.G. Numerical expression of stocking in terms of height. J. For. 1946, 44, 758–761. [Google Scholar]
- Wilson, F.G. Thinning as an orderly discipline: A graphic spacing schedule for red pine. J. For. 1979, 77, 483–486. [Google Scholar]
- Zhao, D.; Kane, M.; Borders, B.E. Development and applications of the relative spacing model for loblolly pine plantations. For. Ecol. Manag. 2010, 259, 1922–1929. [Google Scholar] [CrossRef]
- Pretzsch, H. Forest Dynamics, Growth and Yield; Springer Verlag: Berlin, Germany, 2009; p. 664. [Google Scholar]
- Assmann, E. The Principles of Forest Yield Study; Pergamon Press: Oxford, UK; New York, NY, USA, 1970; p. 506. [Google Scholar]
- Zhang, J.; Oliver, W.W.; Powers, R.F. Reevaluating the self-thinning boundary line for ponderosa pine (Pinus ponderosa) forests. Can. J. For. Res. 2013, 43, 963–971. [Google Scholar] [CrossRef]
- Bi, H. Stochastic frontier analysis of a classic self-thinning experiment. Austr. Ecol. 2004, 29, 408–417. [Google Scholar] [CrossRef]
- Bredenkamp, B.V.; Burkhart, H.E. An examination of spacing indices for Eucalyptus grandis. Can. J. For. Res. 1990, 20, 1909–1916. [Google Scholar] [CrossRef]
- Curtis, R.O. Stand density measures: An interpretation. For. Sci. 1970, 16, 517–534. [Google Scholar]
- Long, J.N.; Vacchiano, G. A comprehensive framework of forest stand property–density relationships: Perspectives for plant population ecology and forest management. Ann. For. Sci. 2014, 71, 325–335. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Newton, P.F. Evaluating the Ecological Integrity of Structural Stand Density Management Models Developed for Boreal Conifers. Forests 2015, 6, 992-1030. https://doi.org/10.3390/f6040992
Newton PF. Evaluating the Ecological Integrity of Structural Stand Density Management Models Developed for Boreal Conifers. Forests. 2015; 6(4):992-1030. https://doi.org/10.3390/f6040992
Chicago/Turabian StyleNewton, Peter F. 2015. "Evaluating the Ecological Integrity of Structural Stand Density Management Models Developed for Boreal Conifers" Forests 6, no. 4: 992-1030. https://doi.org/10.3390/f6040992
APA StyleNewton, P. F. (2015). Evaluating the Ecological Integrity of Structural Stand Density Management Models Developed for Boreal Conifers. Forests, 6(4), 992-1030. https://doi.org/10.3390/f6040992





