Cross-Correlation of Diameter Measures for the Co-Registration of Forest Inventory Plots with Airborne Laser Scanning Data
Abstract
:1. Introduction
2. Material
2.1. Study Areas
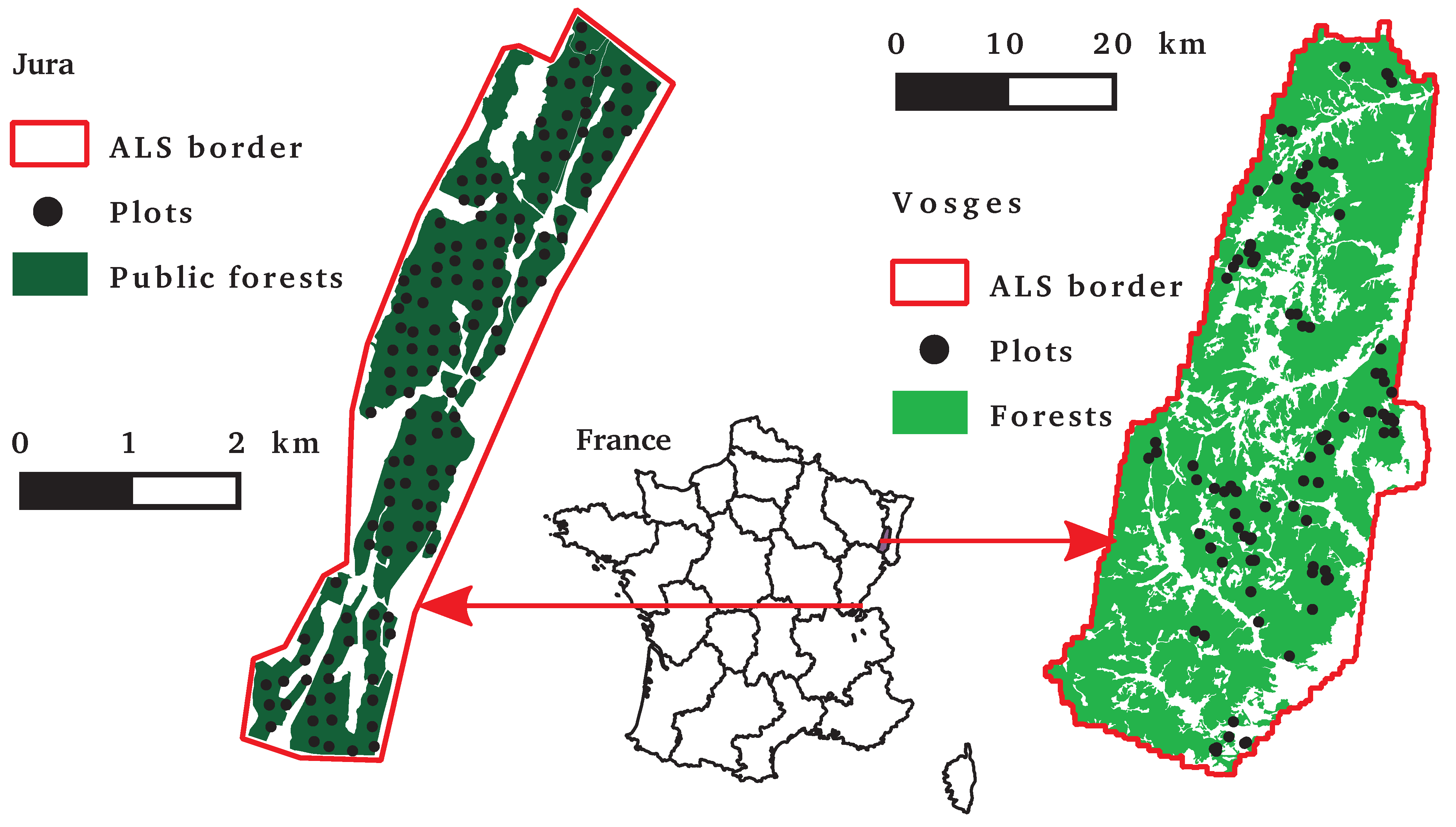
| Study area | Dominant height (m) | Basal area (m2·ha−1) | Coniferous proportion weighted by basal area | Stem density (ha−1) | Mean diameter (cm) |
|---|---|---|---|---|---|
| Jura | 31.8 ± 9.2 | 0.87 ± 0.12 | 510 ± 150 | 25.8 ± 7.0 | |
| np = 139 | 13.3 − 60.5 | 0.49 − 1.0 | 110 − 1, 520 | 14.8 − 54.5 | |
| Vosges | 23.9 ± 7.0 | 40.7 ± 9.2 | 0.53 ± 0.38 | 1, 990 ± 2, 900 | 20.8 ± 11.5 |
| np = 95 | 7.6 − 38.4 | 10.8 − 75.2 | 0 − 1 | 170 − 17, 700 | 2.4 − 51.5 |
2.2. Airborne Laser Scanning Data
3. Methods
3.1. Co-Registration Algorithm

 tree positions with a symbol size proportional to the tree diameter, × plot center); the background is the canopy height model; (b) The correlation image (
tree positions with a symbol size proportional to the tree diameter, × plot center); the background is the canopy height model; (b) The correlation image (  global maximum,
global maximum,  its 3 × 3 neighborhood and
its 3 × 3 neighborhood and  the second maximum); (c) The co-registered plot according to the (−10, −2) shift corresponding to the global maximum in the correlation image.
the second maximum); (c) The co-registered plot according to the (−10, −2) shift corresponding to the global maximum in the correlation image.
 tree positions with a symbol size proportional to the tree diameter, × plot center); the background is the canopy height model; (b) The correlation image (
tree positions with a symbol size proportional to the tree diameter, × plot center); the background is the canopy height model; (b) The correlation image (  global maximum,
global maximum,  its 3 × 3 neighborhood and
its 3 × 3 neighborhood and  the second maximum); (c) The co-registered plot according to the (−10, −2) shift corresponding to the global maximum in the correlation image.
the second maximum); (c) The co-registered plot according to the (−10, −2) shift corresponding to the global maximum in the correlation image.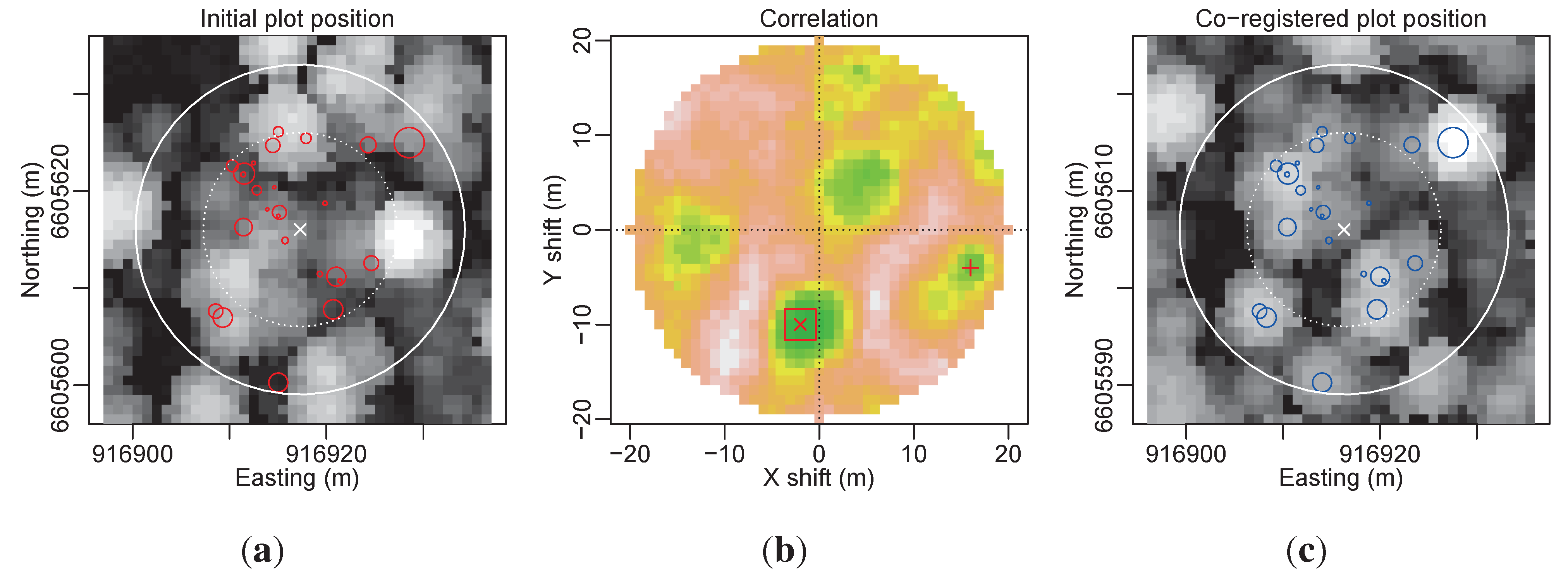
3.2. Influence of Co-Registration on the Accuracy of Prediction Models
3.3. Influence of Forest, Topography and ALS Data Parameters on Co-Registration
3.4. Influence of the Number of Georeferenced Trees on Co-Registration
4. Results
4.1. Co-Registration
4.1.1. Operator Validation
4.1.2. Algorithm Comparison
4.1.3. Comparison of the GNSS, Algorithm and Operator Positions
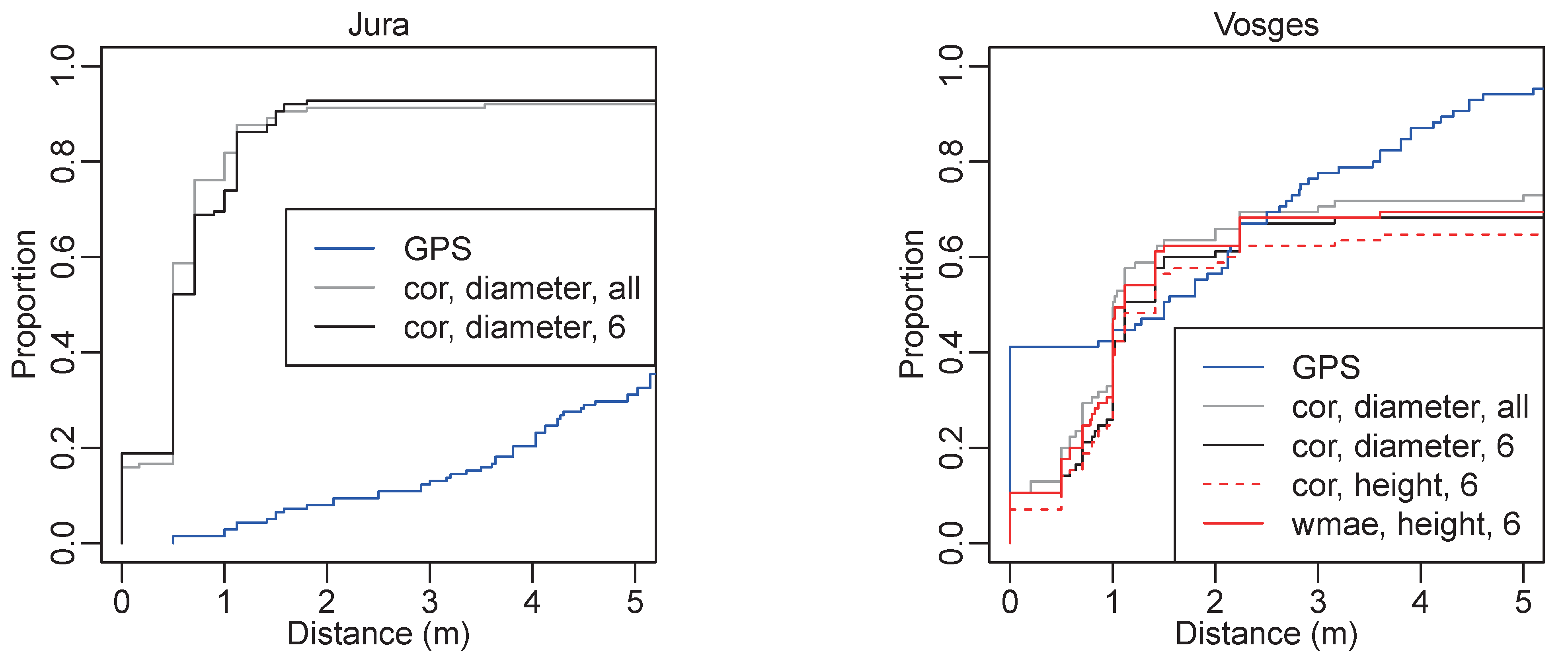
| GNSS | cor, Diameter, All | cor, Diameter, 6 | cor, Height, All | wmae, Height, All | ||
|---|---|---|---|---|---|---|
| Jura | 9.0 ± 8.7 | 3.3 ± 11.0 | 3.1 ± 10.1 | |||
| 4.2, 6.6, 10.7 | 0.5, 0.5, 0.71 | 0.5, 0.5, 1.1 | ||||
| Vosges | 1.8 ± 2.1 | 5.4 ± 7.5 | 5.3 ± 7.0 | 5.4 ± 7.3 | 6.1 ± 7.5 | |
| 0, 1.5, 2.8 | 0.71, 1.0, 11.3 | 0.9, 1.1, 9.8 | 0.8, 1.1, 10.8 | 0.9, 1.4, 12.8 | ||
4.1.4. Influence of Environmental Variables on Co-Registration Error
| Variable | Vosges | Jura | |||
|---|---|---|---|---|---|
| cor, Diameter, All | cor, Height, 6 | wmae, Height, 6 | cor, Diameter, All | ||
| Dominant height | −0.25 ∗ | −0.11 | −0.28 ∗ | ||
| Basal area | −0.43 ∗∗∗ | −0.40 ∗∗∗ | −0.29 ∗∗ | −0.05 | |
| Stem density | 0.2 | 0.09 | 0.28 ∗∗ | 0.03 | |
| Mean diameter | −0.31 ∗∗ | −0.22 ∗ | −0.31 ∗∗ | −0.04 | |
| Coniferous proportion | −0.54 ∗∗∗ | −0.53 ∗∗∗ | −0.31 ∗∗ | −0.15 | |
| Slope | −0.16 | −0.08 | −0.05 | 0.14 | |
| Altitude | −0.12 | −0.36 ∗∗∗ | −0.37 ∗∗∗ | 0.04 | |
| Pulse density | 0.08 | 0.11 | −0.06 | −0.05 | |
| Ground point density | 0.18 | 0.17 | −0.02 | 0.11 | |
| Vegetation point density | −0.08 | −0.21 | −0.29 ∗∗ | −0.02 | |
| Points below 0.5 m density | 0.19 | 0.18 | −0.02 | 0.05 | |
| CHM pit-filling | −0.03 | 0.13 | 0.06 | −0.11 | |
| CHM empty pixels | 0.06 | 0.05 | 0.08 | −0.04 | |
| max1/max2 | −0.41 ∗∗∗ | −0.42 ∗∗∗ | 0.41 ∗∗∗ | −0.20 ∗ | |
| max1/med1 | 0.04 | 0.02 | −0.04 | 0.24 ∗∗ | |
4.1.5. Influence of the Number of Sample Trees
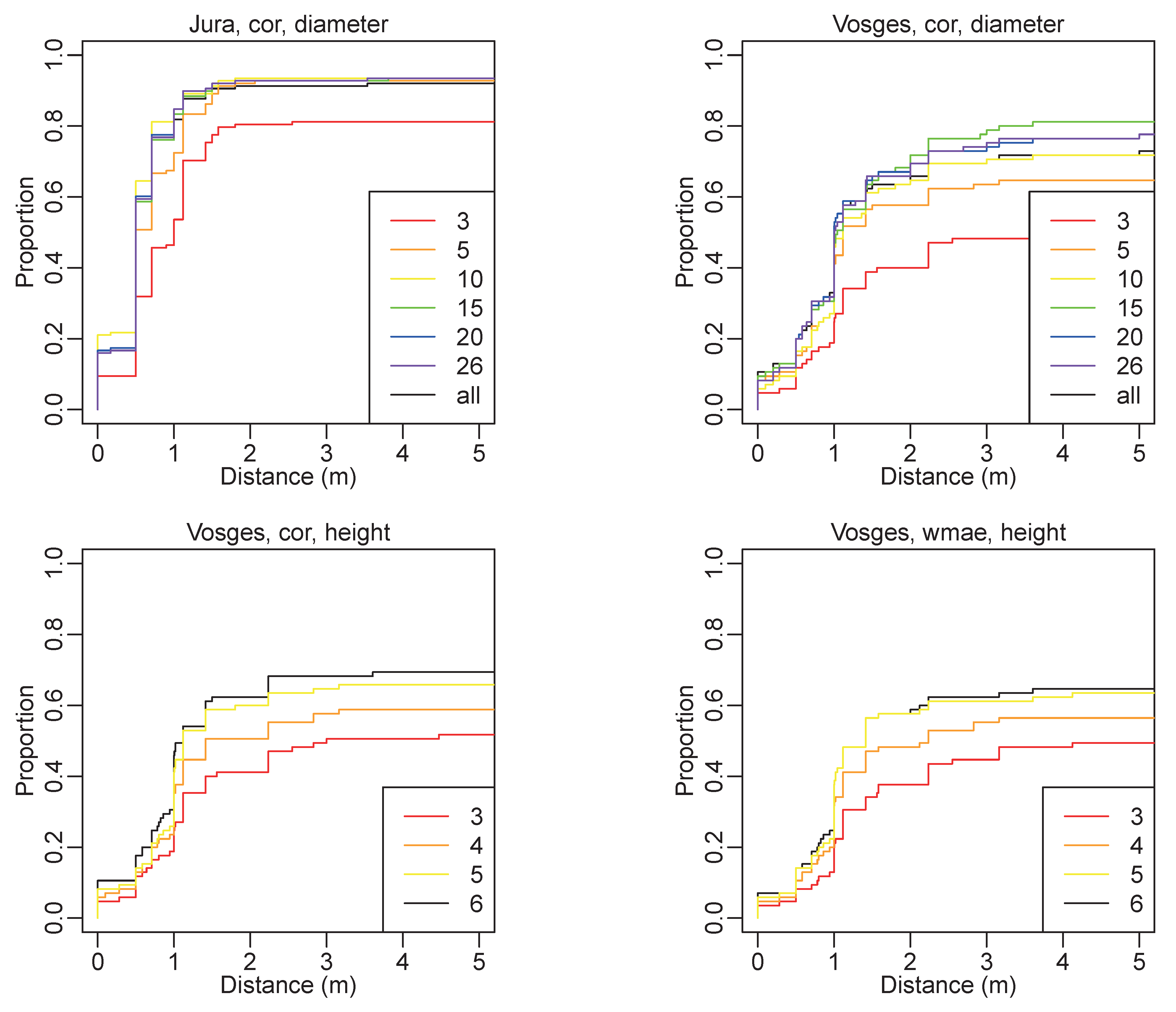
4.2. Prediction Models
| Calibration | Validation (Jura) | Validation (Vosges) | |||||
|---|---|---|---|---|---|---|---|
| GNSS | cor, Diameter, All | Operator | GNSS | cor, Diameter, All | Operator | ||
| GNSS | 7.13 | 6.49 | 6.09 | 9.46 | 9.58 | 9.42 | |
| cor, Diameter, All | 7.17 | 6.44 | 6.03 | 9.72 | 9.31 | 9.62 | |
| Operator | 7.34 | 6.37 | 5.88 | 9.47 | 9.60 | 9.43 | |
5. Discussion
5.1. Limitations of Reference Data
5.2. GNSS Accuracy in Forests
5.3. Possibility of Co-Registration
5.4. Automated Co-Registration
5.5. Factors Affecting the Algorithm Co-Registration Error
5.6. Resulting Co-Registration and Prediction Models
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Duplat, P.; Perrotte, G. L’inventaire par échantillonnage. In Inventaire et Estimation de l’Accroissement des Peuplements Forestiers; Office National des Forêts: Paris, France, 1981; pp. 37–74. [Google Scholar]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Hollaus, M.; Dorigo, W.; Wagner, W.; Schadauer, K.; Höfle, B.; Maier, B. Operational wide-area stem volume estimation based on airborne laser scanning and national forest inventory data. Int. J. Remote Sens. 2009, 30, 5159–5175. [Google Scholar] [CrossRef]
- Baltsavias, E.P. Airborne laser scanning: Basic relations and formulas. ISPRS J. Photogramm. Remote Sens. 1999, 54, 199–214. [Google Scholar] [CrossRef]
- Naesset, E.; Jonmeister, T. Assessing point accuracy of DGPS under forest canopy before data acquisition, in the field and after postprocessing. Scand. J. For. Res. 2002, 17, 351–358. [Google Scholar] [CrossRef]
- Andersen, H.E.; Clarkin, T.; Winterberger, K.; Strunk, J. An accuracy assessment of positions obtained using survey-and recreational-grade global positioning system receivers across a range of forest conditions within the Tanana valley of interior Alaska. West. J. Appl. For. 2009, 24, 128–136. [Google Scholar]
- Korpela, I.; Tuomola, T.; Välimäki, E. Mapping forest plots: An efficient method combining photogrammetry and field triangulation. Silva Fennica 2007, 41, 457–169. [Google Scholar] [CrossRef]
- Gobakken, T.; Næsset, E. Assessing effects of positioning errors and sample plot size on biophysical stand properties derived from airborne laser scanner data. Can. J. For. Res. 2009, 39, 1036–1052. [Google Scholar] [CrossRef]
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Hauglin, M.; Lien, V.; Næsset, E.; Gobakken, T. Geo-referencing forest field plots by co-registration of terrestrial and airborne laser scanning data. Int. J. Remote Sens. 2014, 35, 3135–3149. [Google Scholar] [CrossRef]
- Olofsson, K.; Lindberg, E.; Holmgren, J. A method for linking field-surveyed and aerial-detected single trees using cross correlation of position images and the optimization of weighted tree list graphs. In Proceedings of the SilviLaser 2008: 8th International Conference on LiDAR Applications in Forest Assessment and Inventory, Edinburgh, UK, 17–19 September 2008; Hill, R., Rosette, J., Suárez, J., Eds.; pp. 95–104.
- Hyyppä, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners. IEEE Trans. Geosci. Remote Sens. 2001, 39, 969–975. [Google Scholar] [CrossRef]
- Dorigo, W.; Hollaus, M.; Wagner, W.; Schadauer, K. An application-oriented automated approach for co-registration of forest inventory and airborne laser scanning data. Int. J. Remote Sens. 2010, 31, 1133–1153. [Google Scholar] [CrossRef]
- Pascual, C.; Martín-Fernández, S.; García-Montero, L.; García-Abril, A. Algorithm for improving the co-registration of LiDAR-derived digital canopy height models and field data. Agrofor. Syst. 2013, 89, 967–975. [Google Scholar]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens. 2003, 29, 564–577. [Google Scholar] [CrossRef]
- Hollaus, M.; Wagner, W.; Eberhofer, C.; Karel, W. Accuracy of large-scale canopy heights derived from LiDAR data under operational constraints in a complex alpine environment. ISPRS J. Photogramm. Remote Sens. 2006, 60, 323–338. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkanen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.M.; et al. Comparative testing of single-tree detection algorithms under different types of forest. Forestry 2012, 85, 27–40. [Google Scholar] [CrossRef]
- Monnet, J.-M. Evaluation of a semi-automated approach for the co-registration of forest inventory plots and airborne laser scanning data. In Proceedings of the SilviLaser 2013, Beijing, China, 9–11 October 2013; pp. 167–174.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Monnet, J.-M.; Mermin, É. Cross-Correlation of Diameter Measures for the Co-Registration of Forest Inventory Plots with Airborne Laser Scanning Data. Forests 2014, 5, 2307-2326. https://doi.org/10.3390/f5092307
Monnet J-M, Mermin É. Cross-Correlation of Diameter Measures for the Co-Registration of Forest Inventory Plots with Airborne Laser Scanning Data. Forests. 2014; 5(9):2307-2326. https://doi.org/10.3390/f5092307
Chicago/Turabian StyleMonnet, Jean-Matthieu, and Éric Mermin. 2014. "Cross-Correlation of Diameter Measures for the Co-Registration of Forest Inventory Plots with Airborne Laser Scanning Data" Forests 5, no. 9: 2307-2326. https://doi.org/10.3390/f5092307
APA StyleMonnet, J.-M., & Mermin, É. (2014). Cross-Correlation of Diameter Measures for the Co-Registration of Forest Inventory Plots with Airborne Laser Scanning Data. Forests, 5(9), 2307-2326. https://doi.org/10.3390/f5092307




