Next Article in Journal
Cross-Correlation of Diameter Measures for the Co-Registration of Forest Inventory Plots with Airborne Laser Scanning Data
Previous Article in Journal
Spatial and Temporal Variability of Channel Retention in a Lowland Temperate Forest Stream Settled by European Beaver (Castor fiber)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 5
Issue 9
10.3390/f5092289
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effects of Harvesting Systems and Bole Moisture Loss on Weight Scaling of Douglas-Fir Sawlogs (Pseudotsuga Menziesii var. glauca Franco)

by
Jarred D. Saralecos
*,
Robert F. Keefe
,
Wade T. Tinkham
,
Randall H. Brooks
,
Alistair M. S. Smith
and
Leonard R. Johnson
Department of Forest, Rangeland, and Fire Sciences, College of Natural Resources, University of Idaho, 975 W. 6th St., Moscow, ID 83844-1133, USA
*
Author to whom correspondence should be addressed.
Forests 2014, 5(9), 2289-2306; https://doi.org/10.3390/f5092289
Submission received: 25 June 2014 / Revised: 6 September 2014 / Accepted: 15 September 2014 / Published: 19 September 2014
Browse Figures
Versions Notes

Abstract

:
Characterizing the moisture loss from felled trees is essential for determining weight-to-volume (W-V) relationships in softwood sawlogs. Several factors affect moisture loss, but research to quantify the effects of bole size and harvest method is limited. This study was designed to test whether bole size, harvest method, environmental factors, and the associated changes in stem moisture content of felled Douglas-fir (Pseudotsuga menziesii var. glauca Franco) affected the weight-to-volume relationship of sawlogs. Thirty trees in three size classes (12.7–25.4 cm, 25.5–38.1 cm, 38.2–50.8 cm) were felled and treated with one of two harvesting processing methods. Moisture content was sampled every two days for four weeks. Results showed 6% greater moisture loss in the crowns of stems that retained limbs after felling compared to stems with limbs removed after harvesting. Additionally, moisture loss rate increased as stem size decreased. The smallest size class lost 58% moisture content compared to 34% in the largest size class throughout the study duration. These stem moisture content changes showed a 17% reduction in average sawlog weight within the largest size class, shifting current W-V relationships from 2.33 tons m−3 to 1.94 tons m−3 during the third seasonal quarter for northern Idaho Douglas-fir and potentially altering relationships year-round.

1. Introduction

Since the 1960s, weight scaling of sawlogs for volume based transactions has developed into a widely applied method used by forest industry across North America [1,2], with interior British Columbia uses weight scaling to process 97% of its harvested timber [3]. Developments in timber harvesting techniques and lumber production processes, such as improved supply chain procedures and mechanized machinery, have increased harvesting efficiency and retrievable products from each forest management activity [4]. In order to meet the growing demand for increased forest products while reducing scaling costs for mills, a systematic random sample of trucks arriving at the mill is often used to determine truck weight-to-volume (W-V) relationships. The process of weight scaling, however, relies heavily upon regional knowledge of wood characteristics and seasonal trends to accurately estimate harvested volumes [5].
Water content is among the many variables associated with W-V relationships affecting sawlog inventory [6]. Stem moisture content in weight scaling systems has been found to be significant in southern hardwoods and not significant in some mid-western softwood sawlogs studies [2,7]. Sap flux density and thus log moisture vary spatially within stems, commonly peaking towards the outer edges in the radial direction and declining toward the heartwood, leading to different moisture contents between heartwood and sapwood [8,9]. For softwoods, the moisture content of heartwood is typically considerably lower than for sapwood [10,11,12]. Additional studies have identified seasonal patterns associated with stem moisture content of pulpwood [13]. Previous studies have explored similar methodologies for measuring bole moisture loss of softwoods, with each producing common trends of moisture loss related to season and the presence of tree crowns [14,15,16,17]. Subsequent results have shown faster moisture loss immediately following felling, with trees that have intact crowns losing more moisture over the study duration. However, these studies are characterized by smaller sample sizes (8–20 stems) and narrow sample diameter ranges (6–18 cm).
Although decreasingly common in the northern Rocky Mountain region, operational practices that have been the focus of past research, such as sour-felling and floatation of logs for transportation purposes provide insight into changes in wood moisture content for weight scaling [18]. For example, sour felling works to encourage moisture loss in harvested stems in an effort to increase the amount of volume that can be transported on each truckload [19,20]. Reducing transportations costs to lower biomass moisture content can also provide increased energy yields in forest products burned for energy [20]. This process also increases the buoyancy of logs for transportation through floatation [18]. However, while increased moisture loss benefits harvest operations based on volume based transactions, it negatively impacts profit margins of operations using weight based transactions by removing a source of profit in the bole moisture content and subsequently total stem weight. Finally, fuel moisture content studies have modeled stem moisture changes and rates based on stem size; limitations of such approaches have included the coarse temporal-resolution of samples (weekly) and that key information such as time since felling (i.e., proportion of dead and green stems) is often not included in the regression models [21,22].
Douglas-fir (Pseudotsuga menziesii var. glauca Franco) is one of the predominant species of the forests in the interior Pacific Northwest [23]. The water stored in standing timber is progressively reduced by as much as 50% in sapwood during the summer season, relative to the reduced winter draw down or reduction of sapwood moisture content [24,25]. The relationship between reduced moisture content in the sapwood of felled timber and the ratio of stem W-V is not well understood [26,27,28]. Log buyers and land appraisers are challenged with accurately establishing the value of standing timber; but either stumpage or mill-delivered log values must incorporate changes in order to value the result of felling, processing, and delivery practices. Improved knowledge of the uncertainties in mapping moisture loss within softwood sawlogs with respect to current operational harvesting practices is needed to better understand potential changes to scaled product and ultimately profit margin.
The objective of this study was to determine the effects of bole size, harvesting method, and environmental factors on moisture content of felled Douglas-fir sawlogs and the subsequent effect on sawlog W-V relationships. We hypothesized that stem size and harvest system would affect sawlog moisture content. Specifically, that smaller stems and stem retaining limbs would lose more moisture than larger stems and stems without limbs. In keeping with the concept of seasonal bole water storage and draw-down [13,29], we also hypothesized that stemwood moisture content would be significantly affected by relative humidity, atmospheric temperature, and vapor pressure deficit (VPD). Finally, we believed that including environmental factors such as soil moisture and stem ground contact would not significantly affect changes in moisture content. The change in moisture content observed with respect to the measured variables will help determine the impact of moisture loss on W-V relationships and current weight scaling practices.

2. Methods

2.1. Site Description

The research site was selected to represent high potential evapotranspiration using a southern aspect in late summer in order to provide longer radiation exposure to the felled samples. The mature, second growth, closed canopy Douglas-fir (Pseudotsuga menziesii) stand was located in the West Hatter Creek unit (WHC) of the University of Idaho Experimental Forest in north-central Idaho (46°50′05.15″ N/116°50′25.19″ W). The WHC unit is located 15 km northeast of Moscow, Idaho, on the north slope of the Palouse Range (Figure 1). The Palouse Range is a heterogeneous mosaic of second-growth mixed conifer forest stands distributed across a topographically complex landscape and, consequently, a diverse range of habitat types [30]. The stand was predominantly Douglas-fir, but scattered Grand fir (Abies Grandis (Dougl.) Lindl.) was also present in the understory at less than 20 trees per hectare. The sampled stems showed no visible signs of defect or loss of structural integrity. The site reflected a shelterwood stand following the study treatments. Within the sample area, stems were randomly spaced and mixed between size classes, with canopy cover conditions similar for all sample stems. The site featured the expected seasonal and environmental conditions, including low precipitation and average daily temperatures associated with the time of year (Table 1).
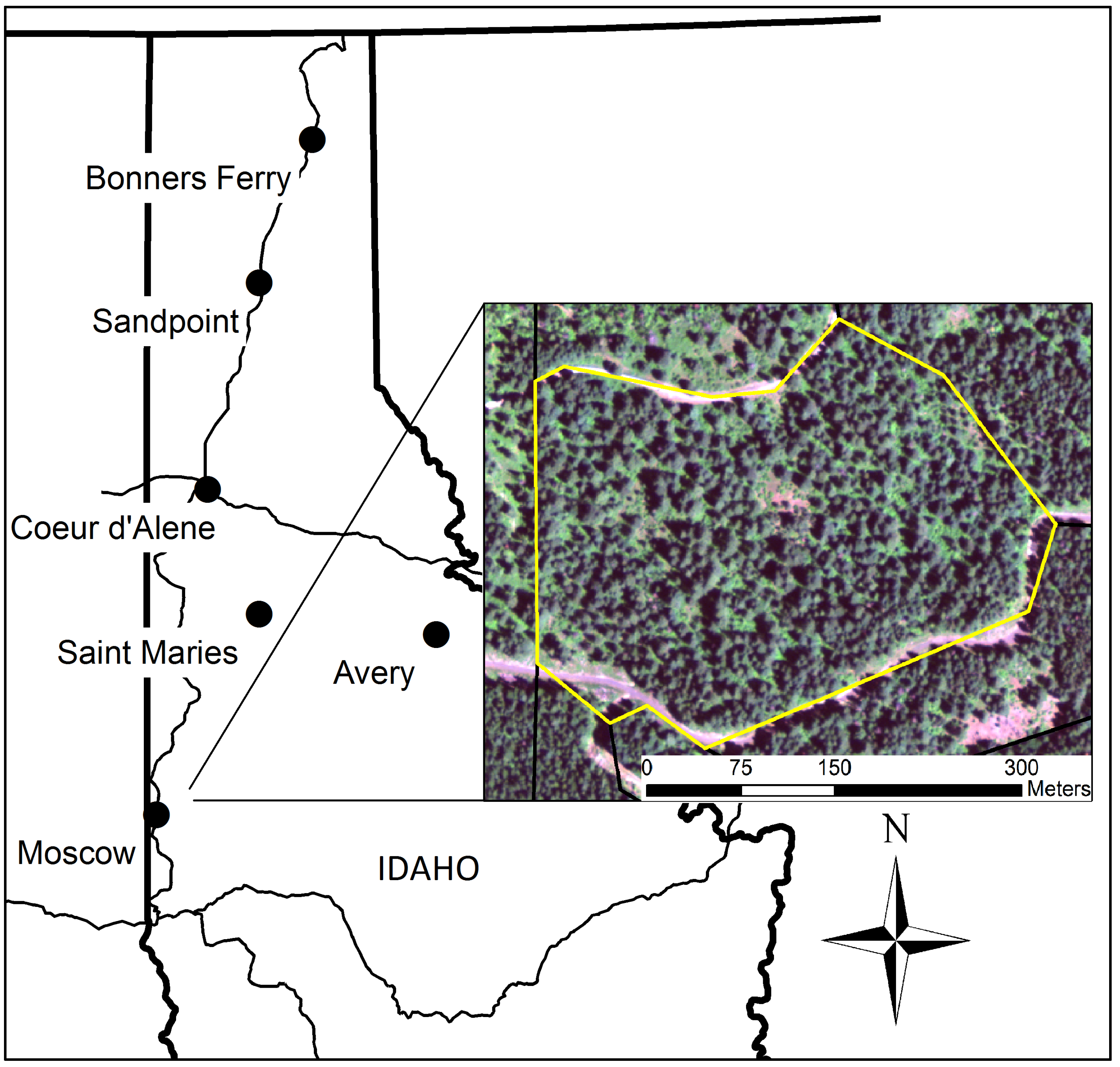
Forests 05 02289 g001 1024
Figure 1. The study unit located Northeast of Moscow, Idaho in the West Hatter Creek Unit of the University of Idaho Experimental Forest (46°50′05.15″ N/116°50′25.19″ W).
Figure 1. The study unit located Northeast of Moscow, Idaho in the West Hatter Creek Unit of the University of Idaho Experimental Forest (46°50′05.15″ N/116°50′25.19″ W).
Forests 05 02289 g001
Table
Table 1. Site characteristics during study duration.
Table 1. Site characteristics during study duration.
Site AttributesUniversity of Idaho Experimental Forest
Longitude/Latitude46°50′05.15″ N/116° 50′25.19″ W
Elevation (m)892
Total study precipitation (mm)3.1
Mean study temperature (°C)21.3
Temperature range (°C)8–39
Slope, aspect17%, Southern
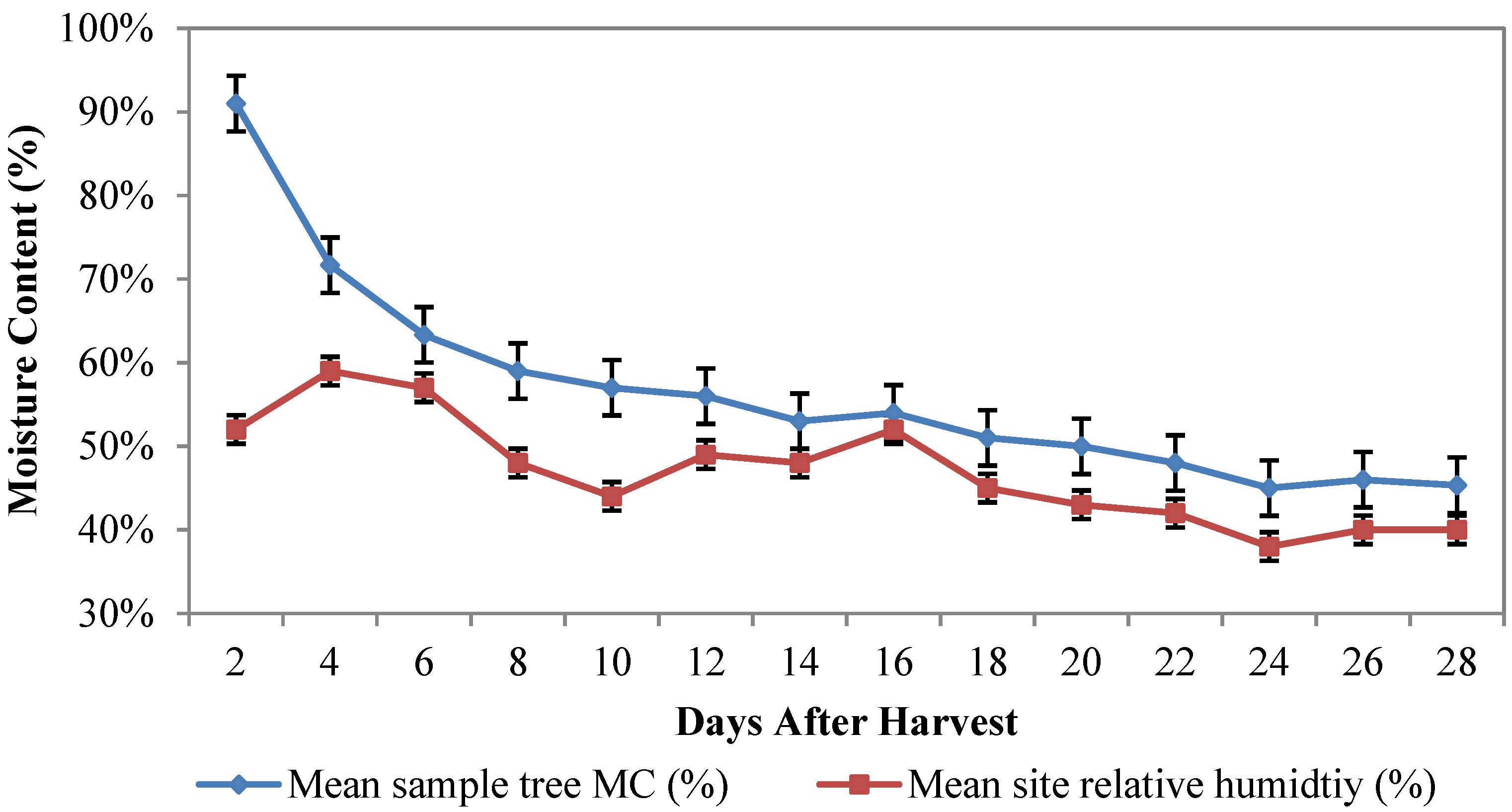
Mean daily vapor pressure deficit (kPa)2.58
Mean daily relative humidity (%)47
Relative humidity range (%)10–84
Mean soil temperature (°C)16.7
Mean soil moisture content (%)7.6
In addition to gathering gravimetric moisture content, we also collected relative humidity (+/− 0.5%), soil moisture (+/− 0.03 m3/m3), soil temperature (+/− 1 °C), air temperature (+/− 1 °C), and precipitation (+/− 0.1mm) throughout the study. The environmental measurements were collected using a Decagon EM50 data logger, Decagon 5-TM soil moisture and temperature sensors, Decagon ECRN-100 high resolution rain gauge, and Hygrochron ™ Ibuttons. Ibuttons are small (1 cm diameter) battery-powered temperature sensors that can be deployed with inexpensive radiation shields to record surface air temperature [31]. Data was collected continuously over the duration of the study at 15 minutes intervals. The data was then structured to represent daily means. Through combining the factors of atmospheric temperature and relative humidity both vapor pressure deficit and adjusted degree days were calculated. Vapor Pressure Deficit (VPD) was calculated by taking the difference in saturation vapor pressure and actual vapor pressure (Equation (1)). Degree days were determined by assessing the daily high temperature (°C) and calculating the difference from 0 °C (Equation (2) (The inclusion of VPD and degree days offered greater ability to assess variation in daily moisture change during the study. VPD was calculated using the formula expressed in [32].
S V P = 0.611 × exp ( 17.3 × T T + 237.3 ) A V P = R H 100 × S V P V P D = A V P − S V P S V P = Saturation Vapor Pressure T = Atmospheric Temperature (°C) A V P = Actual Vapor Pressure R H = Relative Humidity (%) V P D = Vapor Pressure Deficit
Degree Days = Tmax − 0°C
Tmax = Daily maximum temperature (°C)

2.2. Tree Measurements

Co-dominant Douglas-fir trees with complete crowns and free of noticeable signs of injury or disease were selected by diameter at breast height (DBH, 1.37 m) to represent the size range of sample selected. A total of 30 trees were chosen and separated by three size classes of 12.7 cm intervals (Table 2). The diameter classes represent commercial sawlog sizes ranging from lower end merchantability standards to the larger limitation of conventional mechanized felling equipment. Samples were felled according to two treatment types representing harvesting systems commonly applied in the northwestern United States. Ground based harvesting systems comprise a large portion of the timber annually harvested in North America. Within the ground based category, independent procedures and operations are adjusted depending on machinery availability and contractor preference. Two of the most prominent methods are cut-to-length harvesting and whole tree harvesting which vary when and where the felled trees are processed for transportation to mills.
Table
Table 2. Characteristics of the Douglas-fir trees sampled for stem moisture content loss rate.
Table 2. Characteristics of the Douglas-fir trees sampled for stem moisture content loss rate.
Tree Attributes12.7–25.4 cm25.5–38.1 cm38.2–50.8 cm
Number of trees sampled101010
Mean diameter (cm) at 1.37 m20.032.544.7
Diameter range (cm)14.7–25.426.4–38.141.1–49.2
Mean height (m)18.424.228.0
Samples identified as treatment 1 were felled and immediately processed into sawlogs, which included removing all limbs manually with a chainsaw. This method represented a cut-to-length harvesting system where trees are processed at the stump. Samples identified as treatment 2 were felled and left intact. The process of felling-only and leaving the bole with limbs intact represented a whole-tree harvesting system. Trees were sampled every other day for a period of four weeks. The cores were collected using a 5.15 mm diameter increment borer (Haglöf, Sweden). After felling, all stems were measured for height using a steel tape (Feet, 1/10th) and relative proportion in contact with the ground. Ground contact percentage was measured by dividing the length of the stem in contact with the ground by total stem length. Previous studies have assessed field wood moisture content with samples containing some portion of ground contact [33] and alternative research where samples were suspended above the ground [34]. The establishment of ground contact percentage helped to identify the potential effect of soil temperature and moisture on adjusting stem moisture content.
To avoid broken cores or sampling in close proximity to prior cores, grids of each sampling location were identified and each sampling point was separated by 7.62 cm in all directions from other sample points. After the completion of drilling charts on each stem, cores were taken randomly from each sample location throughout the study. In order to better characterize potential vertical variability along the bole, trees were sampled at two locations on each stem. The lower core sample was taken at 1.37 m from the base of the tree established prior to felling, and the upper sample was taken at the mid-point of the crown. The upper stem sample locations averaged diameters of 15.7, 18.5, and 24.1 cm, respectively, for the 12.7–25.4, 25.5–38.1, and 38.2–50.8 cm size classes. For each sample removed, heartwood and sapwood were separated using a razor blade. During analysis, total stem moisture content was derived by accounting for the heartwood to sapwood ratio of from each sample location. Samples were immediately placed into air-tight, pre-weighed plastic bags and placed in an environmental container. The heartwood-sapwood barrier was determined visually. In the laboratory, samples were weighed within three hours of collection and an initial weight was recorded with the samples still in bags. The predetermined bag weight was then subtracted and samples were dried according the ASTM International Standards for drying wood to obtain moisture content [35]. After drying, samples were reweighed and the percentage of moisture content of each sample was calculated as the difference between the original sample mass and oven-dry mass divided by the oven-dry mass, often considered to determine moisture content on a green basis (Equation (3)) [36]. Similar processes using Equation (3), or variations of it, have been implemented in previous studies exploring mositure content of surface fuels in fire models [33,34].
M C = M g − M od M od × 100 M C = Wood moisture content (%) W g = Green weight of wood (pounds or kilograms) W o d = Oven-dry weight of wood (pounds or kilograms)

2.3. Statistical Analysis

All statistical analysis was completed using R Statistical Package [37]. A series of one way ANOVA tests were used to evaluate the significance of the variables days since harvest, treatment type, size class, and sample stem location. To further understand the influence of size class, treatment type, and sample stem location, Tukey’s HSD test was used to evaluate interactions between these variables (α = 0.05). From the ANOVA analysis a series of linear mixed-effects model were developed using the significant variables and also days since harvest, VPD, RH, soil moisture content, soil temperature, atmospheric temperature, and percentage of ground contact for each felled log segment to test the Ho that size class, and environmental factors have no effect on stem moisture content of felled sawlogs. Within the model analysis, sample trees were treated as random variables to reduce the magnitude of temporal effects and limit the influence of standard error across the study days. All models were tested using a similar form to: Y( mc) = β0 + β1 Days Since Harvest + β2 Size Class + β3 VPD + β4 (1|tree) + u. Akaike’s Information Criterion (AIC) test was used to assess which model performed the best in predicting stem moisture content over the study duration. AIC evaluates the statistical quality of a model in comparison to others by balancing goodness of fit against model complexity [38], where individual AIC values are unit-less and non-meaning without other model values to compare it against. When comparing between model AICs, lower values indicate better fitting models [39]. In the case of negative reported values, it is the highest negative value that identifies the best model. The delta AIC (Δi) statistic is commonly used to assess the statistical difference between competing models and is calculated as [40,41] (Equation (4)).
ΔAICi = AICi − min(AIC)
where AICi is the value for an individual competing model and min(AIC) is the minimum AIC value among tested models. The AIC and R2 values from the model were derived from conditional R2 and AIC procedures established in Nakagawa and Schielzeth, 2013 [42].

3. Results

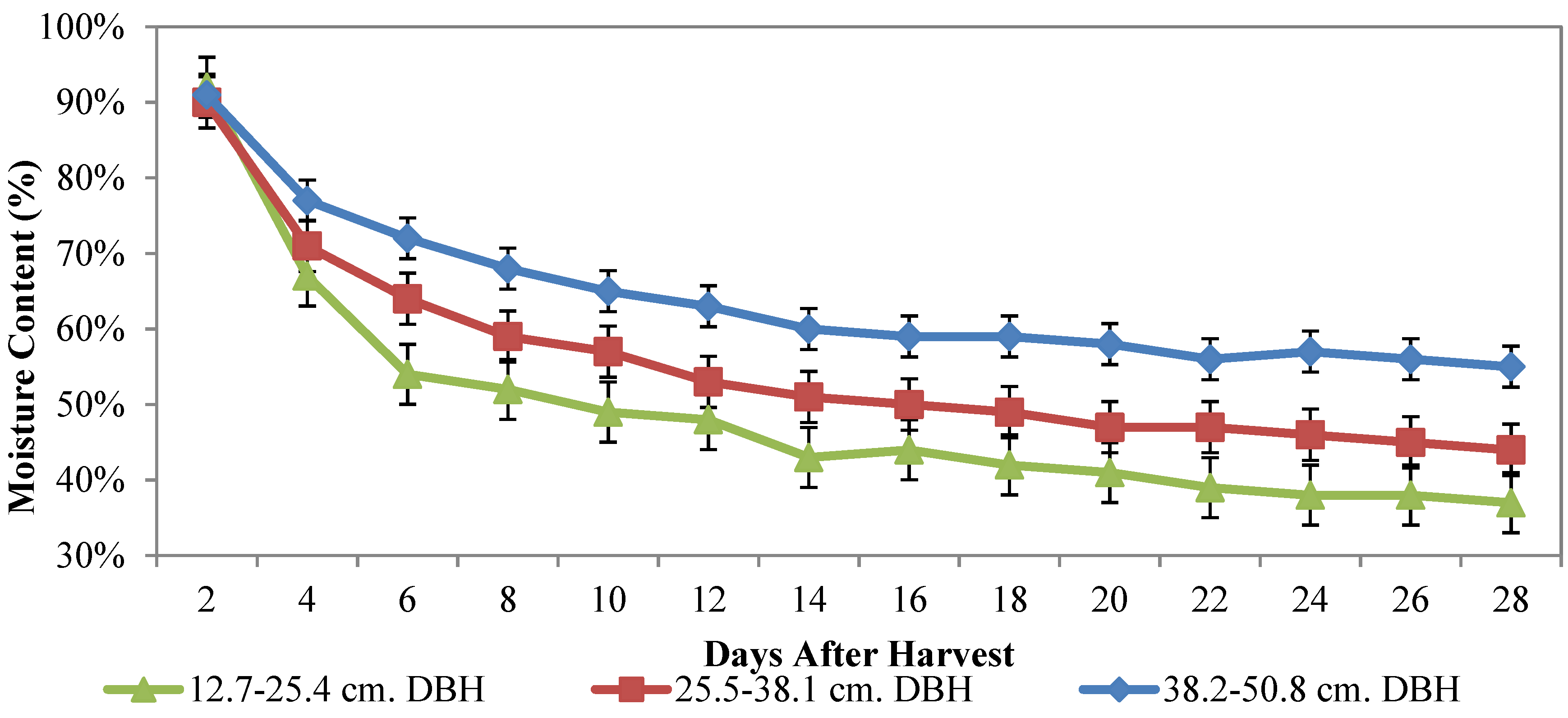
3.1. Moisture Loss

The ANOVA analysis indicated that only size class by itself exhibited significant influence on moisture loss. In testing the interactions between the variables, Tukey’s HSD identified significant differences in moisture loss when considering both the interaction between size class and treatment type, and the interaction between sample location and treatment type (Table 3). Within the smallest size class (12.7–25.4 cm), 58% of the stem moisture content was lost over the four weeks compared to 34% in the largest size class (38.2–50.8 cm) (Figure 2). The interaction between whole-tree harvesting with size class accelerated moisture loss over the rates observed in the cut-to-length harvest system (Table 3). The effect of treatment type on stem moisture loss was also significant when looking at sample location within the stem (Figure 3 and Table 3), with upper stem locations treated with cut-to-length harvesting losing moisture significantly slower than stems treated with whole-tree harvesting. The change in stem moisture content slowed as average atmospheric relative humidity (RH) and stem moisture content drew closer later in the study (Figure 4). Although stem heartwood moisture content was lower to begin with, mean heartwood moisture content experienced less loss than the mean sapwood moisture content over the study period, losing an average of 42% compared to 62% (Table 4).
Table
Table 3. Results of Tukey’s HSD test to determine ad hoc differences in bole moisture content between size classes, stem sample location, and treatment type.
Table 3. Results of Tukey’s HSD test to determine ad hoc differences in bole moisture content between size classes, stem sample location, and treatment type.
Significance Testp-value
Size Class
size class 1–size class 20.0053
size class 1–size class 3<0.0001
size class 2–size class 3<0.0001
Stem Sample Location
upper–lower0.8214
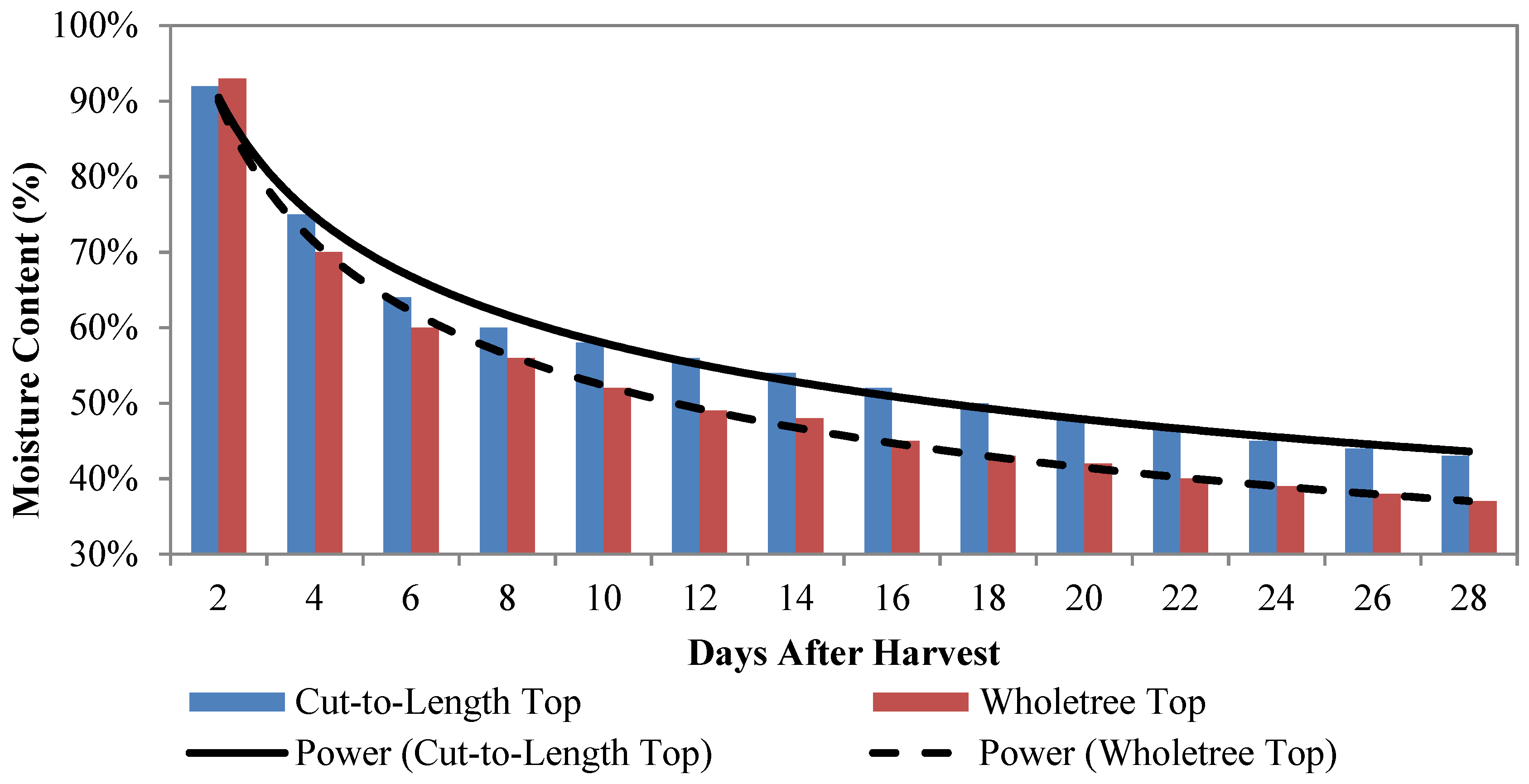
Treatment Type
treatment 1 * upper–treatment 2 * upper0.0008
* Denotes interaction term between two variables.
Forests 05 02289 g002 1024
Figure 2. Moisture content (MC) of stem wood, dry weight basis, over 28 days following harvesting; mean MC values for trees on a given sampling date are shown as solid shapes averaged across both harvest systems, and error bars show one standard error (SE).
Figure 2. Moisture content (MC) of stem wood, dry weight basis, over 28 days following harvesting; mean MC values for trees on a given sampling date are shown as solid shapes averaged across both harvest systems, and error bars show one standard error (SE).
Forests 05 02289 g002
Table
Table 4. The beginning and ending stem moisture contents of all sample stems regardless of size separated by heartwood and sapwood.
Table 4. The beginning and ending stem moisture contents of all sample stems regardless of size separated by heartwood and sapwood.
Sample TreesMean Starting (%)Mean Ending (%)Mean Loss (%)
Sapwood MC 1165462
Heartwood MC672542
Forests 05 02289 g003 1024
Figure 3. The mean moisture content of stem wood separated by treatment type and stem location in the time following harvesting; Treatment 1 represented a cut-to-length harvesting system and Treatment 2 a whole-tree system; these results show the MC in the upper portions of the stems.
Figure 3. The mean moisture content of stem wood separated by treatment type and stem location in the time following harvesting; Treatment 1 represented a cut-to-length harvesting system and Treatment 2 a whole-tree system; these results show the MC in the upper portions of the stems.
Forests 05 02289 g003
Forests 05 02289 g004 1024
Figure 4. The changes in stem wood moisture content and site relative humidity are shown over the duration of the study; mean moisture contents and relative humidity are shown in solid shapes with error bars showing one standard error.
Figure 4. The changes in stem wood moisture content and site relative humidity are shown over the duration of the study; mean moisture contents and relative humidity are shown in solid shapes with error bars showing one standard error.
Forests 05 02289 g004

3.2. Optimal Model

Different combination of size class, treatment type, VPD, RH, days since harvest, soil moisture content, soil temperature, atmospheric temperature, and percentage of ground contact for each felled log segment, and the significant interaction terms were used within the linear mixed-effects model analysis. This rigorous analysis approach has not been previously applied to predicting moisture loss of harvested sawlogs, where each sample tree is utilized as a random variable to account for influences in standard error between sample days on the same tree. The application of a linear mixed-effects model recognized the interaction between sample days through using each sample tree as a random variable. Model evaluation using the AIC showed the strongest model (i.e., smallest integer or highest negative) to be Model 3: Y(mc) = β0 + β1 Days Since Harvest + β2 Size Class + β3 VPD + β4 (1|tree) + u (Table 5). The inclusion of either treatment type or RH by themselves did not improve the models’ fit enough to overcome the added model complexity (Table 5). Model 3 used the covariates days since harvest, harvest treatment, and VPD combined to explain 82% (R2 = 0.819) of the total variability in the bole moisture content of the sampled stems (Table 6). The identification of these variables supported the hypothesis that size class and environmental factors would significantly affect the prediction of stem moisture content, which declined with increasing time after harvest. In contrast though, when including soil temperature, soil moisture, and stem percentage in contact with the ground, there was no significant influence on stem moisture content of the harvested sawlogs.
Table
Table 5. The results of Akaike’s Information Criterion (AIC) testing to determine the significant model variables.
Table 5. The results of Akaike’s Information Criterion (AIC) testing to determine the significant model variables.
ModelFormAIC
1Y(mc) = β0 + β1 Days Since Harvest + β2 (1|tree) + u−620.86
2Y(mc) = β0 + β1 Days Since Harvest + β2 Size Class + β3 (1|tree) + u−697.40
3Y(mc) = β0 + β1 Days Since Harvest + β2 Size Class + β3 VPD + β4 (1|tree) + u−710.42
4Y(mc) = β0 + β1 Days Since Harvest + β2 Size Class + β3 VPD + β4 TRT + β5 (1|tree) + u−688.17
5Y(mc) = β0 + β1 Days Since Harvest + β2 Size Class * TRT + β3 VPD + β4 (1|tree) + u−702.17
* Denotes interaction term between two variables.
Table
Table 6. The regression values of a generalized linear mixed effects model assessing moisture content of felled stems using Treatment 1 as the base treatment.
Table 6. The regression values of a generalized linear mixed effects model assessing moisture content of felled stems using Treatment 1 as the base treatment.
Model: Y log(mc) = β1 Days Since Harvest + β2 Size Class + β3 VPD + β4 (1|tree) + u
Fixed Effects
Co-efficientEstimateStd. errort-value
Intercept−0.49480.0394−12.55
Days Since Harvest−0.02190.0006−33.59
Size Class 20.13510.011711.51
Size Class 30.28510.011724.28
VPD0.00600.00033.79
Random Effects
GroupsNameVarianceStd. Dev.
TreeIntercept0.000010.00001
Residual 0.009650.09825
Marginal R-SquaredConditional R-Squared
0.08180.819

3.3. ΔAIC Analysis: Secondary Model

The ΔAIC analysis identified that Model 5 was moderately comparable (i.e., ΔAIC < 10) and accounted for a higher amount of the model error [39,40,41,43]. Model 5 explained a higher proportion of variation in the response variable based on R2 (0.849 Model 5 vs. 0.819 Model 3). While Model 3 provided the best balance between fit and complexity of the models compared, Model 5 could be argued to have greater implications for management prescriptions as it included the interaction between size class and treatment types. This, as well as the operational significance of the current management shift towards younger harvesting rotations and increased commercial thinning where stems contain greater crown ratio, should be kept in mind. The individual effects of days since harvest, size class * treatment, and VPD are shown in Table 7 using size class 1, treatment 1, and their interaction as the base treatment in the model. While the moisture content loss was significant when comparing stem size regardless of treatment, the impact of the loss was much greater when viewed within the context of active logging operations. The results showed whole tree harvesting stems averaged lower moisture content over the duration of the study than cut-to-length.
Table
Table 7. The regression values of a generalized linear mixed effects model assessing moisture content of felled stems using Size Class 1, TRT 1, and their interaction as the base treatment.
Table 7. The regression values of a generalized linear mixed effects model assessing moisture content of felled stems using Size Class 1, TRT 1, and their interaction as the base treatment.
Model: Y log(mc) = β1 Days Since Harvest + β2 Size Class* TRT + β3 VPD + β4 (1|tree) + u
Fixed Effects
Co-efficientEstimateStd. errort-value
Intercept−0.49480.0439−12.25
Days Since Harvest−0.02160.0006−33.50
Size Class 20.13510.01179.12
Size Class 30.28510.016616.65
TRT 2−0.03970.01684.48
Size Class 2:TRT 20.02470.02332.14
Size Class 3:TRT 20.01580.02351.98
VPD0.00600.00032.79
Random Effects
GroupsNameVarianceStd. Dev.
TreeIntercept0.000010.00001
Residual 0.009250.09805
Marginal R-SquaredConditional R-Squared
0.8430.849
*Denotes interaction term between two variables.

4. Discussion

In support of our hypothesis that stem size would affect the moisture content in felled Douglas-fir, we saw significant correlation between stem moisture content and stem size class. The greatest amount of moisture loss was observed in the days immediately following harvesting. In addition, the majority of the moisture lost was contained in the sapwood compared to the heartwood, which makes sense when considering that the majority of each tree’s pre-treatment moisture was located primarily in the sapwood. The best model identified by the AIC test included the variables days since harvest, size class, and VPD. Although the AIC model with the smallest number should be considered the best overall, limited differences between the best two models (<10) supports using the second best model when operational data is available. In accordance with ΔAIC comparisons [39], the second best AIC model was also evaluated, which included an interaction term between size class and treatment type.
Studies looking at seasonal changes in live tree stem moisture have reported a range of results, including increased sapwood moisture content during the growing season [27,44]. In contrast, several studies show increased stem moisture content in winter months [7,13]. While the standing, seasonal moisture content of conifers fluctuates by region and species, the moisture content of felled trees exhibits more variability. The large quantity of water lost suggests that even under alternative seasonal conditions, the effect of harvest system and time between harvest and delivery could prove significant when working in a weight scaling system. Tree age and size can affect wood characteristics and in turn water storage capacity [45].
The effect of stem size on moisture content over time from this study is consistent with conventional fuel moisture models used to characterize 1000 and 10,000 hours fuel moisture content. These rates classify the time needed for moisture to change 1/3 of the way towards equilibrium moisture content. While these rates prove efficient for fire predictions and fuel modeling, they contain general practices that reduce their effectiveness when applied to weight scaling. For example, they do not account for the time a given species has been dead or downed. In addition, the percentage of bark cover is not identified and base moisture contents for 1000 hours fuels are averaged over 7-day periods.
We found that harvesting and processing of sawlogs affects log moisture content, and that the results depend on sawlog diameter. Because moisture content directly affects sawlog weight, the relationship of W-V, and thus log value, would be affected when using weight scaling systems that do not account for these variables. As identified in the results, stems harvested using whole-tree harvesting system with limbs remaining on the stem after harvesting and prior to processing showed greater moisture loss than stems harvested using cut-to-length harvesting, where processing occurs at the stump and logs are limbed and bucked to length immediately. While the harvest method was important in our study, significant moisture loss occurs in each scenario. In practice, operators may modify practices to minimize loss, depending on which system is being deployed and what current environmental conditions are at the time of harvest. For example, in the current study, 38.2–50.8 cm. sawlogs lost an average of 34% moisture content from each log over a one month period after harvest, regardless of harvest system. Assuming a truckload contains 24,500 kilograms, roughly matching state averages and legal highway limits, a 34% moisture content loss would result in 4.16 metric tons of lost water weight or 17% loss in total truckload value if paid using a weight basis system. Current industry weight-to-volume relationships for Intermountain West Douglas-fir during the third seasonal quarter are 5.51 tons/mbf or 2.33 tons m−3. A 17% loss in weight would shift the ratio to 4.57 tons/mbf or 1.94 tons m−3. This decrease in weight-to-volume ratio could impact the financial productivity of landowners and contractors. Converting between Scribner board foot to cubic volume was derived from Spelter, 2004 [46]. While the very dry, warm conditions during the study may have increased moisture loss, moisture loss was present in all felled trees and should be considered operationally.
Altering harvesting practices to change bole moisture content and improve profit margins greatly depends on the scaling unit employed. Losses in moisture content are viewed negatively when associated with transactions based on weight. However, loss in bole moisture content has long been sought out when product transactions are based on mbf or cubic meter volume. Methods such as “sour felling”, which consists of whole tree harvesting followed by transpirational drying to allow moisture loss have been applied in efforts to increase loaded truck net volume per load [16]. While effective, these practices encourage increased defect in harvested product in the form of checking, insect infestation, and staining [17]. The increase in volume per load profit can be counteracted in the subsequent loss of usable product; retaining the idea that sour felling is best applied when working with pulpwood or woody biomass where profit margins are limited and defect is less important [14,16,17,47]. Sour felling practices are also applicable in harvesting systems where floating logs is used for transportation or storage purposes. Decreases in the bole moisture content result in increased buoyancy for periods of storage or transportation. Log storage in water, when properly executed, reduces checking, insect activity, and staining of logs [48]. Ultimately, the perception of harvesting method and bole size on moisture loss in sawlogs should be considered in direct relation to the unit of volume measure. With western United States scaling practices shifting towards increased transactions through weight scaling, long standing notions of moisture loss in felled sawlogs must be adjusted accordingly in order to maximize profit margin.
Beyond environmental factors present during drying, bark cover and thickness is often assumed to influence drying rates [49,50]. However, when investigating moisture content of branches, Boddy, 1983 [51] did not find drying to be significantly faster in bark-less branches. In contrast, Nicholls and Brackley, 2008 [52], identified bark as a barrier to moisture loss. This is supported by Defo and Brunette, 2006 [53], who found that the stem drying rate of aspen is proportional to the percentage of bark absent. Bark is reported to make up 10–25 percent of the over-bark volume and weight of a tree [54,55]. Therefore, depending on location and season, bark can prove to be beneficial or costly to the forester or contractors [56]. However, felled trees lose moisture through either diffusion or transpiration. While the presence of bark would affect the diffusion process, transpiration would be unaffected. In contrast, remaining tree foliage would be affected by transpiration. Therefore, if stem moisture loss is dominated by transpiration then the effects of bark coverage may go unnoticed. Further investigation concerning the pathway of stem moisture loss could help quantify the importance of bark on stem moisture loss. The simulated processing techniques for the current study were completed using chainsaws as opposed to machinery, leaving the majority of the stem bark intact. This alteration from expected seasonal and operational bark loss from machine processing limits the understanding of bark influence on moisture loss in this study.
While the species characteristics are relevant in mapping stem moisture loss rates, local environmental conditions drive changes to solid wood moisture content. The combination of low relative humidity, high mean daily temperatures, and limited precipitation on the southern aspect provided an extreme setting for moisture loss. The long-term effect of seasonal relative humidity in a region will cause non-living wood to fluctuate with a delayed lag time until equilibrium with the environment is reached. The rate of drying increases with the difference between relative humidity and stem moisture content at the time of harvesting. In order for foresters and contractors to understand and adapt to the variability in sawlog moisture content when working with weight scaling systems in mountainous terrain, sawlog size, harvesting method, and present atmospheric conditions must be considered.

5. Conclusions

The maximum moisture loss occurred in both the smallest size class and stems in the whole-tree harvesting system. The greatest moisture content variation and subsequent moisture loss also took place in the sapwood portion of the stem. With these results, we reject the null hypothesis that harvested stem moisture loss was unrelated to bole size and harvest system of felled Douglas-fir trees. Trees felled and left intact with limbs proceeded to show increased moisture loss vs. stems that were felled and immediately processed into sawlogs. Additionally, we predicted that the moisture content during late summer would not be significantly affected by stem ground contact percentage, bark coverage, or soil characteristics, and the results supported that prediction. Consistent with the concept of evapotranspiration, stem moisture content is best predicted by a combination of VPD, stem size, and harvest system. The probable reason for changes in the moisture content variation among treatment types is the increased surface area present of trees containing limbs and foliage. The effect of stem size on moisture content was also likely driven by the reduced amount of external energy required to extract moisture from a smaller object. These findings suggest that understanding the implications of seasonal harvests exposing harvested timber to strong climatic and environmental conditions can significantly alter expected results from areas utilizing weight scaling practices.

Acknowledgments

We would like to thank the Idaho Department of Lands, Associated Logging Contractors of Idaho, and the University of Idaho Experimental Forest for support of this project.

Author Contributions

  • Jarred D. Saralecos. Responsible for project development, data collection, analysis, writing, and revision process. Oversaw communication and revisions made by co-authors.
  • Robert F. Keefe. Assisted in project development, data collection, writing, and revision process.
  • Wade T. Tinkham. Assisted in data collection, analysis, and writing.
  • Randall H. Brooks. Provided writing assistance and assisted with manuscript revision.
  • Alistair M.S. Smith. Provided help with analysis and manuscript revisions.
  • Leonard R. Johnson. Assisted in manuscript revisions and preliminary project development.

Conflicts of Interest

This manuscript is not being considered for publication in any form in alternative journals, books, or publications. We have acknowledged all published work cited within the manuscript. All authors have read and approved the manuscript. There are no real or perceived conflicts of interest associated with the study.

References

  1. Daniels, R.A. Marketing Your Timber: The Basics of Weight Scaling; Mississippi State University, Cooperative Extension Service: Starkville, MI, USA, 2005. [Google Scholar]
  2. Saucier, J.R.; Phillips, D.R. Weight Loss of Summer-Stored Sweetgum, Yellow-Poplar, Red Oak, and Loblolly Pine Sawlogs; Georgia Forestry Research Division: Athens, GA, USA, 1981; pp. 1–7. [Google Scholar]
  3. British Columbia Ministry of Forests, Lands, and Natural Resource Operations Scaling Manual. Weight Scale Sampling; Crown Publication: Victoria, British Columbia, Canada, 2011; p. 502.
  4. Mann, L.K.; Johnson, D.W.; West, D.C.; Hornbeck, J.W.; Martin, C.W.; Riekerk, H.; Smith, C.T.; Swank, W.T.; Tritton, L.M.; Van Lear, D.H. Effects of whole-tree and stem-only learcutting on postharvest hydrologic losses, nutrient capital, and regrowth. For. Sci. 1988, 34, 412–428. [Google Scholar]
  5. Fonseca, M.A. The Measurement of Roundwood: Methodologies and Conversion Ratios; CABI Pub.: Wallingford, UK, 2005; p. 269. [Google Scholar]
  6. Yerkes, V.P. Weight and Cubic-Foot Relationships for Black Hills Ponderosa Pine Sawlogs; Research Note RM-78; U.S. Forest Service, Department of Agriculture: Fort Collins, CO, USA, 1966.
  7. Yerkes, V.P. Effect of Seasonal Stem Moisture Variation and Log Storage on Weight of Black Hills Ponderosa Pine; Research Note-96; U.S. Forest Service, Department of Agriculture: Fort Collins, CO, USA, 1967.
  8. Raczkowski, J.; Olek, W.; Guzenda, R. Moisture evaporation rates from sapwood and heartwood sample of Douglas-fir (Pseudotsuga menziesii Franco) green wood. Holz als Roh- und Werkstoff 2000, 58, 247–252. [Google Scholar]
  9. Spicer, R.; Gartner, B.L. The effects of cambial age and position within the stem on specific conductivity in Douglas-fir (Pseudotsuga menziesii) sapwood. Trees 2001, 15, 222–229. [Google Scholar] [CrossRef]
  10. Engelund, E.T.; Thygesen, L.G.; Svensson, S.; Hill, A.S. A critical discussion of the physics of wood-water interactions. Wood Sci. Technol. 2013, 47, 141–161. [Google Scholar] [CrossRef]
  11. Pallardy, S.G.; Kozlowski, T.T. Physiology of Woody Plants, 3rd ed.; Elsevier: Amsterdam, the Netherlands, 2008; p. 454. [Google Scholar]
  12. Grainer, A.; Biron, P.; Lemoine, D. Water balance, transpiration and canopy conductance in two beech stands. Ag For. Meteorol. 2000, 100, 291–308. [Google Scholar] [CrossRef]
  13. Marden, R.M.; Lothner, D.C.; Kallio, E. Wood and Bark Percentages and Moisture Contents of Minnesota Pulpwood Species; USDA Forest Service: St. Paul, MN, USA, 1975; pp. 1–9. [Google Scholar]
  14. Klepac, J.; Rummer, B.; Seixas, F. Seasonal Effects on Moisture Loss of Loblolly Pine. In Council on Forest Engineering Conference Proceedings, Charleston, SC, USA, June 22–25; pp. 1–9.
  15. Visser, J.J. Evaportation as a parameter to measure mass loss in biological drying Pinus radiata trees. J. Inst. Wood Sci. 1990, 11, 231–235. [Google Scholar]
  16. Holt, H.A. Delayed processing of felled trees to reduce wood moisture content. For. Prod. J. 1985, 35, 55–59. [Google Scholar]
  17. Johnson, N.E.; Zingg, J.G. Transpirational drying of douglas-fir: Effect on log moisture content and insect attack. J. For. 1969, 67, 816–819. [Google Scholar]
  18. Clark, J.; Gibbs, R.D. Studies in Tree Physiology: IV. Further investigations of seasonal changes in moisture content of certain canadian forest trees. Can. J. Bot. 1957, 3, 219–253. [Google Scholar]
  19. Patterson, W.A.; Post, I.L. Delayed bucking and bolewood moisture content. J. For. 1980, 78, 407–408. [Google Scholar]
  20. Garret, L.D. Delayed processing of felled trees to reduce moisture content. For. Prod. J. 1985, 35, 55–59. [Google Scholar]
  21. Peck, E.C. The Sap or Moisture in Wood; Forest Products Laboratory; Report No. D768; USDA: Madison, WI, USA, 1953.
  22. Fosberg, M.A.; Rothermel, R.C.; Andrews, P.L. Moisture content calculations for 1000-hour timelag fuels. For. Sci. 1981, 27, 19–26. [Google Scholar]
  23. Edmunds, R.L.; Hawk, G.M.; Long, J.N.; Franklin, J.F.; Emmingham, W.H.; Reed, K.L.; Clark, S.G.; Lassoie, J.P.; Johnson, D.W.; Cole, D.W.; et al. Analysis of coniferous forest ecosystems in the Western United States. Conifer. For. Biome 1982, 1–27. [Google Scholar]
  24. Waring, R.H.; Running, S.W. Sapwood water storage: Its contribution to transpiration and effect upon water conductance through the stems of old-growth Douglas-fir. Plant Cell Environ. 1978, 1, 131–140. [Google Scholar] [CrossRef]
  25. Parker, J. Available water in stems of some rocky mountain conifers. Bot. Gaz. 1954, 115, 380–385. [Google Scholar] [CrossRef]
  26. Beedlow, P.A.; Tingey, D.T.; Lee, E.H.; Phillips, D.L.; Andersen, C.P.; Waschmann, R.S.; Johnson, M.G. Sapwood moisture in Douglas-fir boles and seasonal changes in soil water. Can. J. For. Res. 2007, 37, 1263–1271. [Google Scholar] [CrossRef]
  27. Beedlow, P.A.; Tingey, D.T.; Waschmann, R.S.; Phillips, D.L.; Johnson, M.G. Bole water content shows little seasonal variation in century-old Douglas-fir. Tree Physiol. 2007, 27, 1–11. [Google Scholar] [CrossRef] [PubMed]
  28. Pearson, A.F. Natural and logging disturbances in the temperate rain forests of the Central Coast, British Columbia. Can. J. For. Res. 2010, 40, 1970–1984. [Google Scholar] [CrossRef]
  29. Tyree, M.T.; Zimmermann, M.H. Xylem Structure and the Ascent of Sap; Berlin Springer: New York, NY, USA, 2002; p. 283. [Google Scholar]
  30. Cooper, S.V.; Neiman, K.E.; Roberts, D.W. Forest Habitat Types of Northern Idaho: A Second Approximation; General Technical Report INT-236; United States Department of Agriculture: Ogden, UT, USA, 1991; pp. 1–152.
  31. Holden, Z.A.; Klene, A.E.; Keefe, R.F.; Moisen, G.G. Design and evaluation of an inexpensive radiation shield for monitoring surface air temperatures. Agric. For. Meteorol. 2013, 180, 281–286. [Google Scholar] [CrossRef]
  32. Dingman, S.L. Physical Hydrology; Prentice Hall: Upper Saddle River, NJ, USA, 2002; p. 646. [Google Scholar]
  33. Whitehead, R.J.; Russo, G.L.; Hawkes, S.W.; Taylor, B.N.; Barclay, H.J.; Benton, R.A. Effect of a Spaced Thinning in Mature Lodgepole Pine on Within-Stand Microclimate and Fine Fuel Moisture Content; USDA, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; pp. 523–536.
  34. Estes, B.L.; Knapp, E.E.; Skinner, C.N.; Uzoh, F.C.C. Seasonal variation in surface fuel moisture between unthinned and thinned mixed conifer forest, northern California, USA. Int. J. Wildland Fire 2012, 21, 428–435. [Google Scholar] [CrossRef]
  35. Standard Test Methods for Direct Moisture Content Measurement of Wood and Wood Base Materials; ASTM Standard D 4442; ASTM International: West Conshohocken, PA, USA, 2007.
  36. Simpson, W.T. Specific Gravity, Moisture Content, and Density Relationship for Wood; USDA Forest Service, Forest Products Laboratory: Madison, WI, USA, 1993. [Google Scholar]
  37. R Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing: Vienna, Austria, 2013. ISBN 3-900051-07-0. Available online: http://www.R-project.org/ (accessed on 10 November 2004).
  38. Akaike, H. A new look at statistical model identification. IEEE Transact. Autom. Control 1974, 19, 716–722. [Google Scholar] [CrossRef]
  39. Breck, S.W.; Wilson, K.R.; Andersen, D.C. Beaver herbivory and its effect on cottonwood trees: Influence of flooding along matched regulated and unregulated rivers. River Res. Appl. 2003, 19, 43–58. [Google Scholar] [CrossRef]
  40. Burnham, K.P.; Anderson, D.R. Model Selection and Inference: A Practical Information—Theoretic Approach; Springer-Verlag: New York, NY, USA, 1998. [Google Scholar]
  41. Falkowski, M.J.; Gessler, P.E.; Morgan, P.; Hudak, A.T.; Smith, A.M.S. Characterizing and mapping forest fire fuels using ASTER imagery and gradient modeling. For. Ecol. Manag. 2005, 217, 129–146. [Google Scholar] [CrossRef]
  42. Nakagawa, S.; Schielzeth, H. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol. Evol. 2013, 4, 133–142. [Google Scholar] [CrossRef]
  43. Cahill, A.T. Significance of AIC differences for precipitation intensity distributions. Adv. Water Resour. 2003, 26, 457–464. [Google Scholar] [CrossRef]
  44. Wullschleger, S.D.; Hanson, P.J.; Todd, D.E. Measuring stem water content in four deciduous hardwoods with a time-domain reflectometer. Tree Physiol. 1996, 16, 809–815. [Google Scholar] [CrossRef] [PubMed]
  45. Domec, J.C.; Gartner, B.L. Age- and position-related changes in hydraulic versus mechanical dysfunction of xylem: Inferring the design criteria for Douglas-fir wood structure. Tree Physiol. 2002, 22, 91–104. [Google Scholar] [CrossRef] [PubMed]
  46. Spelter, H. Converting among log scaling methods, scribner, international, and doyle versus cubic. J. For. 2004, 102, 33–39. [Google Scholar]
  47. Silversides, C.R. Energy from forest biomass—its effect on forest management practices in Canada. Biomass 1982, 2, 29–41. [Google Scholar] [CrossRef]
  48. Hakkila, P.; Heikkila, P.; Michelsen, P. Leaf-Seasoning in harvesting veneer Birch. Metsatieteellisen Tutkimuslaitoksen Julk. 1970, 70, 42–49. [Google Scholar]
  49. Sollins, P.; Cline, S.P.; Verhoeven, T.; Sachs, D.; Spycher, G. Patterns of log decay in old-growth Douglas-fir forests. Can. J. For. Res. 1987, 17, 1585–1595. [Google Scholar] [CrossRef]
  50. Harmon, M.E.; Sexton, J. Water balance of conifer logs in early stages of decomposition. Plant Soil Sci. 1995, 172, 141–152. [Google Scholar] [CrossRef]
  51. Boddy, L. Microclimate and moisture dynamics of wood decomposing in terrestrial ecosystems. Soil Biol. Biochem. 1983, 15, 149–157. [Google Scholar] [CrossRef]
  52. Nicholls, D.; Brackley, A. House Log Drying Rates in Southeast Alaska for Covered and Uncovered Softwood Logs; General Technical Report PNW-GTR-782; USDA Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2008; p. 18. [Google Scholar]
  53. Defo, M.; Brunette, G. A log drying model and its application to the simulation of the impact of bark loss. For. Prod. J. 2006, 56, 71–77. [Google Scholar]
  54. Meyer, H.A. Bark volume determination in trees. J. For. 1946, 44, 1067–1070. [Google Scholar]
  55. Philip, M.S. Measuring Trees and Forests, 2nd ed.; CAB International: Oxfordshire, UK, 1994; p. 310. [Google Scholar]
  56. Murphy, G.E.; Pilkerton, S.J. Seasonal impacts of bark loss on simulated payloads, bark delivery, and transport costs for freshly harvested logs. For. Prod. J. 2011, 61, 71–76. [Google Scholar]

Share and Cite

MDPI and ACS Style

Saralecos, J.D.; Keefe, R.F.; Tinkham, W.T.; Brooks, R.H.; Smith, A.M.S.; Johnson, L.R. Effects of Harvesting Systems and Bole Moisture Loss on Weight Scaling of Douglas-Fir Sawlogs (Pseudotsuga Menziesii var. glauca Franco). Forests 2014, 5, 2289-2306. https://doi.org/10.3390/f5092289

AMA Style

Saralecos JD, Keefe RF, Tinkham WT, Brooks RH, Smith AMS, Johnson LR. Effects of Harvesting Systems and Bole Moisture Loss on Weight Scaling of Douglas-Fir Sawlogs (Pseudotsuga Menziesii var. glauca Franco). Forests. 2014; 5(9):2289-2306. https://doi.org/10.3390/f5092289

Chicago/Turabian Style

Saralecos, Jarred D., Robert F. Keefe, Wade T. Tinkham, Randall H. Brooks, Alistair M. S. Smith, and Leonard R. Johnson. 2014. "Effects of Harvesting Systems and Bole Moisture Loss on Weight Scaling of Douglas-Fir Sawlogs (Pseudotsuga Menziesii var. glauca Franco)" Forests 5, no. 9: 2289-2306. https://doi.org/10.3390/f5092289

APA Style

Saralecos, J. D., Keefe, R. F., Tinkham, W. T., Brooks, R. H., Smith, A. M. S., & Johnson, L. R. (2014). Effects of Harvesting Systems and Bole Moisture Loss on Weight Scaling of Douglas-Fir Sawlogs (Pseudotsuga Menziesii var. glauca Franco). Forests, 5(9), 2289-2306. https://doi.org/10.3390/f5092289

Article Metrics

Back to TopTop